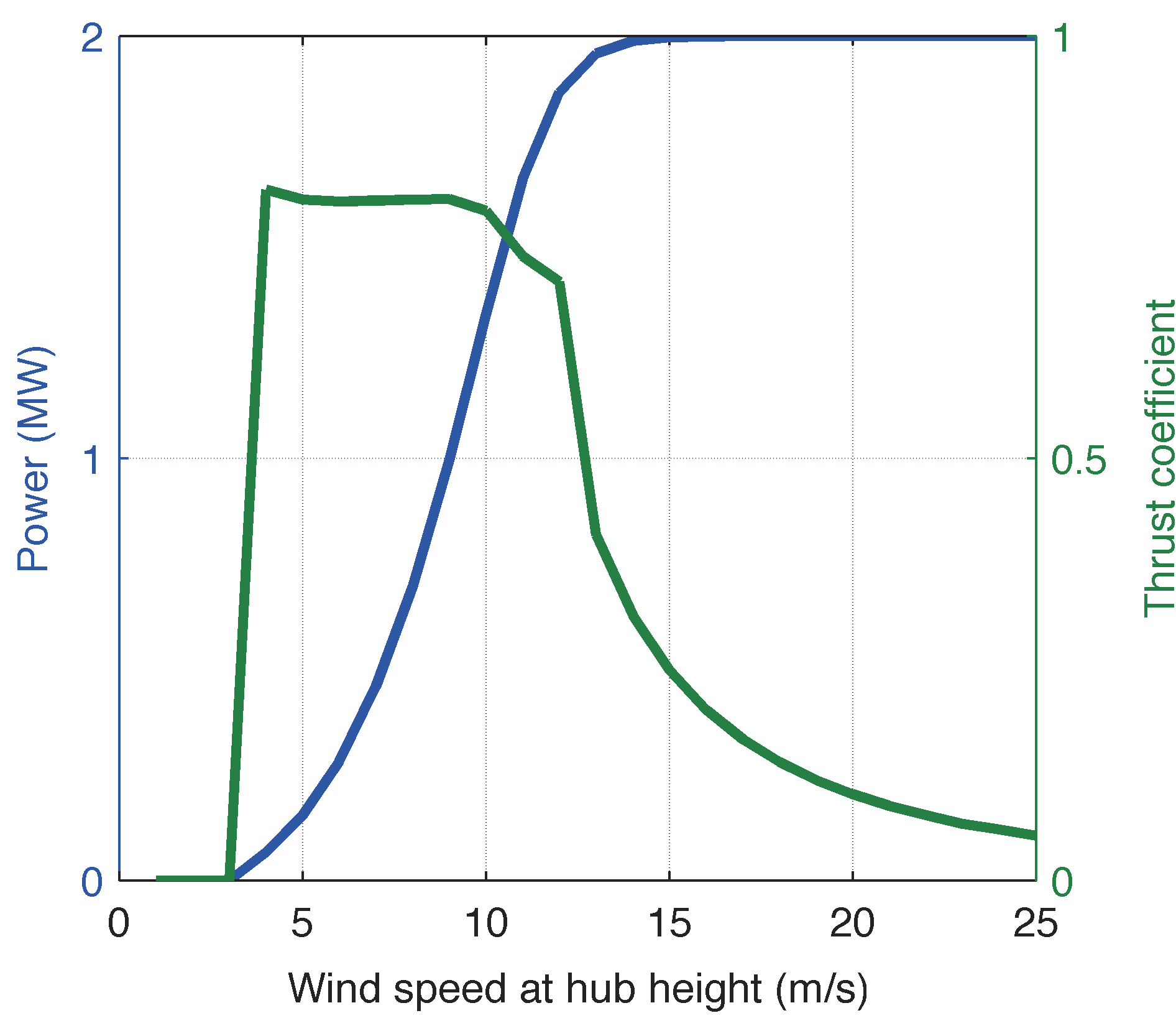
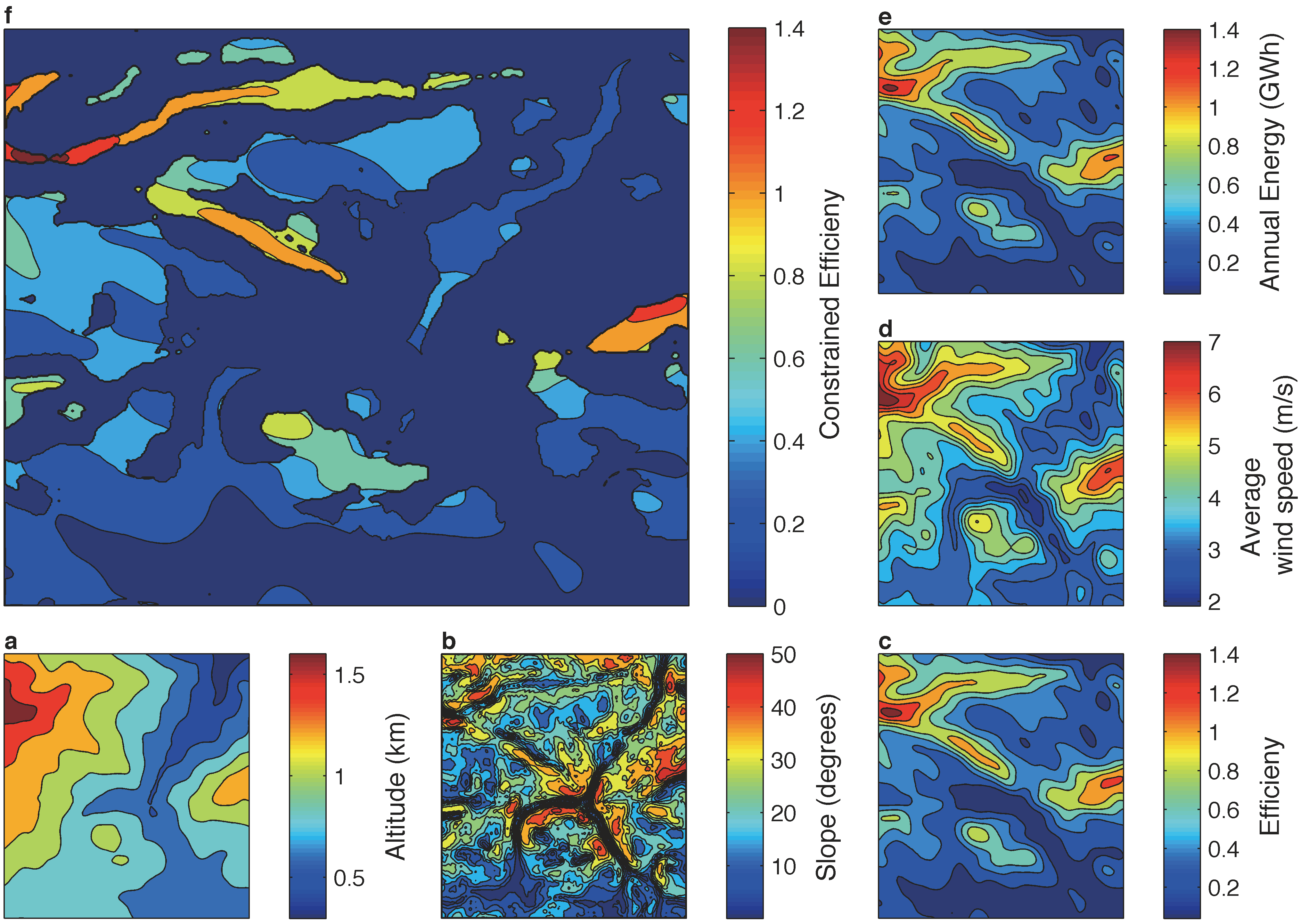
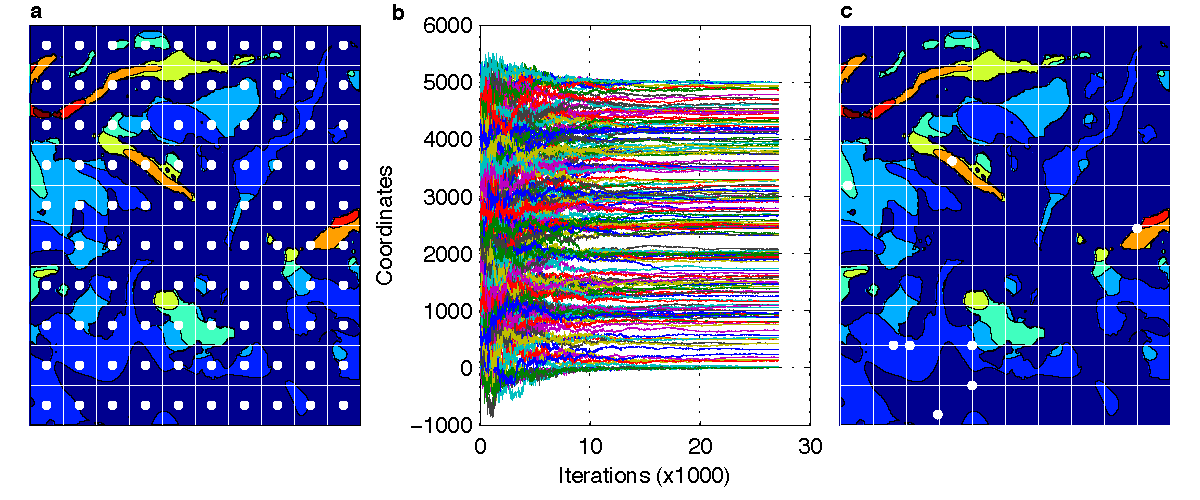
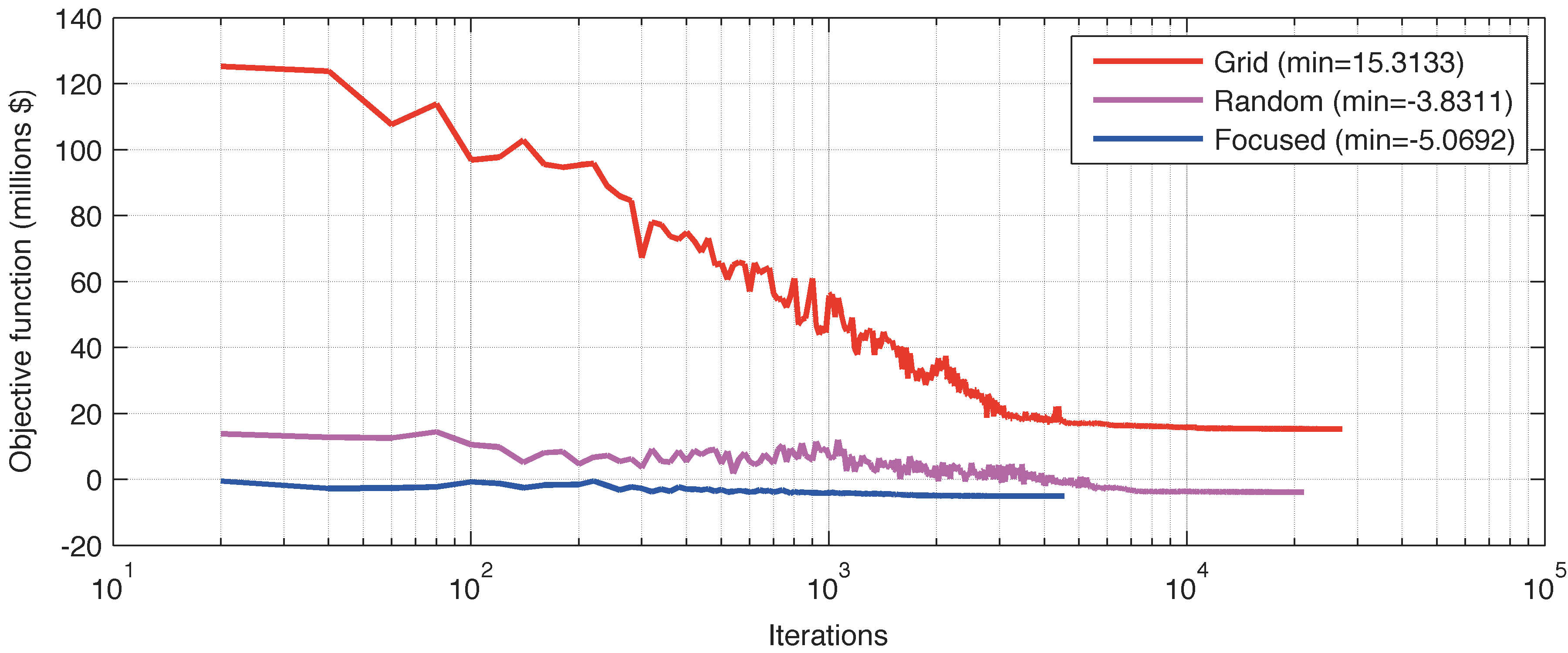
We investigate the problem of wind farm design in isolated mountainous areas. We first describe a remote sensing approach for the terrain reconstruction of complex terrains. We then employ a well--known evolutionary optimization algorithm to find the optimal wind farm layout. Although the algorithm has been efficiently used for off--shore or smooth on--shore areas, we show that its performance is significantly affected by the complex topography. Moreover, we illustrate how a priori information can be exploited to improve both the computational time and efficiency of the optimization algorithm.
1.
Introduction
As an effective and low-cost method to achieve high precision deformation information of large areas, Interferometry Synthetic Aperture Radar (InSAR) technology is widely used in topographic survey, earthquake monitoring, ground surface subsidence monitoring and many other applications [1,2,3]. However, conventional InSAR is affected by the temporal decorrelation and atmospheric effects, which seriously restricts the accuracy and reliability in deformation monitoring [4]. Based on plenty of relatively stable, high coherent points from time-series SAR images and implementing differential Interferometry Synthetic Aperture Radar (DInSAR) on them, Permanent Scatterer InSAR (PSInSAR) can mitigate the spatial and temporal decorrelation and atmospheric delay effect to get relatively high accuracy and reliable information of the earth surface deformation [5,6,7,8,9,10,11,12].
One of the key steps for PSInSAR technology is to analyze and process those stable scatterers with the high coherent characteristic. The phase stability of PS determines that the deformation results of these scatterers is reliable and can reflect the ground deformation if the density of PS is sufficient [13,14]. So how to identify and select PS automatically and effectively from SAR images is one of the most critical procedures in PSInSAR technology.
Ferretti et al. firstly proposed the algorithms of PS identification and selection, including amplitude dispersion thresholding, temporal correlation thresholding and phase deviation thresholding [15,16], and some related experiments were implemented correspondingly. Among them, the amplitude dispersion thresholding needs a large number of images for the statistical analysis. However, in the amplitude dispersion thresholding method, only the varying of amplitude is used without considering the corresponding amplitude value. In addition, its reliability is related to the quality of the image preprocessing and the setting of the threshold [17,18]. The results based on temporal correlation thresholding are actually some stable regions rather than individual pixels. Their reliability is related to the window size and the selection of the threshold directly. Phase dispersion thresholding only considers phase information, so the results are easily affected by decorrelation, system thermal noise and so on [19]. Kampes et al. proposed a new PS selection algorithm by setting an amplitude threshold to identify high coherent points, which can detect high amplitude points easily [20,21]. Considering the phase stability, Hooper presented a new PS identification method based on the spatial correlation analysis of interferometric phase and implemented some related deformation extraction experiments [22,23].
To automatically identify PS, Chen et al. put forward a Double-Thresholding algorithm (DTA) by combining both correlation coefficient threshold and amplitude dispersion index threshold [18]. Luo et al. proposed a method named amplitude information dual-threshold approach (AIDTA). With this method, those points with high amplitude values are firstly selected as permanent scatterer candidates (PSCs), then the eventual PS are taken out of PSCs by setting a suitable amplitude dispersion index (ADI) threshold [24]. Azadnejad et al. presented a new method which is based on minimizing Amplitude Dispersion Index (ADI) by finding the optimum scattering mechanism to increase the number of PSC and PS pixels [25]. Similarly, taking into account the characteristics of strong reflectivity and stable backscattering of PS to radar waves, Hu et al. presented a new method by seriously setting tri-threshold with time-series correlation coefficient, amplitude dispersion index and amplitude index [19]. Based on the characteristics and flaws of all kinds of PS selection methods, such as amplitude stability, phase stability, temporal sequence correlation and amplitude dispersion index threshold, Long et al. proposed a new approach considering the union and intersection of temporal sequence correlation coefficient threshold and amplitude dispersion index threshold [26]. Tao et al. presented a new method for identifying and selecting PS by introducing wavelet phase analysis and taking into account the stability of amplitude and phase [27].
All the above mentioned methods enriched the PS identification technology and achieved superior effects and they are suitable for those land cover with clear characters (e.g. unstable plants and stable man-made buildings) areas. However, these methods identify PS by setting one or several thresholds under the “black or white” rule without taking the fuzzy characteristics of the PS into account and can easily fall into a logical paradox especially in the area covered by objects possessing ambiguous boundary for interested features. For example, in an mountain area covered with various reflective land covers (there is no clear boundary of the reflection intensity), considering both the amplitude and amplitude dispersion index thresholds, it might be obviously unreasonable that if a pixel, with amplitude equal or greater than 64 and amplitude dispersion equal or less than 0.4, is selected as PS, while another pixel with the amplitude 63.99999 and amplitude dispersion 0.2 is excluded from PS. In fact, this can exclude many valuable PS, which usually leads to unreliable subsidence analysis results because of sparse density of PS. Based on this, this paper tries to find a suitable PS selection method to deal with those areas with fuzzy features. The fuzzy set (FS) theory was proposed in 1965 [28], since then it is widely used in various fields [29,30,31]. It adopts quantitative method to study and deal with the fuzzy phenomenon and always makes the solution in conformity with the practical situation. In other words, FS method can achieve more accurate result by a fuzzy point of view. In order to obtain more reasonable PS in those areas covered by objects possessing ambiguous boundary for interested features, a new fuzzy PS (FPS) concept is first proposed based on fuzzy set theory in this paper. Taking the two indexes amplitude and amplitude dispersion in AIDTA as an example, the selection method is presented. Two groups of real data are performed to validate the proposed method. The results indicate that, compared with traditional method, FPS can not only eliminate the negative effect of the “black or white” rule because of setting single threshold on each PS characteristic, but also gain a unified quantitative index to guide the selection and quality classification of PS by fusing different PS characters comprehensively.
The paper is organized as follows. Section 2 introduces the detail description of amplitude information dual-threshold approach (AIDTA). The fuzzy PS identification method is presented in Section 3. Test results and data analysis are given in Section 4. The last part of the paper is the conclusions attained through this study.
2.
Amplitude information dual-threshold approach
Based on the characteristics of PS with strong and stable Radar reflectivity, a method named amplitude information dual-threshold approach (AIDTA) was proposed [24]. Firstly, the pixels with high amplitude values are selected as PS candidates (PSC) using amplitude thresholding in view of their strong reflectivity. Then, PS are selected from PSC according to an amplitude dispersion index thresholding for their stable reflectivity.
1) Consider $N$ time-series images covering the same area. The amplitude threshold is computed as:
where $m$ and $n$ represent the number of rows and columns of the SAR images; ${A_k}$ is the calibrated amplitude array of the ${{\rm{k}}^{th}}$ SAR image [32]. From Eq (1), the minimum of the amplitude mean of each image is set as the amplitude threshold.
For a fixed ${T_A}$, PSC are those pixels satisfying the following formula:
The above amplitude threshold considers only the strong reflectivity without regarding to the scattering stability of PS, making the result not reliable enough. In the following step, PS are further selected from the PSC using amplitude dispersion index threshold for their stable reflectivity.
2) Amplitude dispersion index ${D_A}$ and phase dispersion index ${D_\varphi }$ are used to quantitatively express the stability of the PS scattering. The distribution of the amplitude values $f(A)$ is given by the Rice distribution [16]:
where ${I_0}$ is the modified Bessel function; $\sigma _n^2$ is the power of complex circular Gaussian distributed noise; $g$ is complex reflectivity and $A > 0$.
The shape of the Rice Distribution depends on the SNR (i.e., the ratio ${g \mathord{\left/
{\vphantom {g {{\sigma _n}}}} \right.
} {{\sigma _n}}}$). For low SNR, the probability density function (PDF) tends to a Rayleigh distribution. For high SNR (${g \mathord{\left/
{\vphantom {g {{\sigma _n}}}} \right.
} {{\sigma _n}}} > 4$), $f(A)$ approaches a Gauss distribution, and the following equations hold:
where ${\sigma _{nR}}$ and ${\sigma _{nI}}$ are the noise standard deviation of the real and imaginary part; ${m_A}$ and ${\sigma _A}$ are the mean and the standard deviation of the amplitude values ${A_k}$; ${D_A}$ is called amplitude dispersion index (ADI). According to the above equation, the amplitude dispersion index is a measure of phase stability, at lease for high SNR pixels [16].
Based on the above analysis, the selected PSC can meet the high SNR, and the points are selected as PS if the amplitude dispersion is below a threshold in the second step which means that the final PS are with stable reflectivity. Therefore, PS can be finalized through further analysis of the amplitude dispersion index on PSC.
3.
Fuzzy PS identification method
The basic idea of fuzzy set is to make the absolute membership degree in common sets flexible, specifically, by expanding the membership degree of element from the only 0 or 1 to arbitrary value in [0, 1]. Some relevant concepts are briefly described as follows [33]:
Let $U$ be the universal set. A fuzzy set $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{F} $ of $U$ can be mathematically described as:
where ${\mu _{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{F} }}\left( u \right):U \to \left[ {0, 1} \right]$ represents the membership degree of an element belonging to $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{F} $.
$\lambda {\rm{ - }}$ cut of a fuzzy set $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{F} $ in $U$ can be defined as
where $\lambda $ is called a threshold. Obviously, ${(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{F} )_\lambda }$ is a common set and ${(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{F} )_{{\lambda _1}}} \supset {(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{F} )_{{\lambda _2}}}$ if ${\lambda _1} < {\lambda _2}$.
T-norms, T-conorms and negated function are the basic operations on fuzzy sets to compute the membership degree of their union, intersection and complement, respectively. Minimum, Algebra product and bounded product are common T-norms operators.
PS are with the characteristics of steadier scattering and stronger radar echo signal. While “steadier” and “stronger” are fuzzy descriptions of PS properties. Based on previous research PS and non-PS are classified by setting threshold respectively for each characteristic. One pixel will be excluded from PS once it does not meet any threshold rule. This in turn will lead to an “either this or that” logic paradox especially in the area covered by objects possessing ambiguous boundary for interested features. Because it is very difficult to set a precise and proper threshold in practice. For example, if pixels whose amplitude greater than or equal to 367.54 and amplitude dispersion less than or equal to 0.35 are identified as PS, it is more reasonable to classify the pixel with amplitude 367.30 and amplitude dispersion 0.27 to PS, while the previous method may make a rejection choice. Based on this, the concept of fuzzy PS is proposed and a fuzzy identification method is designed accordingly.
On the base of fuzzy set theory, each point is no longer classified into either “PS” set or “no-PS” set absolutely, but has a membership degree to describe its level belonging to “PS”.
Let $P$ represent all pixels in a study area. Each pixel $p \in P$ has $m$ feature indexes ${{\rm{C}}_1}, \ldots , {C_m}$ which are used to describe the characteristics of “PS”. Accordingly, there will be a fuzzy vector $V(p) = \left( {{u_1}(p), \ldots , {u_m}(p)} \right)$, where ${u_i}(i = 1, \ldots , m)$ is the value of $p$ in ${C_i}$. Define $m$ fuzzy sets ${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{A}}_{1}}, \ldots , {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{A} _m}$, where ${\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{A} _i} = \left\{ {\left( {u, {\mu _{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{A} }_i}}}\left( u \right)} \right)\left| {u \in {U_i}} \right.} \right\}$ is a fuzzy set describing feature ${C_i}$, ${U_i}$ is a universal set containing all values of $p$ in ${C_i}$. Since all the fuzzy sets are to describe the feature of PS, fuzzy PS set $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{P} $ can be given by $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{P} = \bigcap\limits_{i = 1}^m {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{A} }_i}} $ and the membership degree can be calculated by the following formula
where $T$ represents T-norms and Algebra product operation $ \bullet $ is selected in this paper. Thus, the fuzzy PS set can be written as $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{P} = \left\{ {(p, {\mu _{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{P} }}\left( p \right))\left| {p \in P} \right.} \right\}$. Accordingly, the $\lambda {\rm{ - }}$ cut of $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{P} $ can be symbolized as ${\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{P} _\lambda } = \left\{ {p{\rm{ | }}{\mu _{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{P} }}\left( p \right) \geqslant \lambda , p \in P} \right\}$, which means all the pixels whose membership degrees are greater than or equal to $\lambda $.
According to the above theory, each pixel has a corresponding membership degree, which can be considered as the level it belongs to “PS”. A larger membership degree means the higher possibility that a certain pixel will be regarded as PS. It must be pointed out that, how to select a proper membership function in practice will directly affect the identification results. Since there is not a universal law to select a membership function, the reasonable and proper formulas for membership functions are more or less formulated with subjectivity or by experience.
The new PS identification algorithm based on fuzzy set (fuzzy PS identification for short) are as follows:
1) Select the study area. A matrix is used to describe the whole pixels which can be expressed by position.
2) Choose $m$ feature indexes related to properties of PS, written as ${{\rm{C}}_1}, \ldots {C_m}$, such as “amplitude”, “amplitude dispersion” or “time-series correlation coefficient”.
3) Define fuzzy set ${\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{A} _i}$ for ${C_i}$, such as “high” amplitude, “low” amplitude dispersion and so on. They are usually constructed based on some empirical models.
4) Determine fuzzy PS set $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{P} = \bigcap\limits_{i = 1}^m {{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{A} }_i}} $, ${\mu _{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{P} }}\left( p \right) = T_{i = 1}^m{\mu _{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{A} }_i}}}({u_i}(p))$. The operator $T$ is decided on practical problem.
5) Set membership degree threshold $\lambda $ to select the points satisfying ${\mu _{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{P} }}\left( p \right) \geqslant \lambda $. This is usually related to the threshold of traditional method.
6) Determine practical PS considering the traditional method and the fuzzy method.
The proposed method is a new characteristic fusion tool to identify PS. By fusing two or more characteristics, the practical PS can be selected on one hand, and the quality value of each PS can be obtained on the other hand. The former is conducted by controlling the membership degree threshold instead of setting single threshold for each characteristic. From Eq (7), it can be seen that the membership degree in fuzzy PS set $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{P} $ is a fusion result taking the entire feature into account. Therefore, it is more reasonable than the traditional method by setting single threshold one by one.
4.
Cases analysis
4.1. Case 1
Twenty-seven TerraSAR-X images acquired from April 2012 to January 2013 are selected as the first test data set. The cropped images are 500 × 500 pixels, which cover part of 18,207 working face in Tunlan coal mine and its geographical location is about from east longitude 111 to 112 degree, and north latitude 37 to 38 degree.
4.1.1. Experimental method
Taking the amplitude information dual-threshold approach (AIDTA) as an example, the traditional method (AIDTA) and fuzzy amplitude information dual-threshold approach (FAIDTA) are compared to show their relationship and difference. For simplicity, PS selected by AIDTA are shortly written as PS-AIDTA, PS selected by FAIDTA are simply described as PS-FAIDTA, and PS selected by FAIDTA but excluded from AIDTA is expressed as PS-FAIDTA/AIDTA.
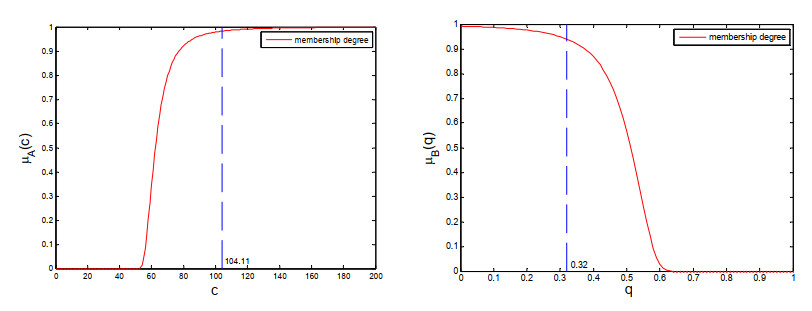
The calculated amplitude threshold for this test data was ${T_A} = 104.11$ based on Eq (1). Meanwhile, the amplitude dispersion threshold was set as ${T_B} = 0.32$ to make sure the selected PS candidates with high amplitude stability. Then, the calculated number of PS-AIDTA is 709. The FAIDTA method can be described as follows:
Define that $ U = {({p}_{i, j})}_{I\times J},(i = 1, \dots , I, j = 1, \dots , J)$ represents all the pixels in study area, ${p_{i, j}}$ is the position of the $i$ row, $j$ column pixel, $I = 500$ and $J = 500$ are the number of rows and columns. The minimum amplitude value of time-series (amplitude value for short) ${c_{i, j}}$ and amplitude dispersion value ${q_{i, j}}$ for pixel ${p_{i, j}}$ were selected to describe the features of PS. Correspondingly, two fuzzy sets were defined.
The first fuzzy set $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{A} $ means that the amplitude value $c$ is high. The second fuzzy set $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{B} $ means that the amplitude dispersion value $q$ is low. As a kind of methods for constructing fuzzy membership function, the assignment method is used in this paper [34,35]. The membership functions of $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{A} $ and $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{B} $ are shown as follows, which are Cauchy distributions
Figure 1 shows the membership functions of amplitude value and the amplitude dispersion value. It can be found that the former is monotone increasing and the latter is monotone decreasing. The membership degrees of the amplitude threshold (${T_A} = 104.11$) and the amplitude dispersion threshold (${T_B} = 0.32$) are greater than 0.9, and the membership function of the latter is more sensitive than the former, which conforms to the real expectation.
According to fuzzy set theory, the membership degree of any pixel belonging to “PS” is
The calculated minimum membership degree of PS-AIDTA is 0.92384.
4.1.2. Test results
Figure 2 shows three overlay sub-graphs. The green ‘*’ means the PS-AIDTA, and the red ‘o’ represents the PS-FAIDTA. PS-AIDTA are all the same in the three sub-graphs because the thresholds of amplitude and amplitude dispersion are fixed, while PS-FAIDTA are different under three membership degree thresholds, and both of them are on top of the mean intensity image in study area. From all the three sub-graphs, it can be found that the PS-AIDTA and the PS-FAIDTA are mostly distributed in the strong reflected intensity area. With the decrease of membership degree threshold, the number of PS-FAIDTA grows. When the membership degree threshold was set as T = 0.92384 (the minimum membership degree of PS-AIDTA), the PS-FAIDTA include all the PS-AIDTA and the former is much more than the latter. This is consistent with the fuzzy PS theory—the $\lambda $ -cut of a fuzzy set is monotone decreasing with $\lambda $.
Table 1 shows the statistic information under different membership degree thresholds. There are some abbreviations: TMD is the threshold of membership degree; n-FAIDTA, n-FAIDTA/AIDTA, and n-intersection stand for the number of PS-FAIDTA, PS-FAIDTA/AIDTA, and the intersection of FAIDTA and AIDTA respectively. It can be found that with the decrease of membership degree threshold, the number of PS-FAIDTA, PS-FAIDTA/AIDTA and their intersection increase. When the membership degree threshold was set as T = 0.92384, the PS-FAIDTA include all the PS-AIDTA and the former is about 37 percent more than the later. Figure 2 and Table 1 indicate that the PS-FAIDTA method is feasible and it can select some different pixels based on FAIDTA method. Following, the quantitative characteristics of these PS-FAIDTA/AIDTA are showed and analyzed.
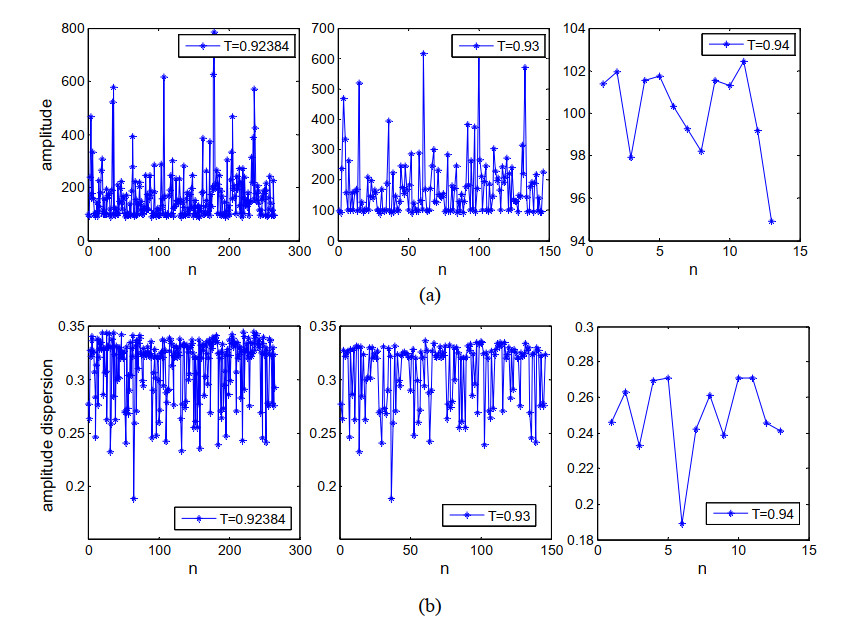
Figure 3 shows the characters of the PS-FAIDTA/AIDTA under different membership degree thresholds. Sub-graph (a) offers the amplitude values of these scatterers, (b) shows their amplitude dispersion values and ${\rm{n}}$ is the number of selected pixels. It is clearly shown that all of them are not far from the “PS” characters. And as the membership degree threshold increases, the number of PS-FAIDTA/AIDTA decreases, while the amplitude values of these scatterers are closer to the threshold of AIDTA and the amplitude dispersion values get smaller and smaller, which conforms to the PS characteristics better. This can be confirmed from the two subplots on the right-most side of Figure 3 especially. According to the traditional method (AIDTA), these scatters should be belonged to “no-PS” because they do not simultaneously meet the requirements that the minimum amplitude value of the pixel sequence should be greater than a fixed threshold 104.11 and the amplitude dispersion should be smaller than 0.32. However, it is not a logical judgment to some extent. For our study, the first requirement is very strong. In practice, there are some pixels whose amplitude values are slightly smaller than the given threshold while their amplitude dispersion values are much lesser than the given threshold. Obviously, they conform to “PS” better. Similarly, there is the same problem for amplitude dispersion index threshold in traditional method. Actually, these problems are embodied in several traditional methods beside AIDTA because the fuzzy properties of PS are not considered. This demonstrates the significance of the FAIDTA method. In addition, it should be worth noting that some PS-FAIDTA/AIDTA may not be selected as practical PS because their characteristics are far from PS somewhat. However, with the increase of the membership degree threshold, the reliability of the PS-FAIDTA/AIDTA is improving. Therefore, we can select those with high membership degree as practical PS.
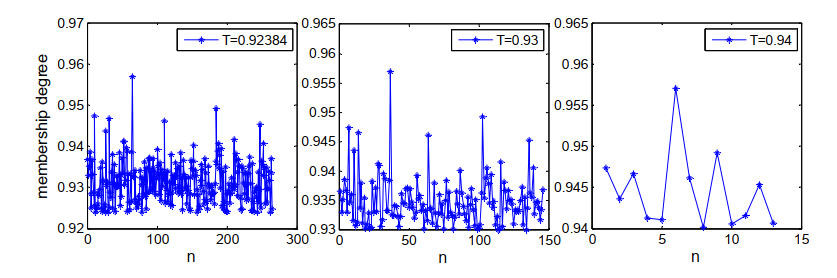
Figure 4 shows the distribution of membership degrees of those PS-FAIDTA/AIDTA under different membership degree thresholds. We find that the membership degrees are relatively greater compared to the minimum membership degree of PS-AIDTA 0.92384 on the whole and the lesser the membership degree threshold is, the more PS-FAIDTA/AIDTA can be selected as. In practice, it is improper for them to be all excluded from PS. Take the sixth point in the third sub-graph for example, its amplitude is 100.31 and amplitude dispersion is 0.1888. Relatively, the former is slightly less than the threshold 104.11, while the latter is much less than 0.32. By our subjective judgment, it is more consistent with the characteristics of “PS”. Its membership degree, greater than 0.955 from the Figure 4, confirms the judgment, which reflects the rationality of the new method.
Table 2 lists eight typical pixels whose membership degrees are greater than 0.94, amplitude are greater than 100 and amplitude dispersion are less than 0.32. Clearly, the amplitude of all the pixels are slightly smaller than the threshold 104.11 relatively. That is why these points are excluded by AIDTA. In fact, it is reasonable for them to be selected as PS based on their high amplitude stability seen from amplitude dispersion and negligible undesirable amplitude information. Taking the eighth pixel of Table 2 for example, its amplitude 102.42 is only a litter below the threshold 104.11 a little relatively, while its amplitude dispersion 0.2711 is much smaller than 0.32. Comprehensively considering, it’s a better choice to classify it as a PS.
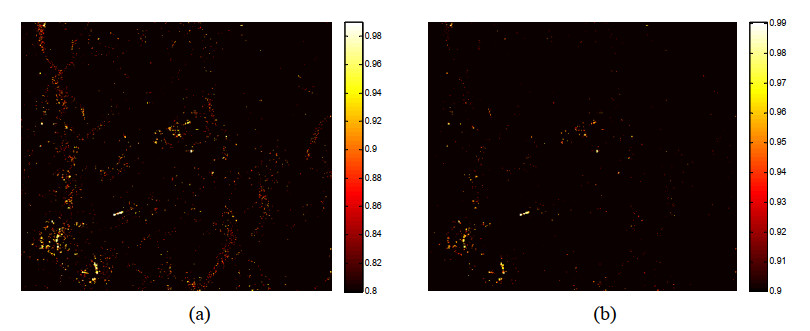
Another merit of FAIDTA is that quality results of all the interested pixels can be achieved based on their membership degrees in study area. Figure 5 shows two typical quality maps about PS-FAIDTA under membership degree threshold T = 0.8 and T = 0.9 respectively (mathematically named 0.8-T cut and 0.9-T cut of fuzzy set $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{P} $). In Figure 5, the brighter the pixel is, the greater the membership degree it has. Thus it can be seen that the FAIDTA method can not only recognize the effective PS, but also obtain the quality result of these pixels. In other words, FAIDTA can also obtain the quantitative description for the selected PS, which may be used for evaluating the reliability of them.
In addition, the proposed method is also compared with the traditional algorithm (AIDTA) from the numerical computational costs. To compare the efficiency of different algorithms objectively, the same hardware and software were adopted. The hardware was a PC with a Core i7-8565U CPU and 16 Gb RAM. Matlab software (version R2017b) running on the Win10 system was used to design the different algorithms. For the test data in this case, the new method costs about 0.5 second and AIDTA costs about 0.05 seconds. Because the membership degrees of the candidate points need more computational costs. It should be pointed that the cost of the new method is closely related to the parameter setting in selecting the candidate points.
4.2. Case 2
Fifty-six ERS images acquired from April 1992 to January 2003 over Luxembourg are selected as the second test data set. The cropped images are 150 × 650 pixels and cover about 39 km2. The same methods and processing strategy are used. The amplitude dispersion threshold is set as 0.35. The calculated amplitude threshold and minimum membership degree of PS-AIDTA PS are 367 and 0.9263 respectively in this test. For keeping the paper concise, parts of the results are shown below.
Figure 6 shows three corresponding overlay sub-graphs. The green ‘*’ and red ‘o’ mean the same as Figure 2. Similar regularity it demonstrates as Figure 1.
Table 3 shows the statistic information about the PS-AIDTA and PS-FAIDTA under different membership degree thresholds. The abbreviations are the same as Table 1. When the membership degree threshold was set as T = 0.9263, the PS-FAIDTA include all the PS-AIDTA. Other analyses are similar to Figure 6.
Table 4 lists nine typical pixels with membership degrees greater than 0.94, amplitude greater than 360 and amplitude dispersion less than 0.35. Clearly, the amplitude values of all the pixels are slightly smaller than the threshold 367.54 calculated by AIDTA method relatively. That is why these points are excluded by AIDTA. In fact, it is reasonable for them to be selected as PS based on their high amplitude stability seen from amplitude dispersion and negligible undesirable amplitude information. Taking the sixth pixel of Table 4 for example, its amplitude value 367.30 is slightly below the threshold 367.54, while its amplitude dispersion 0.2757 is much lesser than 0.35. Comprehensively considering, it’s a better choice to classify it as a PS.
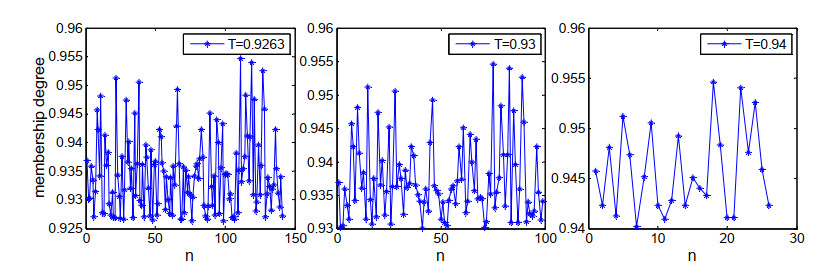
Figure 7 shows the distribution of membership degrees of those PS-FAIDTA/AIDTA under different membership degree thresholds. It can be found that the membership degrees are relatively greater compared to the minimum membership degree of PS-AIDTA 0.9263 on the whole and the lesser the membership degree threshold is, the more PS-FAIDTA/AIDTA can be selected as. The twenty-second point, whose amplitude value is 366.04, amplitude dispersion value is 0.2465 and membership degree is greater than 0.95, indicates the illogical judgment of excluding all of them by AIDTA.
5.
Discussions
From Cases 1 and 2, it can be found that AIDTA method always lose some key pixels which could be identified as PS for application while FAIDTA can make up this shortcoming. In other words, combing the two methods can usually lead to a nicer result for PS identification. Firstly, traditional method AIDTA is used to get some PS with clear characteristics. Then, some supplement pixels with high membership degree selected by FAIDTA method are obtained. As a consequence, it can increase the density of practical PS. Sub-graphs (a), (b) in Figures 2 and 6 show the selection results for the combining method. Moreover, from Tables 1 and 3, we can find that the new method plays a greater role in case 1 (the percent of n-FAIDTA/AIDTA is higher). In other words, the extent of the increase is different for different study areas. This depends on the land cover types. The vaguer the difference between land covers, the greater the extent of increase and the more sensitive the selection result. For instance, if a study area is covered with various reflective land covers, more reasonable PS can be selected based on the FAIDTA method and a slight change of the threshold will lead to great changes of the selection result. However, an opposite result can be shown in areas covered only by crops and some man-made corner reflectors. Therefore, the FAIDTA method can further improve the PS technology. In addition, it is clearly that the quality results of the selected PS can be also obtained, which can be used to evaluate the degree of the reliability for the selected PS. This is a remarkable advantage compared with traditional methods.
6.
Conclusions
Based on the fuzzy sets theory and features of PS pixels, a new concept of fuzzy PS was proposed and a fuzzy identification method was designed. Taking the amplitude information dual-threshold approach (AIDTA) as an example, the characters of PS were quantitatively described by membership degrees of amplitude and amplitude dispersion. Accordingly, a fuzzy AIDTA (FAIDTA) method was formed. Two groups of real data indicated that FAIDTA could recognize more effective and reliable permanent scatterers so as to compensate for traditional method AIDTA. In addition, quality results of the selected PS also could be obtained from the membership degrees, which could be used for quantitative evaluation of the selected points in time-series analyzing step of PSInSAR technology. That is to say, the new method not only can provide more practical PS to promote the time series analysis reliability for ground subsidence, but also can present quality value of each PS which can be used to evaluate the result of deformation based on PSInSAR technology. Generally, the proposed method can be extended based on other traditional PS identification methods, which is an effective feature fusion tool for PS identification and can improve the PSInSAR technology. Furthermore, how to apply the selected PS to subsidence monitoring is our future work. Additionally, heuristic and PSO algorithms can also be used to solve this problem, which are our other further research.
Acknowledgments
This work was supported by Science Foundation of Jiangsu Province (No: BK20170248) and National Natural Science Foundation of China (No: 51804297).
Conflict of interests
The authors declare no conflict of interest.









 DownLoad:
DownLoad: