Open Access Journals

AIMS Energy, 2014, 2(4): 410-423. doi: 10.3934/energy.2014.4.410. Research article Special Issues

Export file:

Format

RIS(for EndNote,Reference Manager,ProCite)
BibTex
Text

Content

Citation Only
Citation and Abstract

Cradle-to-gate life cycle assessment of the dry etching step in the manufacturing of photovoltaic cells

Otto Andersen, Geoffrey Gilpin, Anders S.G. Andrae

1 Western Norway Research Institute, P.O. Box 163, 6851 Sogndal, Norway;
2 Huawei Technologies Sweden AB., P.O. Box 54., 16494, Kista, Sweden

Received date: , Accepted date: , Published date:

Special Issues: Materials for Energy Technologies

Abstract Full Text(HTML) Figure/Table Related pages

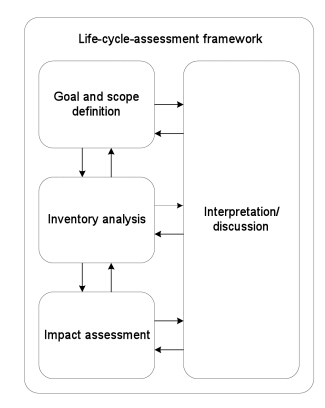
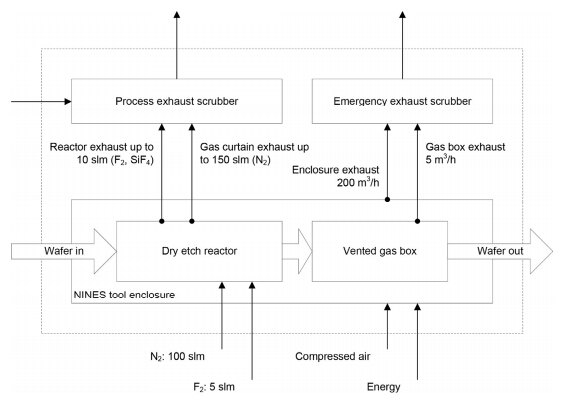
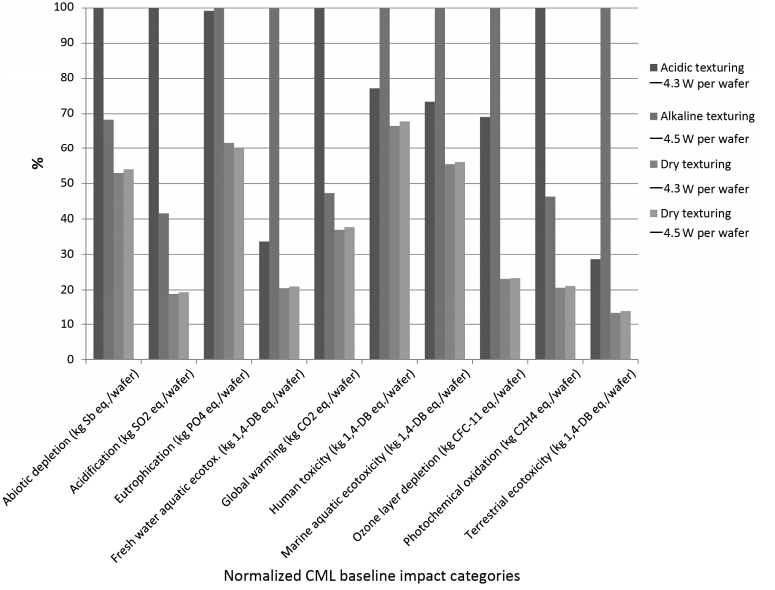
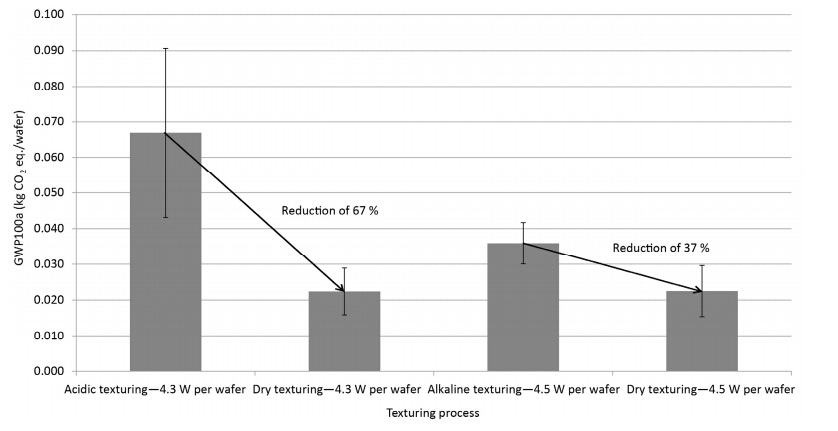
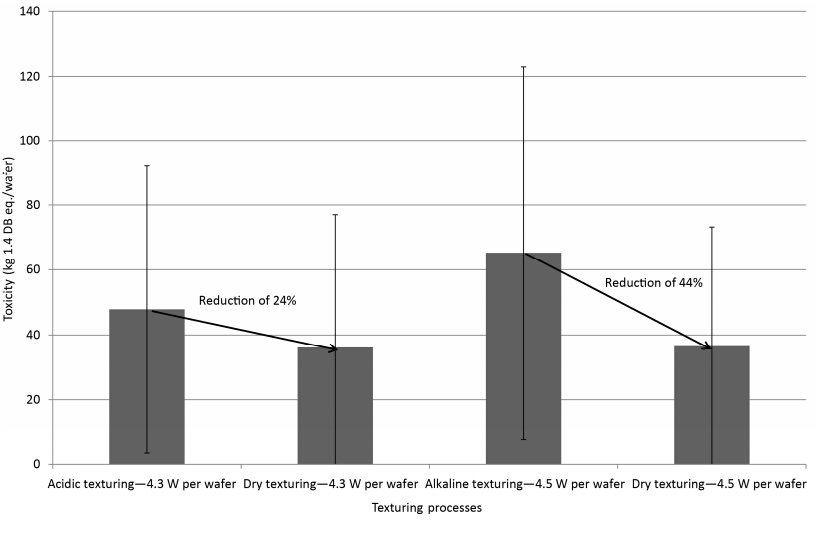
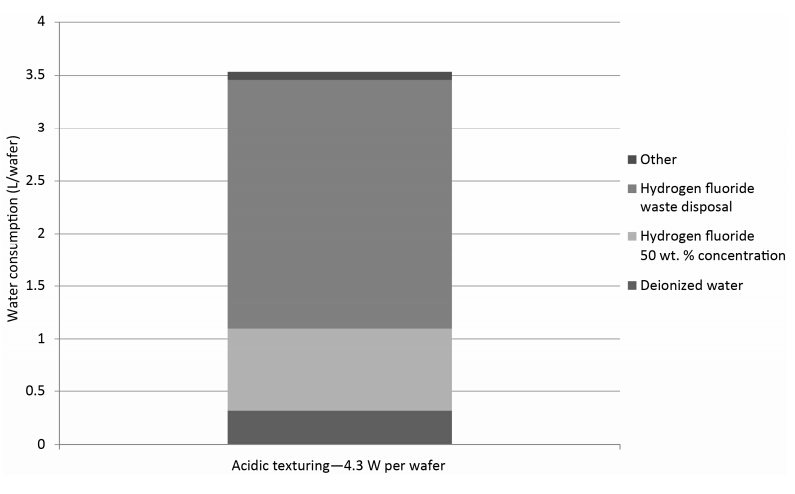
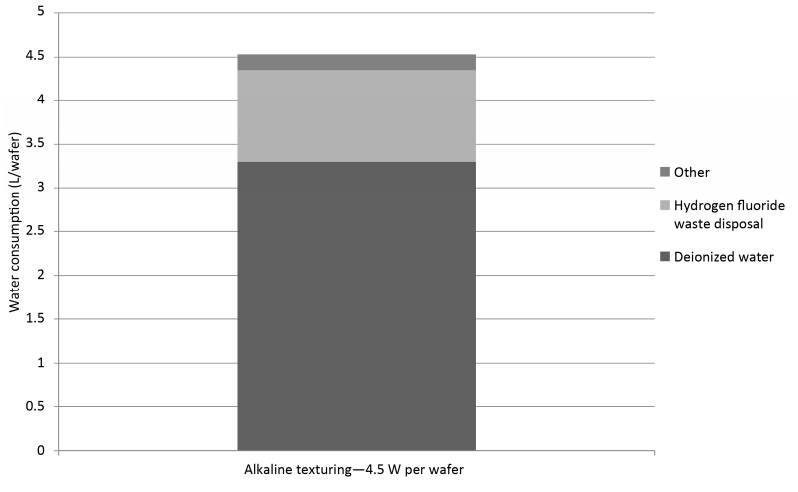
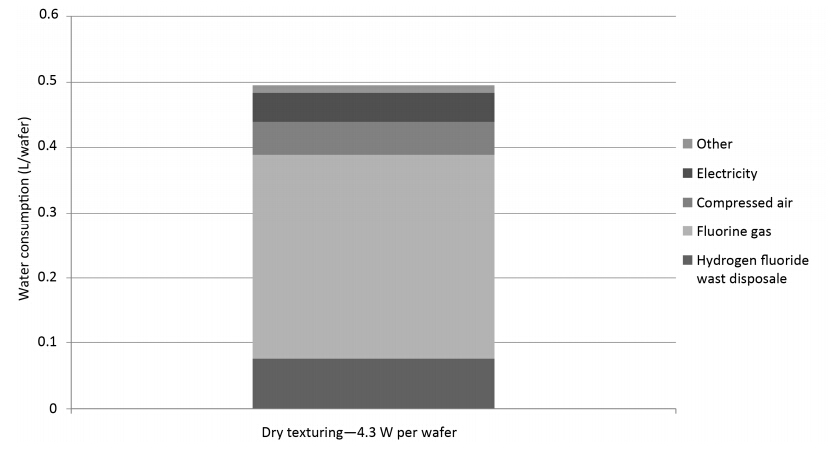
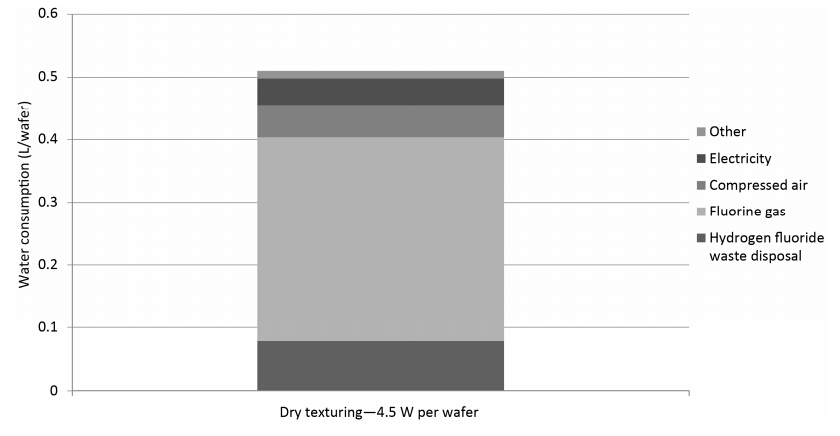
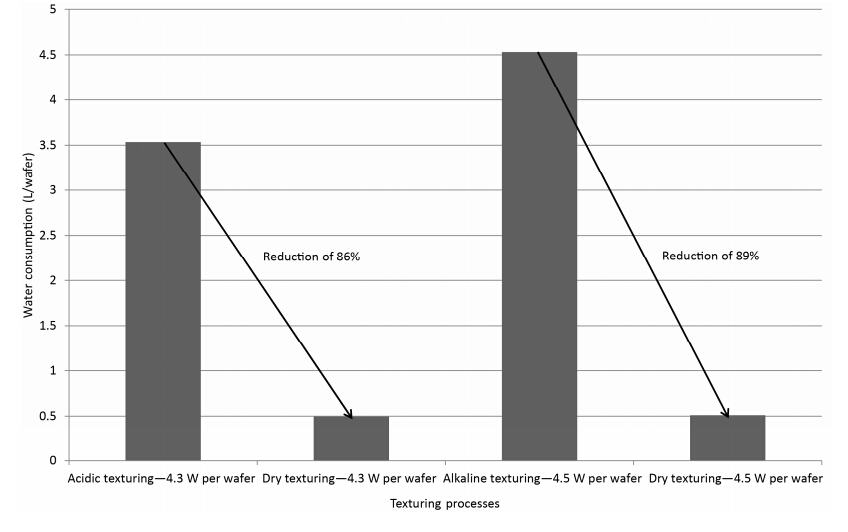
A new photovoltaic silicon crystalline solar cell dry chemical etching process (DCEP) is developed. It is an alternative to the current State-of-the-Art (SoA) wet chemical etching process (WCEP), associated with relatively large environmental loadings in the form of high water consumption and emissions of greenhouse gases with high Global Warming Potential (GWP). In order to compare the environmental impacts of DCEP to the corresponding impacts from WCEP, a comparative attributional life cycle assessment (LCA) is conducted. From the LCA it can be concluded that the DCEP will lead to 86% reduction in water consumption compared to WCEP (acidic), and 89% reduction compared to WCEP (alkaline). The emissions of greenhouse gases, as expressed by the GWP100 indicator of the etching step, are also reduced with 63% and 20% respectively, when compared with current SoA acidic and alkaline WCEP. The toxicity impacts are also assessed to be lower for the DCEP compared to WCEP technologies, although the uncertainty is relatively high for the applied toxicity indicators. All in all, DCEP can reduce the CO₂eq emissions of solar photovoltaic systems production by 5-10%.

Figure/Table

Supplementary

Article Metrics

Keywords: dry etching; global warming potential; life cycle assessment; photovoltaic solar cells; toxicity; water consumption

Citation: Otto Andersen, Geoffrey Gilpin, Anders S.G. Andrae. Cradle-to-gate life cycle assessment of the dry etching step in the manufacturing of photovoltaic cells. AIMS Energy, 2014, 2(4): 410-423. doi: 10.3934/energy.2014.4.410

References:

1 Dominguez-Ramos A, Held M, Aldaco R, et al, (2010) Prospective CO2 emissions from energy supplying systems: Photovoltaic systems and conventional grid within Spanish frame conditions. Int J LCA 15(6): 557-566.
2 Andersen O (2013) Solar Cell Production. In: Unintended Consequences of Renewable Energy. Problems to be Solved. Springer London, London, 81-89.
3 Bianco C, Torrelli A, Squizzato V, et al.. Energy and carbon pay back times for renewable power supply systems for Italian RBS off-grid sites. Telecommunications Energy Conference (INTELEC), 2011 IEEE 33rd International; 2011 9-13 Oct.; Amsterdam, the Netherlands. IEEE. 1-6.
4 Andrae ASG, Dong H, Shudong L, et al.. Added value of life cycle assessment to a business case analysis of a photovoltaic/wind radio base site solution in South Africa. Telecommunications Energy Conference (INTELEC), 2012 IEEE 34th International; 2012 30 Sept.-4 Oct.; Scottsdale, AZ, USA. IEEE. 1-7.
5 Zehner O (2011) Unintended Consequences of Green Technologies. Green Technology. Sage, London, 427-432.
6 Duffy E (2012) SOLNOWAT—Development of a competitive zero Global Warming Potential (GWP) dry process to reduce the dramatic water consumption in the ever-expanding solar cell manufacturing industry. D7.3 Exploitation Plan (interim).
7 Agostinelli G, Dekkers HFW, De Wolf S, et al. (2004) Dry Etching and Texturing Processes for Crystalline Silicon Solar cells: Sustainability for Mass Production. Paris, 423-426.
8 Forster P, Ramaswamy V, Artaxo P, et al. (2007) Changes in Atmospheric Constituents and in Radiative Forcing. In: Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.
9 Piechulla P, Seiffe J, Hoffman M, et al.. Increased Ion Energies for Texturing in a High-Throughput Plasma Tool. European Photovoltaic Solar Energy Conference and Exhibition (EU PVSEC); 2011 5-9 Sept.; Hamburg, Germany. Fraunhofer-Publica. 2024-2027.
10 Alsema E (2000) Energy pay-back time and CO2 emissions of PV systems. Prog Photovoltaics: Res Appl 8(1): 17-25.
11 Alsema E, de Wild-Scholten M. Environmental Impact of Crystalline Silicon Photovoltaic Module Production. 13th CIRP Intern. Conf. on Life Cycle Engineering; 2006 31 May-2 Jun.; Leuven, Belgium. G3.3.
12 Fthenakis VM, Kim HC, Alsema E (2008) Emissions from Photovoltaic Life Cycles. Environ Sci Technol 42:2168-2174.
13 Fthenakis VM, Kim HC (2010) Photovoltaics: Life-cycle analyses. Sol Energ 85:1609-1628.
14 Pehnt M (2006) Dynamic life cycle assessment (LCA) of renewable energy technologies. Renew Energ 31:55-71.
15 Jungbluth N (2005) Life cycle assessment of crystalline photovoltaics in the Swiss ecoinvent database. Prog Photovoltaics: Res Appl 13:429-446.
16 Fthenakis VM, Kim HC (2007) Greenhouse-gas emissions from solar electric- and nuclear power: A life-cycle study. Energ Policy 35:2549-2557.
17 Bergesen J D, Heath GA, Gibon T, et al. (2014) Thin-film photovoltaic power generation offers decreasing greenhouse gas emissions and increasing environmental co-benefits in the long term. Env Sci Tec 48(16): 834-9843.
18 Kim, H. C., Fthenakis, V., Choi, J., & Turney, D. E. (2012). Life cycle greenhouse gas emissions of thin-film photovoltaic electricity generation: Systematic review and harmonization. J Ind Ecol 16(SUPPL.1): S110-S121.
19 Fthenakis V, Kim HC, Alsema E (2008). Emissions from photovoltaic life cycles. Env Sci Tec 42(6): 2168-2174.
20 European Commission (2003) External Costs. Research results on socio-environmental damages due to electricity and transport. European Commission, Directorate-General for Research Information and Communication Unit, Brussels.
21 European Commission (1995) ExternE: Externalities of Energy. Prepared by ETSU and IER for DGXII: Science, Research & Development, Study EUR 16520-5 EN. Luxembourg.
22 Rentsch J, Jaus J, Roth K, Preu R. Economical and ecological aspects of plasma processing for industrial solar cell fabrication. Photovoltaic Specialists Conference, 2005. Conference Record of the Thirty-first IEEE; 2005 3-7 Jan.. IEEE, 931-934.
23 Agostinelli G, Choulat P, Dekkers HFW, et al.. Advanced dry processes for crystalline silicon solar cells. Photovoltaic Specialists Conference, 2005. Conference Record of the Thirty-first IEEE; 2005 3-7 Jan.. IEEE, 1149-1152.
24 Lopez E, Dani I, Hopfe V, et al.. Plasma enhanced chemical etching at atmospheric pressure for silicon wafer processing. European Photovoltaic Solar Energy Conference; 2006 4-8 Sept.; Dresden, Germany. Fraunhofer-Publica. 1161-1166.
25 Lopez E, Beese H, Mäder G, et al.. New developments in plasma enhanced chemical etching at atmospheric pressure for crystalline silicon wafer processing. The compiled state-of-the-art of PV solar technology and deployment. 22nd European Photovoltaic Solar Energy Conference, EU PVSEC 2007. Proceedings of the international conference; 2007 3-7 Sept.; Milan, Italy. Fraunhofer-Publica. 1484-1487.
26 Linaschke D, Leistner M, Mäder G, et al. Plasma Enhanced Chemical Etching at Atmospheric Pressure for Crystalline Silicon Wafer Processing and Process Control by In-Line FTIR Gas Spetroscopy. 21st European Photovoltaic Solar Energy Conference 2006. Proceedings; 2008 1-5 Sept.; Valencia, Spain. Fraunhofer-Publica.1907-1910.
27 Photovoltaics World, Champions of Photovoltaics: Cells and Modules. Photovoltaics World, 2011. Available from: http://www.renewableenergyworld.com/rea/news/article/2011/12/champions-of-photovoltaics-cells-and-modules.
28 Dresler B, Köhler D, Mäder G, et al. (2012) Novel Industrial single sided dry etching and texturing process for silicon solar cell improvement. 27th European Photovoltaic Solar Energy Conference and Exhibition 1825-1828.
29 International Standards Organisation (2006) Environmental management-life cycle assessment-principles and framework. International Organization for Standardization, Geneva, Switzerland.
30 International Standards Organisation (2006) Environmental management-life cycle assessment-Requirements and Guidelines. International Organization for Standardization, Geneva, Switzerland.
31 Andrae ASG (2009) Global life cycle impact assessments of material shifts: the example of a lead-free electronics industry. Springer.
32 Frischknecht R, Stucki M (2010) Scope-dependent modeling of electricity supply in life cycle assessments. Int J LCA 15:806-816.
33 European Commission Joint Research Centre Institute for Environment and Sustainability (2010) International Reference Life Cycle Data System (ILCD) Handbook—General guide for Life Cycle Assessment—Detailed guidance. First edition March 2010. EUR 24708 EN. Luxembourg. Publications Office of the European Union.
34 Institute of Environmental Sciences (CML) Faculty of Science, CML-IA Characterisation Factors. Leiden University Institute of Environmental Sciences (CML), 2013. Available from: http://cml.leiden.edu/software/data-cmlia.html.
35 Dominguez-Ramos A, Aldaco R, Irabien A (2007) Life cycle assessment as a tool for cleaner production: Application to aluminium trifluoride. Int J Chem Reactor Eng 5(1): 1542-6580.
36 Weidema B, Wesnaes M (1996) Data quality management for life cycle inventories—an example of using data quality indicators. J Cleaner Prod 4(3-4):167-174.

show all references

This article has been cited by:

1. Anders Andrae, Mengjun Xia, Jianli Zhang, Xiaoming Tang, Practical Eco-Design and Eco-Innovation of Consumer Electronics—the Case of Mobile Phones, Challenges, 2016, 7, 1, 3, 10.3390/challe7010003
2. Mohammad Masih Edalat, Haroon Stephen, Effects of two utility-scale solar energy plants on land-cover patterns using SMA of Thematic Mapper data, Renewable and Sustainable Energy Reviews, 2017, 67, 1139, 10.1016/j.rser.2016.09.079

Reader Comments

your name: * your email: *

Copyright Info: 2014, Otto Andersen, et al., licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution Licese (http://creativecommons.org/licenses/by/4.0)

Download full text in PDF

Associated material

Metrics