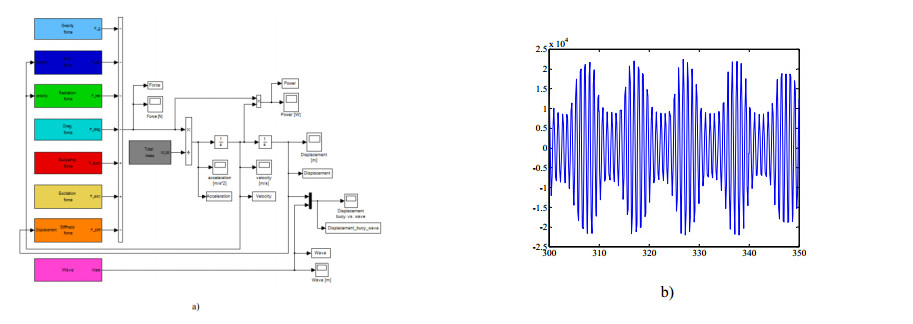
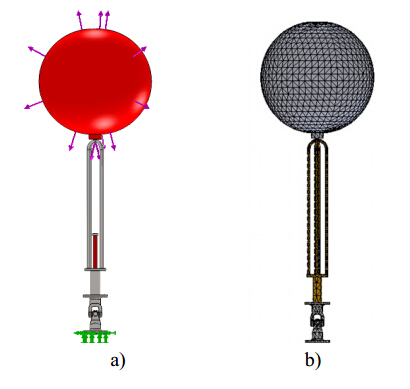
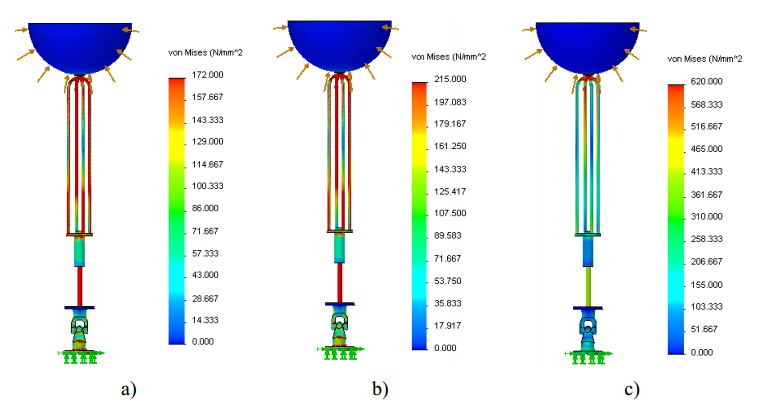
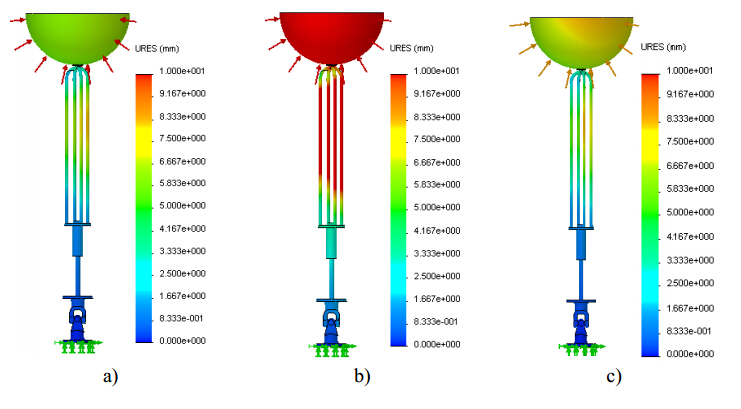
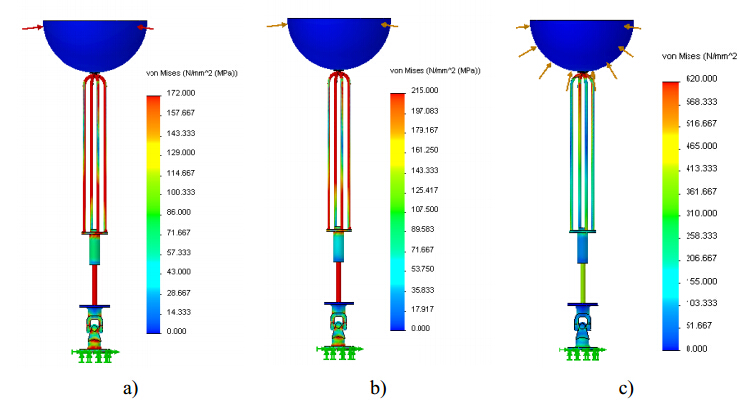
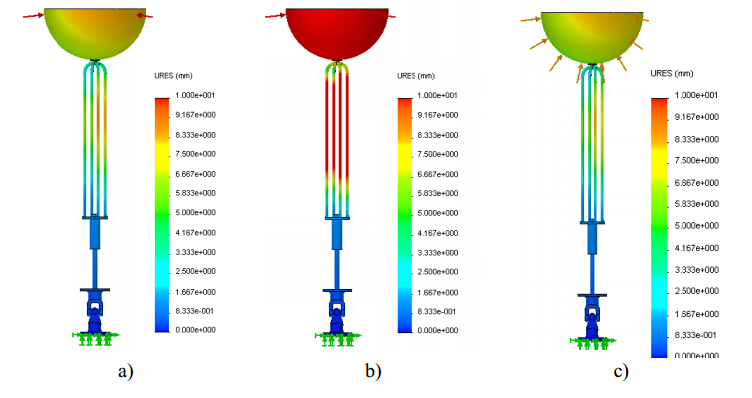
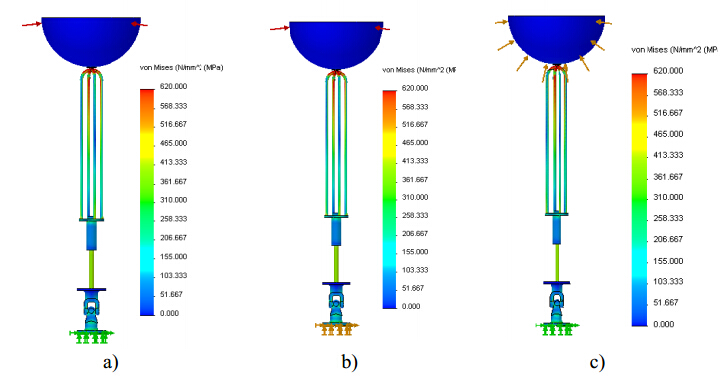
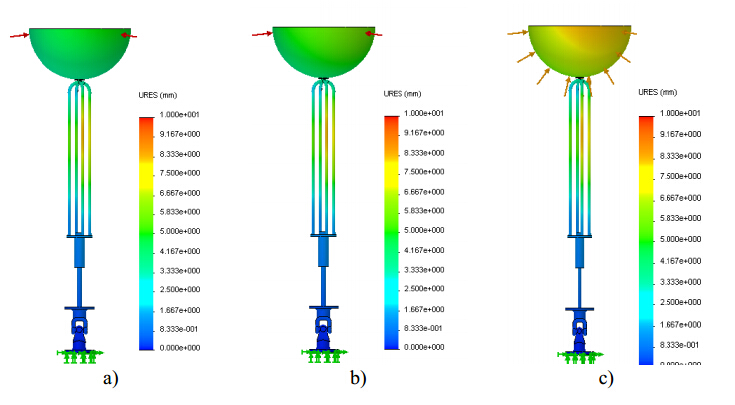
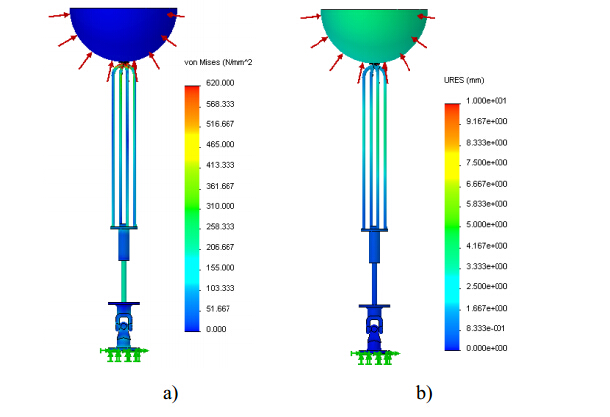
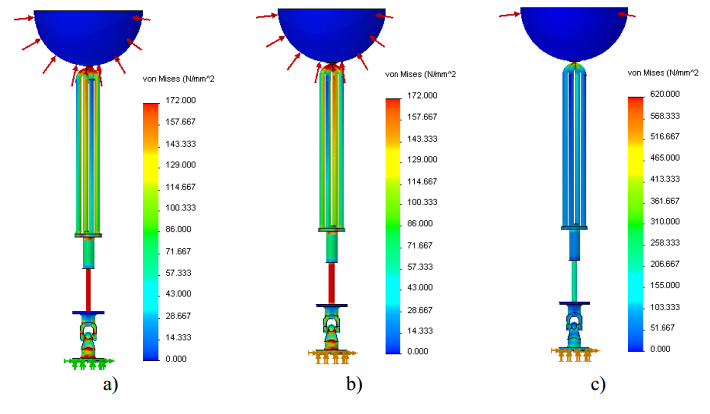
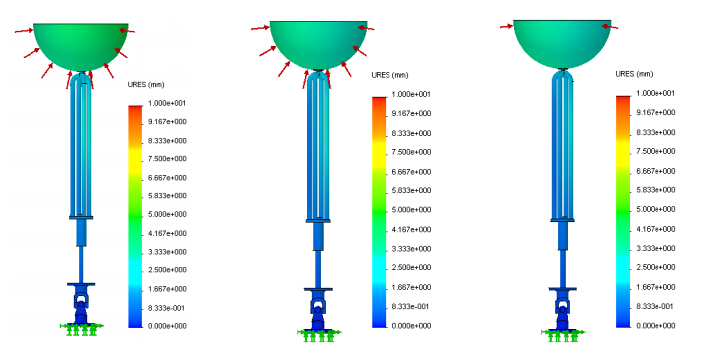
In the last decades, the world energy demand has raised significantly. Concerning this fact, wave energy should be considered as a valid alternative for electricity production. Devices suitable to harness this kind of renewable energy source and convert it into electricity are not yet commercially competitive. This paper is focused on the selection and analysis of different types of elastic materials and their influence on the structural behavior of a wave energy converter (WEC). After a brief characterization of the device, a tridimensional computer aided design (3D CAD) numerical model was built and several finite element analyses (FEA) were performed through a commercial finite element code. The main components of the WEC, namely the buoy, supporting cables and hydraulic cylinder were simulated assuming different materials. The software used needs, among other parameters, the magnitude of the resultant hydrodynamic forces acting upon the floating buoy obtained from a WEC time domain simulator (TDS) which was built based on the WEC dynamic model previously developed. The Von Mises stress gradients and displacement fields determined by the FEA demonstrated that, regardless of the WEC component, the materials with low Young's modulus seems to be unsuitable for this kind of application. The same is valid for the material yield strength since materials with a higher yield strength lead to a better structural behavior of WEC components because lower stress and displacement values were obtained. The developed 3D CAD numerical model showed to be suitable to analyze different combinations of structural conditions. They could depend of different combinations of buoy position and resultant hydrodynamic forces acting upon the buoy, function of the specific sea wave parameters found on the deployment site.
1.
Introduction
The Chinese Sina-Microblog is reported to have 446 million active users per month (32% of the Chinese population) at the end of 2018 and is particularly popular among the young generations. Take the event (Weibo) "304 car theft case" as an example, around 185 thousand of forwarding users were generated into 36 hours since it was posted [1]. This important platform presents some unique characteristics different from other microblogs for public opinion diffusion [2,3] that a systematic approach towards understanding the diffusion patterns and nearcasting the information propagation is called for.
The information propagation of a microblog is created through the action of "follow" connecting as an interaction network, where a following user is called "follower" and a followed user is called "followee" [4,5]. There are a large amount of literature and there seem to be three typical and important information diffusion models developed for microblogs [6] according to the spreading process, influence ability [7,8] and forwarding factors [9,10]. The model we are exploring is based on the propagation process as we focus on the dynamic changes of the status of users during the spreading process.
Our approach follows the classical rumor model that evolved from the epidemic models, in which the population is stratified into three mutually exclusive and exhaustive classes: heard rumor (ignorants), actively spreading rumor (spreaders) and no longer spreading rumor (stiflers). The propagation of information (rumor) occurs through the transitions of infections from ignorants to spreaders, and removals from spreader to stiflers [11]. This is very much similar to epidemic models for infectious disease spreading in the population. Extensions from this classic rumor model to information spreading in microblogs include propagation transition models [12,13,14,15,16] and population classification models [17,18,19,20,21]. In particular, taking into account of different behaviors of differential users in different platforms, Huang et al. [12] extended the rumor spreading model to characterize browsing behaviors of users and examine differentiating rumor refuting effects. This model involves a parameter similar to the birth rate in a standard epidemic model to describe the entry of new susceptibles. Liu et al. [13] proposed a modified rumor spreading model (SIRe), where two contact parameters are used to describe the stifler's broadcasting effect and social intimacy degree. Su et al. [14] developed a Microblog-Susceptible-Infected-Removed (Mb-SIR) model for information propagation by explicitly considering the incomplete reading behaviors of users using the probability that a newly posted or retweeted message will be read by its followers. These models also utilized real data from the Chinese Sina-Microblog in their numerical simulations.
Our framework follows the work of Borge-Holthoefer et al. [15] that considered the situation where spreaders are not always active and an ignorant is not interested in spreading the rumor. Their numerical simulations were based on data from Twitter. A similar model for an information dissemination network was proposed in [16], where different transition probabilities from the spreader stage to stifler stage and from the ignorant stage to stifler stage were used. This set a theoretical foundation to compare microblog information dissemination and epidemic disease spreading.There have been other efforts to incorporate further states during the propagation process, in addition to the states of ignorant, spreader and stifler. In particular, reflecting some information features and diffusion characteristics of Weibos in the Chinese Sina-Microblog, Li et al. [17] incorporated the number of fans of infectious and validated the modified SIR model using actual event data. Liu et al. [18] considered a dynamic model to characterize the super-spreading phenomenon in tweet information propagation. An ignorant spreaders, super-spreaders, stiflers model (ISJR model) was proposed in [19] that considered the role of super-spreaders to show how super-spreaders can accelerate the information dissemination and amplify information influence in microblogging networks. Other models have also been proposed to incorporate the recovery state of users in different platforms including the Chinese Microblogs, Japanese Mixi, and Facebook [20,21].
Here we consider the capacity of using a simple compartmental model for information propagation of Microblog for nearcasting the trend of information propagation in the Chinese Microblogs. Nearcasting is an important issue for assessing public opinions, that aims to project the forwarding trend at the earliest possible stage of a Weibo outbreak so interventions for the information propagation and/or rapid response to the public opinions can be designed and implemented effectively. Our ultimate goal is to develop nearcasting technologies for a group of Weibos (similar to "Tweet" in Twitter) in the ecosystem of Chinese Microblogs. To achieve this goal, we need to develop computable summative indices to characterize each Weibo, and see how these indices can be effectively calculated or at least estimated from the public available information at the early stage of information propagation of the Weibo. Here, we formulate the basic compartmental model (SFI) and introduce the Weibo propagation indices in the Chinese Sina-Microblog (Section 2), and then contrast two methods to use this SFI-model for nearcasting.
2.
The SFI model for forwarding behavior
2.1. Model description
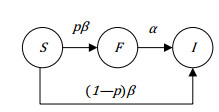
We consider a population of Chinese Sina-Microblog users, stratified in terms of three distinct states: the susceptible state ($ S $), in which users are unaware of but susceptible to the Weibo; the forwarding state ($ F $), in which users have been forwarding the Weibo actively to influence other users; and the immuned state ($ I $), in which users have already forwarded the Weibo, but are no longer forwarding the Weibo and even if receiving it again.
Assuming the populations susceptible to the Weibo is sufficiently large and denoting the total numbers of users in the susceptible, forwarding and immune state at time $ {t\ge0} $ by $ S(t) $, $ F(t) $ and $ I(t) $, respectively, we obtain the following susceptible-forwarding-immune model:
where $ ' = d/dt $ is the derivative with respect to $ t $. The model is illustrated in Figure 1.
In the model, $ \beta $ is the average number of exposures to the Weibo of a susceptible user, $ p $ is the probability that the exposed user will forward the Weibo and $ \alpha $ is the rate at which a user in the $ F $ state becomes inactive to forwarding. The mass action term can also be interpreted as follows: an active forwarding user will contact an average number of $ \beta N $ users per unit time, among which $ p\beta N $ will choose to forward the Weibo and $ (1-p)\beta N $ will not. Since the probability of a contacted user to be a susceptible user is $ {S(t)}/{N} $, the number of exposed users who leave the state $ S $ are $ \beta S(t)F(t) $ among which new forwarding and immuned users are $ p\beta N(S(t)/N)F(t) = p\beta S(t)F(t) $ and $ (1-p)\beta S(t)F(t) $, respectively. As usual, $ 1/\alpha $ is the average duration a F-user remains active in forwarding.
An important distinction between a standard epidemic-SIR model and the Weibo-SFI model is the direct immunity of a susceptible user gained through exposure to the Weibo. The parameter $ 1-p $ reflect the suitability of the Weibo for a susceptible user to trick the activity of forwarding. This SFI model was used in [15,16] as a basic building block of a more complicated framework. We adopt this for the Weibo information spread dynamics model in the hope this can be further expanded to discuss the dynamics of an ecosystem consisting of multiple Weibos sharing a same set of key words. The novelty of our approach here is to develop some analytic indices which will be used in our subsequent studies to consider Weibo spreading dynamics in a complex Weibo ecosystem, and explore the feasibility of using openly available Weibo data from the Chinese Sina-Microlog to estimate these indices for the purpose of nearcasting the propagation trend.
The official Chinese Sina-Microblog only provides limited information of the propagation, an important piece of information we can obtain from the Chinese Sina-Microblog directly is the number of cumulative forwarding users given by
Observe that this is NOT a new compartment from the coupled system (2.1). Instead, from Eq (2.1), we can obtain
It is easy to show that $ S(t) $, $ F(t) $, $ I(t) $ and hence $ E(t) $ all remain nonnegative. We consider the case when the Weibo is posted by a single user at the beginning, leading the initial condition: $ {E_0 = F_0 = 1} $, $ {I_0 = 0} $, $ {S_0 = N-F_0 = N-1} $.
From Eqs (2.1) and (2.5) it follows that $ S(t) $ is decreasing since $ S'(t) = -\beta S(t)F(t) < 0 $, and that the function $ E(t) $ is increasing since $ E'(t) = p\beta S(t)F(t) > 0 $. Therefore, $ S(t) $ decreases to a limit $ S_{\infty}: = \lim \limits_{t \to \infty}S(t) > 0 $, $ E(t) $ increases to a limit $ E_{\infty}: = \lim \limits_{t \to \infty}E(t) < N $, $ F(t) $ tends to 0 ($ F_{\infty} = 0 $), and $ I_{\infty} = N-S_{\infty} $. These limits are shown to be relevant to the so-called final size of the Weibo spreading.
2.2. The Weibo propagation indices
Weibo reproduction ratio $ \Re_o $: The initial growth of the F-population is given by $ r = p\beta S_0-\alpha $, and the propagation of the Weibo will never take off if $ F'(t) > 0 $. Since $ F'(t)\leq(p\beta S_0-\alpha)F(t) $ due to the decreasing property of $ S(t)\, (S(t) < S_0) $. We then define
as the Weibo reproduction ratio. Then $ {\Re_o < 1} $ implies a rapid decline of F-user which results in information propagation never taking off. However, when $ {\Re_o > 1} $ the F-population used grow exponentially initially.
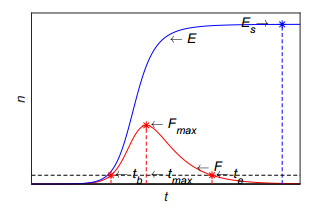
Index $ \Re_o $ denotes the number of F-users generated by one active forwarding user during an active period. A typical curve for F-population with a Weibo with $ {\Re_o > 1} $ has the bell shape as shown in Figure 2. Maximal Weibo forwarding users $ F_{max} $: The maximum of the F-curve is achieved when $ F'(t) = 0 $. At this point, we have $ S(t) = \alpha/p\beta $. We also use Eqs (2.1) and (2.2) to get
Integrating then yields
If we substitute $ F_0 = 1 $, we get (notify $ F_{max} = F(t) $ for $ t $ when $ S(t) = \alpha/p\beta\, ) $ that
Maximum Weibo cumulative forwarding users $ E_s $: The maximum Weibo cumulative forwarding users $ E_s $, which represents the number of users that encountered the Weibo, is also a factor we are interested in. To establish an analytic formula, we integrate from 0 to $ +\infty $ on both sides of Eq (2.1) to get
Adding Eqs (2.1) and (2.2) and integration yields also
From Eqs (2.11) and (2.12), we get
In order to analyze the relation between $ E $ and $ S $, we integrate from Eqs (2.1) and (2.5) to obtain
Similarly, $ E_0 = F_0 = 1 $, $ F_{\infty} = 0 $ and $ \Re_o = p\beta S_0/\alpha $, from Eqs (2.12) and (2.13) we get (notify $ E_s: = E_{\infty} $) that
and then
We observe from Eqs (2.9) and (2.15) that, with a fixed $ \Re_o $, the final outcome of the Weibo spread is determined by parameter $ S_0 $. Note that, differently from an epidemic study, the initial susceptible Weibo users are usually unknown.
Weibo public opinion times and velocities: To understand the global performance of the Weibo ecosystem, we need to know the take-off and extinctive time of a particular Weibo, denoted by $ t_b $ and $ t_e $, respectively. The definitions depend on the threshold $ F^* $ which is set in advance such that $ F(t_b) = F^* = F(t_e) $. In the experiment we design, we let $ F^* = 0.1\times F_{max} $. The difference, $ t_e-t_b $, is the duration during which the Weibo remains active in the ecosystem. We denote this by $ t_i: = t_e-t_b $. Relevant to the timings and the spread duration, we can define the (initial) outbreak velocity $ V_o $, the propagation decline velocity $ V_d $, and the average spreading velocity $ V_a $ as follows:
where $ t_{max} $ is given when $ F(t) = F_{max} $. Note that $ t_b $, $ t_e $, $ t_{max} $, $ V_o $, $ V_d $ and $ V_a $ can be calculated when model parameters are estimated although we do not have the closed form of these quantities. A schematic picture is given in Figure 2.
2.3. An example:
The number of cumulative forwarding users can be collected through the Weibo' Application Programming Interface (API). Table 1 lists such a data set, studied in paper [22], for an actual event lasted 16 days.
The LS method [23] can be used to estimate the parameters of the SFI model (2.1), (2.2), (2.3) and (2.5). The parameter vector is set as $ \Theta = (\beta, \alpha, p, S_0) $, and the corresponding numerical result for $ E(t) $ is denoted by $ f_{E}(t, \Theta) $. The LS error function
can be used, where $ ID $ denotes the real number of cumulative forwarding users given in Table 1, $ t_k = k $ is the sampling time, $ k = 1, 2, ..., 16 $.
We use the standard package (fmincon) of MATLAB to solve a nonlinear LS problem, with parameter initial values and ranges given as follows: $ \beta\in[2\times10^{-6}, 8\times10^{-6}] $, $ p\in[0.1, 0.5] $, $ \alpha\in[0.5, 1.5] $, $ S_0\in[7\times10^{6}, 2\times10^{7}] $, $ \Theta_0 = (4.0\times10^{-6}, 0.3, 1.0, 1.0\times10^{7}) $.
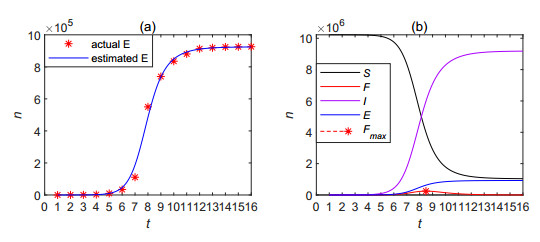
Figure 3 reports our data fitting and simulation results. Figure 3a shows the fitting result between the numerically calculated and the actual numbers of cumulative forwarding users. From the data fitting, we can estimate the model parameters and then inform other information not available from the API. Namely, we can obtain the temporal variations of the numbers of susceptible, forwarding, immunized and cumulative forwarding users, $ S(t) $, $ F(t) $, $ I(t) $ and $ E(t) $, after obtaining the model parameters.
Note that for the Weibo data listed in Table 1, the estimated basic reproductive ratio $ \Re_o = 2.5460 $, and since it is much greater than one, we should expect a rapid information spread at the beginning of the propagation. Figure 3a does confirm this expectation. We should also expect, from surveillance data of infectious disease outbreak such as influenza, a large number of F-users and a large number of E-users for the Weibo. The numerical simulations reported in Figure 3b, however, shows otherwise: despite a large number of susceptibles ($ S_0 = 1.0221\times10^7 $), the cumulative E-users during the entire propagation is only $ E_s = 9.2430\times10^5 $ and maximum F-users at the propagation peak is only $ F_{max} = 2.4724\times10^5 $. A reason is that $ p $ is only 0.1006 and hence a large number of individuals exposed to the Weibo became immunied immediately upon exposure.
3.
Nearcasting capacity of SFI-modelling
3.1. Method 1 (all parameters estimated)
The numerical illustration in the last section indicates a good data fitting results using the numbers of cumulative forwarding users during the entire outbreak period. These numbers can be collected from the API, and therefore a Weibo can now be characterized by the SFI-model parameters ($ \beta, \alpha, p, S_0 $), using the information from API retroactively.
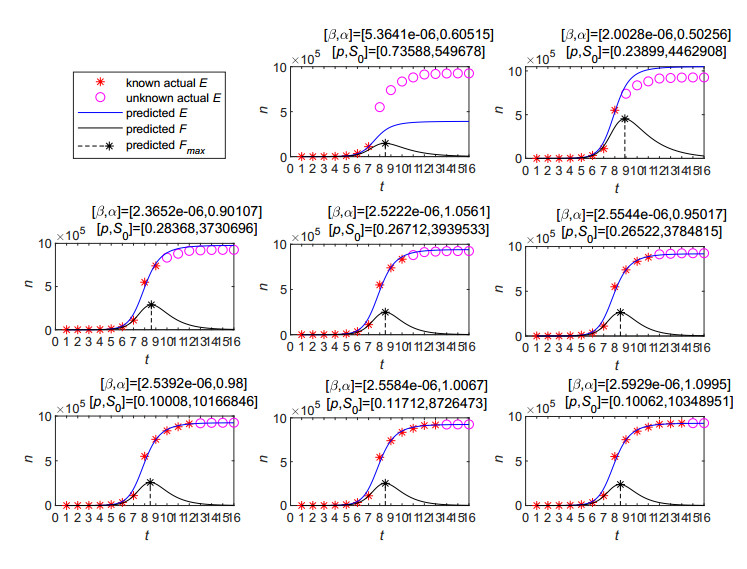
An important question in Weibo information management is how many units (days) of data about the cumulative forwarding users we need to be able to estimate the model parameter and thus make the prediction for the near future about the propagation trend and calculate key Weibo indices. Figure 4 reports our numerical experiments in which parameters ($ \beta, \alpha, p, S_0 $) are estimated from the past days, and then the cumulative F-users are predicted and compared with the actual data from API data.
Comparing with the estimated parameters $ \beta = 2.5651\times10^{-6} $, $ \alpha = 1.0365 $, $ p = 0.1006 $, and $ S_0 = 1.0221\times10^{7} $ from the entire outbreak duration, we observe that the estimated parameter and the resulted SFI-model prediction does not fit the actual data until 7 days have pasted, when the peaking time is 8.49 days.
3.2. Method 2 (a-prior estimation)
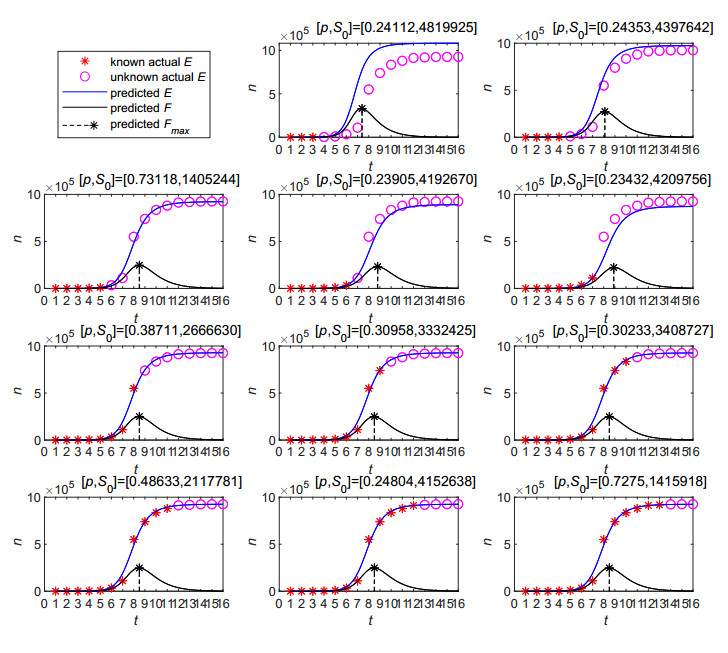
Therefore, the use of an SFI-model for nearcasting is not promising if we need to use the historical data to estimate all the model parameters altogether. On the other hand, in the Chinese Sina-Microblog, parameter $ \beta $ is determined by the compactness of the network structure and parameter $ \alpha $ is usually user-specific rather than Weibo-specific. Thus, it is feasible to estimate parameters $ \beta $ and $ \alpha $ before the outbreak of an event (for example from other events). Figure 5 gives the numerical results with fixed $ \beta $ and $ \alpha $ that are given a-priori.
This experiment indicates the remaining parameters ($ \it p, \it S_0 $) can be estimated from the data in the first 3-days, much ahead of the outbreak peak time. Therefore, the nearcasting capacity of an SFI-model can be significantly enhanced should the network-specific parameter $ \beta $ and user-specific $ \alpha $ be estimated in advance.
3.3. Comparison
The numerical experiments with all parameter estimated (Method 1) and some parameters a-priori estimated (Method 2) clearly show that Method 2 has a much better performance in nearcasting with limited historical data well before the peaking time of the Weibo information outbreak.
Tables 2, 3, 4 give the comparison of indices $ \Re_o $, $ \it F_{max} $, $ \it E_s $, indices $ t_b $, $ t_s $, $ t_i $, $ t_{max} $, and indices $ V_o $, $ V_e $, $ V_a $, separately. For Method 1, Tables 2, 3, 4 show that at the beginning of the Weibo propagation, our predictions have low accuracy when using the historical data until Day 7. Using the historical data until after the propagation peak (Day 8), the predicted maximum F-users ($ F_{max} $), cumulative F-users ($ E_{s} $), reproduction ratio ($ \Re_o $) and the outbreak velocity ($ V_o $) are larger than the actual values, indicating over-estimation of the propagation potential. However, as one gains more and more historical data, the prediction converges to the actual values. For the prediction of key times during the Weibo information outbreak, Method 1 can produce predictions of key instants, after Day 7, such as take-off, extinction, duration and propagation peak time within 1-day error. The predicted maximal forwarding users ($ F_{max} $), the outbreak velocity ($ V_o $), the propagation decline velocity ($ V_e $) and the average spreading velocity ($ V_{a} $) are all consistent with corresponding actual instants. So, the time after which a good nearcasting prediction is possible is Day 7, and the prediction quality is very high if historical data until Day 9 is used.
Method 2 is more effective in nearcasting both in terms of estimating the peaking time at the 3-day, but also estimating all relevant indices. Therefore, it is advised that one should perform the nearcasting by estimating parameters $ \beta $ and $ \alpha $ before the outbreak of the event. This proposed a-priori estimation method for nearcasting emphasizes the importance of understanding the propagation of other previously happened Weibos propagation events in advance, in order to better monitor and respond to public opinion dynamics at a real time.
4.
Discussions
This paper concerned with nearcasting for forwarding behaviors in the Chinese Sina-Microblog based on the use of a simple compartmental SFI model for a Weibo to be forwarded by users exposed to the Weibo. A significant difference of Weibo information propagation from the pathogen of an infectious disease is that an exposed user may gain immunity to the Weibo so the user becomes completely uninterested in forwarding the Weibo.
The relative simplicity of the model permitted the construction of various indices and their calculations/estimations: the Weibo reproduction ratio, the maximal forwarding users, the maximum cumulative forwarding users, and critical propagation peak time, taking off and extinction times, and propagation velocities during different phases of the information outbreak. An important issue, to use this simple model to predict these critical indices and thus contribute to nearcasting propagation trend based on historical Application Programming Interface (API) data, was addressed through some numerical experiments based on a real Weibo event data. We considered two cases, where we can accurately estimate all model parameters with the historical data passing the peaking time, or we can rapidly and accurately estimate two critical parameters relevant to the Weibo when two other model parameters relevant to the network characteristic and forwarding users' waning interest rate are estimated a-priori. This second approach clearly shows the nearcasting capacity of a simple compartmental SFI-model as long as we have some information about the network characteristics and the anticipated public interest in a class of Weibo events.
The simple model provides two important pieces of information about the propagation characteristics of a particular Weibo: the intrinsic growth rate (the basic Weibo reproduction ratio), and the maximal capacity of the network for the particular Weibo event (the maximal number of cumulative forwarding users). As anticipated from long time intensive modeling study of biological ecosystems, the intrinsic growth rate and the maximal capacity gives the logistic growth dynamics [24] of a single Weibo propagation dynamics. A full understanding of this propagation dynamics of a single Weibo event is the first critical step towards examining the propagation dynamics of a group of interactive Weibo events in a complex network.
There are many different model frameworks, as briefly reviewed in the introduction. We have listed existing studies which are directly relevant to our mechanistic approach towards developing a simple compartmental model for characterizing the Weibo information spread in the Sina-Microblog. We refere to [25,26,27] and references therein for further studies at the intersection of mathematics, epidemics, information diffusion and control. Interestingly, the work [25] that introduces a class of infants with maternal antibodies giving passive temporary immunity for the considered infectious disease may find an application for our modeling Weibo spread within the Sina-Microblog as some immediate followers of opinion leaders may inherit a certain immunity for a Weibo. Obviously, the Sina-Microblog possesses all kinds of features of complex networks [26], the sub-network structure and the network topology require much further investigations that our simple mechanistic model can serve as a building block towards a more complicated network framework. A primary goal of nearcasting the propagation trend is to inform optimal design of interventions, so the methodologies designed for the control of infection dynamics [27] may also be adopted in our simple model and its variations.
We mention also that a variant of the epidemiological SIR model was used in [28] to accurately describe the diffusion of online content over the online social network Digg.com. The work examined also qualitative properties of our viral information propagation model, demonstrate the model's applications to nearcasting social media spread in online social networks. Alternatively, a linear diffusive model was proposed and considered in Feng et al. [29,30] using a temporal-spatial partial differential equation model to explain these rates of spread in the DOSN. The PDE and network analogue of the SFI model should be developed to reflect the spatial spread and network heterogeneity.
Acknowledgments
The work was supported by the National Natural Science Foundation of China (Grant numbers: 61801441), the Natural Science and Engineering Research Council of Canada and the Canada Research Chair Program (JWu), and the Fundamental Research Funds for the Central Universities.
Conflict of interest
The authors declare that they have no competing interests.









 DownLoad:
DownLoad: