1. Introduction

In the last decades, the world energy dem and has significantly raised. With the decay of fossil resources, renewable energy sources are facing a growing dem and . Among them, ocean wave energy is one of the most promising alternatives regarding the production of electricity [1]. This renewable energy source provides a high power density when compared, for instance, with solar and wind energies. Additionally it is more reliable than most of the other renewable energy sources, since wave power availability can surpass 90 percent of the time while solar and wind availability only reach 20 to 30 percent of the time [2]. This allows the high utilization of wave power plants over the year, as well as their customization through engineering solutions that match those devices to different ocean climates [3]. Although in an early stage of development when compared with more mature renewable energy sources, different countries with exploitable wave power resources started considering wave energy as a possible source of power supply. However, devices suitable to harness this kind of renewable energy source and convert it into electricity are not yet commercially competitive [1] when compared with more mature renewable energies, such as wind and solar. Currently there are numerous concepts of wave energy converters (WEC) being developed and tested around the world which require a great deal of investigation. Some of them have already been submitted to real ocean conditions and a few full-scale devices have been operating under a more or less continuous basis [4].

This paper is focused on the development of a WEC 3D CAD numerical model suitable to be applied under different combinations of buoy positions and resultant hydrodynamic forces acting upon the buoy, function of specific sea wave parameters found on the deployment site. The sizing of the floating buoy and the materials selected to build the components of the WEC can be optimized and customized to each specific site conditions, leading thus to an improved WEC performance at lower costs.

The selection and analysis of different types of elastic materials and their influence on the structural behavior of a near shore floating point absorber WEC was analyzed. Although the FEA is widespread throughout several engineering domains, it is not so exploited in wave energy domain. Resorting to FEA, the influence of several characteristics such as the dimensions, different wave parameters, hydrodynamic forces and elastic material properties on the structural behavior of a given floating point absorber wave energy converter WEC can be revealed. In order to do this, after a brief characterization of the device, a 3D CAD numerical model was built and several FEA were performed through a commercial finite element code. Among other parameters, the magnitude of the resultant hydrodynamic forces acting upon each buoy is needed. This input data is supplied by the WEC time domain simulator (TDS) implemented in Matlab/Simulink software and based on the WEC dynamic model previously developed [5].

2. WEC working principle, model and simulator

This section briefly describes the working principle of a small scaled WEC equipped with a hydraulic power take-off (PTO) as well as the corresponding dynamic model. This model was used as a basis to develop a TDS, built using Matlab/Simulink software. The TDS was therefore used to obtain the force values used as inputs in the commercial finite element code.

The general WEC architecture is depicted in Figure 1 [5]. It belongs to the point absorber category, since its characteristic dimension has a negligible size when compared to the ocean wavelength [6]. Additionally, this device can also be classified as a near-shore WEC since it should be deployed at intermediate water depth, according with the relative depth criterion [7]. The components of the hydraulic PTO system should be enclosed in a sealed waterproof concrete mooring foundation placed at the seabed. For a detailed description of a hydraulic PTO see [8,9,10] .

Figure 1. 3D CAD model of the WEC.

DownLoad: Full-Size ImgPowerPoint

The main components are a spherical buoy with 200 mm radius, which floats with the sea waves, connected to a double effect hydraulic cylinder by supporting cables. A cardan joint connects the piston rod of the hydraulic cylinder to the concrete mooring. Although three modes of motion are possible (heave, roll and pitch) due to the cardan joint, for simplicity reasons the floating buoy is assumed to oscillate with the sea waves only in heave mode. When submitted to the sea waves the buoy floats and moves upwards under the influence of a wave crest and moves downwards under the effect of a wave trough. Other hydraulic PTO components are four non-returnable valves, an oil tank, a hydraulic accumulator and a hydraulic motor mechanically coupled to an electric generator. The force acting upon the buoy is transmitted through the hydraulic PTO. As a consequence the hydraulic cylinder pumps oil from the tank to the hydraulic accumulator and the fluid returns to the tank through the hydraulic motor. The alternating oil flow is rectified by the non-returnable valves and is smoothed by the hydraulic accumulator which could also be used as energy storage. The goal is to deliver a reasonable smooth electrical output. The continuous oil flow through the hydraulic motor will be converted into rotary motion and will drive an electric generator.

A more detailed description of the entire WEC used here can be found in [11].

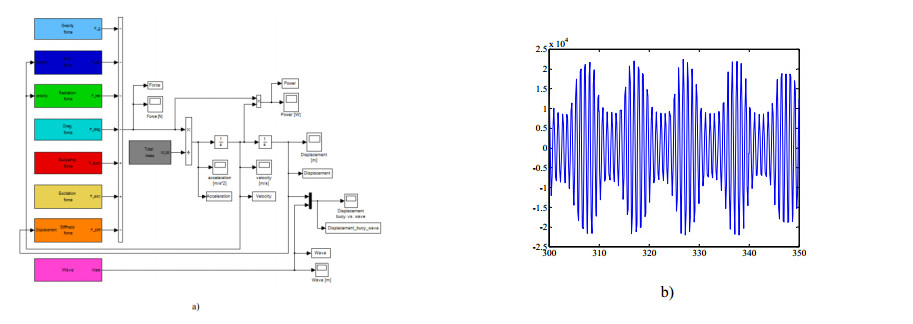
A previously developed WEC dynamic model [5] describes the buoy heave motion with respect to its acceleration. It is based on the second Newton's law and assumes that the buoy heave motion is excited by the sea waves. Due to the model nonlinearities, a simulator in time domain is preferable instead of a simulator in frequency domain. The corresponding WEC TDS was built using Matlab/Simulink software. It intends to simulate the dynamic behavior of the WEC buoy due to the action of sea waves. All equations from the mathematical model were grouped in a dynamic model block under individual subsystems. Another block simulates the sea wave equation. This is shown in Figure 2a) . More details about this subject can be found in [5]. Several inputs such as buoy and wave data, among others are needed to run the simulation. Figure 2b) exemplifies a 50 s detail of the evolution with time of the total hydrodynamic force acting on the spherical buoy. Different results can be obtained if input parameters are changed in the TDS.

Figure 2. a) TDS dynamic model block and b) Total force [N] acting on buoy vs. time [s].

DownLoad: Full-Size ImgPowerPoint

3. WEC finite element model

The WEC 3D CAD numerical model was initially built using SolidWorks^Ò software [11]. The Simulation tool of this software was used to perform FEA in order to simulate different sea conditions and to evaluate the influence of dimensions and material properties of the WEC components on its structural behavior.

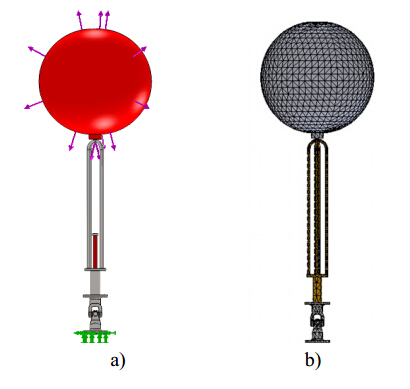
Figure 3a) shows the 3D CAD model that was developed, as well as the boundary and load conditions considered. It can be observed that the inferior half of the cardan joint, represented by green arrows, is rigidly fixed. Therefore, constraints of no displacements and rotations are applied to simulate the WEC mooring system. Based on data retrieved from Figure 2b) , it was assumed a maximum resultant hydrodynamic force of 50 x 10³ N (peak to peak amplitude) , which corresponds to a pressure of 8 × 10^-5 Nm^-2. This pressure, represented in Figure 3a) by the pink arrows, is applied to the surface elements. Its direction is a function of the position of the hydraulic cylinder piston rod and changes if the retracted or the advanced position is simulated.

Figure 3.a) 3D CAD model with boundary and applied load conditions, retracted position of hydraulic cylinder piston rod and b) Mesh geometry of finite element model.

DownLoad: Full-Size ImgPowerPoint

Regarding the finite element model, a relatively fine mesh of triangular tetrahedral solid elements was applied, as depicted in Figure 3b) . A meshing sensitivity study was previously conducted to guarantee that the resultant solid mesh has the required accuracy. In all FEA simulations carried out in this work the whole WEC numerical model was always analyzed, no axis symmetric solutions were used.

Figures 3a) and 3b) represent both the retracted position of the hydraulic cylinder piston rod, corresponding to the wave through. The wave crest situation corresponds to the opposite stroke position. From a structural point of view, the advanced position of the hydraulic cylinder piston rod leads to a higher magnitude of stresses when compared with the retracted position of the hydraulic cylinder piston rod [5]. Therefore the results presented in the following section only reflect the advanced position of the hydraulic cylinder piston rod.

Additionally, only the condition corresponding to the buoy partially submerged was considered in this analysis. When compared with the other two conditions — buoy at the surface and totally submerged buoy — the partially submerged buoy condition leads to a considerable increase on both maximum stress and displacements values. This corresponds to the critical position of the buoy [5]. Furthermore, the partially submerged buoy condition is the most expected position when the spherical buoy heaves due to the action of the sea waves.

In what concerns the buoy dimensions it was also demonstrated that, regardless of the buoy dimensions and the considered WEC components size, the increase of the dimensions leads, for the same level of applied load, to the increase on both stress and displacements values. This is an expected behavior since the area submitted to the pressure resulting from the resultant hydrodynamic forces acting on the buoy is greater [5]. However this is not a desirable situation and can be avoided with the resizing of the WEC.

4. Results and discussion

Several simulations were performed using SolidWorks^Ò software in order to evaluate the structural response of the WEC when submitted to specific loading conditions. The objective was to demonstrate that the developed WEC numerical model is able enough to be optimized in terms of dimensions and materials of the WEC components. Therefore, several materials or combinations between different materials were simulated to demonstrate which lead to the lowest level of stress concentration as well as displacements, when the spherical buoy is submitted to a resultant hydrodynamic force. The magnitude of this resultant hydrodynamic force depends of the specific sea wave parameters found on the deployment site.

Materials such as polyethylene, nylon 6/10 and silicone were considered for both buoy core and shell. Although most of the buoys commercially available have a polyurethane core and a high density polyethylene shell, in this work the same solid material was considered for core and shell. Materials such as AISI 316 stainless steel (SS) , aluminum alloy 6063 T6 (AA) and high strength steel (HSS) were selected for the supporting cables, hydraulic cylinder and cardan joint. Table 1 resumes their relevant elastic material properties: Young’s modulus, Poisson coefficient, yield strength and density.

Table 1. Selected elastic material properties for the WEC main components.

Material	Young’s modulus (Nmm-2)	Poisson coefficient	Yield strength (Nmm-2)	Density (kgm-3)
Polyethylene	1860 × 10-6	0.39	30	940
Nylon 6/10	8300	0.28	139	1400
Silicone	112000	0.28	120	2330
AISI 316 SS	193000	0.27	172	8000
AA 6063 T6	69000	0.33	215	2700
HSS	21000	0.28	620	7700

 | Show Table

DownLoad: CSV

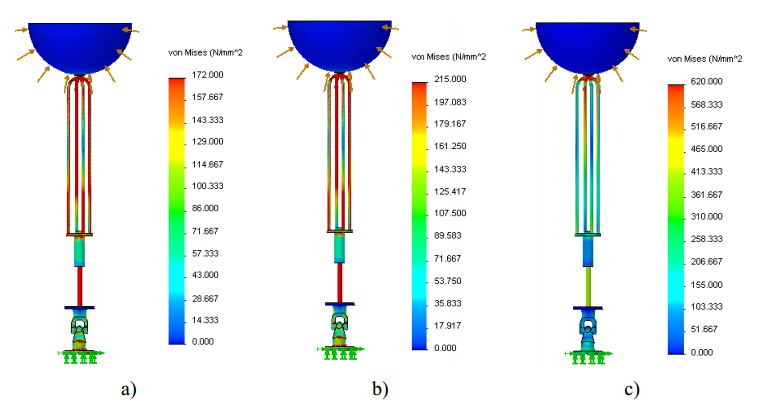
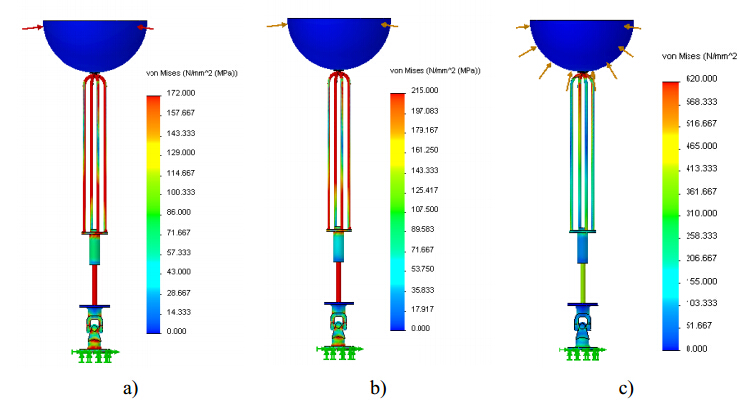
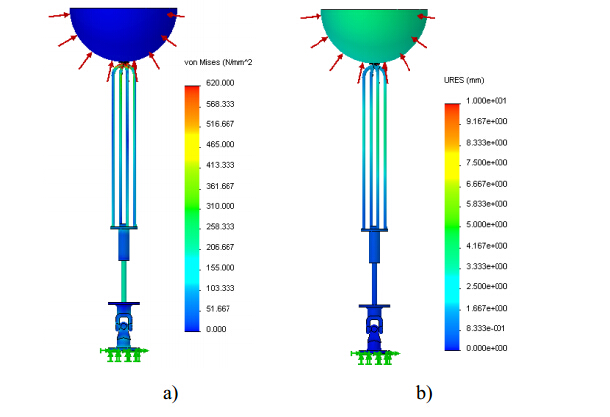
Figure 4 shows the Von Mises stress gradient for a polyethylene spherical buoy partially submerged with a radius of 200 mm, considering the advanced position of the hydraulic cylinder piston rod and assuming that the hydraulic cylinder and cardan joint are both made of SS, AA and HSS, respectively.

Figure 4. Von Mises Stress field for 200 mm radius polyethylene spherical buoy partially submerged assuming remaining WEC components made of: a) SS, b) AA and c) HSS.

DownLoad: Full-Size ImgPowerPoint

The analysis based on the finite element method provides not only an insight into the stress concentration magnitude and location as well as the maximum value of the displacement and their corresponding location, as shown in Figure 4.

For the polyethylene buoy, results reveal that maximum stress (given by the red color in Figure 4) exceeded the yield strength of the material. This means that plastic deformation is reached and , consequently, the collapse of the structure. It should be highlighted that plastic deformation only occurs at the supporting cables within a restricted location when the HSS material is chosen. Otherwise, for the other two materials considered (SS and AA) the maximum stress largely exceeds the yield strength of material at the hydraulic cylinder piston rod and at the cardan joint.

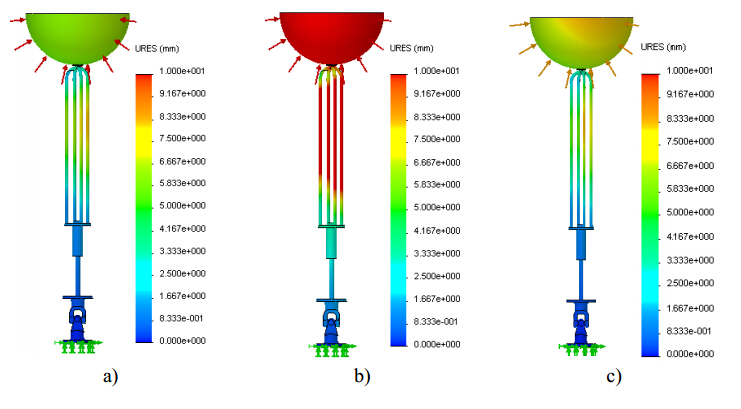
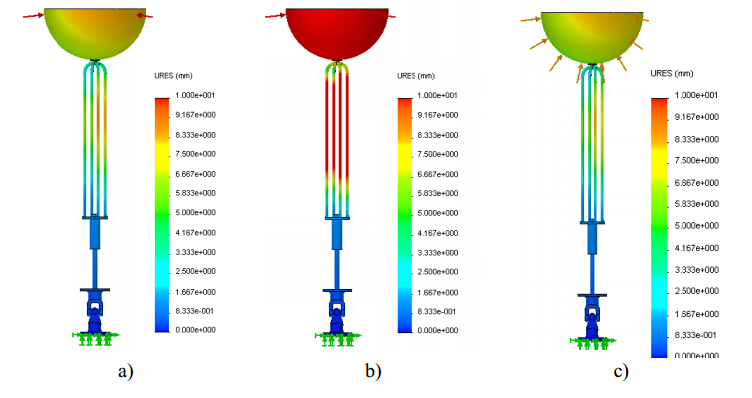
Concerning the displacement fields, it is clear that AA leads to maximum values than those obtained for SS or HSS, where similar values are observed, as depicted in Figure 5. It can be concluded that AA seems to be unsuitable due to the higher stresses and displacements attained for the buoy dimensions and the applied load level considered in this study. This behavior is not surprising if elastic material properties, in particular the Young’s modulus of AA, are compared with those of SS or HSS. The lower AA Young’s modulus corresponds to a low stiffness, which means that the deformation expected will be greater, according with the results presented, namely in Figure 5. However a low stiffness can represent an advantage for the supporting cables since an overdue life can be expected due to the load cycles they are submitted.

Figure 5. Displacement field for 200 mm radius polyethylene spherical buoy partially submerged assuming remaining WEC components made of: a) SS, b) AA and c) HSS.

DownLoad: Full-Size ImgPowerPoint

It should be highlighted that an extremely high hydrodynamic force value was considered during the simulation process, which justifies the results obtained.

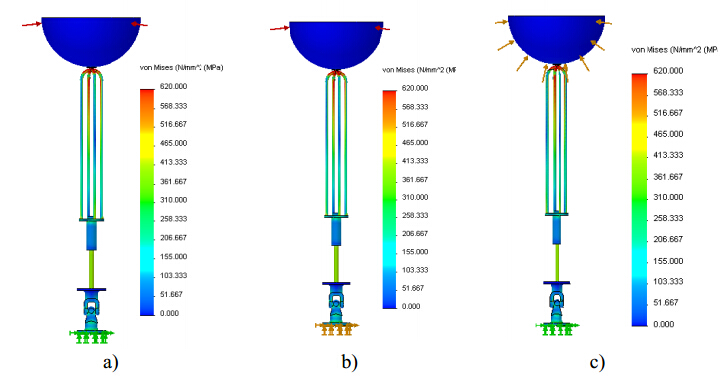
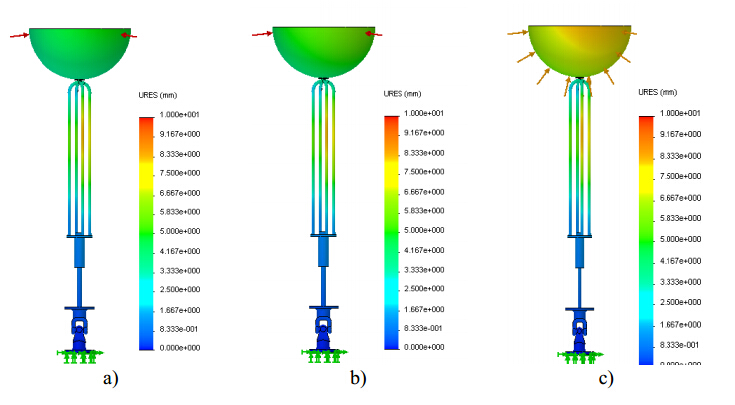
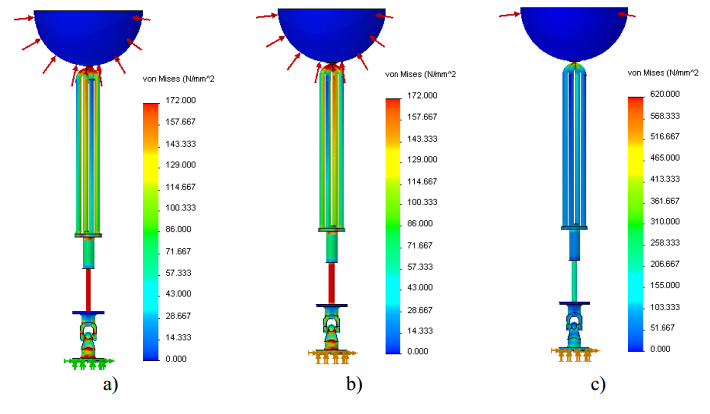
Another simulation was done assuming again a polyethylene spherical buoy and considering that both the hydraulic cylinder and cardan joint are made of HSS. Only the material of the supporting cables was changed: cables made of SS, AA and HSS are analyzed. Figures 6 and 7 show the corresponding Von Mises stress and displacement fields for the described simulation conditions.

Figure 6. Von Mises stress field for supporting cables made of: a) SS, b) AA and c) HSS assuming polyethylene spherical buoy and remaining WEC components made of HSS.

DownLoad: Full-Size ImgPowerPoint

Figure 7. Displacement field for supporting cables made of: a) SS, b) AA and c) HSS assuming polyethylene spherical buoy and remaining WEC components made of HSS.

DownLoad: Full-Size ImgPowerPoint

As expected once again, the areas of higher stress concentration are located in the hydraulic cylinder piston rod and in the supporting cables. Regarding maximum stress distribution, no significant differences were observed between the supporting cables made of SS or AA. However, for the AA cables is observed a slight increase of the stress values on the hydraulic cylinder. The poor mechanical behavior achieved for the AA material is confirmed by the higher displacements obtained, as shown in Figure 7. Thus, materials with a low Young’s modulus seem to be unsuitable.

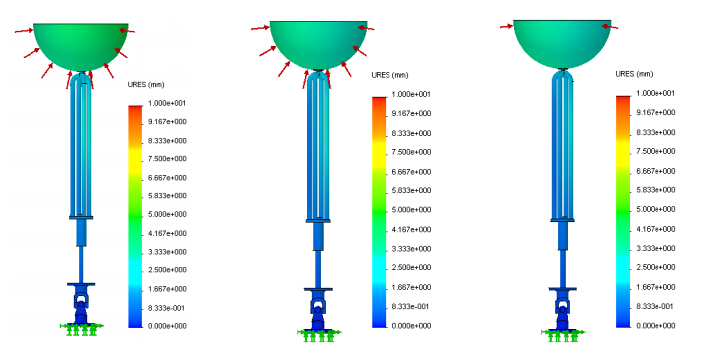
In order to analyze the influence of different buoy materials on the mechanical behavior, all the WEC main components are assumed to be made of HSS. Materials such as nylon and silicone were considered for the buoy. Simulation results revealed that, regardless of the material considered for the buoy, no relevant differences are observed in maximum stress, as illustrated in Figure 8. A significant increase in displacement values is observed at the buoy itself when polyethylene is considered, as demonstrated in Figure 9. Once again, among the several buoy materials, polyethylene is the one that presents the lowest Young’s modulus.

Figure 8. Von Mises Stress field assuming WEC main components made of HSS and spherical buoy made of: a) Silicone, b) Nylon and c) Polyethylene.

DownLoad: Full-Size ImgPowerPoint

Figure 9. Displacement field assuming WEC main components made of HSS and spherical buoy made of: a) Silicone, b) Nylon and c) Polyethylene.

DownLoad: Full-Size ImgPowerPoint

It is important to quantify in what manner the level of the applied load can induce the plastic deformation of the structure. Thus, half of the original resultant hydrodynamic force applied corresponding to a pressure of 4 × 10^-5 Nm^-2, was considered.

Figure 10 presents the influence of the resultant hydrodynamic force on the structural behavior of the WEC, considering a polyethylene spherical buoy and all the main components of the WEC made of HSS. Comparing Figure 10a) , Figure 4c) and Figure 6c) for stresses and Figure 10b) , Figure 5c) and Figure 7c) for displacement fields, it can be concluded that plastic deformation can be avoided with the decrease of the resultant hydrodynamic force, as it was demonstrated in Figure 10, where half of the original values for stresses and displacements are achieved. It is also important to analyze the influence of the size of the components, function of the material properties. The influence of the increased diameters of the supporting cables and hydraulic cylinder piston rod was calculated using the original pressure value (8 × 10^-5 Nm^-2) , a polyethylene spherical buoy and assuming that the WEC main components are made of SS and HSS. An increase of 5 mm on both supporting cables and hydraulic cylinder piston rod diameters was considered.

Figure 10. a) Von Mises Stress field and b) displacement field assuming polyethylene spherical buoy, WEC components made of HSS, 25 kN resultant hydrodynamic force.

DownLoad: Full-Size ImgPowerPoint

Figures 11 and 12 depict the simulation results for the conditions described in the last paragraph, in terms of maximum stress and displacement values, respectively.

Figure 11. Von Mises Stress field assuming polyethylene spherical buoy, 50 kN resultant hydrodynamic force and : a) WEC main components made of SS and 20 mm diameter supporting cables; b) WEC main components made of SS, 20 mm diameter supporting cables and 25 mm hydraulic cylinder piston rod diameter and c) WEC main components made of HSS, 20 mm diameter supporting cables and 25 mm hydraulic cylinder piston rod diameter.

DownLoad: Full-Size ImgPowerPoint

Figure 12. Displacement field assuming polyethylene spherical buoy50 kN resultant hydrodynamic force and : a) WEC main components made of SS and 20 mm diameter supporting cables; b) WEC main components made of SS, 20 mm diameter supporting cables and 25 mm hydraulic cylinder piston rod diameter and c) WEC main components made of HSS, 20 mm diameter supporting cables and 25 mm hydraulic cylinder piston rod diameter.

DownLoad: Full-Size ImgPowerPoint

As expected, from the comparison between Figure 4a) and Figure 11a) as well as between Figure 5a) and Figure 12a) , for SS material and for the increased diameter of the supporting cables, is obtained a significant reduction of stress and displacement values, but only at the supporting cables. For the hydraulic cylinder piston rod, even with the increase on its diameter, the maximum value for the Von Mises Stress is around 200 × 10⁶ Pa, as shown in Figure 11b) .

With the applied load level and since SS has a yield strength of 172 × 10⁶ Pa, plastic deformation is undoubtedly reached, although relatively low displacement values are attained, as depicted in Figure 12b) . Moreover, no relevant differences on displacement field values are obtained with the increase of the diameter of the hydraulic cylinder piston rod. However, the scenario is quite different if HSS is considered. This material leads to the lowest magnitude of stresses and displacements achieved, in particular when the supporting cables and hydraulic cylinder piston rod are resized. This is demonstrated by the comparison between Figure 5c) and Figure 11c) for stress values and Figure 6c) and Figure 12c) for displacement values. Plastic deformation is never attained because the yield strength of the material is not reached even if a higher level of load is applied.

5. Conclusion

The purpose of this work was to provide a WEC 3D CAD numerical model able enough to be customized, depending on different combinations of buoy position and resultant hydrodynamic forces acting upon the WEC floating buoy, function of specific sea wave parameters found on the deployment site. To demonstrate its robustness, several materials or combinations between different materials and sizing of WEC components, as well as loading magnitudes were simulated, using FEA, and their influence on the WEC structural performance was analyzed. For the conditions simulated, it was demonstrated that materials with low stiffness and low strength lead to a structural collapse, for the load level applied and sizes considered. For this kind of materials, even when the dimensions of the main WEC components are increased, plastic deformation tends to occur. Furthermore, the developed model proved that it can be very useful in order to easily test the structural behavior of the main WEC components when different buoy positions are assumed. Regarding the dimensions and materials of the WEC main components, it is possible to optimize the model, according with the applied load level, which is a function of the resultant hydrodynamic forces acting upon the buoy.

Conflict of Interest

All authors declare no conflicts of interest in this paper.