Abbreviations:
| AFM |
atomic force microscopy; |
| DCs |
dendritic cells; |
| EMT |
epithelial to mesenchymal transition; |
| F-actin |
filamentous actin; |
| FRAP |
fluorescence recovery after photobleaching; |
| GEFs |
guanine nucleotide exchange factors; |
| LIC2 |
(cytoplasmic dynein) light intermediate chain 2; |
| MAT |
mesenchymal to amoeboid transition; |
| MT1-MMP |
membrane-type 1 matrix metalloproteinase; |
| MTOC |
microtubule organizing center; |
| PIP3 |
phosphatidylinositol (3, 4, 5)-trisphosphate |
| PKA |
protein kinase A; |
| TAN |
transmembrane actin-associated nuclear (lines); |
| TGF-β |
transforming growth factor β |
1. Introduction
When investigating cell migration and the different migration types, termed the migration modes, the main question is: What do we understand about plasticity of cell migration? The migration of cells is important in many physiological processes such as developmental processes, tissue formation, maintenance and the tissue regeneration by repair mechanisms. Under pathological conditions such as cancer or acute/chronic inflammatory processes the migration of cells seems to be critical for the patients' outcome, therapy and prognosis.
The main determinators for the mode of cell migration are structural and molecular parameters of the surrounding tissue microenvironment. The mechanical properties of tissues are highly important for normal healthy tissue functions such as wound healing, tissue and organ development, proliferation and apoptosis as well as pathological conditions such as inflammation and cancer and its malignant progression, the formation of metastasis. The mechanical properties of tissues enable or restrict the movement of single cells through the extracellular matrix environment, which is on the one hand eminent for immune cells and fibroblasts in normal would healing processes and on the other hand dangerous when single cancer cells spread out of the primary tumor mass and migrate into targeted sites within even other tissues to for metastasis. All these migration modes (types) underly the same physical principles and biochemical regulations acquired by the distinct cell types.
Cellular mechanical properties and tissue mechanical properties can both be seen as active regulators of tumorigenesis and hence are both a target for treating cancer (Figure 1A). The tumor microenvironment is characterized by physical aberrancies and at the first view the non-structured organization of the tumor vascular system is a main characteristic feature (Figure 1B). These structural effects result in increased interstitial pressure leading to increased solid stress within the tissue. Moreover, these effects cause hypoxia within the tissue compartment, which additionally enhances interstitial pressure. Finally, these alterations of the tissue lead to a progressive stiffening of the primary solid tumor and an environment promoting the malignant tumor progression, which involves the cellular mechanical property aberrancies that in turn affect cellular motility. These physical barriers in tumors such as altered tissue mechanics are important obstacles that need to be overcome by single or a collection of cancer cells migrating out of the primary tumor to metastasize. In addition drug delivery systems using nanometer-sized objects such as nanoparticles of 20 to 50 nm in diameter need to consider these mechanical tissue alterations for their efficient uptake by the targeted tumor cells [1]. Moreover, the physical barriers of tissues reduce the infiltration by immune cells fighting the tumor and hence promote the aggressiveness of the disease [2]. Hence, the physical barriers build by the tumor microenvironment affect the hallmarks of cancer [3]. A new target for anticancer therapies seems to be the normalization of the physical abnormalities of solid tumors that facilitate the switch in the migration strategies of cancer cells from a highly motile back to a weak or impaired migration mode, which is currently seen as a paradigm shift in the field. These novel anticancer approaches are based on nanomaterials, which are activated on demand to evoke a spatio-temporal regulated response, and thus may cause a reduction of the resistance rates for current treatments of cancer [4]. The main targets are the reduction of the tumor stiffness and pressure in order to access the tumor tissue with the designed anti-tumoral drugs and subsequently reduce the resistance of the tumor to current treatments including the blocking of cancer cell migration and spreading into the surrounding local microenvironment. Besides the treatment of the tumor, the detection and precise mapping of tumors by using ultrasound elastography or magnetic resonance elastography reveal important tools for earlier diagnosis and personalized treatments [5,6,7].
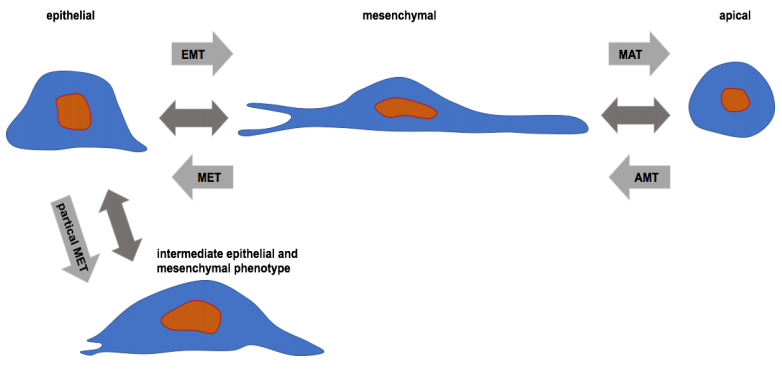
The tumor microenvironment is composed of extracellular matrix, a larger number of non-tumoral tissue cells such as stromal cells and their derived vesicles all affecting the plasticity of cancer cells and hence their individual migration mode. Thus, the extracellular matrix confinement can define the exact mode of cell migration such as the cells migrate individually as single cells by epithelial to mesenchymal transition (EMT) or the mesenchymal to amoeboid transition (MAT) or vice versa MET and AMT, respectively (Figure 2). Whether these migration mode switches occur fully has to be determined and is currently under strong debate [8,9,10]. However, it is clear that the migration mode switches are reversible and cells can actively switch between different modes by to their requirements [9,11]. Moreover, it has been questioned whether the EMT is necessary to from metastasis [10].
Besides single cell migration, collective migration of cells can occur [12,13]. In order to understand the switch between migration modes a multi parameter tuning model has been introduced [14]. Here, spatiotemporal analysis of cell migration in 3D microenvironment comes into play focussing on visualization and computation analysis tools [15]. At one extreme, the mesenchymal cell migration mode involves single cells undergoing a multistep cycle such as the formation of protrusions, cell adhesion to the underlying substrate, stabilization of the cell's leading edge, translocation of the entire cell body followed by the cell's nucleus, deadhesion and detachments of the cell's rear end [16,17,18,19].
2. Historically 2D Cell Migration Mode and Its Switch to Other Migration Modes in 3D Confinements
An advantage of primary human fibroblasts is their ability to adapt to the environmental conditions by exhibiting different migration modes depending on their environment such as rather rigid 2D cell culture dish surfaces and more preferably and physiological more adequate 3D cell and tissue culture systems. In earlier and more historic cell culture based motility assays the so-called crawling behavior of the fibroblasts and other vertebrate cells has been investigated excessively. These experiments built the basement of the concept of the classical elaborate cell motility cycle for 2D cell migration, in which the adhesion of cells is a critical determent for cellular migration speed and directionality of movement [17,20]. When transferring this model to the motility assays in a 3D matrix environment, it can not predict cellular movement as other parameters need to be taken into account such as the cells deforming their nuclei to move carefully through the confinements of a 3D matrix environment. Moreover, the 2D migration model provides no explanation why primary fibroblasts utilized different mechanisms or migration modes to move forward in a 3D environment. Several studies report a special role for the intracellular localization of myosin Ⅱ activity regulated by cell-matrix adhesions pushing the nucleus through the extracellular matrix confinement and hence determining the type of protrusions such as lamellipodial, lobopodial or filopodial extensions of the cell's membrane necessary to move through the 3D environment [21,22,23]. Subsequently mechanical cues of cells, tissues and the extracellular matrix environment play a central role in several diseases such as cancer metastasis and inflammatory processes during wound healing processes.
3. Experimental Cellar Migration Model Systems Turn from 2D to 3D Environments
As the 2D cultures dishes cannot fully describe cellular migration in a real 3D environment of tissues, it is necessary to investigate cellular motility in 3D matrix confinements composed of extracellular matrix proteins such as collagen polymerized to fibers with interconnections and a certain pore size (mesh size) or cross-sectional area in this network depending on the polymerization conditions, fiber crosslinking proteins or chemical drugs, types of collagen and the organism of origin from which the collagen is isolated. Cells manage to migrate through many different 3D environments during several phases of multicellular life stages such as immune cell migration at high speed through structurally variably tissues to search for intruders and fight against microbiological infections. In contrast, fibroblasts move more slowly compared to immune cells through the extracellular matrix of the dermis to the sites at which tissue damage occurred to rebuild the matrix scaffold and restore the physical and biological barrier function of the entire skin. In turn, the increased 3D migration of tumorigenic and hence metastatic cancer cells can be worse for the patients' outcome and survival rate. The knowledge of the underlying molecular and mechanical mechanisms controlling 3D fibroblast migration will shed more light on normal physiological processes such as wound healing and on non-physiological pathological processes such as tissue fibrosis, tumor progression and finally cancer metastasis. The understanding of the principles for normal, primary human cells migrating in 3D environments is essential for revealing and finally defining migration modes, which may also be used directly or altered by single migrating cancer cells. These cancer-specific mechanisms utilized for cellular movement in 3D environments seem to be a promising target for therapeutic approaches to impair or even abolish metastasis, whereas the migration of normal and untransformed cells such as fibroblasts or immune cells is minor or not pronouncedly affected.
Cell migration is regulated in general by the interaction of actin polymerization, deformation of the cell membrane, actomyosin contractility and cell-matrix adhesion [24,25]. It is kown that cancer cells can utilize different migration modes to migrate through tissue [3,26,27]. The mode of migration affects the sensitivity of cancer cells towards certain interventions impacting actin polymerization or actomyosin contractility [23,28]. Cell migration is regulated by graded environmental cues that induce asymmetries in the cell's cytoskeletal properties and subsequently cause directed cell behavior and increase the speed of migration [29,30,31]. The knowledge of parameters that regulate the speed of cell migration in 2D versus 3D environments seems to be essential to reveal insights in the function of key regulators in cell migration. Among these key regulators are adhesion and contractility on cellular level and matrix constraints such as matrix geometry and ligand availability for cell surface receptors [24,32]. It has turned out that the matrix geometry selects the migration mode of cancer cells and affects the response to pharmacological and molecular interventions [24]. Thus, a model of cell motility has been introduced, which includes actin-polymerization dependent protrusions, actomyosin dependent contractility, connections (focal adhesions) between the actin cytoskeleton and the cell membrane, cell-matrix adhesion and matrix geometry alterations [24].
The three main matrix geometries used for migration studies are (ⅰ) a planar surface, (ⅱ) a confined geometry by a continuous environment (similar to cell movement in a tube of between two tissue planes) or (ⅲ) a confined geometry by a discontinuous environment (similar to cells transversing a network scaffold of fibers). When cells migrate on a continuous surface, their cell speed is highest at intermediate cell-matrix adhesion strength [33]. Elevated cell adhesion requires an increased amount of myosin activity to provide optimal migration speeds. In turn, low levels of adhesion and high levels of contractility reduce the cell migration speed, as high contractility is connected to reduced F-actin polymerization-driven protrusion exertion leading subsequently to cell deadhesion. For non-confined surfaces, cells extruding F-actin protrusions displayed highest migration speeds. However, the forces exerted on the matrix are not uniformly distributed over the interface length between the cell and the matrix. Behind the protrusion, relatively high forces are extered, whereas at the cell's rear, forces with a large component perpendicular to the matrix are generated causing a deadhesion at the cell's rear end. At moderate levels of contractility, the extrusion of protrusions is most effective for cell migration, as large forces are exerted parallel to the direction of movement. At high levels of contractility, the blebbing-driven migration mode is performed under confinement. In contrast to unconfined migration, increasing myosin function facilitates enhanced cell migration, as the confinement impairs cell deadhesion caused by high cellular contractility. Hence, the level of confinement impacts the balance between contractility, bleb formation and the destructive effect of high contractility on the initiation of protrusions [24]. Moreover, distinct signaling processes such as the interaction between Rac1 and myosin Ⅱ regulate the migration of cells in unconfined and confined environments. In unconfined environments, the migration speed depends on increased Rac1 activity, which is provided by inhibiting the paxillin binding to the alpha 4 integrin subunit. However, in confined environments, the myosin Ⅱ-dependent contractility is necessary, which is increased by the inhibition of Rac1 through paxillin binding to the alpha 4 integrin subunit [34]. In addition, the myosin Ⅱ isoforms, MIIA and MIIB are required for specific environments: in confined migration MIIA is needed, whereas in unconfined environments MIIB is needed [34]. The alpha 4 beta 1 facilitated migration is a paradigm for cellular plasticity, in which a signaling process is adapted to physical constraints to promote maximal cell migration speed [34].
Besides the natural cellular plasticity, mechanical signals triggered by the physical confinement can additionally induce a cellular response, in which the cells alter their signaling pathways and subsequently their migration mode to optimize cell motility [35,36]. How do cells sense confined 3D microenvironments? Several key mechanisms have been revealed such as a mechanism involving the RhoA/myosin Ⅱ signaling pathway [34,35,37,38]. In contrast to unconfined 2D migration, confined migration does not depend on Rac1-facilitated protrusive activities, whereas the migration requires myosin Ⅱ-based contractility [34,36]. For fast cell migration, cells adapt the signaling pathways to reach a balanced state between Rac1 and RhoA/myosin Ⅱ. An example is the strong Rac1 function in cells migrating in an unconfined environment and another example is the strong myosin Ⅱ function in cells migrating in a confined environment [34]. How can cells regulate Rac1 and RhoA/myoin Ⅱ to precisely tune themselves to different degrees of confinement through which they migrate? In an integrin alpha 4 beta 1 expressing model cell system, the Rac1 activity is regulated by cyclic AMP (cAMP)-dependent protein kinase A (PKA) phosphorylating the cytoplasmic tail of the alpha 4 integrin subunit [39]. Based on these results, PKA is supposed to play a key role in tuning the complex regulatory network of RhoA/Rac1 due to mechanical cues. What is the underlying mechanosensing mechanism that enables cells to respond directly to a physical confinement? Mechanotransduction is a mechanism in which external forces can directly induce a conformational change or activate a mechanosensory protein (termed mechanosensor). Integrins perform an important role in mechanosensing [40]. Alpha 4 and alpha 5 integrin subunits can be used to sense confinement and subsequently downregulate PKA activity. No synergy effect between the alpha 4 integrin subunit with either PDE1 nor myosin Ⅱ has been observed indicating that confined environments favor a rather low adhesion state [36,41,42]. Thus, it is proposed that confinement sensing can utilize two different pathways such as Piezo1 and myosin Ⅱ pathways. These two pathways are regulated by a double negative feedback loop between PKA and myosin Ⅱ or a positive feedback loop between Piezo1/calcium and myosin Ⅱ, in which Piezo is activated by calcium via calmodulin-facilitated pathway [43] or G-protein-facilitated pathway [44].
In discontinuous environments, the blebbing-driven migration mode is preferentially used, which provides high speed migration compared to actomyosin contractility-driven migration. When the blebbing migration mode is used, the effect of adhesion is altered in a discontinuous environment. Since lower cell-matrix adhesion strength in the blebbing migration mode promotes a higher migration speed, the cells adapt to the environmental cues [24]. Lateral expansion during the blebbing of the cell exerts traction forces on the matrix and provides resistance of the cell body to deformation. When the gap-size between the cell and the matrix environment is increased, less interactions are observed and less tractions are generated. Finally, cell-matrix adhesion seems to be the restrictive factor for cell migration in confined discontinuous environments.
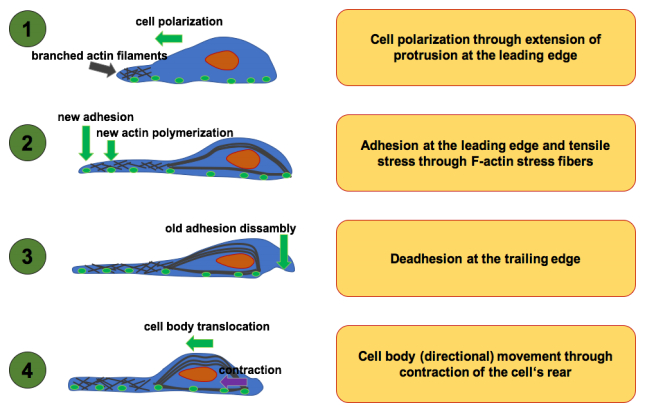
Under idealized conditions, the cellular motility needs to be investigated in a physiologically more relevant 3D tissue or 3D extracellular matrix. Approximately half century ago it has been found that primary fibroblasts have the capacity to crawl out of tissue explants and migrate on relatively rigid 2D plastic surfaces of tissue culture plates, which have been frequently used to investigate the migratory behavior for revealing the underlying molecular mechanisms [45,46]. Moreover, analyzing the migratory behavior by imaging of the dynamic cell movements and determining the biochemistry and genetics backgrounds promoted the establishment of the mechanistic basis for primary fibroblast movement as a conceptual cycle consisting of four consecutive steps, termed cell motility cycle [17,18] (Figure 3).
All the steps of the 2D cell motility cycle act together to generate the directional movement (Figure 3). The first initial step is the polarized signaling by the phosphatidylinositol (3, 4, 5)-trisphosphate (PIP3) [47], the small GTPases Rac1 [48] and Cdc42 [49] directing the actin nucleating proteins such as Arp 2/3 [50] for the development of polymerized branched actin filaments (F-actin) pushing against the cell's membrane to subsequently initiate the protrusion of a lamellipodium [51]. The second step involves integrin receptors in the protruding cell membrane, which interact by binding to extracellular matrix ligands on the 2D surface and subsequently the integrins arrange themselves into clusters to create small nascent focal adhesions [52]. In the third step the small Rho GTPase RhoA and the formin family of actin nucleators such as mDia1 and mDia2 facilitate the polymerization of actin stress fibers linking the nascent adhesions at the cell's leading front to the mature focal adhesions underneath the cell's body [53,54]. The actomyosin contractility of the cell's cytoskeleton subsequently pulls on the nascent focal adhesions facilitating their enlargement in size and increases their adhesion strength to the underlying substrate. Thereby the cell's contractile tension is enhanced between its front leading edge and its rear. All in all, the myosin Ⅱ activity at the cell's rear transmits signals to the local focal adhesions to disassemble and tear off the weakened focal adhesions from the 2D surface retracting the cell's trailing edge [55,56]. When the rear of the cell is fully deadhead, the entire cell body is able to migrate forward. At the same time, the polarized microtubules deliver the transport of lipids and proteins directly to the cell's leading edge together with polarity signals targeting Rac1 and Cdc42 activity to the cell's leading edge [57,58]. At the end, the retrograde cortical flow of F-actin sweeps the cell membrane lipids and proteins rearward facilitating the positioning of the nucleus back to the cell's rear [59].
The great advances in resolution and imaging technology together with the employment of in vitro 3D extracellular matrix migration and invasion assays have uncovered the underlying mechanism, a 2D cell motility cycle, which is not the unique and only possible mechanism used by primary fibroblasts and epithelial-originated cancer cells, but it is very common and frequently used [60]. However, cells can utilize diverse protrusive mechanisms for cell migration such as lamellipodia [16], lobopodia [61] or membrane blebs [62], in dependence on the individual physical nature such as the structure and mechanical properties of the 3D extracellular matrix environment (Figure 4). The plasticity in cellular migration has resulted in novel cellular mechanisms necessary for 3D motility, but is not required for cellular crawling on rigid 2D plastic surfaces of cell and tissue culture flasks or dishes.
4. Cellular Migration Modes in 3D Environments
Unequal to a 2D environment, a 3D extracellular matrix can additionally facilitate the movement of non-adhesive cells migrating at high speed through the extracellular matrix [63]. An example are cancer cells, which are stationary non-adherent and exert membrane blebs on a flat 2D surface, when compressed between two surfaces, these cancer cells get highly motile [41]. Similarly, this phenomenon is also seen when water droplets containing microtubules, kinesin, and ATP are being compressed [64], which enables the friction between the fluid containing the flowing microtubules and the confinement represented by the two surfaces to move the droplet forward. In addition, the compression-dependent cell migration in a low-adhesion microenvironment has been seen for diverse cell types including primary human fibroblasts [36,65]. Besides two glass plate compressing confinements, the fibrillar collagen-based structure of the 3D extracellular matrix represents a physical barrier for cellular migration and invasion. Matrix properties such as the distance between neighboring matrix fibers, their rigidity and their cross-linking points and entanglements with each other are evoking constraints on the cell motility, which are not present in liquid media. Whether a 3D matrix impairs or facilitates cellular motility and invasion, depends on the molecular mechanisms regulating an individual cell. To be more precise, the adhesion strength of the cell-matrix connection and the ability of the nucleus to deform represent two cellular properties that determine the 3D cell migration speed and the directionally of movement. Immune cells such as dendritic cells (DCs) possess very soft and hence deformable nuclei adhering only weakly to the extracellular matrix enabling them to move rapidly with approximately 240 μm/hour between the extracellular matrix fiber network [63]. Conversely, slower fibroblasts with a migration speed of approximately 40 μm/hour possess stiffer nuclei and interact strongly by cell matrix adhesion receptors such as integrins with the surrounding extracellular matrix when they move forward. Despite these important cell type-specific differences, the steric problem of the bulky and relatively stiff nucleus in confinements with pore sizes under the nuclear diameter becomes evident and a universal constraint on 3D cell migration when the cells move their bulky nucleus through the fibrillar 3D extracellular matrix network [63,66,67,68]. Whether a cell is able to migrate at low or high speed, depends on the capacity (power) of the non-muscle myosin Ⅱ to overcome the fundamental restrictions, the individual tissue barrier to migrate through diverse tissues.
5. Small Rho-GTPases and Their Role in Myosin Ⅱ-facilitated Cellular Migration in 3D Environments
Physiological developmental processes and the pathology of cancer can be understood by revealing the signaling pathways involved in the migration of cells as a prerequisite for normal tissue development and regeneration as well as the development and establishment of the metastatic phenotype in carcinoma cells. It is still not clear whether there exist distinct metastatic genes regulating the progression of tumors, which are activated during the progression itself or whether they are in earlier stages of oncogenesis activated oncogenes and inactivated tumor suppressor genes promoting the metastatic phenotype [69].
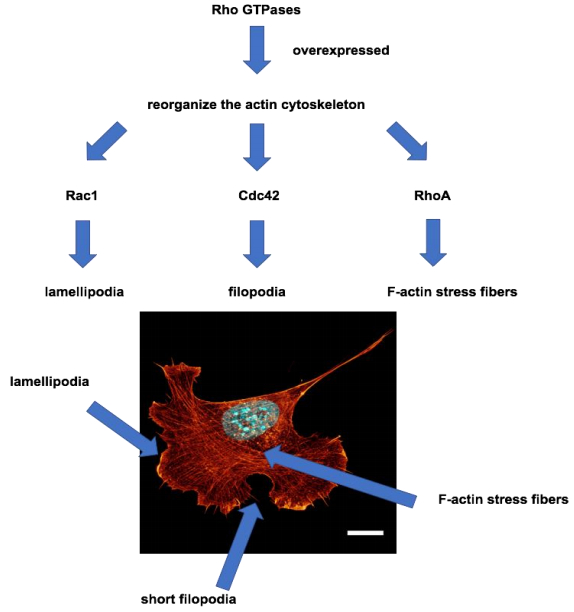
There exists a large family of Rho GTPases that includes at least twenty members in mammals [70,71]. When these Rho GTPases are overexpressed, they mostly cause major reorganizations of the actin cytoskeleton [72]. In more detail, Rac proteins such as Rac1 induce the formation of lamellipodia and membrane ruffles [73,74] (Figure 5). However, not all Rho GTPases induce filopodia or lamellipodia individually, e.g., Rho proteins such as the Rac-related RhoG or Cdc42 may induce lamellipodial structures by increasing Rac1 activity [72,74,75,76].
Moreover, it has been reported that the Rho family of GTPases is deeply involved in cellular motility and invasive phenotypes [77]. Additionally, the Rho family members Rac, Cdc42 and RhoA are key regulators of the cell's actin cytoskeleton [78]. During cellular migration Rac is required for lamellipodia formation at the cell's leading edge of migrating cells and hence, seems to be the driving factor for cellular migration [77]. During the migration of cells Rac is required for lamellipodia formation and the cell's leading factor for cellular migration [77]. Cdc42 is not essential for cellular movement, but it has been suggested to regulate cellular polarity and control the direction (persistence) of motion [79,80]. Rho controls the assembly of F-actin stress fibers and colocalizes in focal adhesions via activation of the downstream effector mDia as well as ROCK Ⅰ and ROCK Ⅱ kinases [81,82]. It is not yet clear whether Rho is required for cell migration [79], as it provides contractility, or whether it impairs motility by increasing the number of F-actin stress fibers [83].
The effectors of the Rho-family GTPases interact solely with the active GTP-bound form of the Rho GTPases and hence the measurement of the amount of active RhoGTPases using an affinity precipitation assay focussed on the binding region for specific effectors is essential in determining which migration mode can be utilized by the cells. The interaction regions between RhoGTPases and their effectors are the GTPase-binding domain of WASP for Cdc42, the Cdc42/Rac1-interactive binding domain (termed RIB) of Pak for Rac1 and the Rho binding domain (termed RBD) of Rhotekin for RhoA [84]. There exist dominant negative mutants of the RhoGTPases RhoA-N19, Rac1-N17 and Cdc42-N17, which bind preferable GDP, but not GTP, inhibiting the activation of the endogenous GTPases by sequestering upstream the guanine nucleotide exchange factors (GEFs). Conversly, there exist constitute active forms of the RhoGTPases such as RhoA-V14, Rac1-V12, Cdc42-V12, RhoA-L63, Rac1-L61 and Cdc42-L61, which are defective in their intrinsic GTPase activity and hence may exist permanently in the active GTP-bound state in the cells. In contrast to movement on 2D substrates, the complexity of a 3D microenvironment such as collagen gels challenge cells to limit the number of their protrusions omitting simultaneously engagement of multiple migration paths within the 3D microenvironment. Therefore, polarity proteins such as the small Rho GTPase Cdc42 are needed to overcome this constraint. These polarity proteins are required for the 3D cellular movement, whereas on 2D substrates they are not essential for movement, an exception is Cdc42, that is solely required for the directionality of cellular movement [63].
6. RhoA Regulates a Contractile Force Dependent Migration Mode
As cell migration in 3D matrices use other mechanisms, these mechanisms do not have to be consistent with the migration on 2D substrates. The actomyosin-dependent contractility is induced by the small GTPase RhoA and is required for 3D migration, whereas it is not essential for 2D migration [85,86]. However, the actomyosin contractility in 2D cell biological model systems such as the production of fibrillar fibronectin [87], inducing the retraction of the cell's leading edge [88] or the enhancement of cell-matrix adhesions [89]. Moreover, myosin Ⅱ has been shown to exert traction forces to the 3D extracellular matrix, which leads to a reorientation and subsequently an alignment of actin stress fibers that restrict the direction of cellular protrusion exertion for promoting the directional movement of cells [90,91]. Besides the actomyosin dependent contractility, the myosin ⅡB isoform is able to push the nucleus through narrow confinements of the tissue environment such as narrow pores [92].
7. Nuclear Limits of Cell Migration
As mentioned before, confinements in a 3D environment such as narrow pores are probing the cell's capacity to deform and squeeze through the confinement in the absence of the ability of the cells to degrade the surrounding extracellular matrix confinement. What restricts the cell in its deformability?
The largest organelle within the cell is the nucleus and hence the size of the nucleus is the critical determent for migration through confined space. As the nucleus is the largest single organelle within a cell, the its capability to pass through the narrow confinements in dense extracellular matrix may be the rate-limiting step in 3D cellular motility of many different cell types [63,66,67,68,93]. There exist at least two mechanisms applied by cells through myosin Ⅱ generated forces towards the nucleus to deform him. The differences in the mechanisms rely on the diverse adhesion strength of the cell types.
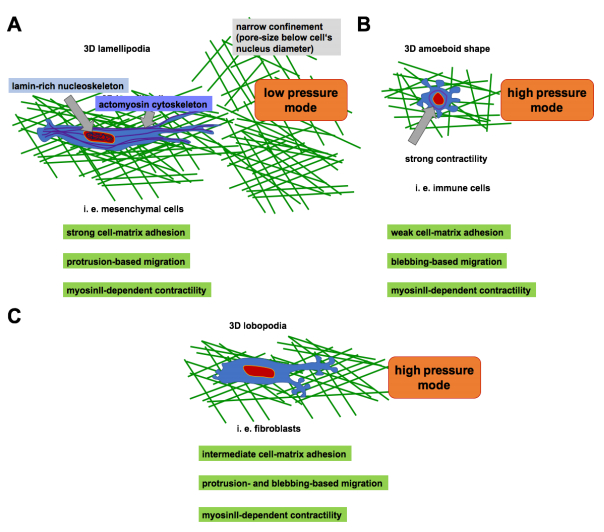
Firstly, in fibroblasts adhering strongly to their microenvironment, can extensively mechanical coupling be found between the lamin-rich nucleoskeleton and the actomyosin cytoskeleton encompassing the force transmission between the cell's nucleus and the extracellular matrix environment [94]. The mechanical linkage and the actomyosin contractility both work together to pull the entire nucleus by large deformation through narrow confinements such as pores of meshes within the extracellular matrix network [66,68,95] (Figure 6A).
Secondly, in weakly adherent cells such as immune cells and certain types of cancer cells, the myosin Ⅱ-dependent contractility is generated behind the cell's nucleus to squeeze the entire nucleus forward through narrow restrictions [63,96,97] (Figure 6B). However, the decision to follow one of these two strategies to transport the large and bulky nucleus forward during migration through a 3D extracellular matrix with narrow structural confinements relies on the mechanical properties of the nucleus, i.e. the degree of nuclear softness and deformability. In the relatively short-lived immune cells is the myosin Ⅱ activity located behind the nucleus and it is reported that a softer nucleus is able to squeeze more easily through narrow restrictions such as small pores of the surrounding microenvironment. For cells with longer life time such as primary fibroblasts this migration strategy is not suitable as cells with a softer nucleus are more vulnerable to DNA damage and subsequently apoptosis-based cell death [67,98].
8. Rac1 Regulates a Lamellipodial Migration Mode, whereas Cdc42 Regulates a Filopodial Migration Mode
As mentioned before, the small GTPase Rac1 is a member of the conserved Rho family of small GTPases [71]. Rac1 promotes migration of singles cells on 2D surfaces by exertion of a lamellipodium [99]. Moreover, collective cell migration such as the movement of epithelial cells within a monolayer, in which a cell gap has been introduced requires the activation of Rac1, which is facilitated by merlin [100]. Merlin interacts with tight junctions and competes with the Rho GTPase-activating protein Rich1, which is then released from the tight junction complex and subsequently leads to inactivation of Rac1 [101]. However, the underlying molecular mechanism regulating coordinated cell migration is still not yet fully understood. A fundamental principle of collective cell movement is that cells moving as a large cluster of cells coordinately polarize the activation of Rac1, Cdc42 and RhoA over a large range of cells [102,103,104]. Thereby, the contractility of the cells and cytoskeletal structural rearrangements need to be timely tuned [105,106,107], which depends critically on the regulation of cell-cell tight, adherence and gap junctions [108]. As the molecular regulator for cell polarization and hence migration is not yet known, biophysical-driven approaches revealed that the coordination of cell-cell junctions and migration seems to be driven by local anisotropic pulling stresses within a cell-cell monolayer [100,109,110,111], which can range over a long distance of hunderts or tausends of cells and result in a long-distance ordering of cells [111].
Cdc42 is a member of the conserved Rho family of small GTPases, which are activated upon binding of GTP and inactive when bound to GDP [112]. Thus, proteins can activate or inactivate Cdc42 such as the GEFs, which catalyze the exchange of GTP to GDP [113]. Cdc42 is capable of regulating actin polymerization, dynamics of microtubules and gene expression [112,114]. By controlling many diverse processes, Cdc42 regulates membrane trafficking, cellular motility, cell-cycle, intercellular adhesion and cellular polarity [112,115,116]. The coordination of the regulation of actin and the microtubule cytoskeleton is facilitated by Cdc42's binding and hence activation of the Wiskott-Aldrich syndrome protein. In particular, Cdc42 regulates actin polymerization through the activation of WASP and N-WASP [117,118], whereas the microtubule assembly is regulated by the Cdc42 interacting protein CIP4, which then induces the deformation of the membrane [119]. Finally, Cdc42 facilitates the interaction between actin and microtubules [120,121].
9. Cellular Plasticity in 3D Fibroblast and Cancer Cell Migration
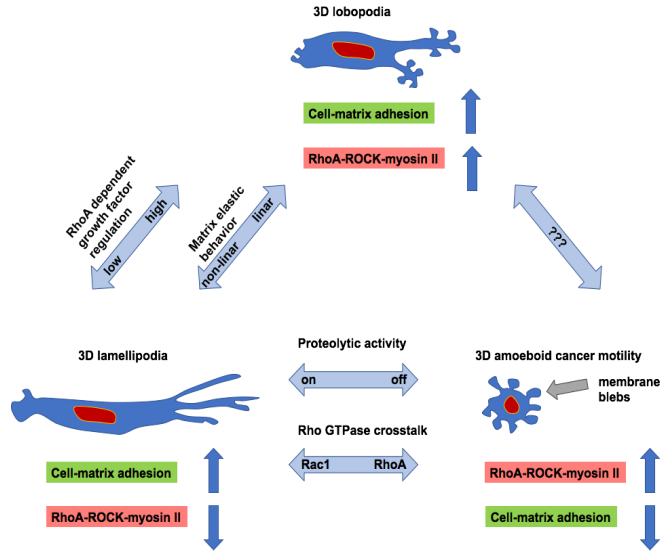
Cellular membrane extensions such as protrusions are defined by their morphology. An example is the protist Amoeba proteus, which employs the actomyosin-based contractility to facilitate cytoplasmic streaming increasing the intracellular pressure. Then blunt, cylindrical protrusions are formed, the so-called lobopodia [122]. In turn, another protist such as Vanella miroides utilizes a low-pressure based mechanism by crawling over a 2D surface involving also actin polymerization, but forms wide, flat and fan-shaped protrusions termed lamellipodia [123]. Similarly, primary human fibroblasts migrate by switching between a low-pressure migration mode based on lamellipodia formation and a high-pressure migration mode based on lobopodia formation and hence fibroblasts are therefore in the need of myosin Ⅱ (Figure 6C). The choice of switching between a low or a high pressure mode of migration depends on the structure and subsequently on the mechanical properties of the 3D matrix [61,124] (Figure 6). As these two modes of migration are protrusion-based, these modes are chosen in the mesenchymal state of cells such as cancer cells migrating through the tissue confinements [7,124]. In addition, there exists a third type of migration mode termed amoeboid migration of fibroblasts (Figure 6C). Moreover, a fourth alternative mechanism of cellular migration through confinements has been proposed that is based on the regulation of the cell's volume through the permeation of water [125]. In the following the major similarities and the largest differences between the three modes of cellular migration of fibroblasts are described. In protists, the involvement of pressure is suitable to select a distinct type of migration mode, however, the generation of pressure is exactly the same as in human cells, whereas the relationship between the pressure generation and the specific formation of a certain protrusion type is highly conserved.
10. Lobopodia-driven Migration Mode or Nuclear Piston Migration Mode
Fibroblasts manage to migrate in linearly elastic 3D extracellular matrices by using blunt cylindrical lobopodial structures (Figure 6B), rather than the classical lamellipodia, which have been observed frequently in cell migration on 2D flat and smooth surfaces. The identification of lobopodia were first performed by revealing lamellipodia lacking the lamellipodial markers such as cortactin [61]. The signaling pathways such as Rac1, Cdc42 and PIP3 are seen to be polarized at the cell's leading edge of lamellipodial cells, whereas in lobopodial cells they are non-polarized [61]. Moreover, lobopodial protrusions utilize intracellular pressure to broaden the cell's leading edge, whereas lamellipodia employ classically actin polymerization driven and Brownian ratchet based mechanisms [124]. However, in cross-linked and hence linearly elastic matrices (material does not undergo strain stiffening), the high cell-matrix adhesion localizes myosin Ⅱ directly in front of the cell's nucleus to pull it forward similarly to a piston to pressurize the lobopodial protrusions [124]. In addition, myosin Ⅱ connects via the linker protein nesprin 3 to the intermediate filament vimentin connecting itself to the lamin-based nucleoskeleton. Another support of this nuclear pulling mechanism comes from the finding that there exists a strong interaction of active myosin Ⅱ and vimentin [126] revealing that vimentin filaments link the cell's entire nucleoskeleton to the extracellular matrix environment [127,128]. Moreover, vimentin filaments' property are to withstand breakage by tensile forces seems to be a suitable mechanism by which vimentin filaments, which is not a property of single F-actin filaments or microtubules [129], and vimentin filaments' position in front of the bulky and rigid nucleus make them suitable for pulling the nucleus through the confinements such as the pores of 3D extracelllular matrix environment. As actomyosin bundles are much stronger than single F-actin filaments [130], the actomyosin contractility is required for the positioning of the nucleus towards the cell's rear before extrusion of the membrane for the formation of the cell's leading-edge building the onset of cellular migration on a 2D substrate [59,131]. The movement of the nucleus involves both the actomyosin contractility and vimentin independently whether the cells migrate in 2D and 3D contexts, it hence can be hypothesized that rearward positioning of the nucleus on 2D substrates and the forward pulling of the nucleus in 3D extracellular matrix environments are based on the same molecular regulatory mechanisms finally needed for the movement of fibroblasts through a 3D extracellular matrix. Finally, the knowledge why myosin Ⅱ can move the nucleus rearward on 2D substrates and pull it forward in 3D may help to reveal the underlying migration mechanism [93]. It has been reported that non-similarly to primary fibroblasts, the nuclear piston is not actively found in fibrosarcoma cells [132]. However, the nuclear piston mechanism can be reactivated in fibrosarcoma cells such as HT1080 and SW684 by inhibition of the proteolytic activity using proteas inhibitors such as GM6001. The inhibition of protease such as matrix metalloproteinases can reintroduce and hence switch the migration mechanism to the nuclear piston migration mode in polarized HT1080 and SW684 cells by generating compartmentalized pressure. The achievement of compartmentalized pressure to the nucleoskeleton-cytoskeleton connecting protein nesprin 3, the actomyosin-driven contractility and the integrin-facilitated cell adhesion is all of which consistent with lobopodia fibroblast migration mode. Moreover, the activation of the nuclear piston migration mode decreases the 3D movement speed of HT1080 cells. Finally, inhibition of the proteolytic activity of cells during polarized cancer cell 3D migration is sufficient to rescue the nuclear piston migration mode associated with compartmentalized pressure, which a characteristic marker of nonmalignant and non tumorigenic cells.
11. 3D Lamellipodia-driven Migration Mode
Cells can adapt a lamellipodia-driven migration mode when migrating through strain-stiffening and non-linearly elastic 3D matrix environments. In addition, cells acquire a lamellipodia-driven migration mode upon a reduction of their actomyosin contractility and hence switch to a rather low pressure based lamellipodial migration mode. The mechanism is not yet precisely revealed. However, the 3D lamellipodia-facilitated migration mode is similar to the classical 2D environment based migration involving the full 2D cell motility cycle including the series of discrete steps, which function tightly during the cell migration such as crawling [18,60]. In more detail, the cell motility cycle starts with stationary cells being activated by mitogenic triggering signals such as growth factors or cytokines and hence cells get motile by extrusion of the leading and trailing edges along their newly polarized cell axis. Moreover, the internal polarization of cytoskeletal structures such as microtubules and the secretory apparatus of the cells confines lateral protrusions and promotes the delivery of vesicles to the leading edge carrying different loads such as recycled cell-matrix adhesion molecules such as integrins [133,134,135,136]. At the cell's leading edge, the two Rho family GTPases Rac1 and Cdc42 regulate the activation of the actin nucleator Arp2/3 turning on the polymerization of actin and subsequently the formation of thin, wide lamellipodial protrusions [49,137,138]. In addition, the lipid second messenger phosphatidylinositol (3, 4, 5)-trisphosphate (PtdIns(3, 4, 5)P3) is enriched in the lamellipodia during the persistent migration [139]. Moreover, the lamellipodia undergo cycles of protrusion exertion and retraction, however, they can be stabilized by the assembly of nascent adhesions at the cell's leading edge [140]. The Arp2/3-dependent actin polymerization to a branched network at the cell's leading edge and the myosin Ⅱ activity lead both to actomyosin-dependent contraction and a retrograde flow of filamentous actin (F-actin) towards the cell body [141]. The basic major components of the cell's motility cycle such as the individual steps of protrusion, attachment, contraction and detachment are precisely defined and are conserved among the diverse migration modes through 3D extracellular matrix confinements, however, the underlying molecular mechanisms are likely different [14,142]. The distinct cell movement mechanisms are determined in alterations of the overall cellular morphology and shape, the adhesion receptor type and the adhesion strength of these cell–matrix adhesions, the speed of actin retrograde flow behind the cell's leading edge or the overall directional persistence of cellular migration and the migration speed through the cellular microenvironment [85,143,144,145,146]. Finally, the structure of the cell's leading edge is the best characteristic feature to determine the current mode of cell migration.
Within these cells, the lamellipodial markers such as cortactin and F-actin are present at high levels at the cell's leading edge together with small Rho GTPases such as Rac1, and Cdc42 and by the PIP3 signal transduction pathway [61]. Moreover, these cells exhibit a relatively low intracellular pressure being uniformly distributed throughout the entire cell. This isotropic pressure distribution impairs the activity of the nuclear piston migration mechanism within lamellipodial cells, although these cells still demand the cell-matrix adhesion to migrate efficiently. However, it is hypothesized that even less force is necessary to move the nucleus forward, when the cells are migrating through non-linearly elastic 3D matrices and solely entangled fiber matrices compared to crosslinked and therefore linearly elastic materials such as such as the dermis of the skin or fibroblast-derived extracellular matrix.
12. Amoeboid-shape Migration Mode (Retrograde Flow-based, Blebbing-based, or Friction-based) and Osmosis-driven Migration Mode
Primary fibroblasts under compression between two surfaces, which are chemically treated to avoid and thus impair integrin-facilitated cell-matrix adhesion, switch to a third type of 3D migration, which has been defined as "fibroblast amoeboid" or simply termed A1 motility [36]. As expected, the cytoplasmic pressure together with the weakening of the focal adhesions between the cell's membrane and its underlying actin cortex facilitated the exertion of dynamic membrane blebs protruding the cell membrane, which does not dependent on the formation of lamellipodia [147]. The amoeboid metazoan-based cell migration mode is a property that can be acquired by single cells such as neutrophilic granulocytes and DCs alternating their cell shape during the movement rapidly compared to adherent fibroblasts migrating through tissue confinements or extracellular matrices [145]. In addition, these amoeboid migrating cancer cells are adopting a round cell morphology exerting continuously membrane blebs at their leading edge [26,27].
There exist two adhesion-independent amoeboid forms of cellular motility which have been characterized in more detail due to their degree of the retrograde actomyosin flow: amoeboid fibroblasts (termed A1) protrude at their leading edge with a pattern of the actomyosin flow differing from the cells applying the A2 mode of amoeboid migration. In contrast to the A1 amoeboid migration mode, the in the A2 migration mode migrating cells such as blebbing mode migrating Walker 256 carcinosarcoma cells and leukocytes utilized a large stable bleb extruded at their leading edge and moreover they need myosin Ⅱ activity to sustain in the blebbing migration mode when restricted between two low-adhesion flat surfaces [3,36,148]. Conversely to lobopodia driven cell migration, during the non-adhesive amoeboid fibroblast migration, myosin Ⅱ can flow fast backward along the cell's leading-edge protrusions and seems to be uniformly distributed referentially over the cell cortex. In addition, this cortex-based myosin Ⅱ is necessary for the rapid migration of the cells [36]. In line with this, the integrin-independent movement of A1 amoeboid fibroblasts is proposed to be also driven by the retrograde flow of the actin cortical cytoskeleton.
As the speed of the primary fibroblast migration through confined fibrillar 3D extracellular matrices has been shown to be pronouncedly diminished upon the inhibition of integrins [61], it has been suggested that this amoeboid fibroblast myosin Ⅱ-independent A1 amoeboid mechanism is not ample to ensure proper and efficient migration in higher structurally confined fibrillar 3D extracellular matrices such as collagen fiber matrices and fibroblast-derived matrices. As the low-adhesion based migration mode of fibroblasts in 3D confinements seems to be provided by relatively low traction forces [41], however, the involved intracellular pressure and the type of protrusion formed need to be figured out precisely. However, the critical determinant such as the pressure or the decreased strength of the cortical attachment is still not yet known for the various types of blebs during the amoeboid migration mode of cancer cells. In addition, it needs to be figured out how the fibroblast A1 and A2 amoeboid migration modes can be transferred to the classical amoeboid migration mode utilized by cancer cells exhibiting a round cell shape. In extremely confined spaces such as two flat plates, a friction-driven movement can be performed, which is also integrin-independent similar are retrograde flow and blebbing driven movements [149].
An alternative strategy for confined cell migration in 3D microenvironments is the osmotic engine based migration that utilizes the semi-permeable cell membrane for movement. However, it is still not yet clear whether cells use this specific migration type in 3D extracellular matrix fiber networks in which cellular contractility and cell-matrix adhesion are necessary to move forward [90,124,150]. In more detail, the cell transports water from the cell's leading edge to the cell's rear end to propel the entire cell body forward [125]. Thereby, the cell uses a low adhesion based migration mode in contrast to the cell's crawling migration mode employed in amoeboid migration of cancer cells [28].
13. Switching between Migration Modes
Common knowledge is that cells can utilize different migration modes to move forward in different confined 3D environments. However, it is still elusive which type of migration mode is preferred by a distinct genotype or specific cell type of cancer cells. The regulation of the migration mode switch is partially known such as the epithelial-mesenchymal transition, which can be facilitated for example by the transforming-factor beta (TGF-beta) or lysophosphatidic acid (LPA) upregulating the expression of class Ⅲ deacetylase SIRT1 [151,152], and the mesenchymal-amoeboid transition of migration modes is known to be facilitated for example by interstitial flow [153] or inhibition of matrix metalloproteinase MT1-MMP [26,27]. Moreover, the microenvironment confinements can affect the transitions of the cells, which then began to migrate or impair migration. However, it is not yet precisely known under which specific biomimetic environmental conditions these switches can be induced to certain types of cells. In addition to these migration modes, there exists also other migration modes such as the protrusive migration based on lamellipodial or filopodial cellular extruding structures. Moreover, there exists another migration mode that is based on the formation of blebs on the cell's surface, which does not contain actin in this lumen. The lobopodial migration mode describes a another mode of migration, which utilizes the exertion of short filopodial structures with blebs on their membrane, representing an intermediate migration mode state [124].
14. Cytoskeletal Confined Migration Mode
The actin cortex or the cortical cytoskeleton is a critical parameter for providing cellular deformability and hence cellular movement in 3D confined extracellular matrices. The deformation of the cell by applying an external force leads to very fast response to stress, which is approximately occurring after 1 s. This fast response may also include membrane defects or represent simply only just a pure membrane effect, which is not yet fully clear. Conversely to the actin cortex, the cytosolic (internal) cytoskeleton is less fast deformed and responds much slower to stress at a larger timescale of approximately 30 s [154]. These two deformation response modes can be probed by adding an actin polymerization inhibitor Cytochalasin D to the cells prior to cell stretching. In order to probe whether the cortical or cytosolic network is involved in cellular mechanical properties such as stiffness, the actin polymerization inhibitor Cytochalasin D can be used as it evokes less pronounced effects on the cortical network than on the cytosolic network [154]. For the cortical network, internal tension generated by actin filaments and stress fibers might not be the primary mechanism, which is responsible for stiffness of the cortical structure, as the actin cross linking proteins such as the Arp2/3 complex, fascia or alpha-actinin may account to the cortical stiffness [155].
15. Nuclear Confined Migration Mode
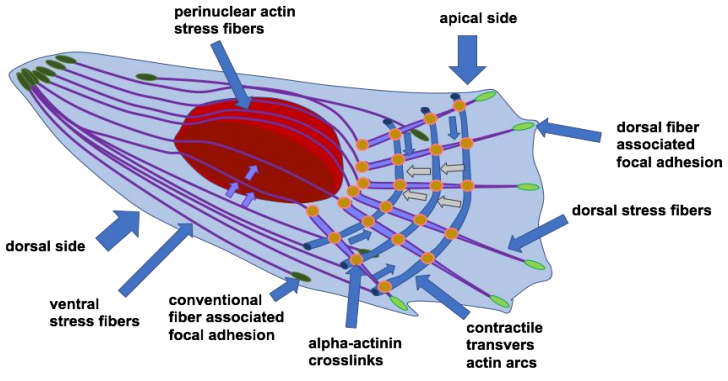
How are nuclear size and cellular rigidity related to cell migration? The movement of the nucleus and overall translocation is a rate-limiting step on planar substrates and also in 3D confinements such as extracellular matrices with relative narrow pore-sizes. In migrating and invading cells, the actin cytoskeleton builds diverse types of stress fibers that display specific structural, morphological and mechanical characteristics due to different contractility [156,157,158,159]. The contractile ventral or basal actin stress fibers are located along the base of the cell at its dorsal side, are commonly arranged in parallel fibers in the direction of cellular movement and are terminating in focal adhesions at each of their two ends. The ventral stress fibers are highly cross-linked due to their high content of the actin-cross-linking proteins alpha-actinin and myosin, which link the neighboring actin stress fibers and subsequently facilitate their contractility. The ventral actin stress fibers fulfill diverse cellular functions such as the focal adhesion maturation, the structuring and formation of the nonprotrusive rear of the cell during its spreading on a substrate [160], the establishment of a polarity between the cell's leading edge in the front and the trailing edge in its rear [56,161,162], the generation and transmission of traction forces, the retraction of the cell's trailing edge [53,163] and subsequently, the determination of the cell's shape on soft substrates [164]. Moreover, the contractile F-actin stress fibers contribute to the mechanical remodeling of the surrounding extracellular matrix [165,166,167].
Besides the ventral stress fibers being restructured to the cell's basal side, a network of dorsal fibers, transverse actin arcs and peri nuclear actin cap fibers emerge from the ventral (lower side of the cells) to the dorsal side (upper side of the cell) of the entire cell (Figure 7). The dorsal fibers start to polymerize from focal adhesions at the cell's leading edge and elongate to the dorsal side of cell's lamella. In more detail, the formation of dorsal fibers involves the actin bundling protein alpha-actinin, as the specific knock-down by RNAi of alpha-actinin alters the dorsal fibers, whereas the ventral F-actin stress fibers and transverse arcs are not affected [168,169,170]. Additionally, the dorsal fibers are devoid of myosin Ⅱ [169,172] and either free of distinct tropomyosin isoforms or they exhibit a distinct pattern of localization [173,174].
Transverse arcs are positioned perpendicular to dorsal fibers, exhibit a bended curved shape and are contractile actomyosin bundles, which are parallel aligned to the cell's leading edge and flow centripetally from the cell's leading edge to the cell's center of mass, where they start to depolymerize [169,171,172,175]. Moreover, transverse arcs consist of myosin ⅡB as a predominant isoform, which increases when these arcs are located in the lamella in close proximity to the nucleus [158,169]. Alpha-actinin is present in these transverse arcs and periodically structures these network into a sarcomeric-like arrangement [172]. Actin arcs are suggested to be crosslinked with the dorsal fibers [173] and hence both arcs and dorsal fibers are moving with the same speed to the cell's center of mass [172]. Moreover, these transverse arcs exert pulling forces to the connecting dorsal fibers facilitating the maturation of focal adhesions and the restructuring of the extracellular matrix [169]. In turn, the linkage of the dorsal fibers to focal adhesions evokes a resisting force to the transvers actin arcs and subsequently in human U2OS bone sarcoma cells, the force causes a flatteving of the lamella, when the cells migrate [172].
Transverse actin arcs and dorsal fibers are usually located at the cell's front, whereas the contractile perinuclear actin cap fibers grow from focal adhesions at the cell's leading edge, span over the entire nucleus and finally, terminate in focal adhesions at the cell's rear leading to the formation of a dome-like structure caging the entire nucleus [176].
16. Arp2/3 Crosslinking of Actin Filaments and Its Effect on Cell Migration Modes
Arp2/3 plays an important role in the regulation of the nucleation of actin filaments in vivo, as it fulfills a key step in the process of actin polymerization. The Arp2/3 is evolutionarily conserved and facilitates the nucleation of branched actin networks. Moreover, the Arp2/3 complex is a stable and clearly a stoichiometric assembly of seven polypeptides among which are Arp2 (Actr2), Arp3 (Actr3) and Arpc1-5. In more detail, the cell migration has two sides: on the one side movement is needed for normal physiological processes such as the migration of immune cells, i. e. dendritic cells (DCs) migrate upon inflammatory responses and on the other side movement needs to be impaired when cancer cells adapt a malignant phenotype and migrate invasively into organs and tissues. The cell migration in vivo faces complex microenvironments and often requires a distinct mechanical phenotype of these invasive cancer cells such as they become highly deformable, which is a cellular mechanical property that is restricted by the cell's nuclear deformability such as the compressibility. In line with this, it has been reported that the compressibility of the nucleus is important for cellular movement in a 3D extracellular matrix confinement [177]. In more detail, the cellular nucleus of adherent and unstimulated HT1080 fibrosarcoma cells has been identified to adapt a stiffness range between 0.2 and 2.5 kPa [177] using atomic force microcopy with a bead-carrying cantilever type. The treatment of the HT1080 cells with a chromatin-decondensating drug trichostatin A (TSA) caused a nuclear softening up to 50%. By pushing the bead-carrying rather stiff cantilever on the cell's nucleus, the nucleus can be deformed up to 20% of its original height. The deformation of the nucleus could even be increased by the pretreatment of the cells with TSA by reducing the original height of the nucleus to remaining 5% indicating that the chromatin organization is essential for providing the nuclear stiffness [177].
In more detail, for a specific type of immune cells such as dendritic cells it has been shown that these cells can acquire a mechanism to migrate through micrometric constrictions. The mechanism relies on a rapid Arp2/3 driven actin nucleation surrounding the nucleus and disrupting the cell's nuclear lamina, which represents the major obstacle for the deformability of the nucleus [177]. However, the cells' requirement of Arp2/3 for transmigration through narrow subnuclear-sized constrictions is decreased when the nuclear stiffness is itself reduced by the suppression of lamin A/C expression. Thereby, a new role for Arp2/3 in three-dimensional cell migration has been revealed, as Arp2/3 enables fast moving cells such as leukocytes (including DCs) to pass at high speed and increased efficiency through narrow gaps of the tissue environment, which represents a process of high importance for immunce cell function such as cleaning up inflammatory regions or tissue ruptures [178]. Similarly, it has been seen in various other cell lines [66,67,68,92] that the nucleus restricts the confined 3D extracellular matrix migration. In more detail, the DCs overcome the physical limitation of the nuclear deformability by generating a dense and dynamic perinuclear actin fiber network, which is nucleated by the Arp2/3 complex acting downstream of Wave2. The Arp2/3-nucleated perinuclear actin fiber network enables the nuclear deformation and finally the passage of the cells through narrow constrictions such as pores, which might be solely possible when the intranuclear lamina shell is disputed. In summary, DCs employ a specific mechanism, based on the Wave2/Arp2/3 actin nucleation around the nucleus allowing them to deform their own nucleus without the presence of a stiff lamin A/C composed intranuclear shell. Subsequently, this mechanism enables DCs to combine a high migration speed with an increased deformability and hence long-term survival of the migrating cells.
17. Coupling of Cytoskeletal and Nuclear Compartments during Confined Migration: What Is the Role of the Nucleus?
Eukaryotic cells have been observed to move through 3D confinements in alternating periods of advancing migration phases represented by high speed and persistent movement and periods of hesitating migration characterized by phases of low speed and non-persistent movement [176,179]. However, it is still under investigation what molecular mechanisms regulate the dynamic switches between the advancing or hesitating migration phases. The switch between the two migration phases is based on changes in cellular morphology, speed and persistence of movement and possibly also in the mechanical state of the cells or its organelles (representing cellular compartments).
The movement of a nucleus in the interphase in a random cellular migration mode can switch immediately between two distinct modes: one mode is a rotation mode and the other mode is a translocation mode [179]. The rotation mode of the nucleus is associated with a rounded phenotype of the nucleus and subsequently of the entire cellular morphology, whereas the translation mode of the nucleus is characterized by an elongated nucleus followed an elongation of the entire cell. Hence, the nuclear rotation and nuclear translocation facilitate the fast and slow motion of the entire cell body by the dynamic assembly and disassembly of the contractile force driven perinuclear actin cap structure being connected to the nuclear lamina and the nuclear envelope via linking complex.
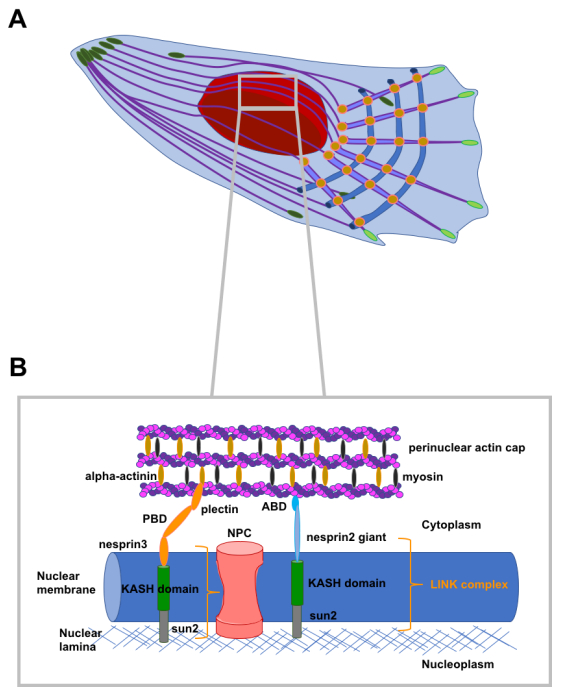
Perinuclear actin fibers or the so-called perinculear actin cap differ from conventional stress fibers, insofar as the conventional stress fibers are confined by the ventral side of the cell and are anchored within focal adhesions located in the cell's leading edge. The conventional stress fibers span over the nucleus and terminate in focal adhesions at the cell's rear building up a dome-like structure, which is aligned to the axis of migration (Figure 7). In contrast, the central part of the perinuclear actin fibers is connected to the nucleus via the linkage complex and hence couples mechanically the focal adhesions of the leading edge to the nucleus [180]. Hence, mechanical signals from the microenvironment can be transferred via cell-matrix adhesion receptors, which are themselves coupled to focal adhesions and hence to the actomosin cytoskeleton, to the cell's nucleus resulting in a mechanotransduction complex regulating the nuclear orientation [181]. In more detail, the nuclear reorientation is regulated by an interconnected network consisting of dorsal actin fibers, transverse actin arcs, and perinuclear actin cap fibers that anchor the focal adhesions of the cell's leading edge to the nucleus. The dorsal actin fibers and transverse actin arcs at the cell's leading front can mechanistically attract the pre-existing ventral actin stress fibers and translocate them to the nucleus' apical side which in turn evokes a rotation of the nucleus to a more favored position for cell movement, i.e. the nucleus represents a smaller steric obstacle in the direction of movement. The linkage between the cytoplasm and the nucleus seem to be critical for the repositing of the nucleus needed for the movement of the cell through a confined environment.
How is the linkage provided? The linkage complex is termed LINC (Linker of the nucleoskeleton with the cytoskeleton) and mechanically combines the nuclear lamina with the cell's cytoskeleton. The position of the nucleus inside the cell is an indicator of the migration-driven cellular polarity and determines the axis of migration (e.g., the direction of movement) [181,182]. The mechanical coupling between the nucleus and the actin cytoskeleton is required for the precise regulation of the nuclear movement caused by external stimuli such as mechanical tissue properties [180,183,184]. Active nuclear movement and its repositioning to the cell's rear during the polarization of cells such as fibroblasts depend on actin fibers, the so-called TAN (transmembrane actin-associated nuclear lines). TAN-lines are located and restricted in an alignment directly above the nucleus and interact with the LINC complex [59,185]. They are composed of nesprin-2G and SUN2, which are coupled to actin fibers. TAN-lines are anchored by A-type lamins enabling the actomyosin forces of the cytoskeleton to be transferred directly across the nuclear envelope into the nucleus [185].
How are these LINC complexes precisely arranged in the cells? The SUN proteins span the inner nuclear membrane and their N-termini interact with the KASH domain of the Nesprin family members, which span the outer nuclear membrane at the cytoplasmic side. At their cytoplasmic side, Nesprin proteins interact with microtubules, intermediate filaments and actin stress fibers linking the nuclear lamina to the cell's cytoplasmic cytoskeleton [180]. The attachment of the perinuclear actin fibers to the LINC complex is still elusive and not well understood. There exists a direct connection between the actin-binding domain of the N-terminus of both nesprin-1 and nesprin-2. In addition, there seems to be an indirect connection through actin-interaction proteins such as fascin that interacts with the short non-overlapping segments of nesprin-1 and nesprin-2 [181].
Another possible way for the indirect interaction is plectin that interacts as a cytolinker by connecting nesprin-3 with the intermediate filaments [186]. In line with this, adherent cells can pull on integrins such as alpha 5 beta 1 by fibronectin-coated beads, cyclic stretching of cells by mechanically applied stress on their adhesion substrate or by the adhesion of cells to restricted adhesive substrates, which are produced by micropatterning and induce a movement (translocation) and a rotation of the nucleus based on actomyosin contractility [32,95,164,187,188,190]. In contrast, the perinuclear actomyosin fibers may stall and hence anchor the nucleus in a non-rotationary state [179]. These results are in line with the findings that the inhibition of actomyosin contractility by specifically inhibiting myosin facilitates the rotation of the nucleus [191,192]. Highly ordered actomyosin fibers arranged as filament bundles span over the apical surface of interphase nuclei and bind to the nuclear envelop and the nuclear lamina via the LINC complexes in numerous adherent cells such as cancer cells of epithelial origin or fibroblasts [176,179]. The structure over the nucleus forms a perinuclear actin cap terminating in focal adhesions that represent the key components of the outside in signaling, which converts extracellular stimuli into intracellular signals [193,194]. As cellular movement enables the continuous mechanosensation of the nearby environment, which is important for driving physiological and pathological processes such as embryonic development and tissue differentiation or cancer metastasis [195,196,197,198], the actin cap has been proposed to regulate cellular migration by connecting the mechanical microenvironment, the cytoskeletal mechanical properties and the nucleoskeletal mechanical properties.
As the complex LINC mechanically combines the nuclear lamina with the cell's cytoskeleton, it enables cytoskeletal-driven forces to move the nucleus or induce a rotation of the nucleus (Figure 8A). However, the role of the LINC complex and perinuclear actin fibers in cancer cell invasion and metastasis is not yet known. Moreover, the signaling mechanisms involved in the assembly of perinuclear actin fibers and their control over the nuclear movement are still elusive. It has been suggested that cytoskeletal forces act on the nucleus by either inducing a displacement of the nucleus or simply compressing it. Cytoskeletal-driven forces are generated by actin fibers building contractile actin fiber bundles together with myosin Ⅱ. These bundles connect the focal adhesions with the LINC complex and subsequently the nucleus (Figure 8B). The main questions are still not answered: What role do these perinuclear actin fibers play in establishing a front-back polarity in the cell? How are these perinuclear actin fibers assembled? How does the assembly of these perinuclear actin fibers assist nuclear movement and finally cellular motility?
It is known that dorsal stress fibers, transvers actin arcs and perinucelar actin fibers assembly an interconnected network face the nucleus and span over the entire cell. In more detail, the central part of the perinuclear actin fibers (or synonymously termed perinuclear actin cap) is attached on its lower nucleus-facing side to the nucleus and its interior through the LINC complex. Perinuclear fibers, actin arcs, and dorsal actin fibers are transiently connected in spots containing a high amount of the actin crosslinking protein alpha-actinin-1, which leads to the suggestion that the three different actin fibers are crosslinked via alpha-actinin-1. The LINC complex is composed of two main proteins termed Sun and Nesprin, which span over the nuclear envelope and interact with the nuclear lamina at the nucleoplasmic side. Subsequently, Sun and Nesprin connect the nucleus mechanically with the actin cytoskeleton [199] (Figure 8). Thus, the peri nuclear actin cap fibers and the LINC complex define the nuclear shape [176,200,201] and moreover facilitate the mechanosensing and mechanotransduction processes during cell migration through a confined environment [194,202,203]. In contrast to the perinuclear fibers, the ventral stress fibers are not attached to the nucleus or connected to the LINC complex [194,200,202,204]. In cancer disease, it has been found that distinct cancer cells such as human bone osteosarcoma epithelial cells U2OS assemble a peri nuclear actin cap structure [202,203].
How plays the nuclear position and shape a role in cell migration? The persistent cell migration mode and the nuclear translocation are facilitated by the presence of an actin cap. The persistence of the cell migration is abolished when the actin cap is disrupted, which causes then the depolymerization of the entire cell (termed hesitating migration mode). When the cell is caught in a hesitating migration mode, the cell can start immediately to polymerize again for the persistent movement phase upon nuclear rotation, which is facilitated by the cytoplasmic dynein light intermediate chain 2.
The described migration behavior is not restricted to eukaryotic cells, however, it seems to be a non-unique phenomenon which can even be acquired by cells without any organelles such as prokaryotic cells. Similarly to eukaryotic cells, motile prokaryotic cells (i.e. bacteria) such as Escherichia coli can switch between high speed and persistent movement facilitated by its flagella, which rotate mainly counterclockwise, and tumbling movement facilitated by the flagella transiently rotating clockwise [205]. During the random migration such as the protrusion-driven mesenchymal migration mode without any chemotactic gradients, the cells alter continuously their entire morphology and switch dynamically from an elongated to a round morphology [206]. The maintenance of the overall cell polarity by a precisely regulated position of the cell's nucleus is essential for the mesenchymal cell migration mode, which is subdivided into sequential steps of polarization, protrusion formation, translocation of the nucleus and the entire cell, and retraction of the cell's rear that are repeated in endless cycles, when the cell migrates in a 2D environment, until the cell stops moving upon the decision to undergo mitosis in order to divide into two daughter cells [207,208,209,210]. In the past, movements of the nucleus have revealed to be facilitated by microtubule-driven processes and hence have been the focus of numerous studies [191,211,212,213,214]. As described before, it has been reported that the actin stress fibers are associated with nuclear dynamics in migrating cells [59] via specific connection points between the nuclear envelope and the actin cytoskeleton [199]. Upon a symmetry-breaking event involving F-actin in polarized cells, cells rapidly react on external stimuli. In addition, microtubules manage to stabilize the asymmetry within the cell by causing actin filament dynamical changes [215]. As mentioned before, the TAN lines connect to the cytoplasmic actin filaments and the LINC complex, which consist of the proteins nesprin-2 giant (nesprin-2G) and SUN2 and restore the reward movement of the nucleus within migrating fibroblasts during their 2D migration into a cell-free gap from sub confluent cell-borders, termed wound healing assay [185].
In summary, the dynamic formation and dissolution of the actin cap are supposed to control tightly the timing and the occurrence of fast persistent migration phases during the entire fibroblast migration. Moreover, the translocation and rotation of interphase nuclei are driven by the dynamically attachment and detachment of the actin cap to the nuclear envelope through the linkage via KASH-SUN interactions in the perinuclear region located in between the inner and outer membranes of the nucleus [132].
18. Actin Cap Migration Model Works in Nuclear Confined Migration Modes
The actin cap migration model describes the highly coupled migration between a cell and its nucleus facilitated by the actin cap structure at the apical side of the nucleus. The non-stimulated and hence random movement of cells is based on the perpetual-like dynamics of alterations of two movement phases: (i) a fast directional movement phase involving the translocation of the nucleus by elongated actin cap structures, which confine the nucleus and hinder the rotation of the nucleus and (ii) a low speed movement phase (termed hesitation migration phase) breaking up the phases of fast directional movement, which is guided by LIC2-facilitated rotation of the round and thus actin cap free nucleus that is not able to translocate. During the migration and invasion of cells, the perinuclear actin cap enables the cell to stabilize a certain degree of polarization for a long duration of half to two hours before the cell is able to repolarize for reorientation of these perinuclear actin fibers in a new direction for the following next persistent and slow movement phase. These results indicate that a cell performing persistent random-walk migration utilizes a two-gear system, which is tightly coupled to the perinuclear actin cap. In addition, the focal adhesions, which specifically terminate actin cap fibers, help cells to perform a long-lived persistent movement of the entire cell body. In contrast to conventional focal adhesions terminating conventional stress fibers, which are found located over the entire basal cell surface, the perinuclear actin cap connected focal adhesions are specifically located at distinct positions within the cell such as the two narrow sectors in the direction of the aligned actin cap fibers, which are located in one direction at the cell's leading lamellipodial edge and in the other direction at the cell's trailing edge [194]. The actin cap dependent focal adhesions are significantly larger and more time stable compared to conventional focal adhesions [194]. Moreover, these focal adhesions seem to stabilize and hence define the principal location and structure of the lamellipodium, which ensure the long-lasting polarization of the cell and its persistent motion in the direction determined by the perinuclear actin cap fibers.
Cellular protrusions such as lamellipodia, filopodia or lobopodia are dynamically and consistently generated at the entire membrane periphery of adherent mesenchymal cells enabling actin assembly and actomyosin contractility mechanisms. The current knowledge is that these protrusions are thought to be short-lived due to the fact that they are not covered and hence not stabilized in their structure by an actin cap, which is connected to focal adhesions. These rather short-lived structures are extrudes from the side, when the actin cap structure is not present in the cells. As these cellular protrusions cannot be fixed in their position by actin cap connected focal adhesions, the cell exhibits a more symmetric shape. In more detail, the non-polarized and short-lived cellular protrusions evoke randomly short-lived cellular movements, whereas the entire cell body stays basically at the same position. The reason for stalled cell movement is that the cells cannot adapt a polarized lamellipodium in order to migrate directionally. The LIC2 facilitated nuclear rotation is likely to take place, as the steroidal hindrance by the actin cap structure is not present. Moreover, the rotating nucleus then inhibits the stable polarization of the cell.
The actin cap can spontaneously vanish due to the finite lifetime of SUN-KASH, which couples the perinuclear actin cap to the nuclear envelope [216]. The differential fluorescent labeling of actin and focal adhesion proteins in living cells showed that the actin cap is able to slide over the apical surface of the entire nucleus and subsequently, hits the bottom of the cell's body turning the actin cap fibers directly into basal F-actin stress fibers [194]. Subsequently, this observation can explain why cells such as mouse embryonic fibroblasts, human lung and foreskin fibroblasts, endothelial cells and human ovarian epithelial cells are described to possess an actin cap structure, do not display an actin cap all the time [176,194,217]. For supporting the model of nuclear driven migration being regulated by a peri nuclear actin cap structure and dynein motors, it has been observed that LIC2 does not facilitate the cell speed, if an actin cap structure is present [218]. However, the actin cap promotes the fast persistent migration mode of protrusive cells. Finally, nuclear and cellular movements are coupled through the actin cap, which can be seen as a gear box switching between the rotation and translocation mode of the cell's nucleus, termed two-gear model of random cell migration. From the physical-point-of view both the actin cap fibers and the nucleus try to avoid strain exposed from the surrounding microenvironment [204].
The perinuclear actin cap structure has been seen to be completely absent from undifferentiated embryonic stem cells, but it can be induced in pluripotent stem cells, where the perinuclear actin cap emerges upon cell differentiation start [217]. As mentioned before, the perinuclear actin cap is not present in all stages of cellular arrangements or cell-types such as epithelial sheets, whereas it becomes rapidly assembled upon the epithelial-to-mesenchymal (EMT) transition [219]. However, the perinuclear actin cap has been found to be either partly disrupted or impaired in cells from laminopathic mice and patients [220] exhibiting disease grounded in mutations in the LMNA gene, which encodes the intermediate filament lain A/C present in the nucleoplasm. In addition, the actin caps are disrupted in several human cancer cells such as the HeLa cervical cancer line [221], U2OS osteosarcoma, MDA-MB-231 breast carcinoma, and MCF-7 breast adenocarcinoma [194]. Thus, these cancer cells exhibit an altered nuclear shape, which is a common feature for many cancer cells, however, the biological significance of the missing perinuclear actin cap structure in these cancer cells needs to be revealed. However, the lack of the perinuclear actin cap cannot explain why cancer cells manage to migrate through the 3D environmental confinements in a directed manner in order to metastasize, which is also known for the cancer cells mentioned above not showing a perinuclear actin cap structure.
The perinuclear actin cap has been found to be highly dynamic. Moreover, live cell imaging video microscopy of cells transfected by a GFP-lifeact plasmid displays high contractility and actin dynamics of the cell's cytoskeleton, as the perinuclear actin cap fibers are undergoing alternating phases of extension and retraction [194], which then lead to an exact positioning of the nucleus and an actively deformation of the entire nucleus [176]. By using fluorescence recovery after photobleaching (FRAP) analysis the perinuclear actin cap fibers possess pronouncedly faster turnover dynamics compared to basal stress fibers [194]. In somatic cells, the perinuclear actin cap is not appearing several hours after cell division [176] demonstrating that the actin cap network is a permanent structure for the fixation of cells in a rather stalled stage and hence nearly immobile state.
19. What Role Has the Nuclear Shape Analysis in Prediting Cellular Migration Capacities?
The migration of cells is associated the formation of the perinuclear actin cap (Figure 8), which in turn regulates the nuclear shape via the LINC complex connection [176]. Hence a question is raised whether the nucleus also displayed two distinct shapes indicating the distinct migratory modes during the migration of the cell. This hypothesis has been tested by analyzing the shape and the movement of the nucleus due to the movement of the entire cell. Indeed, the analysis of the nuclear shape showed that the time-dependent alterations in the projected area of the nucleus and its shape are highly correlated, whereas the movement of the nucleus and the nuclear speed were inversely correlated with the nuclear size and shape [218]. Moreover, it has been revealed that the nucleus alternatively switches between two shapes, as the nucleus exhibits a small elongated shape and a larger more rounded shape. These two different shapes of the nucleus are associated with fast (small and elongated nucleus) and slow movement of the cell (large and rounded nucleus). Indeed, these findings represent a confirmation of the proposed relationship between the nuclear size, the nuclear shape and the nuclear speed. Moreover, the nuclear volume was nearly constant during these two different modes and the movements of the cell [218].
The nucleus may move in fundamentally different ways depending on its nuclear morphology. As alterations in nuclear morphology occurred at a certain critical nuclear size, the fast movement phase of the nucleus can be distinguished from the slow movement phase of the cell, which has been observed in EGFP-histone H2B transfected cells, when monitoring both the nuclear morphology and entire nuclear displacements simultaneously. Indeed, elongated nuclei were smaller and hence can move more rapidly than the rounded nuclei, which are relatively large. Moreover, the rounded nucleus rotated intermittently and the overall longitudinal displacements of the nuclear centroid were smaller compared to the displacements of elongated nuclei as seen in the distribution of instantaneous displacements. In turn, elongated nuclei translocate fast and show thereby no or little rotation.
Finally, it is questioned whether the nuclear translocation and rotation purely rely partly on cell to cell variations or whether a nucleus can dynamically switch between these two movement modes in an individual cell. Indeed, the entire nucleus can switch the migratory mode dynamically between a translocation-driven migration mode or a rotation-driven migration mode corresponding to a more random cell migration pattern [36,61,218]. Moreover, there is a sigmoidal relationship, which has been revealed by the tracking of single individual nuclei between the size and the shape of the nucleus being inversely correlated with the movement speed of the entire nucleus [218]. Additionally, the nuclear size increased with the increased magnitude of the angular alterations between consecutive centroid displacements of the entire nucleus of the cell. In summary, these findings show definitely that the nucleus of a migrating cell is capable of dynamically modifying the nuclear morphology and nuclear movement following a tight relationship between morphology and movement. The nucleus adapts a small and elongated shape when it moves rapidly and the rotation is drastically reduced, and conversely the nucleus adapts to a large and rounded shape when its motion nearly impaired movement (slow movement is still posssible) and the rotation is pronouncedly increased.
20. Synchronized Regulation of the Nuclear Movement by an Actin Cap and the Cellular Polarization through Microtubules
Mesenchymal cells such as invasive and metastatic cancer cells as well as fibroblasts adapt usually polarized conical cell shapes. The two most extreme cell parts differ in their morphology and function: the producing leading edge adapts an outward-curved (convex) cell shape and the inward-curved (concave) non-producing regions are located at the cell sides and the extended cell rear [17]. The polarized cell shape results from the spatial separation of the different actin structures such as the perinuclear actin cap fibers and the peripheral actin fibers. A branched actin polymerization pushes the cellular membrane outward and hence promotes forward underlying cellular protrusion formation, which subsequently promotes overall forward movement of the entire cell. In contrast, peripheral stress fibers and the actomyosin contractility specify the cell's shape at the sides and the rear [222]. Thus, the segregation of protrusive and contractile structures is a critical step in the directional and persistent migration of cells.
For cell migration, the cells polarize along their front-rear axis, which defines the direction of movement and leads to a reorganization of cellular organelles such as the nucleus. Upon cell movement, the nucleus is positioned at the cell's rear, which influences the position of the microtubule organizing center (MTOC) and the Golgi apparatus, as they are located between the leading edge of the cell and the nucleus [182,223]. As a result of the altered MTOC position, the microtubules grow preferentially towards the leading edge and hence build a track for the directional movement of vesicles trafficking to the leading edge [224].
Are there two distinct nucleus/cell migratory modes? Similar to mesenchymal cancer cells, differentiated cells such as fibroblasts employ a microtubule-facilitated cell polarity for building an actin-rich leading edge to facilitate cell migration [225]. The microtubule-driven cell polarity has been analyzed by using EGFP-alpha-tubulin-transfected cells, which enables the tracking of microtubules during the random migration of the cells. The microtubule network exhibited a differently behavior during the translocation and rotation steps of the nucleus compared to the perinuclear actin cap, as the broad and overall organization of the microtubules remained rather unaltered during these two steps. However, the nucleus and the centrosome, which means the MTOCs, were located at different positions within the cell. In general, the nucleus is positioned in the rear of the cell and moves forward during the nuclear translocation, which is seen upon the persistent and fast migration of the cell, whereas the MTOCs are positioned nearby the nucleus, when the nucleus is located in the rear of the cell and undergoes nuclear rotation (migration impaired state of the cell). After repolarization of the cell and the translocation step of the nucleus, the MTOCs were located nearby the nucleus, but away from the center of mass of the cell, when the cell has become meanwhile more polarized.
Several studies reported that MTOCs in polarized motile cells are highly correlated to the directionality of cellular movement, whereas their location is also cell type specific [226,227,228,229,230,231] and depends on the contact inhibition [227] as well as on physical constraints [232]. However, it has been revealed that the position of the MTOC is highly correlated with the polarization state of the cell, which can be detected through the distance between the MTOC and cell's center of mass, which exhibits larger values in polarized and single cells [233]. Indeed, the MTOC stained for gamma-tubulin were away from the cell's center of mass and located in between the cell's leading edge and the nucleus, when the cells are grown in the stripe-pattern consistently with the cell migration direction, however, in circular patterns the MTOC has been found to be close to the cell's center of mass. These results further support the actin cap based model of cell migration, in which the perinuclear actin cap seems to be the critical determent of the coupling between the nucleus and cytoskeleton provided by the nuclear lamin A/C and the LINC complex facilitating the connection to the perinuclear actin cap, which subsequently regulates the migration mode of cells. When the cells are devoid of a perinuclear actin cap structure, the nucleus undergoes rotation, but very weakly translocation. By comparing the nuclear shape and the movement of the nucleus in control and lamin A/C-deficient (Lmna–/–) mouse embryonic fibroblasts (MEFs), it has been reported that the lamin A/C deficiency impairs the perinuclear actin cap formation in these MEFs [176]. The Lmna–/– cells showed normal basal F-actin stress fibers, whereas the perinuclear actin cap was impaired compared to control cells. In more detail, the nucleus of Lmna–/– cells appeared compared to the control cells' nucleus more rounded. Moreover, even the translocation speed of the nucleus in Lmna–/– cells is reduced by half and in turn, the nucleus in Lmna–/– cells rotated more pronouncedly compared to control cells. When there is an lamin A/C deficiency of cells how does it impact cell migration? The perinuclear actin cap is not present in Lmna–/– cells, whereas the overall cell speed and persistence of movement is impaired as the nuclear translocation is reduced pronouncedly. As both the speed and persistence of Lmna–/– cells were nearly abolished, the capability of these cells to spend long time periods in a persistent migration mode before repolarization is toned down. In addition, diverse mechanical, pharmacological and genetic alterations strongly favor the assembly of the perinuclear actin cap structure, which is important for the fast persistent migration mode of cells, nuclear shape elongation, translocation of the nucleus and subsequently entire cell polarization. This dependence was further investigated in elongated cells lacking the perinuclear actin cap structure, as these cells are transfected with EGFP-KASH2, which inhibits the perinuclear actin cap formation and hence reduces the directionality of the cell migration. In a next step, the cells are cultured on fibronectin-coated stripes on which the control cells formed a perinuclear actin structure, their nuclei adapted an elongated shape and the cells migrated longitudinal and persistently [218]. Although the EGFP-KASH2 expressing cells exhibited an elongated cell shape representing the morphology of fast and persistent migrating cells, the perinuclear actin cap cannot be detected in these cells and the nuclei adapted a rounded shape. All of which is consistent with the finding that the perinuclear actin cap adapts the shape of the nucleus in response to environmental conditions or restrictions promoting a cell shape change [176]. Indeed, the lamin A/C and LINC complexes facilitate the coupling between the nucleus and the cell through the actin cap and rather not through the cell's shape, which is crucial for directing persistent and fast cell migration. Finally, the nuclear actin cap formation and the MTOCs need to be precisely regulated during the individual migration modes leading to fast and slow migration phases.
21. How Can Cells Overcome the Physical Limits of the Nucleus during Cell Migration? What Role Play Repair Mechanisms in Cell Migration?
Mostly studies on cell migration have investigated nuclear cap structures using 2D environments for cell migration. Thus, the question whether 3D migration modes rely on such an actin cap structure is still not yet well understood. Besides the squeezing of the nucleus during confined migration, nuclear rupture and DNA damage can promote cell migration, when the environment induces a nuclear deformation such as a compression and therby causes a localized loss of the integrity of the nuclear envelope [234,235,236]. The nuclear envelope itself consists of inner and outer membranes, nuclear pore complexes and the nuclear lamina building the physical barrier between the interior of the nucleus and the surrounding cytoplasm. Without such as protection of the genome and the separation of DNA from RNA synthesis during the process of cell migration under confinements, the cell is susceptable to DNA damage and subsequently cell death (apoptosis). There exists a precisely defined threshold for the nuclear deformation such as nuclear compression. Above a certain threshold the nuclear lamina scaffold breaks by rupturing the bonds, however, the nuclear lamina can rebuild itself by reducing the nuclear volume [237]. The nuclear deformation has been correlated with increased gene expression such as nuclear factors and components involved in classical mechanotransduction pathways [237]. Besides environmental compression of the nucleus, intracellular cues such as the actin cytoskeleton can rupture the nucleus [67,178,238]. A fragmentated nucleus can occur by passing a narrow confinement and may also reveal DNA double-strand breaks. In addition, nuclear blebs occur to overcome nuclear pressurization by the environment and by actomyosin contraction at the rear of the nucleus [234]. The nuclear deformation susceptability increases with cell confinement as well as the depletion of nuclear lamins or depletion of nuclear envelope proteins, which both structure the nucleoplasm. During the rupture of the nculear envelope, multiple DNA repair proteins can move away from DNA and mis-localize in the cytoplasm of U2OS osteosarcoma cells, which may then cause a significant delay of DNA repair upon nuclear envelope rupture [236]. The partial knock-down of DNA repair factors downregulates chromsome copy numbers and increases DNA double strand breaks leading to decreased DNA levels, which finally leads to more stem cell like state of certain cancer cells [236].
For the restorage of the nuclear envelope, components of the endosomal sorting complex required for transport-Ⅲ (ESCRT-Ⅲ) machinary are necessary to repair the nuclear envelope and DNA damage [234]. However, certain cytoskeletal structures such as the formin-family actin filament nucleator 2 (FMN2) have been revealed to prevent nuclear damage and hence prevent DNA damage during migration through confinements [239]. In more detail, FMN2 interacts with the perinuclear actin/focal adhesion (FA) system and alters it to control nuclear shape and positioning in 2D cell migration, whereas in confined 3D environments, FMN2 decreases damage of the nuclear envelope and subsequently damage of DNA [239]. In diseases such as cancer FMN2 has been found to be increased in human melanomas, whereas the disruption of FMN2 in mouse melanoma cells impairs cancer cell metastasis in the lung [239]. Finally, FMN2 plays a key role in providing a perinuclear actin/FA system preventing damage of the nucleus and DNA and leads to cell survival during 3D confined migration and thereby supports the metastatic cascade in cancer [239].
22. Conclusions
The interplay between the cell's nucleus and its actin cytoskeleton seems to be important for cellular movement in 3D confinements such a connective tissues and stroma. In addition, from the biophysical-point-of-view the cytoskeleton represents for the nucleus a similar confinement as the extracellular matrix environment for the entire cell. Thus, the mechanical properties such as the stiffness of the cell's cytoskeleton and the nucleoskeleton seem to be crucial for understanding the different migration modes cells' can adapt due to their own internal structure and the environmental confinement. Moreover, they seem to dependent on differences between the cell types in their individual capacities to adapt to a distinct migration mode. In order to interpret the different migration outcomes, it is necessary to know if and when a distinct cell can exhibit a certain migration mode and how the mechanical parameters of the nucleus and its cytoskeletal confinements regulate the cell's migration mode and subsequently its directionality and speed. An important question remains unanswered: Can the mechanical properties of nucleus be included in the staging of tumors and prediction of metastasis?
Finally, we propose that exact and distinct migration modes of cells will enable us to predict the outcome of diseases such as the malignant progression of cancer or the success wound healing processes. The identification of these migration modes will help us to develop individual and personalized treatment of cancer patients and possible the adaption of a cancer treatment method to the specific conditions present in each patient individually. Thereby, the mechanical characterization of the migration modes will allow us to predict a migration mode such as a persistent mode of migration dependent of the specifities in the individual cells under a distinct environment.
Acknowledgements
This work was supported by the DFG (MI1211/18-1 and INST268/357-1 FUGG).
Conflict of Interest
The author declares no conflict of interest in this paper.









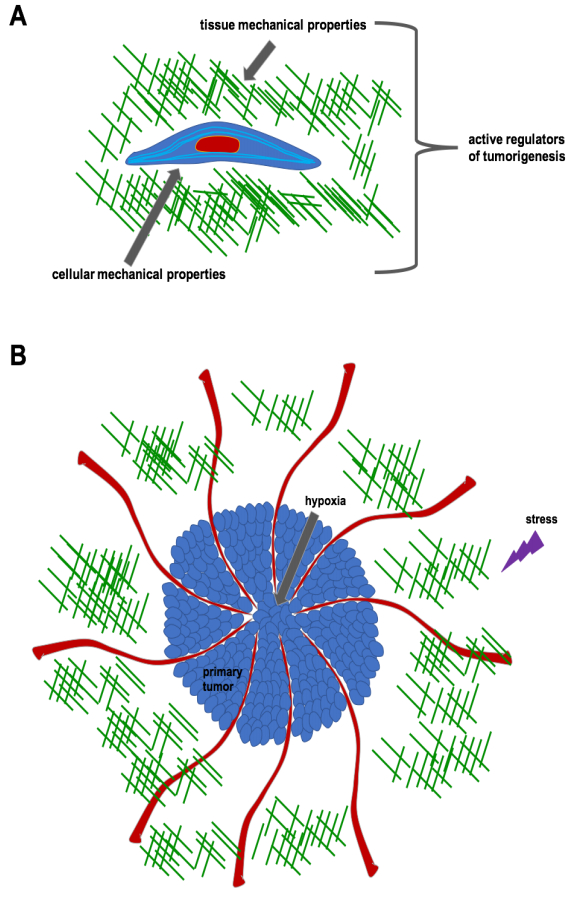
 DownLoad:
DownLoad: