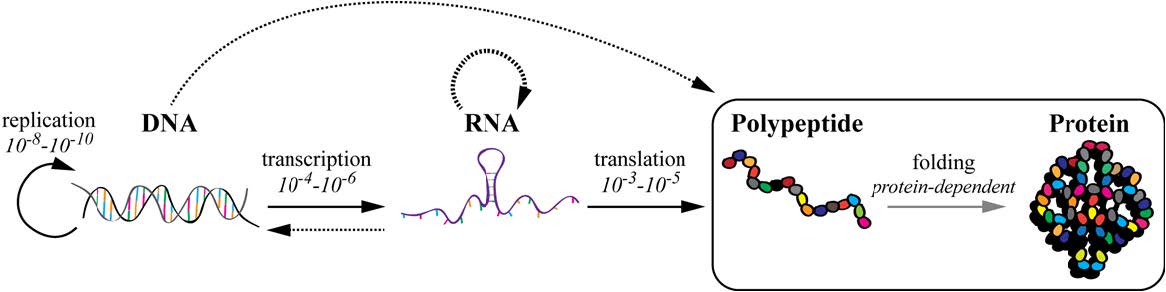
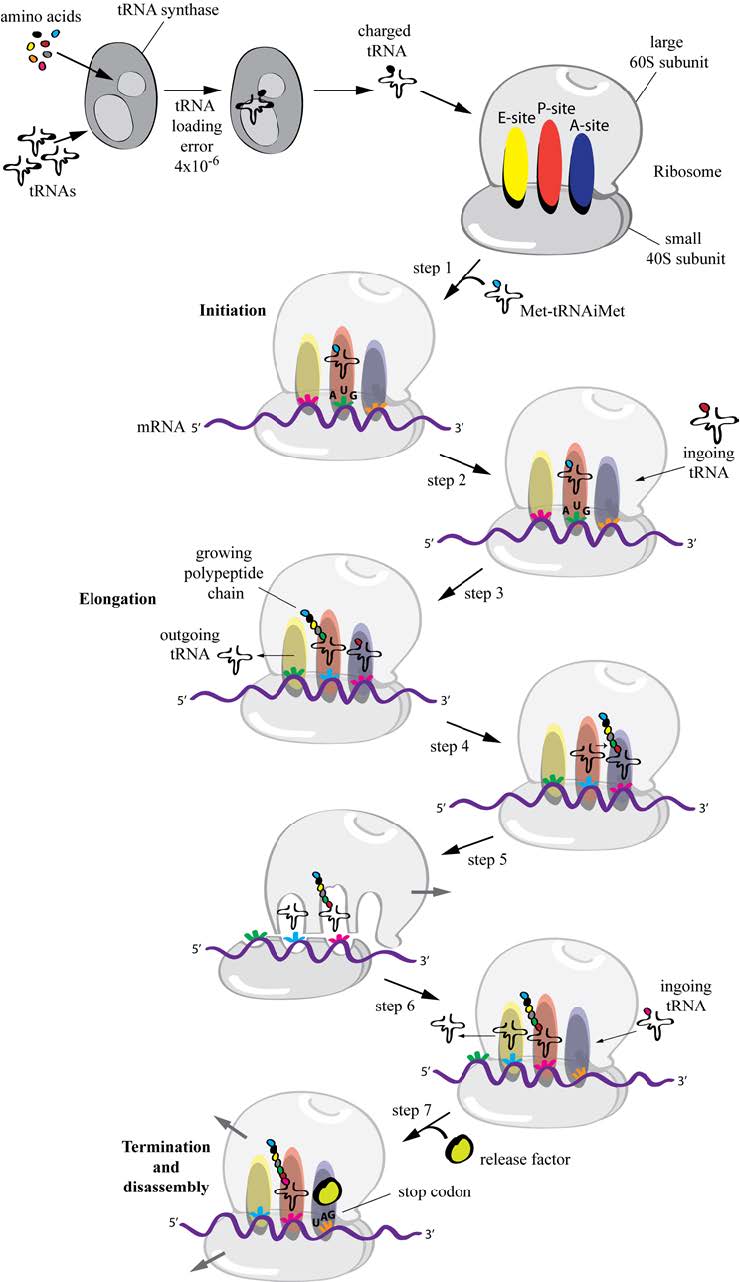
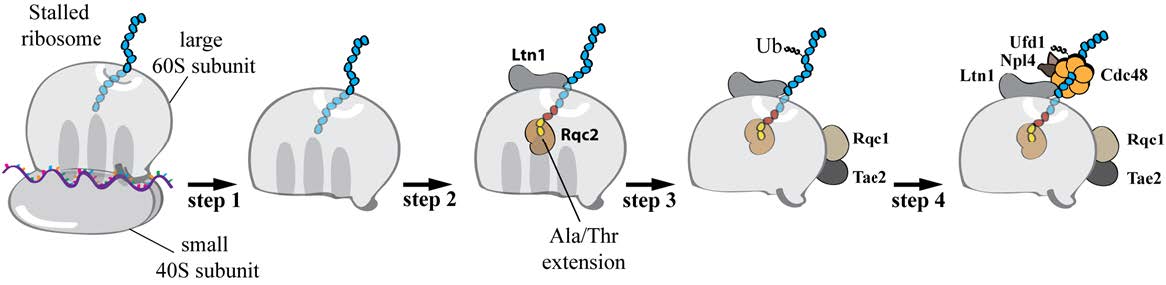
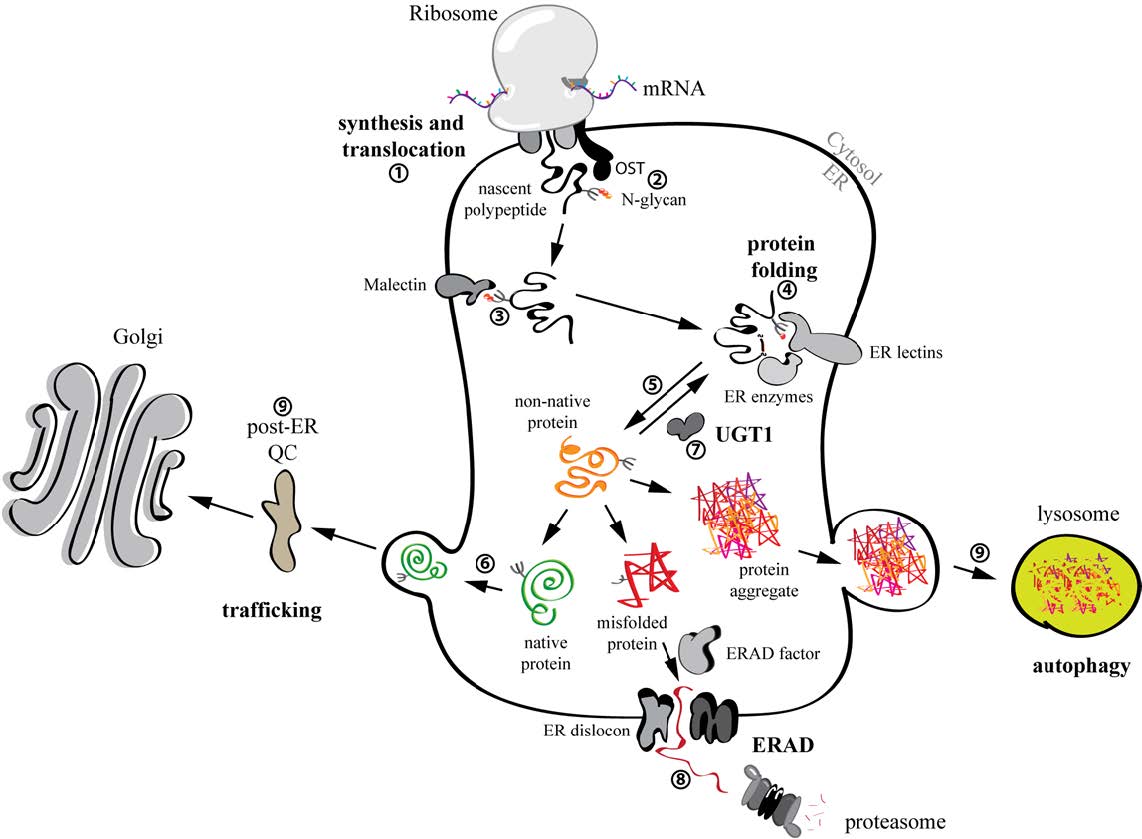
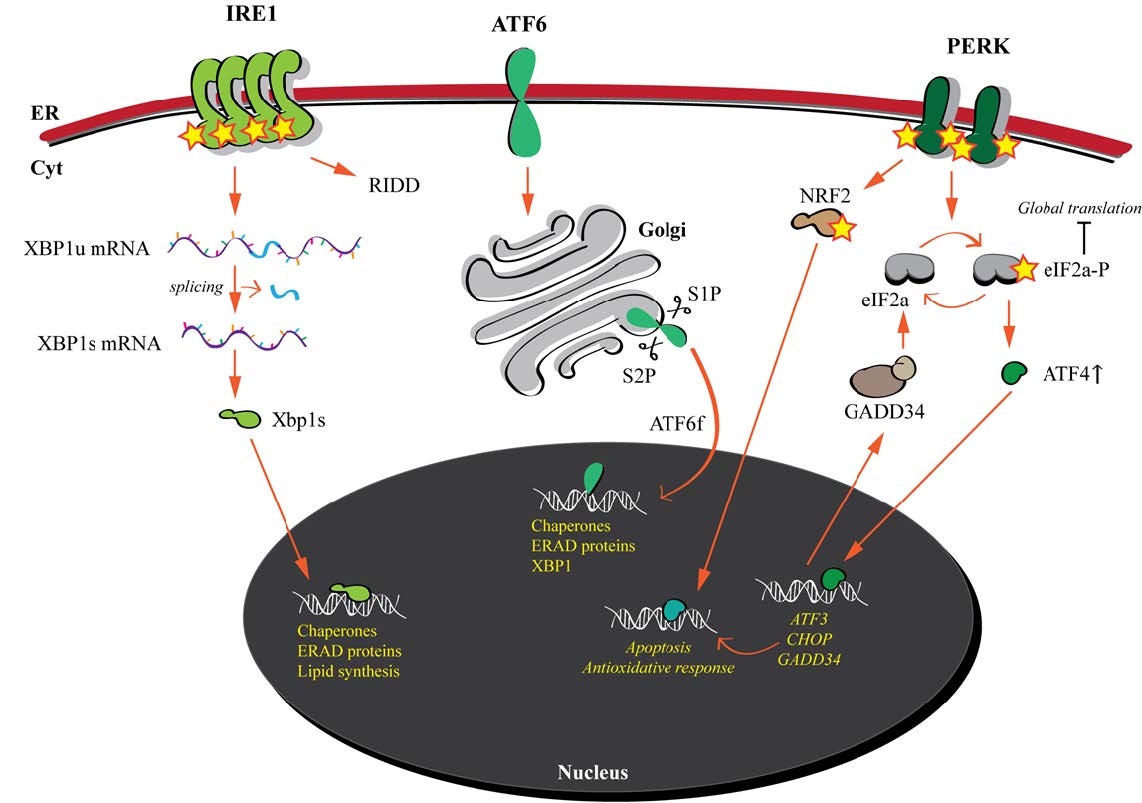
The biosynthesis of proteins entails a complex series of chemical reactions that transform the information stored in the nucleic acid sequence into a polypeptide chain that needs to properly fold and reach its functional location in or outside the cell. It is of no surprise that errors might occur that alter the polypeptide sequence leading to a non-functional proteins or that impede delivery of proteins at the appropriate site of activity. In order to minimize such mistakes and guarantee the synthesis of the correct amount and quality of the proteome, cells have developed folding, quality control, degradation and transport mechanisms that ensure and tightly regulate protein biogenesis. Genetic mutations, harsh environmental conditions or attack by pathogens can subvert the cellular quality control machineries and perturb cellular proteostasis leading to pathological conditions. This review summarizes basic concepts of the flow of information from DNA to folded and active proteins and to the variable fidelity (from incredibly high to quite sloppy) characterizing these processes. We will give particular emphasis on events that maintain or recover the homeostasis of the endoplasmic reticulum (ER), a major site of proteins synthesis and folding in eukaryotic cells. Finally, we will report on how cells can adapt to stressful conditions, how perturbation of ER homeostasis may result in diseases and how these can be treated.
1.
Introduction
The transformations in the power industry have promoted the preference to distributed generation (DG) and renewable energies. Usage of renewable energy based DGs causes free energy generation and decreased environmental pollution [1]. In spite of the numerous advantages of these type of DGs, their variable nature lead to lower reliability in the power system [2]. The ESSs can complement this type of DGs, so, if economical storage systems are available, development of renewable energy will progress more rapidly.
The ESSs are very useful and practical as they can save the extra energy and discharge it in the time of shortage [3]. With increased research and development in this field, the ESS have become more economical.
The applications of energy storage across the grid are diverse, which include energy supply at a large scale, time transference of electricity energy or energy trade, frequency adjustment, spinning and complementary reserves, voltage adjustment, delaying the transmission and distribution grids upgrading, improving the power quality, improving the system reliability, and managing the demand fulfillment [4,5]. These systems should participate in the electricity market under the ownership of an investor and independently. The most important problem of interest in storage units in a restructured environment is requiring higher profit in competition with others.
The ESS can be installed in the power system with different capacities. At larger scales, ESS is more suitable for higher generation levels and voltage compared to the electricity grid, whereas smaller scale ESS can fulfill various targets across the distribution level with lower voltages [6]. Five types of ESS including mechanical, electrochemical, chemical, thermal, and electrical systems are employed for large-scale uses [7].
Many researchers have tried to optimize the performance of the ESSs for different applications. The important factor about the ESS relates to its planning in order to meet the load demands. In [8] a novel approach is introduced for optimal operation of distribution networks at the presence of DG and ESS. Reliability and costs are objective of this study and a hybrid evolutionary algorithm called Hybrid Grey Wolf Optimizer-Particle Swarm Optimization (HGWO-PSO) algorithm is applied. An analysis of the operation mode of energy storage is presented in [9]. The analysis is performed through a mixed integer linear programming (MILP) model programmed via the General Algebraic Modelling System (GAMS) to reduce operation costs.
A multi-objective methodology for locating, sizing and operation of ESSs in distribution network for a day is presented in [10]. The objective functions of the problem are minimization of power losses and the ESS cost that uses non-dominated sorting genetic algorithm Ⅱ and taboo search optimization algorithm. In [11] a method to find the optimal ESS capacity for a peak-shaving application is proposed. This method is based on Dynamic programming to improve voltage profile and energy cost.
Optimal storage operation problem as a finite-horizon dynamic program is formulated in [12] for a grid with renewable DGs and AC/DC load to minimize expected energy cost. Ref. [13] presented mixed-integer second-order cone programing and mixed-integer linear programing models for solving the problem of optimal operation of distribution networks with ESSs. Optimal operation of the grid with DG and ESS for multiple objective functions such as minimization of losses, imbalanced power at the substation, total energy costs, and peak demand is presented in [14]. In [15] and [16] the SSO algorithm is used solving the economic dispatch problem and in [17] the hybrid SSO algorithm is employed to estimate the thermos physical properties of phase change material for the first time.
Study on optimal operation of hybrid storage systems include battery and super-capacitor is presented in [18,19] for distribution system. Optimal operation and energy management of a hybrid power system in smart grid framework is presented in [20]. In this research wind turbine, photovoltaic and ESS are integrated and model predictive control (MPC) is used for optimal management. A novel stochastic planning framework is proposed in [21] to determine the optimal ESS capacity in an isolated micro-grid.
In this paper optimal operation of the ESSs in a distribution system is presented. In this study SSO algorithm is used as a novel method to minimize cost, losses and improve voltage profile. The rest of this paper is organized as follows: problem formulation includes decision variables, objective functions and constraints are illustrated in section Ⅱ. Section Ⅲ is dedicated to backward/forward power flow. The SSO algorithm is explained in section Ⅳ. Simulation results and conclusion are presented in section Ⅴ and Ⅵ, respectively.
2.
Problem formulation
2.1. Decision variables
In this study, contribution of storage units is considered in electricity markets to achieve maximum financial benefit within a specified period. Determining the optimal time of storage unit charge and discharge is the main decision variable. This time should be determined in such a way that the problem objective function is optimized.
2.2. Objective functions
The ESSs are organized and contributed in the market to achieve more profit. The storage units' profit can be expressed as follows:
Where, Pbuyt is the power purchased from the grid, Psalet represents the power sold to the grid, and λgridt shows power cost at t.
2.3. Constraints
2.3.1. Buses voltage limits
The permitted range of the grid voltage level changes is very limited, and standards usually allow for small variations around the nominal value. According to the limitation defined for voltage of buses, the following equation can be expressed:
Where, vi is the bus voltage, vimin and vimax are minimum and maximum voltages of ith bus, respectively and Nbus is the total bus number.
2.3.2. Permitted line current flow
The thermal capacity of the lines is simply determined based on current flow; thus, the following equation can be used for the current flow limitation:
Where, Ii is the current of ith line, Iimax is the maximum allowed current for ith line, and NLine is the total number of lines.
2.3.3. Constraint on ESS
State of charge (SOC) is defined as the ratio of battery remaining energy to total energy saved. Each EES has its specified SOC which must always be within the allowed range, as:
Where, SOCmin and SOCmax are minimum and maximum values of the storage SOC, respectively.
2.4. Load modeling
With respect to the load static features, three general models are proposed in power system studies, including constant power (powers are independent of voltage), constant current (powers are proportional to bus voltage) and constant impedance (powers are proportional to square bus voltage). In this paper, constant power model is considered.
3.
Power flow
Traditional power flow methods in transmission networks are less effective for distribution systems due to radial structure and high R/X ratio. Also, by increasing the DG unit's penetration, the distribution network changes from a passive to an active grid [22]. Therefore, instead of common power flow methods, backward/forward sweep method based on current summation is used.
3.1. Backward/forward sweep method
The backward/forward sweep method is appropriate for radial construction, whose effectiveness has already been proven. Simple structure, fast convergence and suitability for online and offline problems are the main advantages of this method [23]. This method has three step which are explained below:
3.1.1. Backward sweep
In the first iteration, all bus voltages are equal to source voltage (1 p.u.). In the next iteration, bus voltages are calculated from the previous step. With respect to bus voltages, the load current can be calculated as follows:
Where, ILi, Pi, Qi and Vi are the current, active power, reactive power and voltage of ith load, respectively.
Thereafter, it is necessary to calculate the current through lines starting from the farthest line relative to the reference line. For example, line j can be expressed as:
Where, Nbus is the bus number, ILi is the current of jth line, and D represent all the lines connected to bus i. Consequently, backward sweep is finished and the current of lines is updated.
3.1.2. Forward sweep
In the forward sweep starting with source bus, whose voltage is known, and considering impedance and current of lines, the voltage of ith bus is calculated as follows:
Where, Vi is the voltage of ith bus, Vi-1 is the first bus voltage at ith line, ILi shows the current of ith line and Nbus is the bus number. Upon completion of this process, the forward sweep is finished and all bus voltages are updated.
3.1.3. Convergence criterion survey
After backward/forward sweep, the convergence criterion needs to be calculated to assess the need for further iterations.
Where, Viold is the voltage of ith node in the previous iteration, Vinew denotes the voltage of ith node in the last iteration and ε is the permissible voltage deviation value. If the above equation persists, the power flow will end; otherwise, iterations will continue.
3.2. Power flow in distributed network with DG sources
Distributed systems with DGs are similar to multi source networks, so buses with DG are modelled as PQ or PV bus [22]. In this paper, DG units are controlled like a PQ bus and hence, they are considered as a negative load. The PQ buses are modeled as follows:
4.
Social spider optimization (SSO) algorithm
Optimization is a challenging area that has attracted increasing attention in recent decades. Optimization finds the best solution depending on the problem, limits and constraints [24]. Recently, metaheuristic algorithms have gained more popularity as they are superior to traditional gradient-based approaches.
The main advantage of SSO include its optimum search in some complex multimodal optimization problems, the uniform structure of the population, the unique searching pattern and its underlying social animal foraging strategy [25]. The SSO indicates lower convergence potential in some problems, but it is also able to solve multi-objective optimization problems with numerous local optimization points [25].
In many algorithms based on collective intelligence including artificial bee colony (ABC) and group search optimization (GSO), populations are categorized into different types. Different independent agents perform different tasks and the entire population cooperate with each other to search and explore the search space. However, in SSO, all of the independent agents (spiders) are the same and equal. Each agent performs all tasks which should be carried out by several types of species of population in other algorithms.
4.1. Spider
Spiders are optimization agents in SSO. At the beginning of running the algorithm, a number of predetermined spiders lie on the web. Each spider S has a memory, and stores independent information [25].
The position of the spider as well as the degree of eligibility is used for stating the special status of spider S, and other information is employed for navigation of spider S towards new locations.
Based on observations, spiders have a very accurate sense towards vibrations. In addition, they are able to distinguish between different vibrations propagated on the same web, and perceive the intensity associated with each of them. In this way, the spiders lying on a web share their personal information with others to develop a public social awareness.
4.2. Vibration
In SSO, two characteristics including the location of the vibration source and its intensity are used to define a vibration. By transferring each spider to a new position, a vibration is developed in its current position. The position of spider A at the time of t is defined as PA(t), or more simply as PA. Further, G(PA, PB, t) is used to represent the intensity of vibration sensed by a spiders at the time of t. Therefore, G(PS, PS, t) means intensity of vibration produced by spider S at the source position [25,26]. The intensity of vibration at the source position is dependent on the eligibility of its position F(PS):
Where, C is a small constant value. According to (10), it is concluded that all possible values for the intensity of vibration and positions with greater eligibility have greater intensity.
As a type of energy, vibration will attenuate in a specific distance that is considered in SSO. The distance between spiders A and B is defined as D(PA, PB), which is obtained by the following Relation:
The standard deviation of positions of all spiders in each dimension is represented by σ. The attenuated vibration received by a spider can be calculated as follows:
Where, ra∈(0,∞) is fixed parameter of the SSO algorithm. For a weaker attenuation, ra should be considered large.
4.3. Search pattern
In SSO, there are three consecutive stages of initialization, iteration, and finalization. At the stage of initialization, the objective function and search space as well as the numerical value used for the algorithm are defined. After adjusting these values, the algorithm starts generating an initial population of spiders. As the number of spiders along the SSO simulation remains unchanged, a memory with a constant size is considered for storing their information. The positions of spiders are generated randomly and then eligibility values of each of them are calculated and stored. The first target vibration related to each spider present in the population is adjusted and determined at the current position of that spider, and the intensity of the vibration is considered zero. All of the initial data stored for spiders are also valued as zero.
In this way, the stage of initialization is terminated, and the algorithm begins the iteration stage, and deals with searching for the problem solution by the generated spiders. At this stage, a specific number of iterations are run by the algorithm. In each iteration, all spiders move towards a new position on the web and evaluate their degree of eligibility. First, the algorithm calculates the eligibility values of all spiders present on different positions on the web, and if possible it upgrades the Global optimal value. The eligibility values for each spider along every iteration are assessed. Once all vibrations were generated, the algorithm simulates propagation of these vibrations.
In this process, every spider S will receive the number |population| different vibrations generated by other spiders. The information received from these vibrations includes the source of vibration and the extent of its damped intensity. V is used to represent the number |population| of vibration [25].
As soon as the vibration's V is received, the spider S selects the most powerful vibration vsbest among the vibration V and compares its intensity with the intensity of the target vibration vstar. If the intensity of vsbest is higher, spider S stores vsbest as vstar and Cs (number of iterations) is reset to zero. Otherwise, the main vtar is kept, and Cs increase one unit. PSi and PStar represent the positions of the source for generation of V and vtar, in which i = 1, 2, …, |population|.
Thereafter, the algorithm takes some measure causing spider S to move randomly towards vstar. Every spider has a m dimensional cover, which is a binary vector consisting of 0-1, with a length of D, with D showing the number of dimensions of the optimization problem. First, all cover values are zero. In each iteration, spider S alters its cover with the probability of 1-pccs; Here pc∈(0˒ 1) and is defined by the user, which represents probability of cover variation. If it is decided to change the cover, each bit of this vector is replaced by a probability of pm equal to 1, and remains with a probability of 1-pm unchanged and equal to zero.
Once the dimensional cover was determined, the following new position called Psfo it generated based on the cover of spider S. The value of ith dimension of the following position, Ps˒ifo, is generated as follows:
Where, r is a random number within the range of [1, |population|], which is produced separately, while ms, I represents the ith dimension of the dimension m cover associated with the spider S.
After generating PSfo, spider S performs a random movement towards this position. This random movement is conducted and controlled by the following relation:
Where, ⊙ is the element-wise multiplication and R is a vector of decimal random numbers between 0 and 1. Spider S moves along any dimension and with random coefficients within (0, 1) range towards PSfo. These random coefficients are generated independently and individually for each dimension. After running this random movement, spider S stores its manner of displacement in the current iteration to be used in the next iteration. In this way, the sub stage of random movement is finished. The final sub stage of the stage of iterations is controlling establishment of constraints. During the stage of random movement, spiders may leave the web's zone, causing transgression of the optimization problem constraints. Reflective method can be used to develop the constraints, and one can generate a free position from bounded constraints, i.e. PS (t + 1) using the following relation:
Where, ¯xi is the upper bound of the search space in the ith dimension, while xi_ represents the lower bound of its corresponding dimension. The stage of iteration continues iteratively until the final criterion is fulfilled. The final criterion can be defined as achieving the maximum number of iterations, achieving a specific error, or any other suitable criterion. By the completion of the iteration stage, the best solution found with the best eligibility is displayed as the output of the algorithm. The above three stages constitute a complete the SSO algorithm. Table 1 shows the steps of SSO algorithm.
5.
Results and discussion
By introducing problem and the SSO algorithm, proposed optimization method is simulated by MATLAB software under different scenarios.
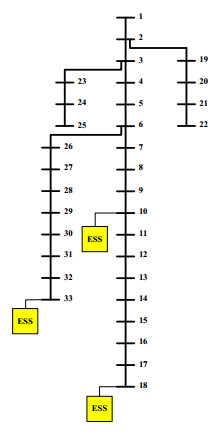
The proposed method is applied to a standard 33-bus radial distribution network with 4 laterals and 33 nodes, as shown in Figure 1. The main data of this network are presented in Appendix. This test network has 32 individual branches and its total active and reactive power are equal to 3715 kW and 2300 kVar, respectively. The nominal voltage is equal to 12.66 kV and three storage units are installed at buses 10, 18 and 33. The charging rate and capacity of three ESSs are 8 kW/h and 40 kWh, respectively. Table 2 presents energy price and hourly load during 24 hours.
5.1. Scenario Ⅰ
Maximizing the operational profit from storage units during 24 hours is the main purpose of the first scenario. The SSO algorithm population and maximum iteration are considered equal to 100 and 200, respectively.
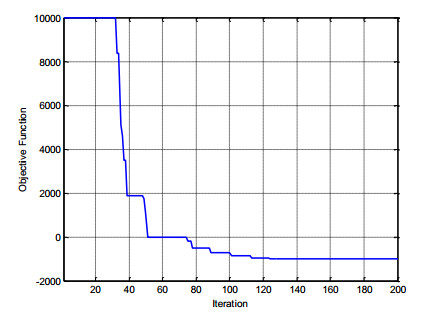
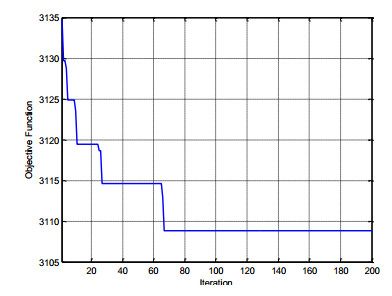
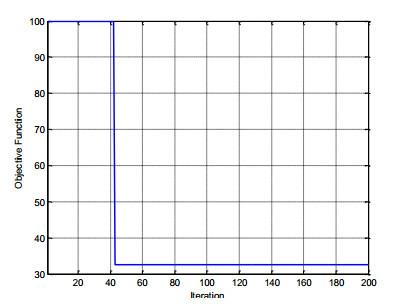
The convergence curve of the first scenario is illustrated in Figure 2. The SSO algorithm has the ability to converge rapidly to the optimal global answer.
The ESSs cost is calculated as about -1016$ which means ESSs have earned 1016$ during a day through energy sales and purchases.
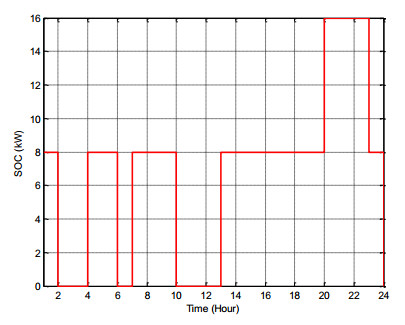
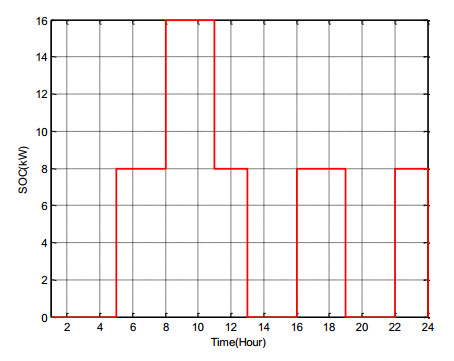
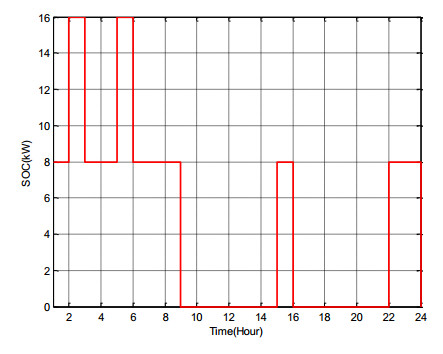
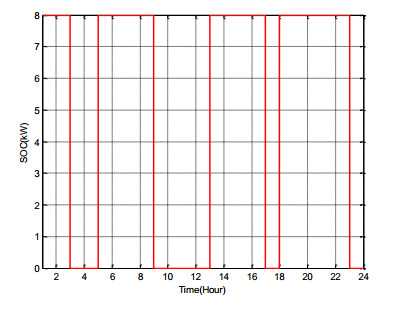
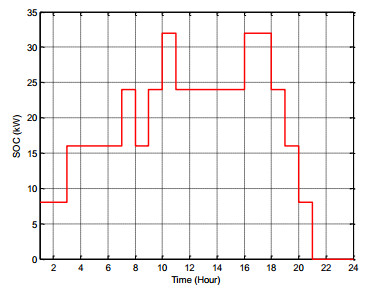
The SOC of installed storage units at buses 10, 18 and 33 is displayed in Figure 3, Figure 4 and Figure 5, respectively. These figures indicate the amount of stored energy, with SOC always satisfying the constraints. Its change rates are 8 kW.
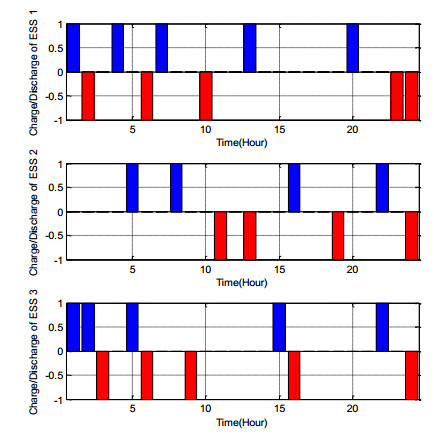
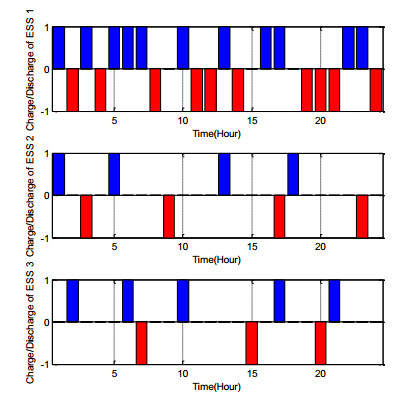
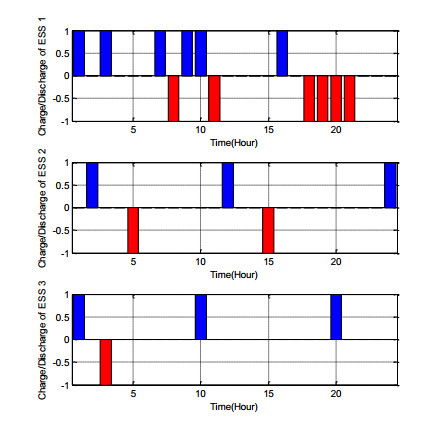
Figure 6 shows the charge and discharge rate of ESSs during 24 hours. The blue sections (positive) represent charge state and red sections (negative) indicate discharge state.
When the energy price is cheap or the load is not heavy, ESSs store energy and vice versa, leading to decreased ESSs operational costs and more profits. For example at hour 24, the price of energy is too high, so three ESSs are produced energy (red section).
According to scenario Ⅰ, ESSs satisfies SOC limits and they produce in expensive time. This figures demonstrate behavior of ESSs for 24 hours so as to obtain high profit.
5.2. Scenario Ⅱ
Reducing power losses is the main purpose of the second scenario. The SSO algorithm population and maximum iteration are similar to the previous scenario. This scenario is investigated in two modes, which are with and without storage units.
Figure 7 shows the convergence curve of the second scenario. According to this figure, the SSO has been converged within a short time.
Total losses for 24 hours a day are 3109 kW, which is equal to 3101 kW before presence of storage units. After optimal charging and discharging, losses grow by about 0.25% which can be ignored. This scenario indicates that ESSs do not have a significant effect on power losses. It should be noted that situation depends on the number of storage units, their capacity as well as charge and discharge rates.
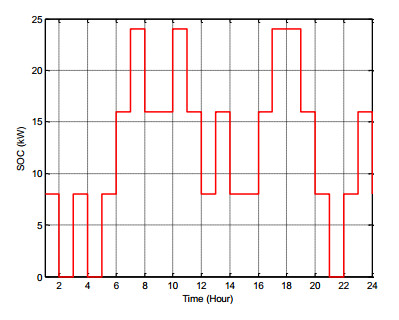
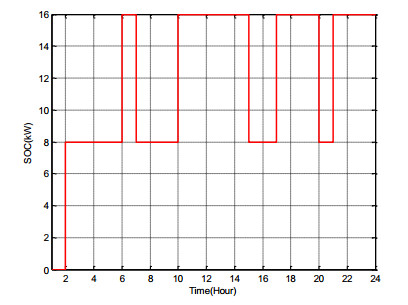
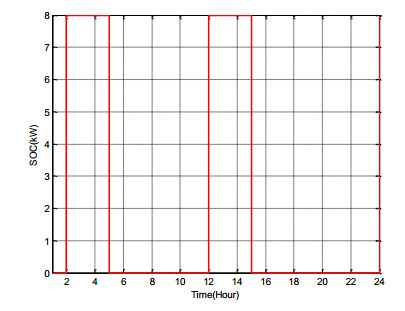
Similar to scenario Ⅰ, the SOC of installed storage units at buses 10, 18 and 33 is shown in Figure 8, Figure 9 and Figure 10, respectively. These figures confirm that the SOC satisfies constraints, with its change rates being equal to 8 kW.
The ESSs charging and discharging rate for one day is shown in Figure 11.
According to proposed information in scenario Ⅱ, the ESSs cannot reduce significantly power losses. Furthermore, since the aim of this scenario is loss reduction, results may different with scenario Ⅰ. similar to previous scenario, all constraints are satisfied.
5.3. Scenario Ⅲ
In this scenario, the problem is solved with the aim of improving the voltage profile. The SSO algorithm population and maximum iteration are considered equal to 100 and 200, respectively. This scenario is investigated in two modes; with and without storage units.
Figure 12 displays convergence curve of the third scenario. The algorithm is converged after 42 iterations.
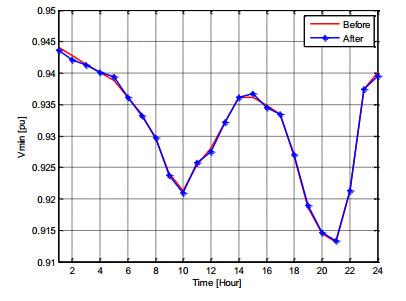
Figure 13 shows the minimum voltage of the system for 24 hours. According to this figure, the grid voltage has satisfied the constraints (between 0.9 and 1.1 p.u.) and grid's voltage profiles with the ESSs are similar to the case without the ESSs. Thus, presence of storage units has no dramatic effect on the voltage profile.
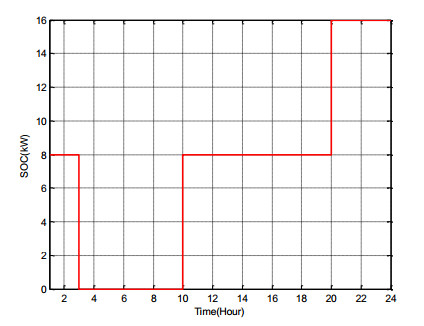
The SOC of connected ESSs at buses 10, 18 and 33 is shown in Figure 14, Figure 15 and Figure 16, respectively. Figure 17 shows the charge (blue) and discharge (red) rate of ESSs during 24-hours.
Improvement of voltage profile with the presence of ESSs is marginally. Moreover, the cost of energy and profit is not the matter of third scenario, so it can be seen ESSs operates in accordance with voltage level as well as constraints. For example, the installed ESSs at bus 10 and 33 don't operate at 24th hour but the ESS at bus 18 produce energy at same time. The behavior of ESSs in this hour is opposite with scenario Ⅰ.
6.
Conclusion
In this paper, contribution of storage units in a sample distribution network is examined with the aim of acquiring the maximum profit for a 24-hour period. The technical limitations including grid constraints, charging and discharging rate of the storage sources and SOC are also taken into account. In order to solve this problem, SSO algorithm is applied to the system.
The results obtained from the SSO algorithm indicated that it is efficient and can be converged to the global optimal solution with a high speed. Also, with the help of this algorithm, optimal charging and discharging of storage units is obtained that cause profitability. This is because when electricity price is cheaper, units usually start charging and vice versa. Although presence of storage units causes increased grid loss, this increase is usually trivial, and is dependent on the number, placement of units as well as their charging and discharging rates. In addition, storage units can improve voltage profile. Thus, their optimal placement is achieved with SSO and this useful algorithm helps the overall distribution system to work properly.
Conflict of interest
The authors declare that there is no conflict of interest in this paper.









 DownLoad:
DownLoad: