1.
Introduction
Privacy attack on remote sensing images has been a new attack field which begins to be concerned.For example, Google Maps often collect the remote sensing images and 360-degree full view video of military bases, including details such as devices, weapons, barracks, obstacles and headquarters. That would be a new security threat once terrorists use them as attack objects. Besides, Google has provided a service called Street View which can even show the details about house number or house windows along the road. It provides possibility for invasion of personal privacy. Therefore, it is necessary for us to figure out how privacy attacks happen on remote sensing images. In this paper, we mainly propose a privacy attack with a deep neural network for remote sensing images classification to support future defense technology.
Large amount of data is the foundation for deep learning on various areas, however, in reality, acquisition of large amount of data sets drains too much on manpower and material resources. Therefore, small-sample data sets are more common in real applications than big data sets. The remote sensing image data is a kind of typical small-sample data. As we all know, commonly a piece of a remote sensing picture is big in size, annotate these big remote sensing pictures needs huge amount of manpower. Actually, large-scale of remote sensing samples are rare in public.
Therefore, how to realize efficient and accurate image classification on small samples has becoming an important task for remote sensing image classification. Traditional machine learning algorithms such as SVM, K-Means requires researchers' domain knowledge and experience to build the models and design parameters, which is a big barrier. With deep learning technology becoming more and more applicable, it is expected to apply deep learning algorithms on small samples of remote sensing for the tasks like traffic detection, fire monitoring, marine oil spill monitoring, since it can extract and learn the features without requirement of much domain knowledge and save more manpower.
However, for small remote sensing samples, deep learning models often perform well on training sets, but perform badly on testing sets. It is called overfitting problem. That is because most of deep learning models are too complex and sample data is too small so that they hard to describe the actual distribution for small samples, thus the trained models may not be reliable.
In this paper, we mainly solve the overfitting problems for privacy attack deep learning models on small samples by proposing a new residual network structure called Joint Residual Network(JRN). By comparing with the experiments results, we analyze how JRN can help deep learning models alleviate overfitting problems. Besides, we analyze how the fine tuning technique can increase the classification accuracy. Our work is helpful for practical applications of remote sensing image classification.
2.
Related work
The image classification of small-sample data is mostly based on the word bag model (BOW) [1] before deep learning model is introduced. In the image classification, the word frequency is the feature descriptor of the image, such as the HOG and SIFT features. Based on the word bag model, Lazebnik [2] and some other scholars adopt a multi-scale block method to analyze the features of each character block respectively, and stitch all the features together to present a structure of the hierarchical pyramid to solve the shortcomings of the location information of the real feature points of the word bag model. In the papers [3,4] the image classification schemes perform well based on the small-sample size of the word bag model. But it needs to make full use of the expert knowledge to express the complex image structure. It is similar to the non-deep learning image classification model on large-scale data. The word bag based scheme still has no generality.
With the accuracy increasing of the deep learning based image classification on large-scale data, many scholars also try to introduce deep learning method into the image classification task on small sample data. Many papers [5,6,7] show that the convolutional neural network is pre trained on the large scale data sets such as ImageNet [8], and then the trained network can be transferred to the image classification of small sample data. Salakhutdinov et al. [9] proposed a HDP-DBM model, which has a better performance than the SVM algorithm on the database CIFAR, handwritten font and human motion capture. Fan Hu [10] and others proposed a deep learning model with pre training method, which can also be well generalized in the classification on the small data such as high resolution remote sensing images. Wei Hu et al. [11] proposed the same idea as Fan Hu and they proved it furthur in the experiment, which has better results for most classification environments, but some classes are relatively poor. While in the papers [12,13] they do not use the pre training method, instead training deep learning model directly on small sample data, and then using SVM to complete classification. Although the result is better than the word bag based model, but the accuracy is too lower than the pre training based model. Therefore, it is a quite reasonable way to use pre train based deep learning model on a large-scale data, and then transfer the model to the small sample data image classification task.
The scheme based on the word bag model requires researchers to have prior knowledge in the related fields and rich experience in image processing and image feature extraction. It has been a limitation for application development. Actually, it is necessary to design various feature extraction strategies for different fields. The possibility of extension on multiple domains is very low, and it is not versatile. Besides, it requires researchers to further abstract and combine the proposed features, and may need to select the features of the extracted features before the classification of discriminant classifiers, but the feature presentation capability of humans is limited. This scheme is not only complex in the process of image classification, but also has a lower classification accuracy.
Therefore, currently most image classification tasks based on small-sample data have gradually abandoned the solution the word bag based models, and turn to the deep learning models. But deep learning model requires to fit more parameters than traditional machine learning methods so that the scale of parameters may be the level of millions or ten millions. Thus, it often occurs some problems such as overfitting if deep learning meets small-sample data. It is of great significance to solve the problems result from deep learning models on small-sample data for practical applications.
3.
Fine-tuning for deep learning on small-sample data
Traditional machine learning based image classification require researchers to extract image features manually, so it is still very demanding for the researchers' domain knowledge. Because of special feature in each field, such as big size, the blurred, multimodal and local effects of remote sensing images, traditional machine learning Image classification schemes still have no universality and weak scalability.
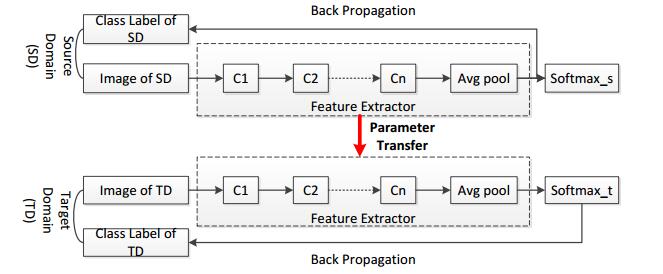
With the continuous improvement of the accuracy of image classification on large-scale data sets, the pre training based deep learning models have becoming applied to the image classification tasks of small-sample remote sensing data, and a typical pre training framework is shown in Figure 1.
Figure 1 shows a general framework for the pre trained deep learning model image classification. When the target task is to classify the small-sample data sets, it usually employs an independent big data set such as the ImageNet data set to pre train a deep learning model, while the trained parameters are transferred to the model for the target domain which is the corresponding small-sample data set. In order to improve the accuracy of classification, many researchers use the deep learning model as a feature extractor, and then use SVM or other discriminant classifiers to fulfill classification.
However, a typical deep learning model such as CNN has a large number of parameters needed to be optimized, therefore, in order to alleviate the overfitting phenomenons, it needs to adopt various techniques to improve the generalization ability of the deep learning model, such as regularization, dropout, and data enhancement, etc. The most commonly used and most effective method in the image classification task on small-sample data sets is the method called fine-tuning. Fine-tuning in a deep learning model can transfer the model parameters of the pre training to the other sample data [14,15], so the technology of fine tuning is widely used in deep learning models.
Besides, in deep learning, the parameter initialization of the model is an important part of the model training, because the gradient descent method is very sensitive to the initialization parameters of the model, and a good set of initialization parameters can make the deep learning model converge faster, and not easy to fall into the local optima. At the same time, in training stage, gradient dispersion is easy to occur because of the deepening of network layers, that is, the gradient will become very small. This is due to the use of the backpropagation algorithm to iterate the weight of the depth learning model. With the depth of the network increasing, the amplitude of the gradient of the reverse propagation will drop sharply because of the characteristics of the chain derivation rule. As a result, the gradient of the initial several layers of the deep learning model tends to zero. Therefore, according to the weight updating formula in the backpropagation algorithm, the values updating of the initial several layers becomes very slow, which make the update of the whole model very difficult, so that they can not execute an effective learning from sample data [16,17,18,19].
The problem of gradient dispersion is an essential problem brought by the gradient descent method in deep learning. The deeper the network structure is, the more serious the problem of the gradient dispersion is. Especially for small-sample data, the problem of gradient dispersion and overfitting becomes particularly significant. Many papers [20,21,22] shows that the first serval layers of CNN usually learn the features of the shallow layer, such as edge, texture and color of the image, therefore it is feasible for different tasks to share the parameters of first several layers, for example, in this paper, a large scale data set is used. The source domain pretrains the deep model, then uses the parameters of the deep model trained as the initial parameters of the deep model of the target domain of the small-sample data set, and then continues to use the small-sample data set to fine tune the depth model, thus modifying the parameter deviation between the target domain and the source domain.
Besides, in practical application, the data set satisfying the demand of CNN is very rare. On the other hand, it takes a long time to train a CNN model from scratch, so that the model can not be applied in time. how to alleviate the over-fitting phenomenon and shorten training time becomes a important research problem for practical application.
4.
Research motivation
In theory, the more layers of the convolutional neural network, the more features can be extracted. Besides, the features are more abstract and have more semantic information in more deep network. Therefore, increasing the depth of the CNN becomes the first choice of the computer vision tasks such as image classification. However, the increasing depth of the network will lead to a more serious problem of gradient dispersion. In order to deal with the problem, Ioffe S et al. [23] proposed a scheme Batch Normalization (BN) that increasing regularization to train dozens of layers of convolutional neural network structure, however, it still can not reach hundreds of layers or deeper network structures. Therefore, He Kaiming [24] and others proposed the deep residual network, fitting the original mapping by fitting residual function.
BN and residual network are all to alleviate the problem of gradient dispersion. Actually, in small-sample data, the problem of gradient dispersion is more serious, besides, overfitting is a more difficult problem. Only through solving the problem of gradient dispersion may not be able to alleviate the overfitting phenomenon, it still needs model optimization to enhance the function of the convolution module, so our research is carried out from this point. Specifically, we need to explore whether it can alleviate the overfitting phenomenon by fusing the bottom feature map and the top feature map of convolutional neural network. Our scheme is based on residual network structure, and improve the residual network by propose a new residual network which fuses the underlying feature map and the top feature map by matrix joint. To evaluate our network, we compare the accuracy with our network and without it by making some experiments on two small-sample data sets, and we explore how our network can alleviate overfitting phenomena.
4.1. Design of joint residual network
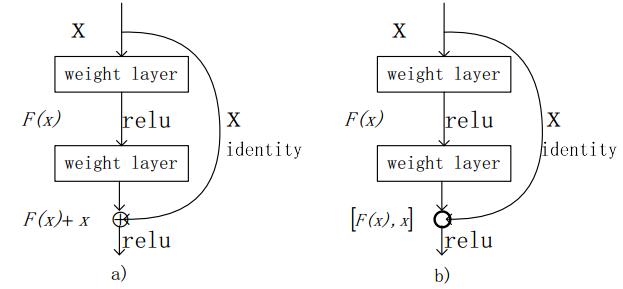
He Kaiming and others [24] propose a residual network model, which is shown in Figure 2 (a). If $ H(x) $ represents the actual mapping expected, the residual network is to make the accumulated nonlinear multi-layer network to fit another mapping relationship $ F(x) = H(x)-x $, then the actual mapping relationship can be represented as $ H(x) = F(x)+x $. The optimization of the residual mapping may be more applicable than the direct mapping. In particular, when $ X $ is already optimal, then it is easier for residuals to fit the zero than to fit a identity mapping by using a stacked nonlinear composite coiling layer.
In the residual network, the residual network uses the accumulated nonlinear network to fit the residual mapping $ F(x) = H(x)-x $, that is, the actual mapping relation is $ H(x) = F(x)+x $, based on the idea of residual network, we propose a new residual network structure shown in Figure 2(b).
In our residual network structure, we called it Joint Residual Network(JRN), the underlying feature graph $ x $ and the top-level feature graph $ F(x) $ are jointed in its own matrix form, so it does not require the linear transformation of the underlying $ x $, which not only ensures the integrity of the original input $ x $, but also does not introduce a new weight matrix; at the same time, the underlying feature graph $ x $ is mixed with the top feature graph $ F(x) $. The type of the feature graph is made so that the generated feature map can cover the latent feature map as far as possible. As a contrast, in traditional residual network, there is a typical limitation in real application. After through two layers of convolution layer, the residual network adds the underlying feature graph $ x $ to the top feature graph $ F(x) $, not only requires the feature graph with the same dimension of the underlying feature graph $ X $ and the top feature graph $ F(x) $, but also requires the underlying feature graph $ x $ to have the same channel as the top feature graph $ F(x) $, that is, the same number of feature graphs. When the number of channels is not equal, the residual network becomes $ H(x) = F(x)+W_sx $, that is, a linear transformation of the underlying feature graph $ x $.
Because the convolutional neural network combines feature learning with the classification task, the characteristics of convolutional neural network are more related to the classification task than the traditional machine learning algorithms. That is, the convolutional neural network has the ability to learn and extract features automatically. The joint residual network structure proposed in this paper splicing the underlying feature map $ x $ and the top layer feature map $ F(x) $. If the underlying feature map $ x $ is a good discriminative and even optimal feature map, it is similar to the traditional residual network structure and the top-level feature map maps $ F(x) $ to zero, therefore it is much easier to learn an identity mapping than using a set of non-linear convolution layers.
In order to avoid the extra burden on the next convolution layer, we use a convolution layer with a kernel $ 1 \times 1 $ to connect JRN so that it can function like dimensionality reduction for the whole network structure. The convolution layer with the kernel $ 1 \times 1 $ can be regarded as a micro network structure, which is inspired by the idea from the NIN model that uses a multilayer perceptron micro network structure to replace the existing linear model, so that it is not easy to occur overfitting problems than the traditional convolutional neural network.
5.
Experiment and analysis
In our experiment, we mainly employ a classical CNN model GoogleNet as the benchmark model. Firstly we delete the Inception Layer of GoogleNet and simply accumulate the convolution layers and the pool layers. Thus the model is called plain convolutional neural network (PlainNet). Based on the PlainNet we integrate JRN structure into it, and the model is called FeatNet. The main operation of our experiment is to compare the classification accuracy of PlainNet and FeatNet on UCMLU [25] and WHU-RS [26] data sets respectively. And based on the UCMLU data set we analyze how FeatNet can alleviate the overfitting problems. Finally, with fine-tuning technique, we compare the classification accuracy of models with JRN and without JRN on the UCMLU and WHU-RS data sets.
5.1. Data set
We use three data sets in this paper, among them ILSVRC2012 data set is mainly used for pre training of deep models, while UCMLU data set and WHU-RS dataset are used to evaluate the scheme of image classification models on small-sample data. The following are brief introduction of three datasets.
5.1.1. ILSVRC2012
The ImageNet data set, [27], the largest image recognition database in the world, was founded by Professor Li Feifei from the Stanford University. They have downloaded nearly 1 billion pictures and labeled these pictures by crowd-sourcing. In recent years, most large-scale visual recognition competition (ILSVRC) only uses a small part of ImageNet. In this paper, we mainly adopt the ILSVRC2012 data set, which contains 1.2 million pictures, contains 1000 different categories. Figure 3 shows a few samples of the ILSVRC2012 data set.
ILSVRC has greatly promoted the development of deep learning, with AlexNet, VGNet, Google Net and RestNet appearing successively, and the top 5 test error rates dropping from 16.4 to 3.57. With the holding of ILSVRC, the theory of deep learning is improved a lot. Many researchers have done a large amount of research work on many aspects such as the activation function [28,29,30], parameter initialization, overfitting and so on [31].
In practical applications, researchers often have a ImageNet data set to pre train a convolutional neural network model, and then use the method of fine-tuning to transfer the learned model parameters to the target task.
5.1.2. UCMLU
The UCMLU data set, which is manually extracted from a collection of big remote sensing images of the city area from the national map Office, has a pixel resolution of 1 feet in the public domain. The UCMLU dataset contains 21 different scene categories, each of which contains 100 images, each with 256*256 pixels, as shown in Figure 4.
5.1.3. WHU-RS
The WHU-RS dataset is an open data set collected from the Google earth. This data set is smaller than UCMLU. It contains only 19 scene categories, and each category has about 50 pictures with a pixel of 600*600. As shown in Figure 5.
5.2. GoogleNet-Feat
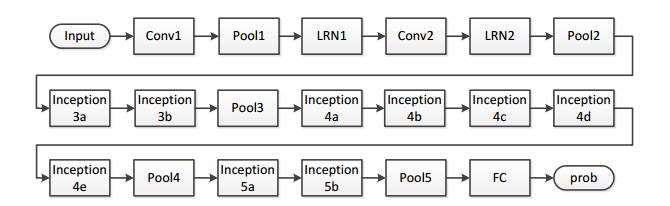
In this paper, the GoogleNet model is used as the benchmark model, and the JRN structure is used to improve the GoogleNet model. Commonly, the ImageNet data set will be used for pre training in the practical application. Besides, many classical convolutional neural networks have been realized in the Caffe framework. Without data enhancement, the top-1 accuracy of the GoogleNet model realized in the Caffe framework on the ILSVRC2012 validation data set is $ 68.7\% $, that is very close to the performance of the GoogleNet model in ILSVRC2012 competition. The original GoogleNet model is shown in Figure 6.
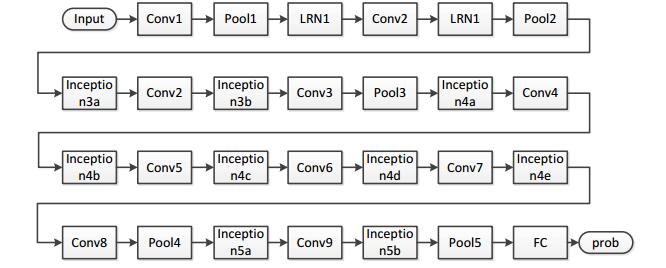
As shown in Figure 6, the first few layers of GoogleNet are the combination of the common convolutional neural network and the pool layer. After the sixth layer, a total of 9 Inception modules are added. The last pool layer is the global average pool layer, and then a full connection layer is connected after that. Based on the GoogleNet model, the GoogleNet-Feat model using JRN structure is shown in Figure 7.
As shown in Figure 6 and Figure 7, in GoogleNet-Feat, it combines the input of the Inception layer and the output of the Inception layer, and then goes through a convolution layer to reduce the dimension, so GoogleNet-Feat is 8 convolution layers more than the original GoogleNet model. Besides, adding the 8 layers can guarantee the layers number of the obtained model to keep consistent with the GoogleNet-R, as shown in Figure 8.
As shown in Figure 8, the GoogleNet-R model seems to be very similar to the GoogleNet-Feat model, but differently, in GoogleNet-R, the input of the Inception layer and the output of the Inception layer are not fused. Therefore, considering the parameters, the parameters of the GoogleNet-R model are very similar to that of the GoogleNet-Feat model.
Since the structure of the GoogleNet model, the GoogleNet-R model, and the GoogleNet-Feat model are similar, so the GoogleNet-R model and the GoogleNet-Feat model can reuse the parameters of the GoogleNet model by the method of fine-tuning. Firstly, we use the ImageNet to train a GoogleNet model, and the parameters of the obtained GoogleNet model can be used to initialize the GoogleNet-R model and the GoogleNet-Feat model, which can save lot of training time, and then use the ImageNet to fine tune the two models.
If the ImageNet is considered as the source domain data set, and then the UC Merced Land Use (UCMLU) data set or the WHU-RS data set can be considered as the target domains, the pre training module of the GoogleNet model, GoogleNet-R model, and GoogleNet-Feat model is shown in figure 1, and then migrates the parameters of the pre trained model to the target domain, UCMLU or WHU-RS classification tasks, by fine-tuning.
5.3. Experiment setup
All the deep learning experiments in this paper are based on the deep learning framework Caffe which uses C++/CUDA architecture to support the command line, Python and MATLAB interfaces, and uses the Google Protocol Buffer data standard [32]. It not only makes the network modification easier to study, but also improves the efficiency of model training and testing. At the same time, the popular deep learning framework used in many academic papers is Caffe, so all our experiments of the convolutional neural network are based on the Caffe framework for convenience of academic comparison.
The hardware and software configuration of the computers used in our experiments are shown in Table 1.
Accuracy(accuracy) is the most used benchmark in the classification task. The accuracy rate is the proportion of the number of samples correctly classified in the total number of samples with a given test data set. For the sample data set D, the accuracy rate is:
$ m $ is the size of the sample data set D, and $ \mathbb{I}(*) $ is the indicator function. Accuracy is the evaluation of the comprehensive accuracy of the classifier. In general, the higher the accuracy, the more effective the classifier is.
5.4. Analysis of the experiments
In order to evaluate the capability to alleviate overfitting, we design four models, which are PlainNet-19 and FeatNet-19 with 19 layers of network structure, as well as PlainNet-31 and FeatNet-31 with 31 layer network structures. By comparing the accuracy of the four models on UCMLU and WHU-RS datasets, we confirm the hypothesis that FeatNet has the ability to alleviate overfitting problems. The specific structures of the four convolutional neural network models are shown in Table 2.
As shown in Table 2, the number of parameters of model FeatNet-19 and PlainNet-19 is millions, and the parameters of FeatNet-31 and PlainNet-31 with 31 layers reach the level of tens of millions, while the size of the UCMLU and WHU-RSI datasets is only 2100, 995 respectively. Therefore, theoretically the four models would be overfitting very appropriately. Moreover, because the parameters of the FeatNet is more than PlainNet and the model structure is more complex, so in theory the overfitting problems of FeatNet would be more than PlainNet. But if the residual network structure of the FeatNet has the ability to alleviate the overfitting problems, then the accuracy of the FeatNet with same layers would be higher than PlainNet. To evaluate the hypothesis, we use two small sample da ta UCMLU and WHU-RS to verify the performance of the four models without fine-tuning.
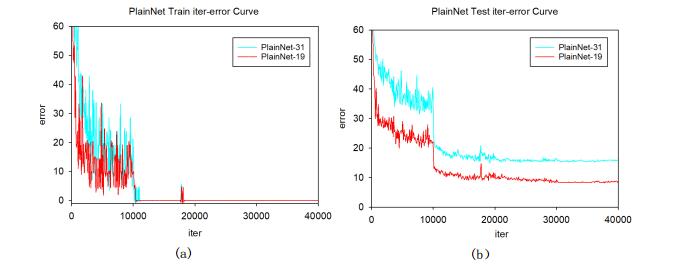
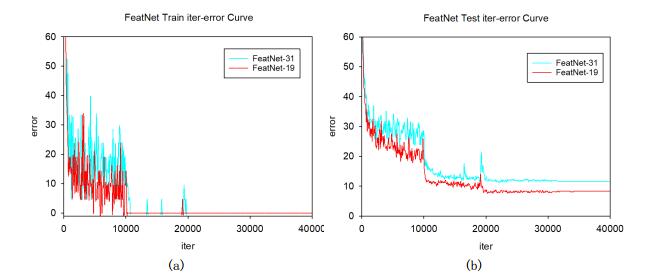
First, evaluate the performance of the PlainNet-31 and the PlainNet-19 on UCMLU data set, and the training errors and testing errors of the two models on UCMLU data set are shown in Figure 9.
As shown in Figure 9, the training error is gradually approaching to 0 with the increase iterations of the PlainNet-31 model and the PlainNet-19 model, but the test error of the PlainNet-31 model is greater than that of the PlainNet-19. It shows that the overfitting phenomenon is becoming more serious with the increase of network depth. However, the problems are not result from gradient dispersion problems with the depth increasing, because the training error of both models in the UCMLU data set converges to 0.
The training error and test error of FeatNet-31 and FeatNet-19 on UCMLU dataset are shown below, as shown in Figure 10.
As shown in Figure 10, with the depth incresing, FeatNet also leads to overfitting problems, but the error interval between the FeatNet-31 model and the FeatNet-19 model on the test set is less than the error interval between the PlainNet-31 model and the PlainNet-19 model. Besides, it can be seen from Table 3 that the accuracy difference of the two 19 layer models is less than one percentage point on the UCMLU data set, and the classification accuracy of the FeatNet-19 model is slightly higher than that of the PlainNet-19 model, while the 31 layer model is 4 percentage points different in the accuracy rate, and the 31 layer is higher than the PlainNet of 31 layers in the 31 layer. On WHU-RS, the accuracy of the two 19-layers models is equal, and the accuracy of the FeatNet model of the 31 layer is obviously higher than the 31 layer PlainNet model, the difference is nearly 20 percentage points. Under the same data set, the accuracy of the 31 layer model is less than the 19 layer model, about 20 percent greater. On the same data set, the accuracy of 31-layers model is less than 19-layers model, although FeatNet also has overfitting phenomenon with the deepening of network depth, it is obvious that FeatNet has stronger ability to alleviate overfitting than PlainNet.
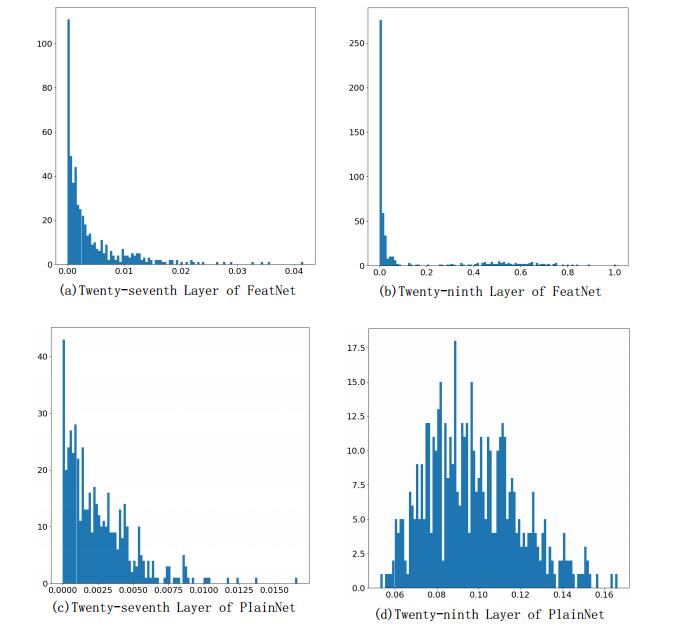
In order to explore the reason why FeatNet can alleviate overfitting problems, we output features of the twenty-seventh layer and the twenty-ninth layer convolution layer of the FeatNet-31 model and the PlainNet-31 model on UCMLU data set in visualized way, which is shown in Figure 11.
As shown in Figure 11, most of the feature maps in the twenty-ninth layer of the FeatNet-31 model are black, while the feature map of the twenty-ninth layer of PlainNet-31 presents diversity. In the convolutional neural network, the last layer of convolution layer usually passes through a global average pooling layer and then connect to a classifier, that is, the feature map is represented by the global average feature maps. The Figure 12 is the global average histogram of the output feature maps of the FeatNet-31 model and the twenty-seventh layer and the twenty-ninth layer convolution layer.
As shown in Figure 12, the feature values of the twenty-ninth layer output of FeatNet-31 are close to 0 after the global average, while PlainNet-31 is relatively homogeneous and diverse after the global average, that is, the FeatNet model using the structure of JRN is only a little activated on the top layer convolution layer. The output feature map is sparse, while the PlainNet model is activated by a large number of feature maps on the top convolution layer, and the output feature map is denser.
Table 4 shows the classification accuracy of only using twenty-seventh layer of FeatNet-31 model and PlainNet-31 model as classification features.
As shown in Table 4, the twenty-seventh layer of FeatNet-31 model and PlainNet-31 model has been able to distinguish the samples. From Figure 12 and Table 4, when JRN of the FeatNet model has a good distinction for the samples, the upper convolution layer tends to be zero, while in PlainNet, the upper convolution layer tends to be identical mapping. Actually, because the convolution layer is nonlinear, the mapping with a set of convolution layers to fit the tendencies of zero will be easier than identical mapping.
Table 5 shows the classification accuracy of using twenty-ninth layer of FeatNet-31 model and PlainNet-31 model as classification features.
As shown in Table 4 and Table 5, the accuracy of the twenty-ninth layer output of the PlainNet-31 model is much higher than twenty-seventh layers on training data set, but on the test set, the accuracy rate of the twenty-seventh layer of the PlainNet-31 model is higher than the twenty-ninth layer. That is, When the number of layers of the network reaches a certain depth, the increased convolution layers can not further improve the generalization ability. It is because the convolution layer has relatively good distinctiveness after reaching a certain depth. While the convolution layer after the convolution layer with good distinguishability of the sample is equivalent to the use of a set of nonlinear stacked convolution layers to fit the identity mapping. Not only fitting process is difficult, but also the complexity of the model increases, including increasing the possibility that the convolution layer gradually extracts noises or abstracts the inherent attributes of the training set. When the learned model is applied to the testing set, those features do not represent the whole sample. Therefore when the model has a good performance on the training set but a poor performance on the testing set, it is the phenomenon of overfitting.
The accuracy of the feature map of the twenty-ninth layer output of FeatNet on testing set is also higher than the the twenty-seventh layer output. As shown in Figure 12, most of the feature maps of the twenty-ninth layers output tend to be zero, that is, most of the feature maps are not activated, thus which reduce the possibility that using the noise or inherent attribute as the whole sample attributes. As a result, comparing with PlainNet, FeatNet has a more capability to alleviate overfitting problems.
The above experiments show that the accuracy of FeatNet with the same depth on the test set is higher than that of PlainNet without fine-tuning, especially with the deepening of convolutional neural networks, the phenomenon of overfitting of PlainNet is more serious, while, with JRN, the FeatNet can alleviate the overfitting phenomena.
In practical applications, data sets satisfying the demand of convolutional neural network are very rare. On the other hand, it takes a long time to train a convolutional neural network model from the beginning, so that the model can not be put into application quickly. Therefore people usually do not randomly initialize the convolutional neural network from the beginning. As an alternative, in order to reuse the trained models and shorten the training time, we often use the weight of the convolutional neural network model trained by large data sets as the initial weight of other related task models, and then save a lot of training time.
The following shows the comparison of the accuracy of convolutional neural networks with JRN and withouth it through experiments. By comparing the classification accuracy of the GoogleNet model, the GoogleNet-R model and the GoogleNet-Feat model on the small-sample data sets, we prove that the model with JRN has the ability to alleviate the overfitting problems.
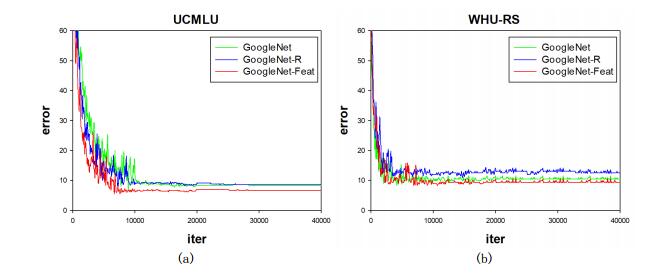
Table 6 shows the classification accuracy of the three models on two small-sample data sets without fine-tuning.
As shown in Table 6, the classification accuracy of the GoogleNet-R model is lower than the original GoogleNet model on the two small-sample data sets without using fine-tuning, that is because the GoogleNet-R model adds 8 layers of convolution layer than the original GoogleNet model, so the GoogleNet-R model is more complex than the GoogleNet model and has more overfitting problems. Especially on WHU-RS data set it is more serious. While, although the GoogleNet-Feat model has the most parameters among the three models, and is also the most complex in the network structure, but the accuracy of the GoogleNet-Feat model on the two small-sample data sets is the highest. On the UCMLU data set, the GoogleNet-Feat model is 1.66% higher than the original GoogleNet model and 1.87% higher than the GoogleNet-R model; on the WHU-RS dataset, GoogleNet-Feat model is 1.04% higher than the GoogleNet model, and is 3.12% higher than the GoogleNet-R model. Compared with the contrast experiments, the classification accuracy of GoogleNet-Feat is highest which shows it has the ability to alleviate overfitting problems.
Figure 13 shows the variation curve of the test errors with the increase of iteration number without the use of fine-tuning.
As shown in Figure 13, under the same super parameter condition, the convergence rate of GoogleNet-Feat is the fastest on the UCMLU data set and the GoogleNet model is the slowest. On the WHU-RS data set, the GoogleNet-R model has the slowest convergence rate among the three models and the GoogleNet model has almost the same convergence speed with the GoogleNet-Feat model. The GoogleNet-Feat model uses a JRN to make it faster to converge because a set of accumulated nonlinear convolution layers is easier to fit a mapping to zero than to fit a identity mapping.
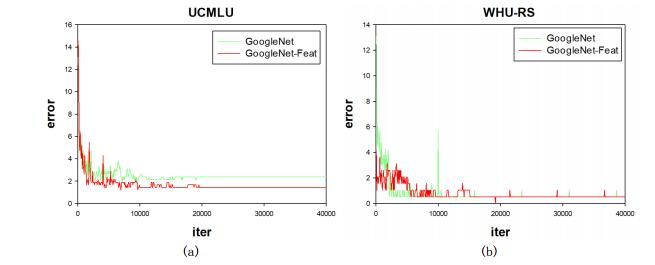
Figure 14 shows the variation curve of the test errors with the increase of iterations in GoogleNet model and GoogleNet-Feat model with fine-tuning.
The classification accuracy of Google Net model and Google Net-Feat model on small-sample datasets is shown in Table 7 under the condition of using in-depth learning model fine-tuning technology.
As shown in Table 6 and Table 7, the classification accuracy of the model on two small-sample data sets has been substantially improved after using fine-tuning technique, which shows that in the image classification task on small sample, fine-tuning technique can alleviate the overfitting phenomenon. on WHU-RS GoogleNet-TL model and the GoogleNet-Feat-TL model both have good performance, while, on UCMLU data set, GoogleNet-Feat-TL model has a better performance than GoogleNet-TL model, and the classification accuracy of the GoogleNet-Feat-TL model is nearly 0.96% higher than the GoogleNet-TL model. Therefore, we can see that with JRN, the image classification effect on the small-sample data sets is improved, besides, the structure of the model with JRN is only a few convolution layers more than the original model, therefore, the new model using JRN can easily be extended from the original model.
In summary, In our experiments, we visualize the output maps from top convolution layer with our joint residual network and without it to explore the reason how it can alleviate the overfitting problems. That is because when the depth increases of the model with JRN, the feature maps output from top layers tend to be zero which means most of feature maps are not activated. Thus it reduces the possibility that convolution layers extract the noise of training set or consider the inherent attributes of training set as the whole sample attributes. So with JRN the deep learning model can alleviate the overfitting problems. Moreover, because only a few feature maps are activated, which fit the sparsity of biological nerve that the neuron responds to a few selective at the same time and a large number of neurons can be quantified. So it can enhance the learning accuracy, in other words, the distinguishability of top convolution layer with JRN on sample data is better than that without JRN. Finally, based on GoogleNet model, we compare the classification accuracy on small-sample data sets with JRN and without it by adding fine-tuning technique, the experiment result shows with JRN the model has a high accuracy.
6.
Conclusion
In this paper, we propose a joint residual network(JRN) model to execute privacy attacks on remote sensing images, and evaluate its effectivity. Besides, we study how the fine-tuning technique can help reducing overfitting problems. The result of experiments shows that the JRN proposed in this paper can enhance the function of convolutional module. It can alleviate overfitting problems. Besides, with fine-tuning technique adopted, JRN model can also enhance the classification effectiveness on small-sample data.
Acknowledgments
This research was supported in part by National Natural Science Foundation of China (No.61572157), grant No.2016A030313660 and 2017A030313365 from Guangdong Province Natural Science Foundation, JCYJ20160608161351559, KQJSCX70726103044992, JCYJ20170811155158682 and JCYJ20160428092427867 from Shenzhen Municipal Science and Technology Innovation Project. The authors thank the reviewers for their comments.
Conflict of interest
We declare that there is no conflict of interests regarding the publication of this article.









 DownLoad:
DownLoad: