1. Mammary Gland
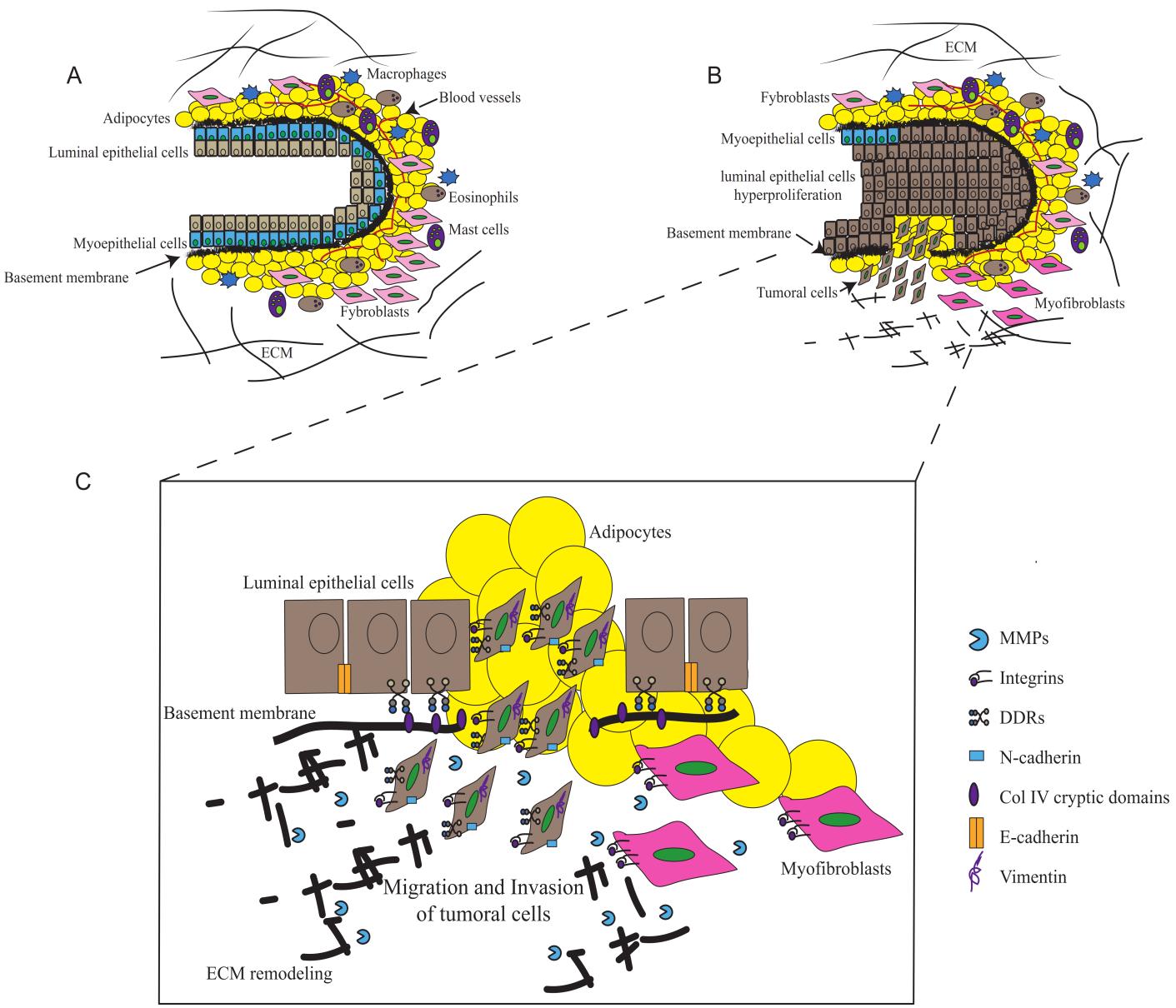
The mammary gland is an organ which is restricted to mammals, the physiological function is milk production to feed new born offspring during lactation [1]. The mammary gland is organized into a network of branched ducts that are composed of an outer layer of myoepithelial cells and an inner layer of luminal epithelial cells, which build the ductal lumen and are able to differentiate into milk-producing alveoli [2]. The mammary ducts are embedded within a stroma consisting mainly of adipocytes, fibroblasts, blood vessels, nerves and immune cells (Figure 1A) [3]. In the mammary gland, myoepithelial cells are surrounded by the basement membrane (BM), which is a specialized extracellular matrix (ECM) composed mainly of type IV collagen, laminins, fibronectin, and different binding proteins, such as nidogen and entactin. The primary function of the BM is to separate the epithelium and the endothelium from connective tissue and connect the different types of collagens with other ECM components. Moreover, BM constitutes a platform for transmission of mechanical forces and induces the activation of signal transduction pathways [4,5,6].
The mammary gland is the only organ that completes its maturation during adulthood in women, however it undergoes several morphological changes from the embryonic stage until puberty and pregnancy [1,7]. In pregnancy, mammary luminal epithelium proliferates and differentiates into milk-producing alveoli; however after lactation it undergoes involution by apoptosis. The apoptosis removes up to 80% of the epithelium and the mammary gland returns back to pre-pregnancy volume and morphology [8,9,10,11]. All of these biological processes are mediate by signal transduction pathways which are activated by several bioactive molecules including proteases, hormones, growth factors, ECM components, receptor tyrosine kinases (RTKs) and G protein-coupled receptors (GPCRs)[1,12,13]. The dysregulation of these signal transduction pathways contributes to development of different pathologies, including breast cancer.
2. Collagens
Collagens are the most abundant proteins in vertebrates and the main component of ECM. Currently, 27 types of collagen has been described and their main functions are structural [14,15]. According to their organization and properties, collagens are classified in fibrillar (types I, II, III) and non-fibrillar (types IV, X) [15,16,17]. Collagens have a typical triple helix molecular conformation characterized as Gly-X-Y motifs, where X- and Y-positions are proline and hydroxyproline respectively. Collagens are usually composed of three identical alpha helices, however certain collagens contain two or three different alpha helices [15]. The function of collagens is not only limited to a structural role in tissues, because they also play important roles in various biological processes such as cell adhesion, migration, growth, differentiation, morphogenesis, chemotaxis, wound healing, and in several pathologies [14,18,19,20].
Epithelial cells are surrounded by an intact BM composed mainly of type IV collagen, and during tissue fibrosis or cancer this BM undergoes remodeling by the action of matrix metalloproteases (MMPs), whereas fibroblast, myofibroblast and transformed epithelial cells secrete specific ECM components [15,21,22]. The secretion of MMPs mediate BM degradation and cell processes that promote migration and invasion of tumor cells, such as the epithelial-mesenchymal transition (EMT) process (Figure 1B) [21,23].
Collagens present several cryptic domains inside of the quaternary structure that are able to bind and activate membrane receptors such as integrins and discoidin domain receptors (DDRs) [24,25]. It has been proposed that ECM degradation exposes cryptic domains on collagen, which are recognized for membrane receptors, which are then activated and induce signal transduction pathways that mediate cell behavior. In breast cancer, integrins and DDRs activated by collagens are able to induce an EMT process and invasion and that, it has been proposed, may contribute to progression and metastasis of tumor cells (Figure 1C) [24,26].
3. Discoidin Domain Receptors
DDRs are RTKs expressed in vertebrates and invertebrates that exist as pre-formed dimers, which are activated by native triple-helical collagens but are not activated by denatured collagens and other ECM components [27,28,29,30,31,32]. Unlike typical RTKs, DDRs present a slow activation (phosphorylation) process and are able to maintain their activated state for several days [30,31]. The DDRs are a family with two members, DDR1 and DDR2. DDR1 is composed of five isoforms, which are generated by alternative splicing. DDR1a, DDR1b and DDR1c are functional, however DDR1d and DDRe are truncated isoforms which do not have a functional kinase domain. Recently, two DDR1 variants which are secreted have been described, but their functions have not been elucidated. DDR1 is expressed during embryonic development and in skin, lung, liver, kidney, intestine, colon, brain pancreas, and mammary epithelium; whereas DDR2 is mainly expressed in cardiac, muscular and connective tissues [4,33,34,35,36,37].
DDRs regulate several biological processes including development, differentiation, cell adhesion, and proliferation. However, DDRs also play an important role in pathological processes such as tumor growth and invasion/metastasis of several cancers [17,38].
3.1. Structure
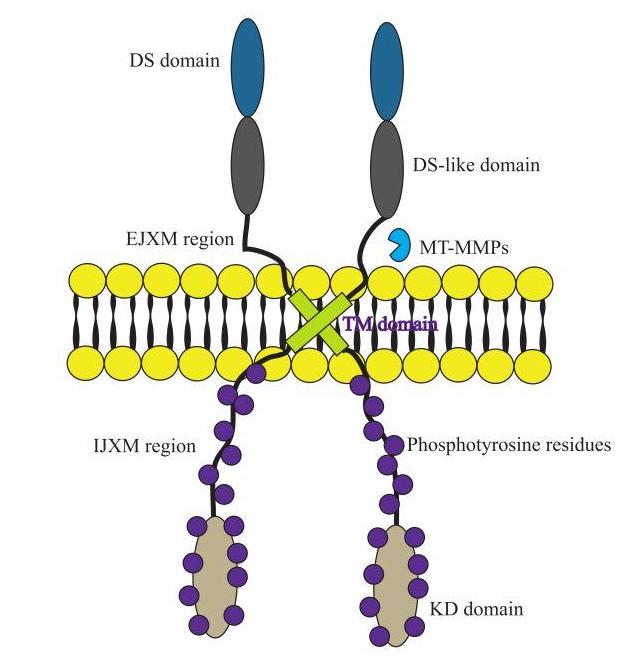
DDRs are type I transmembrane receptors composed of an extracellular discoidin domain (DS), an extracellular discoidin-like domain (DS-like), an outer juxtamembrane region (EJXM), a single-pass transmembrane domain (TM), a large inner juxtamembrane region (IJXM) and one intracellular kinase domain (KD) (Figure 2)[36]. DDRs are present as preformed dimers in the plasma membrane and they are essential for ligand binding. The DS domain contains the motifs that recognize collagen binding sequences and confer the specificity of binding to collagens [36,39,40,41,42,43]. It is proposed that the DS-like domain is involved in the activation of DDRs by collagen, however the specific function remains to be described [44]. The EJXM region contains several N- and O- glycosylation sites that regulate receptor traffic, turnover and activation induced by ligands [39]. The TM domain has a leucine zipper motif that is required for receptor signaling and it plays an important role in receptor dimerization [28]. The IJXM region is large (130-140 residues) and together with KD domain, constitutes the cytoplasmic domain, which presents tyrosine residues that are phosphorylated during DDR activation [17]. The KD domain is composed for a kinase catalytic domain that mediates phosphorylation of target proteins. The phosphorylated tyrosine residues in the IJXM region and KD domain function as attachment sites for different cytoplasmic effector and adaptor proteins that are required for signaling [36]. Additionally, DDR1b and DDR1c have 15 phosphotyrosine residues in their cytoplasmic domain; whereas DDR1a has 13- and DDR2 has 14-phoshphotyrosine residues [17,38].
3.2. Activation and signaling
DDRs have different binding affinities to collagens and are activated by specific collagens. DDR1 and DDR2 are activated by collagen types I, II and III, whereas collagen type IV activates only DDR1. DDR2 binds preferentially to collagen type X and it is not activated by collagen type IV [31,39,45]. Collagens form supramolecular structures; however these structures are not required for DDR activation. DDRs are activated by specific triple-helical peptides containing specific collagen-binding motifs, which are absent in denatured collagens [31,41,43,46].
Upon binding to collagen, several tyrosine residues are autophosphorylated in the cytosolic domains of the DDRs; these are docking sites for different proteins with Src homology 2/3 (SH2/3) and phosphotyrosine binding (PTB) domains that promote the formation of protein complexes and the activation of signal transduction pathways [17,47,48,49]. DDR1 phosphorylation induces its association with several proteins including adaptor proteins (Nck2, ShcA, Csk, Crk-II), regulatory subunits of PI3K (p85), kinases (c-Src, Pyk2), motor proteins (NMHC-IIA), Stat proteins (Stat1a/b, Stat3, Stat5), GEFs (Vav 2/3) and SHIP2 phosphatase [47,49,50,51,52,53]. Moreover, non-phosphorylated DDRs are associated with other proteins including DARP32 phosphatase, KIBRA regulator protein, Syk kinase, Notch1 transcription factor, E-cadherin cell-cell adhesion protein, and Par3/Par6 cell-polarity proteins [54,55,56,57,58].
DDR1 phosphorylation promotes the activation of PI3K/Akt and Ras/MAPK signaling pathways, which mediate activation of transcription factors such as NFκB, Hes1, Hey2 and Notch [58,59,60,61]. DDR2 maximum activation requires Src activity in COS7 cells, whereas in vitro studies demonstrate that Src phosphorylates DDR2 at tyrosine (Y)736, Y740 and Y741 and promotes autophosphorylation of DDR2 at other tyrosine residues [62,63]. In addition, DDR2 promotes proliferation and migration of mouse skin fibroblasts, whereas DDR2 activation induced by collagen I promotes expression of DDR1 and MMP-10 through a JAK2/ERK1/2-dependent pathway in primary human lung fibroblasts [50,64].
The tumor suppressor gene p53 is activated in response to cell damage and stress; activation promotes cell cycle arrest, limits cell proliferation and induces apoptosis or senescence, p53 is inactivated in most human tumors [65,66]. DDR1 is also activated in response to cell damage, and promotes survival through a p53-dependent manner and it does not require the binding of a ligand [60].
3.3. Regulation
DDR regulation has been poorly studied. It is proposed that some activated DDR isoforms are internalized, because DDR1b and DDR1c present NPXY motifs at the IJXM region and these motifs are associated to clathrin-mediated internalization. The absence of NPXY motifs in other DDR1 isoforms and DDR2 suggests that other mechanisms of regulation are utilized [29,36]. However, it is proposed that receptor internalization does not negatively regulate DDR activation, because activation of these receptors persists for long periods of time. It is suggested that DDR1 is phosphorylated during internalization and then it is recycled back to the cell surface [17]. Moreover, DDRs exist as stable dimers which is required for their activation, and therefore the structural changes in the TM domain of dimers are able to modify the activation of DDRs [28].
Another mechanism of regulation involves the EJXM region in DDR1, because this region is processed by some members of membrane-type matrix metalloproteinases (MT-MMPs) such as MT-MMP-14, -15 and -16, which release receptor ectodomain and regulate receptor activation induced by ligands [17,67,68]. In contrast, DDR2 is not regulated for MT-MMPs activity, because EJXM region does not present the recognized sequences for MT-MMPs [69,70]. In addition, phosphatases are implicated in DDR activation, because treatment of cells with pervanadate, a phosphatase inhibitor, in absence of collagen induces phosphorylation of DDR1 [51].
4. DDRs as Mediators of Adhesion and EMT Process
DDR1 is highly expressed in epithelial cells and is associated with E-cadherin. The glycoprotein E-cadherin regulates intercellular junctions, maintenance of cell polarity, and cell architecture; however, loss of E-cadherin expression is associated with EMT processes and tumor progression [54,71,72]. In normal epithelial cells, DDR1 expression induces an increase of E-cadherin levels through a decrease in its degradation rate, which is mediated by inactivation of Cdc42 GTPase. It promotes epithelial differentiation and a reduction of mesenchymal markers expression [73]. E-cadherin also regulates DDR1 activity through sequestration at cell junctions, which prevents DDR1 binding to collagen [74]. In MDCK cells, DDR1 activation mediated by type I collagen inhibits FAK activity and cell spreading through suppression of α2β1 integrin-mediated Cdc42 activity [75].
Integrins are the most studied collagen receptors in mammalian cells. During tumor establishment, there is an aberrant expression of integrins and their dysregulation is associated to cancer progression. Particularly, β1 integrin is the major adhesion receptor for several ECM components [15]. Although DDR1 activation induced by collagens is independent of β1 integrin activity, it has been described that several signaling pathways downstream of DDR1 converge with integrin signaling [76]. In epithelial cells, DDR1 and integrins maintain a close communication in order to maintain morphology, adhesion, differentiation, growth and survival [15]. In MDCK cells, DDR1 prevents adhesion and migration through inhibition of α2β1 and Stat1/3 activity and suppression of SHP2 phosphatase expression [48]. In contrast, collagen I, through activation of DDR1 and α2β1, mediates an EMT process, tumor growth, invasion and metastasis in pancreatic cancer cells [53].
EMT process is characterized by a decrease of E-cadherin and an increase of N-cadherin and vimentin expression, as well as an increase in motility and invasion [53]. In tumor epithelial cells, DDR1 upregulates N-cadherin expression whereas α2β1 integrin promotes a reduction in E-cadherin levels, and these processes induce an increase of migration and invasion [53,75,77]. In 3T3 cells, DDR1 overexpression induces an increase of β1 glycosylation and its recruitment to focal adhesions, also enhancing binding/adhesion to fibrillar collagen, and it is crucial for connective tissue homeostasis [78].
TGFβ dysregulation is associated with tumor progression and its expression in several types of cancers correlates with a decrease of metastatic potential. In pancreatic cells, DDR1 expression promotes a downregulation of TGFβ expression and induces a more aggressive phenotype of cancer; whereas an increase in TGFβ levels downregulates DDR1 expression [79]. In contrast, TGFβ is a promoter of EMT processes in late-stages carcinomas, because it induces Par6 and Smurf1 E3-ubiquitin ligase expression which mediate GTPase RhoA degradation, removal of tight junctions and actin cytoskeleton remodeling and then invasion/metastasis [80,81]. Moreover, high expression levels of TGFβ are detected in early and advanced stages of breast cancer when compared to normal epithelium; whereas it is also associated with an increase of angiogenic potential and metastasis to lung and bone [80,82,83].
TGFβ induces an increase of DDR2 expression and promotes an EMT process through a mechanism that involves collagen I, NFκB and LEF-1 in HK-2 epithelial cells [84]. In addition DDR2 is upregulated in several pathologies including cancer [38]. In head and neck squamous cell carcinoma, DDR2 increases migration and promotes invasion, and its overexpression correlates with lung metastasis [85]. In contrast, DDR1 induces cell cycle arrest and maintains epithelial characteristics, while type I collagen increases DDR2 expression with an increase of proliferation and an EMT process, as well as decrease of DDR1 expression in MDCK epithelial cells [86].
5. DDRs and Breast Cancer
Breast cancer is the most frequent carcinoma in women worldwide. Invasive ductal and lobular carcinomas are the most common histological types of breast cancer, with an average of 70-85 % of all reported cases, whereas 15-30% corresponds to in situ carcinomas [87,88]. Invasive carcinomas arise as a result of loss or gain of genes involved in the expression of tumor suppressors, mutations in GPCRs, RTKs and proteins that mediate adhesion, differentiation, growth and survival [88].
DDRs present differential expression during mammary gland development and breast cancer stages. In normal mammary epithelium, DDR1 is highly expressed and is frequently upregulated in both invasive and in situ ductal carcinomas, while it is downregulated in lobular carcinomas [88,89]. Moreover, knockout mice for DDR1 have defects in the morphology and function of the mammary glands [90]. In normal mammary epithelium DDR2 is not expressed, however it is overexpressed in invasive ductal and lobular carcinomas and is related with node invasion and poor prognosis [91,92]. DDR2 is mainly expressed in mesenchymal cells, and promotes Snail transcription factor stability in ERK1/2 and c-Src pathways-dependent manner, which induce EMT processes, migration and invasion in mammary ductal carcinoma cells [93]. DDRs play an important role in breast cancer progression through regulation of various biological processes including EMT, survival, growth, migration and invasion [17].
The BM is a structure that delimits epithelial cells with the stroma and is mainly composed of type IV collagen. The degradation of BM is a crucial step in invasion/metastasis of cancer cells [94]. In particular, type IV collagen induces expression of mesenchymal markers, activation of transcription factors (Snail1/2, NFκB), migration/invasion and therefore an EMT process in mammary epithelial cells MCF10A [26]. In addition, patients with aggressive breast cancer present an upregulation of NFκB and ZEB1; whereas ZEB1 promotes an EMT process and inhibition of DDR1 expression in mammary epithelial cells [95,96,97].
Invasive cancers show a collective migration pattern that is mediated by integrins, GTPases, and MMP secretion. Particularly, MMPs induce ECM remodeling and promote the invasion process [98]. DDR1 is associated with collective migration because it mediates cell polarity through regulation of Par3/Par6 activity and actomyosin activity suppression at cell-cell contacts [54]. In mammary epithelial cells, Syk kinase inhibits migration, however in breast cancer cells it is reported that a downregulation of Syk expression and its role on inhibition of migration is blocked for DDR1 expression [99]. In breast cancer cells, NMHC-IIA, a protein involved in cell spreading and directional migration, is constitutively associated with DDR1, and treatment with collagen I enhances this association [52].
The Wnt signaling pathway plays an important role in embryogenesis and mammary gland development [100,101]. In mammary epithelial cells Wnt-5a and its receptor, Fz-5, are required for DDR1 phosphorylation induced by type I collagen; however it also requires Gαi/0 and PI3K activity [100,102]. In addition, TGFβ induces Wnt-5a transcription and regulates DDR1 activity [103]. In breast cancer patients, it has been demonstrated that there is a correlation between Wnt-5 downregulation and a poor survival prognosis [103]. However, the relationship between TGFβ, Wnt-5a and DDR1 in breast cancer progression is still unclear.
The Notch signaling pathway is a mediator of breast cancer progression because it participates in various biological processes such as differentiation, proliferation, angiogenesis, apoptosis, and survival [104,105]. In triple negative breast cancer cells, Notch mediates an EGFR transactivation process and its hyperactivation has been associated with a poor survival prognosis [106]. In T47D breast cancer cells, collagen I promotes a functional association between DDR1 and Notch that maintains a constitutive activation of Notch [58].
Angiogenesis is a vital process in tumors, because they require nutrients and oxygen [107]. Angiogenesis involves new blood vessels formation from pre-existing ones, and represents an essential step during tumor growth and metastasis [108]. In angiogenesis induced by hypoxia, the hypoxia-inducible factor 1 (HIF-1) transcription factor and vascular endothelial growth factor (VEGF) play an important role in angiogenesis promotion [108]. In breast cancer cells, hypoxia induces an increase of DDR2 expression and promotes an EMT process, migration, invasion, and metastasis [109].
CD9 is a tetraspanin family member widely expressed in the plasma membrane of several cell types including malignant cells. Tetraspanins are implicated in a variety of physiological and pathological processes and are adapter proteins that mediate signal transduction pathways [110]. Particularly, CD9 is associated with and regulates the signaling of several integrins, such as: α3β1, α4β1, α5β1, α6β1, α6β4, and αIIbβ3 [111]. Furthermore, CD9 is associated with EWI family proteins and EGFR and participates in cytoskeleton remodeling [112], whereas CD9 is able to act like a metastasis suppressor because an inverse correlation between CD9 expression and the malignancy grade/metastasis in several cancers including breast cancer have been described [113]. In contrast, type IV collagen induces a transient CD9 expression at the plasma membrane and promotes migration through a DDR1-dependent pathway in MDA-MB-231 breast cancer cells [114].
6. Conclusion
Breast cancer is a heterogeneous disease and affects women worldwide. Metastasis is the principal cause of death in breast cancer patients and BM degradation plays a crucial role during breast cancer progression and metastasis. BM is composed by collagen type IV, laminins, fibronectin and linker proteins. During BM degradation cryptic domains inside of quaternary structure of collagens can activate two classes of receptors, integrins and DDRs. DDRs are activated by native triple-helical collagen and are involved in several cancer-related biological processes. In the case of breast cancer, DDRs regulate cell adhesion, proliferation, EMT process, migration, invasion, and survival.
Finally, we can summarize that DDRs are expressed and regulated in a differential manner in breast cancer cells and their function depends on the tumor stage and the type of ligands that induce their activation. The crosstalk of DDRs with other receptors such as integrins or Notch and their association with other proteins as Wnt-5a and CD9 tetraspanin shows the great complexity in cell communication mediated by DDRs in breast cancer cells.
Acknowledgments
This work is partly supported by a grant from ICYTDF (224/2012). E. R-U and N. S-M. are supported by a CONACYT predoctoral training grant.
Conflict of Interest
All authors declare that there are no conflicts of interest.









 DownLoad:
DownLoad: