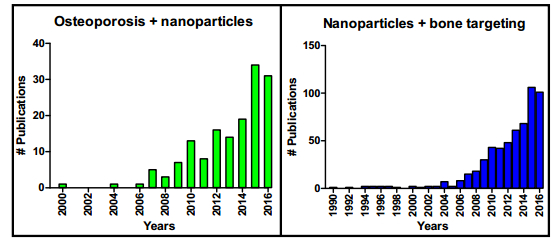
1. Introduction
1.1. Osteoporosis
Osteoporosis is a progressive skeletal disease characterized by reduced bone mass and microarchitectural deterioration of bone tissue, with a consequent increase in bone fragility and susceptibility to fracture. According to the definition given by the World Health Organization, osteoporosis is diagnosed when a patient has a bone mineral density of 2.5 standard deviations or more below the average value of bone mass for young healthy adults [1]. In adults, bone is remodeled by a coordinated process in which bone resorbing osteoclasts remove old bone, and bone-forming osteoblasts synthesize and mineralize new bone matrix [2]. Disturbances in this physiological process lead to a decreased bone mass, namely, osteoporosis. Unfortunately, the current treatments for osteoporosis have notable restrictions, including adequacy and long-term safety issues [3]. It does not exist yet a satisfactory solution to the problem of bone weakening due to osteoporosis [4]. The treatment options of osteoporosis are limited to anti-resorptive drugs, that slow down the excess of bone resorption (principal cause of primary osteoporosis); and anabolic agents, that effectively increase the bone mass that has previously disappeared as a consequence of resorption excess [5]. With increased aging population and life expectancy, bone diseases have become the most prevalent degenerative disorders and a major public health problem in many countries [6,7], which has fuelled the interest in prevention and treatment. According to the International Osteoporosis Foundation, osteoporosis is estimated to affect one in three women and one in five men over the age of 50 years [8]. In fact, a bone will break every 3 seconds because of this disease. This problem has an enormous human and socio-economic impact. In the European Union, the economic burden of incidents and prior fragility fractures mainly due to osteoporosis was estimated at €29 billion in the five largest EU countries (France, Germany, Italy, Spain and UK) and €38, 7 billion in the 27 EU countries [9].
1.2. Current treatments for osteoporosis
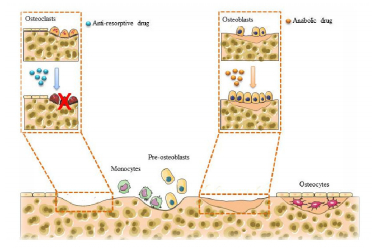
Therapeutic strategies to limit bone loss and prevent fracture are predominantly divided in two main groups (Figure 1) [9], anti-resorptive drugs, that target osteoclasts, and bone forming accelerators or anabolic drugs, designed for osteoblast stimulation [10]. Anti-resorptive drugs act mainly by suppressing osteoclast activity preserving bone mass and increasing bone strength [4,11]. On the other hand, anabolic drugs are able to induce bone formation and can reverse bone deterioration generated by the osteoporosis progression [4,12].
1.2.1. Anti-resorptive drugs
In the last few years osteoporosis therapeutics have been monopolized by bisphosphonates (BP) capable of averting further bone degradation in well-established osteoporosis [13]. BP disrupts osteoclast activity by inhibiting farnesyl pyrophosphate synthase, critical enzyme for membrane protein prenylation and osteoclast detachment from bone [14]. Ultimately, they induce osteoclast apoptosis, thus reducing bone resorption [15]. Even though they are capable of reducing the fracture risk and bone turn over, the effect of these drugs in increasing or recovering bone mass is really small, at < 2% per year [16]. Furthermore, BP are not easily absorbed by intestine, presenting variable bioavailability, being necessary to ingest the drug 2 hours before breakfast and avoid the administration of a second drug for 30 minutes in order to minimize the interactions with cations like calcium, iron, etc. [13]. It is necessary to orally administrate high doses, what causes several side effects like esophagitis [3], due to the local action on the mucosa, or jaw necrosis due to an excessive inhibition of bone resorption [17]. Taking this into consideration, it is relevant to know about long-term treatment with bisphosphonates. Clinical studies have examined the effects of using bisphosphonates in treatments of 3, 5 or 10 years. They showed a persistent antifracture and bone mineral density increasing effects beyond 3 years of treatment [18]. On the other hand, more serious adverse effects, or discontinuation due to adverse effects were reported between patients with 10 years treatment versus those with just 5 years treatment [19].
Another anti-resorptive drug is raloxifene (RLX). RLX is a second generation non-steroidal benzothiophene, selective estrogen receptor modulator (SERM). It acts as estrogen agonist in bone. RLX reduces bone loss by inhibiting the activity of cytokines which increase bone resorption. Although RLX is rapidly absorbed by the intestine, it will suffer an extensive pre-systemic glucuronide conjugation. Consequently, the absolute bioavailability achieved is very low.
Osteoclast differentiation is triggered when Receptor Activator of Nuclear Factor κB ligand (RANKL) binds to its receptor, RANK, present on the surface of osteoclasts and osteoclast precursors [20]. This interaction will promote osteoclast differentiation through preosteoclast fusion and osteoclast survival. Consequently, it generates multinucleated mature bone-resorbing osteoclasts, which increment the bone resorption rate [2,10,20]. According to this concept, a monoclonal humanized anti-RANKL antibody has been developed and currently used as osteoporosis therapy [10].
1.2.2. Anabolic drugs
Recombinant human parathyroid hormone (rPTH) [21] and estrogens [22] are anabolic agents for bone formation that have demonstrated their efficacy in osteoporosis [5,22,23]. rPTH by daily administration has proven to be more efficient than BP therapy by increasing bone mass. This drug is used for its capability of stimulating bone formation [24] and for its ability to suppress apoptosis of osteoblasts [25]. However, the increased hypercalcemic and tumor risk associated with prolonged hormone administration, and need for daily injections, limits the long-term treatment to 24 months [26].
Another way explored to promote bone formation is the administration of growth factors like bone morphogenetic proteins (BMPs). They stimulate bone formation and increase bone strength and density [5,27]. However, supraphysiological doses are necessary to achieve therapeutic effects, what can lead to undesirable effects such as uncontrolled bone formation, inflammation or even tumorigenesis [28]. Furthermore, the short half-life of BMPs limited their systemic administration [29].
More recently, gene silencing through the delivery of small interfering RNA (siRNA) has been used as treatment for bone disease such as osteoporosis. Due to the several advantages that this therapy presents, its study has increased notably [30]. In this type of therapy, siRNA targeted those genes that had been identified to down regulate bone formation without modulating bone resorption. However, high doses of siRNA are necessary to sufficiently stimulate bone formation, what drives to a high risk for adverse effects in non-skeletal tissues [31].
Taking these aspects into consideration, one of the most important and persistent problems of osteoporosis treatment is the several side effects of the different current drugs. It is clear that the development of specific delivery systems for each developed drug is necessary.
2. Drug Delivery and Bone Release by Nanotechnology
Drugs delivered systemically are absorbed into the blood stream and distributed through the body. They are rapidly clear from the body and poorly penetrate into bone tissue. Bone compared to other organs like brain, liver, or kidney is less vascularized which is the principal reason why drugs penetrate less in bone than in other tissues [32]. Thus, they are generally administered in a high dose or/and frequently, what can result in systemic toxicity. It would be safer and more effective if the drug could be delivered specifically to bone tissue through a controllable drug delivery system [33]. Drug delivery systems (DDS) are designed for improving the therapeutic effect of drugs, minimizing their potential toxic side effects. In the last few years the use of nanoparticles as DDS applied to bone diseases has gained growing attention (Figure 2). The drug carrier would transport the drug to bone tissue, there releasing the therapeutic agent, which either promotes bone growth or reduces bone resorption. In this sense DDS optimize the drug doses, protect drug from biodegradation and reduce the drug exposure to non-target cells [23,34]. For example, during the treatment with estrogen, the distribution of the drug to other tissues different from bone can produce several effects such as intrauterine hemorrhage, increasing uterus weight or even endometrial and breast cancer [35,36]. Recent research developed an estradiol-prodrug, consisting of estradiol conjugated with an Asp-oligopeptide carrier. They found that it was selective to bone, and even produced a long-term action on bone, avoiding the side effects of estradiol. The use of this selective bone delivery system would also extend medication intervals, resulting in a better quality of life for patients [37].
A targeted drug delivery system is a system that releases the drug in a preselected site. The bone targeting moieties and the carriers are the most important elements in a drug delivery system targeting bone diseases [36].
2.1. Bone-targeting moieties
In order to guide nanoparticles to bone, it is important to find moieties with strong affinity to it. It is known that bones are made of a mineralized matrix, being hydroxyapatite (HA) its principal component [38]. Since HA crystals are present in a high concentration in bone, it would represent a promising target for selective delivery [39]. Moieties with high affinity to HA should be taken into consideration.
2.1.1. Tetracycline and bisphosphonate
Tetracycline and bisphosphonate have strong affinity with the calcium present on HA, so they can be used as bone-targeting moieties [35]. Tetracycline was the first to be used because of its strong affinity with calcium. It is used as antibiotic but, due to the high affinity to bone it caused children teeth to stain yellow, so its use was discontinued in pediatric medicine. Despite this fact, its use as antibiotic in adults and as bone targeting moiety has persisted [40]. Consequently, smaller molecules with similar bind capacities as tetracycline were designed, as tetracycline analogues [41]. Neale et al. tried to reduce potential side effects caused by tetracycline's biological activity by minimalizing tetracycline structure. The modifications were still able to bind HA but did not retain the biological activity [42]. Despite these efforts, its complicated chemical structure and its poor stability during chemical modifications, pledged its use [36]. Unlike tetracycline, bisphosphonates have attracted the attention as bone-targeting moieties in recent years. They are widely used to treat the osteolysis diseases due to their high affinity to HA, their capacity to bind at sites with osteoclastic activity and their ability to inhibit bone resorption. These facts permit to use the same molecule for targeting and for treating the disease [14].
2.1.2. Oligopeptides
Furthermore, some studies found moieties capable of discriminating between bone-resorption surface and bone-formation surface. It has been reported that eight repeating sequences of aspartate (Asp8) preferentially bind to bone-resorption surface, and (AspSerSer)6 showed favorable binding to bone-formation surface [31]. Thanks to this, it is possible to use one moiety or another depending on the type of drug used. If it is an antiresorptive agent, it should be used Asp8 which guides to bone resorption surface, or if it is an anabolic agent, it should be used instead (AspSerSer)6 that should be guide instead to bone formation surface [43].
2.2. Nanocarriers in osteoporosis therapy
In the last few years, nanoparticles have been found to be promising carriers for efficient therapeutic delivery in bone disease therapy. For bone regeneration in osteoporosis patients, the development of nanoparticles is ideal since bone itself is a nanocomposite. In addition to this dimensional similarity, they can offer drug protection from biodegradation, transport efficiency, and even improve its pharmacokinetic, pharmacodynamics, biodistribution and targeting [36]. Thanks to their capability to be chemically modified they can enhance therapeutic loading, increase tissue specificity, decreasing doses without sacrificing treatment efficacy [44].
Table 1. Summary of bone targeting drug delivery system with therapeutic activity.
| Therapy
|
Bone targeting moiety
|
Carrier
|
Reference
|
| Thermolysis |
ALN |
Fe3O4 NPs |
[45]
|
| ALN |
ALN |
Gold NPs |
[17]
|
| RANKL siRNA |
AspSerSer6
|
Cationic Liposomes |
[46]
|
| ALN |
ALN |
HA NPs |
[47]
|
| RIS |
RIS |
ZnHA NPs |
[13]
|
| RANK siRNA |
*
|
MBGxs |
[10]
|
| RLX |
*
|
Chitosan NPs |
[23]
|
| Ethinylestradiol |
*
|
Liposomes |
[48]
|
| *The targeting moiety is not specified; ALN: Alendronate RANKL: Receptor Activator for Nuclear Factor κB ligand siRNA: small interfering RNA RIS: Risedronate RLX: Raloxifene; Asp: Aspartate Ser: Serine; HA: Hydroxyapatite NPs: nanoparticles MBG: Mesoporous bioactive glass nanospheres. |
2.2.1. Organic nanoparticles for osteoporosis treatment
(1) Liposomes
Liposomes were the first nano-delivery system that succeeded in becoming a clinical application [49]. Generally, liposomes are made by the self-assembly of lipid molecules with a hydrophilic head group and hydrophobic tail. The addition of cholesterol reduces the membrane permeability, and then it improves the mechanical characteristics of the liposome [48,50]. This structure permits to have an aqueous core enclosed within a phospholipid bilayer that permits to load drugs with different solubility. Hydrophobic agents would be in the bilayer membrane, while hydrophilic agents would be in the aqueous core [51]. One of the biggest handicaps of liposomes is the rapid uptake by reticuloendothelial system (RES), which is traduced in a low circulation half-life. Incorporating polyethynel glycol-lipid (PEG-lipid) conjugated with the bilayer will decrease the uptake by RES so the time in blood stream will increase [52].
During the last years a new generation of liposomes was created for the specific delivery of genes to treat bone diseases. Lu et al. prepared ethinylestradiol liposome (EEL) and investigated its action against postmenopausal osteoporosis using the ovarectomized rat model. They concluded that EEL, compared to free ethinylestradiol, were more effective in stimulating the amount of calcium deposition in bone, and also increasing the osteoblast activity and the active bone formation [48]. Zhang et al. linked (AspSerSer)6 with a cationic liposome which encapsulates an osteogenic siRNA. This siRNA targets a negative regulator of osteogenic lineage activity (Plekhol) [53]. Cationic liposomes are made of cationic lipids which have one or more amines present in the polar head. These liposomes bind and condense DNA spontaneously to form complexes with high affinity to cell membranes and capable of delivering the plasmids into the cells [54,55]. This permits the delivery of therapeutic cargos (e.g. siRNAs) to the target osteogenic-linage cells, as an alternative to the modulation of bone-resorption [31]. Compared to the cationic liposomes, neutral liposomes have lower toxicity, longer circulation half-life, and less interaction with proteins [53]. Neutrally charged lipoplexes can be implemented to the cationic liposome system in order to solve these problems. Similar to this, Hengst et al. designed liposomes and used cholesteryl-trisoxyethylenebisphosphonic acid (CHOL-TOE-BP), a new tailor-made bisphosphonate derivate, as bone targeting moiety. These liposomes were designed for the treatment of bone related diseases such as osteoporosis [56].
(2) PLGA-nanoparticles
Compared to liposomes, rigid nanoparticles are promising as delivery system because of their high capacity of cargo and their nano-size. Synthetic biodegradable polymers as poly-lactide (PLA) and the copolymer poly (lactide-co-glycolide) (PLGA) have been extensively used for the synthesis of nanoparticles [57], due to their excellent host biocompatibility, non-toxicity, and tuneable degradation rates [58]. It is possible to achieve different drug release profiles by modifying the molecular weight, the copolymer ratio, the particle size, the porosity, and the manufacturing conditions [34]. Another advantage of PLGA is that it can be functionalized and modified allowing the attachment of biological molecules [59]. Furthermore, it has been FDA-approved for a number of biomedical applications. PLGA properties such as swelling, the molecular interaction potential with the cargo [34], the controllable degradation period (about 1-6 months) [35] make it the perfect candidate for the design of controlled delivery systems. Jiang et al. have developed PLGA-based nanoparticles with a short sequence of poly-aspartic acids that have shown to interact exclusively with hard tissues. Fluorescein isothiocyanate (FITC) was tagged to the nanoparticles in order to study their distribution and binding capacity. The in vitro and ex vivo studies showed the exclusive binding affinity of FITC-poly-Asp nanoparticles to bone tissue [59]. The accumulation of the nanoparticles in bone niches permits a higher local drug concentration, reducing side effects and lengthening the therapeutic window. Similar to this, Fu et al. developed bone-targeting nanoparticles using PLGA-PEG copolymers and Aspn-based bone targeting moieties (1-3). Asp3-nanoparticles showed the best binding capacity to apatite [60]. Moreover, Cong et al. designed PLGA-PEG nanoparticles and functionalized with alendronate (ALN), which is a type of bisphosphonate, as bone targeting moiety [61].
(3) Chitosan NPxs
Chitosan is one of the most used polymers in drug delivery due to its properties like biocompatibility, non-toxicity and biodegradability with ecological safety [23]. Chitosan is a copolymer of β-(1-4) linked 2-acetamido-2-deoxy-β-D-glucopyranose and 2-amino-2-deoxy-β-D-glycopyranose, is obtained by deacetylation of chitin which is widely distributed in nature. The presence of amino groups permits it to be protonated at low pH that makes it soluble in water. On the other hand, when the pH increases over 6 the chitosan amines become deprotonated so the polymer becomes insoluble [62]. Saini et al. prepared nanoparticles by an ionic gelation process of chitosan and tripolyphosphate (Figure 2) [23]. The interactions between the positive amino groups of chitosan and the negative charged tripolyphosphate caused the formation of the nanoparticles [63]. After that the drug raloxifene was loaded in the nanoparticles in order to achieve a new formulation for the intranasal delivery of raloxifene for osteoporosis therapy. Mucoadhesive nature of the polymer helped the nanoparticle in adhering to the nasal mucosa what permits the direct delivery of the drug to systemic circulation. Finally it was concluded that raloxifene loaded chitosan nanoparticles could be a novel drug delivery system for osteoporosis treatment [23].
2.2.2. Inorganic nanoparticles for osteoporosis treatment
(1) Bioactive-silica nanoparticles
Some studies have suggested a beneficial effect of dietary silica on skeletal development in rats [64]. Clinical studies revealed positive associations between dietary silica intake and bone mineral density (BMD) in human cohorts [65]. Silica is famous for being nontoxic in vivo below the concentration of 50, 000 ppm without adverse effects in rats [2]. However the mechanisms by which silica affects skeletal development are unknown. Some studies postulated that silica nanoparticles would be bioactive and beneficial to the skeleton [2]. Beck et al. examined the effect of 50 nm silica-based nanoparticles on the differentiation of osteoclast and osteoblast. The authors of the study finally revealed that the nanoparticles were biologically active; they suppress osteoclast differentiation and stimulate osteoblast differentiation and mineralization in vitro. However, the exact mechanisms are not completely understood. The nuclear factor kappaB (NF-κB) is a transcription factor necessary for osteoclast differentiation [66], and a potent inhibitor of osteoblast differentiation and activity [67]. Therefore, antagonists of NF-κB will promote osteoblast differentiation and will suppress osteoclast formation [68]. It is true that these nanoparticles suppress NF-κB signaling after 24 hours, what could be a partial explanation of how nanoparticles may regulate osteoclast and osteoblast differentiation [2]. Furthermore, in vivo nanoparticles have the capacity to increase BMD in mice, suggesting their possible application in osteoporosis treatment [2]. Recently, Ha et al. investigated the cellular mechanism by which silica-based nanoparticles stimulate differentiation and mineralization of osteoblasts. They revealed that nanoparticles are internalized by caveolae-mediated endocytosis, stimulate ERK1/2 signaling pathway, which is necessary for the processing of LC3β-Ⅰ to LC3β-Ⅱ, stimulating the autophagosome assembly. Although it is not completely understood, this process is stimulatory to osteoblast differentiation and mineralization [69]. This conclusion is supported by a recent study which found that the inhibition of the autophagosome formation blocked bone mineralization [70].
Mesoporous silica nanoparticles (MSNs) have been also reported as a drug delivery system [71,72]. In 2001, the mesoporous material MCM-41 was proposed for the first time as DDS [73]. Sun et al. fabricated MSNs anchored by zolendronate for targeting bone sites, which can be used as DDS of antiosteoporotic drugs [74]. Gene silencing through delivering small interfering RNA (siRNA) has a lot of advantages due to the intrinsic nature of RNA interference (RNAi). SiRNA interferes reducing the expression of a specific gene. This technique has gained great potential as bone disease therapy enhancing bone tissue formation [30]. Among different silica-based nanoparticles, MSNs have great potential to deliver molecules like siRNA. Generally, siRNAs have very short half-life, poor capacity of penetration through the cell membranes, and are immediately degraded by RNase [10]. Consequently, more research is necessary in order to find a nanocarrier which can solve these problems. Because of their unique properties like, large surface area, surface functionality, tunable pore size, loading capacity, and biocompatibility, MSN study as potential delivery systems for genetic molecules have increased [75,76]. Mesoporous bioactive glass nanospheres (MBG) are a type of calcium-added MSNs. They have potential applications for hard tissue repairs and regeneration. Kim et al. demonstrated a novel therapeutic application in which MBGs suppress osteoclastic functions by delivering RANK siRNA [10].
(2) Metal nanoparticles
Thermotherapy has been attractive for the treatment of osteoporosis. It is capable of generating cell death by disrupting cell membranes and denaturing intracellular proteins [77]. It has been used in order to control osteoporosis by destroying osteoclasts through thermolysis. Iron (Ⅱ, Ⅲ) oxide (Fe3O4) nanoparticles are chemically stable, nontoxic, and cost efficient. They have a high magnetic field that can be used to increase local temperature, and in this way trigger osteoclast regulation [78]. Lee et al. synthesized nanoparticles of Fe3O4 by co-precipitation and then coated them with dextran (Dex), in order to increase nanoparticle dispersion in aqueous solvents [45]. After that, to acquire the capacity to bind bone surface, they grafted ALN onto magnetic nanoparticles. ALN has two principal groups, an amino group, responsible for the inhibition of osteoclast activity, and a bisphosphonate group which has high affinity to bone hydroxyapatite. The amino group is responsible for the main side effects observed, namely nausea, abdominal discomfort or vomiting. Thus, they inactivated that group by grafting it with the nanoparticles. Consequently, the ALN/Dex/Fe3O4 nanoparticles have affinity to bone, can be phagocyted by osteoclasts, and then by radiofrequency induce thermolysis and cause osteoclast death [45].
Other metal nanoparticles, like gold nanoparticles, have been studied for osteoporosis applications. Recent studies reported that gold nanoparticles can promote osteoblast differentiation and inhibit osteoclast differentiation [17,79]. Choi et al. reported that chitosan-conjugated-gold nanoparticles at nontoxic concentrations (1 ppm) stimulate osteogenic differentiation of human adipose-derived mesenchymal stem cells (hADMSCs). According to their results, mechanical stimulation by uptake of chitosan-conjugated AuNPs in hADMSCs enhances its differentiation into osteoblasts through the activation of the Wnt/β-catenin signaling pathway. Consequently, the accumulation of β-catenin promotes the differentiation of hADMSCs to osteoblast [79]. Lee et al. showed that 30 nm gold nanoparticles conjugated with ALN have a synergistic effect of inhibiting osteoclast differentiation [17]. As we mentioned previously RANKL is a determinant factor for osteoclasts differentiation, and reactive oxygen species (ROS) play an important role in this respect [80]. Gold nanoparticles reduce the production of ROS by RANKL and also increase the expression of glutathione peroxidase-1 [81], both actions suppress osteoclast formation [82].
(3) Hydroxyapatite nanoparticles
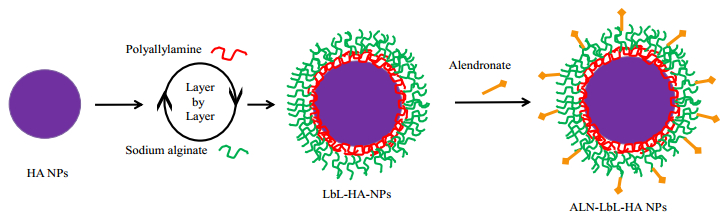
HA is a bio-mineral, one of the principal constituents of human bones matrix and teeth. HA is biocompatible, biodegradable, and has excellent osteoconductive properties [83]. Early studies demonstrated that nano-sized HA promotes osteoblast bioactivity, enhancing bone regeneration [84,85]. In this regard, nanocarrier itself helps bone tissue to grow, and increases bone mass deposition. Hwang et al. [47] designed HA-based nanoparticles which can deliver drugs and bone mineral to bone tissue. In order to functionalize nanoparticles surface, they were coated by a layer-by-layer method with three layers of poly (allylamine) (PAA) and alginate (ALG) (Figure 3). Then, at the outmost layer, ALN was conjugated, which confers the capacity to bind bone tissue. ALN was used as a targeting moiety and also as anti-resoprtive drug. The HA acts like a core for the nanoparticles, and when they arrive to bone matrix they increase bone density by inducing osteoconduction [47].
Some studies reported that HA-based nanoparticles loaded with risendronate (RIS), which is a bisphosphonate, increase bone density and improve stiffness and strength of bone. Compared to the administration of RIS alone, HA-based nanoparticles loaded with RIS were much efficient, even with lower concentrations of RIS, which reduced side effects [83]. Khajuria et al. chose zinc-hydroxyapatite (ZnHA) to design their nanoparticles [13]. They decided to dop the HA with zinc. Since several studies demonstrated that zinc-HA enhanced HA bioactivity. Zinc shares properties with calcium, so it can replace calcium in HA and therefore in bone. Zinc enhances bone growth and bone mineralization by stimulating osteogenesis of osteoblasts, represses osteoclast function [68] and improves bone protein synthesis [84]. However, it is important to know that concentrations over 225 mg of zinc generate cytotoxic effects [85]. These ZnHA-based nanoparticles were loaded with RIS in order to achieve bone targeting. The results demonstrated that ZnHA/RIS nanoparticles present a therapeutic advantage over pure RIS or HA/RIS nanoparticles [13].
Table 2. Summary of advantages and disadvantages of different types of nanoparticles.
| Type of nanoparticle
|
Advantages
|
Disadvantages
|
| Liposomes |
Load drugs with different solubilities *Neutral liposomes: Longer circulation half life, lower toxicity |
Rapid uptake by reticuloendothelial system Toxicity |
| PLGA-nanoparticles |
High capacity of cargo Biocompatibility Different drug release profiles |
More in vivo Tests such as bone targeting and whole body biodistribution are needed |
| Mesoporous silica nanoparticles |
Surface functionality Loading capacity Biocompatibility Bone-bioactivity related to ionic release |
The limited accessibility and high cost of organic template lead to its restricted use in practical applications There are not many studies done in vivo, and this can be challenging for MSN in clinical applications |
| Metal-nanoparticles |
Hyperthermia treatment, inducing thermolysis by radiofrequency. Drug delivery, and can be used as magnetic resonance imaging (MRI) contrast agents |
They can spontaneously aggregate and cause vessel embolism after intravenous application |
| Hydroxyapatite nanoparticles |
HA promotes osteoblast bioactivity, nanocarrier itself helps bone tissue to grow |
Its brittleness that makes it a hardly processed material.
|
3. Conclusion
Osteoporosis is a disease that has become a worldwide challenge, involving clinical, social and economic issues. Health systems and industry should be aware of this problem mainly because of the increase in life expectancy. This has a consequence of an ageing population more susceptible to suffer osteoporosis. Being osteoporosis a disease that affects a increasing proportion of the population, its treatment will have a great economic interest for the pharmaceutical industry. Current pharmacological therapy presents some limitations related to bioavailability issues and toxicity. The emergence of nanotechnology has provided new strategies for improving the properties of these therapies. Among different nanocarries bone-targeted nanoparticles represents a great potential for clinical applications in delivering drugs to bone niches. They are able to increase local drug concentration, reduce off-target side effects, and would lengthen the therapeutic window. However, only limited work has been reported so far on the release pattern and mechanism (s) involved, especially for the newly developed carriers. Consequently, more research is awaiting driven by the optimization of the carriers, focusing on drug release, stability and safety. Although more research is needed for clinical applications, there is an opportunity for prospective treatment options by enhancing nanotechnology.
Acknowledgements
The authors thank funding from the European Research Council (Advanced Grant VERDI; ERC-2015-AdG Proposal no. 694160).
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: