Biotechnological applications of bacterial cellulases

1.   Introduction

In the past decade, robot manipulators have been extensively concerned in industrial assembly, agricultural picking, medical surgery, and other fields ^[1]. Robot manipulators usually face uncertainties such as parameter perturbations, external interferences, frictions, and noises during the service process. Meanwhile, it is expected of high working accuracy such as in position reaching and trajectory tracking. Therefore, the control techniques of robot manipulators are fundamental.

PID controller has been widely used due to its simple structure and acceptable performance during the early stages of the robot industry ^[2]. However, it is quite challenging to obtain the optimum PID parameters because robot manipulators are complex systems with nonlinearity, strong coupling and time varying characteristics. Even worse, for occasions with high precision requirements and complex dynamic constraints, PID is difficult to achieve an ideal performance. To improve the control precision of robot manipulators, sustained efforts have been made to implement robust and optimal control. Many novel control techniques have since emerged, for example, artificial neural network controller ^[3], fuzzy logical controller ^[4,5,6], adaptive nonlinear controller ^[7], sliding mode controller ^[8], linear matrix inequality scheme ^[9], linear quadratic controller ^[10], H∞ controller ^[11,12], reinforcement learning-based controller ^[13], model predictive control (MPC) ^[14,15] and other optimal control strategies ^[16,17,18].

Optimal control techniques always have a distinctive feature, which can simultaneously consider the constraints of input variables, output variables and state variables. Due to robustness, MPC is considered to be a promising controller among the optimal control techniques for the applications in industrial robots ^[19]. Satoh et al. proposed a disturbance observer-based MPC for the tracking control of manipulators ^[20]. Wilson et al. introduced a simplified nonlinear model predictive control (NMPC) for a 2-DoF (degree of freedom) vertical robot manipulator ^[21]. Best et al. put forward a control scheme based on MPC for a 5-DoF soft humanoid robot ^[22]. Based on MPC, Incremona et al. presented a hierarchical multiloop control scheme integrated with a sliding mode controller for a 3-DoF robot manipulator ^[19]. Guechi et al. compared MPC with a linear quadratic controller of a 2‐DoF robot manipulator ^[23]. Carron et al. developed a Gaussian process-based MPC for the offset-free tracking of a robot manipulator ^[24]. MPC and NMPC always encounter some parameters to be determined, and intuitively chosen parameters mostly bring mediocre performance. The aforementioned MPC/NMPC parameters are determined by the trial and error method or the Ziegler Nichols method. Nevertheless, these traditional optimization methods are usually brutal or cumbersome to determine the parameters of MPC/NMPC for robot manipulators due to the nonlinearity and complexity.

The determination of MPC parameters can also be transformed into an engineering optimization problem. In this way, the problem can be extended to take advantage of the benefits from the meta heuristics, which is an efficient strategy for solving complex engineering optimization problems based on computational intelligence. Growing numbers of metaheuristic algorithms have emerged in recent years, such as Particle swarm optimization (PSO) ^[25], Grey wolf optimizer (GWO) ^[26], Monarch butterfly optimization (MBO) ^[27], Sparrow search algorithm (SSA) ^[28], Slime mould algorithm (SMA) ^[29], Moth search algorithm (MSA) ^[30], Hunger games search (HGS) ^[31], RUNge Kutta optimizer (RUN) ^[32], Colony predation algorithm (CPA) ^[33], Multi-tracker optimization (MTO) ^[34], weIghted meaN oF vectOrs (INFO) ^[35], Harris hawks optimization (HHO) ^[36], Mayfly optimization (MO) ^[37], and Satin bowerbird optimizer (SBO) ^[38]. Lately, a new metaheuristic algorithm, Transient search optimization (TSO) ^[39], inspired by the transient physical behavior of switched electrical circuits with inductance and capacitance included, was initiated and it has shown considerable competitiveness for solving engineering optimization problems.

To address the problem of the determination of MPC parameters, Elsisi recently provided an optimal design scheme of NMPC on the basis of MTO, by using the packaged NMPC toolbox in Matlab ^[40]. However, it is noted that NMPC generally requires higher computational time or cost than MPC does. In addition, to our best knowledge, only seldom literature discussed the optimization of MPC/NMPC by metaheuristic algorithm and no existing applications of TSO in MPC parameter optimization have been mentioned yet. This motivated our attempt to propose a new scheme for optimizing MPC parameters of the robotic manipulator by using TSO.

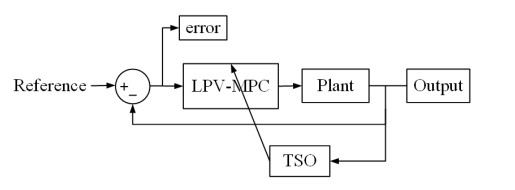
In this paper, inspired by ^[39] and ^[40], aiming of reducing the computational complexity due to nonlinearity of NMPC and extending the application of TSO algorithm, an alternative TSO-based MPC (TSO-MPC for short) controller is proposed. Specifically, the nonlinear dynamics equation of a two-link robot manipulator is transformed into linear parametric-varying (LPV) forms and then the corresponding MPC scheme is established. Afterwards, the TSO algorithm is employed to optimize the objective function, figure of demerit (FoD), of the MPC for the robot manipulator. As will be seen in a later section, the proposed TSO-MPC suggests state-of-the-art performance in solving the tracking problem of the robot manipulator.

The remainder of this paper is organized as follows. Section 2 reviews the dynamic model of the robotic system and establishes the linear parametric-varying MPC (LPV-MPC, also written by MPC for short below). In Section 3, the TSO is described and the objective function and error indices to be optimized are given. Section 4 implements the proposed MPC scheme and optimization process, and discusses the optimized performance of the MPC scheme in set-point tracking, trajectory tracking, and robustness on parameters uncertainties. Section 5 summarizes the full text.

2.   LPV-MPC for robot manipulators

2.1.   Dynamics equation of robot manipulators

When a robot manipulator working in a horizontal plane, the dynamics equation can be denoted by ^[41]

where $ \mathbf{q} $ is the generalized coordinates, $ \mathbf{D}\left(\mathbf{q}\right) $ is the inertia matrix, $ \mathbf{C}\left(\mathbf{q}, \dot{\mathbf{q}}\right) $ is the centrifugal and Coriolis torque, and $ \mathbf{u} $ is the input torque of the links. Let $ \mathbf{x} = [\mathbf{q}, \dot{\mathbf{q}}] $ and $ \mathbf{y} = \mathbf{q} $, then the nonlinear dynamics equation can be reformed as a linear parameter-varying (LPV) model:

where $ \boldsymbol{A} = \left[

$$\begin{array}{cc}{\bf{0}}& \boldsymbol{I}\\ {\bf{0}}& {\boldsymbol{D}}^{-1}(-\boldsymbol{C})\end{array}$$ \right] $, $ \boldsymbol{B} = \left[ $$\begin{array}{c}{\bf{0}}\\ {\boldsymbol{D}}^{-1}\end{array}$$ \right] $, and $ \boldsymbol{C} = \left[ $$\begin{array}{c}\boldsymbol{I}\\ {\bf{0}}\end{array}$$ \right] $. A and B depend on the parameter p(t).

To facilitate digital control, Eq (2) needs to be discretized. Set the sampling period as T_s, then

where $ {\boldsymbol{A}}_{d} = {e}^{\boldsymbol{T}s\boldsymbol{A}}, {\boldsymbol{B}}_{d} = {\boldsymbol{A}}^{+}\left({e}^{\boldsymbol{T}s\boldsymbol{A}}-\boldsymbol{I}\right)\boldsymbol{B} $. And $ {\boldsymbol{A}}^{+} $ is the pseudo inverse matrix of $ {\boldsymbol{A}}_{\mathrm{d}} $.

2.2.   LPV-MPC for robot manipulators

In the LPV-MPC, the objective function needs to minimize the error between the output trajectory and the desired one. Most of the time, extra penalties concerning the input torques are also needed. Thus the objective function can be defined by

where $ {w}_{y} $ and $ {w}_{u} $ are diagonal matrices concerning the output and input weighting values. $ {\boldsymbol{y}}(k + i|k) $, $ {\boldsymbol{r}}(k + i|k) $, and $ {\boldsymbol{u}}(k + i|k) $ respectively represent the prediction output, reference output and prediction input for the (k + i) times during the k^th sampling. $ \left\| . \right\|_2^{} $ is the Euclidean norm.

Let $\boldsymbol{Q}=\boldsymbol{w}_{y}^{T} \boldsymbol{w}_{y} $, $ \boldsymbol{R}=\boldsymbol{w}_{u}^{T} \boldsymbol{w}_{u} $ and $ \boldsymbol{e}(k+i \mid k)=\boldsymbol{y}(k+i \mid k)-\boldsymbol{r}(k+i \mid k)$, then

where Q and R are the error weight matrix and the input torque weight matrix, respectively. They are also the parameter to be optimized in MPC in this article.

Eventually, the objective function at sampling step k can be formulated as:

where u_min and u_max represent the lower and upper limits of the input torque.

3.   Transient search optimization and objective function design

TSO is inspired by the transient physical behavior of the switched electrical circuits rather than by swarm animals' behavior. It has been testified the superiority against other algorithms, simple yet powerful.

3.1.   Transient search optimization

The TSO algorithm includes three main procedures: i) Initialization, the procedure to generate the search agents among the search space; ii) Exploration, the procedure to explore the entire search space to seek diverse solutions; iii) Exploitation, the procedure to search for better solutions close to the local optimal solutions.

Like other metaheuristic algorithms, the initialization of the search agent is generated randomly, as denoted by Eq (7)

where d and n describe the variables' dimension and the total number of search agents therein. For instance, X_nd is the coordinate of the n^th search agent in d^th dimension.

where $ {c_1} = {r_3} \times {k_{\text{c}}} \times {c_2} + 1 $, $ {c_2} = 2\left( {1 - i/{t_{\max }}} \right) $ and $ \Gamma = \left( {2{r_2} - 1} \right) \times {c_2} $; r₁, r₂ and r₃ are random numbers in the interval [0, 1], t is the number of iterations, t_max is the maximum number of iterations; c₁ and $ \Gamma $ are random coefficients, c₂ is an attenuation variable gradually decaying from 2 to 0, and $ {k_{\text{c}}} $ is a constant. $ X_{ij{\text{ }}}^t $ is the search location of the agent $ X_{ij{\text{ }}}^{} $ in iteration t; $ X_{best{\text{ }}}^t $ is the current best solution in iteration t. When r₁ is greater than or equal to 0.5, TSO implements the exploration process; otherwise, TSO implements the exploitation process. Besides, by using the big-oh notation O(n), the computational complexity of TSO is $ O\left( {n\left( {{t_{\max }}d + {t_{\max }} + 1} \right)} \right) $.

3.2.   Objective function and error indices of the TSO-MPC

Many factors can influence the performance of the robot manipulator response. An ideal answer of robot manipulators must have slight maximum overshoot, settling time, and steady-state error in the meantime. In this work, Figure of demerit (FoD) is selected as the objective function to evaluate the control performance of the robot system to minimize the maximum overshoot, steady-state error, and settling time synchronously. The objective function FoD is represented by

where $ M_{os}^i $ is the maximum overshoot (%), $ t_{st}^i $ is the settling time (sec), $ t_r^i $ is the rise time (sec), $ e_{ss}^i $ is the steady‐state error, η is an exponential factor to balance the weights of the term $ \left( {M_{os}^i + e_{ss}^i} \right) $ and the term $ \left( {t_{st}^i - t_r^i} \right) $, and i is the index of robot links.

By setting the value of $ \psi $, one can adjust the penalty degree of the items. Specifically, when η = 0.6932, the weight factor $ \left( {1 - {{\text{e}}^{ - \eta }}} \right) $ and $ {{\text{e}}^{ - \eta }} $ are equal, which means the term of the maximum overshoot, the term of the steady‐state error, and the term of the setting time have fair influences on the objective function FoD.

In addition, for quantitative comparative analysis, four popular error indices are employed to evaluate the performance of the controller approaches ^[42]. The error indices can be denoted as follows.

where ISE is the abbreviation of the integral of the squared error, ITSE is the abbreviation of the integral of the product of time and the square error, IAE is the abbreviation of the integral of the absolute error, ITAE is the abbreviation of the integral time absolute error.

4.   Results and discussion

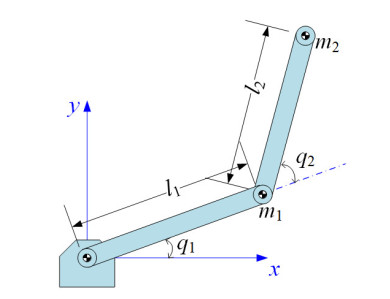
Without loss of generality, a two-link robot manipulator working in a horizontal plane is suggested in Figure 1.

Thus the terms $ \mathbf{D} $ and $ \mathbf{C} $ of the dynamics equation (1) can be presented as

where the structural parameters in this work are set to l₁ = 0.8, l₂ = 0.4, m₁ = 0.1, and m₂ = 0.1; g is the gravity acceleration.

4.1.   Optimization of TSO-MPC of the robot manipulator

The optimization progress of MPC and CTC based on the TSO of robot manipulators was implemented via a unit step reference, as shown in Figure 2.

In the optimization of MPC and CTC, the sampling period is set to T_s = 0.01 s, and a prediction horizon H_p = 10 is employed. In the MPC control, the parameters to be optimized are Q and R; We set $ {\boldsymbol{Q}} = \left[ {

$$\begin{array}{*{20}{c}} {{Q_1} \cdot {{\boldsymbol{I}}_{2 \times 2}}}&{{{\mathit{\pmb{0}}}_{2 \times 2}}} \\ {{{\mathit{\pmb{0}}}_{2 \times 2}}}&{{Q_2} \cdot {{\boldsymbol{I}}_{2 \times 2}}} \end{array}$$ } \right] $, $ {\boldsymbol{R}} = \left[ { $$\begin{array}{*{20}{c}} {{R_1}} \\ {{R_2}} \end{array}$$ } \right] $; $ 0.1 \leqslant {Q_1}, {Q_2} \leqslant 50 $, $ 0 \leqslant {R_1}, {R_2} \leqslant 50 $, and $ {u_{\min }} = - 500 $, $ {u_{\max }} = 500 $. In the CTC control, the parameters to be optimized are k_p and k_d.

During the procedure of the simulation experiment, the search agents of these metaheuristic algorithms are 30, and the maximum iterations of the optimization are 50 times. Expressly, in the TSO method, the constant k_c is set to 1; In GWO, HHO, MO, and SBO, the required parameters are consistent with the original literature. For instance, in GWO, a decreases linearly from 2 to 0; in HHO, β is set to 1.5; in MO, g = 0.8, a₁ = 1.0, a₂ = 1.5, a₃ = 1.5, β = 2, and mutation rate is set to 0.01; in SBO, α = 0.94, mutation rate is set to 0.05, and the percent of the difference between the upper and lower limit is set to 0.02. Afterwards, each algorithm takes the mean value of six independent trials as the final result. After the optimization process, we get the cost function value FoD of these different methods, the standard deviation, the key parameters of the controllers, the settling time, and the maximum overshoot, as tabulated in Table 1. Then the set-point tracking performance on the unit step reference for the robot manipulator using these controllers can be illustrated in Figure 3.

As can be seen from Table 1 and Figure 3, the proposed TSO-MPC has the minimum settling time, overshoot, as well as the performance indices compared with the other methods. Particularly, by employing TSO-MPC, the overshoot of joints 1 and 2 are both zero. To compare with the trial and error method, we set Q₁ = 0.1, Q₂ = 50, R₁ = R₂ = 0; however, the FoD value obtained is 0.06952. It is slightly larger than the optimal value of 0.06455.

In conclusion, the larger the weight coefficient of the angle, the smaller the weight coefficient of the angular speed, and the smaller the weight coefficient of the input torque, the better the performance of the objective function FoD. Although the optimal parameters are not all at the boundaries, they are very close to them.

4.2.   Performance of set-point tracking

Set-point tracking control is an important performance index for the control technique of robot manipulators. Unit step tracking is a typical set-point tracking. In the previous section, MPC and CTC are optimized using a unit step reference trajectory, and key parameters in these control methods are obtained. For quantitative comparative purposes, different error indices are employed to evaluate the performance of different control algorithms in terms of set-point tracking. The implementations of these algorithms under the error indexes are listed in Table 2.

As can be seen from Table 2, all the error indicators of the TSO-MPC algorithm are the smallest. Again, it is proved that TSO-MPC has the best performance among the control schemes.

4.3.   Performance of nonlinear trajectory tracking

In addition to set-point tracking, nonlinear trajectory tracking is also essential in various applications of robot manipulators. Besides, proper nonlinear excitation trajectories for the robot manipulator are required to test the effectiveness of the MPC methods.

For this purpose, the periodic trajectories by a sum of finite Fourier series are utilized hereinafter due to the ascendancy in terms of signal processing and target reaching. The finite-term periodic Fourier series trajectories for joint i of the robot manipulator can be formulated as

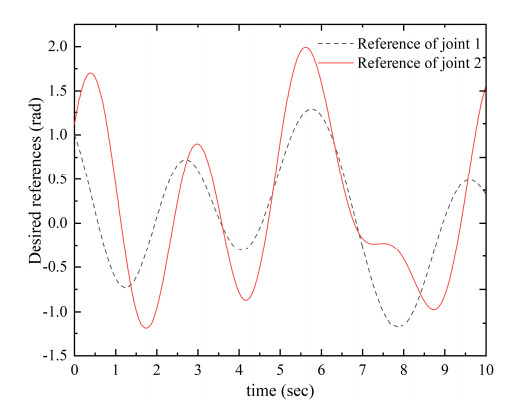
where $ {\omega }_{f} $ is the fundamental frequency, a_i and b_i are amplitudes of the terms, and $ {q}_{io} $ is the offsets of the i^th joint angles. The fundamental frequencies are all set to 0.5, and thus, all of the period of the trajectories is 4π second.

In order to facilitate analysis, we let a₁ = [0.156, -0.478, 0.078, -0.388, -0.070], b₁ = [0.088, 0.253, -0.207, 0.549, 0.150], a₂ = [0.064, -0.335, 0.451, 0.292, 0.746], b₂ = [-0.125, 0.292, -0.369, 0.557, 0.564], q₀ = [0.168, 0.193]; and the initial state of the system is set to $ {q}_{1}\left(0\right) = {\dot{q}}_{1}\left(0\right) = {q}_{2}\left(0\right) = {\dot{q}}_{2}\left(0\right) = 0 $. The final generated nonlinear reference trajectory is presented in Figure 4.

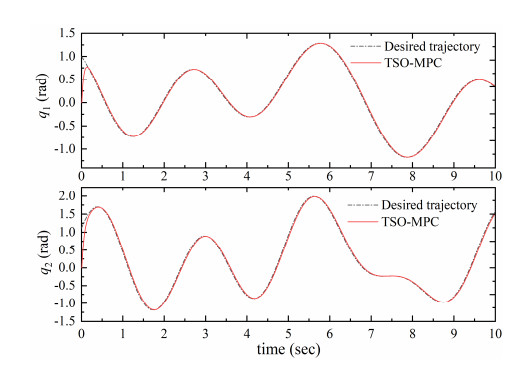
After simulation, the output response of the proposed MPC for tracking nonlinear trajectory is demonstrated in Figure 5. It can be seen that the performance of TSO-MPC still follows the nonlinear trajectory well, and the steady-state error is insignificant.

4.4.   Performance of robustness regarding parameter uncertainties

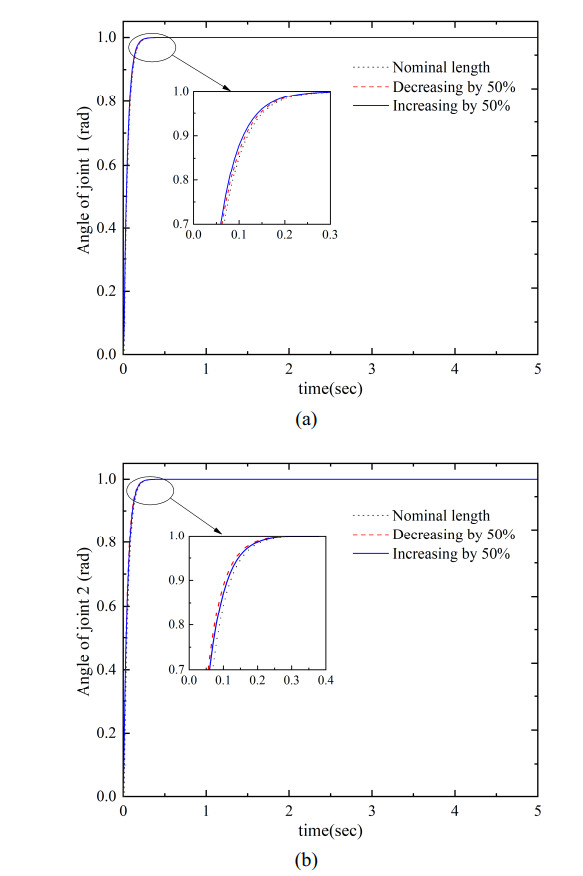
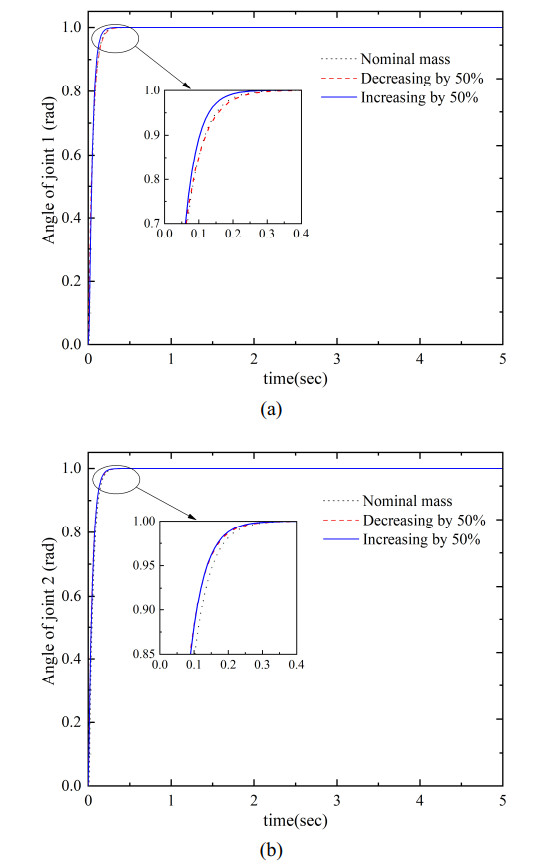
Robot manipulators always encounter varieties of structural and non-structural uncertainties when in service. Uncertainty factors adversely affect the tracking implementation and performance of the robotic system. Therefore, the controllers of robot manipulators are required of good robustness to uncertainty factors. In this section, a pair of trails are conducted to validate the robust performance of the proposed TSO-MPC scheme. Specifically, ± 50% measurement errors in terms of the link masses and the link lengths of the robot manipulator were established to test and verify the robustness of the proposed TSO-MPC.

As demonstrated in Figures 6 and 7, the TSO-MPC can tackle the uncertainties of the system parameters with an ignorable steady-state error in the system response. It should be pointed out that there are many other excellent algorithms that can be used to optimize MPC of the robot manipulator, but they were not yet considered in this work.

5.   Conclusions

A newly proposed metaheuristic, TSO algorithm, was employed for tuning the LPV-MPC parameters of robot manipulators rather than using the trial and error method from experts' experience. The parameters of LPV-MPC were turned using TSO by the minimization of an objective function FoD, which can simultaneously minimize overshoot, steady-state error, and settling time. It is suggested that the larger the weight coefficient of the angle, the smaller the weight coefficient of the angular speed, and the smaller the weight coefficient of the input torque, the better the performance of the TSO-MPC. The control performances achieved with TSO-MPC controllers are then compared with the performances obtained using GWO-CTC, HHO-CTC, MO-CTC, SBO-CTC, and TSO-CTC controllers. Although all the algorithms can achieve small steady-state error, TSO-MPC has better performance in terms of maximum overshoot and settling time than the metaheuristic-algorithm-based CTC schemes. Moreover, TSO-MPC can also effectively track nonlinear trajectories and handle the uncertainty of the robot manipulator parameters. The results can indicate that the proposed TSO-MPC method in some areas is more efficient than other control schemes of robot manipulators.

Acknowledgments

This project is financially supported by the National Natural Science Foundation of China (No. 51875266).

Conflict of interest

The authors declare that there is no conflict of interest.

Appendix