1. Introduction
Medicine as a craft has been practiced for thousands of years. Today, medicine is a pivotal science for the welfare of humanity. The twentieth century has witnessed a plethora of medical innovations ranging from the development of vaccines for infectious diseases such as smallpox and poliomyelitis (polio) to the reduction of deaths caused by cardiovascular diseases by means of early interventions [1]. Nowadays, the current healthcare system faces new challenges such as toxic side effects caused by drugs and the emergence of super bugs. For instance, current cancer treatments (e.g., chemotherapy and radiotherapy) target not only tumor cells, but also normal ones. Therefore, patients undergoing these therapies suffer adverse side effects, impacting the willingness of the patient to undergo treatment. Additionally, treatments that lack specificity negatively impact the cost of treatment, leading to a continued increase in healthcare cost.
To overcome these challenges, researchers have focused on designing smart drug carriers to enhance medical treatments using "on-demand" targeting approaches. Using such an approach, a smart drug vehicle carries therapeutic agents to be released at targeted sites with minimal damage to healthy cells. Metal nanoparticles (NPs) have emerged as a potential material for creating these carriers due to their tunable size and biocompatibility [2,3]. In addition, metal NPs possess unique optical and physical properties [3]. Thus, to create an advanced drug-delivery system using metal NPs, researchers must satisfy three major criteria: (1) effective loading of the drug onto a NP, (2) targeted delivery of the treatment, and (3) successful release of the drugs.
Depending on the chemical composition of the NPs, a variety of organic ligands have been developed to functionalize their surface and to augment their properties. For drug-delivery systems, such surface modifications allow for the creation of adequate drug loading and releasing mechanisms to targeted cells. And while there are several reviews that describe such delivery vehicles in light of the types of nanoparticles or polymeric materials used [2,4,5], this review focuses primarily on recent advances where organic thin films are used as coatings for delivery vehicles. Organic adsorbates, attached to the surface of nanocarriers, provide a suitable platform for immobilizing drug molecules. Over the last two decades, self-assembled monolayers (SAMs) have been widely used to modify metal surfaces. Thus, surface modification using custom-designed SAMs can introduce specific biomolecules to the surface such as small molecule drugs, peptides, proteins, and oligonucleotides [2]. Attachment strategies include electrostatic interactions [6], Diels-Alder reactions [7,8], Huisgen 1, 3-dipolar cycloadditions [9], and thiol-maleimide Michael additions [10] among numerous other strategies. Thus, designing a molecular adsorbate with the appropriate binding site is important for both loading and releasing the drugs. Importantly, the incorporation of several layers of coatings introduces new properties to the particles. The combination of the properties, those arising from the coatings and those of the NPs, give rise to a new nanocomposite with advanced properties. This review discusses examples of effective drug-bearing coatings, the significance of surface modification of nanoparticles, targeted delivery of therapeutic agents, and drug release methods into specific tissues. We will also explore various types of stimuli-responsive ligands for "on-demand" drug release.
2. Drug Loading
Nanotechnology has provided several new strategies for drug delivery due to the unique properties of such materials. However, the immobilization of drugs onto bare NPs has faced fundamental challenges in medicinal applications as drug carriers. Coating a layer (or layers) using SAMs or a polymer provides a variety of excellent and direct routes for fabricating drug-carrying NPs. Herein, we focus on SAMs as a well ordered and reliable coating method to afford enhanced loading capabilities to NPs.
2.1. Functionalization of nanoparticles using SAMs
Studies of nanoparticles coated with thin organic films arose from the initial work of Nuzzo, Allara, and Whitesides on SAMs derived from the adsorption of organosulfur compounds on flat metallic surfaces [11,12,13]. Since their introduction in the 1980s, SAM technology has expanded to various types of colloid-based materials due to their wide range of applicability [14,15,16,17]. Molecular self-assembly is the most widely used method for fabricating functionalized NPs due to its versatility and ease of reproducibility. The self-assembly process typically proceeds via the chemisorption of adsorbates onto the surface of the metal NPs, giving rise to predictable changes in the interfacial properties.
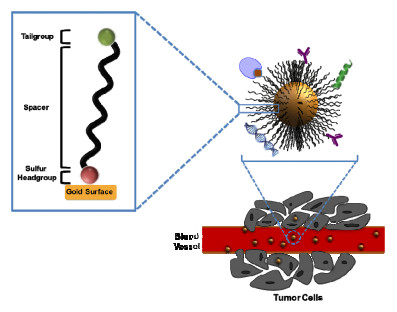
The organic adsorbates are typically composed of a headgroup, a spacer, and a tailgroup (see Figure 1). The headgroup attaches to the metal surface of the particle. Thiolate, dithiolate, disulfide, amine, carboxylate, and phosphine moieties are the most common headgroups used for anchoring molecules onto metal surfaces (especially gold) [18]. Recently, N-heterocyclic carbene (NHC) headgroups have been used to form thin films via the formation of robust Au-C bonds [19]; however, the application of such films has yet to be explored. The spacer groups serve as a barrier between the outer layer of the nanocomposite and the metal surface, thereby enhancing the stability and inert character of the system [20]. The tailgroups, or "terminal groups", dictate the interfacial properties of the surface. Widely used terminal groups include methyl [11,12,13], carboxylate [21], quaternary ammonium [22], azide [10,23], maleimide [10], and biomarkers [23], which provide specific interfacial interactions with their surrounding media. The various terminal moieties introduce specific features to the surface (see Table 1). For example, such coatings might modulate the surface charge of the nanoparticle, their colloidal stability, and their ability to disperse in selected media. Chain termini also serve as platforms for biomolecule attachment as in the case of bioconjugated oligonucleotides, peptides, and proteins in drug-delivery systems and biosensors [24,25].
Table 1. Introduction of interfacial features on NPs using various functional moieties.
| Moieties
|
Interfacial Feature
|
Reference
|
| Oligo (ethylene glycol)
(OEG)
|
Increased hydrophilicity and resistance to non-specific protein adsorption |
[26,27,28]
|
| Perfluorination |
Decreased dispersibility in aqueous media and non-specific protein adsorption |
[27,29,30,31,32]
|
| Quaternary Ammonium |
Interactions with phosphate backbone of oligonucleotides |
[33,34]
|
| Zwitterion |
Increased water dispersibility and lipophilicity |
[35,36,37]
|
| Maleimide |
Undergoes thiol-Michael addition (for attachment of biomolecules)
|
[10,33,38]
|
Adsorbates with multiple binding moieties (i.e., multidentate adsorbates) give rise to SAMs with enhanced stability, which, in turn, leads to highly stable NP systems. The combination of added stability and dispersibility of SAM-coated NPs allows these complex nanostructures to be used as platforms for biomolecule attachment, manipulation, and application, even under forcing conditions.
2.1.1. Stability
Aggregation is a fundamental problem that impacts the stability of nanoparticles and limits their applicability as drug carriers. Collisions of particles due to Brownian motion lead to aggregation and precipitation. Thus, obtaining NPs that are well dispersed and stable in the solution phase (particularly in physiological serum) is highly desirable. A possible solution is to increase the repulsion between NPs, which increases their colloidal dispersion. Coating NPs with SAMs leads to surface passivation and a significant reduction in the agglomeration and sintering of NPs, including: gold [39,40], silver [41] palladium [42], and quantum dots [43]. The modification of NPs with a SAM layer can be employed using two approaches: (1) a direct approach, using the Brust-Schiffrin method, as an example, where the coating takes place at the same time as the synthesis of the NPs to create alkanethiolate-coated gold NPs [44], or (2) using a post-synthesis modification approach, where the NPs are coated via a ligand-exchange process. The latter technique is routinely employed when extending the lifespan of NPs in biological media. For example, ligand exchange has been used to incorporate ligands composed of OEG moieties onto the surface to increase the stability of NPs in aqueous solution [26]. However, for NPs used in biomedical therapies, chemical stability in a biological environment is paramount. For instance, the acidic conditions (pH = 6-7) found in tumor cells causes many NPs to aggregate [45]. Yet, Liu et al. synthesized gold NPs with high stability in acidic conditions by forming a mixed-charge SAM; a 1:1 mixture of a positively-and a negatively-charged alkanethiol [35]. Mixed-charge and zwitterionic SAMs enhance colloidal stability in media having a wide range of acidity and salinity [35,36]. The enhanced stability is due to the formation of a water layer around the particles. Thus, hydrolysis of the surface-bound ligands increases the dispersion of particles in biological media.
2.1.2. Dispersibility
The interfacial properties of SAM-coated NPs are modulated by the chemical nature of the tailgroups. In addition to tailoring properties, certain chemical functionalities also allow for control of the dispersibility of the NPs. For example, fluorinated molecules have strong hydrophobic and lipophobic character [46]. The combination of hydrophobicity and lipophobicity gives rise to NPs with decreased dispersibility in polar solvents [29,46]. However, SAMs derived from fluorinated adsorbates provide low surface energy, which makes them chemically and biologically inert [29,30,31,32]. Therefore, incorporating an OEG moiety along with the fluorinated one in the same chain can circumvent the dispersibility issue while also taking advantage of the physical properties of a fluorinated film. To exemplify, Gentilini et al. designed the first water-dispersible fluorinated NPs using OEG-terminated fluorinated thiols [27]. In this approach, the gold nanoparticles are coated with a monolayer derived from the fluorinated amphiphilic thiolate, HS-F8-OEG, which is composed of eight fluorocarbons underneath an OEG chain. In contrast to the hydrophobicity of the fluorocarbons, these gold NPs show good dispersibility in water along with stability in polar solvents. With such an adsorbate, the authors combine the inertness of fluorocarbons with the biocompatibility of OEGs to develop an interesting nanoscale coating for applications in biomedicine.
2.1.3. Multidentate adsorbates
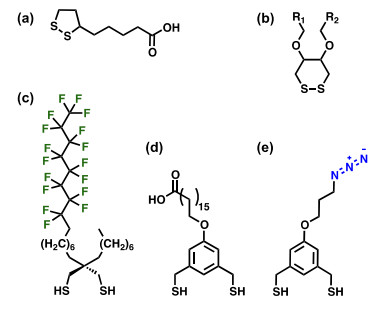
The use of multidentate adsorbates as molecular tools for coating metal nanoparticles expands the versatility of this type of monolayer thin film. Monothiolate-based adsorbates attach to metal surfaces and form stable monolayers at ambient temperature [13]. However, these SAMs exhibit questionable stability at elevated temperatures [47]. In contrast, adsorbate molecules bearing headgroups with multiple binding groups to the metal surface, as shown in Figure 2, form films with enhanced thermal stability [48,49,50].
Lipoic acid (Figure 2a) and analogs with different chain lengths can be used to form highly stable SAMs on gold surfaces [51]. The carboxylic acid tailgroup of such SAMs adds a secondary functionalization site to the multidentate-coated gold [52] and silver NPs [53] or quantum dots [43]. The pioneering work of Nuzzo and Allara introduced disulfide in Figure 2b, which was shown later to have the potential to introduce mixed chains [11,54]. However, disulfide adsorbates are seldom the ideal choice for SAMs on gold surfaces due to their slower adsorption compared to thiols. Shon et al.introduced the "spiro" motif, depicted in Figure 2c, that bridges four substituents at a single branchpoint and binds two sulfur groups to the surface of gold [55]. This type of adsorbate has been shown by Chinwangso et al. to generate mixed SAMs with controlled surface heterogeneity and enhanced thermal stability [56].
Aromatic-dithiol adsorbates are also alternatives for enhancing the stability of SAMs. Studies have shown that the enhancement in stability of SAMs derived from aromatic moieties can be attributed in part to intermolecular π-π interactions [57,58], but more importantly to the chelate effect via the addition of a second anchoring group that increases the thermal stability of the SAMs at elevated temperatures [47]. Lee et al. explored the stability of films generated from carboxy-terminated aromatic dithiol SAMs (Figure 2d) to those of a mono-thiol analog on both flat and colloidal surfaces. The authors found that SAMs derived from the monodentate alkanethiol desorbed from the gold surface in 30 minutes at 90 ℃, which led to aggregation of the monothiol-coated gold NPs. However, gold NPs coated with the bidentate molecules exhibited substantially greater stability at 90 ℃ over 12 h [47].
Furthermore, due to the ability of the aromatic dithiol adsorbates to bind both of the sulfur atoms to the surface, the dithiols adsorbates occupy a larger area on the surface compared to monothiol counterparts [58]. This larger distance between the aromatic dithiol molecules, compared to monothiols, on the surface leads to a lower density of adsorbates on the surface; having less adsorbates on the surface allows for such SAMs to be used as partitioning layers in post surface-attachment modifications. For example, a recent study on an azido-terminated aromatic-dithiol, depicted in Figure 2e, showed a reduction in the steric hindrance for SAMs with a lower packing density compared to well-packed alkanethiol-based SAMs when conjugating poly (L-lysine) [10]. The thermal stability enjoyed by multidentate adsorbates have the capability of enhancing the applicability of SAMs coated NPs for therapies that induce localized heating; examples of these types of drug-releasing treatments are detailed in subsequent sections.
2.2. SAMs as a platform for biomolecular attachment
The attachment of therapeutic agents or biomolecules to the surface of NPs is a crucial step for designing drug carriers. However, the direct interaction of biomolecules and metal surfaces can lead to structural deformation and inactivation of the biomolecule [59]. For example, antimicrobial peptides (AMPs) lose their bactericidal properties when directly attached to a metallic surface [60]. However, moving the AMPs away from the metal surface by incorporating a SAM with a spacer of 2-6 methylene units allows the AMPs to retain their antimicrobial activity against bacteria adsorbed on the surface of the particle [61]. Moreover, Salvati et al. demonstrated that the targeting capability of protein-coated NPs can be deactivated upon the non-specific interaction between the protein and the surface of the NPs. However, distancing the protein targeting sites from the solid surface by using OEG spacers preserves the functionality of the therapeutic proteins [28]. Thus, the spacer group of a SAM protects biomolecules from interacting directly with the surface of the NPs.
Separately, the tailgroup of a monolayer should also be suitable for interacting with biomolecules. Chemical functionality present on the film terminus acts as a platform on which specific biomolecules, such as oligonucleotides and proteins, can bind. While the attachment of biomolecules to the SAM might proceed via covalent or non-covalent interactions, robust interactions between the two entities prevent the loss of biomolecules and increase the efficiency of the drug delivery process. The use of maleimide as a binding platform for biomolecules is a common practice. Maleimide-terminated SAMs provide a specific binding site for biomolecules bearing a thiolate functionality, which bind covalently via a thiol-Michael addition "click" reaction. A facile approach involves tethering a biomolecule at its cysteine residue. Cysteine, an amino acid with a thiol group, can be easily introduced into peptides, proteins, and enzymes. Cysteine reacts rapidly with maleimide, allowing for the attachment of cysteine-containing biomolecules on the surface. A high level of interest in materials chemistry has focused on this type of click reaction since it is efficient and occurs under mild conditions [38]. Yoon et al. functionalized graphene oxide surfaces with maleimide moieties using a stepwise attachment. Subsequently, they bound thiolated NeutrAvidin to the maleimide-functionalized surfaces, and used the generated bio-interface as a platform for the detection of circulating tumor cells in blood samples [62].
The use of non-covalent interactions is another strategy for loading drug molecules onto coated NPs. For example, electrostatic interactions between cationic-terminated SAMs and anionic oligonucleotides can be used to load DNA or RNA molecules on the particles. McIntosh et al. used gold NPs coated with mixed monolayers of tetraalkylammonium (R4N+) and n-alkanethiol, where R4N+ groups can interact electrostatically with the phosphate backbone of DNA molecules [33]. Such interactions assemble DNA onto the surface of AuNPs, which consequently was used to inhibit transcription by T7 RNA polymerase in vitro.
2.3. SAMs as a platform for gene delivery
Gene therapy represents a promising platform for developing novel therapies for diseases such as cancer and acquired immunodeficiency syndrome (AIDS) [63]. The fundamental principle for such therapy is based on the successful delivery of a special sequence of oligonucleotides to infected cells. Plasmid and DNA can be used to repair defective genes, whereas small interfering RNA (siRNA) can be used to regulate relevant processes in a therapeutic fashion [64]. Contrary to small drug molecules, a successful utilization of genes in medicine has been hindered by a number of hurdles including: the inability to cross the lipid-rich cell membranes, low bioavailability, proteolytic and hydrolytic degradation, as well as a short half-life in the circulatory system [65]. To sidestep these obstacles, numerous biomaterials and inorganic surfaces have been studied as potential gene delivery vectors to improve DNA stability and cellular uptake. Functionalized NPs have been used as a potential viral vector in gene therapy due to their tunable size, physical properties, surface modification capabilities, and stability of the particles [66,67,68]. These inherent properties of functionalized NPs can protect them from enzymatic degradation and allow transport through the cell membrane [67].
2.3.1. Small interfering RNA (siRNA) delivery
RNA-interfering technology holds considerable promise in cancer therapy due to its high efficacy and specificity in down-regulating tumor gene expression [68]. Small interfering RNA (siRNA) are 21-23 double stranded nucleotides used to suppress the expression of a specific gene. More specifically, siRNA induce regulation by interacting with argonaute proteins to form an RNA-induced silencing complex, which eventually leads to the degradation of targeted messenger RNA (mRNA) [70]. Controlling the interaction between oligonucleotides and the surface of the NPs is challenging due to the low affinity of these charged agents toward the coated surfaces of NPs. Therefore, designing a material that can facilitate the loading, delivery, and release of siRNA into a target cell is highly desirable. To this end, two approaches have been developed to enhance the effective use of NPs as siRNA-based drug carriers; (1) a direct, covalent attachment of the oligonucleotide via a S-Au bond between thiol-modified nucleotides and the gold surface, (2) electrostatic assembly of negatively charged oligonucleotides and cationic surfactant-coated surfaces. Conde et al. designed multifunctional gold NPs as a platform for siRNA loading via electrostatic approaches [66]. The authors used adsorbates with quaternary ammonium (R4N+) tailgroups to immobilize siRNA on the particles via complementary charge-charge interactions. Further, the absence of R4N+ moieties on the surface led to no induced silencing event, confirming the successful trapping of siRNA using the quaternary ammonium termini. Moreover, the authors also used thiolated oligonucleotides for direct attachment of nucleotides onto gold NPs [34]. However, permanent attachment of nucleotides to the surface of NPs negatively impacts the release stage. Thus, covalent attachment of nucleotides requires high-energy laser irradiation to release the therapeutic agent [71,72]. Further, while both strategies are useful for loading siRNA to the delivery vehicle, the non-covalent strategy might be advantageous due to the ability of NPs to release therapeutic agents under less forcing conditions.
3. Intracellular Uptake
Intracellular targeting refers to the delivery of drug molecules to specific compartments of the cell. Such ability is a pivotal requirement for advanced delivery systems. Factors that limit the intracellular uptake of a drug molecule or a gene include degradation of the drug, poor permeability through the cell membrane, low accessibility to the action site within the cell, and toxicity of the drug to normal cells. Cellular uptake of nanocarriers relates to the inherent, physical properties of the inorganic NPs such as diffusion, size, shape, hydrophilicity, and dispersibility [73,74]. Herein, our discussion focuses on the effect of the chemistry of organic thin layers on delivery systems.
The clinical use of certain drugs has been limited by the stimulated immune response against the drug molecules [75]. Therefore, there is a critical need for a platform capable of transferring and protecting therapeutic agents. Such a carrier is needed to avoid the agglomeration of antibodies, adverse protein interactions, and the degradation by plasma enzymes, as well to cross through cellular barriers for ultimate delivery to a subcellular location. Thus, the attachment or encapsulation of a drug molecule on the surface or inside a nanocarrier, respectively, can enhance the efficiency of drug delivery. Studies have examined the applicability of core-shell materials, including porous and hollow NPs, in drug encapsulation [76,77]. In these types of NPs, monolayer coatings can shield the particles until they reach the biotransformation stage. The nano-assembly of particles coated with cationic surfactants encapsulates negatively charged oligonucleotides such as DNA and siRNA [78,79,80], which then protect therapeutic agents from degradation and facilitate intracellular delivery. For example, Wu and coworkers functionalized gold NPs with a cationic-terminated peptide to assemble DNA molecules electrostatically, reducing the initial degradation rate of DNA molecules to more than ten-fold slower than that of the positive control. Furthermore, this strategy leads to highly efficient cellular delivery of DNA, which shows a significant advantage for using positively charged gold NPs [79].
NP vectors closely associate with outer cell membranes. Lin et al. simulated the interaction of a model lipid membrane with NPs functionalized with a mixture of ammonium-and carboxylate-terminated adsorbates [81]. The charge-charge interactions between the zwitterionic SAM and the lipid-bilayer membrane increased the penetration of the particles into the membrane. Separately, NPs with a high density of surface charge can also disrupt the membrane, suggesting that a controlled-charge density is required to achieve optimal delivery.
In addition, the cytoplasmic delivery of therapeutics can occur via the endocytosis of NPs. Note that a successful intracellular uptake requires the efficient transport of nanocarriers across cellular membranes and the escape of nanocarriers from secondary endosomes. Surface-functionalization of NPs with cationic surfactants or polymers facilitates such interactions between the anionic cell membrane and the NPs, thus enhancing both endocytosis and endosomal escape.
The incorporation of NPs with receptor ligands is another strategy utilized to enhance cellular uptake of drug carriers. A variety of ligands, including antibodies and low molecular weight targeting agents, have been conjugated to the surface of NPs to facilitate receptor-mediated endocytosis [82]. For example, the modification of NPs with folic acid enhances cellular uptake of such particles into cancer cells due to the overexpression of folate receptors on the surface of these cells [83,84]. Effective gene delivery also requires that the oligonucleotide be delivered into the cell nucleus. To achieve such specific delivery, the surfaces of NPs can be modified with nuclear-targeting moieties. For example, liposome-based NPs modified with a nuclear localization signal (NLS) peptide motif interact with cell nuclei [85]. Ma et al. suggested that DNA delivered via NLS-functionalized liposomes is sufficiently expressed for therapeutic purposes.
4. Drug Release Using Stimuli-Responsive Monolayers
Despite progress in the loading and delivery of drugs with NPs, an effective releasing mechanism of the therapeutic agents into the target remains challenging. NPs can be functionalized with a custom-designed monolayer capable of responding to a particular internal, external, chemical, or physical stimulus. Such stimuli include responses to variations in pH, temperature, light, or magnetic fields.
4.1. pH-responsive monolayers
Tumor tissues typically exhibit an acidic environment in the extracellular matrix of pH~6.5, which is significantly lower than that of normal cells (pH = 7.4). Within tumor cells (especially inside endosomes), the pH level is even lower (between 4.5 and 5.5) [86,87] due to the rapid accumulation of lactic acid, high rate of glucose uptake, and reduced rate of oxidative phosphorylation [88,89]. Consequently, NPs coated with a pH-sensitive organic layer can be utilized in smart-release delivery systems. Charged coatings typically possess weak acids and bases (e.g., carboxylic acids, phosphoric acids, and amines) in their structure. The ionization states of these moieties change in response to changes in the pH of the medium. This phenomenon leads to a conformational change in the coating, allowing programmed loading or releasing of drug molecules [90].
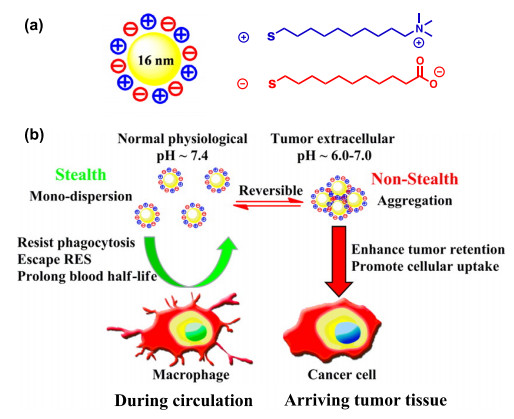
Nanoparticles that are pH-responsive can be generated using a monolayer containing mixed-charge zwitterionic adsorbates. Liu et al. demonstrated that the acidity of tumor cells can enhance the cellular uptake of such coated-NPs [37]. As shown in Figure 3, the authors used gold NPs coated with mixed-zwitterionic SAMs to induce the aggregation of NPs in the acidic environment of tumor cells, leading to the accumulation of NPs in tumor tissue. These findings suggest that the controlled aggregation of coated NPs can be used as a means to enhance the drug availability in target tissue.
4.2. Photo-responsive monolayers
Light has been widely utilized as an external stimulus to control the release of a preloaded drug. Photoactive nanomaterials can be prepared by coating NPs with adsorbates bearing a photo-cleavable linker such as coumarin [91] and o-nitrobenzyl [92]. These commonly used biocompatible functional groups enjoy long-term stability under ambient conditions. However, exposure of such material to UV light cleaves the covalent attachment between these moieties and the nanocarrier [93]. As illustrated in Figure 4, photo-triggered NPs modified with adsorbates bearing an o-nitrobenzyl ester linker and other terminal functionalities provide a binding site for drug molecules, which can be released upon irradiation with UV light.
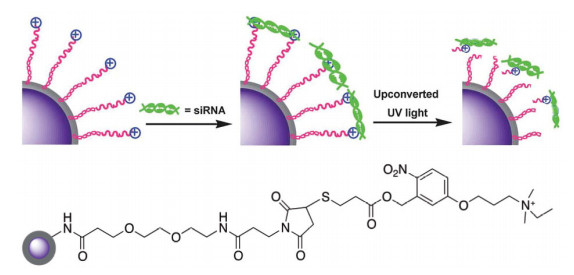
As a specific example, Han et al. designed photo-triggered gold NPs using an adsorbate having a dimethylethylammonium-terminated o-nitrobenzyl ester group to load and subsequently release therapeutic DNA upon irradiation with UV light (λ = 350 nm) [94]. Using fluorescence microscopy and UV spectroscopy, the authors investigated the cleavage of the o-nitrobenzyl ester linkage and the release of therapeutic DNA into living cells [94]. However, the clinical applicability of such an approach is limited due to the low penetration depth of UV light in physiological tissue and the toxicity associated with this high energy radiation. Separately, a specific range of near-infrared (NIR) light (~650-900 nm) has deeper tissue penetration and causes less photo-induced tissue damage [95]. Yet, the energy of NIR photons falls below the energy requirement to break most covalent bonds [96,97]. The photoluminescence of lanthanide upconversion nanoparticles (UCNPs) allows them to convert adsorbed NIR light onto higher energy photons. Several research groups have focused on the use of UCNPs to photo-trigger therapeutic agents in living cells [98,99]. Yang et al. used core-shell lanthanum-doped UCNPs coated with a functionalized silica shell that absorbs NIR light and emits UV light. Monolayers on these UCNPs are composed of two parts: a primary maleimide-terminated adsorbate and a subsequently attached thiolated photoactive linker having a quaternary ammonium terminus [99]. Figure 5 illustrates the drug binding and release mechanisms of the silica-coated UCNPs. The quaternary ammonium termini trap the therapeutic RNA molecules electrostatically, which are subsequently released by cleaving o-nitrobenzyl ester moieties using upconverted UV light.
4.3. Thermally responsive monolayers
Many of the nanocarriers that can be triggered to release drug molecules do so through thermal energy pathways. Various metallic nanoparticles have been used to generate heat and subsequently trigger the release of drug molecules from the coating layer. This type of release takes advantage of the instability of certain chemical bonds used as drug linkers toward thermal stimulus, leading to thermal cleavage, which provides a mechanism for drug release.
4.3.1. Photothermally-triggered monolayers
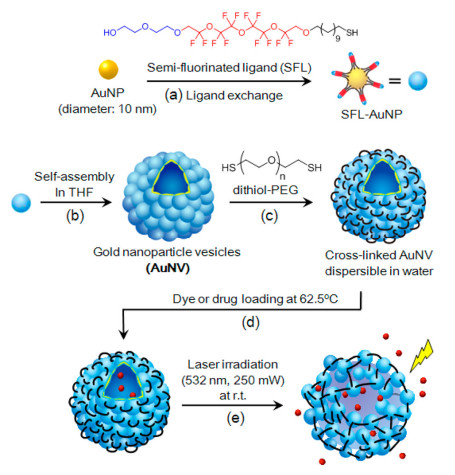
Thermo-sensitive materials manifest a sharp change in their physical properties due to changes in the temperature of their environment. A sharp response can be used as an on-demand release mechanism of preloaded molecules. In plasmonic NPs, such an event occurs by absorbing photon energy via the localized surface plasmon resonance (LSPR) of the particle and converting this light energy into heat [100]. The generated heat can then trigger the release of biomolecules by modulating non-covalent bonds such as electrostatic interactions, hydrogen bonding, or van der Waals (vdW) interactions. Niikura and co-workers engineered a unique light-sensitive drug carrier by trapping drug molecules in hollow NPs [101]. These hollow NPs were formed by the close packing of gold NPs coated with partially fluorinated SAMs [102]. The solvophobic fluorinated segments introduced a driving force for the gold seed to form a hollow shell structure (see Figure 6). Subsequently, these gold seeds were cross-linked using PEGylated-dithiol molecules to improve the dispersibility of the drug carrier in aqueous media. The heat generated by irradiation at 532 nm opened the structure of the nanocarrier by disrupting the vdW interactions between the fluorinated chains. Using this mechanism, the authors released DOX into the cell over five minutes of irradiation by activation with a 532 nm laser. In contrast, disrupting the vdW interaction of the fluorinated moieties via direct heating of the solution at 70 ℃ required more than two hours to release the model drugs.
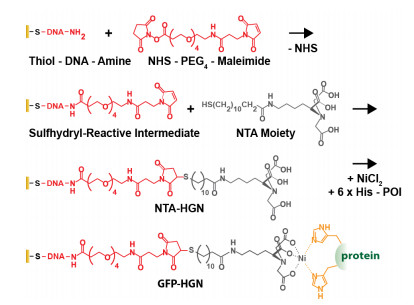
Changing nanoparticle size, shape, and composition allows for tuning of the LSPR band of the particles from the visible region to NIR light. In particular, gold nanoshells and gold nanorods have been extensively explored as potential candidates for targeted drug delivery owing to their ease of surface functionalization [103]. These NPs can be designed to have their LSPR bands appear at the NIR region, allowing for NIR-triggered drug release. Further, various thermal-sensitive coatings have been used to encapsulate drugs and accelerate the release step. Morales et al. designed and employed nickel-chelating tailgroups as a platform for loading a therapeutic protein. The nickel tailgroups provide binding-sites for proteins and allow on-demand release of the functional proteins from hollow, gold nanoshells [104]. As shown in Figure 8, gold nanoshells were functionalized with Ni-chelating SAMs via a two step assembly. First, the amine-terminated DNA SAMs underwent reaction with the N-hydroxysuccinimide (NHS)-activated carboxylic terminus of the PEGylated maleimide linker. Importantly, the bi-functionalized DNA strands used in this study allow for further functionalization of the nanoshells while simultaneously preventing their aggregation [104]. Subsequently, the moiety containing the nitrilotriacetic acid (NTA) group underwent reaction with the maleimide termini to introduce a chelating platform and to secure Ni2+ on the gold nanoshell. To attach therapeutic proteins to Ni2+, the proteins were functionalized with histidine (His). The imidazole moieties of the His residues then chelated to the free coordination sites of Ni2+, immobilizing the proteins onto the surface. Laser irradiation is expected to thermalize the gold-thiol bonds of the linker and, by extension, cause the proteins to be released from the chelating linker.
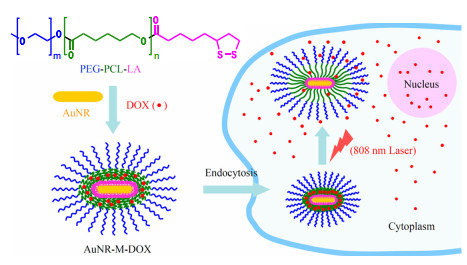
In another study, Zhong et al. used gold nanorods to overcome vdW interactions between the DOX molecules and a tri-block surfactant using NIR irradiation (Figure 8) [105]. The tri-block surfactant contained polyethylene glycol (PEG), polycaprolactone (PCL), and lactide. The tri-block copolymer bound to the surface of gold nanorods via disulfide headgroups in the lactide segment. The PEG segment enhanced both the stability of the NPs in biological media and the efficiency of cellular uptake by tumor cells through the endocytosis pathway. Whereas, the caprolactone segment trapped hydrophobic drugs in the shell structure via vdW interactions.
Thermoresponsive polymers are commonly used as coatings in stimuli-responsive drug carriers. For example, poly (N-isopropylacrylamide) (pNIPAM) exhibits a low critical solution temperature (LCST) of approximately 32 ℃-the coating layer expands below 32 ℃ and holds water in its structure via hydrogen bonding [106]. At temperatures above 32 ℃, the polymer undergoes a phase transition and collapses, disrupting the hydrogen bonding between pNIPAM and water. For medical applications, acrylamide (AAm) has been added to the polymer structure in order to adjust the LCST to a higher temperature. Thus, pNIPAM-AAm co-polymer remains in an expanded form at physiologic temperature (37 ℃) [107]. Many studies have reported the use of pNIPAm-based structures in biomedical applications. Xia et al. for example, used a NIPAm monomer to design thermal-responsive polymer-coated gold nanocages [107]. The heat generated by the nanocage causes the structure of the polymer to collapse, suggesting that initially encapsulated drugs could be released from such a drug carrier [107]. Thereafter, the coating layer returns to its original structure upon decreasing the temperature. However, the use of pNIPAm remains limited due to its non-degradable nature. Non-degradable polymers in the human body can cause a chronic inflammatory response, thus hindering multiple dosing. To overcome such limits, several groups have sought to make NIPAM copolymers biodegradable by modifying the structure of the monopolymer or by introducing a biodegradable copolymer to the polymeric backbone. Examples of biodegradable polymers include those with a significant amount of OEG content, amino acids, or esters in the polymer structure [108].
4.3.2. Control of opening sites via gatekeeper surfactants
Thermally-responsive materials can be used to cap the pore sites of porous nanoparticles. Thomas et al. designed a method to encapsulate magnetic NPs and DOX molecules within a mesoporous silica nanocarrier to later be selectively released [109]. This system uses the pores of the nanocarrier as the drug loading sites and a thermo-sensitive "gatekeeper" as a nanovalve for each pore site. A gatekeeper blocks each pore site and prevents the diffusion of drug molecules. The gatekeeper responds to a specific temperature change and releases the drug molecules from the pore site. This strategy enables the drug release in response to temperature changes.
Phase-change materials (PCMs) have been used as heat-responsive gatekeepers. PCMs change their physical state from solid to liquid and vice versa over a narrow temperature range. Raising the temperature of the medium above the melting point of the PCM will cause the material to change rapidly to the liquid phase; by regulating the surrounding temperature, this feature then facilitates the release of encapsulated drug molecules [110,111]. Porous and hollow nanomaterials have gained enormous attention as a diffusive vehicle to load and control the release of drugs, while the PCM serves to halt or allow the release of drugs from pore sites [112]. Drug molecules that are miscible with the PCM can conveniently diffuse into the hollow interiors and pore sites of the nanocarrier. This requirement can be readily met by choosing PCMs with surfactant-like behavior, such as those containing both long hydrophobic tails and hydrophilic heads. Specifically, 1-tetradecanol with a melting point of 38-39 ℃ and dodecanoic acid with a melting point of 43-46 ℃ are appropriate candidates for demonstrating temperature-regulated drug release systems due to their water-immiscibility, moderate biocompatibility, and melting points close to the temperature of the human body. For example, Moon et al. chose 1-tetradecanol to diffuse a drug model into the hollow interiors of gold nanocages. The authors controlled the subsequent release of the model molecules through a slow diffusion process using ultrasound as the stimulus and, alternatively, heat [113].
4.3.3. Thermolysis via retro Diels-Alder
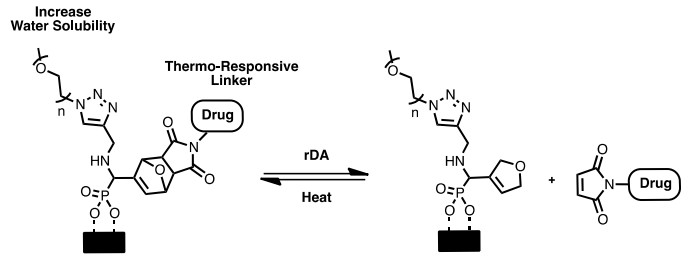
Cleaving a covalent bond using sufficient thermal energy might cause damage to living tissue. Fortunately, covalent bonds of certain linkers can be cleaved by a localized thermal stimulus. Monolayers with such linkers can undergo thermal cleavage in vivo. To this end, Diels-Alder (DA) reactions have been used effectively as a means of making specific chemical modifications to NPs [114,115]. An adsorbate with a diene or dienophile as the tailgroup provides the ideal conditions for a [4+2] cycloaddition, thus attaching molecules to NP surfaces. However, releasing such molecules can be challenging. Retro-Diels-Alder (rDA) reactions have been demonstrated as a suitable release method; however, rDA reactions usually occur above 60 ℃-a temperature that is much higher than that of the human body. Further, such high temperatures can damage healthy cells. Efforts to circumvent these negative sides effects have been explored. For example, Nguyen et al. developed iron oxide nanoparticles as carriers to produce thermal energy in an alternating magnetic field [116]. An alternating magnetic field leads to the production of thermal energy in magnetic NPs via Neel and/or Brownian relaxation [117]. The generated heat can then be utilized to initiate rDA reactions [116]. The localized hyperthermia effect of magnetic NPs provides sufficient localized energy for rDA reactions to occur without significant heating of the medium. Notably, the NPs in this study were coated with mixed SAMs containing diene-and alkyne-terminated adsorbates. As illustrated in Figure 9, the dienes react with the functionalized drug compound, and the alkynes react with an azide-PEG chain to render the particles dispersible in water.
4.3.4. Thermolysis of an azo linker
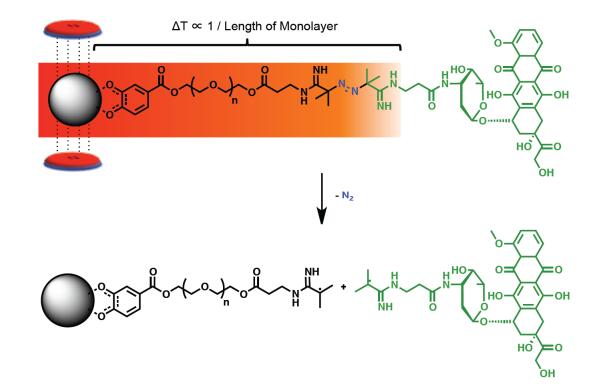
The azo-linker represents an alternative functional group capable of cleavage via thermolysis. Riedinger et al. utilized thermo-labile PEGylated azo-ligands to coat iron oxide NPs, as shown in Figure 10 [118]. Separately, DOX molecules were covalently attached to the ligand through the diazo group. An alternating magnetic field provided the local thermal energy in the surrounding media, which induced cleavage of the azo-bond and consequently the release of DOX molecules. Upon moving away from the surface of NPs that are being stimulated, the temperature decreases. Furthermore, the distance between the azo-group and the surface of the NP can be tuned by adjusting the size of the OEG spacer, thus tuning the effective local temperature at the azo-group. On the other hand, the generated heat increases linearly with the applied magnetic field. Accordingly, drug release can also be achieved by adjusting either the length of the spacer or the strength of the magnetic field. Such an adjustable system also demonstrates the potential for the independent release of multiple drugs from the same particle.
5. Conclusions: Looking Forward to an Ideal System
Due to their tunable properties, coated NPs provide new strategies to improve the efficiency and efficacy of drug-delivery systems. Furthermore, the development of custom-designed SAM-coated NPs is an extremely promising approach for treating diseases without surgical intervention. Custom-designed systems offer enhanced payload sizes that can increase the efficiency of medical treatment. These types of delivery vehicles have the potential to pass through the cell membrane, thus protecting the drug during the delivery process. Finally, stimuli-sensitive monolayers enable the release of the drug into a targeted area. The combination of SAMs and nanoparticles offers a variety of straightforward routes to facilitate drug delivery over the stepwise processes of loading, delivery, and release.
The ultimate goal of this research area is to design systems for more efficient and effective drug treatments that reduce harmful side effects. Furthermore, custom-designed coating materials provide a great platform with all the attributes required to meet emerging drug-delivery challenges. Current efforts in this research area continue to explore potential molecular recognition at the interfaces of biological systems through the utilization of multifunctional moieties on the surfaces of nanoparticles. Moving forward, these custom-designed coated nanomaterials will continue to offer exciting new drug-delivery technologies.
Acknowledgments
We thank the Asian Office of Aerospace Research and Development (AFOSR/AOARD FA2386-16-1-4067), the Robert A. Welch Foundation (E-1320), and the Texas Center for Superconductivity for generously supporting this research.
Conflict of Interest
The authors declare no conflicts of interest in this review.









 DownLoad:
DownLoad: