A recursive pricing method for autocallables under multivariate subordination

1.   Introduction

Autocallables, also known as auto-trigger structures, are very popular in the world of structure products. The autocallables generate a return based on the performance of the reference asset such as equity, commodity or currency. The reference asset can be of single-asset or multi-asset type. We focus on the latter case here as the former can be reduced from the latter. As the name suggests, the autocallable gets automatically redeemed (or autocalled) once a so-called trigger function from the asset spot prices is above the redemption level on one of several predefined observation dates (redemption dates). Usually, another trigger level, often called coupon barrier, is prespecified for each redemption date. If the autocallable does not autocall but the trigger function lies above the coupon barrier, the owner will receive a coupon. The autocallable is an exotic type of barrier option and typically treated as an option class of its own (see e.g., Bouzoubaa and Osseiran, 2010). The main reason for autocallable's growing popularity is the potential for a higher coupon, which is attractive in the current low yield environment for asset investment. Another reason is the autocallable may have a shorter lifespan than other structured products. The investors have the chance to invest in other products with the proceeds from the autocallable once it expires early.

During the period of 2007–2010, the new issuances of autocallables amount to more than 40 billion dollars in the United States (see e.g., Deng et al. (2011)). The autocallables have also been drawing an increasing amount of attention from academics in recent years. Bouzoubaa and Osseiran (2010) describe the features and payoff mechanism of single- and multi-asset autocallables as well as the risks encountered when trading these products. Fries and Joshi (2011) present a reformation of the pricing of a family of generalized autocallables through constructing a Monte Carlo scheme sampling only the survival domain of the autocallables. Alm et al. (2013) show how to adapt a Monte Carlo algorithm in such a way that its results can be stably differentiated by simple finite difference. Their new algorithm possesses a significantly reduced variance and does not require evaluation of multivariate cumulative normal distributions for pricing single- and multi-asset autocallables. Koster and Rehmet (2018) extend the idea of Glasserman (2003) to the multivariate case by means of a coordinate transform and local one-dimensional analytic treatment as in Alm et al. (2013). Their approach does not use importance sampling which has significant algorithmic advantages for the pricing of more complex autocallables or the use of path recycling for the computation of Greeks.

Besides Monte Carlo methods, analytical pricing formulas are also derived for autocallables. Deng et al. (2011) value the autocallables with continuous redemption dates using a closed-form solution based on the Back-Scholes model. Guillaume (2015a) considers two models: a two-asset Black-Scholes one and a Merton jump-diffusion framework combined with a Ho-Lee two-factor stochastic yield curve. A general, flexible form of autocallables is analytically valued under these two models. Guillaume (2015b) provides analytical formula for a general form of autocallables when the equity asset follows a jump-diffusion process, while interest rates are driven by a two-factor model.

This paper contributes to the theoretical literature on the pricing of autocallables in two directions. First, we take the modeling approach of Mendoza-Arriaga and Linetsky (2016) and construct a new model for the valuation of autocallables. Starting from $d$ independent time-homogeneous OU processes $X_i$ and a $d$-dimensional Lévy subordinator ${\bf{T}}$, we construct a new process ${\bf{Y}} = (Y_i)$, $Y_i = X_i(T_i(t))$, by time changing each of the independent OU processes $X_i$ with a coordinate $T_i$ of the multivariate time change process ${\bf{T}}$. The asset price $S_i$ is then modeled by taking an exponential function of $Y_i$.

Our model belongs to a special case of multivariate subordination of Markov processes and has some distinct characteristics. First, the underlying process considered so far for the autocallables is typically geometric Brownian motion (GBM). It is well-known that GBM model does not allow for mean reversion. Instead, we build the underlying process on the OU process, which can capture mean reversion feature that is ubiquitous in various assets such as currency, commodity and even some equities. Second, time changing a continuous time Markov process such as OU process can lead to much wider class of models than the traditional jump-diffusion models. The new process can feature state-dependent mean reverting jumps with the jump direction and the jump amplitude dependent on the current state of the process. Depending on whether the time change process has drift or not, the new process will be a jump-diffusion or a pure jump process. Third, the multivariate subordination is a powerful way to construct dependence among jumps of the asset prices and the dependence is governed by the multi-dimensional Lévy measure of the subordinator. This multivariate subordination procedure enables us to model the autocallables with a basket of assets as underlying.

Second, one novelty of the paper is to derive the recursive pricing formulas for the autocallables in terms of eigenfunction expansion. The OU process belongs to a symmetric pricing semigroup, whose transition semigroup is completely analytically tractable in terms of eigenfunction expansion. The eigenvalues and eigenfunctions of the OU process are discrete and therefore, the price of the autocallables can be expressed in terms of eigenfunction expansion. A crucial advantage of eigenfunction expansion approach is that the subordinate OU process shares the same eigenfunctions with the OU process, while the eigenvalues can be easily obtained via the Laplace transform. This makes the eigenfunction expansion method very convenient for subordinate process. For an overview of the eigenfunction expansion method, we refer to Linetsky (2004) and Linetsky and Mitchell (2008). The applications of eigenfunction expansion method for the univariate subordinate processes in finance can be found in Li et al. (2017), Li and Linetsky (2014), Li et al. (2016), Lim et al. (2012), Mendoza-Arriaga et al. (2010), Mendoza-Arriaga and Linetsky (2013), Tong et al. (2019), Tong and Liu (2017) and Tong and Liu (2018). The applications of eigenfunction expansion method for the multivariate subordinate processes appear recently in Li et al. (2016) and Mendoza-Arriaga and Linetsky (2016).

The structure of the paper is as follows. In Section 2, we introduce the general model framework. Starting from $d$ independent OU processes and a $d$-dimensional Lévy subordinator, we construct a new process by time changing each of the OU processes with a coordinate of the Lévy subordinator. The prices of the underlying assets of autocallables are modeled as an exponential of the subordinate processes. In Section 3, we describe the eigenfunction expansion method for both univariate and multivariate subordinate OU processes. In Section 4, we derive the recursive analytical pricing formulas for the worst-of autocallable prices using the eigenfunction expansion technique, where the expansion coefficients are also given explicitly. In Section 5, we present the numerical analysis of a specific model and provide the pricing sensitivities to some of the key parameters of the model.

2.   The model

Let $(\Omega, \mathcal{F}, Q)$ denote a probability space with an information filtration $(\mathcal{F}_t)$. We assume that under the risk-neutral measure $Q$, the state variables $X_i(t)$, $i = 1, \ldots, d$, are independent OU processes, i.e.,

where $\kappa_i$, $\theta_i$, $\sigma_i$ are constants. $B_i(t)$ is a standard Brownian motion and independent of $B_j(t)$ for $i\ne j$.

We model the joint dynamics of asset prices $S_i$ of a basket with $d$ components as an exponential function of a time changed OU process $Y_i$, that is

and

where ${\bf{T}} = (T_1, \ldots, T_d)$ is a $d$-dimensional time change process and $T_i$ is the $i^{th}$ coordinate of ${\bf{T}}$.

To introduce jumps and correlation into the asset prices dynamics, we follow Mendoza-Arriaga and Linetsky (2016) and model the time change process ${\bf{T}}$ as a $d$-dimensional Lévy subordinator; that is, each of the coordinates of ${\bf{T}}$ is a one-dimensional subordinator, a one-dimensional non-decreasing Lévy process starting at zero. The Laplace transform of ${\bf{T}}$ is given by the Lévy-Khintchine formula (see e.g., Sato, 1999). Here for $u_i\ge 0$ and $\langle {\bf{u}}, {\bf{v}}\rangle = \sum_{i = 1}^nu_iv_i$,

with the Laplace exponent given by

where $\boldsymbol\gamma\in\mathbb{R}^d_+$ is the drift of the subordinator and the Lévy measure $\nu$ is a $\sigma$-finite measure on $\mathbb{R}^d$ concentrated on $\mathbb{R}^d_+\setminus \{0\}$ such that

An important sub-class of multi-dimensional subordinators convenient for applications is the linear factor model (see e.g., Mendoza-Arriaga and Linetsky, 2016). Let $L_k(t)$ be $m$ independent one-dimensional subordinators and ${\bf{A}}$ a $d\times m$ matrix with non-negative entries $A_{i, k}\ge 0$. Define

where the coefficient $A_{i, k}$ is the corresponding loading coefficient. Then the $\mathbb{R}_+^d$-valued ${\bf{T}}(t)$ is a $d$-dimensional subordinator with the Laplace exponent given by

where $\phi_k$ is the Laplace exponents of the $m$ independent one-dimensional subordinators $L_k$. The covariance of $T_i(t)$ and $T_j(t)$ is determined by ${\bf{A}}$:

where $-\phi_k''(0)t$ is the variance of the $k^{th}$ subordinator $L_k(t)$.

The simplest example of subordinators that belongs to the linear factor model is the single-factor model, where $T_i(t) = L(t)$ and $L$ is a one-dimensional Lévy subordinator. In this case, the asset prices are subordinated by the common subordinator. Since the discontinuities of the sample path of prices are due to the subordinator and the same subordinator is acting on all the processes, this implies that all the prices processes will jump together.

The second example is a two-factor model, where

where $\alpha_i\ge 0$, $L_i$ are $d$ independent one-dimensional subordinators, which are also independent of the subordinator $L$. In this case, the asset prices are affected by two sources of uncertainty; one is common to all the assets and can be seen as a global uncertainty and the other is an idiosyncratic uncertainty. The presence of the idiosyncratic clock implies that the assets will not jump together.

3.   Eigenfunction expansion method for subordinate OU process

For the OU process $X_i(t)$ defined in (1), its infinitesimal generator $\mathcal{L}_i$ is given by

where $f$ is transformation function. $f'$ and $f''$ are first- and second-order derivatives of $f$, respectively.

The infinitesimal generator $\mathcal{L}_i$ with domain dom($\mathcal{L}_i$) is always self-adjoint on the Hilbert space $L^2((-\infty, \infty), m_i)$ of functions on $(-\infty, \infty)$ square integrable with the speed measure $m_i(dx) = m_i(x)dx$ and endowed with the inner product $(f, g)$, where

and

We are interested in the transition semigroup $(\mathcal{P}_t^i)_{t\ge 0}$ of $X_i$ defined by

We can use the eigenfunction expansion method for self-adjoint operators in Hilbert spaces to write down the spectral decomposition of $\mathcal{P}_t^if(x)$ (see e.g., Linetsky and Mitchell, 2008).

Proposition 1. For any $f\in L^2((-\infty, \infty), m_i)$, the transition semigroup of the OU process $X_i$ has an eigenfunction expansion of the form

where $f_n = (f, \psi_n^i)$, $\{\lambda_n^i\}$ are the eigenvalues of $-\mathcal{L}_i$ and $\{\psi_n^i\}$ are the corresponding eigenfunctions satisfying the following Sturm-Liouville equation

The eigenvalues and eigenfunctions of OU process can be summarized in the following result (see e.g., Linetsky and Mitchell, 2008):

Proposition 2. For the OU process $X_i$ defined in (1), the eigenvalues $\lambda_n^i$ and eigenfunction $\psi_n^i$, $n = 0, 1, \ldots$, are

and

where $\xi_i = \frac{\sqrt{\kappa_i}}{\sigma_i}(x-\theta_i)$,

and $H_n(x)$ is the Hermite polynomial defined as

For the subordinate OU process $Y_i$ defined in (3), we can also compute the transition semigroup $(\mathcal{P}_t^{i, \phi^i})_{t\ge 0}$ of $Y_i$, where $\phi^i$ is the Lévy exponent for the univariate Lévy subordinator $T_i$:

We can employ the eigenfunction expansion method again to compute the semigroup $\mathcal{P}_t^{i, \phi^i}f(x)$ using the following result (see e.g., Li and Linetsky, 2014):

Proposition 3. For any $f\in L^2((-\infty, \infty), m_i)$, the transition semigroup of the subordinate OU process $Y_i$ has an eigenfunction expansion of the form

where $\{\lambda_n^i\}$ and $\{\psi_n^i\}$ are the eigenvalues and eigenfunctions of OU process and can be obtained from (17) and (18), respectively.

From the above results, it is clear that a key feature of the eigenfunction expansion method is that the temporal and spatial variables are separated. The time variable $t$ enters the expansion only through the exponential function $\exp(-\lambda_n^i t)$. The eigenfunction expansion of time changed process $Y_i$ has the same form as the original process $X_i$, but with $\exp(-\lambda_n^i t)$ replaced by $\exp(-\phi^i(\lambda_n^i)t)$. As long as the Laplace transform of the time change process $T_i$ is known, the time changed model will be as tractable as the original model.

For multivariate OU process ${\bf{X}}(t) = (X_1(t), \ldots, X_d(t))$ and multivariate subordinate OU process ${\bf{Y}}(t) = (Y_1(t), \ldots, Y_d(t))$, we can define the transition semigroups of ${\bf{X}}$ and ${\bf{Y}}$ by

where ${\bf{x}} = (x_1(0), \ldots, x_d(0))$ and

where $\phi$ is the Lévy exponent for the multivariate Lévy subordinator ${\bf{T}}$.

Define $m(d{\bf{x}}): = m_1(dx_1)\ldots m_d(dx_d)$ and $\psi_{\bf{n}}({\bf{x}}) = \prod_{i = 1}^d \psi_{n_i}^i(x_i)$. We can formulate the eigenfunction expansions for the semigroups $\mathcal{P}_tf({\bf{x}})$ and $\mathcal{P}^\phi_tf({\bf{x}})$ using the following results (see e.g., Mendoza-Arriaga and Linetsky, 2016).

Proposition 4. For any $f\in L^2((-\infty, \infty)^d, m)$, the transition semigroup of the multivariate OU process ${\bf{X}}$ has an eigenfunction expansion of the form

where $\sum_{{\bf{n}}\in\mathbb{Z}_+^d}: = \sum_{n_1 = 0}^\infty\ldots\sum_{n_d = 0}^\infty$ and

Proposition 5. For any $f\in L^2((-\infty, \infty)^d, m)$, the transition semigroup of the multivariate subordinate OU process ${\bf{Y}}$ has an eigenfunction expansion of the form

where $f_{\bf{n}}$ can be obtained from (26).

It is clear that the eigenfunction expansion of ${\bf{Y}}$ has the same form as ${\bf{X}}$, but with $\exp\left(-\sum_{i = 1}^d\lambda_{n_i}^i t\right)$ replaced by $\exp\left(-\phi(\lambda_{n_1}^1, \cdots, \lambda_{n_d}^d) t\right)$. Thus, the eigenfunction expansion method makes the multivariate time changed model as tractable as the original model. This result explains why eigenfunction expansion method provides powerful analytical and computational tool for multivariate securities pricing.

4.   Autocallables pricing with eigenfunction expansion method

Generally, the autocallables have discrete autocall dates. Let the observation dates be $0 = t_0 < t_1 < \cdots < t_N$, where $t_N$ is the expiry date of the product. For simplicity, we assume equally discrete observations so that $t_i = i\Delta$. We consider a standard multi-asset worst-of autocallable (see e.g., Bouzoubaa and Osseiran, 2010) which pays coupons depending on the underlying basket components' worst performance reaching two triggers $H$ (autocall trigger) and $B$ (coupon trigger) with $H\ge B$. The basket's worst performance at time $t_i$ is defined by

The autocallable has a payoff defined as follows:

● At each observation date $t_i$, $1\le i < N$, if $WRet(t_j) < H$, $0 < j\le i-1$, and

${\rm{(i)}}$ $WRet(t_i)\ge H$, then the autocallable is redeemed and the holder receives the initial notional $L$.

${\rm{(ii)}}$ $WRet(t_i)\ge B$, then the holder receives a predetermined coupon $C_i$.

${\rm{(iii)}}$ $WRet(t_i) < B$, then the holder will miss the coupon and the autocallable continues.

● At expiry date $t_N$, if $WRet(t_j) < H$, $0 < j\le N-1$, and

${\rm{(i)}}$ $WRet(t_N)\ge B$, then the holder receives the initial notional $L$ plus coupon $C_N$.

${\rm{(ii)}}$ $WRet(t_N) < B$, then the holder only gets back the notional $L$.

The payoff function at date $t_i$, $1\le i\le N$, can then be expressed as

Our goal is to determine the price of the autocallable with the above payoff. We will demonstrate that eigenfunction expansion method enables us to derive the analytical formulas for the autocallable price under the multivariate subordinate OU process.

Before applying eigenfunction expansion method, we notice that for our new pricing model, the eigenvalues and eigenfunctions of OU process can be calculated easily from Proposition 2. To employ the eigenfunction expansion method to calculate the autocallable price, we still need to obtain the eigenfunction expansion coefficients. In this section, we provide the formulas for several integrals that will later be employed to calculate those coefficients.

The following integrals can be computed using the results of Lim et al. (2012) and Prudnikov et al. (1986):

Lemma 1.

(i)

(ii)

where $\Phi(x)$ is the CDF of standard normal distribution.

(iii)

(iv) Define

Then, $\gamma_{m, n}(u)$ can be calculated recursively as follows:

and for $m\neq n$,

Using Lemma 1, we can also prove the following results (see also Tong et al., 2019):

Corollary 1.

(i)

(ii)

(iii)

(iv)

Using backward iteration and eigenfunction expansion method, we can obtain the analytical formula for the autocallable prices recursively. We can prove the following result:

Proposition 6. Assume that the stochastic processes for the asset prices ${\bf{S}}(t) = (S_1(t), \ldots, S_d(t))$ are specified in (1), (2), (3) and the time change process ${\bf{T}}(t)$ is a multivariate Lévy subordinator with Lévy exponent $\phi$, then the time $t = 0$ price $V({\bf{s}})$ of an autocallable with the payoff function defined in (29), conditioning on ${\bf{S}}(0) = {\bf{s}} = (s_1, \ldots, s_d)$, is

where $\sum_{{\bf{n}}\in\mathbb{Z}_+^d}: = \sum_{n_1 = 0}^\infty\ldots\sum_{n_d = 0}^\infty$ and $\psi_{\bf{n}}(\log({\bf{s}})) = \prod_{i = 1}^d \psi_{n_i}^i(\log(s_i))$. $r$ is the risk-free spot rate. $\lambda_{n_i}^i$ and $\psi_{n_i}^i$ are the eigenvalues and eigenfunctions of univariate OU process $X_i$, respectively. The eigenfunction expansion coefficient $g_{n_1, \ldots, n_d}$ can be obtained recursively as follows:

where

and for $i = N-2, \ldots, 0$,

where $\boldsymbol\varpi = \{1, 2, \ldots, d\}$. $a_n^i$, $b_n^i(\cdot)$, $c_{m, n}^i(\cdot)$ and $d_{m, n}^i(\cdot)$ are the functions that can be calculated using Corollary 1.

Proof. Denote $V^{(i)}({\bf{Y}}(t_i))$ the value of the autocallable at time $t_i = i\Delta$, $i = 0, 1, \ldots, N$. Clearly, $V({\bf{s}}) = V^{(0)}(\log({\bf{s}}))$. At time $t_N$,

For $i = N-1$, we have

where ${\rm{E_{N-1}[\cdot]: = {\rm{E}}[\cdot|\mathcal{F}_{t_{N-1}}]}}$.

By eigenfunction expansion, we have

where using Corollary 1, we have

Therefore,

Next, we consider $V^{(N-2)}({\bf{Y}}(t_{N-2}))$. We have

Again using eigenfunction expansion, we obtain

where using Corollary 1, we have

We can continue this backward iteration until we reach time $t_0$ and hence prove the result.

5.   Numerical results

In this section we report numerical results for autocallables written on a two-asset basket based on the multivariate subordinate OU model (MSub-OU). The trigger functions for the autocall and coupon payment are of worst-of type. For simplicity we let the predetermined coupon to be a deterministic function, that is $C_i = L\times C\times\Delta$, where $C$ is the coupon rate. We also specify the two-dimensional subordinator ${\bf{T}}$ as a linear combination of three independent subordinators $L_i$, $i = 1, 2, 3$, as follows:

and

where $L_1$ and $L_2$ are two idiosyncratic components to influence only the first and second asset, respectively and $L_3$ is the systematic component common to both assets. The parameters $\alpha_i$, $i = 1, 2$, control the correlation between two assets. When $\alpha_i = 0$, $i = 1, 2$, the two subordinators $T_1$ and $T_2$ are independent and hence, the two asset price processes $S_1$ and $S_2$ also become independent. The three subordinators are taken to be pure-jump driftless IG subordinators with the Lévy exponents:

where $\delta_i > 0$ and $\eta_i\ge 0$. From Tankov and Cont (2003), we know that the scale parameter $\delta_i$ alters the arrival rates of jumps of all sizes simultaneously, while the parameter $\eta_i$ controls the decay of large jumps. The set of parameters for the benchmark model is given in Table 1. For simplicity we assume that the parameters for the two components of underlying OU processes are taking the same values. Similarly, the parameters of two idiosyncratic components of time change process are also the same. We evaluate the effect of parameter value changes on the autocallable prices by varying the selected parameters while keeping other parameters taking the values in Table 1.

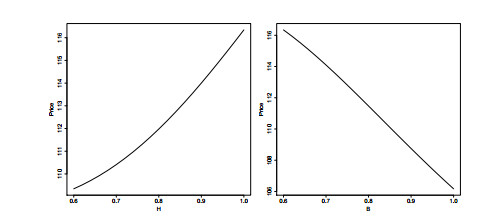
In practice, to employ the eigenfunction expansion to calculate the autocallable prices, we need to truncate the eigenfunction expansion after a finite number of terms. We will follow Li et al. (2017) by truncating the infinite series when a given error tolerance level is reached. To check if our model has been implemented correctly, we plot the autocallable prices for different levels of autocall trigger $H$ and coupon trigger $B$. We expect that the prices should be an increasing (decreasing) function of $H$ ($B$) as the probability of hitting the autocall (coupon) trigger is a decreasing function of $H$ ($B$) and therefore, the chance of missing coupon payment will be a decreasing (increasing) function of $H$ ($B$). The results in Figure 1 confirm that the model behaves as expected.

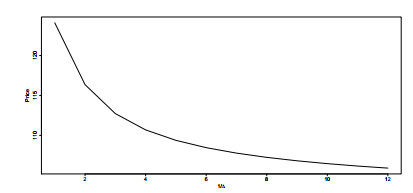
In Figure 2, we also plot the sensitivities of prices to the autocall frequency $1/\Delta$. We find the prices decrease with the frequencies, which is due to the fact the autocallables will be less probable to stay between the coupon trigger $B$ and autocall trigger $H$ when the frequencies increase. When the autocallable prices go above the $H$ or below $B$ more often, the prices of autocallables will decrease.

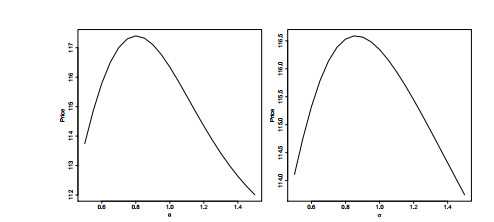
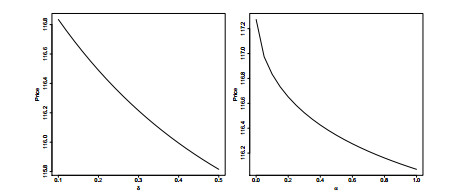
We also evaluate the effect of other parameter value changes on the autocallable prices. We consider the sensitivity of autocallable prices with respect to four parameters: the long term mean parameter $\theta = \theta_i$ and the volatility term $\sigma = \sigma_i$ for the process $X_i$, $i = 1, 2$ and the scale parameter $\delta = \delta_i$ and loading coefficient $\alpha = \alpha_i$ for the time change process $T_i$, $i = 1, 2$.

Figure 3 shows that the autocallable prices are an inverted U-shaped function of both $\theta$ and $\sigma$. Since the underlying state variable $X_i(t)$ is the OU process with long term mean $\theta$, $X_i$ will fluctuate around $\theta$. When $\theta$ is low, an increases in $\theta$ will decrease the chances of missing the coupons for the autocallables and therefore, the prices will increase with $\theta$ at the beginning. However, when $\theta$ becomes much larger, the probability of hitting the autocall trigger will increase as well, which will reduce the values for autocallables. When the volatility term $\sigma$ is low but increases initially, the asset prices will have more chances to stay between $B$ and $H$, which will increase the autocallable values. However, when $\sigma$ becomes larger, an increase in $\sigma$ will make the asset prices more probably go below $B$, which will decrease the autocallable prices.

In Figure 4, we find the autocallable prices are a decreasing function of both $\delta$ and $\alpha$ of the subordinators $T_i$. In both cases, the increases in the parameters will increase the means of $T_i$. In our model, the log asset prices are $X_i(T_i(t))$ and hence when $T_i$ becomes larger, the asset prices will more likely take values close to the long term mean $\theta$. In our case, the effective autocall trigger in terms of the log asset prices is $\log(H)+X_i(0)$ and according to the set of parameters given in Table 1, $\theta$ is higher than this effective trigger. As a result, the asset prices will lie above the trigger more often when the means of $T_i$ increase and this will lower the autocallable prices.

We also compare our new model with two popular competing models. The first is an OU model without time change, which is currently one of the most popular models for the asset class with mean reversion. The OU model is nested in our model by setting $T_i(t) = t$, $i = 1, 2$. Note that in this model, there are no jumps in the asset prices and the assets are independent to each other. The second one is an subordinate OU model with independent time changes (Sub-OU), which is nested in our model by setting $\alpha_1 = \alpha_2 = 0$. Note that in this model, the asset price processes are independent. We compare three models with varying maturities based on the parameters in Table 1. From Table 2, it is clear that the autocallable prices are increasing with maturity for each model. Furthermore, the differences in the prices across the models become larger when the maturity increases.

6.   Conclusion

This paper proposes a new modeling framework for pricing autocallables based on multivariate time changes of OU processes. Staring with $d$ independent OU processes and time changing each of them with a coordinate of a $d$-dimensional Lévy subordinator, we obtain a subordinate OU processes with jumps in the product space. The dependence among jumps is governed by the Lévy measure of the $d$-dimensional subordinator. We then model the underlying asset prices of autocallables as an exponential function of the subordinate OU processes. We employ the eigenfunction expansion method for multivariate subordinate OU processes to derive the analytical formulas for the prices of worst-of autocallable prices. We also numerically implement our model and test its sensitivity to some of the key parameters of the underlying processes.

In practice, there are more complicated variants of autocallables such as outperformance autocallables where coupon value may be a function of the asset prices. Another complication is to add a worst-of down-and-in put feature to the autocallable structure, where the capital is no longer protected as the owner is short a put option at maturity. We need to emphasize our techniques can be extended to handle these more complex structures with minor changes and we leave these applications for future research.

Acknowledgments

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Conflict of interest

The author declares no conflicts of interest in this paper.