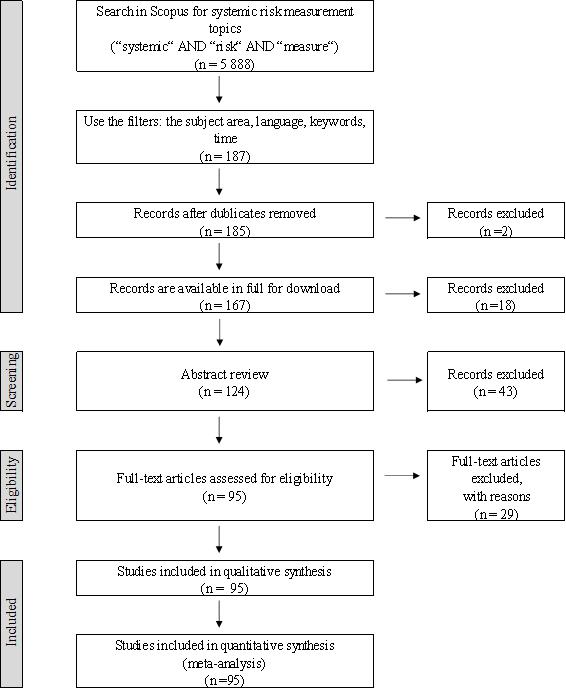
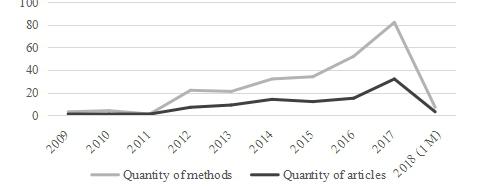
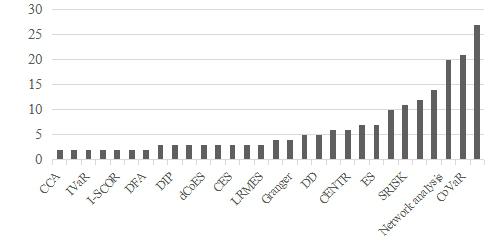
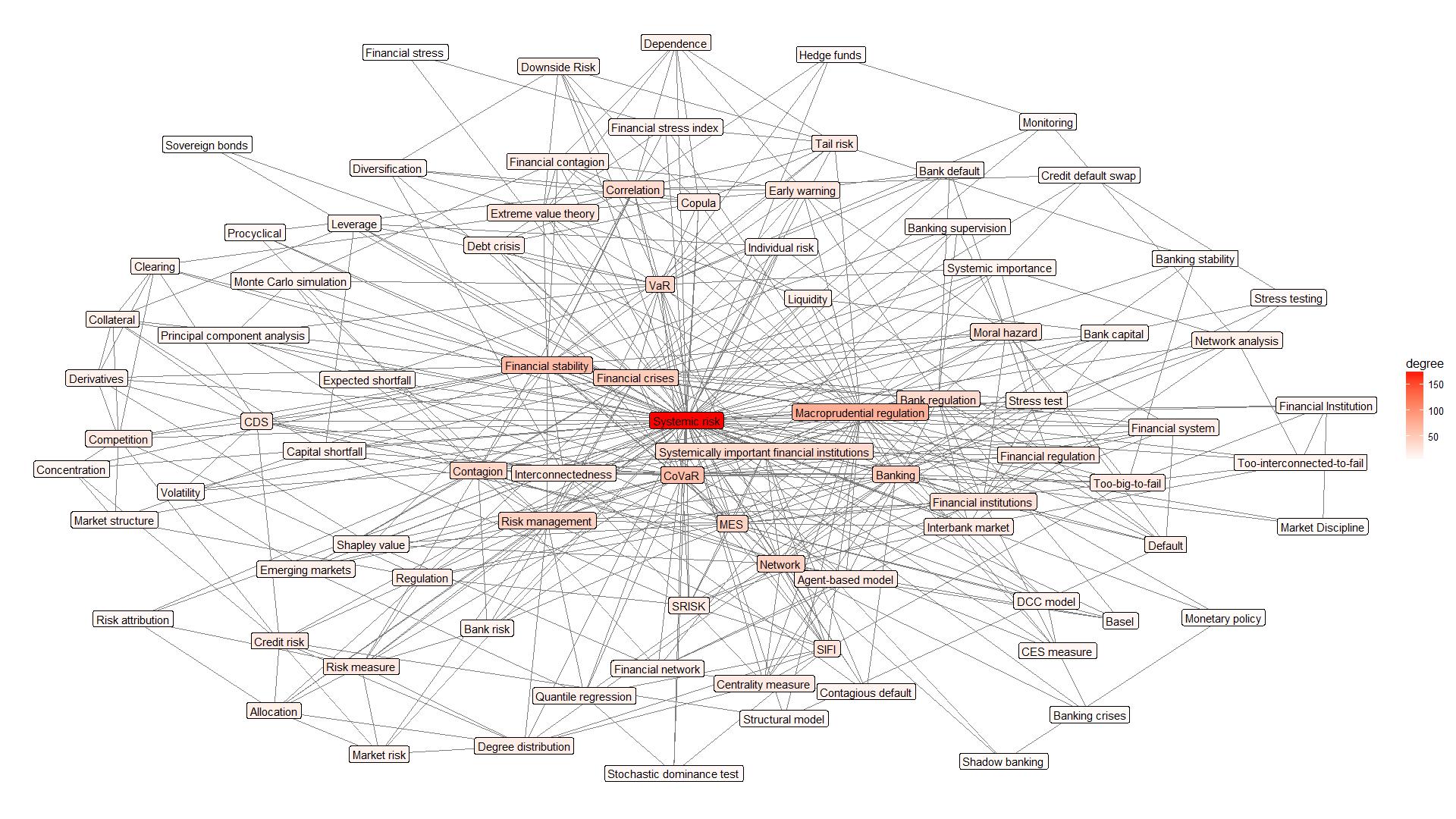
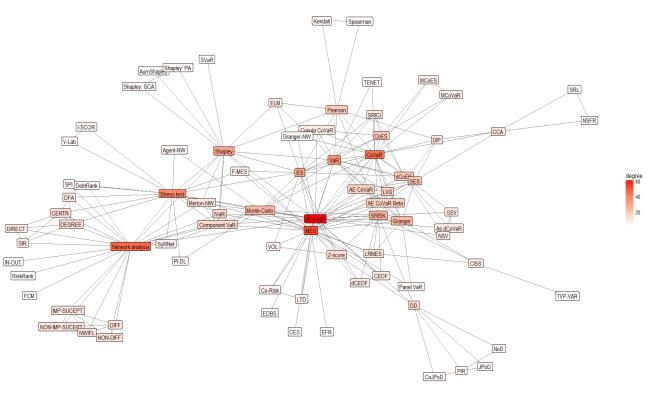
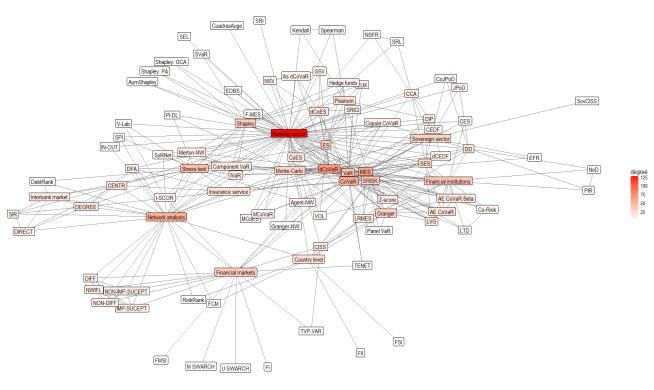
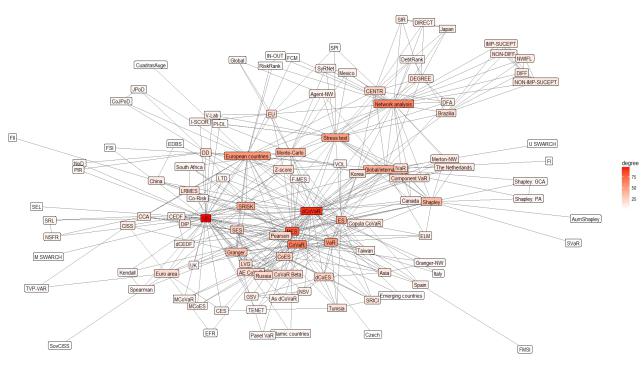
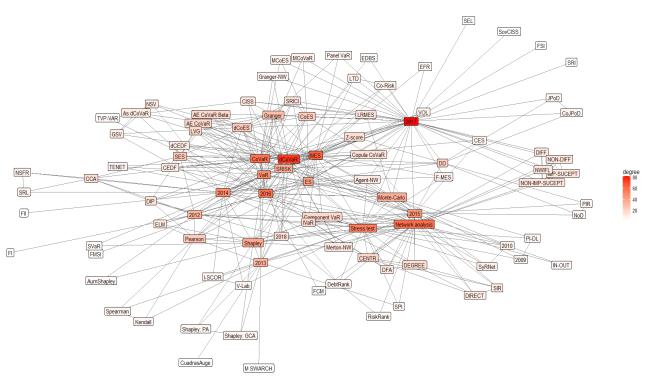
This article presents an analysis of the literature on systemic risk measurement methods. Only the recent global crisis has particularly attracted the attention of researchers on systemic risk measurement. Global challenges such as Big Data, AI, IoF, etc. also have an impact on expanding the systemic risk measurement capabilities. The growing number of publications in the last decade opens the door to deeper insights into the systemic risk measurement features, summarizing the contribution of research and analyse the mainstream research on systemic risk, identify the strengths and weaknesses of the studies. Therefore, the main objective of this study is to provide a framework to address the relevant gaps in the current discussion on systemic risk measurement by conducting a wide search in Scopus database to identify the studies that used different systemic risk measurement in the period from 2009 to January 2018. A meta-analysis of scientific articles is performed based on the Preferred Reporting Items for Systematic Reviews and Meta-Analyses (PRISMA) method and using network approach presents the main interconnection of the methods used to measure systemic risk. A critical analysis of these articles addresses some important key issues. The results of this review are important: they will help researchers to develop better research methods and models around systemic risk measurement. Based on the results, it has allowed us to identify the key issues in choosing a method to assess systemic risk and to help researchers avoid pitfalls in using these methods.
1.
Introduction
A lot of variations of Adaptive Kalman Filters (AKFs) have been developed in the post Kalman Filter (KF) era where process and observation noise covariances are mostly assumed to be known a priori or calculated indirectly. Recently, some AKFs were evolved by Ding (2007), Almagbile et al. (2010), Das and Ghoshal (2010), Senyurek et al. (2014), Kownacki (2015), Das (2016) and Bel et al. (2017) where those noise covariances are assumed to be time varying and made known within the filter iterations. Process noise has been scaled during each filter iterations by available other parameters where as observation noise covariance is revealed using innovations based noise covariance matching principle. These techniques have been applied specially for state and parameter estimations of control and navigational problems (Ding et al., 2007) where any one of these two covariances was assumed to be known and other covariance is calculated. These techniques are suffering from parameter inconsistency problem. To deal with this problem some suitable modifications is introduced in this work. The next target is to develop AKFs and its modifications (if any) where both these noise covariances are not known a priori and calculated during each filter iterations, may be simultaneously. The next target is to characterize these methods for market risk beta (β) estimation in a simple stochastic financial system modelled by Capital Asset Pricing Model (CAPM) (Shah and Moonis, 2003; Bel et al., 2017) and auto-regressive β movement with Gaussian noise components.
CAPM changes the concept of risk identification by volatility (Kai et al., 2018) as only risk measure to that by another variable denoted by β known as systematic (or market) risk. β measures the asset sensibility to the variations on the market returns. Though β is assumed to be time invariant in the classical financial literature, the estimation problem becomes complicated when it is assumed to be time varying. There are substantial evidences that the stability assumption is invalid in several financial markets in US, Itali, Malaysia, Australia and even in India (Mohamed and Schwarz, 1999; Shah and Moonis, 2003). This study explores Indian financial market data describing the relation (β) between the assets return (identified by sectorial indices) and the market index return (identified by gross market index).
One of the important uses of β is for VaR estimation usually estimated using volatility (Das et al., 2008; Das, 2014). The VaR calculation methods are thus named after the estimation techniques of the β. β is estimated using OLS, KF and improved KF (Berardi, 2002; Shah and Moonis, 2003; Gastaldi and Nardecchia, 2003; Wang et al., 2009) in a linear framework and hence the names follow. After β estimation the VaR calculation formula of a portfolio is given by:
where σ2m is the estimated variance of the market index return, β is the vector of βs of individual assets in the portfolio with corresponding weight vector w of portfolio composition.
Unfortunately VaR alone cannot answer the question of how large can the losses be when the VaR is exceeded. However, there is one measure which can complement VaR to make available the information that is missing on tail losses (i.e. losses in excess of VaR). This is the Expected Shortfall (ES) (Yamai and Yoshiba, 2002), which is the expected value (i.e. the average) of the suffered losses, L, if a loss is emerging in excess of VaR. In mathematical terms:
VaR enlightens us the most we can expect to lose if a bad (i.e. tail) event does not occur, and the ES tells us what we can expect to lose if a tail event does occur. In short, the ES has the same appeal as the VaR. ES presents a common consistent risk measure across different positions. It also has many of the same uses as VaR.
The goodness of the models along with considered methods is evaluated by comparing the in-sample forecasting accuracy of the estimated returns through β estimates (Mergner, 2008). In-sample forecasting accuracy of returns is determined by two measures namely mean absolute error (MAE) and the root mean squared error (RMSE). The focus of the present study is to conduct time evolving beta estimation (market risk) through different methods and comparing the performances thereof. The performance of the empirically estimated βs are judged by (1) VaR estimation with the estimated empirical βs, primarily as indirect method of performance evaluation, (2) In-sample return forecasting performance analysis with those estimated βs, secondarily as direct method of performance evaluation as far as beta estimation forecasting is concern. VaR backtesting using traffic light approach and expected shortfall analysis are presented to justify how best that VaR estimates are.
This paper is organised as follows. In section 2, related literature and background theory are reviewed. Section 3 demonstrates the techniques used in this work where as section 4 depicted the results of the explorations carried out with realizations. Section 5 presents some conclusions based on the evidence obtained in this study.
2.
Background theory
According to CAPM if the market portfolio is efficient, then the i-th asset return is described by ri=αi+βirm+εi where ri and rm is the returns of the i th asset and market index respectively, αi is the risk free rate of return (risk free interest), εi is the random error term (with variance σ2t), βi is the relationship of the asset return with market index return, or in other words, it is the sensitivity of the i-th asset return with respect to the market. βi can be expressed as a ratio of covariance (σim) between specific asset returns and market index returns and variance (σ2m) of market index returns. i.e. βi=σim/σ2m. If asset returns is completely uncorrelated to the market returns i.e. βi=0, then according to CAPM asset return will be equal to the risk-free rate of return. The CAPM changes concept of the risk from the volatility to β.
In the simpler model, the sensitivity term β is a constant and the noise term is zero mean, Gaussian IID samples. As the describing equation ri=αi+βirm+εi is linear, the constants αi and βi can be determined in the least square (Barth et al., 2018) sense from the time series data of ri and rm. Analysis of the time series of residuals εi also reveals interesting aspects. For example, one can verify whether εi is zero mean (a violation would indicate computational error), from the standard deviation of εi, one can deduce the quality of fit by statistical techniques, whether εi is a Gaussian sequence, whether the terms in εi are really uncorrelated noise etc. The last criterion, namely, whether the terms in εi are really uncorrelated noise would really put a question mark on the assumption that the sensitivity term β is a constant.
Literature shows that there have been quite a number of techniques for β estimation among which Ordinary Least Square (OLS), KF (Berardi et al., 2002; Shah and Moonis, 2003) are used conventionally and AKF are used rarely. Shah and Moonis (2003) used modified KF for estimating daily βs with high frequency Indian data exhibiting significant non-Gaussianity in the distribution of β. Gastaldi and Nardecchia (2003) approached to estimate time varying β using KF.
3.
Methodology
Application of OLS technique is common for estimation of static β of an industry sector. However the first focus here is towards the utilization of two adaptive estimation techniques namely, RLS (Simon, 2006) and LMS (Haykin, 2001; Nazin and Ljung, 2002) for time varying β estimation. Though these adaptive filters have huge applications in control and navigation literature, but these are rarely found in finance and econometric. The other focus is the applications of KF (Gastaldi and Nardecchia, 2003; Snyder et al., 1996) and newly proposed Modified Adaptive Kalman Filters (MAKF) using regression model of CAPM. Sectorial indices data from Indian market together with Nifty has been analysed in this section to get the time varying adaptive estimates of β parameter of the specific sectors. Those existing and newly proposed adaptive estimation techniques are presented below.
3.1. RLS
OLS gives a way to compute the optimal estimate of constant parameters of a linear regression equation. If we obtain measurements sequentially and want to update our estimate of state we need to augment the measurement transition coefficient and completely recomputed the state estimates. If number of outputs becomes large, then the computational effort could become excessive. A linear recursive estimator for β of regression model of CAPM given by ri,t=rm,tβt+υt with α=0, can be written as ˆβt=ˆβt−1+Kt(ri,t−rm,tˆβt−1), i.e. we compute ˆβt on the basis of the previous estimate ˆβt−1 and the new output ri,t. Kt is a coefficient to be determined called the estimation gain coefficient. The quantity (ri,t−rm,tˆβt−1) is called the correction term. Since the estimator is unbiased regardless of what value of Kt we use, we must choose some optimality criteria in order to determine Kt. The optimality criterion that we choose to minimize is the sum of the variances of the estimation error at time t. We use the RLS algorithm given in the appendix following section 3.3 of Simon (2006) for the purpose of RLS β estimation. Compared to most of its contestants, the RLS demonstrate extremely fast convergence. However, this benefit comes at the cost of high computational complexity, and potentially poor tracking performance when the "true system" changes. The detail RLS algorithm (Algorithm 1) is given in appendix.
3.2. LMS
The LMS is an adaptive algorithm which incorporates an iterative procedure that makes successive corrections to the weight vector in the direction of the negative of the gradient vector which eventually leads to the minimum mean square error. Compared to other algorithms LMS algorithm is relatively simple; it does not require correlation function calculation nor does it require matrix inversions. Although the LMS algorithm is very simple in computational terms, its mathematical analysis is profoundly complicated because of its stochastic and nonlinear nature. The stochastic nature of the LMS technique manifests itself in the fact that in a stationary environment, and under the assumption of a small step-size parameter, the method executes a form of Brownian motion. We have used LMS algorithm given below following Equation 8 of Nazin and Ljung (2002) which demonstrated a parameter estimation technique using LMS filter. The detail LMS algorithm (Algorithm 2) is given in appendix.
3.3. AKF and their modifications
Ordinary state estimation methods require nearly complete knowledge of the "signal model" which includes system model, measurement model, covariance of process noise (Q) and covariance of measurement noise (R). The estimation would be optimal only when the "signal model" is known with acceptable accuracy. When such accurate model is not available, one may use adaptive estimators like AKF (Mehra, 1972). In the present work, variants of AKF would be employed to filter financial time series data. In such applications covariance matrices Q and/or R are usually unknown. The AKF would be used in such restricted situations and the nominal (noise-free) process and observation models would be assumed to be known.
Many KF applications for β estimation (Gastaldi and Nardecchia, 2003) assume the Q and R to be known to the filter. However, in reality, such assumptions are not correct. Over the past few decades AKF algorithms have been intensively investigated to reduce the influence of the Q and R definition errors. However, applications of AKF to financial time series are rare. In the present work we characterize one of the recent AKF techniques found successful in GIP/INS applications developed by Mohamed and Schwarz (1999), Ding et al. (2007), Almagbile et al. (2010) and Senyurek et al. (2014). A total of five AKF algorithms have been characterized and modifications of those algorithms have also been proposed to address the failures.
The simple state-space representation of a dynamical system is given by
where yt is the output, xt is the state variable, Ht is known time varying output transition coefficient, Ft is the state transition coefficient and dt is known feedback (additive constant) at time t. Also wt is a serially uncorrelated zero mean process noise with covariance Qt, and νt is serially uncorrelated zero mean output noise with covariance Rt at time t.
Define innovation sequence as:
and the residual sequence as:
We can write from Equation (5) that:
Covariance matching principles (Mehra, 1972) give:
when E{vtv′t} is available, the covariance of the observation noise Rt can be estimated directly from the equation:
where m is the estimation window size and for Equation (9) to be valid, the innovation sequence has to be ergodic and stationary over the m steps.
Mohamed and Schwarz (1999) and Senyurek et al. (2014) used innovation based adaptive estimation techniques which give ˆQt=KtˆCtK′t, where ˆCt=1mm−1∑i=0vt−iv′t−i and Kt is the Kalman gain at time t. This Q is formulated using maximum likelihood based technique. To improve the robustness of the adaptive filtering algorithm, a new process noise scaling method is proposed by Ding et al. (2007) given by:
Adaptive estimation of R is associated with the Q due to the fact that the derivation is based on the KF process. This can be noticed from (9), that in order to estimate Rt, the calculation of the predicted state covariance Pt|t−1 has used the Qt. The normal practice is to fix one, say Q, and estimate the other one (i.e. R). The variation of the AKF algorithms in this way should be as follows: (1) R known and Q unknown (QAKF), (2) Q known and R unknown (RAKF), (3) Q unknown with known R at first (QRAKF), (4) R unknown with known Q at first (RQAKF) and (5) Q and R both simultaneously unknown (SRQAKF). Among these variations, the first two concepts have been introduced by Ding et al. (2007) but without formal algorithmic representations. Last three techniques are newly proposed here with formal algorithmic approach. The following sub-sections present and modified the above algorithms for a first order financial state-space model.
3.3.1. Modified QAKF algorithm
Algorithm QAKF is developed with the assumption that the R is known. The algorithm concerns about estimating adaptive Q with the Q adaptation formula given in (10). Estimated Qs are used in the next KF iterations. The detail QAKF algorithm (Algorithm 3) is given in appendix.
To deal with parameter inconsistency problem (Q become negative after time iterations) arrived while characterizing this QAKF through simulation study and also in empirical explorations (Das and Ghoshal, 2010) the following modification is introduced. The detail MQAKF algorithm (Algorithm 4) is given in appendix.
3.3.2. Modified RAKF algorithm
Algorithm RAKF is developed with the assumption that the Q is known. The algorithm is concerned about estimating time evolving R with the R adaptation formula given in (9). Estimated R's are used in the next filter iterations. The parameter inconsistency problem is also taken place here (R becomes negative while characterizing through simulation and empirically) and corresponding new modification is introduced. The detail MRAKF algorithm (Algorithm 5) is given in appendix.
3.3.3. Modified QRAKF algorithm
This is one of the proposed algorithms when both Q and R have to be adapted. Algorithm QRAKF is developed with the assumption that the R is known at the first iteration cycle and goes on estimating unknown adaptive Q using formulae in (10). The next iteration cycle deals with estimating adaptive R using formulae in (9) assuming it as unknown where estimated Q in the last iteration is used in this iteration. Similarly, the next iteration concerns estimating Q where estimated R in the last iteration is used in this iteration. This algorithm also suffers from parameter inconsistency problem and corresponding modified version MQRAKF is developed and presented in Algorithm 6 at appendix.
3.3.4. Modified RQAKF algorithm
This is another proposed algorithm where both Q and R have to be estimated. Algorithm RQAKF is developed with the assumption that Q is known at the first iteration and concerns on estimating unknown R using formulae in (9). The next iteration deals with estimating Q using formulae in (10) assuming it as unknown where estimated Q in the last iteration is used in this iteration. Similarly, the next iteration concerns estimating R where estimated Q in the last iteration is used in this iteration. This RQAKF also suffers from the same problem like earlier and hence its modified version MRQAKF is developed and presented in Algorithm 7 at appendix.
3.3.5. Modified SRQAKF algorithm
Algorithm SRQAKF is developed, likewise (Das and Ghoshal, 2010), with the assumption that both the Q and R are not known at the first iteration and concerns on first estimating unknown adaptive R estimation using formulae in Equation (9) and then estimating unknown adaptive Q estimation using formulae in Equation (10) where estimated R in this iteration is used. Since Q calculation needs the value of R, we estimated R before Q estimation where estimated value of R is used. The same parameter inconsistency problem (Q and R both become negative) occurred in this case also and hence it is modified as MSRQAKF and presented in Algorithm 8 at appendix.
4.
Empirical investigations
4.1. Data source and preparation
The stock indices data from National Stock Exchange (NSE) of India has been collected from NSE website (http://www.nseindia.com). The daily closing data during 1st January, 2001 to 31st, December, 2008, total of 2003 days data, are considered for the study. The stock market indices are reasonably representative of a mixture of industry sectors and trading activity mostly revolves around the stocks comprising the indices. The sectoral indices, suitably designed portfolios of equities from specific sector, are considered as representatives of portfolios and gross index Nifty (S & P CNX NIFTY) data are fair representative of the diversified market together. The considered sectoral indices are Bank (BANK NIFTY), Midcap (CNX MIDCAP), Defty (S & P CNX DEFTY) and Junior (CNX NIFTY JUNIOR). The literature on formation and composition of the selected indices are available on NSE websites.
4.2. Results and discussions
4.2.1. OLS
OLS was used to estimate β of the four considered portfolios (viz. Bank, Midcap, Defty and Junior) with respect to market index Nifty. The results are tabulated in table 1.
4.2.2. RLS
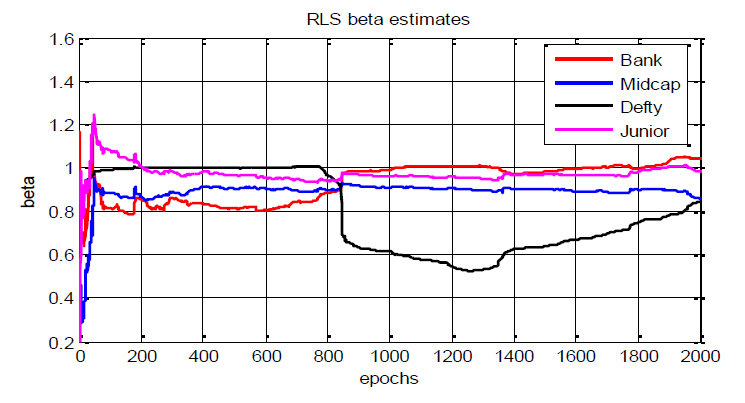
Figure 1 depicts the β estimates using RLS with initialization β0= 0.2 and P0 = 1. Selected indices β are estimated with respect to Nifty.
It is observed that the β estimates emerged by the RLS technique with suitable parameter choice for all four indices are comparable to one another. The range of β estimates as evident from the figure is 0.5 to 1.2. It is also noticed that the estimated β of three indices is close to unity, where as the Defty index behaves differently. Defty incorporates the Dollar-Rupee exchange rates and therefore is very likely affected by factors other than the security market. Its behaviour may differ from other indices.
It may also be noted that the RLS is in effect, a degenerate form of KF, with the process noise set zero and the system matrix equaling unity. Both of these favour near constant value of the state variable and effectively smoothen out fluctuations.
4.2.3. LMS
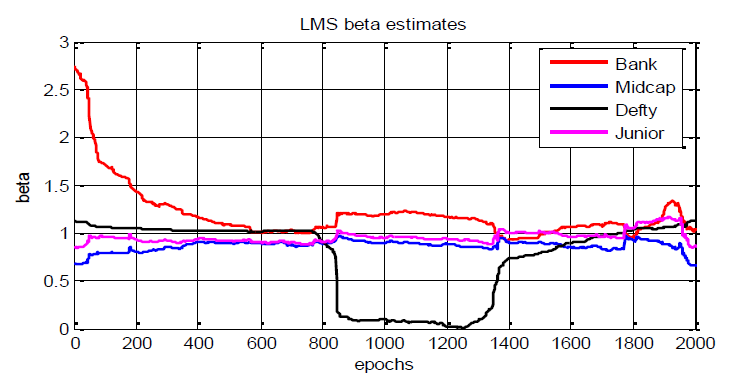
LMS adaptive filter is relatively simple and the computational complexity of this algorithm is low compared to its competitors. It has convergence property as well. Moreover, it does not require correlation function calculation nor does it require matrix inversions. Numerical experiments were carried out with above LMS algorithm for empirical β estimation of the selected Indian indices. Figure 2 presents the β estimates using LMS estimator where μ = 20 (suitable choice of μ to get the convergence results of the β estimates). Selected indices β are estimated here with respect to Nifty returns (rm,t). Such choice of μ provided the β estimates comparable to that provided by other competing estimators.
It is observed that the β estimates emerged by the LMS technique for all four indices are comparable to one another with suitable parameter choice. The Figure 1 and 2 show that the LMS β estimates are very similar to the RLS β estimates for all considered indices except for some initial 'burn-in' period.
4.2.4. Beta estimation with modified AKF techniques
Simulation investigations were carried out with the following first order state-space model given by the following equations
where ri,t is the single asset return, rm,t is the return of the market index in which the asset is traded at time t, αi is the additive constant, βi,t is the beta coefficient which indicates the sensitivity of ri,t to the changes in rm,t, εi,t is the output noise component at time t.
Comparing state-space model of Equations (11) and (12) with state-space model Equations (3) and (4), we have used the following for our simulation experiments: xt=βit, yt = rit~N(0, 1) Ht=rmt=1Tx1, dt=αit=0.02, ct=0, Qt=var(ξit), Rt=var(εit), and F=1. Return rit is taken from Gaussian distribution since it is known that any distribution can be approximated with a sum or mixture of Gaussian distributions (Gastaldi and Nardecchia, 2003; Das and Ghoshal, 2010).
All the modified AKF methods have been applied and thus estimated β have been compared with the observed β from applying standard ordinary KF. In all these cases considered system and filtering parameter set are F = 1, β0 = 0.5, d = α = 0.02, P0 = 0.05. The chosen values of Q are given in the appropriate section below.
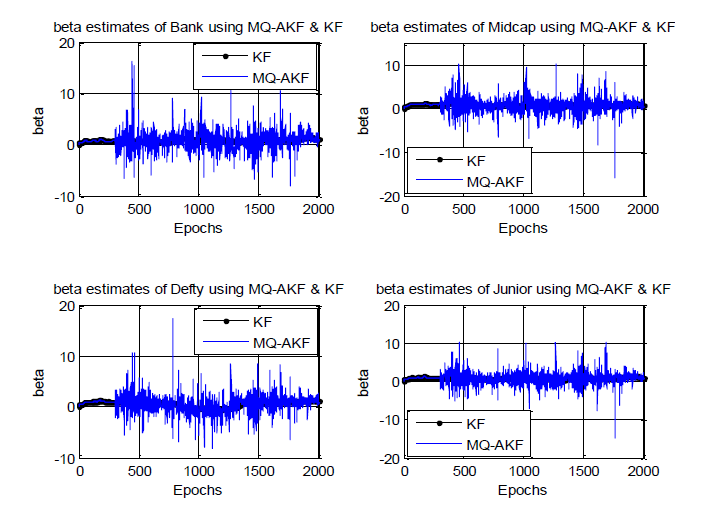
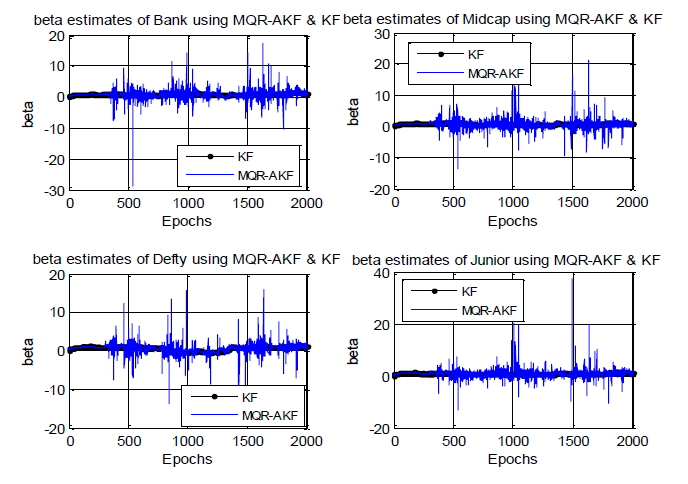
Investigation with MQAKF: The following graphs of Figure 3 present the β estimates using MQAKF with R = 0.01 where initial considered value of Q being 0.01 in comparison to ordinary KF with Q = 0.01 and R = 0.01 for all four considered indices.
It may be seen that the adaptive (MQAKF) filter output of β estimate exhibits substantial high frequency noise. However, the mean value ricks the KF value well.
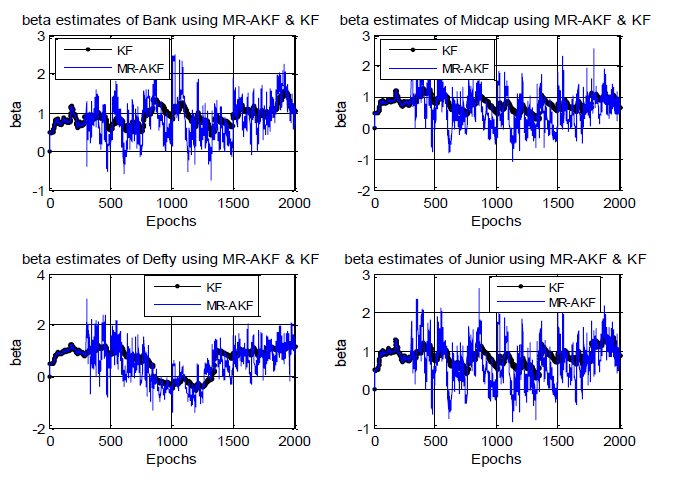
Investigation with MRAKF: The following graphs of Figure 4 present the β estimates using MRAKF with Q = 0.01 where initial considered value of R being 0.01 in comparison to ordinary KF with Q = 0.01 and R = 0.01 for all four considered indices.
From Figure 4, it may again be seen that the adaptive (MRAKF) filter output of β estimate exhibits substantial high frequency noise. However, the mean value tracks the KF value well. However, the amplitude of the noise has reduced considerably compared to MQAKF.
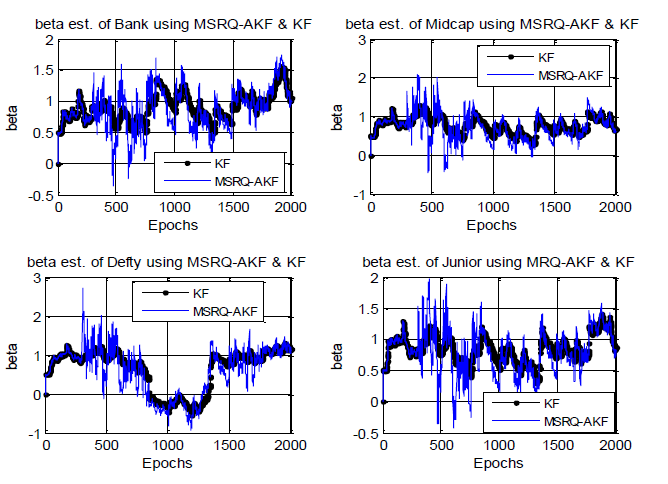
Investigation with MQRAKF: The following graphs of Figure 5 present the β estimates using MQRAKF where initial considered value of Q and R both being 0.005 (= 0.01/2) in comparison to ordinary KF with Q = 0.01 and R = 0.01 for all four considered indices.
Here again it may be seen that the β estimates by MQRAKF exhibits substantial high frequency noise. However, the mean value tracks the KF value well.
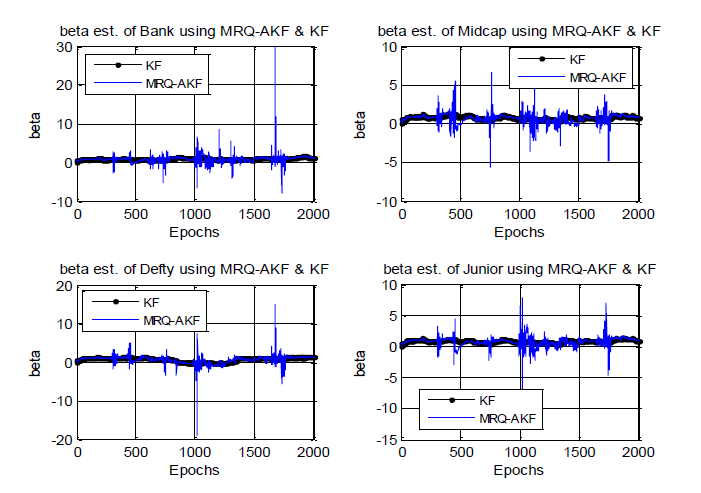
Investigation with MRQAKF: The following graphs of Figure 6 present the β estimates using MRQAKF where initial considered value of Q and R both being 0.005 (= 0.01/2) in comparison to standard ordinary KF with Q = 0.01 and R = 0.01 for all four considered indices.
Here again it may be seen that the adaptive (MRQAKF) filter output of β estimate exhibits substantial high frequency noise. However, the mean value tracks the KF value well.
Investigation with MSRQAKF: The following graphs of Figure 7 present the β estimates using MSRQAKF where initial considered value of Q and R both being 0.005 (= 0.01/2) in comparison to ordinary KF with Q = 0.01 and R = 0.01 for all four considered indices.
Here again it may be seen that the adaptive (MSRQAKF) filter output of β estimate exhibits substantial high frequency noise. However, the mean value tracks the KF value well. However, the amplitude of the noise has reduced considerably compared to MQAKF, MQRAKF and MRQAKF.
4.3. Analysis of empirical results
4.3.1. Backtesting VaR
To evaluate the goodness of a VaR model, banks, financial institutions as well as regulators use backtesting to confirm their judgments. Backtesting a VaR model simply means checking whether the realized daily returns are consistent with the corresponding daily VaR. Necessary literature and interpretation principles on backtesting VaR using "Traffic Light" are explained and used in (Berardi et al., 2002; Das et al., 2008). VaR estimations are carried out using the formula given in Equation 1 in this present context. The results of the backtesting analysis are reported in the table 2. The calculated number of violations for every type of VaR is expressed as percentage over the total number of VaR estimations spanned during the whole considered period. VaR estimation and corresponding backtesting is reported for the considered least squares (OLS, RLS and LMS), KF and modified AKF β estimation techniques at 95% and 99% confidence level and 1 day and 10 days time horizon. The considered value of Q or initial Q is 0.01 where as two values (0.01 and 1) of R or initial R is taken care while reporting backtesting. The corresponding traffic lights of backtesting methods are also indicated in the said table.
The percentage violations of all the considered methods tends to decrease considerably from 1 day to 10 day horizon due to the fact that the relation between the daily volatility and the volatility for a longer time period is smaller (the coefficient √Δt is commonly used for this purpose). It is also noted that RLS shows better performance than OLS as expected due to its dynamic nature. Backtesting performances of KF and modified AKF methods show that the said performance is better while Q and R are equal or initial Q and initial R are equal wherever the case may be. Backtesting results also show that the above considered techniques are highly acceptable and recommended while considering 10 days VaR. For 1 day VaR estimation and backtesting most of the considered methods are not recommended from the above results except a few mildly recommended like RLS, LMS, KF (0.01 equals Q and R), MQAKF and MQRAKF in case of 99% confidence level. MQAKF noticed to be the best performer in the considered adaptive AKF family. Surprisingly, MRAKF shows worse results in respect to empirical VaR backtesting compared to other modified AKF methods. These noted unnatural behaviours may be due to the typical portfolio composition considered for the VaR backtesting.
43.2. Expected shortfall analysis
The table 3 presents the ES of the VaR estimates of the considered portfolio at the same considered level of confidence and time horizon. ES analysis shows that all the least square methods (OLS, RLS and LMS) show performance very nearby to one another specific to confidence level and time horizon. RLS and LMS both provided the better performance than OLS at 99% confidence and 10 days horizon. ES results do not uniformly decreases unlike VaR backtesting with the increase of time horizon. Moreover, KF and modified AKF methods did not shown uniformly better or worse results with equal and unequal Q and R or initial Q and initial R combinations unlike VaR backtesting. The ES analysis also shows that the effect of change of R or initial R is much higher in case of 10 days ES than 1 day ES. However, it is noted that MQAKF is the overall best performer with respect to ES analysis.
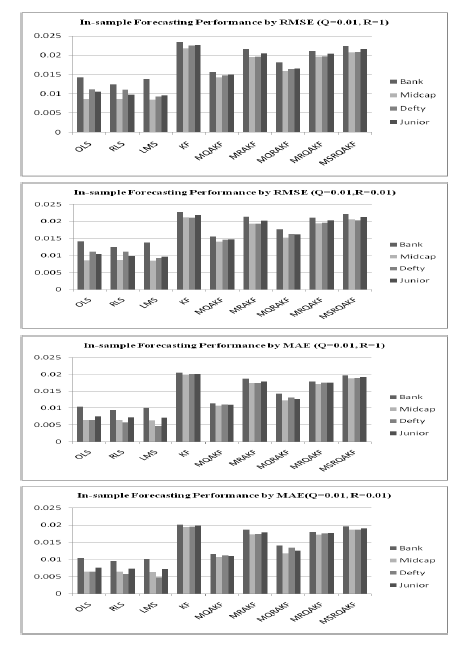
4.3.3. In-sample forecasting performance analysis
In-sample forecasting accuracy (Mergner, 2008) of returns is determined by two measures namely mean absolute error (MAE) and the root mean squared error (RMSE) given by MAE=1TT∑t=1|ˆri,t−ri,t|, and RMSE=√1TT∑t=1[ˆri,t−ri,t]2where T is the number of observations and ˆri,t denotes the series of return forecasts for sector i, calculated from the estimated time varying β series.
The results in Figure 8 indicate that time-varying sector β can suitably be described by a random walk process estimated via both the least square family and the adaptive KF family. The in-sample forecasting performance results generally support all the considered approaches. It is noted that the least square family outperformed over KF family in respect of in-sample forecasting performances. In considerations of KF family of estimators, it is observed that change of R or initial R did not affect much of the in-sample performance of the filters.
5.
Conclusion
The empirical analysis presented in this work contributes to the investigation of time-varying β for four Indian industry (sectoral) portfolios designed by NSE of India with respect to its gross index Nifty. The results of these investigations confirmed previous findings that sector βs are not constant but time varying. Though RLS and KF have earlier been used, but applications of LMS and modified AKFs method for β estimation are novel as far as our knowledge goes. Noise covariance adaptation based Modified AKF techniques are empirically characterized and show that Indian market β can be tracked and estimated successfully without assuming the noise covariance (i.e. uncertainties). The performance of the modified AKF techniques are compared with KF estimates and revealed that the said modified AKF techniques with unknown process and observation noise covariances perform at least as good as (or better than) KF (where both noise covariances Q and R are assigned a priori from previous knowledge).
Variations of observed empirical β estimates show similar trends to that of earlier workers using KF. β trends obtained from Modified AKFs generally show larger and more frequent fluctuations. Among these techniques two broad categories may be formed according to the trends of observed empirical β estimates. MRAKF and MSRQAKF belongs to a category (say Category 1) where as other techniques (MQAKF, MQRAKF and MRQAKF) belong to a different category (say Category 2). Fluctuations observed in the Category 1 are much higher than that in the Category 2. Earlier literature (Shah and Moonis, 2003) reporting β estimates on Indian market shows β estimates closer to the Category 1. It should also be noted that the range of variations of β estimates by Category 2 is much higher than that of Category 1. Whether the larger fluctuations in β estimates can be utilized for better predictions of say VaR needs further investigations.
It is also found that any single method could not provide best results across all three performance measures. RLS and LMS both provided the best performance among all methods where as MQAKF provided best performance in Modified AKF family with respect to VaR backtesting. MQAKF also provided the best performance with respect to ES analysis among all. Least square methods provided the best performance with respect to in-sample forecasting performance analysis. So any single technique could not be recommended for the empirical β and corresponding VaR estimation. Though in-sample return forecasting performance is found capable of evaluating the beta estimation performances since considered time duration is of ten years length, out-of-sample forecasting performances analysis may also be suggested for better realizations. Loss functions and other statistical tests oriented VaR analysis may also be suggested as future work besides VaR backtesting and expected shortfall analysis having comprehensible indications of beta estimation performances.
Acknowledgments
This manuscript benefited from the valuable comments of two anonymous reviewers.
Conflict of interest
The author declares no conflict of interest in this paper.









 DownLoad:
DownLoad: