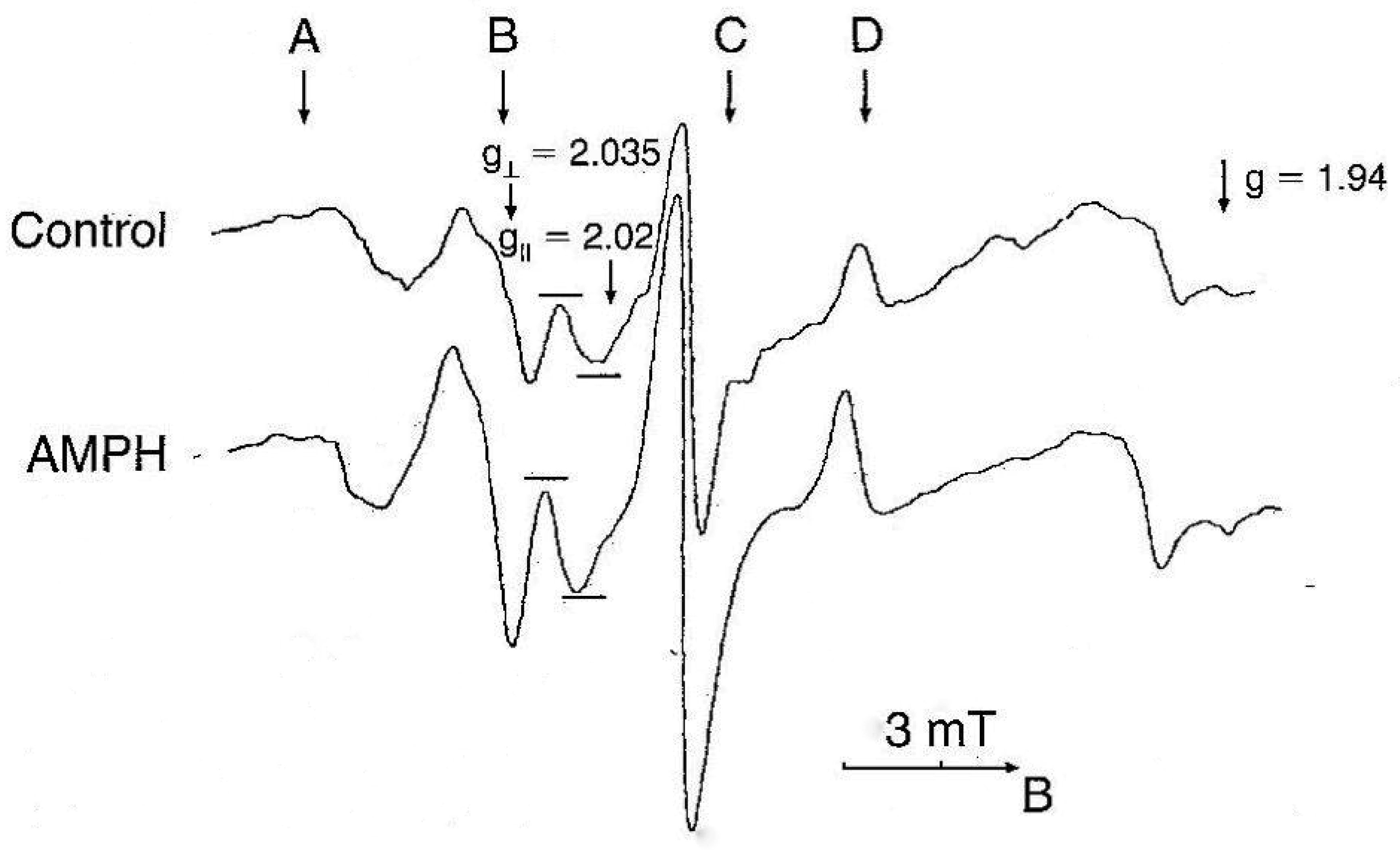
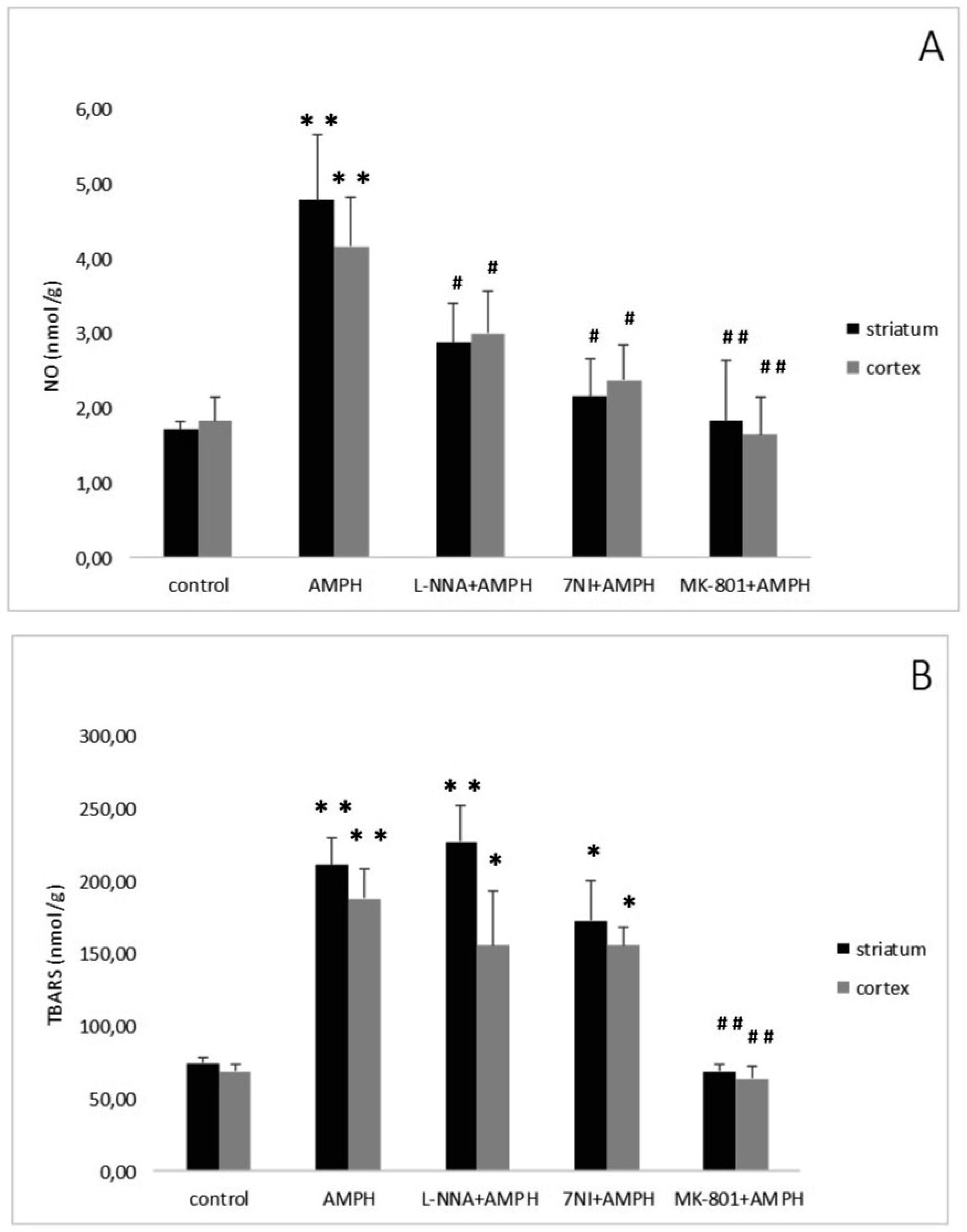
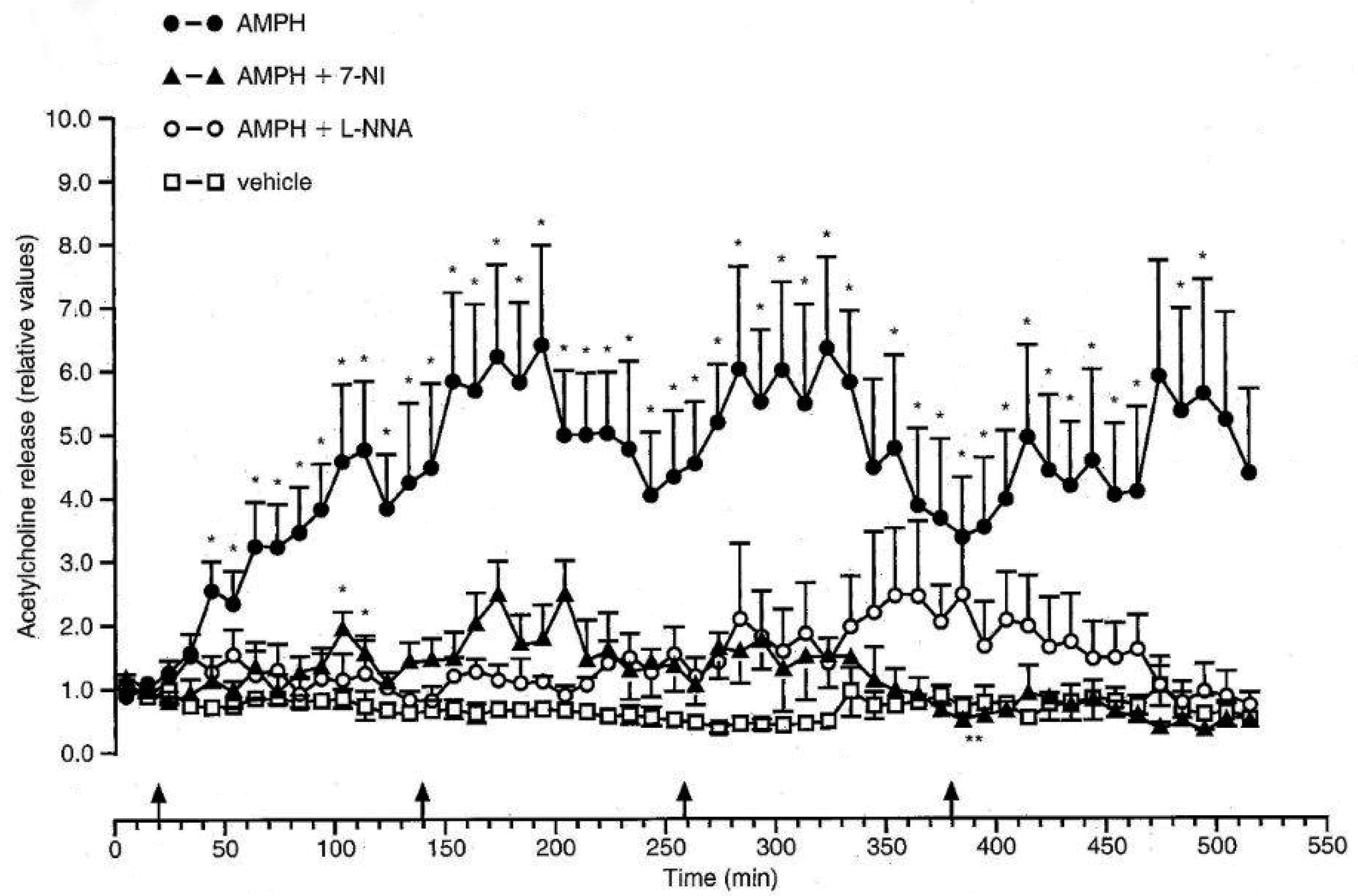
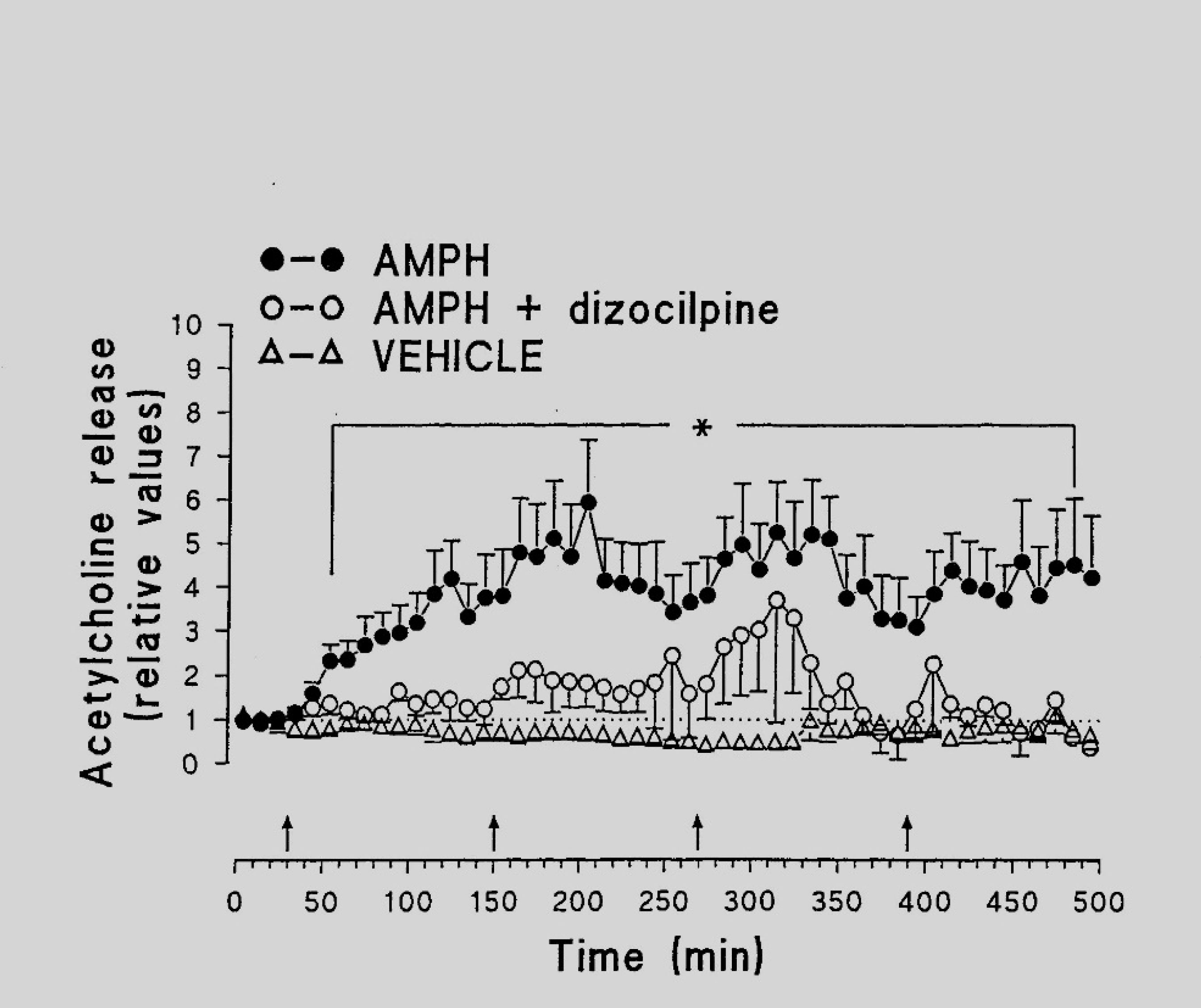
In recent decades, consumption of psychostimulants has been significantly increased all over the world, while exact mechanisms of neurochemical effects of psychomotor stimulants remained unclear. It is assumed that the neuronal messenger nitric oxide (NO) may be involved in mechanisms of neurotoxicity evoked by psychomotor stimulants. However, possible participation of NO in various pathological states is supported mainly by indirect evidence because of its short half- life in tissues. Aim of this review is to describe the involvement of NO and the contribution of lipid peroxidation (LPO) and acetylcholine (ACH) release in neurotoxic effects of psychostimulant drugs. NO was directly determined in brain structures by electron paramagnetic resonance (EPR). Both NO generation and LPO products as well as release of ACH were increased in brain structures following four injections of amphetamine (AMPH). Pretreatment of rats with the non-selective inhibitor of NO- synthase (NOS) N-nitro-L-arginine or the neuronal NOS inhibitor 7-nitroindazole significantly reduced increase of NO generation as well as the rise of ACH release induced by AMPH. Both NOS inhibitors injected prior to AMPH had no effect on enhanced levels of LPO products. Administration of the noncompetitive NMDA receptor antagonist dizocilpine abolished increase of both NO content and concentration of LPO products induced by of the psychostimulant drug. Dizocilpine also eliminated the influence of AMPH on the ACH release. Moreover, the neurochemical and neurotoxic effects of the psychostimulant drug sydnocarb were compared with those of AMPH. Single injection of AMPH showed a more pronounced increase in NO and TBARS levels than after an equimolar concentration of sydnocarb. The findings demonstrate the crucial role of NO in the development of neurotoxicity elicited by psychostimulants and underline the key role of NOS in AMPH-induced neurotoxicity.
1.
Introduction
Transparent photoelastic materials represent an exciting alternative to the experimental study of stress and strain distributions induced in solids by carges. When subjected to carges, these materials present the double refraction phenomenon, or birefringence, changing the polarization state of the transmitted light through the solids, which can be used to analyze the stress distribution [1]. The effect of double refraction, first described by Bartholinus [2,3,4] and related with the stress state by Brewster in the early 19th century [5], advanced throughout the 20th century with a non-destructive set of techniques and methods which associates the study of material stresses with optics, the photoelasticity [6,7,8]. Since the pioneering work of Coker and Filon [9,10,11], photoelasticity became a fundamental base for determining stress and strain distributions in photoelastic materials. Thus, great interest was generated in several fields, such as Engineering and Odontology [12,13,14], which validated and contributed to developing the theoretical method of finite elements [15,16].
Despite advances, most studies are qualitative or indirectly quantitative [13,14] due to the difficulties in obtaining direct optical information. Improvements in qualitative data and quantitative analysis methods are needed so that non-destructive, fast, and reliable optical methods become a reference for determining stress distribution in materials. Although holographic techniques have advanced significantly in recent years, the various works have invested very little in the stresses distribution analysis in photoelasticity using holography. The dynamics of holography allow the results to be more precise, as they are based on optical properties such as intensity, phase, refractive index, etc., which are provided directly or almost directly, thus offering a great perspective in the more quantitative treatment of problems involving elasticity mechanics [17].
We present an alternative approach to determine the stress distribution profile through a non-destructive procedure based on digital holography (DH) [18,19], allowing us to obtain quantitative intensity and phase information from light transmitted through a photoelastic material. The DH produces remarkably accurate results when combined with appropriate statistical processing of optical data, facilitating the quantitative treatment of the specific problem as outlined in the proposed methods [20]. An off-axis holographic setup was used to obtain two cross-holograms with two orthogonally polarized reference waves and a birefringent system with photoelastic samples under static loads [21,22,23,24,25]. After digitally reconstructed with DH, the received data generates the phase differences used to calculate the distributions of elastic stresses. The validation of the method was carried out with the methods finite elements and RGB (red, green, and blue) photoelasticity [14,16,26,27].
2.
Materials and methods
2.1. Samples and Techniques
Four standard rectangular blocks, composed of mixtures of epoxy resin solutions, were prepared according to the traditional procedures [28] of the photoelastic technique, constituting the samples used in this work. The preparation of the samples involved two stages: making the silicone molds, from curing in a liquid solution and catalyst, and the photoelastic samples, from curing, in silicone molds, a liquid solution of epoxy resin and hardener. Details are presented in the work [17]. For the determinations of the mechanical and holographic parameters, two samples with different thicknesses were made, one more flexible and one less flexible. Two other samples with different thicknesses, one more and one less flexible, were also made to determine the stress distributions. Details of the procedures are presented in [17]. The more or less flexible samples were intended to help verify the order of magnitude of the stress-optical coefficient (C) and to provide a greater range of comparison with the photoelastic methodology.
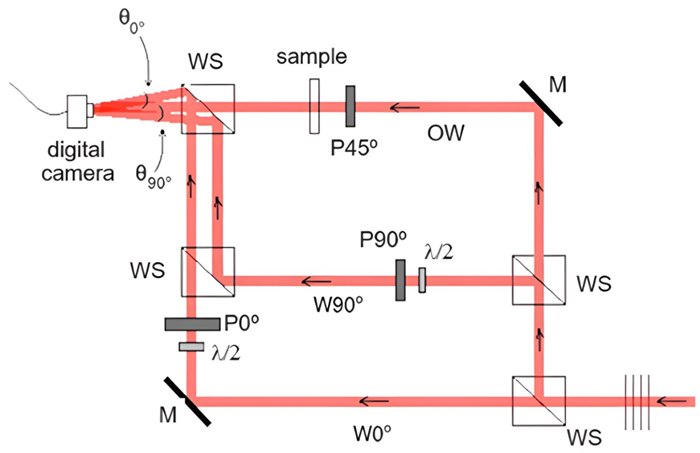
The utilized holographic technique is shown in Figure 1.
A laser light source (1) was used to generate three independent waves: one object wave (OW), with the direction of polarization at 45º concerning two orthogonal reference waves, one with the direction of polarization at 0º (W0º), and another with the direction of polarization at 90º (W90º). Two distinct holograms were produced from the resulting interference patterns among OW, W0º, and W90º, propagating with different angles to the digital camera, as shown in Figure 1: θ(0º) between the OW and W0º, and θ (90º) between OW and W90º, as limited by the N-quest Theorem [29,30,31]. Two sets of holograms were recorded from each sample for compression and decompression in the birefringent system. The compression occurs by the progressive addition of load on the samples, and the decompression occurs by progressive removal of these loads.
The photoelastic images were obtained by blocking both reference waves, removing the wave splitter (WS), near the digital camera, and exchanging the polarizer, P45º, of the object wave for two polarizers with orthogonal polarizations, one before and another after the photoelastic sample. Figure 2 presents an experimental configuration scheme used in photoelasticity.
2.2. Methods
2.2.1. Stress-optic law
The optical information obtained through photoelasticity is related to the difference between the stresses considered in the components longitudinal ($ {\mathsf{σ}}_{\parallel } $) and transverse ($ {\mathsf{σ}}_{\perp } $) to the applied load, defined by Eq 1, as given by the stress-optic law [6,17,28]:
where $ {\rm{C}} $ is the stress-optical coefficient, and $ {(\mathrm{n}}_{\parallel }-{\mathrm{n}}_{\perp }) $ is the difference between the refraction indexes in the components longitudinal ($ {\mathrm{n}}_{\parallel } $) and transverse ($ {\mathrm{n}}_{\perp } $) to the effort. For a material with thickness e, the refractive index difference is also associated with the phase difference Δϕ, so Eq 1 can be rewritten as Eq 2:
where $ \mathrm{N} = \frac{\mathrm{\Delta }{\mathsf{ϕ}}}{2{\mathsf{π}}} $ is defined as the relative retardation, $ {\mathrm{f}}_{\mathsf{σ}} = \frac{{\mathsf{λ}}}{{\rm{C}} } $ is the fringe value that indicates the degree of rigidity of the material, and λ is the wavelength of the light source. Using the matrix of stress-strain $ ({\mathsf{σ}}-\mathsf{ε} $) of the material in the stress state plane [26], the difference between the stresses in the orthogonal components, defined by Eq 3, is [17]:
$ \mathrm{E} $ is the mechanical elasticity modulus, and ν is the Poisson's coefficient. Therefore, comparing Eqs 2 and 3, with $ \mathrm{N} = \left({\mathsf{ε}}_{\parallel }-{\mathsf{ε}}_{\perp }\right) $, the material fringes value can be determined by their intrinsic properties through Eq 4 [17]:
2.2.2. Holographic analogy
The holographic method was empirically inferred and correlated with the stress-optic law. The stress difference $ \left({\mathsf{σ}}_{\parallel }-{\mathsf{σ}}_{\perp }\right) $ occurs in the plane normal to the passage of light [26]. Due to angular displacements, the shear stresses were not considered to limit the boundary conditions and obtain the desired equation. In analogy with photoelasticity, the stress-strain matrix for the holographic parameters is given by Eq 5 [17]:
considering, by Eq 6, that
$ \mathfrak{E} $ is defined as the holographic elasticity modulus, and $ \mathrm{a} $ is a dimensionless constant that relates the holography elasticity with the mechanical elasticity. $ {\mathsf{ε}}_{\mathrm{H}} = \frac{1}{\mathrm{a}}\mathsf{ε} $ is defined as the relative holographic deformation and $ \mathrm{\aleph } = \frac{{\left({\mathsf{ϕ}}_{\parallel }-{\mathsf{ϕ}}_{\perp }\right)}_{\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}\mathrm{i}\mathrm{c}}}{2{\mathsf{π}}} = \left({{\mathsf{ε}}_{\mathrm{H}}}_{\parallel }-{{\mathsf{ε}}_{\mathrm{H}}}_{\perp }\right) $ as the relative holographic retardation. Thus, the holographic dispersion can be written as the Eq 7 [17]:
where, by Eq 8,
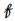 and $ {\mathrm{f}}_{\mathsf{σ}} $ are the fringe values obtained in holography and photoelasticity, respectively. The photoelastic fringe value is related to the wavelength of light ($ {\mathsf{λ}} $) and the photoelastic stress-optical coefficient ($ {\rm{C}} $). Then, analogously to what occurs with photoelasticity, there comes the holographic dispersion term, $ \mathrm{H}\left({\mathsf{λ}}\right), $ an intrinsic property of the material whose value depends on the light wavelength, resultant from the relation between the component differences in refractive indexes, $ {\left({\mathrm{n}}_{\parallel }-{\mathrm{n}}_{\perp }\right)}_{\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}\mathrm{i}\mathrm{c}} $ and the plane stresses $ {\left({\mathsf{σ}}_{\parallel }-{\mathsf{σ}}_{\perp }\right)}_{\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}\mathrm{i}\mathrm{c}} $. For a given wavelength, the stress-holographic law is given by Eq 9 [17]:
and $ {\mathrm{f}}_{\mathsf{σ}} $ are the fringe values obtained in holography and photoelasticity, respectively. The photoelastic fringe value is related to the wavelength of light ($ {\mathsf{λ}} $) and the photoelastic stress-optical coefficient ($ {\rm{C}} $). Then, analogously to what occurs with photoelasticity, there comes the holographic dispersion term, $ \mathrm{H}\left({\mathsf{λ}}\right), $ an intrinsic property of the material whose value depends on the light wavelength, resultant from the relation between the component differences in refractive indexes, $ {\left({\mathrm{n}}_{\parallel }-{\mathrm{n}}_{\perp }\right)}_{\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}\mathrm{i}\mathrm{c}} $ and the plane stresses $ {\left({\mathsf{σ}}_{\parallel }-{\mathsf{σ}}_{\perp }\right)}_{\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}\mathrm{i}\mathrm{c}} $. For a given wavelength, the stress-holographic law is given by Eq 9 [17]:
We have experimentally confirmed these equations in [21,22].
2.2.3. Fresnel transform
The off-axis configuration separates the diffraction orders during the digital reconstruction performed with FTM's fresnel transform method [17,32,33]. The image field (ψmn) and phase (ϕmn) were calculated using Eqs 10 and 11, and the corresponding maps were reconstructed.
where $ {\rm{F}}\left[\rm{\Delta }{\rm{k}}_{{\mathsf{ξ}}}, \rm{\Delta }{\rm{k}}_{{\mathsf{η}}}\right] = \rm{F}\left[{\rm{I}}_{\rm{H}}\left({\mathsf{ξ}}, {\mathsf{η}}\right)\bullet {{\mathsf{ψ}}}_{\rm{R}}\left({\mathsf{ξ}}, {\mathsf{η}}\right)\bullet {\rm{e}}^{\frac{{\mathsf{π}}\rm{i}}{\rm{z}\rm{\lambda }}\left[{\left(\rm{n}\bullet \rm{\Delta }{\mathsf{ξ}}\right)}^{2}+{\left(\rm{m}\bullet \rm{\Delta }{\mathsf{η}}\right)}^{2}\right]}\right] $ is the Fourier Transform of the discretized field, $ \rm{\Delta }{\rm{k}}_{{\mathsf{ξ}}} = -\frac{\rm{k}\rm{\lambda }}{\rm{N}\rm{\Delta }{\mathsf{ξ}}}$, $\rm{\Delta }{\rm{k}}_{{\mathsf{η}}} = -\frac{\rm{k}\rm{\lambda }}{\rm{M}\rm{\Delta }{\mathsf{η}}}$, $\rm{\Delta }{\mathsf{ξ}} = \frac{\rm{z}\rm{\lambda }}{\rm{N}\rm{\Delta }\rm{h}}$, $\rm{\Delta }{\mathsf{η}} = \frac{\rm{z}\rm{\lambda }}{\rm{M}\rm{\Delta }\rm{v}}$, $\rm{\Delta }\rm{h} $ and $ \rm{\Delta }\rm{v} $ are the horizontal and vertical pixel dimensions, respectively. All the phase maps were demodulated with the Volkov Method [34].
The calibration of the setup followed the work of Colomb et al. [24] and was carried out using a quarter-wave plate as a sample. Two-phase maps reconstructed by FTM, one for each polarization, were subtracted to obtain the maps of phase differences in the function of the angle of orientation of the quarter-wave plate. The general expression for the phase difference (Δφ) as a function of the orientation of the quarter-wave, by Eq 12:
The process to obtain the demodulated phase maps for compression and decompression. The area selected (the rectangle on the hologram) of the hologram was processed with the FTM to obtain the frequency spectrum [17]. The chosen area (the rectangle on the frequency spectrum) of the frequency spectrum was obtained from the modulated phase map, and the Volkov method [34] was obtained from the demodulated phase map. The mean phase was determined from the phases of the pixels in the area selected from the demodulated phase map. To reduce the noise, in each phase map, a region of the phase map with no object was chosen, and the mean phase value of this region was subtracted from the phase map [17].
From the vertical phase maps of each stress applied, the load, $ {\mathsf{σ}}_{\mathrm{i}} $, was calculated in the vertical holographic deformations, $ {{\mathsf{ε}}_{\mathrm{H}}}_{\mathrm{v}-\mathrm{i}} $, in both processes: compression and decompression. In the same way, with the phase values of the horizontal phase maps, the horizontal holographic deformations, $ {{\mathsf{ε}}_{\mathrm{H}}}_{\mathrm{h}-\mathrm{i}} $, were calculated. The mean value $ \langle \mathfrak{E}\rangle $ was calculated from various values $ \mathrm{E} $ by fitting the linear function, by Eq 13:
The mean value of the Poisson's coefficient, $ \langle {\rm{\nu }}\rangle $, was calculated from various values ν by fitting the linear function, by Eq 14:
In both cases, the Least Squares Method [34] was utilized.
For each horizontal line j, the phase differences, $ {\left({\mathsf{ϕ}}_{\mathrm{v}}-{\mathsf{ϕ}}_{\mathrm{h}}\right)}_{\mathrm{j}} $, were obtained and, from the result, the relative retardation, $ {\mathrm{\aleph }}_{\mathrm{j}} = {\left({\mathsf{ϕ}}_{\mathrm{v}}-{\mathsf{ϕ}}_{\mathrm{h}}\right)}_{\mathrm{j}}/2{\mathsf{π}} $, was calculated between the dark fringes. These results, associated with the holographic parameters $ \left\langle{\mathfrak{E}}\right\rangle $ and$ \langle {\rm{\nu }}\rangle $, allowed us to find the stress differences $ {\left({\mathsf{σ}}_{\mathrm{v}}-{\mathsf{σ}}_{\mathrm{h}}\right)}_{\mathrm{j}-\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}\mathrm{i}\mathrm{c}} $ using Eq 5. The graphic $ {\left({\mathsf{σ}}_{\mathrm{v}}-{\mathsf{σ}}_{\mathrm{h}}\right)}_{\mathrm{j}-\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}\mathrm{i}\mathrm{c}} $ as a function of the number of pixels produced the distributions of stress differences in the selected region.
A dimensionless constant parameter from Eq 6 gives the relation between holographic and mechanical elasticity. According to Eq 4, using the photoelastic images, mechanical parameters, $ \left\langle{\mathrm{E}}\right\rangle $ and$ \langle {\rm{\nu }}\rangle $, and the thicknesses, e, it is possible to calculate the photoelastic fringes, $ {\mathrm{f}}_{\mathsf{σ}} $, and the photoelastic dispersions, $ {\rm{C}} \left({\mathsf{λ}}\right) $. Using Eq 8, the holographic parameters, $ \mathrm{E} $ and ν, the thickness e, and the constant a, the holographic fringes, 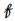 , can be calculated using the phase maps. Using Eq 7 and the wavelength, $ {\mathsf{λ}} $, the holographic dispersion, $ \mathrm{H}\left({\mathsf{λ}}\right) $, can be calculated.
, can be calculated using the phase maps. Using Eq 7 and the wavelength, $ {\mathsf{λ}} $, the holographic dispersion, $ \mathrm{H}\left({\mathsf{λ}}\right) $, can be calculated.
3.
Results and discussion
The mechanical parameters were measured with samples sized 4.15, 2.25, and 1.03 cm, and the stress distribution was tested in samples sized 4.15, 2.25, and 4.90 cm, both in holography and photoelasticity.
Each technique was applied to only one block from each pair of standard blocks, which were prepared with identical flexibilities and labeled as −F low flexibility and +F high flexibility. Stresses were applied to the top surface of the sample blocks via a loading device, as illustrated in Figure 1.
The modified Mach-Zehnder interferometer apparatus was built with a He-Ne laser (632.8 nm CW, 20 mW, model 1135PUniphase). The photoelastic images and hologram registers were captured with a Thorlabs digital camera, model DCC1240C-HQ color, CMOS sensor, 1280 × 1024 pixels, size pixel 5.3 μm (square).
The calibration process of the holographic system generated an experimental distribution that, when compared to a theoretical curve, Figure 3, showed the reliability of the system [24].
The continuous line represents the theoretical curve, Eq 12, and the circles of the experimental distribution. The distribution of the point around the curve indicates that the adjustment of the polarization of waves is correct.
Two sets of holograms were recorded for each sample for compression and decompression. The stresses, applied to the upper central phase of the sample, ranged from 0.3 to 1.5 MPa. In holography, the mean phases were obtained from the statistics of ten selected areas in each demodulated phase map. The final mean was calculated using the values of compression and decompression.
The photoelasticity RGB method, in transmission mode, was associated with the finite elements method to determine the distributions of the stress differences in the same selected regions as those used with the holographic method. These results were used to evaluate the proposed method by comparing holography and photoelasticity by stress-optic and stress-holographic law, given by Eqs 1 and 9, respectively.
All the fitted functions used the least square method [27]. A third-degree polynomial function was fitted to the points, but all the results showed that they were linear functions.
Figure 4 presents the graphics of the experimental values of the $ {\mathsf{σ}} $ versus $ {\mathsf{ε}}_{\mathrm{v}} $ for the +F sample under compression and decompression. This graphic is used to determine the mechanical and holographic modulus of elasticity.
Figure 5 presents the graphics of the experimental values of $ {\mathsf{σ}} $ versus $ {{\mathsf{ε}}_{\mathrm{H}}}_{\mathrm{v}} $ for the +F samples under compression and decompression, and they are used to obtain the Holographic and Mechanical modulus of elasticity.
Similar graphs were made for the −F samples. Table 1 summarizes the holographic and mechanical modules of elasticity. The values are similar for the samples with different flexibilities in analysis. However, the rate $ \mathfrak{E}/\mathrm{E} $ differed for each method (holographic and mechanical). Considering the uncertainties, the values of $ \langle \mathfrak{E}/\mathrm{E}\rangle $ are practically equal for all samples in both flexibilities.
It was verified, in all graphics, using polynomials up to the third degree, that the best-fit function was a first-degree polynomial, related function, agreeing with Robert Hooke's theory of elasticity for the elastic regime.
Figure 6 presents the values of the $ {\mathsf{ε}}_{\mathrm{h}}\left(\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{e}\right) $ versus $ {\mathsf{ε}}_{\mathrm{v}} $ (longitudinal), used to calculate the mechanical Poisson's coefficient under the compression and decompression processes, using samples +F.
Figure 7 presents the values of the $ {{\mathsf{ε}}_{\mathrm{H}}}_{\mathrm{h}}\left(\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{e}\right) $versus $ {{\mathsf{ε}}_{\mathrm{H}}}_{\mathrm{v}}\left(\mathrm{l}\mathrm{o}\mathrm{n}\mathrm{g}\mathrm{i}\mathrm{t}\mathrm{u}\mathrm{d}\mathrm{i}\mathrm{n}\mathrm{a}\mathrm{l}\right) $ used to determine the holographic Poisson's coefficient under the compression and decompression processes, using samples +F to determine the stress distribution.
Similar graphs were made for the −F samples. Table 2 summarizes the Poisson's coefficients: holographic and mechanical. Considering the uncertainties, the Poisson's coefficients ν are practically equal for the sample with the same flexibility.
With these parameters, it was possible to determine the mean stress-optical coefficients in photoelasticity and holography, whose values are presented in Table 3.
The difference between the values of the samples with the same flexibility is due to the dependence of the stress-optical coefficient with sample thickness, e. However, for the same flexibility, the values agree both in holography and in photoelasticity. An important observation is that in holography, the precision of the results is better since the values are of the order of 10−6 N/m2.
The graphics in Figure 8 show the distribution of stress difference over the vertical lines between two dark fringes obtained using the holographic method (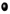 ), photoelasticity RGB ($ + $), and analytical method (
), photoelasticity RGB ($ + $), and analytical method ( ). The load, in mass, applied was 600 g for all samples.
). The load, in mass, applied was 600 g for all samples.
The behavior of curves in graphics exhibits similarities, indicating that the theoretical model of the proposed method is correct. The +F samples are less rigid and suffer more significant vertical deformation, reducing the modulus of elasticity under the same load. This behavior is observed graphically due to the smaller and more scattered peaks about the −F sample distribution.
In photoelasticity, the intensity of the images of the fringes pattern depends on the characteristics of the experimental configuration: transmittance of the materials, anisotropic behavior level, spectral radiation distribution of the light source (white light), the conversion factor of the light-signal control and electric-signal control, and the temporary birefringence effect. In digital holography, these effects are less relevant due to the subtractions performed in the numerical reconstruction process, which eliminate much of this noise, and also due to the optical retardations obtained directly from the phase differences maps.
4.
Conclusions
We present an alternative method to obtain the stress differences in photoelastic materials, as verified by the experiments. The similar results for the modulus of elasticity obtained through the different methods (photoelasticity, mechanical, and holographical) allowed the assumption of an analogy between Hooke's law and holography. The photoelastic and holographic dispersions are equal, allowing the establishment of the stress-holographic law in analogy with the stress-optic law. The experimental stress distributions in holography presented the same behavior as the analytic and photoelastic distributions. The results of stress distributions in holography were more accurate than in photoelasticity when compared to the theoretical results. Thus, the proposed method presents efficiency and independence in procedures since it uses only the extracted parameters obtained directly from the phase maps.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors are grateful for the financial support from Fundação de Amparo à Pesquisa do Estado de São Paulo (2012/18162-4, 2019/23700-4, 2022/15276-0); the physical support from Faculdade de Tecnologia de Pompeia (Fatec Pompeia), Faculdade de Tecnologia de Itaquera (Fatec Itaquera), Instituto de Física da Universidade de São Paulo (IFUSP) and Instituto de Pesquisas Energéticas e Nucleares de São Paulo (IPEN-SP).
Author contributions
The lead author (Sidney Leal da Silva) contributed theory, data, and analysis from his doctoral work [17]. The other co-authors helped with the preparation and first revisions of the article.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad:


 and $ {\mathrm{f}}_{\mathsf{σ}} $ are the fringe values obtained in holography and photoelasticity, respectively. The photoelastic fringe value is related to the wavelength of light ($ {\mathsf{λ}} $) and the photoelastic stress-optical coefficient ($ {\rm{C}} $). Then, analogously to what occurs with photoelasticity, there comes the holographic dispersion term, $ \mathrm{H}\left({\mathsf{λ}}\right), $ an intrinsic property of the material whose value depends on the light wavelength, resultant from the relation between the component differences in refractive indexes, $ {\left({\mathrm{n}}_{\parallel }-{\mathrm{n}}_{\perp }\right)}_{\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}\mathrm{i}\mathrm{c}} $ and the plane stresses $ {\left({\mathsf{σ}}_{\parallel }-{\mathsf{σ}}_{\perp }\right)}_{\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}\mathrm{i}\mathrm{c}} $. For a given wavelength, the stress-holographic law is given by Eq 9 [
and $ {\mathrm{f}}_{\mathsf{σ}} $ are the fringe values obtained in holography and photoelasticity, respectively. The photoelastic fringe value is related to the wavelength of light ($ {\mathsf{λ}} $) and the photoelastic stress-optical coefficient ($ {\rm{C}} $). Then, analogously to what occurs with photoelasticity, there comes the holographic dispersion term, $ \mathrm{H}\left({\mathsf{λ}}\right), $ an intrinsic property of the material whose value depends on the light wavelength, resultant from the relation between the component differences in refractive indexes, $ {\left({\mathrm{n}}_{\parallel }-{\mathrm{n}}_{\perp }\right)}_{\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}\mathrm{i}\mathrm{c}} $ and the plane stresses $ {\left({\mathsf{σ}}_{\parallel }-{\mathsf{σ}}_{\perp }\right)}_{\mathrm{h}\mathrm{o}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{p}\mathrm{h}\mathrm{i}\mathrm{c}} $. For a given wavelength, the stress-holographic law is given by Eq 9 [
 ) and the experimental distribution (
) and the experimental distribution ( ).
).