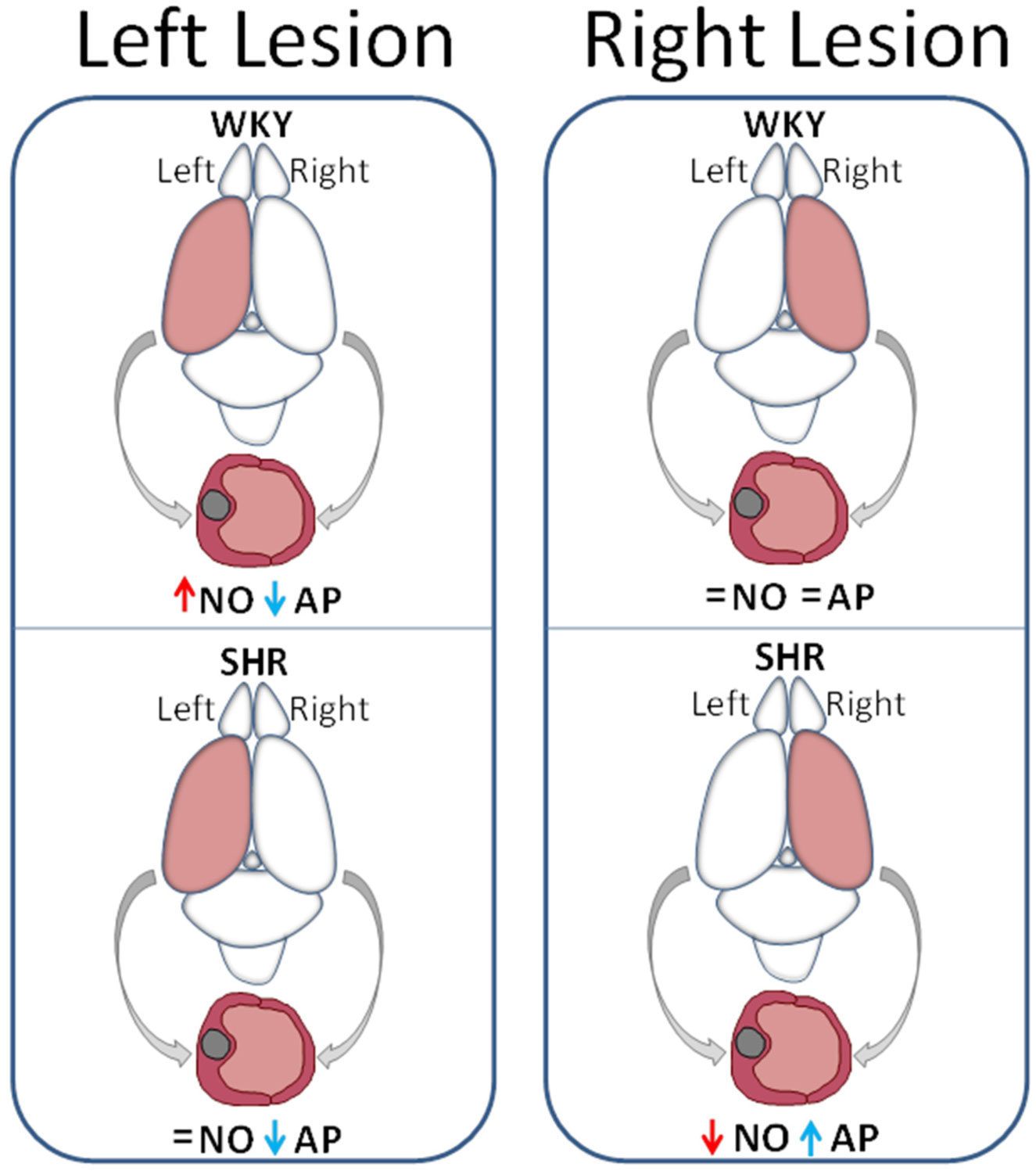
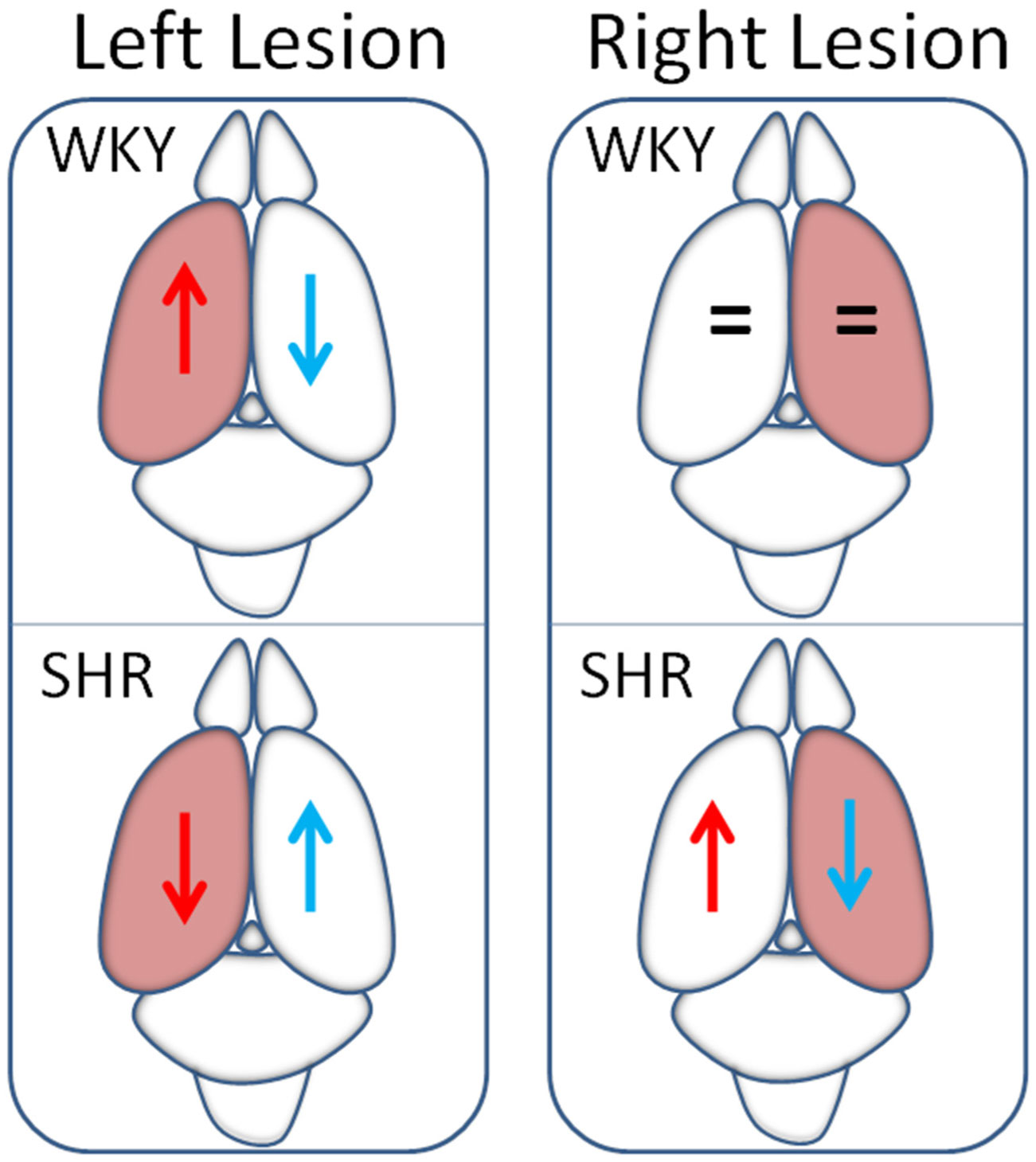
Vital functions, such as blood pressure, are regulated within a framework of neurovisceral integration in which various factors are involved under normal conditions maintaining a delicate balance. Imbalance of any of these factors can lead to various pathologies. Blood pressure control is the result of the balanced action of central and peripheral factors that increase or decrease. Special attention for blood pressure control was put on the neurovisceral interaction between Angiotensin II and the enzymes that regulate its activity as well as on nitric oxide and dopamine. Several studies have shown that such interaction is asymmetrically organized. These studies suggest that the neuronal activity related to the production of nitric oxide in plasma is also lateralized and, consequently, changes in plasma nitric oxide influence neuronal function. This observation provides a new aspect revealing the complexity of the blood pressure regulation and, undoubtedly, makes such study more motivating as it may affect the approach for treatment.
1.
Introduction
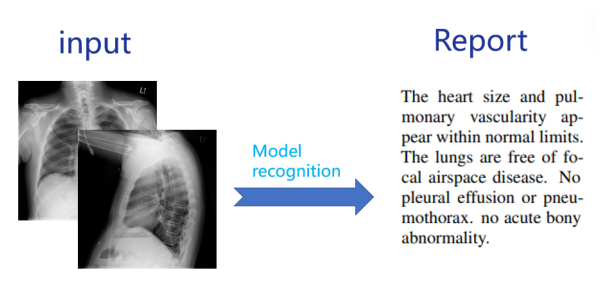
The reading and interpretation of medical images is usually performed by medical professionals. But even for experienced experts, this process of medical image interpretation and reporting is also prone to error. Staff shortages and overworked work-loads can also lead to misjudgments in radiology reports. Writing accurate medical imaging reports is necessary for inexperienced radiologists and pathologists, especially in rural areas and in areas where the quality of care is relatively low. For experienced radiologists and pathologists, writing imaging reports is tedious and time-consuming, and automated generation of medical reports can effectively reduce the doctors' workload and mistakes.
There are several issues that must be addressed to automate the generation of auxiliary reports. First, a complete diagnostic report consists of several different forms of information. Second, how to locate the image region and describe it correctly. You et al. [1] automatically extracted machine-learnable annotations from regression data, but the description results were still not ideal. Third, the description in the image re-port contains multiple sentences. Krause et al. [2] used the combined structure of image and language to generate hierarchical descriptive paragraphs, while generating such a long text is still relatively difficult to achieve. Fourth, the automatically generated statements are still unreadable and cannot be colloquial in a human voice. The current single-layer LSTM method cannot model long word sequences. The traditional RNN-+CNN architecture is difficult to generate long statement sequences. Multimodal recurrent model with attention (MRNA) can be used to model long word sequences, but the accuracy is very low and lacks readability.
In view of the above problems, the following conclusions are drawn. 1) The verbal information of medical reports is more important than the image information. 2) The final results are often more concerned with the degree of imitation of the doctor's tone. Based on this, RCLN model is proposed in this paper. RCLN model solves the problem of multiple forms of information by establishing a multi-task framework. On the area localization problem, a research team proposed a new real-time automatic calibration scheme based on scanning sources. The proposed method allows accurate calibration regardless of the path length variation caused by the non-planar topography of the sample or the scanning of the galvanometer [3]. Previously, the application of multimodal imaging technology in the study of density changes of melanosomes and lipofuscin granules in the retinal pigment epithelium (RPE) cells [4]. There is also an efficient direct time-domain resampling scheme based on phase analysis, which shows significant performance improvements in terms of accuracy and speed and silica-coated silver nanostructures can be excellent contrast agents for optical coherence tomography (OCT) imaging [5]. Multi-label classification is a multi-label classification task processing model, it regards label prediction as a multi-label classification task and long description generation as a text generation task. To solve the problem of image region localization, the MRNA model introduced a cooperative attention mechanism, and explored the synergistic effect of visual features and semantics in the grouping while biased towards im-ages and prediction labels. In view of the difficulty in generating long text, RCLN uses hierarchical LSTM to induce long text by taking advantage of the constituent nature of reports. Combined with the cooperative attention mechanism, the hierarchical LSTM first generates high-level topics, and then generates fine-grained descriptions according to the topics.
1) Aiming at the confusion of long sentences in traditional medical report generation and the difficulty in locating diseased areas, a new cycle sentence generation model and LSTM word-by-word generation model with attention were proposed to solve the problems of long text and colloquialism and achieve theoretical innovation.
2) Through comparative experiments, it is proved that the model is more effective than the traditional model in the generation of chest X-ray reports.
2.
Related technologies
2.1. Problem definition
First of all, the first task is to predict the label of a given image. The label prediction task is processed in the way of multi-label classification task. Specifically, features of the given image I are firstly extracted:
where I ∈R, L is the label vector, li = 1/0 indicates whether there is the ith label, and MLCi represents the ith output of the network. A complete diagnostic report is composed of multiple internal reports with different forms of information. The chest X-ray report contains the impression description, usually in one sentence. Findings are a description. Tags are a list of keywords. Generating such disparate information from a unified framework is technically demanding.
Secondly, it is still difficult to locate the lesion area in the image and attach the correct description.
Finally, descriptions in imaging reports are often long, containing multiple sentences or even paragraphs. y has S sentences, the ith sentence has N words, and y(i, j) is the jth word in the ith sentence. The loss ℓ(x, y) in long sentences produced by producing distribution values on each word of each sentence consists of two weighted and intersecting terms and a sentence loss ℓ shifts the distribution values when stopped, and the word loss ℓ on the word distribution p(i, j).
However, it is indispensable to generate long texts, and this traditional method cannot meet the needs of long texts.
2.2. Main technologies
Both CNN and RNN are extensions of traditional neural networks, which can generate results by forward calculation, and update the model by reverse calculation. Each layer of neural network can have multiple neurons horizontally, and there can be multiple layers of neural network connections vertically. The significance of the combination is that the combination can process a large amount of information and has the characteristics of time and space, such as video, image and text combination. There are also real scene dialogues and dialogues with images to make text expressions more specific, and videos are more complete than pictures description.
Feature extraction mainly adopts convolution kernel, whose width and height are greater than 1, and which only performs cross-correlation operation with each position of the same size in the image. Therefore, the output size is equal to the input size nh × nw minus the convolution kernel size kh × kw, which is:
Image description technology can automatically generate text descriptions for a given image. Most of the image text models studied recently are based on CNN-RNN framework. Vinyals et al. [6] provided image features extracted from the last hidden layer of CNN to LSTM network to generate text. Fang et al. [7] first used CNN to detect anomalies in the image which were used to generate a complete sentence through the language model. Karpathy et al. [8] put forward the use of multimodal recursive neural network to fuse visual and semantic features and then generate image description.
Scientists have been devoted to studying the attention in the field of cognitive neuroscience since the 19th century. Kernel regression [9] in 1964 was a simple demonstration of machine learning with attention mechanism. Described in mathematical language, suppose there is a query q ∈ Rq and m key-value pairs (k1, v1)..., (km, vm), where ki ∈ Rk, vi ∈ R (v). The attention convergence function F is expressed as a weighted sum of values:
The attention weight (scalar) of the query q and the key ki is obtained by mapping the two vectors into scalars through the attention scoring function a, and then through the softmax operation:
Attention mechanisms have proven useful for adding image text. Xu et al. introduced spatial visual attention mechanism into image features extracted from CNN middle layer [10]. Wang et al. [11] proposed a semantic attention mechanism for given image tags. In order to make better use of visual features and generate semantic labels.
The design of LSTM network was inspired by the logic gates of computers. LSTM introduces memory cells, or cells for short, whose hidden layer outputs include hidden states and memory elements. Only the hidden state is passed to the output layer, while the memory element is entirely internal information. Suppose there are h hidden units, the batch size is n, and the input number is d. Therefore, the input is X ∈ R (n × d), and the hidden state of the previous time step is H (t − 1) ∈ R (n × h). Accordingly, the gate of time step t is defined as follows: the input gate is It ∈ Rn × h, the forgetting gate is Ft ∈ Rn × h, and the output gate is Ot ∈ Rn × h. They are calculated as follows:
where Wxi, Wxf, Wxo ∈ R (d * h) Whi, Whi, Who ∈ Rh is the weight parameter, bi, bf, bo ∈ R (l * h) is offset parameters.
As an improved recurrent neural network, LSTM can solve the problem of the long-distance dependence in the process of medical report generation which RNN cannot deal with [12]. Tong et al. [13] are studying intensive text, requiring the model to generate a text description for each detected image region. Lei et al. [14] generated paragraph descriptions for images through layered LSTM.
3.
RCLN model
3.1. Model definition
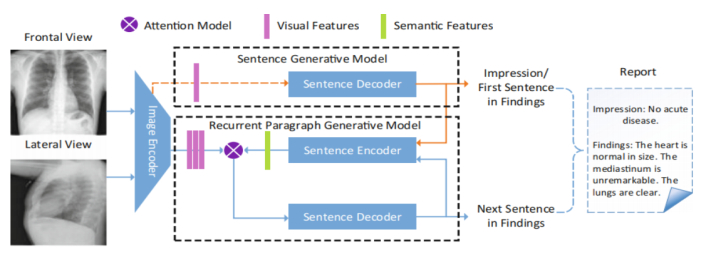
The visual features of the image and the semantic features of the previous sentence are combined into a multimodal cyclic generation network model (MRNA) that generates the next sentence. The RCLN model proposed in this paper proposes a new cyclic generation model to generate results sentence by sentence, in which subsequent sentences are conditional on multi-modal input, including the preceding sentence and the original sentence image [15]. The multimodal model proposed in this paper adopts attention mechanism to improve performance. The overall architecture presented in this paper takes medical images as input from multiple views and generates a framework for radiology reports with impressions and findings. To generate the survey result paragraphs, this paper first uses an encoder-decoder model, which takes image pairs as inputs and generates the first sentence. The first sentence is then input into the sentence coding network to output the semantic representation of the sentence [16]. Suppose a result paragraph containing L sentences is being generated. The probability of generating the ith sentence of length T satisfies:
where V is the given medical image, θ is the model parameter (θ on the right is omitted in this paper), Si represents the ith sentence, wt is the tth mark in the ith sentence. Similar to the n-gram hypothesis in the language model, this paper adopts Markov hypothesis to generate the 2-gram model at sentence level, which means the current sentence being generated depends only on its previous sentence and image. This simplifies the steps to estimate the probability:
It can be noted that for small-scale data sets, the verbal information of medical reports is more important than the image information, and the final results tend to care more about the degree of imitation of doctors' tone.
3.2. Image encoder
The medical reporting task is easily related to the Image2Text task, so this paper utilizes the Image Captions method to solve the problem of this task. In this model, an image encoder is applied to extract global and regional visual features from the input image. The background variable C output by the image encoder encodes the information of the entire image input sequence x1, …, xT. Given the output sequence y1, y2, …, yT′ in the training samples, for each time step t′, the conditional probability of output yt of the image decoder will be based on the previous output sequence y1, …, yt′−1 and the background variable c, which is P(yt′∣y1, …, yt′−1, c).At this time, another cyclic neural network can be used as the decoder to output the time step t 'of the sequence. The decoder takes the output yt′ −1 of the previous time step and background variable c as the input, and transforms them with the hidden state st′−1 of the previous time step into the hidden state st′ of the current time step. Therefore, function g (cyclic neural network unit) can be used to express the transformation of the hidden layer of the image decoder:
Image encoders automatically extract visual features of hierarchical CNN images. The image encoder of this model uses pre-trained Resnet-152 [10]. In this paper, the size of the input image is adjusted to 224 × 224 to keep consistent with the image of pre-trained Resnet encoder. Then, the local eigenmatrix f ∈ R1024 × 19 (reconstructed from 1024 × 14 × 14) res layer of Resnet [17]. Each column of f is a regional eigenvector. So, each image has 196 subregions. At the same time, this paper extracts the global feature vector f ∈ R2048 from the last mean pooling layer of Resnet. For multiple input images from multiple views (for example, the front and side views shown in the body text), their regional and global features are connected accordingly before feeding into the following layers [18]. For efficiency, all parameters in the layer built from Resnet-152 are fixed during training. Then, the maximum pooling operation is applied to the feature maps extracted from each convolution layer to generate 1024-dimension feature vectors. The final sentence feature is a concatenation of feature vectors from different layers. To generate a long paragraph description, a hierarchical cycle network was chosen in this paper. A two-level RNN is generally used for paragraph generation: first, some topics are generated by paragraph-level RNN which are then taken as input by a sentence-level RNN to generate sentences. The pre-trained dense subtitle model can be used to detect the semantic regions of images.
3.3. Sentence generation model
Natural language is a complex system used to express the human mind. In this system, words are the basic units of meaning. As the name suggests, a word vector is a vector used to represent the meaning of a word, and can also be considered a feature vector or representation of a word. The technique of mapping words to real vectors is called word embedding. In recent years, word embedding has gradually become the basic knowledge of natural language processing. Word vector is used to represent the word meaning which can also be regarded as the word feature vector. Each word is mapped to a fixed-length vector that better expresses similarities and analogies between different words. Word embedding consists of two models, namely skip-gram and continuous bag of words. For semantically meaningful representations, their training relies on conditional probability, which can be seen as the use of some words in a corpus to predict other words [19]. Word embedding models are self-supervised models since it is unlabeled data.
3.4. Cyclic paragraph generation model
For the Impression and Findings description of medical reports, QA + Hierarchical RNN method was used in this paper to solve this problem [20]. By introducing hidden state variables to store past information and current input, current output can be determined. Hidden state is a kind of modeling of the way data is generated. It considers that data generation is divided into two steps: first, select a hidden state and then generate observation results from the hidden state [21]. Hiding means you can only see the observation sequence and not the hidden state sequence when the data generation is on the run, but it doesn't affect the hidden state being exposed to you during training [22]. All of this is done in the basic unit of time step, and the time step is the time interval of the load sub-step in the load step [23]. In rate-independent analysis such as static analysis and (static) nonlinear analysis, in a load step, the time step does not reflect the real time, it is accumulated to reflect the sequence of load sub-steps [24]. However, in rate-dependent analysis such as transient analysis, the size of time step reflects actual length of time.
4.
Experiment
4.1. Dataset
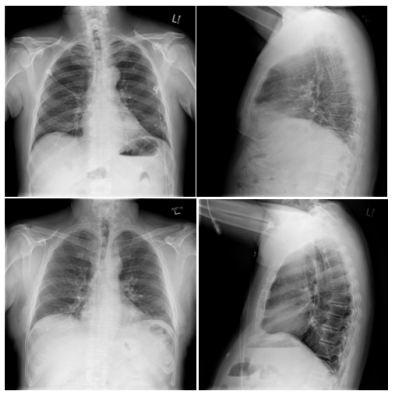
The original dataset was collected from Openi's chest radiography open data, which contained 3955 radiology reports from two large hospital systems in the Indiana Patient Care Network database and 7470 related chest X-rays from the Hospital Image Archiving System.
First, the original data set contained 7470 images, 3391 pairs of positive side chest radiographs and 3631 pairs of sentences of which the number of sentences is greater than 4. In order to ensure that the largest subset of data information can be obtained, the maximum number of sentences was set to 8 since more than 90% of report statements are between 4 and 8 sentences. There were 3111 applications that met both conditions. Secondly, the training and validation dataset are spilt into 2811/300 with a ratio of about 1/10, using Adam optimization function based on stochastic gradient descent. The unused part of the dataset is then used as the test set. In this paper, 300 reports were randomly selected to form a test set on which all evaluations were performed.
4.2. Evaluation indicator
Some common image caption evaluation metrics, including bilingual evaluation understudy (BLEU), metric for evaluation of translation with explicit ordering (METEOR), and recall-oriented understudy for gisting evaluation (ROUGE), are used to provide quantitative comparisons in this paper. BlEU-1 measures the accuracy of words in medical reports, and higher-order BlEU can measure the fluency of sentences. For a sentence to be translated, candidate translations can be expressed as, and the corresponding group of reference translations can represent the phrase set of n words and the possible grams of the kth group.
The purpose of METEOR is to prevent mistranslations of the reported results due to synonyms [25]. The measurement of METEOR is based on weighted harmonic mean value of single precision and single word recall rate. To calculate METEOR, a set of alignments needs to be given in advance, which is based on the thesaurus of WordNet. The alignments are calculated as harmonic average of accuracy and recall rate between the corresponding best candidate translation and reference translation the METEOR is calculated as the harmonic mean of precision and recall rate between corresponding best candidate translation and reference translations by minimizing successive ordered chunks in the corresponding statement:
where α, γ and θ are the default parameters for evaluation. Therefore, the final evaluation of METEOR is based on a harmonic average of decomposition matching and characterization decomposition matching quality of chunk, and contains a penalty coefficient Pen which is different from BLEU. Accuracy and recall rate based on the whole corpus are taken into account to obtain the final measure.
ROUGE evaluates abstracts based on the co-occurrence information of n-grams in abstracts, and it is a method for evaluating the recall rate of n-gram words based on the co-occurrence information of n-gram words [26]. The basic idea is that several experts generate artificial abstracts respectively to form a standard abstract set. The quality of the abstract is evaluated by counting the number of overlapping basic units (n-element grammar, word sequences and word pairs) through comparing the automatic abstracts generated by the system with the standard abstracts generated by the manual.
The stability and robustness of the evaluation system can be improved by comparing with the expert manual abstract. Neural machine translation (NMT) used in this paper is more powerful than its predecessor Statistical machine translation (SMT). The word order of medical reports is often correct but the error frequency increases. Therefore, a recall rate indicator like ROUGE is needed to evaluate the error frequency.
4.3. Contrast test
Firstly, an image encoder is used to extract global and regional visual features from the input image. Image encoder is a CNN, which automatically extracts hierarchical visual features from images. More specifically, we adjust the size of the input image to 224 × 224. (Corresponding to the image size parameter).
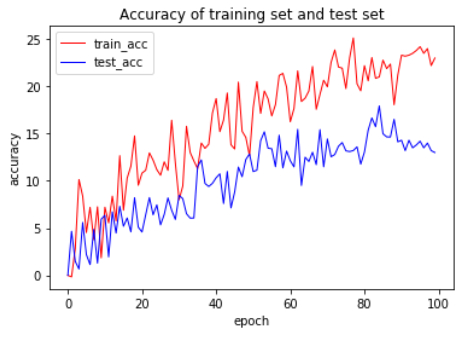
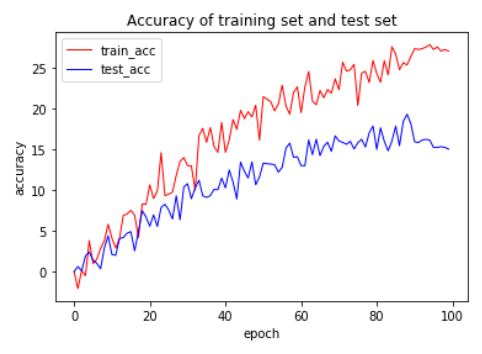
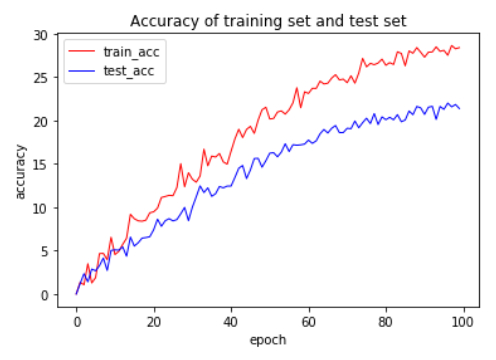
As shown in Figures 3–5, a dropout layer (corresponding to the dropout rate parameter) with a value of [0.3, 0.5 or 0.7] has been added to the network to reduce overfitting and this dropout layer represents the probability that the layer's output is discarded.
Word embedding is mainly responsible for processing the title of each image given as input during training. The output of the word embedding is also a vector of size 1 × 256 (corresponding to the argument word_embedding_size parameter), which is another input to the decoder sequence.
Start the training, set the batch size to 32 (corresponding to the parameter batch size), Adam optimizer makes the learning rate from 1E-2 to 1E-4 (corresponding to the parameter learning rate), a total of 50 iterations (parameter epoch num).
The probability and accuracy influence of network layer output being discarded are discussed.
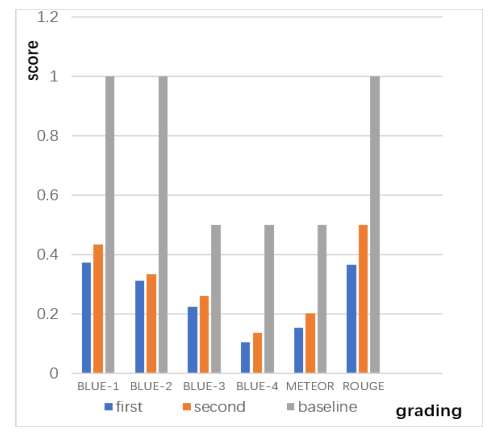
In the following two model tests, the data output of the first and second tests both met the evaluation benchmark range. The label position of the model was adjusted before the second test. The performance of various indicators was improved when the label at the end of the whole sentence was changed to the half of the sentence and the training time was increased. The time complexity of this model is O(n^2). As shown in Figures 6 and 7, the minimum values of the baseline range are all 0. It can be seen that each score index is lower than the maximum value, proving that this model can generate relatively standard medical reports.
In this paper, two comparative models for medical report generation are also implemented. The same Resnet pre-training model was used for pre-training. The data results are shown in Table 1.
CNN-NN, the prototype CNN, was published by Lecun in 1998 [27]. He formally proposed that he applied the back propagation to neural networks and proposed a new neural network convolution NN. Ronald Williams and David Zipser put forward real-time circular learning of RNN as the basis in 1989 [28].
CNN-RNN-Att: The Attention mechanism was added on the basis of the previous one. The Attention mechanism was published by google mind team in 2014 [29]. In 2017, the article "Attention is All You Need" was published by Google Machine Translation team in which self-attention mechanism was extensively used to learn text representation.
By comparing the results of other models and RCLN models, it can be seen that the model based on the multi-attention mechanism is superior to similar models in terms of BLUEs, METEOR and ROUGE, indicating the effectiveness of multi-attention mechanism on medical report generation [30]. The scores of RCLN model were much higher than CNN-RNN series model and higher than MRNA model, proving its effectiveness. Some statements in reports generated by other models are continuous but not coherent. In contrast, the model proposed in this paper is more coherent in context and more colloquial.
5.
Conclusions
This paper mainly focusses on generating detailed findings for chest radiographs medical reports. For impression generation, classification-based methods may be better at distinguishing anomalies and then drawing final conclusions. But from the results, we can see that in the first line the results and impressions are consistent with the actual situation. However, the results and impressions generated in the second line leave out some exception descriptions. The main reason may be that I was training on a small training set, with fewer training samples for anomalies, and some inconsistencies caused by real noise from the original report. Furthermore, the current model does not create high-quality new sentences that never appear in the training set. The reason may be that it is difficult to learn correct grammar from a small corpus because syntactic correctness is not considered in the training objective function.
In conclusion, it is believed that with more control data sets and better noise reduction processing of data set preprocessing, better results will appear [31]. At the same time, multiple loop processing statements can also increase the depth, making the result more accurate. In the data labeling process, the addition of more high-quality sentences is expected to effectively ensure the enhancement of the quality of the results.
Acknowledgments
The research is supported by the National Natural Science Foundation of China (No.12105120, No.72174079, No.72101045), Natural Science Foundation of the Jiangsu Higher Education Institutions of China (No.19KJB520004, No.21KJB520033), Jiangsu Province "333" project (BRA2020261), Jiangsu Qinglan Project, Lianyungang "521 project", Science and Technology project of Lianyungang High-tech Zone (No.ZD201912).
Conflict of interest
The authors declare that there is no conflict of interest.









 DownLoad:
DownLoad: