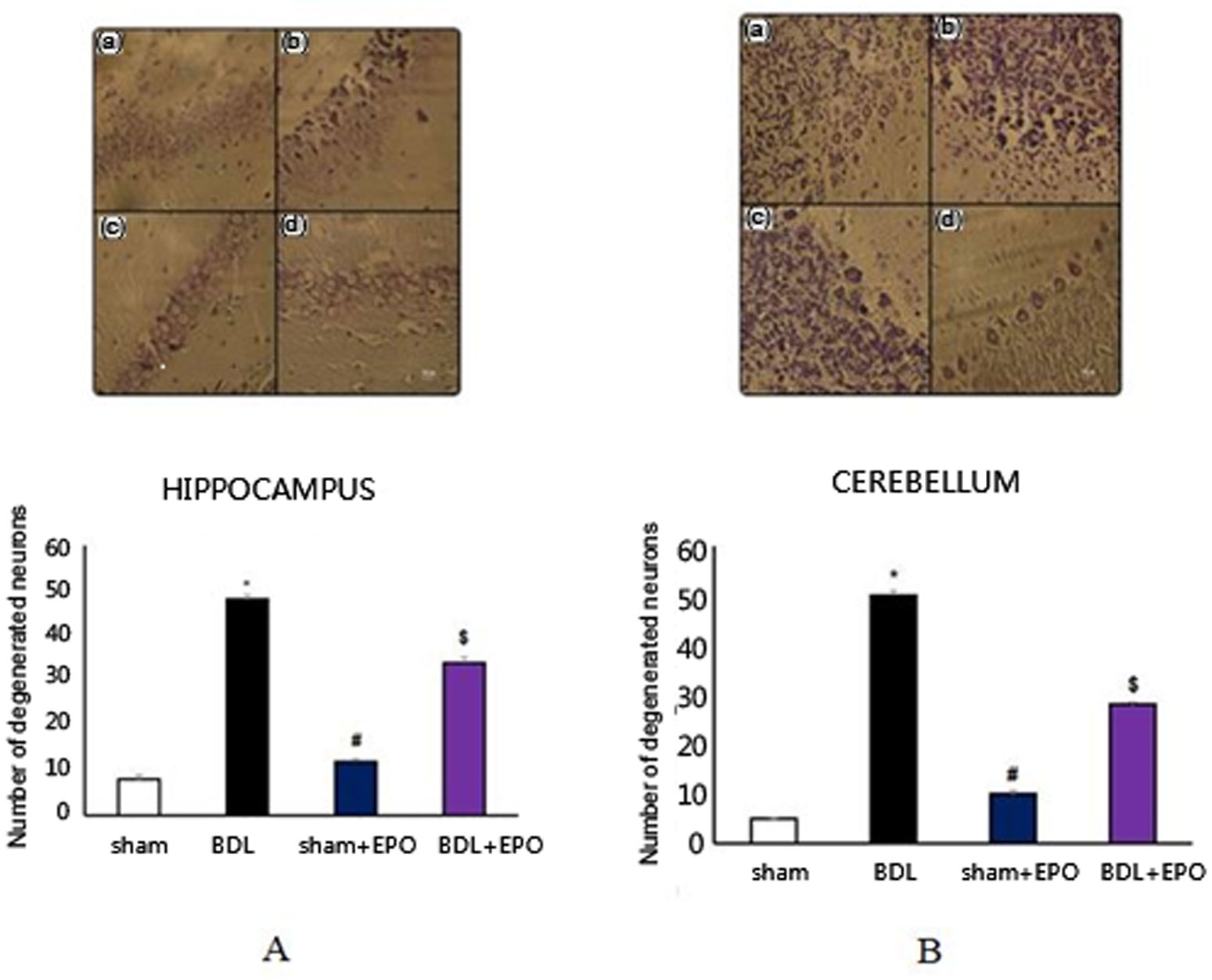
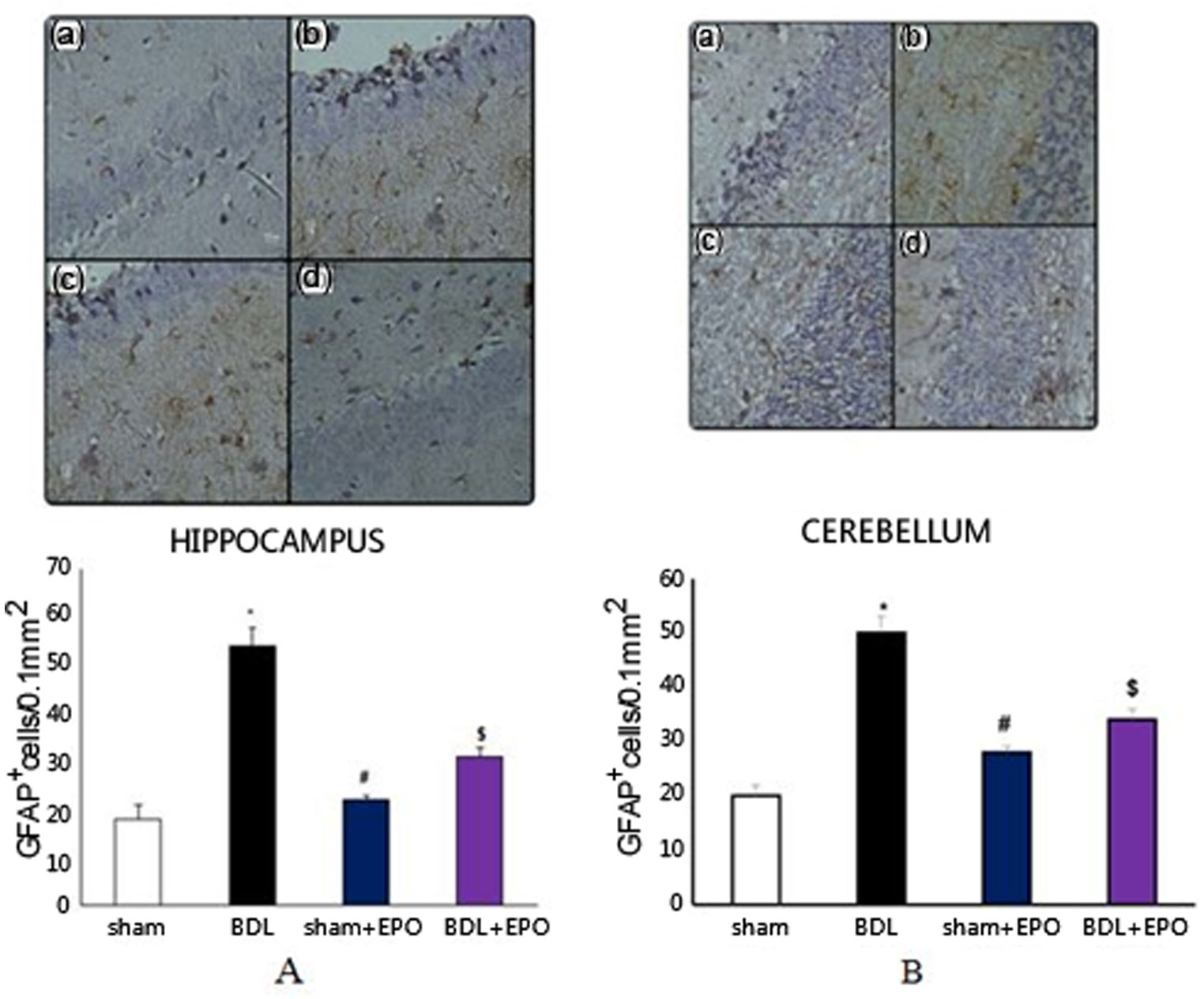
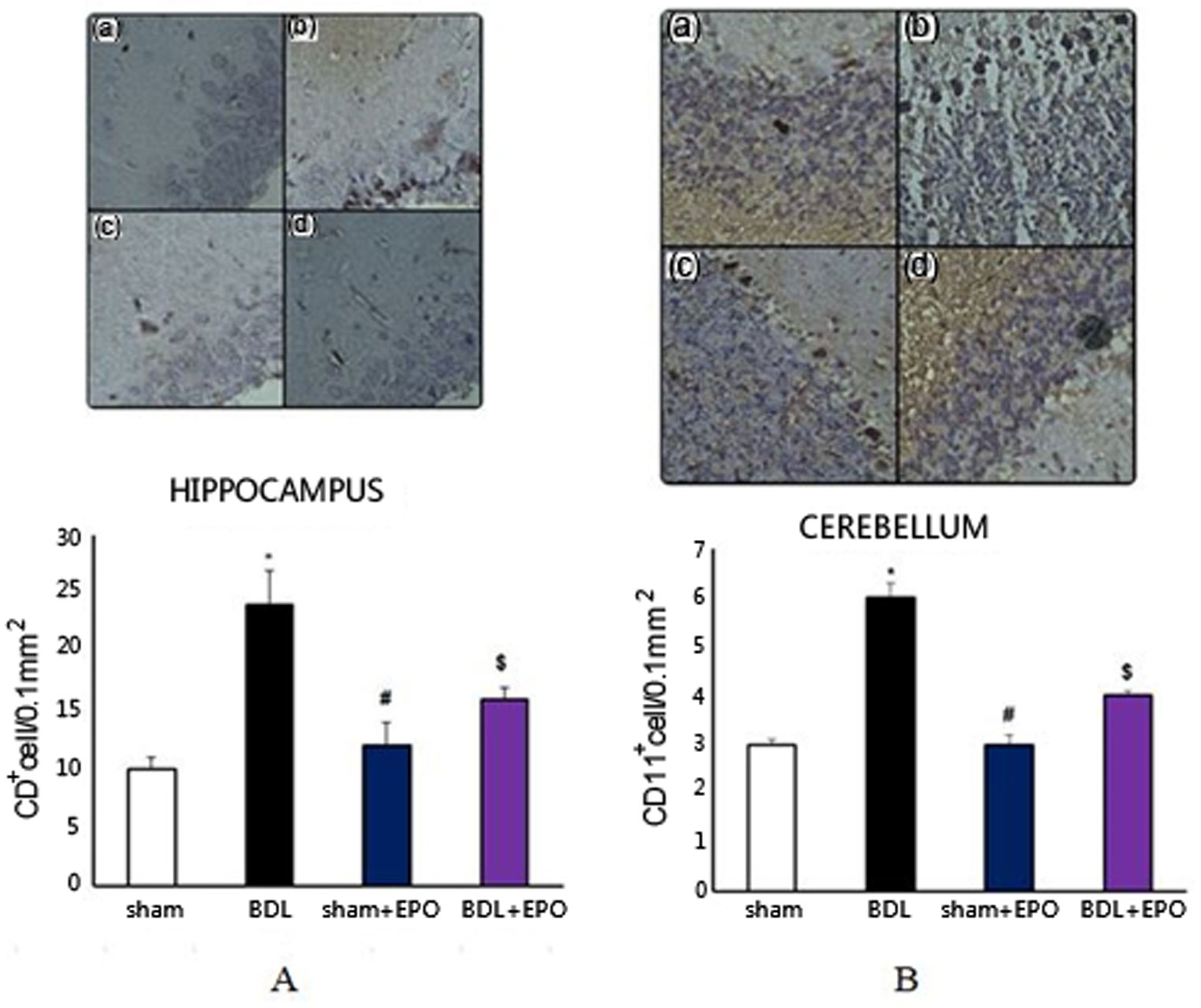
Hepatic encephalopathy (HE) is a brain disorder as a result of liver failure. Previous studies have indicated that erythropoietin (EPO) has neuroprotective effects in different neurological diseases. This study addressed the therapeutic effect of a four-week treatment with EPO on neuronal damages in bile duct-ligated rats. Forty male Wistar rats (250–280 g) were used in the present study. The animals were randomly divided into four groups consisting of 10 animals each, including sham, sham + EPO, bile duct ligation (BDL), and BDL + EPO. EPO was intraperitoneally administered every other day (5,000 U/Kg) in the last four weeks after BDL. Biochemical and histological studies were performed to evaluate neurodegeneration. The results revealed that BDL increases the level of hepatic enzymes and total bilirubin. Furthermore, neurodegeneration was significantly increased in the BDL group compared to sham groups. EPO preserved hepatic enzymes and total bilirubin in the treated group. In addition, EPO significantly decreased the neurodegeneration in BDL + EPO compared to the BDL group. Results of this study showed that EPO has neuroprotective effects in the rat model of HE, possibly due to its anti-inflammatory and anti-oxidant properties. Complementary studies are required to clarify the exact mechanisms.
1.
Introduction
Contact collision is a common phenomenon in engineering practice. With the deepening of scholars' research, the frontal collision model cannot describe the oblique collision system with tilt angle more accurately. Therefore, the oblique collision system with collision angle should be studied in depth. In addition, friction is inevitable in the process of oblique collision. The vibration caused by friction affects the stability of the system, accelerates the wear failure of the parts, and has potential safety hazards. Duan and Ding [1] discussed the influence of collision parameters such as mass clearance and contact surface inclination on the vibration reduction effect of turbine shroud blade group system through phase trajectory diagram, bifurcation diagram, and Poincare section diagram. Ling et al. [2] established a mechanical model of oblique collision between freight cars and trains at railway crossings and studied the dynamic response and derailment mechanism of trains in this scenario using the multi-body dynamics method. Dong and Ding [3] established the oblique collision model and equation of the whole ring bladed disk system with a shroud and analyzed the dynamic response of the blade when the gap between the shrouds and the stiffness of the blade are misaligned. In [4,5,6,7,8], the mechanical model with oblique collision was simplified for the actual engineering model, and the dynamic behaviors such as oblique collision motion and bifurcation phenomenon of the system in engineering practice were studied. Considering the dynamic friction of LuGre, Liu et al. [9] established a friction model of blade crown collision, and studied the bifurcation characteristics of contact collision and friction motion of shrouded blades. For the single-degree-of-freedom system with improved LuGre dynamic friction, Saha et al. [10] analyzed the sticking phenomenon of the system through the phase diagram, and compared and analyzed the dynamic characteristics of the system under LuGre and improved LuGre dynamic friction. Zhang et al. [11] introduced the Dankowicz dynamic friction model into the single-degree-of-freedom vibration system, analyzed the motion state and judgment conditions, and studied the friction-induced system vibration and the dynamic behavior of the system under the influence of two parameters.
The wedge friction damper is one of the key components of the three-piece bogie [12], which has an important influence on the dynamic performance of the vehicle. Li [13] analyzed the vibration characteristics of a 100 t heavy-duty truck with a wedge friction damper and found the influence of the relative friction coefficient of the damping system on the stability of the truck. Based on vehicle system dynamics, Song et al. [14] used SIMPACK software to establish a nonlinear dynamic model of six-axle flat car and analyzed the influence and variation of different friction angles on the dynamics of three-axle bogie. Li et al. [12] used SIMPACK software to establish the mechanical model of the wedge friction damper and analyzed the spatial force and vibration reduction performance of the model. Liu [15] introduced the structure of wedge friction damper for three-piece bogie of freight train bogie, analyzed the design value of the relative friction coefficient of the product, and gave the value suggestion.
On the basis of [12,13,14,15], aiming at the wedge friction damper for freight train bogie, in order to be closer to the actual working conditions and describe the friction-induced vibration characteristics more comprehensively, the dynamic friction between the wedge and the side frame is considered, and a three-degree-of-freedom oblique collision vibration system with Dankowicz dynamic friction and gap is simplified. The motion equation of the system is established, and the motion state of the system and its judgment conditions are analyzed. Based on C language programming and variable step size fourth-order Runge-Kutta algorithm, the numerical simulation analyzes the evolution process of the system motion and the frequency range of the viscous and flutter phenomena when the external excitation frequency changes, which can provide a certain reference for the selection of system structure parameters in engineering practice.
2.
Modeling of the wedge friction damper system
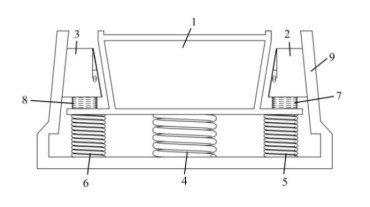
The following Figure 1 shows a wedge friction damper. The numbers 1–9 in the figure are bolster, right wedge, left wedge, intermediate bolster spring, right bolster spring, left bolster spring, right sub-wedge spring, left sub-wedge spring, and side frame.
In order to be closer to the actual working conditions and consider the influence of vibration reduction and lubrication, the bolster 1 is simplified into a mass block $ {M}_{1} $; the wedge blocks 2 and 3 are simplified into block $ {M}_{2} $ and block $ {M}_{3} $, respectively. The damping spring 7 and 8 connected by the wedge block 2 and 3 are simplified to the nonlinear spring $ {K}_{2} $ and the nonlinear spring $ {K}_{3} $, respectively. The lubricating oil between the bolster 1 and the wedge block is simplified as a nonlinear damping sum $ {C}_{2} $ and $ {C}_{3} $, respectively. The bolster spring 4, 5, 6 is simplified into a nonlinear spring $ {K}_{1} $; the air damping of the bolster is simplified to linear damping $ {C}_{1} $; the contact surfaces between the wedge block 2, 3 and the side frame 9 are A and B surfaces, and there is sliding friction force between the contact surfaces; and a dynamic model of the wedge damper with dynamic friction and gap is obtained, as shown in Figure 2.
Between two adjacent collisions, the differential equation of system motion is:
In Eq (1): $ {F}_{d} $ is the dynamic friction generated between the contact surface of the bolster 1 and the side frame 9 during the movement of the wedge friction damper; $ {F}_{i} $ is the nonlinear spring force of the damping spring $ {K}_{i} $, where $ E $ is a small parameter; $ {\bar{F}}_{i} $ is a nonlinear damping force [16].
In Eq (2), $ i = 1, \mathrm{ }2, \mathrm{ }3 $
In Eq (3), $ i = 2, \mathrm{ }3 $, $ \mathrm{H} $ is the asymmetry coefficient, which represents the unequal degree of damping force between the recovery stroke and the compression stroke of the shock absorber, where
Select the initial displacement $ {\mathrm{L}}_{1} = {\mathrm{x}}_{1} $(0) as the length scale, construct the time scale $ {T}_{1} = \sqrt{\frac{{M}_{1}}{{K}_{1}}} $, and take the dimensionless parameter as:
Substituting the above dimensionless parameters into Eq (1), the dimensionless equation of the system motion can be obtained:
The dimensionless expression Eq (6) of Dankowicz dynamic friction model is [17]:
In Eq (6), $ {f}_{r} $ represents the normal total load on the contact surface, $ \mu $ represents the friction coefficient, $ \sigma $ represents the standard deviation of the roughness height, $ \delta $ represents the maximum allowable asperity deformation, $ {v}_{r} = {\dot{x}}_{1}-{\dot{x}}_{i} $ represents the relative slip velocity between mass 1 and mass 2 or mass 3, $ {\mathrm{y}}_{\mathrm{\infty }} $ represents the separation distance from the radius of the asperity to the normal direction, $ {\sigma }_{1} $ is the bristle damping, $ {\alpha }_{1} $ is an ordinary parameter, and $ \dot{z} $ is the internal damping term. The evolution of the internal variable $ z $ of the dynamic friction model is dominated by Eq (7):
In Eq (7), for $ {v}_{r} > $0, z tends to $ \delta $; for $ {v}_{r} < $0, z tends to $ -\delta $; therefore $ z\in \left[-\delta, \delta \right] $.
The motion of the state variable y is dominated by Eq (8):
In Eq (8): $ \beta > 0 $, $ \gamma > 0 $ are free parameters. The first term on the right side of Eq (8) becomes from the asperity shape in the normal direction, and the second term is the normal component of the force generated by the collision of the asperities.
When the displacement difference $ \left|{x}_{1}-{x}_{i}\right| = d $, the system collides. Since the nonlinear system contains collision and friction, the motion state of the system will be converted between chatter, sticking and collision. In order to more fully understand the changes in the motion process of the system, according to the force and velocity changes of the mass 1, the motion process of the system is divided into the following situations.
Case 1: Mass $ {M}_{1} $ moves under the action of harmonic excitation force $ F\mathit{cos}(\varOmega T+\varphi) $, and the system force analysis of mass $ {M}_{1} $ is carried out. Let $ {f}_{1} $ represent the resultant force of mass $ {M}_{1} $, the $ {f}_{1} = fcos(\omega t+\varphi)-{\xi }_{1}{\dot{x}}_{1}-{k}_{1}{x}_{1}-\varepsilon {k}_{1}{x}_{1}^{3}+{k}_{2}{x}_{2}+\varepsilon {k}_{2}{x}_{2}^{3}+{k}_{3}{x}_{3}+\varepsilon {k}_{3}{x}_{3}^{3}$+${\xi }_{2}[1+\eta sgn\left({\dot{x}}_{2}-{\dot{x}}_{1}\right)]{\left({\dot{x}}_{2}{-\dot{x}}_{1}\right)}^{1/3}+{\xi }_{3}[1+\eta sgn\left({\dot{x}}_{3}-{\dot{x}}_{1}\right)]{\left({\dot{x}}_{3}{-\dot{x}}_{1}\right)}^{1/3} $. When the difference between the motion displacement of the mass $ {M}_{1} $ and the mass $ {M}_{2} $ or the mass $ {M}_{3} $ is equal to gap d, the system collides, due to the symmetry of the left wedge and the right wedge, the resultant force on mass $ {M}_{1} $ is the resultant force in the vertical direction as shown in the Figure 3, and the judgment expression is:
According to the law of conservation of momentum and the relationship between the velocity before and after the collision, it can be obtained that:
Among them, R is the collision recovery coefficient.
Case 2: If the resultant force of the mass $ {M}_{1} $ is greater than zero or equal to zero and the relative velocity of mass $ {M}_{1} $ and mass $ {M}_{1} $ or $ {M}_{1} $ is not zero, the mass $ {M}_{1} $ performs accelerated slip motion, and then $ {f}_{1}\ge $0, $ \left|{\dot{x}}_{1}-{\dot{x}}_{2}\right|\ne $0.
Case 3: If the resultant force of the mass $ {M}_{1} $ is less than zero and the relative velocity of mass $ {\mathrm{M}}_{1} $ and mass $ {M}_{1} $ or $ {M}_{1} $ is not zero, the mass $ {M}_{1} $ performs decelerated slip motion, and then $ {f}_{1}\le $0, $ \left|{\dot{x}}_{1}-{\dot{x}}_{2}\right|\ne $0.
Case 4: If the resultant force of mass $ {M}_{1} $ is less than zero and the relative velocity between mass $ {M}_{1} $ and mass $ {M}_{2} $ or mass $ {M}_{3} $ is zero, that is, $ {f}_{1} < $0, $ \left|{\dot{x}}_{1}-{\dot{x}}_{2}\right| = $0, mass $ {M}_{1} $ is in a sticking state.
Based on the above four cases, the numerical simulation of the wedge friction damper oblique collision system with gap and friction is carried out to analyze its dynamic behavior. In order to study the periodic motion and bifurcation characteristics of the wedge damper system, the Poincaré section $ \sigma = \left\{\left({x}_{1}, {\dot{x}}_{1}, {x}_{i}, {\dot{x}}_{i}, \theta \right)\in {\mathrm{R}}^{4}\times \mathrm{S}, {x}_{1}-{x}_{i} = d, {\dot{x}}_{1} = {\dot{x}}_{1+}, {\dot{x}}_{i} = {\dot{x}}_{i+}\right\} $ is selected.
The Poincare mapping is established:
Of which:
In Eqs (11) and (12), $ i = 2, \mathrm{ }3, X\in {\mathrm{R}}^{4} $, $ v $ is a real parameter. The periodic motion in the following discussion is represented by n-p-q-l, where n represents the number of excitation periods, p represents the number of collisions, q represents the number of chatters, and l represents the number of stickings.
3.
The influence of Dankowicz friction on the system
In advance, through a large number of data simulation experiments, we find the different dynamic behavior of the system under different parameters, and select the system parameters of the wedge friction damper combined with the engineering practice: $ {M}_{1} $ = 489 kg, $ {M}_{2} $ = 537.9 kg, $ F $ = 112 N, $ {K}_{1} $ = 2.4 × 104 N/mm, $ {K}_{2} $ = $ {K}_{3} $ = 2.04 × 104 N/mm, $ {C}_{1} $ = 171 N∙s/m, $ {C}_{2} $ = $ {C}_{3} $ = 643 N∙s/m. Take the parameters into Eq (1), and calculate the dimensionless parameters of the system: $ {k}_{1} $ = 0.8, $ {k}_{2} $ = 0.85, $ {k}_{3} $ = 0.85, $ {m}_{2} $ = 1.1, $ {m}_{3} $ = 1.1, $ R $ = 0.85, $ {\xi }_{1} $ = 0.05, $ {\xi }_{2} $ = 0.15, $ {\xi }_{3} $ = 0.15, $ {\mu }_{m} $ = 0.4, $ \mu $ = 0.2, $ \beta $ = 100, $ {y}_{\infty } $ = 2000, $ \delta $ = 0.0001, $ \gamma $ = 3000, $ \sigma $ = 0.01, $ {\alpha }_{1} $ = 2.2, $ f $ = 1, $ {f}_{r} $ = 0.2, $ \theta $ = 53. Set the initial value: $ {x}_{1} $ = 0, $ {x}_{2} $ = 0, $ {\dot{x}}_{1} $ = 0, $ {\dot{x}}_{2} $ = 0. Taking the dimensionless frequency as the bifurcation control parameter, the global and local bifurcation diagrams of the system motion obtained by numerical simulation are shown in Figure 4. From the bifurcation diagram in Figure 4, it can be seen that as the frequency ω increases from 1 to 8, the system motion undergoes inverse periodic doubling bifurcation, periodic doubling bifurcation, Grazing bifurcation, and Hopf bifurcation to each other between single-period, multi-period, quasi-period, and chaos. As shown in Figure 4(a), when ω∈[1, 1.454], the system is in a chaotic state, and when ω∈[1.454, 3.2], the system is in period three motion. As shown in Figure 4(b), when ω∈[3.2, 4.1], the system is in chaotic and multi-period motion. As shown in Figure 4(c), when ω∈[4.3, 4.66], the system is in period six motion and period nine motion successively, and then Hopf bifurcation occurs. When ω∈[4.66, 4.93], the system is in almost periodic motion. As shown in Figure 4(a), when [4.93, 6.33], the system transitions between periodic three motions, periodic six motions and periodic twelve motions. As shown in Figure 4(d), when [7, 8], the system transitions between multi-period motion and chaos. By analyzing the motion process of the system with frequency change, it is found that the system is a stable periodic motion in the parameter interval ω∈[1.75, 3.24], ω∈[4.029, 4.65], ω∈[5, 6.33] and ω∈[6.6, 7.225]. The elastic force, damping force, and external excitation force are coupled to each other due to collision and friction in the motion system of the wedge shock absorber, which leads to chatter. Through the phase diagram, poincare section diagram, and time history diagram of the system motion with the change of bifurcation control parameters, the chatter, collision, and sticking of the wedge damper during the train operation are studied in detail.
When the system frequency is $ \omega = 1.75 $, as shown in Figure 5(a), (b), the corresponding phase diagram and displacement-time history diagram of the system are in the 1-3-2-0 periodic motion. Under the action of an external excitation, the system has three collisions and two chatters. As the external excitation frequency of the system increases, the system undergoes a period-doubling bifurcation and transits to a short period of twelve motions. When the system frequency $ \omega = 3.24 $, as shown in phase diagram 5(c) and displacement-time history diagram 5(d), the system is in a 1-12-9-0 periodic motion. Under the action of an external excitation, the system undergoes twelve collisions and nine chatters. As the system frequency continues to increase, when $ \omega \in [3.35, \mathrm{ }3.55] $ is selected, the sticking phenomenon occurs, and the system motion state is converted between sticking and chatter. As shown in Figure 5(e)–(p), the amplitude of the system chatter first decreases from large to small, reaches the minimum value at $ \omega = 3.395 $, and then decreases from small to large. Furthermore, the duration of the sticking phenomenon first increases from less to the longest at $ \omega = 3.395 $, and then the phenomenon gradually weakens until it disappears. The excitation frequency $ \omega = 3.922 $ is selected, as shown in Figure 5(q), (r). The system is in a 1-8-6-0 periodic motion. Under the action of an external excitation, the system has eight collisions and six chatters. When the excitation frequency $ \omega = 4.029 $, it can be seen from Figure 5(s), (t) that the system has a Grazing bifurcation. Because the displacement difference between mass $ {M}_{1} $ and mass $ {M}_{2} $ and mass $ {M}_{3} $ is exactly d, the direction of the resultant force of mass $ {M}_{1} $ suddenly changes, and under the action of the resultant force, it moves away from mass $ {M}_{2} $ and mass $ {M}_{3} $. At this time, the system is in a 1-6-6-0 periodic motion. Under the action of an external excitation, the system has six collisions and six chatters.
When the excitation frequency $ \omega = 4.187 $ is selected, as shown in Figure 6(a), (b), the corresponding phase diagram and displacement-time history diagram of the system are in the 1-3-3-0 periodic motion. Under the action of an external excitation, the system has three collisions and three chatters. Then, the system undergoes periodic doubling bifurcation, as shown in Figure 6(c)–(e). It can be seen that the system is in a 1-6-4-1 periodic motion. Under the action of an external excitation, the system undergoes six collisions, four chatters and one sticking. When the excitation frequency $ \omega = 4.4258 $, as shown in Figure 6(f)–(h), the system enters the period 1-9-7-2 motion, and the system appears the Grazing collision behavior through the Grazing bifurcation. When the excitation frequency $ \omega \in [4.65, \mathrm{ }4.9] $, as shown in Figure 6(i)–(l), with the increase of $ \omega $, the inverse Hopf bifurcation occurs in the system, and the system enters the periodic 1-3-2-1 motion through phase locking. Under the action of an external excitation, the system undergoes three collisions, two chatters and one sticking.
The excitation frequency $ \omega = 6.12 $ is selected, such as Figure 7(a)–(c), which shows that the system is in period 1-12-12-1 motion. Under the action of an external excitation, the system has twelve collisions, twelve chatters and one sticking. The excitation frequency $ \omega = 6.34 $ is selected, as shown in Figure 7(d), (e), which shows that the system enters the period 1-6-6-0 motion through the grazing bifurcation, and the sticking phenomenon disappears. Select the excitation frequency $ \omega = 7.05 $. As shown in Figure 7(f), (g), the system is in periodic 1-3-3-0 motion. Under the action of an external excitation, the system undergoes three collisions and three chatters. When the excitation frequency $ \omega = 7.276 $, the system enters the period 1-5-5-0 motion. Under the action of an external excitation, the system has five collisions and five chatters. As the system frequency continues to increase, when $ \omega \in [7.34, \mathrm{ }7.578] $ is selected, the system motion state is converted between sticking and chatter. As shown in Figure 7(e)–(p), the amplitude of the system chatter first decreases from large to small, reaches the minimum value at $ \omega = 3.395 $, and then decreases from small to large. At the same time, the duration of the sticking phenomenon increases from less to more, and the duration is the longest when $ \omega = 3.395 $, and then the phenomenon gradually weakens until it disappears. When the excitation frequency $ \omega = 7.877 $ is selected, the inverse Hopf bifurcation occurs in the system, and the chaotic state enters the periodic motion state through phase locking. When the excitation frequency $ \omega = 7.905 $, the system enters a period of 1-4-4-0 motion. Under the action of an external excitation, the system undergoes four collisions and four chatters.
4.
Effect of mass ratio on system motion
The change of the system motion transfer process and the parameter interval of the system stable motion is analyzed further. Through numerical simulation, it is found that the periodic bubble phenomenon of the system is very sensitive to parameter $ {\mathrm{m}}_{2} $, and the slight change of parameter $ {\mathrm{m}}_{2} $ makes the number of periodic bubbles of the system change or disappear. In order to better understand the influence of parameters on the dynamic behavior of the system, the system parameters $ {m}_{2} $ = 1.15, $ {m}_{2} $ = 1.125, $ {m}_{2} $ = 1.1, $ {m}_{2} $ = 1.05, $ {m}_{2} $ = 1, $ {m}_{2} $ = 0.95, $ {m}_{2} $ = 0.9, $ {m}_{2} $ = 0.85 are taken, and the remaining parameters remain unchanged. As the mass ratio decreases, when $ {m}_{2}\in [1.1, \mathrm{ }1.15] $, as shown in Figure 8(a)–(c), the number of periodic bubble structures in the system increases from 4 to 7 and then to 11. When $ {m}_{2}\in [1, \mathrm{ }1.05] $, as shown in Figure 8(d), (e), the periodic bubble structure disappears, and the system presents six chaotic bubble structures. When $ {m}_{2}\in [0.85, \mathrm{ }0.95] $, as shown in Figure 8(f)–(h), the chaotic bubble structure disappears and the periodic bubble structure appears. The number of periodic bubble structures is 17, 6, and 3, respectively. Moreover, with the decrease of mass ratio, the transition region between flutter and viscosity of the system gradually moves to the left, and the period of period three motion window in the low frequency band is reduced. The Hopf bifurcation phenomenon before the periodic bubble phenomenon or the chaotic bubble phenomenon gradually weakens until it disappears, and the window period of the periodic motion in the corresponding frequency band gradually increases.
5.
Conclusions
In this paper, the dynamic model of a kind of wedge damper with dynamic friction is simplified, and the differential equation of system motion is established. According to the change of mass force, the motion situation of the system and the judgment conditions of each situation are discussed. The dynamic characteristics of the system are analyzed by a large number of data simulation. The simulation results show that:
Under certain parameters, with the change of excitation frequency, the system undergoes periodic doubling bifurcation, inverse periodic doubling bifurcation, Grazing bifurcation and Hopf bifurcation between single period, multi period, quasi period, and chaos. In addition, when the excitation frequency of the system is between [5.2, 6.1], there is a periodic bubble phenomenon in the system motion. When the excitation frequency of the system is between [3.35, 3.55], [4.425, 6.12], and [7.34, 7.758], there are chatter and sticking phenomena in the system motion. When the excitation frequency of the system is between [1.75, 3.24] and [3.92, 4.425], the sticking phenomenon disappears, and only the chatter phenomenon exists.
When other parameters remain unchanged, as the mass ratio decreases, the number of periodic bubble structures of the system motion increases exponentially, that is, the number of cycles of the system motion increases exponentially. Then, the periodic bubble structure disappears and the chaotic bubble structure appears. Finally, the chaotic bubble structure disappears and the system enters periodic motion.
Through the theoretical analysis and numerical simulation of the wedge friction damper oblique collision system with Dankowicz dynamic friction, it provides a certain reference basis for the selection of structural parameters and system motion process control of wedge friction damper for freight train bogies in practical engineering. Furthermore, the method of applying the bifurcation theory of mapping to study the stability, bifurcation, and chaos formation process of periodic motion of multi-degree-of-freedom impact vibration system can also be used to study the periodic motion, stability and bifurcation of other types of impact vibration systems, such as double-mass impact vibration molding machine, pile driver, vibration hammer, wheel-rail collision of high-speed train, etc., and can also be applied to the dynamic analysis of some mechanical systems with clearance and elastic constraints.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The work was supported by the Gansu Provincial Science and Technology Plan Project (21YF5WA060) and the National Natural Science Foundation of China (11302092). The author is grateful for the financial support.
Conflict of interest
The authors declare that there are no conflicts of interest.









 DownLoad:
DownLoad: