AIMS Neuroscience, 2015, 2(4): 280-293. doi: 10.3934/Neuroscience.2015.4.280 Research article Topical Section

Export file:

Format

RIS(for EndNote,Reference Manager,ProCite)
BibTex
Text

Content

Citation Only
Citation and Abstract

Relevance of Brain-derived Neurotrophic Factor Levels in Schizophrenia: A Systematic Review and Meta-Analysis

Ian M Rowbotham, Franco F Orsucci, Mohamed F Mansour, Samuel R Chamberlain, Haroon Y Raja

1 Cambridgeshire and Peterborough NHS Foundation Trust;
2 Department of Psychiatry, University of Cambridge;
3 North Essex Partnership Foundation Trust;
4 University College London

Received date: , Accepted date: , Published date:

Topical Section: Advances in Cellular and Molecular Neuroscience Theory

Abstract Full Text(HTML) Figure/Table Related pages

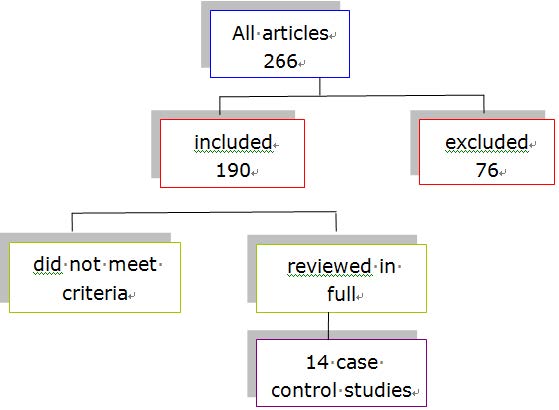
Background: Brain Derived Neurotrophic Factor (BDNF) is one of the neuromodulators crucial for the survival, development and function of neurones in the brain and nervous system. Several authors linked its changes in production and concentration to Schizophrenia syndromes. Aim: This systematic review examined the available evidence to clarify the association between plasma BDNF levels and Schizophrenia. Method: Initial searches revealed 266 records. After screening of abstracts, 20 studies were selected. Following a preliminary review, 14 studies were included in this systematic review and meta-analysis. Results: Of the 14 studies (910 patients, 717 controls) 8 reported decreased BDNF levels in patients with schizophrenia as compared to controls; 3 studies (274/128) found increased BDNF levels; while 3 (62/62) reported no group differences. Meta-analysis of all pooled studies confirmed reduced BDNF levels in schizophrenia versus controls (medium effect size); however, the group difference was not significant when studies using unmedicated cases were considered. Conclusion: The cumulative evidence indicates reduced BDNF levels existing in schizophrenia. However, findings are less clear in unmedicated cases, suggesting that reduced BDNF levels in schizophrenia may be associated with symptom chronicity and/or chronic effects of antipsychotic medication.

Figure/Table

Supplementary

Article Metrics

References

1. Anastasia A, Hempstead BL (2014) BDNF function in health and disease. Nat Rev Neurosci 15.

2. Altar CA, Cai N, Juhasz M, et al. (1997) Anterograde transport of brain-derived neurotrophic factor and its role in the brain. Nature 389: 856-860.

3. Hyman C, Hofer M, Barde Ya, et al. (1991) BDNF is a neurotrophic factor for dopaminergic neurons of the substantia nigra. Nature 350: 230-232.

4. Shoval G, Weizman A (2005) The possible role of neurotrophins in the pathogenesis and therapy of schizophrenia. Eur Neuropsychopharmacol 15: 319-329.

5. De Lisi LE, Sakuma M, Tew W, et al. (1997) Schizophrenia as a chronic active brain process: a study of progressive brain structural change subsequent to the onset of schizophrenia. Psychiatry Res Neuroimaging 74: 129-140.

6. Weinberger DR (1987) Implications of normal brain development for the pathogenesis of schizophrenia. Arc General Psychiatry 44: 660-669.

7. Lawrie SM, Abukmeil SS (1998) Brain abnormality in schizophrenia: a systematic and quantitative review of volumetric magnetic resonance imaging studies. Br J Psychiatry 172: 110-120.

8. Mathalon DH, Sullivan EV, Lim Ki, et al. (2001) Progressive brain volume changes and the clinical course of schizophrenia in men: a longitudinal magnetic resonance imaging study. Arc General Psychiatry 58: 148-157.

9. Kapur S, Mizrahi R, Li M (2005) From dopamine to salience to psychosis: linking biology, pharmacology and phenomenology of psychosis. Schizophr Res 79: 59-68.

10. Palamino A, Vallejo-Illarramendi A (2006) Decreased levels of plasma BDNF in first-episode schizophrenia and bipolar patients. Schizophrenia Res 86: 321-322.

11. Buckley PF, Pillai A, Evans D, et al. (2007) Brain derived neurotrophic factor in first-episode psychosis. Schizophrenia Res 91: 1-5.

12. Grillo RW, Ottonin GL, Leke R, et al. (2007) Reduced serum BDNF levels in schizophrenic patients on clozapine or typical antipsychotics. J Psychiatric Res 41: 31-35.

13. Gama CS, Andreazza AC, Kunz M, et al. (2007) Serum levels of brain-derived neurotrophic factor in patients with schizophrenia and bipolar disorder. Neurosci Letter 42: 45-48.

14. Mei HX, Hui L, Dang YF, et al. (2009) Decreased serum BDNF levels in chronic institutionalized schizophrenia on long term treatment with typical and atypical antipsychotics. Progress Neuropsychopharma Biol Psychiatry 33: 1508-1512.

15. Zhang XY, Tan YL, Zhou DF, et al. (2007) Serum BDNF levels and weight gain in schizophrenic patients on long-term treatment with antipsychotics. J Psychiatric Res 41: 997-1004.

16. Tan YL, Zhou DF, Cao LY, et al. (2005) Decreased BDNF in serum of patients with chronic schizophrenia on long-term treatment with antipsychotics. Neurosci Letter 382: 27-32.

17. Ikeda Y, Yahata N, Ito I, et al. (2008) Low serum levels of brain-derived neurotrophic factor and epidermal growth factors in patients with chronic schizophrenia. Schizophrenia Res 101: 58-66.

18. Toyooka K, Asama K, Watanabe K, et al. (2002) Decreased levels of brain-derived neurotrophic factor in serum of chronic schizophrenic patients. Psychiatry Res 110: 249-257.

19. Rizos EN, Rontos I, Laskos E, et al. (2008) Investigation of serum BDNF levels in drug-naïve patients with schizophrenia. Progress Neuropsychopharma Biol Psychiatry 32: 1308-1311.

20. Huang TL, Lee CT (2006) Associations between serum brain-derived neurotrophic factor levels and clinical phenotypes in schizophrenia patients. J Psychiatric Res 40: 664-668.

21. Shimizu E, Hashimoto K, Watanabe H, et al. (2003) Serum BDNF levels in schizophrenia are indistinguishable from controls. Neurosci Letters 351: 111-114.

22. Pirildar S, Gönül AS, Taneli F, et al. (2004) Low serum levels of brain-deived neurotrophic factor in patients with schizophrenia do not elevate after antipsychotic treatment. Progress Neuropsychopharma Biol Psychiatry 28: 708-713.

23. Jockers-Scherübl MC, Danker-Hopfe H, Mahlberg R, et al. (2004) Brain-derived neurotrophic factor serum concentrations are increased in drug-naïve schizophrenic patients with chronic cannabis abuse and multiple substance abuse. Neurosci Letters 1: 79-83.

24. Kuo FC, Lee CH, Hsieh CH, et al. (2012) Lifestyle modification and behavior therapy effectively reduce body weight and increase serum level of brain-derived neurotrophic factor in obese non-diabetic patients with schizophrenia. Psychiatry Res 6.

25. Fatemi SH, Folsom TD (2009) The neurodevelopmental hypothesis of schizophrenia, revisited. Schizophrenia Bulletin 35: 528-548.

26. Van de Kerkhoff NW, Fekkesa D, van der Heijden FMMA, et al. (2014) BDNF an S100B in psychotic disorders: evidence for and association with treatment responsiveness. Acta Neuropsychiatry 4: 223-229.

27. Rizos E, Papathanasiou MA, Michalopolu PG, et al. (2014) A longitudinal study of alterations of hippocampal volumes and serum BDNF levels in association to atypical antipsychotics in a sample of first episode patients with schizophrenia. PLoS One 9: e87997.

28. Gonzalez-Pinto A, Mosquera F, Palomini A, et al. (2010) Increase in brain-derived neurotrophic factor in first-episode psychotic patients after treatment with atypical antipsychotics. Int Clin Psychopharmacology 4: 241-245.

29. Durany N, Michel T, Zochling R, et al. (2001) Brain-derived neurotrophic factor and neurotrophin 3 in schizophrenic psychoses. Schizophrenia Res 52: 79-86.

30. Green MJ, Matheson SL, Shepherd A, et al. (2011) Brain-derived neurotrophic factor levels in schizophrenia: a systematic review with meta-analysis. Mol Psychiatry 16: 960-972.

31. Walker MP, la Ferla F, Salvador S, et al. (2013) Reversible epigenetic histone modifications and BDNF expression in neurons with aging and from a mouse model of Alzheimer's disease. AGE 35: 519-531.

Copyright Info: © 2015, Ian M Rowbotham, et al., licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution Licese (http://creativecommons.org/licenses/by/4.0)

Download full text in PDF

Export Citation

Article outline

Show full outline