Citation: Frank O. Bastian. Is Alzheimers Disease Infectious?Relative to the CJD Bacterial Infection Model of Neurodegeneration[J]. AIMS Neuroscience, 2015, 2(4): 240-258. doi: 10.3934/Neuroscience.2015.4.240
| [1] | Chris Cadonic, Benedict C. Albensi . Oscillations and NMDA Receptors: Their Interplay Create Memories. AIMS Neuroscience, 2014, 1(1): 52-64. doi: 10.3934/Neuroscience.2014.1.52 |
| [2] | Robert A. Moss, Jarrod Moss . The Role of Dynamic Columns in Explaining Gamma-band Synchronization and NMDA Receptors in Cognitive Functions. AIMS Neuroscience, 2014, 1(1): 65-88. doi: 10.3934/Neuroscience.2014.1.65 |
| [3] | Mazyar Zahir, Amir Rashidian, Mohsen Hoseini, Reyhaneh Akbarian, Mohsen Chamanara . Pharmacological evidence for the possible involvement of the NMDA receptor pathway in the anticonvulsant effect of tramadol in mice. AIMS Neuroscience, 2022, 9(4): 444-453. doi: 10.3934/Neuroscience.2022024 |
| [4] | Valentina Bashkatova, Athineos Philippu . Role of nitric oxide in psychostimulant-induced neurotoxicity. AIMS Neuroscience, 2019, 6(3): 191-203. doi: 10.3934/Neuroscience.2019.3.191 |
| [5] | Tevzadze Gigi, Zhuravliova Elene, Barbakadze Tamar, Shanshiashvili Lali, Dzneladze Davit, Nanobashvili Zaqaria, Lordkipanidze Tamar, Mikeladze David . Gut neurotoxin p-cresol induces differential expression of GLUN2B and GLUN2A subunits of the NMDA receptor in the hippocampus and nucleus accumbens in healthy and audiogenic seizure-prone rats. AIMS Neuroscience, 2020, 7(1): 30-42. doi: 10.3934/Neuroscience.2020003 |
| [6] | Martina Valencia, Odra Santander, Eloísa Torres, Natali Zamora, Fernanda Muñoz, Rodrigo Pascual . Environmental enrichment reverses cerebellar impairments caused by prenatal exposure to a synthetic glucocorticoid. AIMS Neuroscience, 2022, 9(3): 320-344. doi: 10.3934/Neuroscience.2022018 |
| [7] | Masatoshi Takita, Yumi Izawa-Sugaya . Neurocircuit differences between memory traces of persistent hypoactivity and freezing following fear conditioning among the amygdala, hippocampus, and prefrontal cortex. AIMS Neuroscience, 2021, 8(2): 195-211. doi: 10.3934/Neuroscience.2021010 |
| [8] | Suresh D Muthukumaraswamy . Introduction to AIMS Special Issue “How do Gamma Frequency Oscillations and NMDA Receptors Contribute to Normal and Dysfunctional Cognitive Performance”. AIMS Neuroscience, 2014, 1(2): 183-184. doi: 10.3934/Neuroscience.2014.2.183 |
| [9] | Robert A. Moss, Jarrod Moss . Commentary on the Pinotsis and Friston Neural Fields DCM and the Cadonic and Albensi Oscillations and NMDA Receptors Articles. AIMS Neuroscience, 2014, 1(2): 158-162. doi: 10.3934/Neuroscience.2014.2.158 |
| [10] | Fatemeh Aghighi, Mahmoud Salami, Sayyed Alireza Talaei . Effect of postnatal environmental enrichment on LTP induction in the CA1 area of hippocampus of prenatally traffic noise-stressed female rats. AIMS Neuroscience, 2023, 10(4): 269-281. doi: 10.3934/Neuroscience.2023021 |
SARS-CoV-2, as a novel coronavirus, was first identified by the Chinese authorities in Wuhan, Hubei Province of China, which has caused the pneumonia (COVID-19) outbreak in China and other countries [1,2]. Until 05 March 2020, it has spread to all provinces of the mainland China and led to a total of 80552 confirmed cases with 3042 deaths [3]. The number of the confirmed cases is still increasing and the restriction of work causes a tremendous hit on Chinese society and economic.
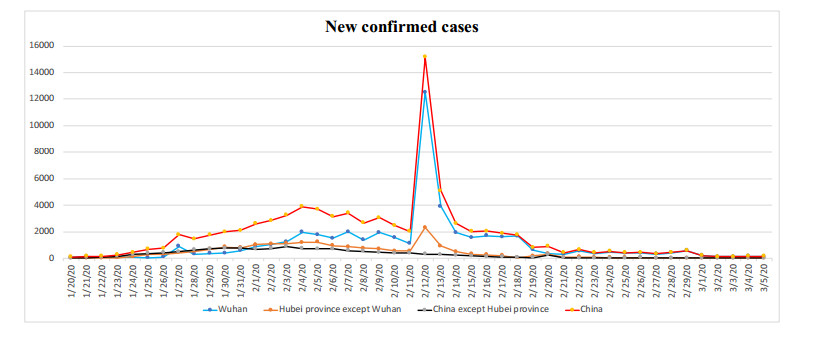
Since December 2019, a series of pneumonia cases emerged in Wuhan, Chinese public health authorities have taken very rapidly responsive strategies including active case finding, closing Huanan Seafood Wholesale Market, improving public awareness of self-protection measures and so on [4]. Despite all of those, the number of infection cases has been continuously increasing. Due to the quick increase in confirmed cases of COVID-19, the Chinese government revised the law to add COVID-19 as class B agent on 20 January 2020, and then Public health officials classified the novel virus as class A agent [5]. In order to prevent further spread of COVID-19 nationally and globally, the government of Wuhan carried out a lockdown at 10:00 on 23 January 2020 [6]. Some interventions, including intensive contact tracing followed by quarantine of individuals, isolation of infected individuals and travel restrictions have been implemented, while the number of new confirmed cases increased in Wuhan and other cities continuously (see Figure 1).
COVID-19 is difficult to diagnose, and a delay between the onset of symptoms and accurate diagnosis is frequently observed. It is worth noting that, except reported confirmed cases of pneumonia, there are still many undiagnosed and delayed-diagnosis infections due to lacks of diagnostic reagents for the virus and the long waiting time for diagnosis [7,8]. Considering the person-to-person transmission [9,10], the undiagnosed infections have the ability and possibility to transmit the virus to other public susceptible people or family members during their searching for or waiting for a diagnosable hospital, and hence increase the risk of spatial transmission and potential infection of COVID-19. The most important aspects are the ability to diagnose and identify the infected in time, and the treatment of the confirmed patients.
The impact of delay in diagnosis on the infectious diseases such as foot-and-mouth disease, mycobacterium tuberculosis and African viral hemorrhagic fever has been extensively studied [11,12,13]. Those studies indicate that delay in diagnosis could increase both infections and economical loss. In particular, for Ebola, the rapid diagnostic tests and early detection of Ebola could allow early triaging of patients, thereby reduce the potential for nosocomial transmission and epidemic size [14,15,16]. In addition, the delay in diagnosis is closely associated with the substantially case fatality. Therefore, assessing the effect of delay in diagnosis is of crucial importance for the transmission and control of COVID-19.
Mathematical modeling studies on COVID-19 focused on the prediction of confirmed cases of the novel coronavirus pneumonia in Wuhan and other cities[17,19,20,21], the estimation of basic reproduction number ($ R_0 $) based on the data of reported confirmed cases[17,18,22,23], the estimation of the unreported number of COVID-19 cases in China in the first stage of the outbreak [24], and also the potential risks of disease spreading [25,26]. Some authors [27,28] evaluated effects of the Wuhan travel restrictions or lock-down of the city in response to the novel coronavirus outbreak. However, the effect of delay in diagnosis on the dynamic evolution of COVID-19 has not been studied yet.
The principal purpose of this study is to present a dynamical model for transmission dynamics of COVID-19 and to evaluate the effect of delay in diagnosis on epidemic trend and characteristics of COVID-19. The main findings shed new insight on the disease interventions and control.
The data of confirmed COVID-19 cases in mainland China was collected from the National Health Commission of the People's Republic of China [5]. Data information includes the cumulative number of confirmed cases and the new number of confirmed cases, shown in Tables 1 and 2. The number of cumulative confirmed cases remained at 41 from 1 to 15 January 2020 according to the official report, i.e., no new case was reported during these 15 days, which appears inconsistent with the following rapid growth of the epidemic since 16 January 2020. The data set from 15 January to 02 February 2020 is used for model calibration, while the data set from 03 February to 05 March 2020 is applied for model validation.
| Date(day/month) | 15 Jan | 16 Jan | 17 Jan | 18 Jan | 19 Jan | 20 Jan | 21 Jan |
| Cumulative cases | 41 | 45 | 62 | 121 | 224 | 291 | 440 |
| New cases | 0 | 4 | 17 | 59 | 78 | 77 | 149 |
| Date(day/month) | 22 Jan | 23 Jan | 24 Jan | 25 Jan | 26 Jan | 27 Jan | 28 Jan |
| Cumulative cases | 571 | 830 | 1287 | 1975 | 2744 | 4515 | 5974 |
| New cases | 131 | 259 | 444 | 688 | 769 | 1771 | 1459 |
| Date(day/month) | 29 Jan | 30 Jan | 31 Jan | 01 Feb | 02 Feb | ||
| Cumulative cases | 7711 | 9692 | 11791 | 14380 | 17205 | ||
| New cases | 1737 | 1982 | 2102 | 2590 | 2829 |
DownLoad:
CSV
| Date(day/month) | 03 Feb | 04 Feb | 05 Feb | 06 Feb | 07 Feb | 08 Feb | 09 Feb |
| Cumulative cases | 20438 | 24324 | 28018 | 31161 | 34546 | 37198 | 40171 |
| New cases | 3235 | 3887 | 3694 | 3143 | 3399 | 2656 | 3062 |
| Date(day/month) | 10 Feb | 11 Feb | 12 Feb | 13 Feb | 14 Feb | 15 Feb | 16 Feb |
| Cumulative cases | 42638 | 44653 | 59804 | 63851 | 66492 | 68501 | 70549 |
| New cases | 2478 | 2015 | 15152 | 5090 | 2641 | 2009 | 2048 |
| Date(day/month) | 17 Feb | 18 Feb | 19 Feb | 20 Feb | 21 Feb | 22 Feb | 23 Feb |
| Cumulative cases | 72436 | 74185 | 74579 | 75456 | 76288 | 76936 | 77150 |
| New cases | 1886 | 1749 | 820 | 889 | 397 | 648 | 409 |
| Date(day/month) | 24 Feb | 25 Feb | 26 Feb | 27 Feb | 28 Feb | 29 Feb | 01 Mar |
| Cumulative cases | 77658 | 78604 | 78497 | 78824 | 79251 | 79824 | 80026 |
| New cases | 508 | 406 | 443 | 327 | 427 | 573 | 202 |
| Date(day/month) | 02 Mar | 03 Mar | 04 Mar | 05 Mar | |||
| Cumulative cases | 80151 | 80270 | 80409 | 80552 | |||
| New cases | 125 | 119 | 139 | 143 | |||
DownLoad:
CSV
According to the clinical progression of COVID-19 and epidemiological status of individuals, we establish a compartmental model of SEIR type, where delay in diagnosis is considered. Assume that the infected individuals are in two different situations, some are in resource-rich setting and can be diagnosed in time while others are in resource-poor setting and can not be timely diagnosed with a longer diagnostic waiting time. Everyone in the population is susceptible. All the infected individuals will be admitted into hospitals as soon as they are diagnosed.
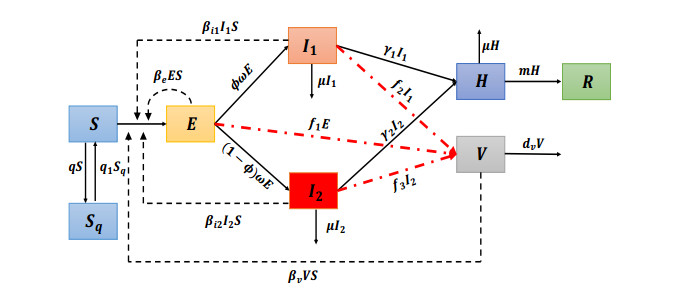
The population is divided into susceptible ($ S $), self-quarantine susceptible ($ S_q $), exposed ($ E $), infectious with timely diagnosis ($ I_1 $), infectious with delayed diagnosis ($ I_2 $), hospitalized ($ H $) and recovered ($ R $). $ V $ denotes the virus in the environment. A schematic description of the model is depicted in Figure 2.
The susceptible individuals can move to the compartment $ S_q $ at rate $ q $ by staying at home for quarantine. The self-quarantined individuals are released from quarantine and become susceptible again at rate $ q_1 $. The susceptible individuals are infected via contact with exposed individuals, infectious individuals, and also virus. All the newly SARS-CoV-2-infected individuals are assumed to be asymptomatic but are capable of infecting the susceptible (move into $ E $). The exposed individuals become infectious (symptomatic) after incubation period $ 1/\omega $. In reality, only a proportion $ \phi $ of symptomatic patients could be diagnosed in time, while the rest may be delayed to be diagnosed due to limited hospital or diagnostic resources. Then the infectious with timely diagnosis $ I_1 $ are decreased after $ 1/\gamma_1 $ days as soon as they are diagnosed (move into $ H $). The infectious with delayed diagnosis $ I_2 $ are diagnosed and hospitalized after $ 1/\gamma_2 $ days, where $ 1/\gamma_1 < 1/\gamma_2 $. The hospitalized individuals are decreased at recovery rate $ m $. All infections ($ I_1 $, $ I_2 $, $ H $) are decreased by diseased-induced death rate $ \mu $. The virus in the environment comes from both the exposed and the infectious at rate $ f_i $ ($ i = 1, 2, 3 $) and it is cleared at rate $ d_v $. The transfer diagram in Figure 2 leads to
|
$ {dSdt=−(βeE+βi1I1+βi2I2+βvV)S−qS+q1Sq,dSqdt=qS−q1Sq,dEdt=(βeE+βi1I1+βi2I2+βvV)S−ωE,dI1dt=ϕωE−γ1I1−μI1,dI2dt=(1−ϕ)ωE−γ2I2−μI2,dHdt=γ1I1+γ2I2−mH−μH,dRdt=mH,dVdt=f1E+f2I1+f3I2−dvV, $
|
(2.1) |
where $ \beta_{e} $, $ \beta_{i1} $, $ \beta_{i2} $, and $ \beta_v $ denote the transmission rates from the exposed, infectious with or without timely diagnosis, and virus in the environment to the susceptible, respectively. $ f_i $, $ i = 1, 2, 3 $ is the virus released rate via the exposed and the infectious. Here all parameters are assumed to be positive and their biological significance, default values, and reference resources are summarized in Table 3.
| Parameter | Description | Value (Range) | Unit | Source |
| $ q $ | Self-quarantined rate of the susceptible | $ 1/10 $ | day$ ^{-1} $ | Estimated |
| $ q_1 $ | Transition rate of self-quarantined individuals to the susceptible | $ 1/200000 $ | day$ ^{-1} $ | Estimated |
| $ \beta_e $ | Transmission rate from the exposed to the susceptible | $ 3.511\times 10^{-8} $ $ (10^{-8}, 10^{-7}) $ | day$ ^{-1} $ | Estimated |
| $ \beta_{i1} $ | Transmission rate from the infectious with timely diagnosis to the susceptible | $ 3.112 \times 10^{-8} $ $ (0.91*10^{-8}, 10^{-7}) $ | day$ ^{-1} $ | Estimated |
| $ \beta_{i2} $ | Transmission rate from the infectious with delayed diagnosis to the susceptible | $ 1.098 \times 10^{-7} $ $ (1.1*10^{-8}, 3*10^{-7}) $ | day$ ^{-1} $ | Estimated |
| $ \beta_v $ | Transmission rate from the susceptible to the exposed (infected by virus) | $ 1.009 \times 10^{-10} $ $ (10^{-11}, 9*10^{-10}) $ | day$ ^{-1} $ | Estimated |
| $ 1/\omega $ | Incubation period | $ 5.2 $ | day | [10] |
| $ \phi $ | Proportion of the infectious with timely diagnosis | $ 0.4\; (0.3, 0.65) $ | – | Estimated |
| $ 1/\gamma_1 $ | Waiting time of the infectious for timely diagnosis | $ 2.9\; (1, 5) $ | day | [29] |
| $ 1/\gamma_2 $ | Waiting time of the infectious for delayed diagnosis | $ 10 $ $ (5, 20) $ | day | Estimated |
| $ \mu $ | Disease-induced death rate | $ 1.7826 \times 10^{-5} $ | day$ ^{-1} $ | [17] |
| $ m $ | Recovery rate of the hospitalized | 1/14 | day$ ^{-1} $ | [9] |
| $ f_1 $ | Virus released rate of the exposed | $ 1440 $ $ (864, 2160) $ | day$ ^{-1} $ | Estimated |
| $ f_2 $ | Virus released rate of the infectious with timely-diagnosis | $ 1008 $ $ (432, 1440) $ | day$ ^{-1} $ | Estimated |
| $ f_3 $ | Virus released rate of the infectious with delayed-diagnosis | $ 1728 $ $ (864, 2592) $ | day$ ^{-1} $ | Estimated |
| $ d_v $ | Clear rate of virus in the environment | $ 144 $ $ (115.2, 172.8) $ | day$ ^{-1} $ | Estimated |
| $ S(0) $ | Initial value of the susceptible | $ 11081000 $ | – | [30] |
| $ S_q(0) $ | Initial value of the self-quarantined susceptible | $ 159 $ | – | Estimated |
| $ E(0) $ | Initial value of the exposed | $ 399 $ | – | [5] |
| $ I_1(0) $ | Initial value of the infectious with timely diagnosis | $ 28 $ | – | Estimated |
| $ I_2(0) $ | Initial value of the infectious with delayed diagnosis | $ 54 $ | – | Estimated |
| $ H(0) $ | Initial value of the hospitalized | $ 41 $ | – | [5] |
| $ R(0) $ | Initial value of the recovered | $ 12 $ | – | [5] |
| $ V(0) $ | Initial value of virus in the environment | $ 21080 $ | – | Estimated |
DownLoad:
CSV
We use the least-square method to carry out the parameter estimation, which is implemented by the command fmincon, a part of the optimization toolbox in MATLAB. The least-square estimation is to find the parameter values to minimize the following objective function
|
$ f(Θ,n)=n∑j=1(I(t)−ˆI(t))2, $
|
where $ \Theta $ is a parameter vector to be estimated, $ n $ is the number of reported data, $ \hat{I}(t) $ is the actual reported confirmed cases, and $ I(t) $ is the theoretical confirmed at day $ t $. The dynamics of $ I(t) $ is governed by
|
$ dI(t)dt=γ1I1+γ2I2, $
|
where $ I_1 $ and $ I_2 $ are determined by model (2.1).
From the data of confirmed cases in mainland China and in Wuhan, we set 15 January 2020 as the initial time. Since the COVID-19 infectious cases before 15 January 2020 were all in Wuhan, we set the population size of Wuhan as the initial value of the susceptible, i.e., $ S(0) = 11081000 $. On 15 January, 41 cases were confirmed and hospitalized, then $ H(0) = 41 $; $ 12 $ cases were recovered, hence $ R(0) = 12 $. We set $ E(0) = 399 $ because the suspected cases on 15 January 2020 is 399. The incubation period of COVID-19 is estimated to be 5.2 [10], hence $ \omega = 1/5.2 $. The average waiting time of the infectious with timely diagnosis is $ 2.9 $ day [29], thus $ \gamma_1 = 1/2.9 $. It is reported that the infectious individuals can recover within two weeks [30], thus the recovery rate $ m $ is $ 1/14 $.
We use the method in §2.3 to estimate parameter values by fitting model with the data of confirmed cases of COVID-19 (see Table 1). The fitting results of model (2.1) with the confirmed cases are given in Figure 3 and the estimated parameter values are listed in Table 3.
With the increase of the medical supply and reasonable allocation of medical resources, the resources-dependent parameters $ \phi $, $ \gamma_1 $ and $ \gamma_2 $ increase with respect to time $ t $ and the correlation of those parameters with $ t $ are estimated as $ \phi = 0.4+0.6t/(t+3) $, $ 1/\gamma_1 = 2.9-0.9t/(t+5) $ and $ 1/\gamma_2 = 10-7t/(t+5) $. From Table 3, it is observed that, among the transmission rates ($ \beta_{i1} $, $ \beta_{i2} $, $ \beta_e $, $ \beta_v $), the transmission rate $ \beta_{i2} $ of the infectious with delayed diagnosis is the biggest. It indicates that the infectious with delayed diagnosis plays a critical role in the spread of COVID-19. Although the transmission rate $ \beta_v $ is much smaller than the other threes, it may ignite the spread of COVID-19. Even if there are no exposed or infectious individuals, the susceptible could be infected by accidental contacts with virus in environment.
Moreover, Figure 3 shows the fitting results of model (2.1) with the reported data of confirmed cases. It is seen that our model prediction shows a similar trend to the reported data of both the new confirmed cases and cumulative confirmed cases. In particular, if the efficiency of diagnosis keeps increasing as $ \phi = 0.4+0.6t/(t+3) $, $ 1/\gamma_1 = 2.9-0.9t/(t+5) $ and $ 1/\gamma_2 = 10-7t/(t+5) $, the predicted values of cumulative confirmed cases will increase further and provide very good fit with the reported data of cumulative confirmed cases. From Figure 3(a), it is observed that, from 06 to 13 February, the prediction of model (2.1) somewhat deviates from the reported data of new confirmed cases. The possible reason is that the diagnosed-efficiency parameters $ \phi $, $ \gamma_1 $ and $ \gamma_2 $ in the model keep increasing with time $ t $ continuously, while in the real-world application, the medical supply and medical resources increased intermittently. The intermittent increase of medical resources makes the actual diagnosis efficiency being different from the model estimation. In addition, from 12 February, the clinically diagnosed cases were statistically seen as the new confirmed cases in Hubei province, and the inclusion of those cases drives the surge in the number of new confirmed on 12 and 13 February. Model (2.1) makes a good prediction of the new confirmed cases from 14 February to 05 March 2020.
The basic reproductive number $ R_0 $ is a measure of the potential for an infectious disease to spread through an immunologically naive population. It is defined as the average number of secondary cases generated by a single infectious case in a completely susceptible population. Based on (2.1), by the next generation matrix method [31], the basic reproduction number reads
|
$ R0=S0[βeω+βi1ϕγ1+μ+βi2(1−ϕ)γ2+μ+βv(f1(γ1+μ)(γ2+μ)+f2ϕω(γ2+μ)+f3(1−ϕ)ω(γ1+μ))dv(γ1+μ)(γ2+μ)ω], $
|
(3.1) |
where $ S_0 $ is the initial value of the susceptible.
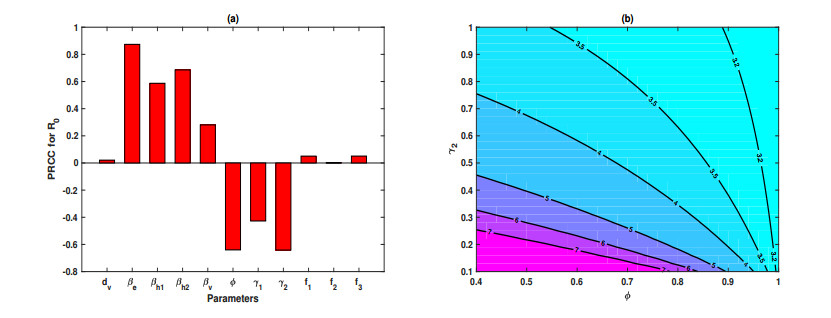
The basic reproduction number $ R_0 $ is a significant indicator in both transmission risks and control of an infectious disease. In order to provide a comprehensive understanding of the influence of different input parameters and their variations on the model outcomes, and to characterize the most important parameters, the sensitivity analysis is conducted by obtaining the partial rank correlation coefficients (PRCCs) [32] for various parameters against $ R_0 $.
The parameters considered in the sensitive analysis include transmission rates ($ \beta_e $, $ \beta_{i1} $, $ \beta_{i2} $, $ \beta_v $), factors related to the diagnosis efforts ($ \gamma_1 $, $ \gamma_2 $, $ \phi $), virus released rates ($ f_1 $, $ f_2 $, $ f_3 $) and clear rate of virus ($ d_v $). Figure 4 (a) illustrates the PRCCs of $ R_0 $ with respect to model parameters. It suggests that $ R_0 $ is more sensitive to $ \beta_e $, $ \beta_{i2} $, $ \beta_{i1} $ and $ \beta_v $ in order among the transmission rates. That is to say, the exposed and the infectious with delayed diagnosis contribute more to the transmission and spread of COVID-19, compared with the infectious with timely diagnosis and virus. In addition, the PRCCs values of $ \gamma_1 $, $ \gamma_2 $, and $ \phi $ are also big. From Figure 4(b), the increase of $ \phi $ and $ \gamma_2 $ can significantly reduce the value of $ R_0 $, which verifies that delay in diagnosis plays a critical role in the transmission of COVID-19. Therefore, the richness and distribution of medical resources and the early timely diagnosis are also very important for the prevention and control of COVID-19.
In order to further explore the possible impact of enhanced diagnosis efficiency and resources richness on the disease transmission, we plot the predicted new confirmed cases ($ \gamma_1 I_1(t)+\gamma_2 I_2(t) $) and new infections ($ I_1(t)+I_2(t) $) with respect to the proportion of the infectious with timely diagnosis $ \phi $ and delayed diagnosed rate $ \gamma_2 $.
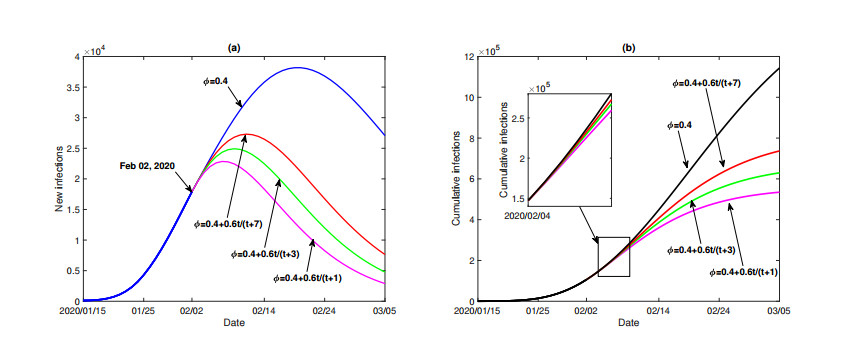
In reality, resources such as abundant diagnostic test kits, diagnosable hospitals, and available beds have been supplied to support the diagnosis and treatment of COVID-19 since 02 February, the proportion $ \phi $ of the infectious with timely diagnosis is gradually improved as time goes on due to the increasing supply of diagnostic resources. We set $ \phi = \phi_0+(1-\phi_0)t/(t+a) $, where $ \phi_0 $ (its estimated value is $ 0.4 $ listed in Table 3) is the basic proportion and $ a $ represents the time when the proportion improves to $ (1+\phi_0)/2 $.
Figure 5 depicts the effect of the proportion $ \phi $ of the infectious with timely diagnosis on the number of confirmed cases. With the increasing of $ \phi $, the number of new confirmed cases increases first and then decreases, while the number of cumulative confirmed cases always decreases; the peak value of the new confirmed cases decreases and the peak time of the new confirmed cases arrives much earlier. Specifically, compared with the baseline scenario with $ \phi = 0.4 $, when $ \phi $ is increased to $ 0.7 $ in one week ($ \phi = 0.4+0.6t/(t+7) $), three days ($ \phi = 0.4+0.6t/(t+3) $), or one day ($ \phi = 0.4+0.6t/(t+1) $), then the peak time of new confirmed cases arrives $ 5 $ days, $ 7 $ days, or $ 8.5 $ days earlier, the peak value of new confirmed cases decreases by $ 33.4\% $, $ 37.8\% $, or $ 42.5\% $, and the number of cumulative confirmed cases decreases by $ 14.7\% $, $ 21.3\% $, or $ 28.2\% $ on 05 March 2020, respectively. Similarly, the increasing of $ \phi $ leads to the decrease of both new infections (include confirmed cases and potential infections) and cumulative infections (see Figure 6). In particular, compared with the basic scenario with $ \phi = 0.4 $, the number of new infection and cumulative infection with $ \phi = 0.4+0.6t/(t+1) $ decreases by $ 88.8\% $ and $ 51.6\% $ on 05 March 2020, respectively. In summary, increasing $ \phi $ can significantly shorten the peak time and reduce the peak value of new confirmed cases and new infections, then reduce the cumulative number of confirmed cases and total infections (Figures 5 and 6).
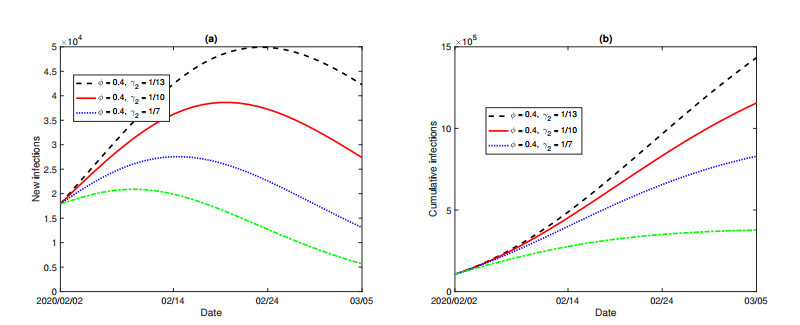
In resource-poor setting, the infectious individuals have to wait for longer time for diagnosis due to limited amount of diagnostic equipments and low diagnostic efficiency of the test kits etc. The waiting time for delayed diagnosis is critical for disease transmission and control. Note that the estimated value of delayed diagnosis rate $ \gamma_2 $ is $ 1/10 $, we consider $ 1/\gamma_2 = 10 $ (days) as the baseline scenario. Next, we investigate the effect of the waiting time for delayed diagnosis on the new and cumulative infection. In Figure 7, compared with the baseline scenario, when the waiting time for delayed diagnosis is extended by $ 3 $ days (i.e., $ 1/\gamma_2 = 13 $) since 02 February, the number of new infected individuals on 05 March 2020 increases by $ 52.1\% $, while if the waiting time for delayed diagnosis is shorten by $ 3 $ days ($ 1/\gamma_2 = 7 $) or by $ 7 $ days ($ 1/\gamma_2 = 3 $), the number of new infections reduces by $ 51.0\% $ or $ 78.2\% $ on 05 March 2020, respectively. Moreover, the number of cumulative infections on 05 March 2020 will decrease drastically (by $ 66.7\% $) if all the infectious can be diagnosed within three days of onset ($ 1/\gamma_2 = 3 $ and $ 1/\gamma_1 = 2.9 $). In summary, increasing $ \gamma_2 $ shortens the peak time, decreases the peak value of new infections, and reduces the number of cumulative infections.
In this study, based on the reported data of COVID-19 in mainland China, a compartmental dynamic model of SEIR type is formulated to investigate the effect of delay in diagnosis on the transmission and spread of COVID-19. Sensitive analysis evaluates the PRCCs for various parameters against $ R_0 $, which together with the contour plot, reveals that the proportion $ \phi $ of the infectious with timely diagnosis and the delayed diagnosis rate $ \gamma_2 $ are of considerable importance for the control of COVID-19. Numerical simulations prove that increasing $ \phi $ (i.e., improve the richness of diagnostic resources) and $ \gamma_2 $ (i.e., improve the diagnosis efficiency) can shorten the peak time, reduce the peak value of new confirmed cases and new infection, the cumulative number of confirmed cases and total infection, and hence can significantly reduce the transmission risk and further infections of COVID-19. Therefore, the resources supply and diagnosis efficiency are essential for an early diagnosis and timely and definitive treatment.
Note that, with the increasing of $ \phi $, the number of new confirmed cases increases first and then decreases, as shown in Figure 5(a). This finding is consistent with the scenario in Wuhan and Hubei province (Figure 1). During the early stage of COVID-19 in Wuhan and Hubei province, the insufficiency and unbalanced distribution of diagnostic resources (e.g., lack of diagnosable hospital, available beds, diagnostic test kits, diagnostic equipments and low diagnostic efficiency of the test kits etc) caused a delay in the diagnosis and an increased mortality. So that COVID-19 incidence and prevalence are increasing very quickly.
As a matter of fact, extraordinary efforts have been made by national and provincial governments of China, especially in Hubei province and Wuhan. 'Compartment hospitals' have been built to treat mild cases, and nationwide support such as plenty of healthcare staff and treatment equipments has been employed to treat more infections in Wuhan since 02 February 2020. As of 03 February, the novel coronavirus nucleic acid testing capability of Wuhan have increased to 4196 samples per day from an initial 200 samples. On 08 February 2020, the National Health Commission of the People's Republic of China issued the fifth edition of the Diagnosis and Treatment Plan for the Coronavirus, which adds CT and clinical standards to provide evidence for diagnosis and treatment. So that the COVID-19 patients can receive timely diagnosis and early standardized treatment as soon as possible and the diagnosis efficiency is quickly improved. The timely diagnosis and treatment of patients are greatly speeded up in Wuhan. As of 13 February, a total of ten 'compartment hospitals' with 6960 beds have been available and about 5600 patients have been admitted. As a result, the number of new confirmed cases in Wuhan increased sharply on 12 February and then showed a decline since February 13 (Figure 1), the evolution trend is consistent with the fitting result in Figure 3 (a).
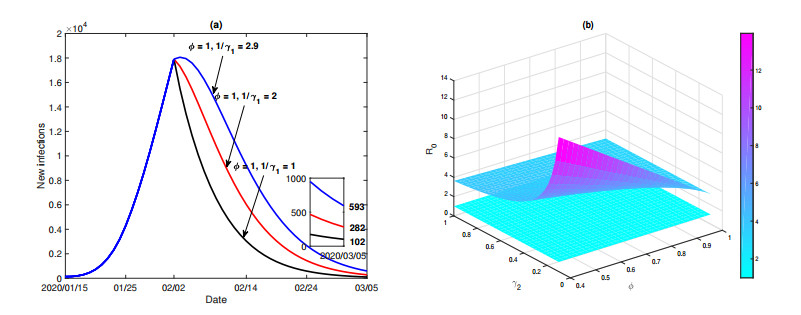
A precise and early diagnosis/treatment is highly important in COVID-19. As mentioned above, it is effective to reduce the transmission risk by reducing the waiting time and increasing the proportion of infections with timely diagnosis, and hence can facilitate the prevention and control of COVID-19. However, only the early diagnosis and effective treatment can not eliminate COVID-19. Figure 8(a) depicts that the new confirmed cases remain at some positive level even if all the infective individuals can be timely diagnosed as soon as possible. Figure 8(b) shows that, the basic reproduction number $ R_0 $ sharply decreases with the increasing of $ \phi $ and $ \gamma_2 $, but $ R_0 $ can not decrease to the level less than $ 1 $, $ R_0 $ is still $ 3.1021 > 1 $ and the new infection on 05 March 2020 is $ 102 $ even when $ \phi = 1 $, $ \gamma_1 = \gamma_2 = 1 $. From the web-news [33,34], Italy will adjust its policy that to do less samples so that they will not report so many cases to avoid public panic, Japanese Government said they will only focus on the treatment of serious patients, and they will limit the tests only for the samples that would meet the 'criteria'. Our findings warn that such ideas are very dangerous.
The prevention, control, diagnosis, and treatment are among the most crucial issues in COVID-19, they are highly integrated and can never be separated. The timely diagnosis and effective treatment can destock the capacity of the infected individuals and reduce nosocomial infection while the prevention and control can suppress the increment of new infection and hence reduce the burden in the hospitals. The principles for the prevention and control of infectious disease are to control the source of infection, to cut off the routes of transmission, and to protect susceptible individuals. A combining multiple measures must be simultaneously implemented. The most key and useful strategy and measures for the control of COVID-19 in China are to detect cases early, isolate every patients, trace every contacts, provide quality clinical care, prevent hospital outbreaks, prevent community transmission, avoid public panic and rumor, progress vaccines and therapeutics. In this light, it is important to thoroughly understand transmission dynamics and implement effective prevention and control programs as well as early diagnosis and timely treatment. It is crucial and important to establish a joint strategy involving prevention, control, and medical treatment. The strategy should be systematic, scientific, normative, and works perfectly.
This research was supported by National Natural Science Foundation of P. R. China (Nos. 11671072, 11271065).
The authors declare no conflict of interest.
| [1] |
Stoeck K, Schmitz M, Ebert E, et al. (2014) Immune responses in rapidly progressive dementia: a comparative study of neuroinflammatory markers in Creutzfeldt-Jakob disease, Alzheimer's disease and multiple sclerosis. J Neuroinflam 11: 170-178. doi: 10.1186/s12974-014-0170-y
|
| [2] | Kojima G, Tatsuno BK, Inaba M, et al. (2013) Creutzfeldt-Jakob disease: a case report and differential diagnosis. Hawai'i J Med Public Health 72: 136-139. |
| [3] |
Manuelidis EE, Manuelidis L (1989) A clinical series with 13% of Alzheimer's disease actually CJD. Alz Dis Assoc Disorders 3: 100-109. doi: 10.1097/00002093-198903010-00009
|
| [4] |
Bastian FO, McDermont ME, Perry AS, et al. (2005) Safe method for isolation of prion protein and diagnosis of Creutzfeldt-Jakob disease. J Virol Methods 130: 133-139. doi: 10.1016/j.jviromet.2005.06.024
|
| [5] |
Nicolson GI (2008) Chronic bacterial and viral infections in neurodegenerative and neurobehavioral diseases. Lab Med 39: 291-299. doi: 10.1309/96M3BWYP42L11BFU
|
| [6] | Bastian FO (1991) Author, Creutzfeldt-Jakob Disease and Other Transmissible Spongiform Encephalopathies, New York, Mosby/Year Book 256 pp |
| [7] |
Matthews WB (1978) Creutzfeldt-Jakob disease. Postgrad Med J 54: 591-594. doi: 10.1136/pgmj.54.635.591
|
| [8] |
Manuelidis EE, De Figuriredo JM, Kim JH, et al. (1988) Transmission studies from blood of Azheimer disease patients and healthy relatives. Proc Natl Acad Sci (USA) 85: 4898-4901. doi: 10.1073/pnas.85.13.4898
|
| [9] | Manuelidis EE, Gorgacz EJ, Manuelidis L (1978) Transmission of Creutzfeldt-Jakob disease with scrapie-like syndromes to mice. Nature 271: 778-779. |
| [10] |
Hainfellner JA, Wanschitz J, Jellinger K, et al. (1998) Coexistence of Alzheimer-type neuropathology in Creutzfeldt_Jakob disease. Acta Neuropathol 96: 116-122. doi: 10.1007/s004010050870
|
| [11] | Solito E, Sastre M (2012) Microglia function in Alzheimer's disease. Frontiers Pharmacol 3: 1-10. |
| [12] | Tousseyn T, Bajsarowicz K, Sanchez H, et al. (2015) Prion disease induces Alzheimer disease-like neuropathologic changes. J Neuropathol Exp Neurol 74: 873-888. |
| [13] |
Dheen ST, Kaur C, Ling EA (2007) Microglial activation and its implications in the brain diseases. Current Med Chem 14: 1189-1197. doi: 10.2174/092986707780597961
|
| [14] |
Mattson MP (2002) Oxidative stress, perturbed calcium homeostasis, and immune dysfunction in Alzheimer's disease. J Neurovirol 8: 539-550. doi: 10.1080/13550280290100978
|
| [15] |
Garcao P, Oliveira CR, Agostinho P (2006) Comparative study of microglia activation induced by amyloid-β and prion peptides. J Neurosci Res 84: 182-193. doi: 10.1002/jnr.20870
|
| [16] | Lee DY, Lee J, Sugden B (2009) The unfolded protein response and autophagy: herpes viruses rule! J Virol 83: 1168-1172. |
| [17] |
Unterberger U, Hoftberger R, Gelpi E, et al. (2006) Endoplasmic reticulum stress features are prominent in Alzheimer's disease but not in prion disease in vivo. J Neuropathol Exp Neurol 65: 348-357. doi: 10.1097/01.jnen.0000218445.30535.6f
|
| [18] | Sorce S, Nuvolone M, Keller A, et al. (2014) The role of NADPH oxidase NOX2 in prion pathogenesis. PLoS Pathogens 10: e1004531. |
| [19] | Bastian FO (2014) Cross-roads in research on neurodegenerative diseases. J Alzheimer's Dis Parkinsonism 4: 141. doi:10.4172/21610460.1000141. |
| [20] | Moreno JA, Radford H, Peretti D, et al. (2012) Sustained translational repression of eIF2α mediates prion neurodegeneration. Nature 485: 507-511. |
| [21] |
Greenlee JJ, Greenlee MH (2015) The transmissible spongiform encephalopathies of livestock. Ilar J 56: 7-25. doi: 10.1093/ilar/ilv008
|
| [22] |
Baker CA, Martin D, Manuelidis L (2002) Microglia from Creutzfeldt-Jakob disease-infected brains are infectious and show specific mRNA activation profiles. J Virol 76: 10905-10913. doi: 10.1128/JVI.76.21.10905-10913.2002
|
| [23] |
Murali A, Maue RA, Dolph PJ (2014) Reversible symptoms and clearance of mutant prion protein in an inducible model of a genetic prion disease in Drosophilia melanogaster. Neurobiol Dis 67: 71-78. doi: 10.1016/j.nbd.2014.03.013
|
| [24] |
Sala I, Marquie M, Sanchez-Saudinos MB, et al. (2012) Rapidy progressive dementia: experience in a tertiary care medical center. Alzheimer Dis Assoc Disorders 26: 267-271. doi: 10.1097/WAD.0b013e3182368ed4
|
| [25] |
Armitage WJ, Tullo AB, Ironside JW (2009) Risk of Creutzfeldt-Jakob disease transmission by ocular surgery and tissue transplantation. Eye 23: 1926-1930. doi: 10.1038/eye.2008.381
|
| [26] |
Wemheuer WM, Benestad SL, Wrede A, et al. (2009) Similarities between forms of sheep scrapie and Creutzfeldt-Jakob disease are encoded by distinct prion types. Amer J Pathol 175: 2566-2573. doi: 10.2353/ajpath.2009.090623
|
| [27] | Cassard H, Torres JM, Lacroux C, et al. (2014) Evidence for zoonotic potential of ovine scrapie prions. Nature communications 5: 5821 doi:10.1038/ncomms6821. |
| [28] | Merz PA, Somerville RA, Wisniewski HM, et al. (1983) Scrapie-associated fibrils in Creutzfeldt-Jakob disease. Nature 306: 474-476. |
| [29] |
Wisniewski T, Aucouturier P, Soto C, et al. (1998) The prionoses and other conformational disorders. Amyloid 5: 212-224. doi: 10.3109/13506129809003848
|
| [30] | Serrano-Pozo A, Frosch MP, Masliah E, et al. (2011) Neuropathological alterations in Alzheimer Disease. Cold Spring Harb Perspect Med 1: a006189. |
| [31] | Kessels HW, Nguyen LN, Nabavi S, et al. (2010) The prion protein as a receptor for amyloid-β. Nature 466: 7308 E3-4. |
| [32] |
Kumar A, Pate KM, Moss MA, et al. (2014) Self-propagative replication of A-β oligomers suggests potential transmissibility in Alzheimer disease. PLoS ONE 9: e111492. doi: 10.1371/journal.pone.0111492
|
| [33] | Guo JL, Lee VM (2011) Seeding of normal Tau by pathological Tau conformers drives pathogenesis of Alzheimer-like tangles. J Biol Chem 286: 15317-15331. |
| [34] |
Liu L, Drouet V, Wu JW, et al. (2012) Trans-synaptic spread of Tau pathology in vivo. PloS ONE 7: e31302. Doi:10.1371. doi: 10.1371/journal.pone.0031302
|
| [35] |
Eisele YS, Bolmont T, Heikenwalder M, et al. (2009) Induction of cerebral β-amyloidosis: intracerebral versus systemic Aβ inoculation. PNAS 106: 12926-12931. doi: 10.1073/pnas.0903200106
|
| [36] | Morales R, Duran-Aniotz C, Castilla J, et al. (2011) De novo induction of amyloid-β deposition in vivo. Mol Psychiatry 17: 1347-1353. |
| [37] |
Volpicelli-Daley LA, Luk KC, Patel TP, et al. (2011) Exogenous α-synuclein fibrils induce Lewy body pathology leading to synaptic dysfunction and neuron death. Neuron 72: 57-71. doi: 10.1016/j.neuron.2011.08.033
|
| [38] |
Luk KC, Kehm VM, Zhang B, et al. (2012) Intracerebral inoculation of pathological α-synuclein initiates a rapidly progressive neurodegenerative α-synucleinopathy in mice. J Exp Med 209: 975-986. doi: 10.1084/jem.20112457
|
| [39] | Stöhr J, Watts JC, Mensinger ZL, et al. Purified and synthetic Alzheimer's amyloid β (Aβ) prions. PNAS 109: 11025-11030. |
| [40] | Ghoshal N, Cali I, Perrin RJ, et al. (2009) Co-distribution of amyloid β plaques and spongiform degeneration in familial Creutzfeldt-Jakob disease with the E200K-129M haplotype. Arch Neurol 66: 1240-1246. |
| [41] |
Salvadores N, Shahnawaz M, Scarpini E, et al. (2014) Detection of misfolded Aβ oligonmers for sensitive biochemical diagnosis of Alzheimer's disease. Cell Reports 7: 261-268. doi: 10.1016/j.celrep.2014.02.031
|
| [42] |
Morales R, Moreno-Gonzalez I, Soto C (2013) Cross-seeding of misfolded proteins: implications for etiology and pathogenesis of protein misfolding diseases. PLOS 9: e1003537. doi: 10.1371/journal.pgen.1003537
|
| [43] |
Chi EY, Frey SL, Winans A, et al. (2010) Amyloid-β fibrillogenesis seeded by interface-induced peptide misfolding and self-assembly. Biophy J 98: 2299-2308. doi: 10.1016/j.bpj.2010.01.056
|
| [44] |
Tateishi J, Kitamoto T, Hoque MZ, et al. (1996) Experimental transmission of Creutzfeldt-Jakob disease and related diseases to rodents. Neurology 46: 532-537. doi: 10.1212/WNL.46.2.532
|
| [45] |
Kovacs GG, Seguin J, Quadrio I, et al. (2011) Genetic Creutzfeldt-Jakob disease associated with the E200K mutation: characterization of a complex proteinopathy. Acta Neuropathologica 121: 39-57. doi: 10.1007/s00401-010-0713-y
|
| [46] |
Vital A, Canron M-H, Gil R, et al. (2007) A sporadic case of Creutzfeldt-Jakob disease with β-amyloid deposits and α-synuclein inclusions. Neuropathology 27: 273-277. doi: 10.1111/j.1440-1789.2007.00755.x
|
| [47] | Kasai T, Tokuda T, Ishii R, et al. (2014) Increased α-synuclein levels in the cerebrospinal fluid of patients with Creutzfeldt–Jakob disease. J Neurol 261: 7334-7337. |
| [48] |
Zhang M, Hu R, Chen H, et al. (2015) Polymorphic cross-seeding amyloid assemblies of amyloid-β and human islet amyloid peptide. Phys Chem Chem Phys 17: 23245-23256. doi: 10.1039/C5CP03329B
|
| [49] |
O'Nuallain B, Williams AD, Westermark P, et al. (2004) Seeding specificity in amyloid growth induced by heterologous fibrils. J Biol Chem 279: 17490-17499. doi: 10.1074/jbc.M311300200
|
| [50] | Westermark P, Westermark GT (2013) Seeding and cross-seeding in amyloid diseases, in Zucker M, Christen Y (eds.) Proteopathic Seeds and Neurodegenerative Diseases, Research and Perspectives in Alzheimer' Disease, Berlin, Springer-Verlag pp. 47-60. |
| [51] |
Zhou Y, Smith D, Leong BJ, et al. (2012) Promiscuous cross-seeding between bacterial amyloids promotes interspecies biofilms. J Biol Chem 287: 35092-35103. doi: 10.1074/jbc.M112.383737
|
| [52] |
Prusiner SB (1987) Prions causing degenerative neurological diseases. Ann Rev Med 38: 381-398. doi: 10.1146/annurev.me.38.020187.002121
|
| [53] |
Vila-Vicosa D, Campos SR, Baptista AM, et al. (2012) Reversibility of prion misfolding: insights from constant –pH molecular dynamics simulations. J Physical Chem 116: 8812-8821. doi: 10.1021/jp3034837
|
| [54] |
Eisenberg D, Jucker M (2012) The amyloid state of proteins in human diseases. Cell 148: 1188-1203. doi: 10.1016/j.cell.2012.02.022
|
| [55] |
Mayer RJ, Landon M, Laszlo L, et al. (1992) Protein processing in lysosomes: the new therapeutic target in neurodegenerative disease. Lancet 340: 156-159. doi: 10.1016/0140-6736(92)93224-B
|
| [56] |
Rigter A, Priem J, Langeveld JP, et al. (2011) Prion protein self-interaction in prion disease therapy approaches. Vet Quarterly 31: 115-128. doi: 10.1080/01652176.2011.604976
|
| [57] |
Safar JG (2012) Molecular pathogenesis of sporadic prion diseases in man. Prion 6: 108-115. doi: 10.4161/pri.18666
|
| [58] |
Tuite MF, Cox BS (2003) Propagation of yeast prions. Nature Rev Mol Cell Biol 4: 878-890. doi: 10.1038/nrm1247
|
| [59] |
Bellinger-Kawahara C, Diener TO, McKinley MP, et al. (1987) Purified scrapie prions resist inactivation by procedures that hydrolyze, modify, or shear nucleic acids. Virology 160: 271-274. doi: 10.1016/0042-6822(87)90072-9
|
| [60] |
Hearst JE (1981) Psoralen photochemistry and nucleic acid structure. J Investigative Dermatol 77: 39-44. doi: 10.1111/1523-1747.ep12479229
|
| [61] | Miyazawa K, Kipkorir T, Tittman S, et al. (2012) Continuous production of prions after infectious particles are eliminated: implications for Alzheimer's disease. PLoS ONE 7: 1-8. |
| [62] | Sun R, Liu Y, Zhang H, et al. (2008) Quantitative recovery of scrapie agent with minimal protein from highly infectious cultures. Viral Immunol 21:293-302. |
| [63] |
Soto C, Estrada L, Castilla J (2006) Amyloids, prions and the inherent infectious nature of misfolded protein aggregates. Trends Biochem Sci 31: 150-155. doi: 10.1016/j.tibs.2006.01.002
|
| [64] |
Klingeborn M, Race B, Meade-White KD, et al. (2011) Lower specific infectivity of protease-resistant prion protein generated in cell-free reactions. PNAS 108: E1244-E1253. doi: 10.1073/pnas.1111255108
|
| [65] | Manuelidis L (2011) Nuclease resistant circular DNAs copurify with infectivity in scrapie and CJD. J Neurovirol 17: 131-145. |
| [66] | Sonati T, Reimann RR, Falsig J, et al. (2013) The toxicity of antiprion antibodies is mediated by the flexible tail of the prion protein. Nature 501: 102-106. |
| [67] |
Miyazawa K, Emmerling K, Manuelidis L (2011) Replication and spread of CJD, kuru and scrapie agents in vivo and in cell culture. Virulence 2: 188-199. doi: 10.4161/viru.2.3.15880
|
| [68] | Watarai M, Kim S, Erdenebaatar J, et al. (2003) Cellular prion protein promotes Brucella infection into macrophages. J Exp Med 198: 5-17. |
| [69] | Bastian FO (2005) Spiroplasma as a candidate causal agent of transmissible spongiform encephalopathies. J Neuropathol Exp Neurol 64: 833-838. |
| [70] | Bastian FO (2014) The case for involvement of spiroplasma in the pathogenesis of transmissible spongiform encephalopathies. J Neuropathol Exp Neurol 73: 104-114. |
| [71] | Baker C, Martin D, Manuelidis L (2002) Microglia from Creutzfeldt-Jakob disease-infected brains are infectious and show specific mRNA activation profiles. J Virol 76: 10905-10913. |
| [72] | Marlatt MW, Bauer J, Aronica E, et al. (2014) Proliferation in the Alzheimer hippocampus is due to microglia, not astroglia, and occurs at sites of amyloid deposition. Neural Plasticity 2014: 693851 1-12. |
| [73] |
Miklossy J, Kis A, Radenovic A, et al. (2006) Β-amyloid deposition and Alzheimer's type changes induced by Borrelia spirochetes. Neurobiol Aging 27: 228-236. doi: 10.1016/j.neurobiolaging.2005.01.018
|
| [74] | Balin BJ, Little CS, Hammond CJ, et al. (2008) Chlamydophila pneumonia and the etiology of late-onset Alzheimer's disease. J Alzheimer's Dis 13: 371-380. |
| [75] | Poole S, Singhrao SK, Kesavalu L, et al. (2013) Determining the presence of peridontopathic virulence factors in short-term postmortem Alzheimer's disease brain tissue. J Alzheimer's Dis 36: 665-677. |
| [76] | Singhrao SK, Harding A, Poole S, et al. (2015) Porphyromonas gingivalis periodontal infection and it putative links with Alzheimer's disease. Mediators Inflam 2015: 137357. |
| [77] | Singhrao SK, Harding A, Simmons T, et al. (2014) Oral inflammation, tooth loss, risk factors, and association with progression of Alzheimer's disease. J Alzheimer's Dis 42: 723-737. |
| [78] | Miklossy J (2008) Chronic inflammation and amyloidogenesis in Alzheimer's disease- role of spirochetes. J Alzheimer's Dis 13: 381-391. |
| [79] | Friedland RP (2015) Mechanisms of molecular mimicry involving the microbiota in neurodegeneration. J Alzheimer's Dis 45: 349-362. |
| [80] | Little CS, Joyce TA, Hammond CJ, et al. (2014) Detection of bacterial antigens and Alzheimer's disease-like pathology in the central nervous system of BALB/c mice following intranasal infection with a laboratory isolate of Chlamydia pneumoniae. Frontiers Aging Neurosci 6: 304. doi: 10.3389/fnagi.2014.00304 1-9. |
| [81] |
Goto S, Anbutsu H, Fukatsu T (2006) Asymmetrical interactions between Wolbachia and Spiroplasma endosymbionts coexisting in the same insect host. Applied Environmental Microbiol 72: 4805-4810. doi: 10.1128/AEM.00416-06
|
| [82] |
Takahashi Y, Mihara H (2004) Construction of chemically and conformationally self-replicating system of amyloid-like fibrils. Bioorg Med Chem 12: 693-699. doi: 10.1016/j.bmc.2003.11.022
|
| [83] | Barnhart MM, Chapman MR (2006) Curli biogenesis and function. Annu Rev Microbiol 60: 131-147. |
| [84] |
Wang X, Chapman MR (2008) Curli provide the template for understanding controlled amyloid propagation. Prion 2: 57-60. doi: 10.4161/pri.2.2.6746
|
| [85] |
Lundmark K, Westermark G, Olsen A, et al. (2005) Protein fibrils in nature can enhance amyloid protein A amyloidosis in mice: cross-seeding as a disease mechanism. PNAS 102: 6098-6102. doi: 10.1073/pnas.0501814102
|
| [86] | Bastian FO (1979) Spiroplasma-like inclusions in Creutzfeldt-Jakob disease. Arch Pathol Lab Med 103: 665-669. |
| [87] | Bastian FO, Hart MN, Cancilla PA (1981) Additional evidence of spiroplasma in Creutzfeldt-Jakob disease. Lancet 1: 660. |
| [88] | Gray A, Francis RJ, Scholtz CL (1980) Spiroplasma and Creutzfeldt-Jakob disease. Lancet 2, 660. |
| [89] |
Reyes JM, Hoenig EM (1981) Intracellular spiral inclusions in cerebral cell processes in Creutzfeldt-Jakob disease. J Neuropathol Exp Neurol 40: 1-8. doi: 10.1097/00005072-198101000-00001
|
| [90] |
Alexeeva I, Elliott EJ, Rollins S, et al. (2006) Absence of spiroplasma or other bacterial 16s rRNA genes in brain tissue of hamsters with scrapie. J Clin Microbiol 44: 91-97. doi: 10.1128/JCM.44.1.91-97.2006
|
| [91] |
Bastian FO, Dash S, Garry RF (2004) Linking chronic wasting disease to scrapie by comparison of Spiroplasma mirum ribosomal DNA sequences. Exp Mol Pathol 77: 49-56. doi: 10.1016/j.yexmp.2004.02.002
|
| [92] | Bastian FO, Sanders DE, Forbes WA, et al. (2007) Spiroplasma spp. from transmissible spongiform encephalopathy brains or ticks induce spongiform encephalopathy in ruminants. J Med Microbiol 56: 1235-1242. |
| [93] | Bastian FO, Boudreaux CM, Hagius SD, et al. (2011) Spiroplasma found in the eyes of scrapie affected sheep. Vet Ophthalmol 14: 10-17. |
| [94] | Bastian FO, Purnell DM, Tully JG (1984) Neuropathology of spiroplasma infection in the rat brain. Am J Pathol 114: 496-514. |
| [95] | Tully JG, Bastian FO, Rose DL (1984) Localization and persistence of spiroplasmas in an experimental brain infection in suckling rats. Ann Microbiol (Paris) 135A: 111-117. |
| [96] |
Bastian FO, Jennings R, Huff C (1987) Neurotropic Response of Spiroplasma mirum following peripheral inoculation in the rat. Ann Microbiol (Inst Pasteur) 138: 651-655. doi: 10.1016/0769-2609(87)90143-8
|
| [97] | Jeffrey M, Scott JR, Fraser H (1991) Scrapie inoculation of mice: light and electron microscopy of the superior colliculi. Acta Neuropathol 81: 562-571. |
| [98] | Trachtenberg S, Gilad R (2001) A bacterial linear motor: cellular and molecular organization of the contractile cytoskeleton of the helical bacterium Spiroplasma melliferum BC3. Mol Microbiol 41: 827-848. |
| [99] | Bastian FO, Jennings R, Gardner W (1987) Antiserum to scrapie associated fibril protein cross-reacts with Spiroplasma mirum fibril proteins. J Clin Microbiol 25: 2430-2431. |
| [100] | Bastian FO, Elzer PH, Wu X (2012) Spiroplasma spp. biofilm formation is instrumental for their role in the pathogenesis of plant, insect and animal diseases. Exp Mol Pathol 93: 116-128. |
| [101] | Forloni G, Iussich S, Awan T, et al. (2002) Tetracyclines affect prion infectivity. PNAS 99: 10849-10854. |
| [102] | Guo YJ, Han J, Yao HL, et al. (2007) Treatment of scrapie pathogen 263K with tetracycline partially abolishes protease-resistant activity in vitro and reduces infectivity in vivo. Biomed Environ Sci 20: 198-202. |
| [103] |
Haig DA, Pattison IH (1967) In-vitro growth of pieces of brain from scrapie-affected mice. J Path Bact 93: 724-727. doi: 10.1002/path.1700930243
|
| [104] | Pattison IH (1969) Scrapie- a personal view. J Clin Pathol (Supp) 6: 110-114. |
| [105] | Sinclair SH, Rennoll-Bankert KE, Dumier JS (2014) Effector bottleneck: microbial reprogramming of parasitized host cell transcription by epigenetic remodeling of chromatin structure. Front Genetics 5: 274. doi: 10.3389/fgene.2014.00274 1-10. |
| [106] | Di Francesco A, Arosio B, Falconi A, et al. (2015) Global changes in DNA methylation in Alzheimer's disease peripheral blodd mononuclear cells. Brain Behav Immun 45: 139-144. |
| [107] | Drury JL, Chung WO (2015) DNA methylation differentially regulates cytokine secretion in gingival epithelia in response to bacterial challengs. Pathogens Dis 73: 1-6. |
| [108] |
Cal H, Xie Y, Hu L, et al. (2013) Prion protein (PrPc) interacts with histone H3 confirmed by affinity chromatography. J Chromat Analytical Tech Biomed Life Sci 929: 40-44. doi: 10.1016/j.jchromb.2013.04.003
|
| [109] |
Derail M, Mill J, Lunnon K (2014) The mitochondrial epigenome: a role in Alzheimer's disease? Epigenomics 6: 665-675. doi: 10.2217/epi.14.50
|
| [110] |
Choi HS, Choi YG, Shinn HY, et al. (2014) Dysfunction of mitochondrial dynamics in the brains of scrapie-infected mice. Biochem Biophys Res Comm 448: 157-162. doi: 10.1016/j.bbrc.2014.04.069
|
| [111] | Razin S, Yogev D, Naot Y (1998) Molecular biology and pathogenicity of mycoplasmas. Microbiol Mol Biol Rev 62: 1094-1156. |
| [112] | Nur I, Szyf M, Razin A, et al. (1985) Procaryotic and eukaryotic traits of DNA methylation in spiroplasmas. J Bacteriol 164: 19-24. |
| [113] |
Halfmann R, Lindquist S (2010) Epigenetics in the extreme: prions and the inheritance of environmentally acquired traits. Science 330: 629-632. doi: 10.1126/science.1191081
|
| [114] | Bastian FO (2014) Cross-roads in research on neurodegenerative diseases. J Alzheimer's Dis Parkinsonism 4: 1000141. |
| [115] | Bleme H, Hamon M, Cossart P (2012) Epigenetics and bacterial infections. Cold Spring Harb Perspect Med 2: a010272. |
| 1. | Srikanya Kundu, Molly E. Boutin, Caroline E. Strong, Ty Voss, Marc Ferrer, High throughput 3D gel-based neural organotypic model for cellular assays using fluorescence biosensors, 2022, 5, 2399-3642, 10.1038/s42003-022-04177-z |
Frank O. Bastian. Is Alzheimers Disease Infectious?
| Date(day/month) | 15 Jan | 16 Jan | 17 Jan | 18 Jan | 19 Jan | 20 Jan | 21 Jan |
| Cumulative cases | 41 | 45 | 62 | 121 | 224 | 291 | 440 |
| New cases | 0 | 4 | 17 | 59 | 78 | 77 | 149 |
| Date(day/month) | 22 Jan | 23 Jan | 24 Jan | 25 Jan | 26 Jan | 27 Jan | 28 Jan |
| Cumulative cases | 571 | 830 | 1287 | 1975 | 2744 | 4515 | 5974 |
| New cases | 131 | 259 | 444 | 688 | 769 | 1771 | 1459 |
| Date(day/month) | 29 Jan | 30 Jan | 31 Jan | 01 Feb | 02 Feb | ||
| Cumulative cases | 7711 | 9692 | 11791 | 14380 | 17205 | ||
| New cases | 1737 | 1982 | 2102 | 2590 | 2829 |
DownLoad:
CSV
| Date(day/month) | 03 Feb | 04 Feb | 05 Feb | 06 Feb | 07 Feb | 08 Feb | 09 Feb |
| Cumulative cases | 20438 | 24324 | 28018 | 31161 | 34546 | 37198 | 40171 |
| New cases | 3235 | 3887 | 3694 | 3143 | 3399 | 2656 | 3062 |
| Date(day/month) | 10 Feb | 11 Feb | 12 Feb | 13 Feb | 14 Feb | 15 Feb | 16 Feb |
| Cumulative cases | 42638 | 44653 | 59804 | 63851 | 66492 | 68501 | 70549 |
| New cases | 2478 | 2015 | 15152 | 5090 | 2641 | 2009 | 2048 |
| Date(day/month) | 17 Feb | 18 Feb | 19 Feb | 20 Feb | 21 Feb | 22 Feb | 23 Feb |
| Cumulative cases | 72436 | 74185 | 74579 | 75456 | 76288 | 76936 | 77150 |
| New cases | 1886 | 1749 | 820 | 889 | 397 | 648 | 409 |
| Date(day/month) | 24 Feb | 25 Feb | 26 Feb | 27 Feb | 28 Feb | 29 Feb | 01 Mar |
| Cumulative cases | 77658 | 78604 | 78497 | 78824 | 79251 | 79824 | 80026 |
| New cases | 508 | 406 | 443 | 327 | 427 | 573 | 202 |
| Date(day/month) | 02 Mar | 03 Mar | 04 Mar | 05 Mar | |||
| Cumulative cases | 80151 | 80270 | 80409 | 80552 | |||
| New cases | 125 | 119 | 139 | 143 | |||
DownLoad:
CSV
| Parameter | Description | Value (Range) | Unit | Source |
| $ q $ | Self-quarantined rate of the susceptible | $ 1/10 $ | day$ ^{-1} $ | Estimated |
| $ q_1 $ | Transition rate of self-quarantined individuals to the susceptible | $ 1/200000 $ | day$ ^{-1} $ | Estimated |
| $ \beta_e $ | Transmission rate from the exposed to the susceptible | $ 3.511\times 10^{-8} $ $ (10^{-8}, 10^{-7}) $ | day$ ^{-1} $ | Estimated |
| $ \beta_{i1} $ | Transmission rate from the infectious with timely diagnosis to the susceptible | $ 3.112 \times 10^{-8} $ $ (0.91*10^{-8}, 10^{-7}) $ | day$ ^{-1} $ | Estimated |
| $ \beta_{i2} $ | Transmission rate from the infectious with delayed diagnosis to the susceptible | $ 1.098 \times 10^{-7} $ $ (1.1*10^{-8}, 3*10^{-7}) $ | day$ ^{-1} $ | Estimated |
| $ \beta_v $ | Transmission rate from the susceptible to the exposed (infected by virus) | $ 1.009 \times 10^{-10} $ $ (10^{-11}, 9*10^{-10}) $ | day$ ^{-1} $ | Estimated |
| $ 1/\omega $ | Incubation period | $ 5.2 $ | day | [10] |
| $ \phi $ | Proportion of the infectious with timely diagnosis | $ 0.4\; (0.3, 0.65) $ | – | Estimated |
| $ 1/\gamma_1 $ | Waiting time of the infectious for timely diagnosis | $ 2.9\; (1, 5) $ | day | [29] |
| $ 1/\gamma_2 $ | Waiting time of the infectious for delayed diagnosis | $ 10 $ $ (5, 20) $ | day | Estimated |
| $ \mu $ | Disease-induced death rate | $ 1.7826 \times 10^{-5} $ | day$ ^{-1} $ | [17] |
| $ m $ | Recovery rate of the hospitalized | 1/14 | day$ ^{-1} $ | [9] |
| $ f_1 $ | Virus released rate of the exposed | $ 1440 $ $ (864, 2160) $ | day$ ^{-1} $ | Estimated |
| $ f_2 $ | Virus released rate of the infectious with timely-diagnosis | $ 1008 $ $ (432, 1440) $ | day$ ^{-1} $ | Estimated |
| $ f_3 $ | Virus released rate of the infectious with delayed-diagnosis | $ 1728 $ $ (864, 2592) $ | day$ ^{-1} $ | Estimated |
| $ d_v $ | Clear rate of virus in the environment | $ 144 $ $ (115.2, 172.8) $ | day$ ^{-1} $ | Estimated |
| $ S(0) $ | Initial value of the susceptible | $ 11081000 $ | – | [30] |
| $ S_q(0) $ | Initial value of the self-quarantined susceptible | $ 159 $ | – | Estimated |
| $ E(0) $ | Initial value of the exposed | $ 399 $ | – | [5] |
| $ I_1(0) $ | Initial value of the infectious with timely diagnosis | $ 28 $ | – | Estimated |
| $ I_2(0) $ | Initial value of the infectious with delayed diagnosis | $ 54 $ | – | Estimated |
| $ H(0) $ | Initial value of the hospitalized | $ 41 $ | – | [5] |
| $ R(0) $ | Initial value of the recovered | $ 12 $ | – | [5] |
| $ V(0) $ | Initial value of virus in the environment | $ 21080 $ | – | Estimated |
DownLoad:
CSV
| Date(day/month) | 15 Jan | 16 Jan | 17 Jan | 18 Jan | 19 Jan | 20 Jan | 21 Jan |
| Cumulative cases | 41 | 45 | 62 | 121 | 224 | 291 | 440 |
| New cases | 0 | 4 | 17 | 59 | 78 | 77 | 149 |
| Date(day/month) | 22 Jan | 23 Jan | 24 Jan | 25 Jan | 26 Jan | 27 Jan | 28 Jan |
| Cumulative cases | 571 | 830 | 1287 | 1975 | 2744 | 4515 | 5974 |
| New cases | 131 | 259 | 444 | 688 | 769 | 1771 | 1459 |
| Date(day/month) | 29 Jan | 30 Jan | 31 Jan | 01 Feb | 02 Feb | ||
| Cumulative cases | 7711 | 9692 | 11791 | 14380 | 17205 | ||
| New cases | 1737 | 1982 | 2102 | 2590 | 2829 |
| Date(day/month) | 03 Feb | 04 Feb | 05 Feb | 06 Feb | 07 Feb | 08 Feb | 09 Feb |
| Cumulative cases | 20438 | 24324 | 28018 | 31161 | 34546 | 37198 | 40171 |
| New cases | 3235 | 3887 | 3694 | 3143 | 3399 | 2656 | 3062 |
| Date(day/month) | 10 Feb | 11 Feb | 12 Feb | 13 Feb | 14 Feb | 15 Feb | 16 Feb |
| Cumulative cases | 42638 | 44653 | 59804 | 63851 | 66492 | 68501 | 70549 |
| New cases | 2478 | 2015 | 15152 | 5090 | 2641 | 2009 | 2048 |
| Date(day/month) | 17 Feb | 18 Feb | 19 Feb | 20 Feb | 21 Feb | 22 Feb | 23 Feb |
| Cumulative cases | 72436 | 74185 | 74579 | 75456 | 76288 | 76936 | 77150 |
| New cases | 1886 | 1749 | 820 | 889 | 397 | 648 | 409 |
| Date(day/month) | 24 Feb | 25 Feb | 26 Feb | 27 Feb | 28 Feb | 29 Feb | 01 Mar |
| Cumulative cases | 77658 | 78604 | 78497 | 78824 | 79251 | 79824 | 80026 |
| New cases | 508 | 406 | 443 | 327 | 427 | 573 | 202 |
| Date(day/month) | 02 Mar | 03 Mar | 04 Mar | 05 Mar | |||
| Cumulative cases | 80151 | 80270 | 80409 | 80552 | |||
| New cases | 125 | 119 | 139 | 143 | |||
| Parameter | Description | Value (Range) | Unit | Source |
| $ q $ | Self-quarantined rate of the susceptible | $ 1/10 $ | day$ ^{-1} $ | Estimated |
| $ q_1 $ | Transition rate of self-quarantined individuals to the susceptible | $ 1/200000 $ | day$ ^{-1} $ | Estimated |
| $ \beta_e $ | Transmission rate from the exposed to the susceptible | $ 3.511\times 10^{-8} $ $ (10^{-8}, 10^{-7}) $ | day$ ^{-1} $ | Estimated |
| $ \beta_{i1} $ | Transmission rate from the infectious with timely diagnosis to the susceptible | $ 3.112 \times 10^{-8} $ $ (0.91*10^{-8}, 10^{-7}) $ | day$ ^{-1} $ | Estimated |
| $ \beta_{i2} $ | Transmission rate from the infectious with delayed diagnosis to the susceptible | $ 1.098 \times 10^{-7} $ $ (1.1*10^{-8}, 3*10^{-7}) $ | day$ ^{-1} $ | Estimated |
| $ \beta_v $ | Transmission rate from the susceptible to the exposed (infected by virus) | $ 1.009 \times 10^{-10} $ $ (10^{-11}, 9*10^{-10}) $ | day$ ^{-1} $ | Estimated |
| $ 1/\omega $ | Incubation period | $ 5.2 $ | day | [10] |
| $ \phi $ | Proportion of the infectious with timely diagnosis | $ 0.4\; (0.3, 0.65) $ | – | Estimated |
| $ 1/\gamma_1 $ | Waiting time of the infectious for timely diagnosis | $ 2.9\; (1, 5) $ | day | [29] |
| $ 1/\gamma_2 $ | Waiting time of the infectious for delayed diagnosis | $ 10 $ $ (5, 20) $ | day | Estimated |
| $ \mu $ | Disease-induced death rate | $ 1.7826 \times 10^{-5} $ | day$ ^{-1} $ | [17] |
| $ m $ | Recovery rate of the hospitalized | 1/14 | day$ ^{-1} $ | [9] |
| $ f_1 $ | Virus released rate of the exposed | $ 1440 $ $ (864, 2160) $ | day$ ^{-1} $ | Estimated |
| $ f_2 $ | Virus released rate of the infectious with timely-diagnosis | $ 1008 $ $ (432, 1440) $ | day$ ^{-1} $ | Estimated |
| $ f_3 $ | Virus released rate of the infectious with delayed-diagnosis | $ 1728 $ $ (864, 2592) $ | day$ ^{-1} $ | Estimated |
| $ d_v $ | Clear rate of virus in the environment | $ 144 $ $ (115.2, 172.8) $ | day$ ^{-1} $ | Estimated |
| $ S(0) $ | Initial value of the susceptible | $ 11081000 $ | – | [30] |
| $ S_q(0) $ | Initial value of the self-quarantined susceptible | $ 159 $ | – | Estimated |
| $ E(0) $ | Initial value of the exposed | $ 399 $ | – | [5] |
| $ I_1(0) $ | Initial value of the infectious with timely diagnosis | $ 28 $ | – | Estimated |
| $ I_2(0) $ | Initial value of the infectious with delayed diagnosis | $ 54 $ | – | Estimated |
| $ H(0) $ | Initial value of the hospitalized | $ 41 $ | – | [5] |
| $ R(0) $ | Initial value of the recovered | $ 12 $ | – | [5] |
| $ V(0) $ | Initial value of virus in the environment | $ 21080 $ | – | Estimated |
