Citation: Daniel A. Barone, Ana C. Krieger. The Function of Sleep[J]. AIMS Neuroscience, 2015, 2(2): 71-90. doi: 10.3934/Neuroscience.2015.2.71
| [1] | Rujing Zhao, Xiulan Lai . Evolutionary analysis of replicator dynamics about anti-cancer combination therapy. Mathematical Biosciences and Engineering, 2023, 20(1): 656-682. doi: 10.3934/mbe.2023030 |
| [2] | Abeer S. Alnahdi, Muhammad Idrees . Nonlinear dynamics of estrogen receptor-positive breast cancer integrating experimental data: A novel spatial modeling approach. Mathematical Biosciences and Engineering, 2023, 20(12): 21163-21185. doi: 10.3934/mbe.2023936 |
| [3] | Urszula Ledzewicz, Heinz Schättler, Mostafa Reisi Gahrooi, Siamak Mahmoudian Dehkordi . On the MTD paradigm and optimal control for multi-drug cancer chemotherapy. Mathematical Biosciences and Engineering, 2013, 10(3): 803-819. doi: 10.3934/mbe.2013.10.803 |
| [4] | Yi Liu, Long Cheng, Xiangyang Song, Chao Li, Jiantao Zhang, Lei Wang . A TP53-associated immune prognostic signature for the prediction of the overall survival and therapeutic responses in pancreatic cancer. Mathematical Biosciences and Engineering, 2022, 19(1): 191-208. doi: 10.3934/mbe.2022010 |
| [5] | Samantha L Elliott, Emek Kose, Allison L Lewis, Anna E Steinfeld, Elizabeth A Zollinger . Modeling the stem cell hypothesis: Investigating the effects of cancer stem cells and TGF−β on tumor growth. Mathematical Biosciences and Engineering, 2019, 16(6): 7177-7194. doi: 10.3934/mbe.2019360 |
| [6] | Hongli Yang, Jinzhi Lei . A mathematical model of chromosome recombination-induced drug resistance in cancer therapy. Mathematical Biosciences and Engineering, 2019, 16(6): 7098-7111. doi: 10.3934/mbe.2019356 |
| [7] | Baba Issa Camara, Houda Mokrani, Evans K. Afenya . Mathematical modeling of glioma therapy using oncolytic viruses. Mathematical Biosciences and Engineering, 2013, 10(3): 565-578. doi: 10.3934/mbe.2013.10.565 |
| [8] | Farinaz Forouzannia, Sivabal Sivaloganathan, Mohammad Kohandel . A mathematical study of the impact of cell plasticity on tumour control probability. Mathematical Biosciences and Engineering, 2020, 17(5): 5250-5266. doi: 10.3934/mbe.2020284 |
| [9] | Cassidy K. Buhler, Rebecca S. Terry, Kathryn G. Link, Frederick R. Adler . Do mechanisms matter? Comparing cancer treatment strategies across mathematical models and outcome objectives. Mathematical Biosciences and Engineering, 2021, 18(5): 6305-6327. doi: 10.3934/mbe.2021315 |
| [10] | Erin N. Bodine, K. Lars Monia . A proton therapy model using discrete difference equations with an example of treating hepatocellular carcinoma. Mathematical Biosciences and Engineering, 2017, 14(4): 881-899. doi: 10.3934/mbe.2017047 |
Nosocomial infections caused by antibiotic-resistant bacteria are a major threat to global public health today. According to the Centers for Disease Control and Prevention (CDC) [1]:" Each year in the United States, at least 2 million people become infected with bacteria that are resistant to antibiotics, and at least 23,000 people die each year as a direct result of these infections." Furthermore, CDC identifies methicillin-resistant Staphylococcus aureus (MRSA), a Gram-positive bacterium, as one of the most common causes of hospital-acquired infections, especially in newborns and intensive-care unit patients. MRSA infections are usually treated by antibiotics, however, due to overprescribing and misprescribing, MRSA has been resistant to multiple commonly used antibiotics, which makes MRSA infections harder to be treated and even causes life-threatening cases in intensive care units.
An observation that patients with MRSA are about 64$ \% $ more possible to die than patients with a non-resistant form of the infection in hospitals was revealed by a World Health Organization report in April 2014 [2]. In fact, some studies have observed a clear association between antibiotic exposure and MRSA isolation (Dancer [3], Tacconelli [4], Tacconelli et al. [5]). It has been shown that patients with prior antibiotic exposure are vulnerable to skin infections and are more likely to be colonized by MRSA. Furthermore, due to antibiotic exposure, patients may have a lower probability of successful treatment, a lengthier stay in hospitals and extra costs of treatment. Hence, it is necessary to take antibiotic exposure into account in modeling MRSA infections in hospitals. It is also found that under certain circumstances MRSA is capable of surviving for days, weeks or even months on environmental surfaces such as door handles, healthcare facilities, health-care workers' gloves (Boyce et al. [6], Dancer [7]). So environmental contamination is also a necessarily essential factor when we study the transmission of MRSA in hospitals.
In order to understand the diverse factors contributing to infections of antibiotic-resistant bacteria such as MRSA in hospitals, various models have been proposed and studied, see for example Austin and Anderson [8], Austin et al. [9], Bergstrom et al. [10], Bonhoeffer et al. [11], Bootsma et al. [12], Browne et al. [13], Browne and Webb [14], Chamchod and Ruan [15], Cooper et al. [16], D'Agata et al. [17,18], Hall et al. [19], Huang et al. [20,21], Lipsitch et al. [22], Smith et al. [23], Wang et al. [24], Wang and Ruan [25], Wang et al. [26,27], Webb [28], Webb et al. [29]. We refer to survey papers of Bonten et al. [30], Grundmann and Hellriegel [31], Temime et al. [32], van Kleef et al. [33] and the references cited therein on modeling antimicrobial resistance. These studies showed quantitatively how infection control measures such as hand washing, cohorting, and antibiotic restriction affect nosocomial cross-transmission. It is observed that the direct transmission via the hands of health-care workers (HCWs) is a crucial factor in the transmission of MRSA. In particular, D'Agata et al. [34] developed models to investigate the impact of persistent gastrointestinal colonization and antibiotic exposure on transmission dynamics of vancomycin resistant enterococci (VRE). Chamchod and Ruan [15] proposed models to investigate the effect of antibiotic exposure on the transmission of MRSA in hospitals. Mathematical models have also been developed to study the effect of environmental contamination on the spread of antibiotic-resistant bacteria in hospitals (Browne and Webb [14], McBryde and McElwain [35], Plipat et al. [36], Wang and Ruan [25], Wang et al. [26,27], Wolkewitz et al. [37]). Especially, Wang et al. [26,27] used both deterministic and stochastic models to focus on exploring the interaction between volunteers and their environment in the hospital system with a special care pattern in China. However, to the best of our knowledge, the combined effects of antibiotic exposure and environmental contamination have not been studied. This is the motivation for the current study.
In our previous studies (Wang et al. [24] and Wang and Ruan [25]) on nosocomial infections of MRSA in the emergency ward and respiratory intensive care unit in Beijing Tongren Hospital, Beijing, China, data on HCW, volunteers, patients, and environmental contamination were obtained. Wang et al. [24] constructed a mathematical model to determine the role of volunteers in the prevalence and persistence of MRSA in Beijing Tongren Hospital. Wang and Ruan [25] studied the effect of environmental contamination on the transmission MRSA in Beijing Tongren Hospital. Based on the data in [24,25], in this article, we first develop a deterministic ordinary differential equations model (ODE) to investigate the combined effects of antibiotic exposure and environmental contamination on the transmission dynamics of MRSA in hospitals. When there is no admission of colonized patients, we study the steady-states and estimate the basic reproduction number. Numerical simulations and sensitivity analysis are also provided. However, in hospital subunits, where the population is usually small, randomness may matter. Then we formulate a stochastic differential equations model (SDE) to study the transmission dynamics of MRSA that are not well described by the deterministic ODE model. Numerical simulations show that the average of multiple stochastic outputs aligns with the ODE output.
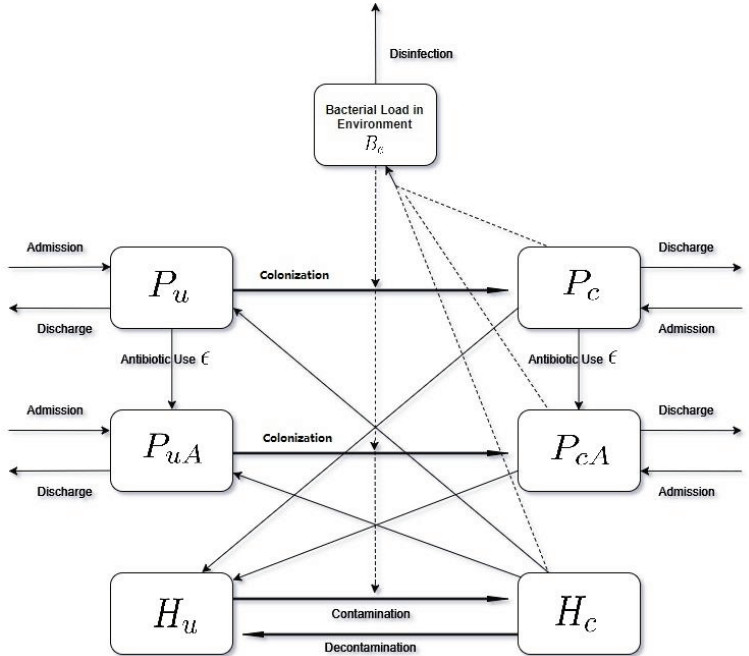
The patients, healthcare workers (HCWs), and free-living bacteria in the environment in hospitals are divided into the following seven compartments (see Figure 1):
$ P_u(t) $ – number of uncolonized patients without antibiotic exposure at time $ t; $
$ P_{uA}(t) $ – number of uncolonized patients with antibiotic exposure at time $ t; $
$ P_c(t) $ – number of colonized patients without antibiotic exposure at time $ t; $
$ P_{cA}(t) $ – number of colonized patients with antibiotic exposure at time $ t; $
$ H_u(t) $ – number of uncontaminated healthcare workers at time $ t; $
$ H_c(t) $ – number of contaminated healthcare workers at time $ t; $
$ B_e(t) $ – density of the free-living bacteria in the environment at time $ t. $
We define antibiotic exposure as having received antibiotics within one month on admission or receiving any antibiotics treatment currently in hospital [38]. We also assume that there is no cross-infection between patients, the hospital is always fully occupied, and the bacteria in the environment are uniformly distributed. Patients are in four compartments according to their status: uncolonized without or with antibiotic exposure ($ P_u $ and $ P_{uA} $, respectively), colonized without or with antibiotic exposure ($ P_c $ and $ P_{cA} $, respectively). Patients are recruited at a total rate $ \Omega(t) $ from any of these four compartments with the corresponding fractions $ \theta_u $, $ \theta_{uA} $, $ \theta_c $, and $ \theta_{cA} $, respectively, and can be discharged from any of these four compartments at corresponding rates $ \gamma_u $, $ \gamma_{uA} $, $ \gamma_c $, and $ \gamma_{cA} $, respectively. We calculate the discharge rate as the reciprocal of the length of stay specific for each compartment.
Based on the assumption that the hospital is always fully occupied, it is reasonable to see that the inflow of patients is equivalent to the outflow of patients, that is $ \Omega(t) = \gamma_uP_u+\gamma_cP_c+\gamma_{uA}P_{uA}+\gamma_{cA}P_{cA} $, which results in a constant population size of patients $ N_p = P_u+P_{uA}+P_c+P_{cA} $. Note that the total number of HCWs is also a constant $ N_h = H_u+H_c $. Besides, patients without antibiotic exposure would move to patients with antibiotic exposure at an antibiotic prescribing rate of $ \epsilon $ per day [39]. Since we assume that there is no cross-infection between patients, uncolonized patients without antibiotic exposure $ P_u $ can be colonized either by direct contacting contaminated HCWs, $ \alpha_p\beta_p(1-\eta)P_uH_c $, or indirect transmission via free-living bacteria in the environment, $ \kappa_pP_uB_e $. A similar process occurs as uncolonized patients with antibiotic exposure move to colonized patients with antibiotic exposure, $ \alpha_p\beta_{pA}(1-\eta)P_{uA}H_c+\kappa_{pA}P_{uA}B_e $. $ \alpha_p $ is the contact rate per day per person, $ \beta_p\ (\beta_{pA}) $ is the probability of colonization after a contact with contaminated healthcare worker for $ P_u\ (P_{uA}) $, $ \eta $ is the compliance rate with the hand hygiene, and $ \kappa_p\ (\kappa_{pA}) $ is the colonization rate from the environment for $ P_u (P_{uA}) $. Meanwhile, HCWs move from uncontaminated state to contaminated state either by contacting colonized patients (without or with antibiotic exposure), $ \alpha_p\beta_h(1-\eta)P_cH_u+\alpha_p\beta_{hA}(1-\eta)P_{cA}H_u $, or by the indirect transmission via free-living bacteria in the contaminated environment, $ \kappa_hH_uB_e $, where $ \kappa_h $ is the contamination rate from the environment for HCWs. Because of hygiene standard of HCWs in hospitals, contaminated HCWs can move to uncontaminated HCWs, $ \mu_c H_c $, in which $ \mu_c $ is the decontamination rate for the HCWs. Even though free-living bacteria in the environment can survive for months, they cannot reproduce themselves in hospitals due to lack of enough reproduction conditions. Hence shedding bacteria into the environment from colonized patients, $ \upsilon_pP_c+\upsilon_{pA}P_{cA} $, serves as an important source of transmission. As well contaminated HCWs contaminate the environment wherever they touch at the rate of $ \upsilon_hH_c $. Here $ \upsilon_p $, $ \upsilon_{pA} $, and $ \upsilon_h $ are the corresponding contaminated rates to the environment from $ P_c $, $ P_{cA} $, and $ H_c $. $ \gamma_b $ is the cleaning/disinfection rate of the environment.
Due to antibiotic exposure, patients may be more likely to have thrush, skin rashes, and gastrointestinal symptoms, and they have a higher probability of colonization, a lower probability of successful treatment, a lengthier stay, and a larger contamination rate to HCWs and the environment. We therefore assume that $ \beta_{pA} \geq \beta_p $, it was estimated that uncolonized patients with antibiotic exposure $ P_{uA} $ is 1.67 times more likely to be colonized than uncolonized patients without antibiotic exposure $ P_u $ [39,15]. We also assume that $ \beta_{hA} \ge \beta_h $ (a higher contamination rate to HCWs), $ \gamma_{cA} \le \gamma_c \le \gamma_{uA}\le \gamma_u $ (a lengthier stay or a lower discharge rate), $ \upsilon_{pA} \ge \upsilon_p $ (a higher contamination (shedding) rate to the environment). Besides, of new admission, the fraction of patients having antibiotic exposure ($ \theta_{uA}+\theta_{cA} $) is assumed to be 0.38 [40,15]. As this article is a continuation of our previous studies on modeling the effect of antibiotic exposure [15] and impact of environmental contamination in Beijing Tongren Hospitals [24,25], we adapt most parameter values from these papers.
Detailed parameter values are listed in Table 1. From the flowchart shown in Figure 1, we formulate an ordinary differential equations model describing the transition between compartments as follows:
| Symbol | Description | Value | Reference |
| $ \epsilon_0 $ | Antibiotic prescription rate (day$ ^{-1} $) | 0.12 | [39][41] |
| $ \epsilon_1 $ | Magnitude of change of antibiotic prescription rate (no dimension) | 0.25 | [56] |
| $ \theta_u $ | Proportion of $ P_u $ on admission (day$ ^{-1} $) | 0.617 | [15][39] |
| $ \theta_{uA} $ | Proportion of $ P_{uA} $ on admission (day$ ^{-1} $) | 0.349 | [15][40] |
| $ \theta_c $ | Proportion of $ P_c $ on admission (day$ ^{-1} $) | 0.003 | [15][39] |
| $ \theta_{cA} $ | Proportion of $ P_{cA} $ on admission (day$ ^{-1} $) | 0.031 | [15][40] |
| $ \gamma_u $ | Discharge rate of $ P_u $ (day$ ^{-1} $) | 0.2 | [15] |
| $ \gamma_{uA} $ | Discharge rate of $ P_{uA} $ (day$ ^{-1} $) | 0.2 | [15] |
| $ \gamma_c $ | Discharge rate of $ P_c $ (day$ ^{-1} $) | 0.06 | [39] |
| $ \gamma_{cA} $ | Discharge rate of $ P_{cA} $ (day$ ^{-1} $) | 0.055 | [15][39] |
| $ \gamma_b $ | Disinfection (cleaning) rate of environment (day$ ^{-1} $) | 0.7 | [25] |
| $ \alpha_p $ | Contact rate (day$ ^{-1} $ person$ ^{-1} $) | 0.0435 | [25] |
| $ \beta_p $ | Probability of colonization for $ P_u $ after a contact with $ H_c $ (no dimension) | 0.42 | [25] |
| $ \beta_{pA} $ | Probability of colonization for $ P_{uA} $ after a contact with $ H_c $ (no dimension) | 0.42*1.67 | [39][15] |
| $ \beta_h $ | Probability of contamination for HCW after a contact with $ P_c $ (no dimension) | 0.2 | [25][15] |
| $ \beta_{hA} $ | Probability of contamination for HCW after a contact with $ P_{cA} $ (no dimension) | 0.25 | [15] |
| $ \eta $ | Hand hygiene compliance with HCWs (no dimension) | 0.4 | [25] |
| $ \mu_c $ | Decontamination rate of HCWs (day$ ^{-1} $) | 24 | [25] |
| $ \upsilon_p $ | Shedding rate to environment from $ P_c $ (day$ ^{-1} $ person$ ^{-1} $ ACC/$ cm^2 $) | 235 | [25] |
| $ \upsilon_{pA} $ | Shedding rate to environment from $ P_{cA} $ (day$ ^{-1} $ person$ ^{-1} $ ACC/$ cm^2 $) | 470 | [26][39] |
| $ \upsilon_h $ | Contamination rate to environment by $ H_c $ (day$ ^{-1} $ person$ ^{-1} $ ACC/$ cm^2 $) | 235 | [25] |
| $ \kappa_p $ | Colonization rate from environment for $ P_u $ (day$ ^{-1} $ (ACC/$ cm^2 $)$ ^{-1} $) | 0.000004 | [25] |
| $ \kappa_{pA} $ | Colonization rate from environment for $ P_{uA} $ (day$ ^{-1} $ (ACC/$ cm^2 $)$ ^{-1} $) | 0.000005 | [15][25] |
| $ \kappa_h $ | Colonization rate from environment for $ H_u $ (day$ ^{-1} $ (ACC/$ cm^2 $)$ ^{-1} $) | 0.00001 | [25] |
| $ N_p $ | Total number of patients | 23 | [25] |
| $ N_h $ | Total number of HCWs | 23 | [25] |
DownLoad:
CSV
|
$ dPudt=θu(γuPu+γcPc+γuAPuA+γcAPcA)−αpβp(1−η)PuHc−κpPuBe−γuPu−ϵPu,dPcdt=θc(γuPu+γcPc+γuAPuA+γcAPcA)+αpβp(1−η)PuHc+κpPuBe−γcPc−ϵPc,dPuAdt=θuA(γuPu+γcPc+γuAPuA+γcAPcA)−αpβpA(1−η)PuAHc−κpAPuABe−γuAPuA+ϵPu,dPcAdt=θcA(γuPu+γcPc+γuAPuA+γcAPcA)+αpβpA(1−η)PuAHc+κpAPuABe−γcAPcA+ϵPc,dHudt=−αpβh(1−η)PcHu−αpβhA(1−η)PcAHu−κhHuBe+μcHc,dHcdt=αpβh(1−η)PcHu+αpβhA(1−η)PcAHu+κhHuBe−μcHc,dBedt=υpPc+υpAPcA+υhHc−γbBe $
|
(2.1) |
with initial conditions $ P_u(0) = P_u^0 $, $ P_{uA}(0) = P_{uA}^0 $, $ P_c(0) = P_c^0 $, $ P_{cA}(0) = P_{cA}^0 $, $ H_u(0) = H_u^0 $, $ H_c(0) = H_c^0 $, $ B_e(0) = B_e^0 $ specified at time 0.
We know that one disadvantage of deterministic models is that they cannot directly reflect randomness in epidemic events. For nosocomial models in hospital subunits where randomness may matter, there is a need to formulate randomness more precisely. The natural extensions of a deterministic ordinary differential equations model are usually two types of stochastic setting, continuous-time Markov chains (CTMCs) and stochastic differential equations (SDEs), where the time variable is continuous, but the state variables are discrete or continuous, respectively. In the formulation of CTMCs, forward Kolmogorov differential equations for the transition probability density functions can be derived and they, in turn, lead directly to the SDEs. Even though it is difficult to find analytical solutions for multivariate processes, SDEs are useful to numerically simulate stochastic realizations (sample paths) of the process. It is believed that the SDEs are easier to solve numerically than the Kolmogorov differential equations and faster than simulating sample paths of the CTMCs model for multivariate processes [42]. Thus, we develop a CTMCs model, an SDE model and its simulations in the following ([43,25]).
By the assumption $ P_u+P_{uA}+P_c+P_{cA} = N_p, H_u+H_c = N_h, \forall t\geq0 $, we have the process $ (P_c, P_{uA}, P_{cA}, H_c, B_e) $ in $ \mathbb{R}^5 $ with $ P_u(t) = N_p-P_{uA}-P_c-P_{cA} $ and $ H_u(t) = N_h-H_c $. These five variables have a joint probability denoted by
| $ p_{(s, j, k, m, n)}(t) = \Pr(P_c(t) = s, P_{uA}(t) = j, P_{cA}(t) = k, H_c(t) = m, B_e(t) = n) $ |
with $ s \ge 0, j \ge 0, k \ge 0, 0 \le s+j+k \le N_p, 0 \le m \le N_h $ and $ n \ge 0 $. Assume that $ \triangle t > 0 $ is sufficiently small, the transition probabilities associated with the stochastic process are defined for a small period of time $ \triangle t > 0 $ as follows:
|
$ p(s+i1,j+i2,k+i3,m+i4,n+i5);(s,j,k,m,n)(△t)=Pr[(Pc(t+△t),PuA(t+△t),PcA(t+△t),Hc(t+△t),Be(t+△t))=(s+i1,j+i2,k+i3,m+i4,n+i5)|(Pc(t),PuA(t),PcA(t),Hc(t),Be(t))=(s,j,k,m,n)], $
|
where $ i_1, i_2, i_3, i_4, i_5\in \{ -1, 0, 1 \} $, Hence the transition probability is as follow:
|
${\mathit{\boldsymbol{p_{(s+i_1, j+i_2, k+i_3, m+i_4, n+i_5);(s, j, k, m, n)}(\triangle t)}}}\\ ={{θc(γu(Np−s−j−k)+γcs+γuAj+γcAk)+αpβp(1−η)(Np−s−j−k)m+κp(Np−s−j−k)n}△t(i1,i2,i3,i4,i5)=(1,0,0,0,0)γcs△t(i1,i2,i3,i4,i5)=(−1,0,0,0,0)ϵs△t(i1,i2,i3,i4,i5)=(−1,0,1,0,0){θuA(γu(Np−s−j−k)+γcs+γuAj+γcAk)+ϵ(Np−s−j−k)}△t(i1,i2,i3,i4,i5)=(0,1,0,0,0)(κpAjn+γuAj)△t(i1,i2,i3,i4,i5)=(0,−1,0,0,0)αpβpA(1−η)jm△t(i1,i2,i3,i4,i5)=(0,−1,1,0,0){θcA(γu(Np−s−j−k)+γcs+γuAj+γcAk)+κpjn}△t(i1,i2,i3,i4,i5)=(0,0,1,0,0)γcAk△t(i1,i2,i3,i4,i5)=(0,0,−1,0,0){αpβh(1−η)s(Nh−m)+αpβhA(1−η)k(Nh−m)+κh(Nh−m)n}△t(i1,i2,i3,i4,i5)=(0,0,0,1,0)μcm△t(i1,i2,i3,i4,i5)=(0,0,0,−1,0)(υps+υpAk+υhm)△t(i1,i2,i3,i4,i5)=(0,0,0,0,1)γbn△t(i1,i2,i3,i4,i5)=(0,0,0,0,−1)0otherwise. $
|
(2.2) |
We must choose the time step $ \triangle t $ sufficiently small. In our case it is too complicated to express the transition matrix. Instead, we still are able to express the probabilities $ p_{(s, j, k, m, n)}(t+\triangle t) $ by using the Markov property:
|
$ p(s,j,k,m,n)(t+△t)=p(s−1,j,k,m,n)(t)[θc(γu(Np−s+1−j−k)+γcs+γuAj+γcAk)+αpβp(1−η)(Np−s+1−j−k)m+κp(Np−s+1−j−k)n]△t+p(s+1,j,k,m,n)(t)γc(s+1)△t+p(s+1,j,k−1,m,n)(t)ϵ(s+1)△t+p(s,j−1,k,m,n)(t)[θuA(γu(Np−s−j+1−k)+γcs+γuAj+γcAk)+ϵ(Np−s−j+1−k))]△t+p(s,j+1,k,m,n)(t)[κpA(j+1)n+γuA(j+1)]△t+p(s,j+1,k−1,m,n)(t)αpβpA(1−η)(j+1)m+p(s,j,k−1,m,n)(t)[θc(γu(Np−s−j−k+1)+γcs+γuAj+γcA(k+1))+κpjn]△t+p(s,j,k+1,m,n)(t)γcA(k+1)△t+p(s,j,k,m−1,n)(t)[αpβh(1−η)s(Nh−m+1)+αpβhA(1−η)k(Nh−m+1)+κh(Nh−m+1)n]△t+p(s,j,k,m+1,n)(t)μc(m+1)+p(s,j,k,m,n−1)(t)(υps+υpAk+υhm)△t+p(s,j,k,m,n+1)(t)γb(n+1)△t+∘(△t). $
|
Naturally, a system of forward Kolmogorov differential equations can be derived:
|
$ dps,j,k,m,ndt=p(s−1,j,k,m,n)[θc(γu(Np−s+1−j−k)+γcs+γuAj+γcAk)+αpβp(1−η)(Np−s+1−j−k)m+κp(Np−s+1−j−k)n]+p(s+1,j,k,m,n)(t)γc(s+1)+p(s+1,j,k−1,m,n)(t)ϵ(s+1)+p(s,j−1,k,m,n)(t)[θuA(γu(Np−s−j+1−k)+γcs+γuAj+γcAk)+ϵ(Np−s−j+1−k))]+p(s,j+1,k,m,n)(t)[κpA(j+1)n+γuA(j+1)]△t+p(s,j+1,k−1,m,n)(t)αpβpA(1−η)(j+1)m+p(s,j,k−1,m,n)(t)[θc(γu(Np−s−j−k+1)+γcs+γuAj+γcA(k+1))+κpjn]+p(s,j,k+1,m,n)(t)γcA(k+1)+p(s,j,k,m−1,n)(t)[αpβh(1−η)s(Nh−m+1)+αpβhA(1−η)k(Nh−m+1)+κh(Nh−m+1)n]+p(s,j,k,m+1,n)(t)μc(m+1)+p(s,j,k,m,n−1)(t)(υps+υpAk+υhm)+p(s,j,k,m,n+1)(t)γb(n+1). $
|
We now try to develop a stochastic differential equations model (SDE) from the deterministic epidemic model (2.1). The system has five variables with a joint probability defined by:
| $ p_{(s, j, k, m, n)}(t) = \Pr\{ P_c(t) = s, P_{uA}(t) = j, P_{cA}(t) = k, H_c(t) = m, B_e(t) = n \} $ |
with $ s, j, k = 0, ..., N_p, m = 0...N_h $, and $ n\geq 0 $, with transition probabilities given in (2.2). Let $ X(t) = (P_c(t), P_{uA}(t), P_{cA}(t), H_c(t), B_e(t))^T $ with infinitesimal
| $ \triangle X(t) = (\triangle P_c(t), \triangle P_{uA}(t), \triangle P_{cA}(t), \triangle H_c(t), \triangle B_e(t))^T. $ |
We express the infinitesimal mean matrix $ f(X(t), t) $ as follows:
|
$ E(\triangle X(t)|X(t) = (eceuAecAeheb) \triangle t = f(X(t), t)\triangle t, $
|
where
$ e_c = \theta_c(\gamma_u(N_h-P_c-P_{uA}-P_{cA})+\gamma_cP_c+\gamma_{uA}P_{uA}+\gamma_{cA}P_{cA})+\alpha_p\beta_p(1-\eta)(N_h-P_c-P_{uA}-P_{cA})H_c+\kappa_pP_uB_e-\gamma_cP_c-\epsilon P_c $,
$ e_{uA} = \theta_{uA}(\gamma_u(N_h-P_c-P_{uA}-P_{cA})+\gamma_cP_c+\gamma_{uA}P_{uA}+\gamma_{cA}P_{cA})-\alpha_p\beta_{pA}(1-\eta)P_{uA}H_c-\kappa_{pA}P_{uA}B_e-\gamma_{uA}P_{uA}\\ +\epsilon (N_h-P_c-P_{uA}-P_{cA}) $,
$ e_{cA} = \theta_{cA}(\gamma_u(N_h-P_c-P_{uA}-P_{cA})+\gamma_cP_c+\gamma_{uA}P_{uA}+\gamma_{cA}P_{cA})+\alpha_p\beta_{pA}(1-\eta)P_{uA}H_c+\kappa_{pA}P_{uA}Be-\gamma_{cA}P_{cA}+\epsilon P_c $,
$ e_h = \alpha_p\beta_h(1-\eta)P_c(N_h-H_c)+\alpha_p\beta_{hA}(1-\eta)P_{cA}(N_h-H_c)+\kappa_h(N_h-H_c)B_e-\mu_cH_c $,
$ e_b = \upsilon_pP_c+\upsilon_{pA}P_{cA}+\upsilon_hH_c-\gamma_bB_e $.
and also the infinitesimal variance matrix $ \Sigma (X(t)t) $:
|
$ E(△X(t)(△X(t))T|X(t))=(δc0−ϵPc000δuA−αpβpA(1−η)PuAHc00−ϵPc−αpβpA(1−η)PuAHcδcA00000δh00000δb)△t=Σ(X(t),t)△t, $
|
where
$ \delta_c = \theta_c(\gamma_u(N_h-P_c-P_{uA}-P_{cA})+\gamma_cP_c+\gamma_{uA}P_{uA}+\gamma_{cA}P_{cA})+\alpha_p\beta_p(1-\eta)(N_h-P_c-P_{uA}-P_{cA})H_c+\kappa_pP_uB_e+\gamma_cP_c+\epsilon P_c, $
$ \delta_{uA} = \theta_{uA}(\gamma_u(N_h-P_c-P_{uA}-P_{cA})+\gamma_cP_c+\gamma_{uA}P_{uA}+\gamma_{cA}P_{cA})+\alpha_p\beta_{pA}(1-\eta)P_{uA}H_c+\kappa_{pA}P_{uA}B_e+\gamma_{uA}P_{uA}\\ +\epsilon (N_h-P_c-P_{uA}-P_{cA}), $
$ \delta_{cA} = \theta_{cA}(\gamma_u(N_h-P_c-P_{uA}-P_{cA})+\gamma_cP_c+\gamma_{uA}P_{uA}+\gamma_{cA}P_{cA})+\alpha_p\beta_{pA}(1-\eta)P_{uA}H_c+\kappa_{pA}P_{uA}B_e+\gamma_{cA}P_{cA}+\epsilon P_c, $
$ \delta_h = \alpha_p\beta_h(1-\eta)P_c(N_h-H_c)+\alpha_p\beta_{hA}(1-\eta)P_{cA}(N_h-H_c)+\kappa_h(N_h-H_c)B_e+\mu_cH_c, \\ \delta_b = \upsilon_pP_c+\upsilon_{pA}P_{cA}+\upsilon_hH_c+\gamma_bB_e $.
It is easy to check that $ \delta_c, \delta_{uA}, \delta_{cA}, \delta_h, \delta_b $ are all nonnegative. Hence we have a matrix $ G $ satisfying $ GG^T = \Sigma $, where $ G $ is a 5$ \times$ matrix to order $ \triangle t $,
|
$ G = (√a1−√a2−√a3000000000000√a4−√a5−√a600000000√a300√a6√a7−√a8000000000000√a9−√a10000000000000√a11−√a12) , $
|
where
$ a_1 = \theta_c(\gamma_u(N_h-P_c-P_{uA}-P_{cA})+\gamma_cP_c+\gamma_{uA}P_{uA}+\gamma_{cA}P_{cA})+\alpha_p\beta_p(1-\eta)(N_h-P_c-P_{uA}-P_{cA})H_c+\kappa_pP_uB_e $,
$ a_2 = \gamma_cP_c $,
$ a_3 = \epsilon P_c $,
$ a_4 = \theta_{uA}(\gamma_u(N_h-P_c-P_{uA}-P_{cA})+\gamma_cP_c+\gamma_{uA}P_{uA})+\epsilon (N_h-P_c-P_{uA}-P_{cA}) $,
$ a_5 = \kappa_{pA}P_{uA}Be+\gamma_{uA}P_{uA} $,
$ a_6 = \alpha_p\beta_{pA}(1-\eta)P_{uA}H_c $,
$ a_7 = \theta_{cA}(\gamma_u(N_h-P_c-P_{uA}-P_{cA})+\gamma_cP_c+\gamma_{uA}P_{uA}+\gamma_{cA}P_{cA})+\kappa_{pA}P_{uA}B_e $,
$ a_8 = \gamma_{cA}P_{cA} $,
$ a_9 = \alpha_p\beta_h(1-\eta)P_c(N_h-H_c)+\alpha_p\beta_{hA}(1-\eta)P_{cA}(N_h-H_c)+\kappa_h(N_h-H_c)B_e $,
$ a_{10} = \mu_cH_c $,
$ a_{11} = \upsilon_pP_c+\upsilon_{pA}P_{cA}+\upsilon_hH_c $,
$ a_{12} = \gamma_bB_e $.
Then the stochastic differential equations have the following form:
| $ dX(t) = f(X(t), t)dt+G(X(t), t)dW(t). $ |
More precisely,
|
$ {dPc(t)=ecdt+√a1dW1−√a2dW2−√a3dW3,dPuA(t)=euAdt+√a4dW4−√a5dW5−√a6dW6,dPcA(t)=ecAdt+√a3dW3+√a6dW6+√a7dW7−√a8dW8,dHct=ehdt+√a9dW9−√a10dW10,dBe(t)=ebdt+√a11dW11−√a12dW12. $
|
(2.3) |
where $ W_1, \cdots, W_{12} $ are twelve independent Wiener processes. Next we are able to run stochastic simulations.
In this section we provide detailed analysis of the deterministic ODE model (2.1).
Based on the biological background of model (2.1), we only consider solutions of model (2.1) starting at $ t = 0 $ with nonnegative initial values:
| $ P_u^0 \ge 0, P_{uA}^0 \ge 0, P_c^0 \ge 0, P_{cA}^0 \ge 0, H_u^0 \ge 0, H_c^0 \ge 0, B_e^0 \ge 0. $ |
Lemma 1. If $ P_u^0, P_{uA}^0, P_c^0, P_{cA}^0, H_u^0, H_c^0, B_e^0 \ge 0 $, then $ (P_u(t), P_{uA}(t), P_c(t), P_{cA}(t), H_u(t), H_c(t), B_e(t)) $ the solutions of model (2.1) are nonnegative for all $ t \ge 0 $ and ultimately bounded. In particular, if $ P_u^0, P_{uA}^0, P_c^0, P_{cA}^0, H_u^0, H_c^0, B_e^0 > 0 $, then the solutions $ (P_u(t), P_{uA}(t), P_c(t), P_{cA}(t), H_u(t), H_c(t), B_e(t)) $ are also positive for all $ t \ge 0 $.
Proof. Firstly, by the continuous dependence of solutions with respect to initial values, we only need to prove that when $ P_u^0, P_{uA}^0, P_c^0, P_{cA}^0, H_u^0, H_c^0, B_e^0 > 0 $, $ (P_u(t), P_{uA}(t), P_c(t), P_{cA}(t), H_u(t), H_c(t), B_e(t)) $ the solutions are also positive for all $ t \ge 0 $. That is, the solutions remain in the positive cone if the initial conditions are in the positive cone of $ \mathbb{R}^7 $. Set
| $ m(t) = \min\{P_u(t), P_{uA}(t), P_c(t), P_{cA}(t), H_u(t), H_c(t), B_e(t)\}, \forall t \gt 0. $ |
Clearly, $ m(0) > 0 $. Assuming that there exists a $ t_1 > 0 $ such that $ m(t_1) = 0 $ and $ m(t) > 0 $ for all $ t \in [\ 0, t_1) $.
If $ m(t_1) = P_u(t_1) $, from the first equation of model (2.1) it follows that $ \frac{dP_u}{dt} \ge -(\alpha_p\beta_p(1-\eta)H_c(t)+\kappa_pB_e(t)+\gamma_u+\epsilon)P_u $ for all $ t \in [\ 0, t_1) $. Since $ H_c(t) > 0, B_e(t) > 0 $ for all $ t \in [\ 0, t_1) $, we have
| $ 0 = P_u(t_1) \ge P_u^0 \exp(-\int_{0}^{t_1}(\alpha_p\beta_p(1-\eta)H_c(s)+\kappa_pB_e(s)+\gamma_u+\epsilon)ds) \gt 0, $ |
which leads to a contradiction. Similar contradictions can be deduced in the cases of $ m(t_1) = P_{uA}(t_1), m(t_1) = P_c(t_1), m(t_1) = P_{cA}(t_1), m(t_1) = H_u(t_1), m(t_1) = H_c(t_1), m(t_1) = B_e(t_1) $. Hence, the solutions remain in the positive cone if the initial conditions are in the positive cone $ \mathbb{R}^7 $.
Secondly, let $ T(t) = P_u(t)+P_{uA}(t)+P_c(t)+P_{cA}(t)+H_u(t)+H_c(t)+B_e(t) $. Then
|
$ dT(t)dt=dBe(t)dt=υpPc+υpAPcA+υhHc−γbBe≤υpNp+υpANp+υhNh−γbBe(t), $
|
where $ N_p = P_u(t)+P_{uA}(t)+P_c(t)+P_{cA}(t) $ and $ N_h = H_u(t)+H_c(t) $, which implies that
| $ B_e(t) \le \frac{(\upsilon_pN_p+\upsilon_{pA}N_p+\upsilon_hN_h)}{\gamma_b}(1-e^{-\gamma_b t})+B_e^0 e^{-\gamma_b t}. $ |
So $ B_e(t) $ is bounded by a fixed number
| $ M = \frac{(\upsilon_pN_p+\upsilon_{pA}N_p+\upsilon_hN_h)}{\gamma_b}+B_e^0. $ |
Let $ N = N_p+N_h+M $, we have
| $ T(t) = P_u(t)+P_{uA}(t)+P_c(t)+P_{cA}(t)+H_u(t)+H_c(t)+B_e(t) \le N. $ |
Thus, the solutions remain bounded in a positive cone of $ \mathbb{R}^7 $, and the system induces a global semiflow in the positively invariant set of $ \mathbb{R}^7 $. This completes the proof.
Remark 2. Denote set G as follows
| $ G: = \{(P_u, P_{uA}, P_c, P_{cA}, H_u, H_c, B_e) \in \mathbb{R}^7_{+} : P_u+P_{uA}+P_c+P_{cA}+H_u+H_c+B_e \le N )\}. $ |
Then Lemma 1 implies that G is a positively invariant set with respect to model (2.1).
When $ \theta_c $ = 0, $ \theta_{cA} $ = 0, that is, there are no colonized patients admitted into hospitals, model (2.1) has a unique infection-free equilibrium (IFE) which is defined by
| $ E_0 = (P_u, P_c, P_{uA}, P_{cA}, H_u, H_c, B_e) = (N^*, 0, N_p - N^*, 0, N_h, 0, 0), \;\; N^* = \frac{\theta_u\gamma_{uA}N_p}{\theta_{uA}\gamma_u+\theta_u\gamma_{uA}+\epsilon}. $ |
We derive the basic reproduction number $ R_0 $ for model (2.1) by using the techniques in Diekmann et al. [44] and van den Driessche and Watmough [45], which involves linearizing the original nonlinear ordinary differential equations at the infection-free equilibrium. Re-order the components of $ E_0 $ as
| $ E_0 = (P_c, P_{cA}, H_c, B_e, P_u, P_{uA}, H_u) = (0, 0, 0, 0, N^*, N_p-N^*, N_h) $ |
and set
|
$ \mathcal{F} = (αpβp(1−η)PuHc+κpPuBeαpβpA(1−η)PuAHc+κpAPuABeαpβh(1−η)PcHu+αpβhA(1−η)PcAHu+κhHuBe0000) , $
|
|
$ \mathcal{V} = (γcPc+ϵPc−θcΩγcAPcA−[ϵPc+θcAΩ]μcHcγbBe−(υpPc+υpAPcA+υhHc)αpβp(1−η)PuHc+κpPuBe+γuPu+ϵPu−θuΩαpβpA(1−η)PuAHc+κpAPuABe+γuAPuA−[ϵPu+θuAΩ]αpβh(1−η)PcHu+αpβhA(1−η)PcAHu+κhHuBe−μcHc) , $
|
where $ \Omega = (\gamma_uP_u+\gamma_cP_c+\gamma_{uA}P_{uA}+\gamma_{cA}P_{cA}) $,
|
$ \mathcal{V}^- = (γcPc+ϵPcγcAPcAμcHcγbBeαpβp(1−η)PuHc+κpPuBe+γuPu+ϵPuαpβpA(1−η)PuAHc+κpAPuABe+γuAPuAαpβh(1−η)PcHu+αpβhA(1−η)PcAHu+κhHuBe) , \;\; \mathcal{V}^+ = (θcΩϵPc+θcAΩ0υpPc+υpAPcA+υhHcθuΩϵPu+θuAΩμcHc) . $
|
Since $ \theta_c $ = 0, $ \theta_{cA} $ = 0, then we can derive that
|
$ F = (00αpβp(1−η)N∗κpN∗00αpβpA(1−η)(Np−N∗)κpA(Np−N∗)αpβh(1−η)NhαpβhA(1−η)Nh0κhNh0000) , $
|
|
$ V = (γc+ϵ000−ϵγcA0000μc0−υp−υpA−υhγb) . $
|
Therefore, let $ \omega_1 = \frac{\upsilon_p\gamma_{cA}+\upsilon_{pA}\epsilon}{\gamma_b\gamma_{cA}(\gamma_c+\epsilon)} $, $ \omega_2 = \frac{\upsilon_{pA}}{\gamma_b\gamma_{cA}} $, $ \omega_3 = \frac{\upsilon_h}{\gamma_b\mu_c} $, we have
|
$ FV^{-1} = (ω1κpN∗ω2κpN∗ω3κpN∗+αpβp(1−η)N∗μcκpN∗γbω1κpA(Np−N∗)ω2κpA(Np−N∗)ω3κpA(Np−N∗)+αpβpA(1−η)(Np−N∗)μcκpA(Np−N∗)γbω1κhNh+βhγcA+βhAϵγcA(γc+ϵ)αp(1−η)Nhω2κhNh+αpβhA(1−η)NhγcAω3κhNhκhNhγb0000) $
|
and the basic reproductive number is defined as the spectral radius of $ FV^{-1} $:
|
$ R0=sp(FV−1)=α3α1+α1+α2 $
|
(3.1) |
where
|
$
α1=(√(α3627μ3cγ3cA+α5+α4)2−α33+α3627μ3cγ3cA+α5+α4)13,α2=α63μcγcA, α3=α73μcγcA+α269μ2cγ2cA, α4=α6α76μ2cγ2cA,α5=(βpκpA−βpAκp)N∗(Np−N∗)Nhα2p(1−η)2[ ω1βhA(γc+ϵ)−ω2(βhγcA+βhAϵ)] 2μcγcA(γc+ϵ),α6=μcγcA(ω1κpN∗+ω2κpA(Np−N∗)+ω3κhNh),α7=Nhα2p(1−η)2[βhAβpA(Np−N∗)+βhγcA+βhAϵγc+ϵβpN∗]+(Np−N∗)Nhαp(1−η)[ω2κhβpAγcA+ω3κpAβhAμc]+N∗Nhαp(1−η)[ω1βpκhγcA+ω3κpμcβhγcA+βhAϵγc+ϵ].
$
|
By Theorem 2 in van den Driessche and Watmough [45], we have the following theorem:
Theorem 3. If $ R_0 < 1 $, then the infection-free equilibrium $ E_0 $ is locally asymptotically stable; If $ R_0 > 1 $, then $ E_0 $ is unstable.
Moreover, from the proof of Theorem 2 in van den Driesshce and Watmough [45] or the proof of Lemma 2.1 in Wang and Zhao [46], we have the following observation: Denote
|
$ J_1 = F-V = (−γc−ϵ0αpβp(1−η)N∗κpN∗ϵ−γcAαpβpA(1−η)(Np−N∗)κpA(Np−N∗)αpβh(1−η)NhαpβhA(1−η)Nh−μcκhNhυpυpAυh−γb) . $
|
Let $ s(J_1) $ be the maximum real part of the eigenvalues of $ J_1 $. Since $ J_1 $ is irreducible and has non-negative off-diagonal elements, $ s(J_1) $ is a simple eigenvalue of $ J_1 $ with a positive eigenvector. Then we have the following corollary:
Corollary 4. There hold two equivalences:
| $ R_0 \lt 1 \iff s(J_1) \lt 0; \;\;\; R_0 \gt 1 \iff s(J_1) \gt 0. $ |
The existence and stability of the infection-free equilibrium $ E_0 $ indicates that the MRSA infection is vanishing.
Theorem 5. If $ R_0 < 1 $, then the infection-free equilibrium $ E_0 $ is globally asymptotically stable.
Proof. From Theorem 3 we know that $ E_0 $ is locally asymptotically stable. Now we prove the global attractivity of the infection-free equilibrium $ E_0 $.
By the first equation of model (2.1), non-negativity of the solutions and previous assumptions, we get
| $ \frac{dP_u}{dt} \le \theta_u[\gamma_uP_u+\gamma_{uA}(N_p-P_u)]-\gamma_uP_u-\epsilon P_u. $ |
Since $ \gamma_{uA} = \max\{\gamma_{uA}, \gamma_c, \gamma_{cA}\} $, it implies that
| $ \frac{dP_u}{dt} \le \theta_u\gamma_{uA}N_p-(-\theta_u\gamma_u+\theta_u\gamma_{uA}+\gamma_u+\epsilon)P_u = \theta_u\gamma_{uA}N_p-(\theta_{uA}\gamma_u+\theta_u\gamma_{uA}+\epsilon)P_u. $ |
So $ \forall \delta > 0 $, there exists $ t_1 > 0 $, such that $ P_u \le N^*+\delta, $ for all $ t\ge t_1 $.
Similarly, by the third equation of model (2.1), non-negativity of the solutions and previous assumptions, we get
| $ \frac{dP_{uA}}{dt} \le (1-\theta_u)[\gamma_u(N_p-P_{uA})+\gamma_{uA}P_{uA}]-\gamma_{uA}P_{uA}+\epsilon(N_p-P_{uA}), $ |
that is,
| $ \frac{dP_{uA}}{dt} \le (\theta_{uA}\gamma_u+\epsilon)N_p-(\theta_{uA}\gamma_u+\theta_u\gamma_{uA}+\epsilon)P_{uA}. $ |
Then $ \forall \delta > 0 $, there exists $ t_2 > 0 $, such that $ P_{uA} \le N_p-N^*+\delta, $ for all $ t\ge t_2 $.
Let $ T = \max \{ t_1, t_2\}. $ If $ t > T $, since $ \theta_c = \theta_{cA} = 0 $, then
|
$ {P′c(t)≤αpβp(1−η)(N∗+δ)Hc+κp(N∗+δ)Be−γcPc−ϵPc,P′cA(t)≤αpβpA(Np−N∗+δ)Hc+κpA(Np−N∗+δ)Be−γcAPcA+ϵPc,H′c(t)≤αpβh(1−η)NhPc+αpβhA(1−η)NhPcA+κhNhBe−μcHc,B′e(t)≤υpPc+υpAPcA+υhHc−γbBe. $
|
(3.2) |
Considering the following auxiliary system:
|
$ {~P′c(t)=αpβp(1−η)(N∗+δ)˜Hc+κp(N∗+δ)˜Be−γc˜Pc−ϵ˜Pc,~P′cA(t)=αpβpA(Np−N∗+δ)˜Hc+κpA(Np−N∗+δ)˜Be−γcA˜PcA+ϵ˜Pc,~H′c(t)=αpβh(1−η)Nh˜Pc+αpβhA(1−η)Nh˜PcA+κhNh˜Be−μc˜Hc,~B′e(t)=υp˜Pc+υpA˜PcA+υh˜Hc−γb˜Be. $
|
(3.3) |
Define
|
$ J_1(\delta) = (−γc−ϵ0αpβp(1−η)(N∗+δ)κp(N∗+δ)ϵ−γcAαpβpA(1−η)(Np−N∗+δ)κpA(Np−N∗+δ)αpβh(1−η)NhαpβhA(1−η)Nh−μcκhNhυpυpAυh−γb) . $
|
It follows from Corollary 4 that if $ R_0 < 1 $, then $ s(J_1(0)) < 0 $. Since $ s(J_1(\delta)) $ is continuous for small $ \delta $, so there exists $ \delta $ small enough such that $ s(J_1(\delta)) < 0 $. Thus there is a negative eigenvalue of $ s(J_1(\delta)) $ with a positive eigenvector. Obviously if $ t \to \infty $, then $ \tilde{ P_c}, \tilde{P_{cA}}, \tilde{H_c}, \tilde{B_e } \to 0 $. Then by the comparison principle we get
| $ \lim\limits_{t \to\infty} P_c = 0, \lim\limits_{t \to\infty} P_{cA} = 0, \lim\limits_{t \to\infty} H_c = 0, \lim\limits_{t \to\infty} B_e = 0. $ |
Therefore, $ E_0 $ is globally attractive when $ R_0 < 1 $. This completes the proof.
Uniform persistence of system (2.1) demonstrates that all components of the dynamical model have positive lower bounds which in turn indicates that MRSA infection persists in the hospital.
Theorem 6. If $ R_0 > 1 $, then model (2.1) is uniformly persistent.
Proof. We first define
| $ X = \{(P_u, P_c, P_{uA}, P_{cA}, H_u, H_c, B_e): P_u \ge 0, P_c \ge 0, P_{uA} \ge 0, P_{cA} \ge 0, H_u \ge0, H_c\ge0, B_e\ge0 \}, $ |
| $ X_0 = \{(P_u, P_c, P_{uA}, P_{cA}, H_u, H_c, B_e) \in X: P_c \gt 0, P_{cA} \gt 0, H_c \gt 0, B_e \gt 0 \}, \;\; \partial X_0 = X\backslash X_0. $ |
It can be seen that both $ X $ and $ X_0 $ are positively invariant with respect to model (2.1). Clearly, $ \partial X_0 $ is relatively closed in $ X $. Lemma 1 implies that model (2.1) is point dissipative, which implies that the solutions of model (2.1) admit a global attractor. Then we define
|
$ M∂={(Pu(0),Pc(0),PuA(0),PcA(0),Hu(0),Hc(0),Be(0)):(Pu(t),Pc(t),PuA(t),PcA(t),Hu(t),Hc(t),Be(t))∈∂X0,∀t≥0}. $
|
Now we prove that
| $ M_{\partial} = \{ (P_u, 0, P_{uA}, 0, H_u, 0, 0):P_u \ge 0 , P_{uA}\ge0, H_u = N_h \}. $ |
For any point $ \varphi_0 = (P_u(0), P_c(0), P_{uA}(0), P_{cA}(0), H_u(0), H_c(0), B_e(0)) $ in $ M_{\partial} $, we suppose that one of $ P_c(0), P_{cA}(0), H_c(0), B_e(0) $ is not zero, that is to say, $ \varphi_0 \notin \{ (P_u, 0, P_{uA}, 0, H_u, 0, 0):P_u \ge 0, P_{uA}\ge0, H_u = N_h \} $. Without loss of generality, we suppose that $ P_c(0) = 0, P_{cA}(0) = 0, H_c(0) = 0, B_e(0) > 0 $. By the second, fourth, and sixth equations, we have
| $ \frac{dP_c(0)}{dt} \ge \kappa_pP_u(0)B_e(0) \gt 0; \frac{dP_{cA}(0)}{dt} \ge \kappa_{pA}P_{uA}(0)B_e(0) \gt 0; \frac{dH_c(0)}{dt} \ge \kappa_hH_u(0)B_e(0) \gt 0. $ |
Thus, there exists $ \delta_0 > 0 $, if $ 0 < t < \delta_0 $ then $ P_c(t) > 0, P_{cA}(t) > 0, H_c(t) > 0, B_e(t) > 0 $, which imply that $ \varphi_0 \notin \partial X_0 $. we will get the similar result for other cases ($ P_c(0) > 0 $, or $ P_{cA}(0) > 0 $, or $ H_c(0) > 0 $). Thus $ \varphi_0 \notin M_{\partial} $. This gives us a contradiction. Hence $ \varphi_0 \in \{ (P_u, 0, P_{uA}, 0, H_u, 0, 0):P_u \ge 0, P_{uA}\ge0, H_u = N_h \} $. So $ M_{\partial} \subseteq \{ (P_u, 0, P_{uA}, 0, H_u, 0, 0):P_u \ge 0, P_{uA}\ge0, H_u = N_h \} $. Obviously we have $ \{ (P_u, 0, P_{uA}, 0, H_u, 0, 0):P_u \ge 0, P_{uA}\ge0, H_u = N_h \} \subseteq M_{\partial} $, therefore, $ M_{\partial} = \{ (P_u, 0, P_{uA}, 0, H_u, 0, 0):P_u \ge 0, P_{uA}\ge0, H_u = N_h \} $. Let $ \varphi_0 $ be an initial value. Clearly there is only one equilibrium $ E_0 = (N^*, 0, N_p - N^*, 0, N_h, 0, 0) $ in $ M_{\partial} $, so $ \cup_{\varphi_0 \in M_{\partial}}\omega(\varphi_0) = E_0 $. Therefore, $ \{E_0\} $ is a compact and isolated invariant set in $ \partial X_0 $.
Next we claim that there exists a positive constant $ \ell $ such that for any solution of model (2.1), $ \Psi_t(\varphi_0), \varphi_0 \in X_0 $, we have
| $ \limsup\limits_{t \to\infty} d(\Psi_t(\varphi_0), E_0) \ge \ell, $ |
where $ d $ is a distant function in $ X_0 $. We construct by contradiction so that we suppose the claim is not true. Then $ \limsup_{t \to\infty} d(\Psi_t(\varphi_0), E_0) \le \ell $ for any $ \ell > 0 $, namely, there exists a positive constant $ T $, such that $ N^*-\ell \le P_u(t) \le N^*+\ell, \ P_c(t) \le \ell, \ N_p-N^*-\ell \le P_{uA}(t) \le N_p-N^*+\ell, \ P_{cA}(t) \le \ell, \ N_h-\ell \le H_u(t) \le N_h+\ell, \ H_c(t) \le \ell, \ B_e(t) \le \ell, $ for any $ t > T $. While $ t > T $, we have,
|
$ {P′c(t)≥αpβp(1−η)(N∗−ℓ)Hc+κp(N∗−ℓ)Be−γcPc−ϵPc,P′cA(t)≥αpβpA(Np−N∗−ℓ)Hc+κpA(Np−N∗−ℓ)Be−γcAPcA+ϵPc,H′c(t)≥αpβh(1−η)(Nh−ℓ)Pc+αpβhA(1−η)(Nh−ℓ)PcA+κh(Nh−ℓ)Be−μcHc,B′e(t)≥υpPc+υpAPcA+υhHc−γbBe. $
|
(3.4) |
Consider the following auxiliary system:
|
$ {~P′c(t)=αpβp(1−η)(N∗−ℓ)~Hc+κp(N∗−ℓ)~Be−γc~Pc−ϵ~Pc,~P′cA(t)=αpβpA(Np−N∗−ℓ)~Hc+κpA(Np−N∗−ℓ)~Be−γcA~PcA+ϵ~Pc,~H′c(t)=αpβh(1−η)(Nh−ℓ)~Pc+αpβhA(1−η)(Nh−ℓ)~PcA+κh(Nh−ℓ)~Be−μc~Hc,~B′e(t)=υp~Pc+υpA~PcA+υh~Hc−γb~Be. $
|
(3.5) |
we define
|
$ J_1(\ell) = (−γc−ϵ0αpβp(1−η)(N∗−ℓ)κp(N∗−ℓ)ϵ−γcAαpβpA(1−η)(Np−N∗−ℓ)κpA(Np−N∗−ℓ)αpβh(1−η)(Nh−ℓ)αpβhA(1−η)(Nh−ℓ)−μcκh(Nh−ℓ)υpυpAυh−γb) . $
|
For $ R_0 > 1 $, by Corollary 4, we have $ s(J_1(0)) > 0 $. Since $ s(J_1(\ell)) $ is continuous for small $ \ell $, so there exists a positive constant $ \ell $ small enough such that $ s(J_1(\ell)) > 0 $. Thus, there is a positive eigenvalue of $ s(J_1(\delta)) $ with a positive eigenvector. It is easy to see if $ t \to \infty $, then $ \tilde{ P_c}, \tilde{P_{cA}}, \tilde{H_c}, \tilde{B_e } \to \infty $. Then by the comparison principle we get
| $ \lim\limits_{t \to\infty} P_c = \infty, \; \lim\limits_{t \to\infty} P_{cA} = \infty, \; \lim\limits_{t \to\infty} H_c = \infty, \; \lim\limits_{t \to\infty} B_e = \infty. $ |
This contradicts our assumption and completes the proof of the claim.
The claim implies that $ \{E_0\} $ is an isolated invariant set in $ X $ and $ W^s(E_0) \cap X_0 = \emptyset $. Therefore, system (2.1) is uniformly persistent if $ R_0 > 1 $ by Theorem 1.3.1 in [47]. This completes the proof.
In this section we present numerical simulations on the deterministic model and sensitivity analysis of the basic reproduction number in terms of model parameters.
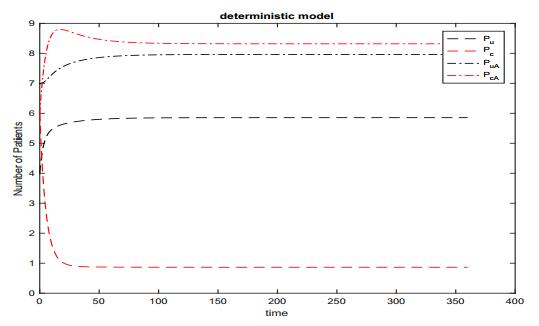
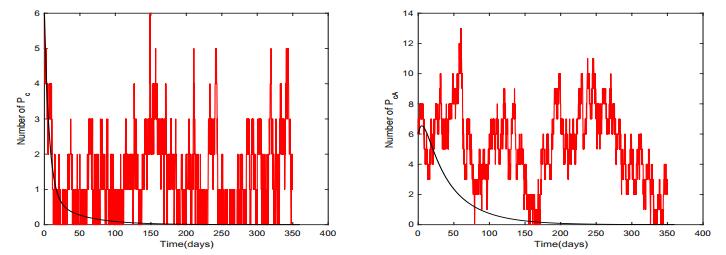
Our deterministic model is simulated for 365 days. Data [24] collected in Beijing Tongren Hospital, where a total of 23 beds were in the emergency ward and were always fully occupied, are used to estimate the initial values of patients and healthcare workers. We assume an initial bacteria density being $ 1000\ ACC/cm^2 $ as comparable to the measurement scale obtained by Bogusz et al. [48]. With the initial values $ (P_u^0, P_{uA}^0, P_c^0, P_{cA}^0, H_u^0, H_c^0, B_e^0) = (4, 6, 7, 6, 17, 6, 1000) $ and parameter values shown in Table 1, we simulate the following outcomes: numerical solutions of the deterministic model (2.1), prevalences of colonized patients without or with antibiotic exposure, and the basic reproduction number $ R_0 $. Simulations are also performed to evaluate the effect of various interventions on changing the prevalence of colonized patients and $ R_0 $.
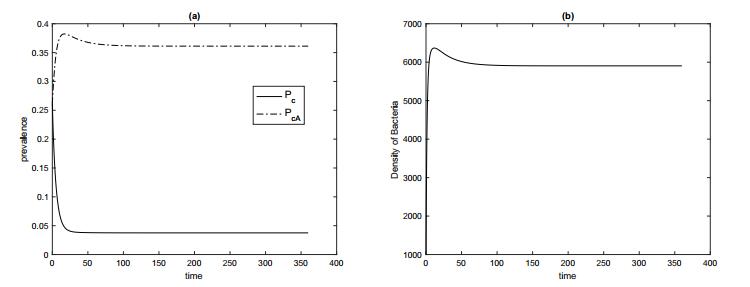
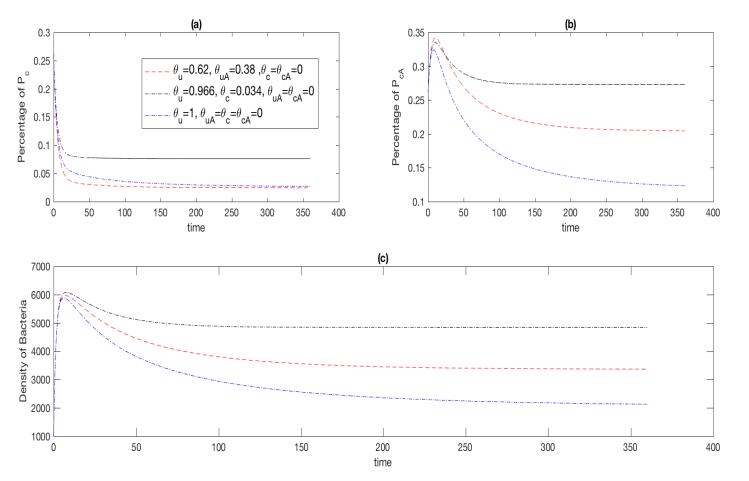
Using the baseline parameters in Table 1, Figures 2 and 3 give the behaviors of solutions to the deterministic model (2.1), which imply that 36$ \% $ of patients are colonized with MRSA with antibiotic exposure, and 4$ \% $ are colonized without antibiotic exposure; Figure 4 shows that, while with no admission of MRSA-positive patients ($ \theta_c = \theta_{cA} = 0 $), 21$ \% $ of patients are colonized with MRSA with antibiotic exposure and 3$ \% $ are colonized without antibiotic exposure; while with no admission of patients with history of antibiotic exposure ($ \theta_{uA} = \theta_{cA} = 0 $), 27$ \% $ of patients are colonized with MRSA with antibiotic exposure, and 7.5$ \% $ are colonized without antibiotic exposure; while with no admission of patients with history of antibiotic exposure and MRSA-positive ($ \theta_{uA} = \theta_c = \theta_{cA} = 0 $), 14$ \% $ of patients are colonized with MRSA with antibiotic exposure, and 3.5$ \% $ are colonized without antibiotic exposure. Hence, to control hospital infections, we may need to reduce the proportion of colonized patients ($ \theta_c $ and $ \theta_{cA} $) at admission by increasing the detection and isolation of the admitted MRSA patients and also reduce the proportion of uncolonized patients with antibiotic exposure ($ \theta_{uA} $) by strengthening the public education about how to use antibiotics properly in the community.
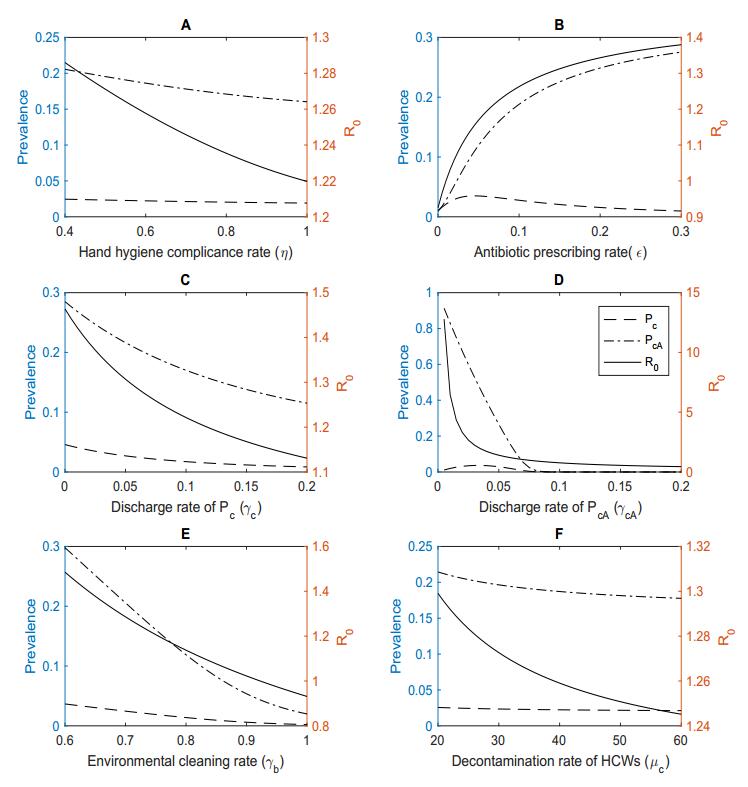
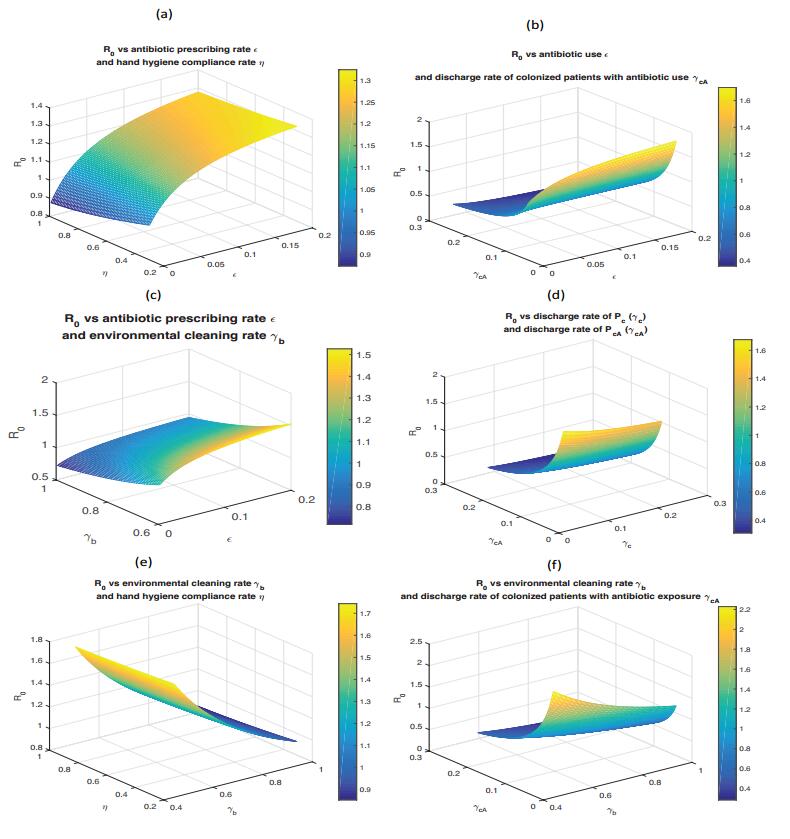
In the case where colonized patients are admitted into hospitals, the infections will always persist. When $ \theta_c = 0, \theta_{cA} = 0 $, that is no colonized patients are admitted into hospital, the infection-free equilibrium (IFE) is defined to be $ E_0 = (P_u, P_c, P_{uA}, P_{cA}, H_u, H_c, B_e) = (N^*, 0, N_p - N^*, 0, N_h, 0, 0) $ where $ N^* $ = $ \frac{\theta_u\gamma_{uA}N_p}{\theta_{uA}\gamma_u+\theta_u\gamma_{uA}+\epsilon} $. By parameters listed in Table 1, the basic reproduction number is estimated to be 1.2860, which means that the infections are persistent. We want to reduce $ R_0 $ to below unity by some interventions. Here we perform some simulations to evaluate the effect of the following interventions in reducing the prevalence of colonized patients with or without antibiotic exposure, and $ R_0 $: (1) Prescription rate of antibiotics $ \epsilon $; (2) Hand hygiene compliance of HCWS $ \eta $; (3) The discharge rate for colonized patients with or without antibiotic exposure $ \gamma_c $ and $ \gamma_{cA} $, respectively; (4) Environmental cleaning rate $ \gamma_b $; and (5) Decontamination rate of HCWs $ \mu_c $.
The predicted effects of individual interventions on reducing the prevalence of MRSA and the reproduction number $ R_0 $ are shown in Figure 5. Figure 5A shows that increasing the compliance rate of hand hygiene for HCWs, $ \eta $, from 0.4 (baseline) to 1, just reduces $ R_0 $ from 1.2860 to 1.2197, and reduces the prevalence of colonized patients with or without antibiotic exposure by 4.51$ \% $ (from 20.56$ \% $ to 16.04$ \% $) and 0.54$ \% $ (from 2.45$ \% $ to 1.91$ \% $), respectively. When antibiotic prescribing rate is reduced from 0.12 (baseline) to 0 (no antibiotic use), we get a result in around 19$ \% $ reduction in the prevalence of colonized patients with antibiotic exposure, while a little increase and then decrease in the prevalence of colonized patients without antibiotic exposure, and a change from 1.2860 to 0.9251 in $ R_0 $ in Figure 5B. We investigate the discharge rate (i.e., the reciprocal of the length of stay) of colonized patients without antibiotic exposure $ \gamma_c $, and with antibiotic exposure $ \gamma_{cA} $, respectively, in Figures 5C-5D. When the discharge rate of $ P_c $ is increased from the baseline value 0.06 to 0.2 (i.e., the length of stay of $ P_c $ is decreased from 16.6 days to 5 days), $ R_0 $ reduces to 1.1308, and the prevalence of $ P_{cA} $ and $ P_c $ reduces by 9.58$ \% $ (from 21.08$ \% $ to 11.50$ \% $) and 1.72$ \% $ (from 2.57$ \% $ to 0.85$ \% $), respectively. Especially, we notice that if we decrease the discharge rate of $ P_{cA} $ a little bit from the baseline value 0.055, there are dramatic increases in both $ R_0 $ and the prevalence of $ P_{cA} $. However, many studies show that colonized patients with antibiotic exposure $ P_{cA} $ usually lead to a lengthier stay [15], which in turns makes the situation worse. Hence, the rapid and efficient treatment of colonized patients, especially those with antibiotic exposure, is key in controlling MRSA infections. Furthermore, we find that improving environmental cleaning rate $ \gamma_b $ is the most effective intervention from Figure 5E. When the environmental cleaning rate is increased from 0.7 (baseline) to 1, we are able to decrease the prevalence of $ P_{cA} $ and $ P_c $ from 20.56$ \% $ to 1.99$ \% $ and from 2.45$ \% $ to 0.21$ \% $, respectively, and successfully reduce $ R_0 $ to below unity. Figure 5F shows that decontamination rate of HCWs has little effect.
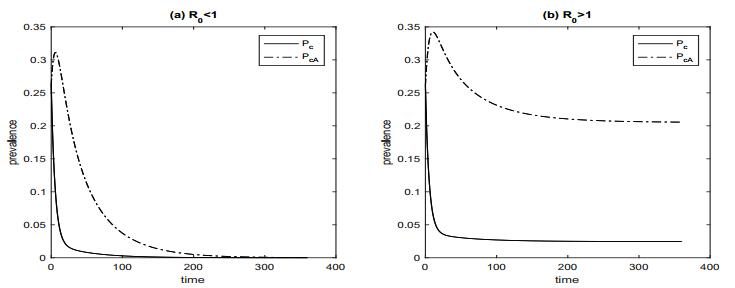
Furthermore, Figure 6 presents a direct simulation of the stability transition at $ R_0 = 1 $ to support our above conclusion that when $ R_0 < 1 $ the infection-free equilibrium is globally asymptotically stable and when $ R_0 > 1 $ the infection is uniformly persistent.
Observing that individual invention is hard to reduce $ R_0 $ to below unity, we examine the effects of combined interventions (Figure 7). When we decrease antibiotic use and in the meanwhile increase the discharge rate of $ P_{cA} $, we reduce $ R_0 $ to below unity efficiently (Figure 7(b)). Similar result occurs when combining the increased environmental cleaning rate and decreased discharge rate of $ P_{cA} $ (Figure 7(f)).
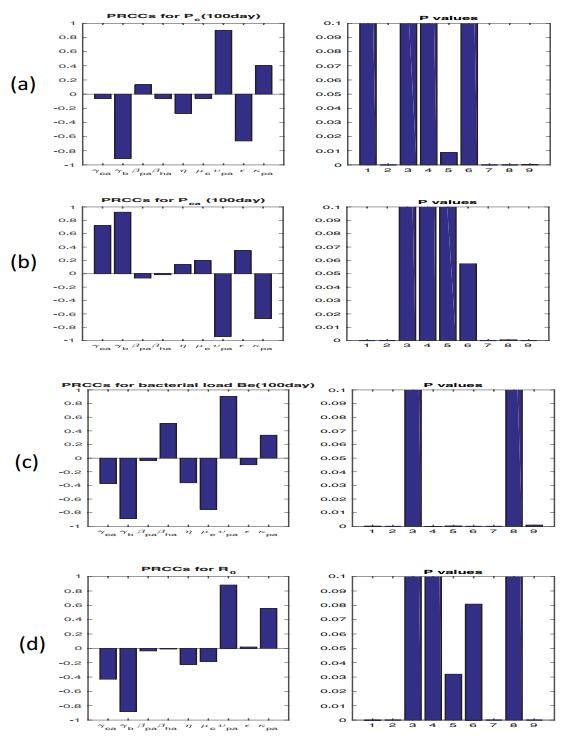
Latin hypercube sampling (LHS) method is used to engage a sensitivity analysis [49,50]. Partial rank correlation coefficients (PRCCs) are calculated for the following nine parameters against the prevalence of colonized patients and $ R_0 $ over time: discharge rate for colonized patients with antibiotic exposure $ \gamma_{cA} $, environmental cleaning rate $ \gamma_b $, probability of colonization for $ P_{uA} $ after a contact with a contaminated HCW $ \beta_{pA} $, probability of contamination for HCW after a contact with a colonized patient with antibiotic exposure $ \beta_{hA} $, hand hygiene compliance rate $ \eta $, decontamination rate of HCWs $ \mu_c $, shedding rate to the environment by colonized patients with antibiotic exposure $ \upsilon_{pA} $, antibiotic prescribing rate $ \epsilon $, contamination rate from environment for uncolonized patients with antibiotic exposure $ \kappa_{pA} $. We also test for significant PRCCs for the above parameters to evaluate which parameters are essential to our model. Since we find that the PRCC values vary little after about 100 days, it is reasonable and efficient for us to just study the PRCC values on this specific day 100 (Figure 8). Figure 8(d) implies that the first four parameters have the most impact on the outcome of $ R_0 $, which are the environmental cleaning rate $ \gamma_b $, shedding rate to the environment by colonized patients with antibiotic exposure $ \upsilon_{pA} $, contamination rate from the environment for uncolonized patients with antibiotic exposure $ \kappa_{pA} $, and antibiotic prescribing rate $ \epsilon $. From Figures 8(a)-8(c), we illustrate the PRCC values of the nine examined parameters and corresponding p-values for different outcome parameters for $ P_c $, $ P_{cA} $, and $ B_e $. All simulations are done by MATLAB and input parameters are assumed to be normally distributed, due to the lack of present data concerning distribution functions, as shown in Table 2.
| Symbol | Distribution | reference |
| $ \gamma_{cA} $ | $ N(0.055, 0.005) $ | estimated by [26] |
| $ \gamma_b $ | $ N(0.7, 0.2) $ | estimated by [26] |
| $ \beta_{pA} $ | $ N(0.43, 0.1) $ | estimated by [26] |
| $ \beta_{hA} $ | $ N(0.2, 0.05) $ | estimated by [26] |
| $ \eta $ | $ N(0.4, 0.1) $ | estimated by [26] |
| $ \mu_c $ | $ N(24, 5) $ | estimated by [26] |
| $ \upsilon_{pA} $ | $ N(470,150) $ | estimated by [26] |
| $ \epsilon $ | $ N(0.12, 0.02) $ | estimated by [26] |
| $ \kappa_{pA} $ | $ N(0.000005, 0.0000006) $ | estimated by [26] |
DownLoad:
CSV
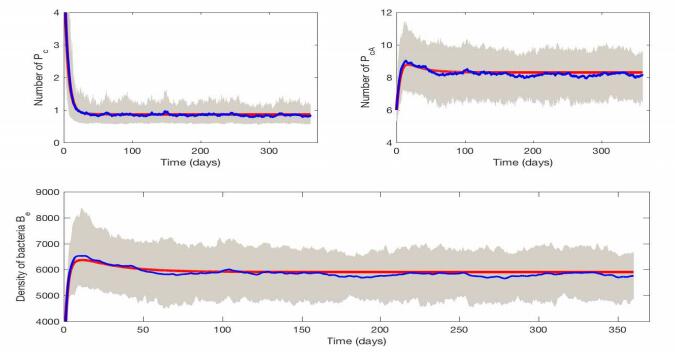
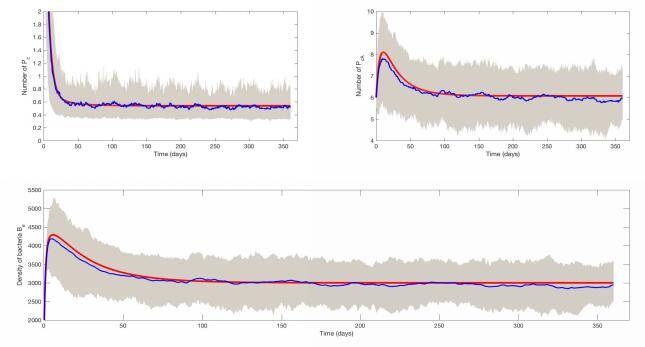
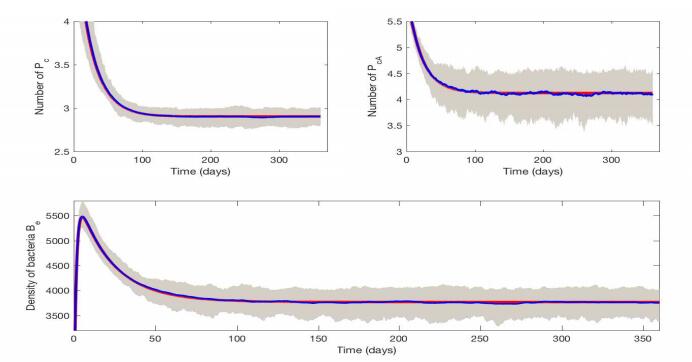
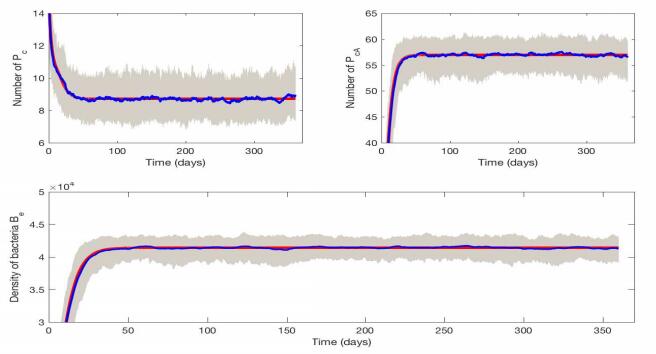
Finally we run some numerical simulations of the stochastic model. Using the baseline parameters in Table 1 and initial values $ (P_u^0, P_{uA}^0, P_c^0, P_{cA}^0, H_u^0, H_c^0, B_e^0) = (4, 6, 7, 6, 17, 6, 1000) $, we run 100 stochastic simulations of the SDE model (2.3). In Figure 9, the blue curves, red curves, and shaded regions represent the averages of 100 runs, outputs of the deterministic model (2.1), and $ 90\% $ bound of 100 runs, respectively. It is shown that the average of stochastic runs is consistent with the outcome of the deterministic model; however, randomness does make a difference in a single stochastic case. Also, we study the effect of environmental cleaning rate $ \gamma_b $ and antibiotic prescribing rate $ \epsilon $ on the number of colonized patients in Figures 10 and 11, respectively. Compared with Figure 9, we increase environmental cleaning rate, $ \gamma_b = 1 $, in Figure 10, which shows that increasing environmental cleaning rate can reduce the average number of colonized patients in the SDE model. Similarly, compared with Figure 9, we reduce the antibiotic use to an extreme case, $ \epsilon = 0 $, in Figure 11, which reduces the average number of colonized patients greatly in the SDE model.
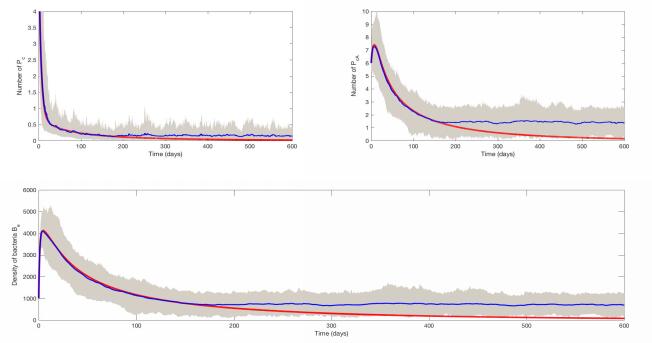
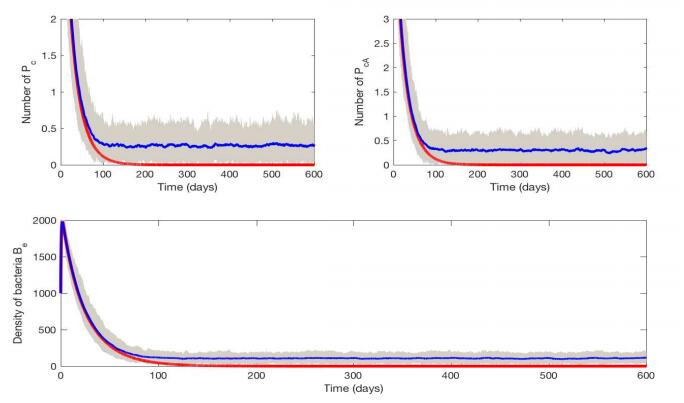
Next, we consider the case with no admission of MRSA-positive patients, i.e., $ \theta_c = \theta_{cA} = 0 $, so $ R_0 $ can be calculated. We have proved that when $ R_0 < 1 $, MRSA infections will go to extinction in the deterministic model (2.1). By choosing different parameter values to make $ R_0 < 1 $ in both Figures 12 and 13, it is shown that MRSA infections do go to extinction in the deterministic model. However, the average number of colonized patients in the SDEs model persists, even though it is small, in Figures 12 and 13. In the above simulations, the number of colonized patients was treated as a real number rather than an integer. In order to intuitively see a difference between deterministic and stochastic models for a small population, in Figure 14, we round the real number to the nearest integer. This shows that with no admission of colonized patients, there are still reinfections after the number of colonized patients drops to zero, which indicates that the free-living bacteria may persist in the environment and later be transmitted back to the patients. That is to say, the free-living bacteria in the environment may be able to cause a later outbreak even though the infections have been died out from patients. Hence, hospitals should pay attention to environmental cleaning strategies to prevent MRSA infections.
Furthermore, in a relatively large population, where we consider initial values
| $ (P_u^0, P_{uA}^0, P_c^0, P_{cA}^0, H_u^0, H_c^0, B_e^0) = (34, 16, 17, 16, 17, 6, 1000), $ |
Figure 15 shows that the average of multiple stochastic runs is consistent with the deterministic outcome.
We developed a comprehensive study of MRSA infections in hospitals, which includes crucial factors such as antibiotic exposure and environmental contamination. Both deterministic and stochastic mathematical models were developed to study the transmission dynamics of MRSA infections in hospitals, including uncolonized patients without and with antibiotic exposure, colonized patients without and with antibiotic exposure, uncontaminated and contaminated health-care workers, and free-living MRSA. Under the assumption that there is no admission of the colonized patients, the basic reproduction number $ R_0 $ was calculated. It was shown that when $ R_0 < 1 $ the infection-free equilibrium is globally asymptotically stable, and when $ R_0 > 1 $ the infection is uniformly persistent.
For the deterministic model, numerical simulations were performed to demonstrate the behavior of the solutions, the effect of several interventions on reducing the prevalence of colonized patients and the basic reproduction number, and the dependence and sensitivity of the basic reproduction number of various parameters. Until recently, control strategies focus on the direct transmission between HCWs and patients, however, our results strongly supported that the environmental cleaning is the most effective intervention. When we increased the environmental cleaning rate, we could decrease the prevalence of colonized patients greatly and successfully reduce $ R_0 $ to below unity in Figure 5. Sensitively analysis in Figure 8 also showed that the environmental cleaning rate $ \gamma_b $, shedding rate to the environment by colonized patients with antibiotic exposure $ \upsilon_{pA} $, contamination rate from the environment for uncolonized patients with antibiotic exposure $ \kappa_{pA} $, and antibiotic prescribing rate $ \epsilon $ had remarkable impacts on the number of colonized patients and $ R_0 $. Even though it is difficult to quantify the environmental cleaning, we suggest that hospitals should try to use more effective cleaning products, improve monitoring strategies such as providing feedback to cleaning teams, and even use new technology (cleaning robots) to supplement the manual cleanings. Besides, it was shown that a higher discharge rate is associated with a lower prevalence of MRSA. The rapid and efficient treatment of colonized patients, especially those with antibiotic exposure, is key in controlling MRSA infections. However, the discharge rate depends on the time required for treatment and cannot be arbitrarily modified at will, which makes the control of MRSA infections challenge. In the cases of outbreaks, hospitals should try proper isolation of those colonized patients. Also, screening and isolating colonized patients at admission are important control strategies. Our study also emphasized the importance of effective antimicrobial stewardship programs in reducing antibiotic usage both in hospitals and communities.
For the stochastic model, numerical simulations were also carried out to study the behavior of the stochastic model and the effect of antibiotic prescribing rate $ \epsilon $, and environmental cleaning rate $ \gamma_b $, on the number of colonized patients, respectively. Moreover, we chose different parameter values to make $ R_0 < 1 $ and found that MRSA infections go to extinction in the deterministic model; however, the average number of colonized patients in multiple stochastic runs persisted in Figures 12 and 13. In order to intuitively see a difference between deterministic and stochastic models for a small population, in Figure 14, we rounded the real number to the nearest integer. This shows that the free-living bacteria in the environment may be able to cause a later outbreak even though the infections have been died out from patients. Hence, hospitals should pay attention to environmental cleaning strategies to prevent MRSA infections.
In the proposed model, the heterogeneity in infection risk among different types of wards was omitted and free-living bacteria were assumed to be uniformly distributed for the sake of simplicity; however, heterogeneity should be taken into account in the future work for a more realistic consideration [12,14]. Also, model parameters were regarded as a constant, however, it is not necessarily true in the real world. In applications, parameters in the model need to be inferred from noisy data. Recent works have developed several methods to infer parameters in models with complex and flexible structures [51,52,53], which should be potentially considered in future works. In addition, in current model the complex contact pattern was simplified to a full mixing, however, it may be useful to take into account the contact network structure in future works to represent heterogeneity in population behavior, locations and contact patterns [54,55]. In current model setting, patients were assumed to be hospitalized and under antibiotic treatments because of other diseases, then for those patients with antibiotic treatment, they were just more likely to be colonized by MRSA, and then had a lower probability of successful treatment, a lengthier stay in hospitals and extra costs of treatment. That is to say, we ignored the difference between colonized patients and infected patients since treatment should be needed for infected patients. A more comprehensive work may be done in the future [15]. Furthermore, an extension should be specifically compared with this proposed model and its conclusions and applied to actual MRSA infection data in hospitals ([25,57]).
This research was partially supported by the University of Miami Provost's Research Award (UM PRA 2019-409). We would like to thank Dr. Xi Huo and three anonymous reviewers for their helpful comments and suggestions which helped us to improve the presentation of the paper.
All authors declare no conflicts of interest in this paper.
| [1] | Banks S, Dinges DF (2007) Behavioral and physiological consequences of sleep restriction. J Clin Sleep Med 3: 519-528. |
| [2] | Van Dongen HP, Maislin G, Mullington JM, et al. (2003) The cumulative cost of additional wakefulness: dose-response effects on neurobehavioral functions and sleep physiology from chronic sleep restriction and total sleep deprivation. Sleep 26: 117-126. |
| [3] |
Knutson KL, Spiegel K, Penev P, et al. (2007) The metabolic consequences of sleep deprivation. Sleep Med Rev 11: 163-178. doi: 10.1016/j.smrv.2007.01.002
|
| [4] |
Dixit A, Mittal T (2015) Executive Functions are not Affected by 24 Hours of Sleep Deprivation: A Color-Word Stroop Task Study. Indian J Psychol Med 37: 165-168. doi: 10.4103/0253-7176.155615
|
| [5] |
Mignot E (2008) Why we sleep: the temporal organization of recovery. PLoS Biol 6: e106. doi: 10.1371/journal.pbio.0060106
|
| [6] |
McCormick DA, Bal T (1997) Sleep and arousal: thalamocortical mechanisms. Annu Rev Neurosci 20: 185-215. doi: 10.1146/annurev.neuro.20.1.185
|
| [7] |
Pace-Schott EF, Hobson JA (2002) The neurobiology of sleep: genetics, cellular physiology and subcortical networks. Nat Rev Neurosci 3: 591-605. doi: 10.1038/nrn895
|
| [8] |
Villablanca JR (2004) Counterpointing the functional role of the forebrain and of the brainstem in the control of the sleep-waking system. J Sleep Res 13: 179-208. doi: 10.1111/j.1365-2869.2004.00412.x
|
| [9] | Krueger J CL, Rector D (2009) Cytokines and other neuromodulators. Stickgold R, Walker M (eds) The neuroscience of sleep. |
| [10] | Porkka-Heiskanen T (2011) Methylxanthines and sleep. Fredholm BB (ed) Methylxanthines, handbook of experimental pharmacology 331-348. |
| [11] |
Krueger JM, Rector DM, Roy S, et al. (2008) Sleep as a fundamental property of neuronal assemblies. Nat Rev Neurosci 9: 910-919. doi: 10.1038/nrn2521
|
| [12] |
Vyazovskiy VV, Olcese U, Hanlon EC, et al. (2011) Local sleep in awake rats. Nature 472: 443-447. doi: 10.1038/nature10009
|
| [13] |
Llinas RR, Steriade M (2006) Bursting of thalamic neurons and states of vigilance. J Neurophysiol 95: 3297-3308. doi: 10.1152/jn.00166.2006
|
| [14] |
Coulon P, Budde T, Pape HC (2012) The sleep relay--the role of the thalamus in central and decentral sleep regulation. Pflugers Arch 463: 53-71. doi: 10.1007/s00424-011-1014-6
|
| [15] | Steriade M MR (1990) Brainstem control of wakefulness and sleep. Plenum, New York. |
| [16] |
Haas HL L, JS (2012) Waking with the hypothalamus. Pflugers Arch 463: 31-42. doi: 10.1007/s00424-011-0996-4
|
| [17] |
Basheer R SR, Thakkar MM, McCarley RW (2004) Adenosine and sleep-wake regulation. Progr Neurobiol 73: 379-396. doi: 10.1016/j.pneurobio.2004.06.004
|
| [18] |
Obal F, Jr., Krueger JM (2003) Biochemical regulation of non-rapid-eye-movement sleep. Front Biosci 8: d520-550. doi: 10.2741/1033
|
| [19] |
De Sarro G, Gareri P, Sinopoli VA, et al. (1997) Comparative, behavioural and electrocortical effects of tumor necrosis factor-alpha and interleukin-1 microinjected into the locus coeruleus of rat. Life Sci 60: 555-564. doi: 10.1016/S0024-3205(96)00692-3
|
| [20] |
Manfridi A, Brambilla D, Bianchi S, et al. (2003) Interleukin-1beta enhances non-rapid eye movement sleep when microinjected into the dorsal raphe nucleus and inhibits serotonergic neurons in vitro. Eur J Neurosci 18: 1041-1049. doi: 10.1046/j.1460-9568.2003.02836.x
|
| [21] |
De A, Churchill L, Obal F, Jr., et al. (2002) GHRH and IL1beta increase cytoplasmic Ca(2+) levels in cultured hypothalamic GABAergic neurons. Brain Res 949: 209-212. doi: 10.1016/S0006-8993(02)03157-8
|
| [22] | Huber R, Tononi G, Cirelli C (2007) Exploratory behavior, cortical BDNF expression, and sleep homeostasis. Sleep 30: 129-139. |
| [23] |
Porkka-Heiskanen T, Alanko L, Kalinchuk A, et al. (2002) Adenosine and sleep. Sleep Med Rev 6: 321-332. doi: 10.1053/smrv.2001.0201
|
| [24] |
Oishi Y, Huang ZL, Fredholm BB, et al. (2008) Adenosine in the tuberomammillary nucleus inhibits the histaminergic system via A1 receptors and promotes non-rapid eye movement sleep. Proc Natl Acad Sci U S A 105: 19992-19997. doi: 10.1073/pnas.0810926105
|
| [25] | Rosenberg PA, Li Y, Le M, et al. (2000) Nitric oxide-stimulated increase in extracellular adenosine accumulation in rat forebrain neurons in culture is associated with ATP hydrolysis and inhibition of adenosine kinase activity. J Neurosci 20: 6294-6301. |
| [26] |
MM H (2011) Thalamocortical dynamics of sleep: roles of purinergic neuromodulation. Semin Cell Dev Biol 22: 245-251. doi: 10.1016/j.semcdb.2011.02.008
|
| [27] |
Steriade M, McCormick DA, Sejnowski TJ (1993) Thalamocortical oscillations in the sleeping and aroused brain. Science 262: 679-685. doi: 10.1126/science.8235588
|
| [28] |
Brown RE, Basheer R, McKenna JT, et al. (2012) Control of sleep and wakefulness. Physiol Rev 92: 1087-1187. doi: 10.1152/physrev.00032.2011
|
| [29] | Rechtschaffen A KA (1968) A manual of Standardized Terminology, Techniques and Scoring System for Sleep Stages of Human Subjects. National Institue of Health Publication Washington, DC: NIH US Goverment Printing Office |
| [30] |
Jeanneret PR, Webb WB (1963) Strength of grip on arousal from full night's sleep. Percept Mot Skills 17: 759-761. doi: 10.2466/pms.1963.17.3.759
|
| [31] |
Tassi P, Muzet A (2000) Sleep inertia. Sleep Med Rev 4: 341-353. doi: 10.1053/smrv.2000.0098
|
| [32] | Klemm WR (2011) Why does rem sleep occur? A wake-up hypothesis. Front Syst Neurosci 5: 73. |
| [33] |
Roffwarg HP, Muzio JN, Dement WC (1966) Ontogenetic development of the human sleep-dream cycle. Science 152: 604-619. doi: 10.1126/science.152.3722.604
|
| [34] | Endo T, Roth C, Landolt HP, et al. (1998) Selective REM sleep deprivation in humans: effects on sleep and sleep EEG. Am J Physiol 274: R1186-1194. |
| [35] | Barone DA, Krieger AC (2014) Muscle Tone Control of REM Sleep. REM Sleep: Characteristics, Disorders, and Physiological Effects / Editor: Chelsea L Saylor |
| [36] |
Kamphuis J, Lancel M, Koolhaas JM, et al. (2015) Deep sleep after social stress: NREM sleep slow-wave activity is enhanced in both winners and losers of a conflict. Brain Behav Immun 47:149-54. doi: 10.1016/j.bbi.2014.12.022
|
| [37] |
Benington JH, Heller HC (1995) Restoration of brain energy metabolism as the function of sleep. Prog Neurobiol 45: 347-360. doi: 10.1016/0301-0082(94)00057-O
|
| [38] | H. Blake RWG (1937) Brain potentials during sleep. Am J Physiol 119 692-703. |
| [39] | Friedman L, Bergmann BM, Rechtschaffen A (1979) Effects of sleep deprivation on sleepiness, sleep intensity, and subsequent sleep in the rat. Sleep 1: 369-391. |
| [40] |
Tobler I, Borbely AA (1986) Sleep EEG in the rat as a function of prior waking. Electroencephalogr Clin Neurophysiol 64: 74-76. doi: 10.1016/0013-4694(86)90044-1
|
| [41] |
Dijk DJ, Beersma DG, Daan S (1987) EEG power density during nap sleep: reflection of an hourglass measuring the duration of prior wakefulness. J Biol Rhythms 2: 207-219. doi: 10.1177/074873048700200304
|
| [42] |
Franken P, Tobler I, Borbely AA (1991) Sleep homeostasis in the rat: simulation of the time course of EEG slow-wave activity. Neurosci Lett 130: 141-144. doi: 10.1016/0304-3940(91)90382-4
|
| [43] |
Lancel M, van Riezen H, Glatt A (1992) The time course of sigma activity and slow-wave activity during NREMS in cortical and thalamic EEG of the cat during baseline and after 12 hours of wakefulness. Brain Res 596: 285-295. doi: 10.1016/0006-8993(92)91559-W
|
| [44] |
Huber R, Deboer T, Tobler I (2000) Effects of sleep deprivation on sleep and sleep EEG in three mouse strains: empirical data and simulations. Brain Res 857: 8-19. doi: 10.1016/S0006-8993(99)02248-9
|
| [45] | Sanchez-Vives MV, Mattia M (2014) Slow wave activity as the default mode of the cerebral cortex. Arch Ital Biol 152: 147-155. |
| [46] |
Meerlo P, Pragt BJ, Daan S (1997) Social stress induces high intensity sleep in rats. Neurosci Lett 225: 41-44. doi: 10.1016/S0304-3940(97)00180-8
|
| [47] |
Meerlo P, de Bruin EA, Strijkstra AM, et al. (2001) A social conflict increases EEG slow-wave activity during subsequent sleep. Physiol Behav 73: 331-335. doi: 10.1016/S0031-9384(01)00451-6
|
| [48] |
Berger RJ, Phillips NH (1995) Energy conservation and sleep. Behav Brain Res 69: 65-73. doi: 10.1016/0166-4328(95)00002-B
|
| [49] |
Berger RJ (1984) Slow wave sleep, shallow torpor and hibernation: homologous states of diminished metabolism and body temperature. Biol Psychol 19: 305-326. doi: 10.1016/0301-0511(84)90045-0
|
| [50] |
Siegel JM (2009) Sleep viewed as a state of adaptive inactivity. Nat Rev Neurosci 10: 747-753. doi: 10.1038/nrn2697
|
| [51] |
Rechtschaffen A (1998) Current perspectives on the function of sleep. Perspect Biol Med 41: 359-390. doi: 10.1353/pbm.1998.0051
|
| [52] |
Zepelin H, Rechtschaffen A (1974) Mammalian sleep, longevity, and energy metabolism. Brain Behav Evol 10: 425-470. doi: 10.1159/000124330
|
| [53] | Horne J (2002) Why sleep? Biologist (London) 49: 213-216. |
| [54] | Schmidt MH (2014) The energy allocation function of sleep: A unifying theory of sleep, torpor, and continuous wakefulness. Neurosci Biobehav Rev 47c: 122-153. |
| [55] |
Adam K (1980) Sleep as a restorative process and a theory to explain why. Prog Brain Res 53: 289-305. doi: 10.1016/S0079-6123(08)60070-9
|
| [56] |
Oswald I (1980) Sleep as restorative process: human clues. Prog Brain Res 53: 279-288. doi: 10.1016/S0079-6123(08)60069-2
|
| [57] |
Landgraf D, Shostak A, Oster H (2012) Clock genes and sleep. Pflugers Arch 463: 3-14. doi: 10.1007/s00424-011-1003-9
|
| [58] |
Wisor JP (2012) A metabolic-transcriptional network links sleep and cellular energetics in the brain. Pflugers Arch 463: 15-22. doi: 10.1007/s00424-011-1030-6
|
| [59] |
Cirelli C, Gutierrez CM, Tononi G (2004) Extensive and divergent effects of sleep and wakefulness on brain gene expression. Neuron 41: 35-43. doi: 10.1016/S0896-6273(03)00814-6
|
| [60] |
Mackiewicz M, Shockley KR, Romer MA, et al. (2007) Macromolecule biosynthesis: a key function of sleep. Physiol Genomics 31: 441-457. doi: 10.1152/physiolgenomics.00275.2006
|
| [61] |
Cirelli C (2006) Cellular consequences of sleep deprivation in the brain. Sleep Med Rev 10: 307-321. doi: 10.1016/j.smrv.2006.04.001
|
| [62] | Clugston GA, Garlick PJ (1982) The response of protein and energy metabolism to food intake in lean and obese man. Hum Nutr Clin Nutr 36c: 57-70. |
| [63] | Clugston GA, Garlick PJ (1982) The response of whole-body protein turnover to feeding in obese subjects given a protein-free, low-energy diet for three weeks. Hum Nutr Clin Nutr 36: 391-397. |
| [64] | Golden MH, Waterlow JC (1977) Total protein synthesis in elderly people: a comparison of results with [15N]glycine and [14C]leucine. Clin Sci Mol Med 53: 277-288. |
| [65] |
Horne JA (1980) Sleep and body restitution. Experientia 36: 11-13. doi: 10.1007/BF02003942
|
| [66] |
Meddis R (1975) On the function of sleep. Anim Behav 23: 676-691. doi: 10.1016/0003-3472(75)90144-X
|
| [67] |
Rial RV, Nicolau MC, Gamundi A, et al. (2007) The trivial function of sleep. Sleep Med Rev 11: 311-325. doi: 10.1016/j.smrv.2007.03.001
|
| [68] |
Webb WB (1974) Sleep as an adaptive response. Percept Mot Skills 38: 1023-1027. doi: 10.2466/pms.1974.38.3c.1023
|
| [69] | Villafuerte G, Miguel-Puga A, Rodriguez EM, et al. (2015) Sleep deprivation and oxidative stress in animal models: a systematic review. Oxid Med Cell Longev 2015: 234952. |
| [70] |
Komoda Y, Honda K, Inoue S (1990) SPS-B, a physiological sleep regulator, from the brainstems of sleep-deprived rats, identified as oxidized glutathione. Chem Pharm Bull (Tokyo) 38: 2057-2059. doi: 10.1248/cpb.38.2057
|
| [71] |
Honda K, Komoda Y, Inoue S (1994) Oxidized glutathione regulates physiological sleep in unrestrained rats. Brain Res 636: 253-258. doi: 10.1016/0006-8993(94)91024-3
|
| [72] |
Kimura M, Kapas L, Krueger JM (1998) Oxidized glutathione promotes sleep in rabbits. Brain Res Bull 45: 545-548. doi: 10.1016/S0361-9230(97)00441-3
|
| [73] |
Krueger JM, Obal F, Jr., Fang J (1999) Why we sleep: a theoretical view of sleep function. Sleep Med Rev 3: 119-129. doi: 10.1016/S1087-0792(99)90019-9
|
| [74] |
Basner M, Rao H, Goel N, et al. (2013) Sleep deprivation and neurobehavioral dynamics. Curr Opin Neurobiol 23: 854-863. doi: 10.1016/j.conb.2013.02.008
|
| [75] |
Hennevin E, Huetz C, Edeline JM (2007) Neural representations during sleep: from sensory processing to memory traces. Neurobiol Learn Mem 87: 416-440. doi: 10.1016/j.nlm.2006.10.006
|
| [76] |
Tononi G, Cirelli C (2014) Sleep and the price of plasticity: from synaptic and cellular homeostasis to memory consolidation and integration. Neuron 81: 12-34. doi: 10.1016/j.neuron.2013.12.025
|
| [77] |
Xie L, Kang H, Xu Q, et al. (2013) Sleep drives metabolite clearance from the adult brain. Science 342: 373-377. doi: 10.1126/science.1241224
|
| [78] |
Mendelsohn AR, Larrick JW (2013) Sleep facilitates clearance of metabolites from the brain: glymphatic function in aging and neurodegenerative diseases. Rejuvenation Res 16: 518-523. doi: 10.1089/rej.2013.1530
|
| [79] | Spira AP, Gamaldo AA, An Y, et al. (2013) Self-reported sleep and beta-amyloid deposition in community-dwelling older adults. JAMA Neurol 70: 1537-1543. |
| [80] |
Hahn EA, Wang HX, Andel R, et al. (2014) A change in sleep pattern may predict Alzheimer disease. Am J Geriatr Psychiatry 22: 1262-1271. doi: 10.1016/j.jagp.2013.04.015
|
| [81] |
Lim AS, Yu L, Kowgier M, et al. (2013) Modification of the relationship of the apolipoprotein E epsilon4 allele to the risk of Alzheimer disease and neurofibrillary tangle density by sleep. JAMA Neurol 70: 1544-1551. doi: 10.1001/jamaneurol.2013.4215
|
| [82] |
Ambrosini MV, Giuditta A (2001) Learning and sleep: the sequential hypothesis. Sleep Med Rev 5: 477-490. doi: 10.1053/smrv.2001.0180
|
| [83] | Ribeiro S, Mello CV, Velho T, et al. (2002) Induction of hippocampal long-term potentiation during waking leads to increased extrahippocampal zif-268 expression during ensuing rapid-eye-movement sleep. J Neurosci 22: 10914-10923. |
| [84] |
Ribeiro S, Gervasoni D, Soares ES, et al. (2004) Long-lasting novelty-induced neuronal reverberation during slow-wave sleep in multiple forebrain areas. PLoS Biol 2: E24. doi: 10.1371/journal.pbio.0020024
|
| [85] |
Huber R, Ghilardi MF, Massimini M, et al. (2004) Local sleep and learning. Nature 430: 78-81. doi: 10.1038/nature02663
|
| [86] |
Walker MP, Stickgold R (2004) Sleep-dependent learning and memory consolidation. Neuron 44: 121-133. doi: 10.1016/j.neuron.2004.08.031
|
| [87] |
Stickgold R, Walker MP (2005) Memory consolidation and reconsolidation: what is the role of sleep? Trends Neurosci 28: 408-415. doi: 10.1016/j.tins.2005.06.004
|
| [88] | Maquet P, Schwartz S, Passingham R, et al. (2003) Sleep-related consolidation of a visuomotor skill: brain mechanisms as assessed by functional magnetic resonance imaging. J Neurosci 23: 1432-1440. |
| [89] |
Tononi G, Cirelli C (2006) Sleep function and synaptic homeostasis. Sleep Med Rev 10: 49-62. doi: 10.1016/j.smrv.2005.05.002
|
| [90] |
Kavanau JL (1997) Memory, sleep and the evolution of mechanisms of synaptic efficacy maintenance. Neuroscience 79: 7-44. doi: 10.1016/S0306-4522(96)00610-0
|
| [91] |
Stickgold R (2006) Neuroscience: a memory boost while you sleep. Nature 444: 559-560. doi: 10.1038/nature05309
|
| [92] |
Eichenbaum H (2007) To sleep, perchance to integrate. Proc Natl Acad Sci U S A 104: 7317-7318. doi: 10.1073/pnas.0702503104
|
| [93] |
Fenn KM, Nusbaum HC, Margoliash D (2003) Consolidation during sleep of perceptual learning of spoken language. Nature 425: 614-616. doi: 10.1038/nature01951
|
| [94] |
Ferrara M, Iaria G, De Gennaro L, et al. (2006) The role of sleep in the consolidation of route learning in humans: a behavioural study. Brain Res Bull 71: 4-9. doi: 10.1016/j.brainresbull.2006.07.015
|
| [95] |
Peigneux P, Laureys S, Fuchs S, et al. (2004) Are spatial memories strengthened in the human hippocampus during slow wave sleep? Neuron 44: 535-545. doi: 10.1016/j.neuron.2004.10.007
|
| [96] |
Gottselig JM, Hofer-Tinguely G, Borbely AA, et al. (2004) Sleep and rest facilitate auditory learning. Neuroscience 127: 557-561. doi: 10.1016/j.neuroscience.2004.05.053
|
| [97] |
Peters KR, Smith V, Smith CT (2007) Changes in sleep architecture following motor learning depend on initial skill level. J Cogn Neurosci 19: 817-829. doi: 10.1162/jocn.2007.19.5.817
|
| [98] |
Ellenbogen JM, Payne JD, Stickgold R (2006) The role of sleep in declarative memory consolidation: passive, permissive, active or none? Curr Opin Neurobiol 16: 716-722. doi: 10.1016/j.conb.2006.10.006
|
| [99] |
Ellenbogen JM, Hulbert JC, Stickgold R, et al. (2006) Interfering with theories of sleep and memory: sleep, declarative memory, and associative interference. Curr Biol 16: 1290-1294. doi: 10.1016/j.cub.2006.05.024
|
| [100] |
Roth TC, 2nd, Rattenborg NC, Pravosudov VV (2010) The ecological relevance of sleep: the trade-off between sleep, memory and energy conservation. Philos Trans R Soc Lond B Biol Sci 365: 945-959. doi: 10.1098/rstb.2009.0209
|
| [101] | Fogel SMS, C. T. (2006) Declarative learningdependent changes in theta power during REM sleep. Sleep: A375-A375. |
| [102] |
Born J, Rasch B, Gais S (2006) Sleep to remember. Neuroscientist 12: 410-424. doi: 10.1177/1073858406292647
|
| [103] |
Wyatt RJ, Fram DH, Kupfer DJ, et al. (1971) Total prolonged drug-induced REM sleep suppression in anxious-depressed patients. Arch Gen Psychiatry 24: 145-155. doi: 10.1001/archpsyc.1971.01750080049007
|
| [104] |
Siegel JM (2001) The REM sleep-memory consolidation hypothesis. Science 294: 1058-1063. doi: 10.1126/science.1063049
|
| [105] |
Rasch B, Pommer J, Diekelmann S, et al. (2009) Pharmacological REM sleep suppression paradoxically improves rather than impairs skill memory. Nat Neurosci 12: 396-397. doi: 10.1038/nn.2206
|
| [106] |
Irwin MR (2015) Why sleep is important for health: a psychoneuroimmunology perspective. Annu Rev Psychol 66: 143-172. doi: 10.1146/annurev-psych-010213-115205
|
| [107] |
Baglioni C, Battagliese G, Feige B, et al. (2011) Insomnia as a predictor of depression: a meta-analytic evaluation of longitudinal epidemiological studies. J Affect Disord 135: 10-19. doi: 10.1016/j.jad.2011.01.011
|
| [108] |
Dryman A, Eaton WW (1991) Affective symptoms associated with the onset of major depression in the community: findings from the US National Institute of Mental Health Epidemiologic Catchment Area Program. Acta Psychiatr Scand 84: 1-5. doi: 10.1111/j.1600-0447.1991.tb01410.x
|
| [109] | Lee E, Cho HJ, Olmstead R, et al. (2013) Persistent sleep disturbance: a risk factor for recurrent depression in community-dwelling older adults. Sleep 36: 1685-1691. |
| [110] |
Cho HJ, Lavretsky H, Olmstead R, et al. (2008) Sleep disturbance and depression recurrence in community-dwelling older adults: a prospective study. Am J Psychiatry 165: 1543-1550. doi: 10.1176/appi.ajp.2008.07121882
|
| [111] | Jaussent I, Bouyer J, Ancelin ML, et al. (2011) Insomnia and daytime sleepiness are risk factors for depressive symptoms in the elderly. Sleep 34: 1103-1110. |
| [112] | Manber R, Edinger JD, Gress JL, et al. (2008) Cognitive behavioral therapy for insomnia enhances depression outcome in patients with comorbid major depressive disorder and insomnia. Sleep 31: 489-495. |
| [113] |
Giedke H, Schwarzler F (2002) Therapeutic use of sleep deprivation in depression. Sleep Med Rev 6: 361-377. doi: 10.1016/S1087-0792(02)90235-2
|
| [114] |
Grozinger M, Kogel P, Roschke J (2002) Effects of REM sleep awakenings and related wakening paradigms on the ultradian sleep cycle and the symptoms in depression. J Psychiatr Res 36: 299-308. doi: 10.1016/S0022-3956(02)00022-5
|
| [115] |
Killgore WD, Kamimori GH, Balkin TJ (2011) Caffeine protects against increased risk-taking propensity during severe sleep deprivation. J Sleep Res 20: 395-403. doi: 10.1111/j.1365-2869.2010.00893.x
|
| [116] |
McKenna BS, Dickinson DL, Orff HJ, et al. (2007) The effects of one night of sleep deprivation on known-risk and ambiguous-risk decisions. J Sleep Res 16: 245-252. doi: 10.1111/j.1365-2869.2007.00591.x
|
| [117] | Venkatraman V, Chuah YM, Huettel SA, et al. (2007) Sleep deprivation elevates expectation of gains and attenuates response to losses following risky decisions. Sleep 30: 603-609. |
| [118] | Killgore WD, Killgore DB, Day LM, et al. (2007) The effects of 53 hours of sleep deprivation on moral judgment. Sleep 30: 345-352. |
| [119] |
Trinder J, Waloszek J, Woods MJ, et al. (2012) Sleep and cardiovascular regulation. Pflugers Arch 463: 161-168. doi: 10.1007/s00424-011-1041-3
|
| [120] |
Barone DA, Krieger AC (2013) Stroke and obstructive sleep apnea: a review. Curr Atheroscler Rep 15: 334. doi: 10.1007/s11883-013-0334-8
|
| [121] |
Mullington JM, Haack M, Toth M, et al. (2009) Cardiovascular, inflammatory, and metabolic consequences of sleep deprivation. Prog Cardiovasc Dis 51: 294-302. doi: 10.1016/j.pcad.2008.10.003
|
| [122] |
Vgontzas AN, Fernandez-Mendoza J, Liao D, et al. (2013) Insomnia with objective short sleep duration: the most biologically severe phenotype of the disorder. Sleep Med Rev 17: 241-254. doi: 10.1016/j.smrv.2012.09.005
|
| [123] |
Meng L, Zheng Y, Hui R (2013) The relationship of sleep duration and insomnia to risk of hypertension incidence: a meta-analysis of prospective cohort studies. Hypertens Res 36: 985-995. doi: 10.1038/hr.2013.70
|
| [124] |
Palagini L, Bruno RM, Gemignani A, et al. (2013) Sleep loss and hypertension: a systematic review. Curr Pharm Des 19: 2409-2419. doi: 10.2174/1381612811319130009
|
| [125] |
Suka M, Yoshida K, Sugimori H (2003) Persistent insomnia is a predictor of hypertension in Japanese male workers. J Occup Health 45: 344-350. doi: 10.1539/joh.45.344
|
| [126] | Vgontzas AN, Liao D, Bixler EO, et al. (2009) Insomnia with objective short sleep duration is associated with a high risk for hypertension. Sleep 32: 491-497. |
| [127] |
Fernandez-Mendoza J, Vgontzas AN, Liao D, et al. (2012) Insomnia with objective short sleep duration and incident hypertension: the Penn State Cohort. Hypertension 60: 929-935. doi: 10.1161/HYPERTENSIONAHA.112.193268
|
| [128] | Chung WS, Lin CL, Chen YF, et al. (2013) Sleep disorders and increased risk of subsequent acute coronary syndrome in individuals without sleep apnea: a nationwide population-based cohort study. Sleep 36: 1963-1968. |
| [129] |
Vozoris NT (2013) The relationship between insomnia symptoms and hypertension using United States population-level data. J Hypertens 31: 663-671. doi: 10.1097/HJH.0b013e32835ed5d0
|
| [130] | Phillips B, Buzkova P, Enright P (2009) Insomnia did not predict incident hypertension in older adults in the cardiovascular health study. Sleep 32: 65-72. |
| [131] | Phillips B, Mannino DM (2007) Do insomnia complaints cause hypertension or cardiovascular disease? J Clin Sleep Med 3: 489-494. |
| [132] |
Ayas NT, White DP, Manson JE, et al. (2003) A prospective study of sleep duration and coronary heart disease in women. Arch Intern Med 163: 205-209. doi: 10.1001/archinte.163.2.205
|
| [133] | Hoevenaar-Blom MP, Spijkerman AM, Kromhout D, et al. (2011) Sleep duration and sleep quality in relation to 12-year cardiovascular disease incidence: the MORGEN study. Sleep 34: 1487-1492. |
| [134] |
Mallon L, Broman JE, Hetta J (2002) Sleep complaints predict coronary artery disease mortality in males: a 12-year follow-up study of a middle-aged Swedish population. J Intern Med 251: 207-216. doi: 10.1046/j.1365-2796.2002.00941.x
|
| [135] |
Wang Q, Xi B, Liu M, et al. (2012) Short sleep duration is associated with hypertension risk among adults: a systematic review and meta-analysis. Hypertens Res 35: 1012-1018. doi: 10.1038/hr.2012.91
|
| [136] |
Cappuccio FP, Cooper D, D'Elia L, et al. (2011) Sleep duration predicts cardiovascular outcomes: a systematic review and meta-analysis of prospective studies. Eur Heart J 32: 1484-1492. doi: 10.1093/eurheartj/ehr007
|
| [137] | Sabanayagam C, Shankar A, Buchwald D, et al. (2011) Insomnia symptoms and cardiovascular disease among older American Indians: the Native Elder Care Study. J Environ Public Health 2011: 964617. |
| [138] |
Heslop P, Smith GD, Metcalfe C, et al. (2002) Sleep duration and mortality: The effect of short or long sleep duration on cardiovascular and all-cause mortality in working men and women. Sleep Med 3: 305-314. doi: 10.1016/S1389-9457(02)00016-3
|
| [139] |
Kronholm E, Laatikainen T, Peltonen M, et al. (2011) Self-reported sleep duration, all-cause mortality, cardiovascular mortality and morbidity in Finland. Sleep Med 12: 215-221. doi: 10.1016/j.sleep.2010.07.021
|
| [140] | Ikehara S, Iso H, Date C, et al. (2009) Association of sleep duration with mortality from cardiovascular disease and other causes for Japanese men and women: the JACC study. Sleep 32: 295-301. |
| [141] |
Suzuki E, Yorifuji T, Ueshima K, et al. (2009) Sleep duration, sleep quality and cardiovascular disease mortality among the elderly: a population-based cohort study. Prev Med 49: 135-141. doi: 10.1016/j.ypmed.2009.06.016
|
| [142] |
Dew MA, Hoch CC, Buysse DJ, et al. (2003) Healthy older adults' sleep predicts all-cause mortality at 4 to 19 years of follow-up. Psychosom Med 65: 63-73. doi: 10.1097/01.PSY.0000039756.23250.7C
|
| [143] |
Kripke DF, Garfinkel L, Wingard DL, et al. (2002) Mortality associated with sleep duration and insomnia. Arch Gen Psychiatry 59: 131-136. doi: 10.1001/archpsyc.59.2.131
|
| [144] | LeBlanc M, Merette C, Savard J, et al. (2009) Incidence and risk factors of insomnia in a population-based sample. Sleep 32: 1027-1037. |
| [145] |
Morin CM, LeBlanc M, Daley M, et al. (2006) Epidemiology of insomnia: prevalence, self-help treatments, consultations, and determinants of help-seeking behaviors. Sleep Med 7: 123-130. doi: 10.1016/j.sleep.2005.08.008
|
| [146] | Ohayon M (1996) Epidemiological study on insomnia in the general population. Sleep 19: S7-15. |
| [147] |
Ohayon MM (2002) Epidemiology of insomnia: what we know and what we still need to learn. Sleep Med Rev 6: 97-111. doi: 10.1053/smrv.2002.0186
|
| [148] | Buysse DJ (2014) Sleep health: can we define it? Does it matter? Sleep 37: 9-17. |
| [149] |
Besedovsky L, Lange T, Born J (2012) Sleep and immune function. Pflugers Arch 463: 121-137. doi: 10.1007/s00424-011-1044-0
|
| [150] | Redwine L, Hauger RL, Gillin JC, et al. (2000) Effects of sleep and sleep deprivation on interleukin-6, growth hormone, cortisol, and melatonin levels in humans. J Clin Endocrinol Metab 85: 3597-3603. |
| [151] |
Meier-Ewert HK, Ridker PM, Rifai N, et al. (2004) Effect of sleep loss on C-reactive protein, an inflammatory marker of cardiovascular risk. J Am Coll Cardiol 43: 678-683. doi: 10.1016/j.jacc.2003.07.050
|
| [152] | Haack M, Sanchez E, Mullington JM (2007) Elevated inflammatory markers in response to prolonged sleep restriction are associated with increased pain experience in healthy volunteers. Sleep 30: 1145-1152. |
| [153] |
Vgontzas AN, Zoumakis E, Bixler EO, et al. (2004) Adverse effects of modest sleep restriction on sleepiness, performance, and inflammatory cytokines. J Clin Endocrinol Metab 89: 2119-2126. doi: 10.1210/jc.2003-031562
|
| [154] |
van Leeuwen WM, Lehto M, Karisola P, et al. (2009) Sleep restriction increases the risk of developing cardiovascular diseases by augmenting proinflammatory responses through IL-17 and CRP. PLoS One 4: e4589. doi: 10.1371/journal.pone.0004589
|
| [155] |
Abedelmalek S, Chtourou H, Aloui A, et al. (2013) Effect of time of day and partial sleep deprivation on plasma concentrations of IL-6 during a short-term maximal performance. Eur J Appl Physiol 113: 241-248. doi: 10.1007/s00421-012-2432-7
|
| [156] | Schmid SM, Hallschmid M, Jauch-Chara K, et al. (2011) Disturbed glucoregulatory response to food intake after moderate sleep restriction. Sleep 34: 371-377. |
| [157] |
Stamatakis KA, Punjabi NM (2010) Effects of sleep fragmentation on glucose metabolism in normal subjects. Chest 137: 95-101. doi: 10.1378/chest.09-0791
|
| [158] |
Faraut B, Boudjeltia KZ, Dyzma M, et al. (2011) Benefits of napping and an extended duration of recovery sleep on alertness and immune cells after acute sleep restriction. Brain Behav Immun 25: 16-24. doi: 10.1016/j.bbi.2010.08.001
|
| [159] |
Shearer WT, Reuben JM, Mullington JM, et al. (2001) Soluble TNF-alpha receptor 1 and IL-6 plasma levels in humans subjected to the sleep deprivation model of spaceflight. J Allergy Clin Immunol 107: 165-170. doi: 10.1067/mai.2001.112270
|
| [160] |
Irwin M, Rinetti G, Redwine L, et al. (2004) Nocturnal proinflammatory cytokine-associated sleep disturbances in abstinent African American alcoholics. Brain Behav Immun 18: 349-360. doi: 10.1016/j.bbi.2004.02.001
|
| [161] |
Irwin M, Mascovich A, Gillin JC, et al. (1994) Partial sleep deprivation reduces natural killer cell activity in humans. Psychosom Med 56: 493-498. doi: 10.1097/00006842-199411000-00004
|
| [162] | Irwin M, McClintick J, Costlow C, et al. (1996) Partial night sleep deprivation reduces natural killer and cellular immune responses in humans. Faseb j 10: 643-653. |
| [163] | Vgontzas AN, Pejovic S, Zoumakis E, et al. (2007) Daytime napping after a night of sleep loss decreases sleepiness, improves performance, and causes beneficial changes in cortisol and interleukin-6 secretion. Am J Physiol Endocrinol Metab 292: E253-261. |
| [164] |
Faraut B, Nakib S, Drogou C, et al. (2015) Napping reverses the salivary interleukin-6 and urinary norepinephrine changes induced by sleep restriction. J Clin Endocrinol Metab 100: E416-426. doi: 10.1210/jc.2014-2566
|
| [165] | Chaput JP, Despres JP, Bouchard C, et al. (2008) The association between sleep duration and weight gain in adults: a 6-year prospective study from the Quebec Family Study. Sleep 31: 517-523. |
| [166] |
Patel SR, Malhotra A, White DP, et al. (2006) Association between reduced sleep and weight gain in women. Am J Epidemiol 164: 947-954. doi: 10.1093/aje/kwj280
|
| [167] |
Cappuccio FP, D'Elia L, Strazzullo P, et al. (2010) Quantity and quality of sleep and incidence of type 2 diabetes: a systematic review and meta-analysis. Diabetes Care 33: 414-420. doi: 10.2337/dc09-1124
|
| [168] |
Cooper AJ, Westgate K, Brage S, et al. (2015) Sleep duration and cardiometabolic risk factors among individuals with type 2 diabetes. Sleep Med 16: 119-125. doi: 10.1016/j.sleep.2014.10.006
|
| [169] |
Lou P, Qin Y, Zhang P, et al. (2015) Association of sleep quality and quality of life in type 2 diabetes mellitus: A cross-sectional study in China. Diabetes Res Clin Pract 107: 69-76. doi: 10.1016/j.diabres.2014.09.060
|
| [170] |
Spiegel K, Tasali E, Penev P, et al. (2004) Brief communication: Sleep curtailment in healthy young men is associated with decreased leptin levels, elevated ghrelin levels, and increased hunger and appetite. Ann Intern Med 141: 846-850. doi: 10.7326/0003-4819-141-11-200412070-00008
|
| [171] |
Spiegel K, Leproult R, Van Cauter E (1999) Impact of sleep debt on metabolic and endocrine function. Lancet 354: 1435-1439. doi: 10.1016/S0140-6736(99)01376-8
|
| [172] |
Conlon M, Lightfoot N, Kreiger N (2007) Rotating shift work and risk of prostate cancer. Epidemiology 18: 182-183. doi: 10.1097/01.ede.0000249519.33978.31
|
| [173] |
Kubo T, Ozasa K, Mikami K, et al. (2006) Prospective cohort study of the risk of prostate cancer among rotating-shift workers: findings from the Japan collaborative cohort study. Am J Epidemiol 164: 549-555. doi: 10.1093/aje/kwj232
|
| [174] |
Kubo T, Oyama I, Nakamura T, et al. (2011) Retrospective cohort study of the risk of obesity among shift workers: findings from the Industry-based Shift Workers' Health study, Japan. Occup Environ Med 68: 327-331. doi: 10.1136/oem.2009.054445
|
| [175] |
Parent ME, El-Zein M, Rousseau MC, et al. (2012) Night work and the risk of cancer among men. Am J Epidemiol 176: 751-759. doi: 10.1093/aje/kws318
|
| [176] |
Schwartzbaum J, Ahlbom A, Feychting M (2007) Cohort study of cancer risk among male and female shift workers. Scand J Work Environ Health 33: 336-343. doi: 10.5271/sjweh.1150
|
| [177] |
Haus EL, Smolensky MH (2013) Shift work and cancer risk: potential mechanistic roles of circadian disruption, light at night, and sleep deprivation. Sleep Med Rev 17: 273-284. doi: 10.1016/j.smrv.2012.08.003
|
| [178] |
von Ruesten A, Weikert C, Fietze I, et al. (2012) Association of sleep duration with chronic diseases in the European Prospective Investigation into Cancer and Nutrition (EPIC)-Potsdam study. PLoS One 7: e30972. doi: 10.1371/journal.pone.0030972
|
| [179] |
Jiao L, Duan Z, Sangi-Haghpeykar H, et al. (2013) Sleep duration and incidence of colorectal cancer in postmenopausal women. Br J Cancer 108: 213-221. doi: 10.1038/bjc.2012.561
|
| [180] | Zhang X, Giovannucci EL, Wu K, et al. (2013) Associations of self-reported sleep duration and snoring with colorectal cancer risk in men and women. Sleep 36: 681-688. |
| [181] |
Bishop D (2008) An applied research model for the sport sciences. Sports Med 38: 253-263. doi: 10.2165/00007256-200838030-00005
|
| [182] |
Drust B, Waterhouse J, Atkinson G, et al. (2005) Circadian rhythms in sports performance--an update. Chronobiol Int 22: 21-44. doi: 10.1081/CBI-200041039
|
| [183] | Fullagar HH, Skorski S, Duffield R, et al. (2015) Sleep and Athletic Performance: The Effects of Sleep Loss on Exercise Performance, and Physiological and Cognitive Responses to Exercise. Sports Med 45(2):161-86. |
| [184] |
Hausswirth C, Louis J, Aubry A, et al. (2014) Evidence of disturbed sleep and increased illness in overreached endurance athletes. Med Sci Sports Exerc 46: 1036-1045. doi: 10.1249/MSS.0000000000000177
|
| [185] |
Gleeson M (2007) Immune function in sport and exercise. J Appl Physiol (1985) 103: 693-699. doi: 10.1152/japplphysiol.00008.2007
|
| [186] |
Samuels C (2008) Sleep, recovery, and performance: the new frontier in high-performance athletics. Neurol Clin 26: 169-180; ix-x. doi: 10.1016/j.ncl.2007.11.012
|
| [187] |
Durmer JS, Dinges DF (2005) Neurocognitive consequences of sleep deprivation. Semin Neurol 25: 117-129. doi: 10.1055/s-2005-867080
|
| [188] | Venter RE (2014) Perceptions of team athletes on the importance of recovery modalities. Eur J Sport Sci 14 Suppl 1: S69-76. |
| [189] |
Erlacher D, Ehrlenspiel F, Adegbesan OA, et al. (2011) Sleep habits in German athletes before important competitions or games. J Sports Sci 29: 859-866. doi: 10.1080/02640414.2011.565782
|
| [190] |
Juliff LE, Halson SL, Peiffer JJ (2015) Understanding sleep disturbance in athletes prior to important competitions. J Sci Med Sport 18: 13-18. doi: 10.1016/j.jsams.2014.02.007
|
| [191] |
Hanton S, Fletcher D, Coughlan G (2005) Stress in elite sport performers: a comparative study of competitive and organizational stressors. J Sports Sci 23: 1129-1141. doi: 10.1080/02640410500131480
|
| [192] |
Chen JC, Brunner RL, Ren H, et al. (2008) Sleep duration and risk of ischemic stroke in postmenopausal women. Stroke 39: 3185-3192. doi: 10.1161/STROKEAHA.108.521773
|
| [193] | Chien KL, Chen PC, Hsu HC, et al. (2010) Habitual sleep duration and insomnia and the risk of cardiovascular events and all-cause death: report from a community-based cohort. Sleep 33: 177-184. |
| [194] | Gangwisch JE, Malaspina D, Boden-Albala B, et al. (2005) Inadequate sleep as a risk factor for obesity: analyses of the NHANES I. Sleep 28: 1289-1296. |
| [195] | Cappuccio FP, D'Elia L, Strazzullo P, et al. (2010) Sleep duration and all-cause mortality: a systematic review and meta-analysis of prospective studies. Sleep 33: 585-592. |
| [196] | Machado RM, Koike MK (2014) Circadian rhythm, sleep pattern, and metabolic consequences: an overview on cardiovascular risk factors. Horm Mol Biol Clin Investig 18: 47-52. |
| [197] | Petrov ME, Lichstein KL (2015) Differences in sleep between black and white adults: an update and future directions. Sleep Med Jan 23, in press. |
| 1. | Fuli Wang, Rongxiang Zhang, Yong Cui, Liping Sheng, Yinping Sun, Wei Tian, Xiao Liu, Shuzeng Liang, Design, synthesis and biological evaluation of 3,4-dihydronaphthalen-1(2H)-one derivatives as Bcl-2 inhibitors, 2017, 43, 0922-6168, 5933, 10.1007/s11164-017-2972-x | |
| 2. | Ning Li, Wen-Yu Xin, Bin-Rong Yao, Chun-Hua Wang, Wei Cong, Feng Zhao, Hong-Juan Li, Yun Hou, Qing-Guo Meng, Gui-Ge Hou, Novel dissymmetric 3,5-bis(arylidene)-4-piperidones as potential antitumor agents with biological evaluation in vitro and in vivo, 2018, 147, 02235234, 21, 10.1016/j.ejmech.2018.01.088 | |
| 3. | Ning Li, Binrong Yao, Chunhua Wang, Qingguo Meng, Guige Hou, Synthesis, crystal structure and activity evaluation of novel 3,4-dihydro-1-benzoxepin-5(2H)-one derivatives as protein–tyrosine kinase (PTK) inhibitors, 2017, 73, 2053-2296, 1003, 10.1107/S2053229617015145 | |
| 4. | Binrong Yao, Ning Li, Chunhua Wang, Guige Hou, Qingguo Meng, Ke Yan, Novel asymmetric 3,5-bis(arylidene)piperidin-4-one derivatives: synthesis, crystal structures and cytotoxicity, 2018, 74, 2053-2296, 659, 10.1107/S2053229618006605 | |
| 5. | Fereshteh Nazari, Alexandra E. Oklejas, Jacques E. Nör, Alexander T. Pearson, Trachette L. Jackson, In Silico Models Accurately Predict In Vivo Response for IL6 Blockade in Head and Neck Cancer, 2020, 80, 0008-5472, 1451, 10.1158/0008-5472.CAN-19-1846 | |
| 6. | Michelle Przedborski, David Sharon, Steven Chan, Mohammad Kohandel, A mean-field approach for modeling the propagation of perturbations in biochemical reaction networks, 2021, 165, 09280987, 105919, 10.1016/j.ejps.2021.105919 |
Daniel A. Barone, Ana C. Krieger. The Function of Sleep[J]. AIMS Neuroscience, 2015, 2(2): 71-90. doi: 10.3934/Neuroscience.2015.2.71
| Symbol | Description | Value | Reference |
| $ \epsilon_0 $ | Antibiotic prescription rate (day$ ^{-1} $) | 0.12 | [39][41] |
| $ \epsilon_1 $ | Magnitude of change of antibiotic prescription rate (no dimension) | 0.25 | [56] |
| $ \theta_u $ | Proportion of $ P_u $ on admission (day$ ^{-1} $) | 0.617 | [15][39] |
| $ \theta_{uA} $ | Proportion of $ P_{uA} $ on admission (day$ ^{-1} $) | 0.349 | [15][40] |
| $ \theta_c $ | Proportion of $ P_c $ on admission (day$ ^{-1} $) | 0.003 | [15][39] |
| $ \theta_{cA} $ | Proportion of $ P_{cA} $ on admission (day$ ^{-1} $) | 0.031 | [15][40] |
| $ \gamma_u $ | Discharge rate of $ P_u $ (day$ ^{-1} $) | 0.2 | [15] |
| $ \gamma_{uA} $ | Discharge rate of $ P_{uA} $ (day$ ^{-1} $) | 0.2 | [15] |
| $ \gamma_c $ | Discharge rate of $ P_c $ (day$ ^{-1} $) | 0.06 | [39] |
| $ \gamma_{cA} $ | Discharge rate of $ P_{cA} $ (day$ ^{-1} $) | 0.055 | [15][39] |
| $ \gamma_b $ | Disinfection (cleaning) rate of environment (day$ ^{-1} $) | 0.7 | [25] |
| $ \alpha_p $ | Contact rate (day$ ^{-1} $ person$ ^{-1} $) | 0.0435 | [25] |
| $ \beta_p $ | Probability of colonization for $ P_u $ after a contact with $ H_c $ (no dimension) | 0.42 | [25] |
| $ \beta_{pA} $ | Probability of colonization for $ P_{uA} $ after a contact with $ H_c $ (no dimension) | 0.42*1.67 | [39][15] |
| $ \beta_h $ | Probability of contamination for HCW after a contact with $ P_c $ (no dimension) | 0.2 | [25][15] |
| $ \beta_{hA} $ | Probability of contamination for HCW after a contact with $ P_{cA} $ (no dimension) | 0.25 | [15] |
| $ \eta $ | Hand hygiene compliance with HCWs (no dimension) | 0.4 | [25] |
| $ \mu_c $ | Decontamination rate of HCWs (day$ ^{-1} $) | 24 | [25] |
| $ \upsilon_p $ | Shedding rate to environment from $ P_c $ (day$ ^{-1} $ person$ ^{-1} $ ACC/$ cm^2 $) | 235 | [25] |
| $ \upsilon_{pA} $ | Shedding rate to environment from $ P_{cA} $ (day$ ^{-1} $ person$ ^{-1} $ ACC/$ cm^2 $) | 470 | [26][39] |
| $ \upsilon_h $ | Contamination rate to environment by $ H_c $ (day$ ^{-1} $ person$ ^{-1} $ ACC/$ cm^2 $) | 235 | [25] |
| $ \kappa_p $ | Colonization rate from environment for $ P_u $ (day$ ^{-1} $ (ACC/$ cm^2 $)$ ^{-1} $) | 0.000004 | [25] |
| $ \kappa_{pA} $ | Colonization rate from environment for $ P_{uA} $ (day$ ^{-1} $ (ACC/$ cm^2 $)$ ^{-1} $) | 0.000005 | [15][25] |
| $ \kappa_h $ | Colonization rate from environment for $ H_u $ (day$ ^{-1} $ (ACC/$ cm^2 $)$ ^{-1} $) | 0.00001 | [25] |
| $ N_p $ | Total number of patients | 23 | [25] |
| $ N_h $ | Total number of HCWs | 23 | [25] |
DownLoad:
CSV
| Symbol | Distribution | reference |
| $ \gamma_{cA} $ | $ N(0.055, 0.005) $ | estimated by [26] |
| $ \gamma_b $ | $ N(0.7, 0.2) $ | estimated by [26] |
| $ \beta_{pA} $ | $ N(0.43, 0.1) $ | estimated by [26] |
| $ \beta_{hA} $ | $ N(0.2, 0.05) $ | estimated by [26] |
| $ \eta $ | $ N(0.4, 0.1) $ | estimated by [26] |
| $ \mu_c $ | $ N(24, 5) $ | estimated by [26] |
| $ \upsilon_{pA} $ | $ N(470,150) $ | estimated by [26] |
| $ \epsilon $ | $ N(0.12, 0.02) $ | estimated by [26] |
| $ \kappa_{pA} $ | $ N(0.000005, 0.0000006) $ | estimated by [26] |
DownLoad:
CSV
| Symbol | Description | Value | Reference |
| $ \epsilon_0 $ | Antibiotic prescription rate (day$ ^{-1} $) | 0.12 | [39][41] |
| $ \epsilon_1 $ | Magnitude of change of antibiotic prescription rate (no dimension) | 0.25 | [56] |
| $ \theta_u $ | Proportion of $ P_u $ on admission (day$ ^{-1} $) | 0.617 | [15][39] |
| $ \theta_{uA} $ | Proportion of $ P_{uA} $ on admission (day$ ^{-1} $) | 0.349 | [15][40] |
| $ \theta_c $ | Proportion of $ P_c $ on admission (day$ ^{-1} $) | 0.003 | [15][39] |
| $ \theta_{cA} $ | Proportion of $ P_{cA} $ on admission (day$ ^{-1} $) | 0.031 | [15][40] |
| $ \gamma_u $ | Discharge rate of $ P_u $ (day$ ^{-1} $) | 0.2 | [15] |
| $ \gamma_{uA} $ | Discharge rate of $ P_{uA} $ (day$ ^{-1} $) | 0.2 | [15] |
| $ \gamma_c $ | Discharge rate of $ P_c $ (day$ ^{-1} $) | 0.06 | [39] |
| $ \gamma_{cA} $ | Discharge rate of $ P_{cA} $ (day$ ^{-1} $) | 0.055 | [15][39] |
| $ \gamma_b $ | Disinfection (cleaning) rate of environment (day$ ^{-1} $) | 0.7 | [25] |
| $ \alpha_p $ | Contact rate (day$ ^{-1} $ person$ ^{-1} $) | 0.0435 | [25] |
| $ \beta_p $ | Probability of colonization for $ P_u $ after a contact with $ H_c $ (no dimension) | 0.42 | [25] |
| $ \beta_{pA} $ | Probability of colonization for $ P_{uA} $ after a contact with $ H_c $ (no dimension) | 0.42*1.67 | [39][15] |
| $ \beta_h $ | Probability of contamination for HCW after a contact with $ P_c $ (no dimension) | 0.2 | [25][15] |
| $ \beta_{hA} $ | Probability of contamination for HCW after a contact with $ P_{cA} $ (no dimension) | 0.25 | [15] |
| $ \eta $ | Hand hygiene compliance with HCWs (no dimension) | 0.4 | [25] |
| $ \mu_c $ | Decontamination rate of HCWs (day$ ^{-1} $) | 24 | [25] |
| $ \upsilon_p $ | Shedding rate to environment from $ P_c $ (day$ ^{-1} $ person$ ^{-1} $ ACC/$ cm^2 $) | 235 | [25] |
| $ \upsilon_{pA} $ | Shedding rate to environment from $ P_{cA} $ (day$ ^{-1} $ person$ ^{-1} $ ACC/$ cm^2 $) | 470 | [26][39] |
| $ \upsilon_h $ | Contamination rate to environment by $ H_c $ (day$ ^{-1} $ person$ ^{-1} $ ACC/$ cm^2 $) | 235 | [25] |
| $ \kappa_p $ | Colonization rate from environment for $ P_u $ (day$ ^{-1} $ (ACC/$ cm^2 $)$ ^{-1} $) | 0.000004 | [25] |
| $ \kappa_{pA} $ | Colonization rate from environment for $ P_{uA} $ (day$ ^{-1} $ (ACC/$ cm^2 $)$ ^{-1} $) | 0.000005 | [15][25] |
| $ \kappa_h $ | Colonization rate from environment for $ H_u $ (day$ ^{-1} $ (ACC/$ cm^2 $)$ ^{-1} $) | 0.00001 | [25] |
| $ N_p $ | Total number of patients | 23 | [25] |
| $ N_h $ | Total number of HCWs | 23 | [25] |
| Symbol | Distribution | reference |
| $ \gamma_{cA} $ | $ N(0.055, 0.005) $ | estimated by [26] |
| $ \gamma_b $ | $ N(0.7, 0.2) $ | estimated by [26] |
| $ \beta_{pA} $ | $ N(0.43, 0.1) $ | estimated by [26] |
| $ \beta_{hA} $ | $ N(0.2, 0.05) $ | estimated by [26] |
| $ \eta $ | $ N(0.4, 0.1) $ | estimated by [26] |
| $ \mu_c $ | $ N(24, 5) $ | estimated by [26] |
| $ \upsilon_{pA} $ | $ N(470,150) $ | estimated by [26] |
| $ \epsilon $ | $ N(0.12, 0.02) $ | estimated by [26] |
| $ \kappa_{pA} $ | $ N(0.000005, 0.0000006) $ | estimated by [26] |
