1. Introduction

In 1924, Hans Berger invented the cortical electroencephalogram (EEG). He discovered the alpha frequency (~10 Hz) rhythm, which is recorded particularly in the occipital cortex during the resting state, that is, during relaxed wakefulness and in the absence of sensory stimulation or conscious mental activity [1]. Once eyes are open, baseline alpha oscillations are reduced in the cerebral cortex. They are also reduced during drowsiness and sleep. The Berger’s waves would be generated by a thalamic pacemaker [2]. Berger was the first to suggest that brain rhythmic electric oscillations in the human EEG are associated with mental processes, including cognition, memory, arousal, and consciousness. Since then, a growing body of studies has been consolidating the notion that EEG oscillations, including gamma frequency (30-80 Hz) oscillations (GFO), are biomarkers of brain state and function. Brain field oscillations are versatile and directly linked to the structure of the neural networks and to the neurotransmitter systems.

When and how field or network GFO and N-methyl D-aspartate glutamate type receptors (NMDAr) contribute to normal and dysfunctional cognitive performances? This open question is currently the object of intensive clinical, experimental and theoretical investigations and of passionate debates. In the previous issue, three reviews written by Moss and Moss [3], Cadonic and Albensi [4], and by Pinotsis and Friston [5] provide three appealing non-exclusive theoretical viewpoints. Moss and Moss [3] discuss the possible roles in health and disease of cortical columns through the notion of the “dimensional systems model”, paying attention to the generation of “signal and noise” in neural circuits. Cadonic and Albensi [4] introduced the basic physical model of “damped and forced harmonic oscillators”, which are under the constraints of inhibitory or driving “forces” that impede or amplify network oscillations. Pinotsis and Friston [5] show how GFO, neural field models and “Dynamical Causal Modeling” can be combined to understand the generation of relevant signal (visual perception) and noise in dynamic neural circuits and the connectivity between brain regions. This challenges lateral connections which, by generating a functional excitatory centre-inhibitory surround, play a crucial role in GFO-based information processing. Lateral inhibitions might be vulnerable during cognitive disorders. Interestingly, simulations of neural field models can yield predictions of recorded field GFO and on the anatomofunctional properties of the related cortical circuits.

Here I take this opportunity to discuss these different theoretical perspectives while integrating them in a basic-clinical translational framework in an attempt to understand neurophysiological and pathophysiological aspects regarding the relation between NMDAr-mediated activities and GFO in mental disorders and brain illnesses. I argue that spontaneously-occurring field GFO (or network gamma noise), which are usually mostly intracerebrally generated (e.g, from resident cognitive information), can―during neurological and neuropsychiatric diseases―increase in a manner such that they can become the source of abnormal activities (e.g, during hallucinations) and disturb function-related synchronized oscillations (or network gamma signal). The gamma signal-to-noise ratio is considered as a potential neurophysiological biomarker of the state and function of neural circuits.

2. Baseline and Function-Related Network Gamma Oscillations

Natural, spontaneously-occurring, synchronized and non-synchronized GFO are dominant in the desynchronized cortical EEG [6], a EEG state that can be recorded during conscious awareness in the awake state, executive functions, selective attention [7,8,9], Rapid Eye Movement sleep [10,11], hallucinations [12,13,14,15,16], in early psychosis [17,18], and in the process of meditation [19]. At rest, in the visual cortex, differences in peaks of GFO variations are associated with a γ-aminobutyric acid (GABA)-related inhibitory drive [5].

Large-scale, ephemeral synchronized field GFO emerge during the performance of cognitive tasks, that is, during global brain operations like attention, perception and memory [20,21,22]. They also arise during pain perception [23]. They are thought to play a key role in the temporal interaction and coordination between multiple cortical and subcortical brain regions during information integration (binding-by-synchronization) [24,25,26,27,28,29], the focused arousal, the resting wake state [30] and synaptic plasticity [31]. Field GFO can be recorded as local extracellular field potentials associated with irregular firing of single nerve cells [32]. Network GFO are multiple and operate in combination with theta frequency and other (slower and faster) brain rhythms [32,33,34]. Field GFO principally result from subthreshold synaptic and intrinsic membrane potential oscillations triggering action potentials at a precise instant during the oscillatory period. Their functions and mechanisms are still matter of debate.

3. From Vertical to Horizontal Network Gamma Oscillations

Function-related synchronized field GFO are usually recorded principally in adult small- and large-scale cortico-cortical networks. These “horizontal” cortical network GFO correspond to binding-by-synchronization of multiple cortical areas, which are also connected to subcortical structures including the thalamus. In human, ongoing and function-related synchronized GFO emerge during early childhood, and their spatiotemporal properties continue to mature until early adulthood, suggesting they are associated with synaptic and network plasticity involving myelination processes and the development of GABAergic neurotransmission [35].

In the rodent, the somatosensory vibrissae-related cortico-thalamo-cortical system is composed of topographically organized and interacting anatomofunctional modules, the barreloid-barrel circuits, each of them being already active at birth [36,37,38]. Field GFO start to play functional and structural roles early during the development of the neocortex. Remarkably, in the rodent, early “vertical” thalamically-generated GFO start to emerge in response to the ongoing activity of sensory inputs during the neurodevelopment of thalamocortical circuits, especially during the critical period for activity-dependent plasticity in thalamocortical synapses and before the appearance of intracortical GABAergic-dependent inhibition [39,38]. These synchronized GFO are very likely driven by the GABAergic thalamic reticular nucleus, the pacemaker of thalamic GFO [40,41]. These sensory-evoked, thalamically-generated early GFO appear when thalamocortical connections present enhanced plasticity (long-lasting potentiation of thalamocortical excitatory postsynaptic potentials) Highly localized spontaneous and sensory-related thalamocortical and corticothalamic GFO can be recorded at birth in the newborn rat barrel cortex [38]. These rhythmic events spread to adjacent ontogenetic columns at the end of the first postnatal week. Early GFO trigger repetitive synchronization of thalamic and cortical neurons during the neurodevelopment and maturation of the topographical organization of cortico-thalamo-cortical connections. The development of the column 6-layers architecture is driven by spontaneous and sensory-related thalamocortical activity [38]. In short, vertical field GFO start to play an anatomofunctional role early during the development of the topographic maps in the somatosensory cortex, a natural neurodevelopmental process that requires precise temporal binding-by-synchronization in thalamocortical networks. Then, vertical and horizontal GFO work together during adult global brain operations.

4. The Dimensional Systems Model and Memory

In the previous issue, Moss and Moss [3] argue that a cortical column is a basic unit having all the ingredients to compute ongoing information during global brain operations or functional integration. In their theory, the anatomofunctional integrity of the cortical column relies on the emergence of network GFO. The notion that the neocortex operates on a basic principle based on modular elements, that is, the cortical columns, took its roots in the pioneering neurophysiological discoveries of Mountcastle [42], who later proposed every column is made of “minicolumns” [43]. Since then, the cortical column becomes the unit of computation and a focus of interest to investigate the anatomofunctional properties of neuronal circuits [44]. Whether or not the cortical column has a function remains an open debate and the object of intensive investigations [44,45].

Moss and Moss [3] consider their theoretical cortical column, with its hundreds of minicolumns [each containing ~100-200 neurons], as an elementary unit involved in cognitive processes. Their theory, the so-called “DSM or Dimensional Systems Model”, suggests functional overlapping between columns and minicolumns during cortical processing, leading to a dynamic column formation based on synchronized GFO. In their model, there is room for series and parallel “light-buzzer” circuits, thereby providing multiple patterns of connections, like electrical devices (electrical circuits with power supplies and switches). The DSM takes into consideration 5 systems: sensory inputs, arousal system, attention-memory system, cortical system (information processing) and motor system (output). Thus, their theoretical model provides a system definition of the simplest to the more complex memory, including multisensory and association memories. It also allows the implication of subcortical structures, in particular the thalamus and hippocampus.

In their DSM, Moss and Moss [3] highlight the importance of AMPA (α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid), NMDA and GABA receptors in the formation and consolidation of memory. Initial AMPAr-based activity would be strengthened by NMDAr-mediated synaptic potentiation; then a horizontal spreading would allow the consolidation of connections between the first activated minicolumns and the follower ones. The spreading would involve the pyramidal cell-parvalbumine positive GABAergic interneuron gamma-based feed-forward inhibition. The authors also highlight the importance of diverse types of interneurons (expressing parvalbumine, somatostatin and vasoactive intestinal polypeptide), which play a crucial GFO-based role in cortical information processing.

In their theory, a set of cortical columns that is coherently consolidated during a memory process would form the relevant “signal” while the other, overlapping and adjacent, columns that display irrelevant and distractive “noise” would be inhibited. Such a concept is nothing other than the principle of lateral inhibition, which consists in sharpening the receptive field by generating consolidated patterns of center-on (signal) surround-off (noise) connections. Moreover, local and distant lateral neuronal interactions play important roles in facilitating contrast augmentation during information processing in sensory and other systems. Furthermore, Pinotsis and Friston [5] emphasize the notion of intimate relationship between stimulus contrast, GFO and lateral inhibition in the visual cortex (excitatory-inhibitory balance).

5. Ketamine Amplifies Baseline Network Gamma Oscillations

The glutamatergic systems mediate most of the excitatory neuronal transmissions through the activation of ionotropic and metabotropic receptors. The ionotropic NMDAr play a key role in the synaptic plasticity, memory processes and in the modulation of field oscillations (see Cadonic and Albensi, the previous issue [4]). Ketamine, a non-competitive NMDAr antagonist, can safely be administered in humans under clinical monitoring. It has dose-dependent multiple properties, including positive and negative effects. For instance, a single subanesthetic administration can disturb cognitive and sensory-perceptual processes and induce schizophreniform psychosis in healthy subjects [46,47,48,49]; puzzlingly but of importance, ketamine can generate a durable antidepressant effect in patients refractory to conventional antidepressant therapies [50,51,52].

More specifically, brain scans recently revealed that a single subanesthetic administration of ketamine in healthy subjects at rest produces in the prefrontal cortex a state of hyperconnectivity, which resembles that recorded in people in the early stages of schizophrenia but not in patients with chronic (since several years) schizophrenia [53]. Also, using fMRI in healthy human subjects, it was demonstrated NMDAr antagonist ketamine increases global brain functional connectivity and reduces negative symptoms [54]. The acute ketamine effects are quick, transient and reversible. These findings (hyperconnectivity and hyperactivity) are consistent with preclinical studies demonstrating that, in rodents, non-competitive NMDAr antagonists increase the amount of field GFO in cortical and subcortical regions (see below). In healthy subjects, ketamine increases the power of GFO during auditory-evoked network oscillations [55].

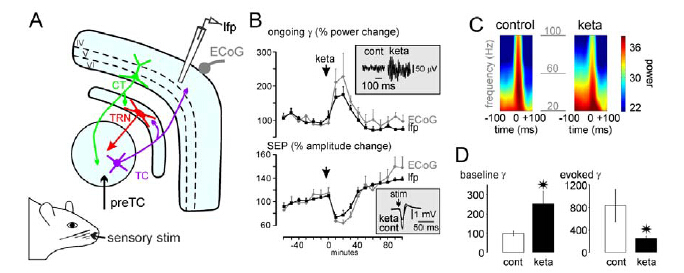
In rodents a single subanesthetic administration of ketamine (or other NMDAr antagonists like dizocilpine [MK-801] and phencylidine) quickly and transiently induces abnormal behavior (hyperlocomotion, ataxy), memory deficits and abnormally persistent and generalized hypersynchronized (200%-400% increased power) ongoing GFO [56,57,58,59,60,61] (Figure 1B, top panel). The gamma frequency at maximal power is significantly increased by approximately 10 Hz on average [56]. Interestingly, using conductance and convolution models, Pinotsis and Friston [5] suggest that such a gamma frequency shift reflects an increase in the strength of inhibition. The amount of ongoing higher-frequency (> 80 Hz) oscillations is also increased following a single subanesthetic administration of ketamine [60,62,63].

Figure 1. In the thalamocortical system, ketamine increases the power of baseline GFO and decreases both the power of sensory-evoked GFO and the synaptic plasticity. (A): Experimental design showing the simplified three-neuron circuit involving the neocortex (CT, corticothalamic [from layer VI]), GABAergic thalamic reticular nucleus (TRN) and thalamus with its principal neurons that project to the cerebral cortex (TC, thalamocortical). Natural-like mechanical stimulus (sensory stim) of the vibrissae is provided by a piezo bender actuator. Baseline cortical activity and sensory-evoked potentials (SEP) are recorded simultaneously with the surface electrocorticogram (ECoG) electrode and intracortical (layer IV) lfp (local field potential) micro-electrode. (B): Ketamine transiently disrupts the expression of the sensory-induced long-term potentiation. Top: changes in the baseline GFO power; bottom: changes in the SEP amplitude before and after ketamine (keta) injection. Each point is an average of 15 values x 4 rats (± SEM). The insets in gray show traces of ongoing GFO (top) and of averaged (n = 12) SEP under the two conditions (cont, keta). (C): Time-frequency graph of the ECoG for each condition (90 SEP trials, stimulus given at 0 ms). (D): Quantitative and statistical analysis (t-test, P < 0.0001) shows that ketamine (keta) administration increases the power of baseline GFO and decreases the power of sensory-evoked GFO. The averaged power of the baseline GFO is measured during the 100 ms epoch before the sensory stimulation (from at least 45 trials, three rats). The power of the sensory-evoked GFO is directly measured from the averaged SEP (12 values from the post-stimulus 100 ms epoch from three rats per condition). Adapted from Kulikova et al., 2012.

DownLoad: Full-Size ImgPowerPoint

In the ketamine (or MK-801)-treated rodent, the persistent generalized and hypersynchronized GFO are not dependent on muscle activity, locomotion-related brain state or conscious sensorimotor processing. Moreover, they are also recorded in anesthetized and immobilized rodents in almost all cortical and subcortical structures implicated in sensory, motor, limbic and associative/cognitive systems [60]. The ketamine-induced persistent generalized and hypersynchronized GFO are thought to represent an aberrant diffuse network noise, a potential electrophysiological correlate of a psychotic(-like) state (see below).

In addition, NMDAr antagonists transiently disrupt the expression, not the induction, of long-term potentiation in the thalamocortical system (Figure 1B, bottom panel; [63]), disorganize action potential firing in rat prefrontal cortex [64], increase the firing in fast spiking neurons and decrease that in regular spiking neurons [65].These results suggest that the amount of ongoing GFO is inversely related to synaptic potentiation (assessed from the amplitude of the sensory-evoked potential) at least in the thalamocortical system [63]. They also suggest that the ketamine-induced state results in part from dysfunction of cortical GABAergic interneurons that would lead to hyperexcitation of projection glutamatergic neurons [65].

It may be worth precising that the acute, single low-dose (< 10 mg/kg) ketamine rat model models more hyperfrontality, which can be observed in first-episode schizophrenia [53,54,66], than the hypofrontality of patients diagnosed with the chronic disease schizophrenia. Therefore, the acute ketamine model may be appropriate to model the pathogenesis of acute psychotic states, a model translatable in humans [47,48,53,54,67]. The advantages and weaknesses and possible mechanisms of the acute ketamine model are still a matter for discussion [68,69,70].

6. Damped and Forced Harmonic Oscillators

Cadonic and Albensi [4] introduced the basic physical model of “damped and forced harmonic motion” referring to mechanical vibrations in real-world systems. The motion of the oscillator is under the constraint of inhibitory or driving “forces” that impede or amplify the motion of the oscillator. Such a model can be applied to neural oscillations although, as stressed by the authors, the activity of individual nerve cells is not representative of the corresponding field activity, which is the integration of collective activities from local and sparse neuronal populations. So, mathematical models, which approximate electrical properties (capacitance, conductances, voltage and current sources) of nerve cells, are necessary to describe how, in neurons, firing patterns are generated. Network systems can be described for instance with the Wilson-Cowan model, which considers at least two types, excitatory and inhibitory, of interconnect neurons.

As above-mentioned, both the duration and the amplitude of spontaneously-occurring EEG bursts of GFO significantly increase in the rat frontoparietal cortex following the administration of ketamine at a subanesthetic dose [56]. So, from the mathematical viewpoint presented by Cadonic and Albensi [4], it is tempting to propose that natural, physiological ongoing GFO operate like damped harmonic oscillators, which would leave room for synaptic potentiation, learning and memory, whereas ketamine-induced persistently amplified GFO run like forced harmonic oscillators, which would brake the expression of synaptic potentiation. From this perspective, one may wonder what are the so-called inhibitory or driving forces that are responsible for the acute persistent amplification of network ongoing GFO that appear following the systemic administration of the NMDAr antagonist ketamine.

It is well known that, in health and disease, GFO interact with other neural oscillations, in particular with theta oscillations [71,72]. Such interactions are termed cross-frequency-couplings [73], which are of several types (power-to-power, phase-to-phase, phase-to-frequency and phase-to-power). The functional role of cross-frequency-coupling is not yet understood [71,74]. The ketamine-induced increase in ongoing GFO might in part be the result of privileged interactions with theta oscillations, dual oscillations forming a spatiotemporal code that would be implicated in processes underlying learning and memory.

Further investigations are necessary to understand the contribution of the possible inhibitory or driving forces that work from one rhythm to the other and vice versa. Indeed, there is a growing body of evidence suggesting that the NMDAr antagonist ketamine modulates not only GFO and higher frequency oscillations, as above-mentioned, but also lower frequency oscillations, including alpha, theta and delta oscillations [55,61,75,76]. However, this broad-spectrum effect depends on the injected dose, the experimental and recording conditions and on the anatomofunctional properties of the structures under investigation. For instance, in in vivo conditions, a single low-dose (< 10 mg/kg) ketamine administration alters more specifically GFO and higher frequency oscillations [56,59,60,69] while higher doses in addition affect slower rhythms [61,62,75,77,78,79,80]. Therefore, we must be prudent when comparing results and inferring mechanisms from studies using different doses of NMDAr antagonists and various and diverse animal and network models. This is fundamental for basic-clinical translational understanding.

7. NMDAr-Related Network Dysfunction Modulates the Gamma Signal-To-Noise Ratio

Interestingly, in an attempt to understand the functional role of NMDAr and minicolumns, Moss and Moss [3] introduced the concept of “disrupted column formation” as a neuronal substrate of mental disorders and brain illnesses, like schizophrenia and Alzheimer’s disease.

The notion of disrupted column formation comforts the universal concept of “Disconnection Syndrome” or “Cerebral Dis/Dysconnections”, which attempts to explain disorders of sensory-perception, thought, cognition, emotion and of sensorimotor integration that are observed in many complex brain diseases, including Alzheimer’s disease, autism, dementia, schizophrenia, bipolar and attention deficit hyperactivity disorders [81,82,83,84,85]. Nowadays, it is clear from the literature that many of these mental disorders, each arising from more than one etiology, share common pathophysiological mechanisms, which include at least three essential facets: 1) brain abnormal rhythms, in particular in GFO [86,87,88,89,90,91], 2) dysfunction of cortical and subcortical networks, including cortico-thalamo-cortical circuits [92,93,94,95,96,97] and 3) NMDAr hypofunction [98,99].

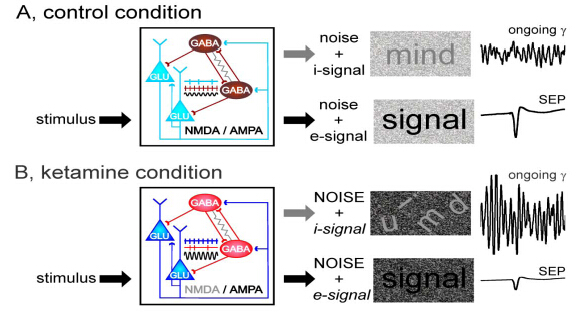
Here, I would like to further argue on the notion of “signal-to-noise ratio” pointed out in the previous issue in their terms by Moss and Moss [3] and by Pinotsis and Friston [5]. In any neuronal system, baseline field oscillations [recorded with EEG and local field potential electrodes] represent a dynamic “network noise”. The oscillation properties (frequency, period, amplitude, power, etc.) depend on the physiological or pathological brain state and on the recording conditions. Under a given pathological condition, such a noise (background activity) can increase in a manner such that it can mask or interfere with function-related synchronized oscillations, thereby affecting the ratio signal power to noise power. Here, the notion of signal―more precisely “network signal” - is a function-related response (e.g, sensory-evoked potential―with its related wave components - that is time-locked to the stimulus) of the system under investigation challenged by the activation of an afferent pathway (e.g, sensory stimulus). In short, in any system, both the amount of the ongoing (background or baseline) activity and the amplitude (or power) of its global response to the activation of its inputs are indicators of its state and functionality (Figure 2). The possible noise-signal interplay(s) might in part explain some disparities between findings (e.g., increases and decreases in GFO in patients with schizophrenia).

Figure 2. Ketamine decreases the signal-to-noise ratio in a network model composed of interconnected glutamatergic and GABAergic neurons. (A): The simplified cortical network shows local anatomofunctional interactions between GABAergic parvalbumine positive interneurons that are interconnected, electrically and synaptically, and that innervate (recurrent and lateral inhibitions) glutamatergic (GLU) pyramidal cells. Both GLU and GABA neurons have operational NMDA and AMPA receptors. Natural ongoing GFO are locally generated through interactions in the GLU-GABA network, thereby inhibiting pyramidal neurons that display irregular firing with action potentials (in blue) phase-locked with the positive wave of ongoing GFO recorded in the extracellular local field potential (in black). The ongoing intrinsically-generated network activity generates a certain amount of gamma noise (ongoing y) and intrinsically-generated signals (noise + i-signal). This ongoing activity characterizes the “normal or natural” network state (mind). When challenging the system by the activation of a sensory afferent pathway (stimulus), it produces a measurable sensory-evoked signal (e-signal), here the averaged sensory-evoked potential (SEP) of a given amplitude, which reflects synaptic potentiation. The averaging procedure attenuates or eliminates the ongoing noise as it is not time-locked to the stimulus. (B): Following a single administration of ketamine at a subanesthetic dose, NMDAr are less operational than AMPAr. The GABAergic interneurons, assumed as being more sensitive to the NMDAr antagonist, emit less action potentials leading to reduced inhibition of pyramidal neurons. These latter disinhibited GLU neurons, which are more numerous than the GABAergic neurons (~85% vs. 15%), spontaneously generate (locally and distantly), through their numerous axon collaterals, massive synchronized rhythmic activity at the gamma frequency. This “generalized” disinhibited pyramidal rhythmic activity is recorded as abnormally high amplitude (high power) ongoing GFO, which corresponds to a huge gamma noise and intrinsically-generated signal (NOISE + i-signal). Under such a pathological condition, the averaged SEP is recorded with an amplitude lower than that of the SEP recorded under the normal (control) condition, revealing an apparent decrease in synaptic potentiation. In short, ketamine alters both the state and the function of the GLU-GABA network, thereby affecting the network noise and accompanying intrinsically generated and sensory-evoked signals (i-signal and e-signal, respectively).

DownLoad: Full-Size ImgPowerPoint

More precisely, in the rat thalamocortical system, ketamine simultaneously increases the power of spontaneously-occurring GFO (signature of a change in the state of the system) and decreases sensory-evoked GFO (signature of a disturbance of the functionality of the system) [56,60,63] (Figure 1C, D). Assuming that sensory-evoked GFO include a “true” sensory-related component, the ketamine-induced gamma noise amplification decreases the ability of the thalamocortical system to discriminate the sensory-evoked gamma signal drowned in the noise. In other words, the NMDAr antagonist ketamine decreases the gamma signal-to-noise ratio during sensory information processing (Figure 2). Such a ratio is considered as a suitable neurophysiological marker of neural networks to evaluate their function and dysfunction [61,100,101,102].

This abnormally excessive ongoing gamma noise is thought to affect global brain state and operation and to contribute to psychosis. Moreover, continuous and stereotyped GFO might be responsible for clinical positive symptoms [103]. Furthermore, ongoing abnormally hypersynchronized GFO have been recorded in patients experiencing sensory hallucinations [12,13,14,15,16]. Hypersynchronized GFO in cortico-thalamo-cortical systems are thought to play a key role during the appearance of hallucinations [12,14], arising the question as to whether persistent amplification of ongoing GFO somehow could generate aberrant signals and conceal function-related GFO in the corresponding brain networks.

8. Conclusion

Healthy neural networks have the ability to discriminate, from ongoing intracerebrally generated background activities―under or not the influence of external world’s stimuli-, the appropriate signal(s) at the right time during cognitive and sensorimotor processes. During information processing, neuronal interactions play important roles in facilitating, via lateral GABAr-mediated inhibitions, contrast augmentation. As against, many mental disorders and brain pathologies have, in spite of their respective etiology, common pathophysiological characteristics, in particular dysfunction of brain networks leading them to exhibit abnormal GFO. Abnormally hypersynchronized ongoing GFO might be the source of distorted thoughts and hallucinations [14]. In the cortico-thalamo-cortical system, NMDAr antagonism dramatically amplifies baseline network GFO, impedes synaptic plasticity and disturbs function-related GFO [63]. The mechanisms underlying network dysfunction might in part involve hypofunction of NMDAr on GABAergic interneurons, which would lead to a deficit in GABAr-mediated inhibitions, a subsequent hyper-excitation of the postsynaptic projection glutamatergic neurons [99,104,105], and disruption of lateral inhibitions [95]. Testing theoretical and pathophysiological hypotheses is an appealing and effective basic-clinical translational approach to understand how, in health and disease, our brain at work combines its various and miscellaneous molecular, synaptic, cellular and architectural complexities.

Acknowledgement

This work is supported by the French Institute of Health and Medical Research (INSERM, Institut National de la Santé et de la Recherche Médicale) and by the Université de Strasbourg.

Conflict of Interest

The author reports no conflict of interest associated with this article.