Business and policy models to incentivise utilities to engage with demand-side management (DSM) have received more attention in the grey literature than the academic literature. This review paper contributes to filling this gap by reviewing theoretical frameworks for four key categories of business models and how they relate to policy models that enable their implementation. The paper proposes a theoretical lens through which to visualise the different frameworks. The review discusses the key benefits and challenges for utilities to engage with DSM, and finds that deferred investment in new generation capacity, new business opportunities and services, and dealing with variable power production are the primary benefits, and limited incentives to invest in markets based on the quantity of energy sold and cost recovery issues (such as DSM programme costs) are the main challenges. The paper reviews four primary business and policy models: decoupling, demand-side participation in capacity markets, utility obligations and Energy Service Companies (ESCOs), and finds that despite the limitations of the evidence base on the applicability of decoupling in fully liberalised markets, demand-side participation in capacity markets, utility obligations and ESCOs appear to be applicable across contexts.
1.
Introduction
The traditional business model of energy utilities is based on increasing revenue through selling greater quantities of energy, such as gas or electricity. The link between sales and revenues encourages utilities to sell more energy regardless of the impacts of increased sales on customers (Hirst and Blank, 1994). In the 21st century, the role that the demand-side can play in contributing to meeting energy policy objectives, such as carbon emissions reduction, energy security, reducing consumer energy bills and energy access, is receiving increasing interest from governments around the world. Demand-side management (DSM) includes activities on the demand-side of energy meters, such as energy efficiency, energy conservation, demand response, on-site generation and behind-the-meter storage that seek to meet these policy objectives (Warren, 2018; 2014a). However, DSM runs contrary to the traditional business model of energy utilities, except where on-site back-up generation (historically from diesel generators in industry) is used to manage demand during peak times when supply-side options are constrained or too expensive.
DSM is a crucial part of meeting the goals of the Paris Agreement, agreed at COP 21 in 2015, and improving the efficiency of resource use. Utilities are key actors in the energy system and consequently have an important role to play in accelerating the implementation of DSM activities. A number of theoretical and practical business models have been proposed and developed since the energy crises of the 1970s to put the profitability of demand-side activities on an equal basis to supply-side options. However, much of the work has been undertaken outside of the academic literature and existing academic reviews have focused on specific types of DSM, such as demand response, rather than a more holistic consideration of DSM. More importantly, there is limited theoretical work on developing frameworks to understand incentives from a private finance perspective. As such, this review aims to contribute to filling these gaps by reviewing theoretical frameworks for four key categories of business models and how they relate to policy models that enable their implementation.
Section two reviews the benefits and challenges for utilities to engage with demand-side management. Section three then discusses theoretical frameworks for four key categories of business and policy models: Decoupling, capacity market participation, utility obligations and Energy Service Companies (ESCOs). These categories were chosen due to their promising potential to meet environmental, economic and social goals (as identified in the academic and grey literatures), the diversity between them in their design and implementation, and the tendency for previous research to look at them in isolation rather than together. Section four provides the paper's conclusions and identifies important areas for further research.
2.
Benefits and challenges
2.1. Benefits of DSM for utilities
In the energy system, there has been much academic debate over the role of demand-side management (DSM). Many of the arguments are in broad agreement that DSM is a useful and complementary solution to current energy policy challenges, alongside interconnections, energy storage and increased low carbon generation capacity. It is clear from the literature review that there are numerous benefits to the implementation of DSM. For society, Gillingham et al. (2009) argue that it is a cost-effective way to contribute to overcoming energy security issues, and Pachauri et al. (2012) highlight that DSM (particularly energy efficiency) can contribute to addressing energy access issues. For Governments, DSM reduces the risk of 'black-outs' (power supply disruptions), which can have important political repercussions during energy crises, and can help to reduce greenhouse gas (CO2e) emissions (Cooke, 2011) in order to meet policy targets. Furthermore, DSM can be an effective way to facilitate behaviour change by increasing the awareness of consumers with regards to their energy consumption patterns (Owens and Driffill, 2008; Devine-Wright and Devine-Wright, 2004). However, the focus of this section is on the benefits and challenges for utilities to engage with the demand-side, rather than the benefits and challenges with DSM more broadly, which have been covered elsewhere (e.g., Strbac, 2008; Paterakis et al., 2017 (in relation to demand response specifically); Parrish et al., 2016 (in relation to demand response specifically)).
Strbac (2008) highlights that DSM prevents or defers the need to invest in new generation capacity, which is a costly option if the generators are used infrequently during times of peak load (and are usually carbon-intensive plants, such as diesel generators). Historically, this has been the primary reason for utility engagement with DSM outside of undertaking activities due to mandatory regulation. Torriti et al. (2010) extends this point by stating that due to the political pressure on the energy industry to invest in low carbon generation in a growing number of countries (particularly following the Paris Agreement in 2015), energy utilities have an effective way to deal with more variable sources, such as wind power, by using demand response tariffs (for example, time-of-use pricing for consumers where prices vary at different times of the day or year). Furthermore, Strbac (2008) argues that DSM improves transmission and distribution grid investment and operation efficiency, which highlights the benefits of demand-side activities across the total energy system.
Increased engagement between utilities and their customers is mutually beneficial. For consumers, DSM can allow them to more actively engage in energy markets and to monitor their specific patterns of energy consumption (Darby 2006). DSM can be used as an educational tool, which may lead to cost savings through behaviour change, demand response tariffs and energy efficiency, and (where available) the production of capital through feed-in tariffs for micro-generation (such as solar photovoltaics or heat pumps). Feed-in tariffs are payments from energy utilities to consumers for each unit of low carbon energy produced from micro-generation. Such activities help utilities to balance supply and demand at least cost. Darby (2006) and Stromback et al. (2011) argue that in the face of energy price rises in the 2010s, making energy more 'visible' to consumers could help them to mitigate such rises. As Capgemini (2008) notes, the success of demand-side activities depends on being simple, affordable, empowering and reliable for consumers.
For the market, Hirst (2002) argues that permitting and encouraging retail customers to respond to dynamic prices will improve economic efficiency, discipline wholesale market power, improve reliability and reduce the need to build new generation and transmission facilities. DSM can also facilitate the development of a 'negawatts' market, where reduced energy has an equal value to megawatts (Steinberger et al., 2009). Amory Lovins, who first coined the term 'negawatts', states that it refers to electricity saved and he argues for the development of a negawatts market where negawatts are treated as a commodity (Lovins, 1990). Such a market would involve a certain number of megawatts being reduced by participating customers when called on to do so by agammaegators, utilities or system operators, in order to help balance supply and demand. In the industrial sector, many large consumers are involved in demand response programmes, such as interruptible/curtailment programmes, where upfront payment incentives or rate discounts are given to reduce load to pre-defined values (Albadi and El-Saadany, 2008). These concepts are explored further in section three.
Globally, different types of demand response programmes have been well-tested with large consumers but not to the same degree with small energy users (the domestic sector and small-to-medium-sized enterprises (SMEs)). Newborough and Augood (1999) provide the example of automation, which refers to the direct control of certain appliances and equipment by energy utilities during peak periods. They show that automation can be adapted to smaller consumers to achieve up to 60% peak-power reductions in appliance use through the controlled modulations of appliances, such as cooking and washing machines. For example, automation devices may be installed on air conditioners to change the temperature by a few degrees for a few hours during peak periods (Albadi and El-Saadany, 2007; Walawalkar et al., 2010). The contracts are designed so that direct load control has minimal impact on the welfare of consumers. Spees and Lave (2007) showed that 65% of firms included in their study reported that direct load control had minimal impact on facility operation. Suitable domestic equipment for automation include: Fridges, washing machines, tumble dryers, lighting, air conditioning, hot water storage heaters and electric heaters.
A further example of residential demand response is É lectricité de France (EDF)'s Tempo tariff, which was introduced in the 1960s. The tariff involves the days of the year being divided into three categories: 300 days are 'blue' (with low electricity prices), 43 days are 'white' (with medium electricity prices) and 22 days are 'red' (with high electricity prices) (IEA DSM, 2008). EDF informs consumers in advance of what colour the days will be based on forecasts of electricity demand, usually determined by the weather (IEA DSM, 2008) or if the French transmission network operator informs them of significant congestion on the electricity network (Crossley, 2011). However, tariff structures like Tempo are currently not very common and < 20% of residential consumers in France use it (IEA DSM, 2008).
Simpler tariffs, such as higher electricity prices for peak times of the day and lower electricity prices for off-peak times, are available in some countries. Off-peak times are generally during the night, such as 10pm-6am under EDF's tariff (IEA DSM, 2008). In the UK, heat stored in bricks, hot water storage tanks and electric storage heaters allow residential consumers to store thermal energy during the night when electricity prices are cheaper, and use the energy during the day using Economy 7 tariffs (Hamidi et al., 2009) or Economy 10 tariffs, where there are seven and ten hours of off-peak electricity prices respectively. Out of the estimated 11–12 million hot water storage tanks in the UK (BEIS, 2016; Saker et al., 2013), ~2 million have radio tele-switching (RTS) technology installed that could be utilised to enable demand response (Owen et al., 2012), 3–3.5 million households have Economy 7 tariffs (Owen et al., 2012), and 1.8 million households have electric storage heating (BEIS, 2016). These examples show that demand response has been useful in helping utilities to match supply and demand, but it is clear that they do not highlight the full potential of demand response and the ability of utilities to profit from it.
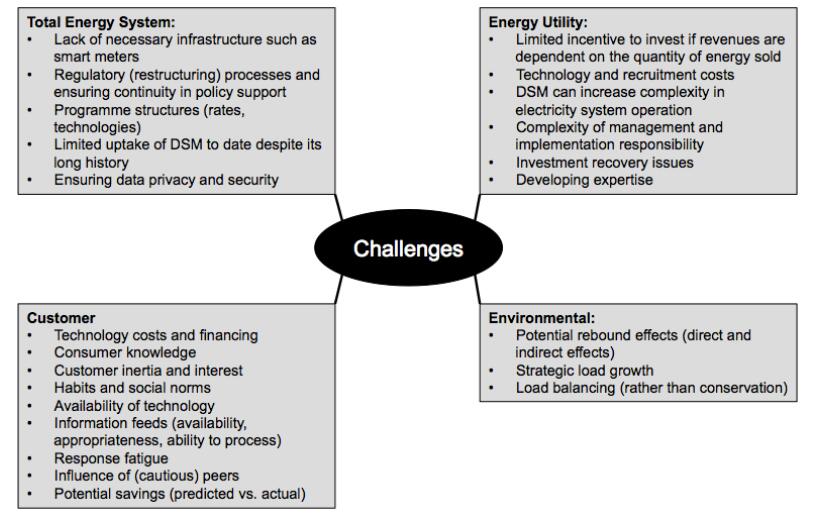
Drawing on this literature review, the benefits of DSM are summarised in Figure 1. The diagram is broken down into four boxes: Benefits to the total energy system, benefits to consumers, benefits to utilities and environmental benefits. However, it is important to note that all of the bullet points relate to utility benefits either directly or indirectly through operational costs, regulatory requirements or corporate social responsibility.
2.2. Challenges of DSM for utilities
Despite the benefits of demand-side activities for utilities, there are a number of key implementation challenges that exist. Kim and Shcherbakova (2011) argue that the challenges are primarily social, political and economic rather than technical. From an economic perspective, Didden and D'haeseleer (2003) emphasise the implementation and incentives issues that have developed as a result of energy market liberalisation. Energy market liberalisation refers to the privatisation of the energy industry and/or the introduction of competition. Full market liberalisation involves moving from vertically-integrated monopolies to retail competition with full customer choice of energy supplier (Bhattacharyya, 2011; Lise and Kruseman, 2008). Didden and D'haeseleer (2003) claim that Integrated Resource Planning (IRP) is theoretically appropriate and partly applicable in the open market, but as its history indicates, there are better frameworks for developing DSM, such as energy services and mandated energy efficiency goals (explored in section three). IRP is a regulatory framework that ensures that energy utilities evaluate all options (including the demand-side) for meeting future energy demands and provide energy services at minimal societal costs to customers (Cheng, 2005). The most fundamental economic barrier to DSM development is the limited incentive for energy utilities to invest in DSM in a market based on the quantity of electricity or gas sold if there are no clear financial returns (Cheng, 2005), or if DSM is not cost-competitive with traditional approaches (Strbac, 2008).
Although Kim and Shcherbakova (2011) argue that the main barriers are social, political and economic rather than technical, they exclude information-based infrastructure from their category of technical issues and instead highlight it as an important limiting factor. This is strongly evident in the literature. For example, Strbac (2008) conveys how a lack of information and communications infrastructure is an important hindrance to the successful implementation of many DSM measures, such as demand response tariffs and the effective management of micro-generation technologies. In the latter case, the micro-management of a collective number of local micro-generation installations to form a 'Virtual Power Plant' (El Bakari et al., 2009) is dependent on the necessary information and communication infrastructure being in place. Currently, the rollout of smart meters in many countries aims to overcome this challenge in the domestic and SME sectors. For example, the European Union (EU)'s Directive 2009/72/EC mandates that member states must achieve at least an 80% rollout of smart meters to small consumers by 2020. Smart meters are advanced energy meters that measure consumption in real-time, providing detailed information to utility companies and allowing bidirectional communication, which enables the collection of information about electricity (or gas) fed back into the grid from customers' premises (Depuru et al., 2011), such as from solar photovoltaic panels. Warren (2017) analyses the potential of smart technologies and micro-generation in SMEs in the UK and, in contrast to Kim and Shcherbakova (2011), finds that the main barriers are more diverse and context-specific, such as the importance of the initial costs, technical feasibility and planning permission on historical buildings.
Kim and Shcherbakova (2011) convey how smart meters with In-Home Displays (IHDs) (display monitors showing energy consumption, prices and other information such as carbon emissions) could overcome some of the commonly cited barriers to DSM development: Consumer knowledge, consumer engagement, information feeds and two-way communication between utilities and customers. They state that consumer knowledge refers to consumers' limited practical knowledge of the functioning of energy markets. They highlight that consumer engagement is linked to a lack of effective utility strategies to incentivise consumers to take part in demand response programmes. Thus, the success of utility engagement with DSM, particularly demand response, is strongly correlated with the ability of utilities to engage their customers in such activities.
Kim and Shcherbakova (2011) define information feeds as the lowering of search costs for consumers to find information about energy prices and consumption, and what they need to do to reduce consumption if they are signed up to a demand response programme. The authors argue that In-Home Displays (IHDs) have an important role to play here. The key challenge in this respect is the ability of utilities to incentivise consumers to continue to engage with IHDs and demand-side activities over the long-term. Some studies, such as Hargreaves et al. (2010) and Darby (2006), show that consumer engagement with DSM is a short-term phenomenon and is not maintained as a part of every day life over the long-term.
Two-way communication between utilities and customers refers to the installation of smart meters to integrate information on consumption to and from the supplier, including the use of demand response programmes and micro-generation technologies if present. Key challenges of two-way communication are the management of large volumes of data by energy utilities, as well as cyber security issues (Depuru et al., 2011; Chinnow et al., 2011). In the UK, the government introduced a Data and Communications Company (DCC) to ensure the effective management of data, and to ensure the security of communications and data privacy during its rollout of smart meters to small consumers by the end of 2020.
The provision and appropriateness of information by utilities is arguably the most fundamental social barrier, as there is much research from behavioural economics, which demonstrates that simply providing consumers with information (the 'information deficit model') does not result in the uptake of demand-side measures by consumers. For example, Ürge-Vorsatz and Hauff (2001) found that, despite Hungary's success with the market transformation of Compact Fluorescent Lighting (CFL), a high level of consumer awareness does not necessarily guarantee market success. Family, friends and peers are important influences on people's decision-making (Johnson-Brown and Reingen, 1987; Granovetter, 1973), as well as the influence of neighbours or competing companies and social norms (Mau et al., 2008; Strachan and Warren, 2011). This poses an important challenge for utilities in successfully engaging their customers in DSM.
Drawing on this literature review, the challenges of DSM are summarised in Figure 2, which is broken down using the same format as Figure 1.
3.
Incentivising utilities: Business and policy models
3.1. Overview
There are various business models that have been discussed in the academic and grey literature with regards to how to incentivise utilities to engage with DSM. The business models discussed in this section are linked where relevant to the policy models that may be required to implement them, and the discussions draw on practical examples where possible (though the paper primarily focuses on theoretical frameworks). The paper narrows the scope of the review by focusing on four broad types: Decoupling (sub-section 3.2), capacity market participation (sub-section 3.3), utility obligations (sub-section 3.4) and energy services companies (sub-section 3.5). Much of the evidence base is dominated by grey literature rather than academic literature, such as from regulatory papers, consultancy or institutional reports, and company material, which this section will highlight. As a result, this paper aims to contribute to the academic literature on this topic.
3.2. Decoupling
There has been growing interest in the concept of decoupling utility profits from the quantity of energy sold. It is possible that this has stemmed from broader discussions of the idea of decoupling economic growth from energy consumption. The USA has been the pioneering country in developing alternative utility business models to enable decoupling, though this has been driven at a state-level rather than at a national level (discussed further below).
Decoupling is a broad term that encompasses a range of business models that vary based on the balance between the revenue received by the utility and the costs to other parties, such as consumers and regulators. The revenue is affected by potential reduced sales from selling less energy due to demand-side activities, the costs of undertaking DSM programmes and the ability to obtain additional profit beyond what could be achieved through supply-side options. The academic literature on the topic has been relatively limited outside of Utilities Policy and The Electricity Journal, where much of the practical examples from the USA are published. In the grey literature, the Regulatory Assistance Project (RAP), the Natural Resources Defense Council (NRDC) and the American Council for an Energy-Efficient Economy (ACEEE) have been the key institutions driving research in the area, and draw on practical examples from the USA and Australia.
Decoupling policies usually require utilities to be either fully regulated (such as through state-owned models) or to accept a high degree of regulatory control (such as through partially-privatised models). Most of the policy models vary based on cost recovery mechanisms. However, some focus on the direct regulation of revenues or the provision of direct incentives for DSM. The models are summarised in Table 1.
The business models in table one can be split into those that focus on decoupling directly and those that focus on providing shareholder incentives. Decoupling (without recovery) is achieved through the regulation of utility revenues by making sure that utilities do not receive less than the authorised fixed costs nor more from increased sales (Hayes et al., 2011). Thus, the disincentive to engage with DSM is removed and the incentive to sell more electricity or gas is removed. However, the recovery of DSM programme costs is not allowed under this model. Lost Revenue Adjustment Mechanisms (LRAMs) are business models that allow partial cost recovery. Utilities can recover lost revenue through rate adjustments, though unlike the decoupling (without recovery) business model, they can still increase returns from increased sales (Baxter, 1995). Thus, this is a form of partial decoupling.
Shareholder incentives aim to take the previous concepts a step further by allowing utilities to profit from DSM programmes, and they can be categorised into three main types: Shared benefits, performance targets and rates of return (Hayes et al., 2011). Shared benefits involve the utility sharing the benefits of DSM programmes between ratepayers and utility shareholders (Schultz and Eto, 1990), with the utility benefiting from some of the value of the energy savings achieved. Performance targets aim to financially reward utilities for achieving certain targets (Kushler et al., 2006), such as previously defined energy or carbon savings goals through investments in energy efficiency. These targets are usually set on a 1–3-year basis. Rates of return seek to give utilities a return based on energy efficiency spending or savings (Hayes et al., 2011).
In terms of policy models, revenue regulation reflects the decoupling (without recovery) and LRAMs business models to ensure that utilities receive consistent revenues regardless of the amount of electricity or gas that they sell, but with periodic adjustments to the revenues based on actual sales. Any over- or under-collection of revenues during a given year is corrected in determining the level of revenues for the following year (Crossley, 2013). Direct incentives for DSM is a policy model that primarily refers to financial payments given directly to utilities by regulators or government bodies for DSM activities. Such payments are not usually provided through changes to rates paid by consumers, but instead through other channels, such as regular payments over a designated time scale or through tax credits.
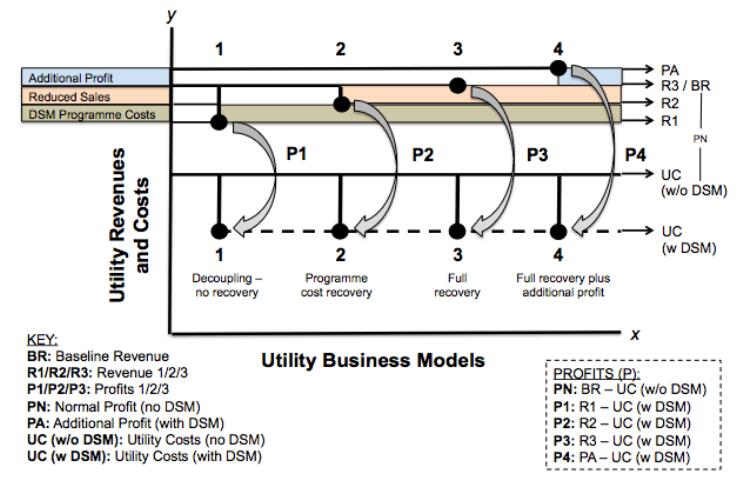
The four remaining policy models in table one are variations of the same concept and are focused on cost recovery mechanisms through adjustments to the rates paid by consumers. They vary based on the amount of revenue the utility receives. The higher the amount, the higher the rates paid by consumers. In contrast, the lower the amount, the lower the energy bills are for consumers. The four policy models are visualised in figure three. The graph builds on previous work by the ACEEE (e.g., Hayes et al., 2011; Molina and Kushler, 2015; Nowak et al., 2015; Berg et al., 2016), RAP (e.g., Crossley, 2013; Crossley, 2010; Crossley et al., 2000) and the NRDC (e.g., NRDC, 2016; NRDC, 2013).
The recovery of DSM programme costs model refers to utilities being allowed to raise rates in order to cover the costs of demand-side activities. However, this is a form of partial cost recovery, as potential revenue losses from reduced sales as a result of DSM programmes cannot be recovered. Similarly, the recovery of reduced sales model allows utilities to recover what cannot be recovered in the first model. However, they are not allowed to recover the costs of demand-side activities. Thus, this is also a form of partial decoupling, as it deals only with revenue losses (Eto, 1994; Eto et al., 1997). The third model (full recovery) allows both DSM programme costs and potential reduced sales to be recovered. The fourth model (enhanced full recovery) is the most interesting for utilities as it ensures that demand-side activities are more profitable than supply-side activities, rather than simply placing them on an equal basis, as in the first three models. However, there is little practical experience of this model. It allows utilities to increase rates further by an agreed percentage to provide additional profit (Warren, 2015).
Drawing on this literature review, this paper proposes the theoretical lens presented in Figure 3 to summarise how the different business and policy models impact the revenues and general costs of the utility. The graph only focuses on the cost recovery models rather than revenue regulation and direct incentives for DSM. Utility costs include investments in generation capacity, infrastructure, operations and maintenance. In each model (1–4), utility costs decrease overall (by the same amount), but this is primarily due to deferred investment in generation capacity and improved efficiency of operation rather than general operation and maintenance (as DSM can sometimes increase utility costs due to potentially increased administrative complexity). The x-axis is not scaled and simply shows the four main utility business models, whereas the y-axis is scaled to show how utility revenues and costs vary with each model.
Introducing decoupling policies without any recovery of potential lost revenue from reduced sales and DSM programme costs (1) leads to a reduction in utility revenue but still leads to an overall benefit as the reduced utility costs are greater than the reduced sales. In this case the utility funds any additional costs. However, the model is theoretical and in practice, the degree to which there is a net financial benefit under (1) depends on local, contextual factors, such as variations in administrative costs for DSM programmes between utilities in the same or different jurisdictions and countries, the impact of current, local energy prices on potential reduced sales, the importance of the financial benefit from deferred investment in infrastructure (such as generation infrastructure) for a particular utility, the willingness of a utility's customers to engage in DSM programmes, the skills and capacity of utilities to undertake demand-side activities, and the degree to which the senior management of a given utility is innovative or traditional in its strategic approach for generating revenues.
Introducing policies to recover DSM programme costs (2) increases the utility benefit as it can recover the administrative costs of DSM programmes (primarily through surcharges on consumer bills). This is partial cost recovery, and LRAMs fit into this category in reverse where potential lost revenue from reduced sales can be recovered but not DSM programme costs. In other words, either reduced sales or DSM programme costs can be recovered but not both. This model helps to overcome any potential issues with not achieving a net financial benefit due to the contextual factors listed above. Some studies, such as Satchwell et al. (2011), have demonstrated viable business models through applying a revenue-per-customer decoupling mechanism, which is designed to recover revenues on a per-customer basis.
In (3), full recovery is allowed where both DSM programme costs and potential lost revenue from reduced sales can be recovered (again primarily through surcharges on consumer bills). Enhanced full recovery (4) allows the full recovery of costs as in (3) but allows additional profit to also be recovered.
The incentive for utilities increases as one moves from (1) to (4), though the practical implementation of such policies depends on the individual circumstances and contexts of the country or region where they are being introduced. Costs to consumers tend to increase from (1) to (4) as utility revenues increase, as utilities usually recover costs through consumer energy bills.
There has been limited practical implementation of these business and policy models outside of North America, though there have been some developments in Australia and Northern Ireland as a result of the Northern American experiences (Crossley, 2013). Although implementation has been driven at a state-level rather than the national-level in the USA, a growing number of states have introduced decoupling policies within their jurisdictions (Nowak et al., 2015). In 2016, almost half of US states had implemented gas decoupling (23/50 states) with four states considering it, and almost a third of US states had implemented electric decoupling (15/50 states) with eight states considering it (NRDC, 2016). Although it is unlikely that decoupling will be implemented at the national level due to contextual differences between the states, it is probable that most states will individually implement some form of decoupling in the future. Some studies have sought to examine the transferability of DSM policies between countries and sub-national states. For example, Warren (2017) examined twelve different types of DSM policy, including decoupling policies, and concluded that context is key and the level of contextual detail included in methods to analyse DSM policy transferability will affect the level of policy transfer (direct copying, adaptation and inspiration) that is appropriate.
The US experiences with decoupling have generally been successful, particularly shareholder incentives (Molina and Kushler, 2015), but a key challenge is in determining the applicability of such policies in other regions, such as Europe, Asia and Australasia. As stated previously, there have been some developments in the implementation of decoupling policies in Australia and Northern Ireland (Crossley, 2013), but as yet it has received limited introduction globally in comparison with the three other categories of models discussed in this paper: capacity market participation, utility obligations and Energy Service Companies (ESCOs).
In the USA, a large number of utilities operate locally or regionally and are usually publicly- or investor-owned but with a strong degree of regulation from state public commissions. In Europe, utilities are often large, private and operate in fully liberalised, competitive markets across different countries. Thus, decoupling policies implemented in one country of operation may need to be implemented in the other countries where the utility operates, as well as being applied to all utilities in the markets within which a given utility is active. In such contexts, decoupling policies are arguably less suitable. However, there could be a role for decoupling business models for vertically-integrated transmission and distribution providers in liberalised markets (Crossley, 2013), which tend to be natural monopolies, though not for retail companies. Further research should identify which countries and sub-national states beyond the USA and Australia are suitable for the introduction of decoupling policies.
3.3. Capacity market participation
The role of the demand-side in capacity markets is receiving increased attention from governments around the world. On-site generation, such as diesel generators in industry, have long been used to provide capacity during peak times in order to help contribute to balancing supply and demand. Demand response provided through 'turn-down' activities has been used in capacity markets in some countries and regions for a number of decades (such as in the PJM, NYISO, ISO-NE, CAISO and MISO regional markets in the USA), whilst in others it has only recently been introduced (such as in the UK). There are two main types of demand response: price-based and incentive payment-based (Albadi and El-Saadancy, 2008; Warren, 2014b). The former refers to the response of consumers to price changes, whereas the latter refers to the response of consumers to incentive payments (Albadi and El-Saadany, 2008; Warren, 2014b). For capacity markets, it is the latter that is included through direct load control (automation), interruptible/curtailment contracts, demand bidding and ancillary services market provision, emergency demand response, and relieving network constraints in specific locations. There is much academic literature on demand-side participation in a range of energy markets (for example, see Chapman and Verbic, 2017, Fattahi et al., 2018 and Otashu and Baldea, 2018 for specific applications and Poudineh and Jamasb, 2014and Paterakis et al., 2017 for comprehensive overviews).
In practice, where the demand-side can participate in capacity markets (or other markets), on-site generation makes up the vast majority of the demand-side capacity that is bid with 'turn-down' demand response only making up a small proportion of this. This may partly be explained by the perceived risk by utilities of non-response from consumers that have signed up to demand-side contracts. Despite this, direct load control can contribute to overcoming the risk, and demand-side agammaegators can also spread the risk over a larger pool of consumers (i.e., rather than focussing on a few consumers with large loads, they instead concentrate on agammaegating a larger number of small loads—however, this increases administrative costs for demand response organisers). Prior to the implementation of the UK's capacity market in 2014, demand-side resources through demand response could participate in the balancing market. Ward et al. (2012) estimated that of the 1.5 GW of demand-side capacity that was contracted in the 2011–2012 period, only 200 MW was provided through 'turn-down' demand response (the rest was provided through on-site generation, primarily industrial diesel generators). The total back-up requirements for the period were 4.7 GW—thus, the demand-side (including on-site generation) contributed 20–25% of the requirements (Ward et al., 2012).
The role of on-site generation and demand response in capacity markets has been explored in much depth in the academic and grey literature. However, the role of the third pillar of DSM, energy efficiency, in capacity markets has received much less attention, particularly in the academic literature. The concept of energy efficiency in capacity markets is based on the bidding of permanent reductions over the lifetime of measures that can provide the required capacity in a given period (e.g., winter peak periods). As Behrangrad (2015) notes, the reduction in load caused by energy efficiency allows generation and transmission capacity to freed up by affecting the load-generation balance.
There have been limited practical experiences of energy efficiency in capacity markets globally. The ISO-NE capacity market was the first market to introduce energy efficiency as a resource in 2006, with the first 'delivery' of capacity in 2009 (Fetter et al., 2012). The PJM capacity market followed soon after this in 2009 with the first 'delivery' of capacity in 2012 (Fetter et al., 2012; Titus et al., 2009). The UK government followed the US experiences and implemented a pilot scheme in 2014 to explore the potential of permanent reductions through electricity efficiency as a resource in the capacity market that was introduced in 2014 (BEIS, 2017a). To date the pilot has held two auctions (in January 2015 and January 2016) and is targeted at the private and public sectors. In the first auction (phase one), £1.28 million of funding was allocated for ~5.589 MW of electricity demand reduction for the 2015–2016 winter period (spread across 22 projects) (Murray, 2015; BEIS, 2017a), and in the second auction (phase two), £4.74 million of funding was allocated for ~23.307 MW of electricity demand reduction for the 2016–2017 and 2017–2018 winter periods (spread across 37 projects) (Stoker, 2017; BEIS, 2017a). The interim government report highlights that phase one delivered 2.595 MW of electricity demand reduction of an estimated 4.517MW, which represents a realisation rate of around 57% (BEIS, 2017a). Liu (2017) provides a comprehensive comparative assessment of energy efficiency and demand response in the ISO-NE, PJM and UK capacity markets.
There is much potential globally for demand response and energy efficiency to play a much greater role in capacity markets. However, regulatory support and appropriate incentives are required to put demand-side options beyond on-site generation on an equal basis with supply-side options (Warren, 2019; 2015). Furthermore, in removing the barriers to the inclusion of demand response and energy efficiency in capacity markets, consideration must be given to the capability of providers in addressing risks of unstable funding and forward planning (Liu, 2017).
3.4. Utility obligations
Alongside performance standards (minimum energy performance standards for appliances, equipment and buildings), utility obligations have been one of the most successful DSM policies globally in terms of policy objectives for energy savings and carbon emissions reduction (Warren, 2019; 2015). Much research and analysis has been conducted on utility obligations in both the academic and grey literatures, so this sub-section provides only a brief discussion in order to highlight the importance of utility obligations in fully liberalised energy markets to stimulate new business arms and innovative business models.
Utility obligations refer to usually mandatory (though sometimes voluntary) obligations placed on suppliers, distributors, public entities, or building owners or users (THINK, 2012). Nevertheless, the evidence base is dominated by evaluations of obligations on energy suppliers and distributors. In the USA, they are referred to as Energy Efficiency Resource Standards (EERS) and in Europe, they are known as supplier (or distributor) obligations. The obligations aim to meet various policy objectives, and there are a number of ways in which the targets can be expressed. Targets are commonly set in terms of energy or carbon savings with sub-targets for fuel poverty (consumers living on a low income in a home that cannot be kept warm at a reasonable cost, as defined in the UK's Warm Homes and Energy Conservation Act 2000 and reviewed in the Hills Fuel Poverty Review, 2012).
The USA and the UK have the longest history of utility obligations, and in the 2000s and 2010s a large number of other countries have begun introducing them. In Europe, the UK has had utility obligations since 1994, in Italy since 2005, in France since 2006 and in Denmark since 2006 (Eyre et al., 2009; Bundgaard et al., 2013a; 2013b). The Energy Efficiency Directive (Directive 2012/27/EU) requires all Member States of the European Union (EU) to introduce utility obligations (or to implement an equivalent, agreed alternative). This has increased the number of utility obligations globally. Comprehensive comparative assessments of different European utility obligations, particularly those in the UK, Italy and France, have been undertaken by leading researchers in the field, such as Rosenow (e.g., Rosenow et al., 2013; Rosenow, 2012; Rosenow and Galvin, 2013), Bertoldi (e.g., Bertoldi et al., 2013; 2011; 2010) and Oikonomou (e.g., Oikonomou et al., 2012; 2009; 2008).
Unlike the decoupling model, where the focus is on adapting the underlying business models of utilities, utility obligations aim to make it mandatory that all utilities (usually over a certain size) must meet specific targets for energy savings or carbon savings by investing in energy efficiency in their customer base. Thus, the primary business model is not affected and utilities can still increase profits by selling more electricity and/or gas. Furthermore, unlike the decoupling model, which appears to work well only in certain types of market (regulated, monopoly markets with vertically integrated utilities), utility obligations have been found to be successful across market types (vertically integrated electricity utilities with regulated markets, markets with unbundled electricity providers, competitive wholesale electricity generation markets with regulated electricity retailers, and fully competitive electricity generation and retail markets) (Crossley, 2013; Warren, 2019; 2015). Nevertheless, in fully liberalised energy markets, utility obligations are encouraging traditional utilities to set up new business arms to create value from demand-side activities, such as energy efficiency, 'smart' technologies, demand response and micro-generation.
3.5. Energy services companies
The concept of energy services is not new and some countries, such as the USA, have being trying to develop energy services markets (particularly at a state-level) since the energy crises in the 1970s without large-scale success. Some US states, such as Vermont, have introduced separate utilities to offer energy services. In 2000, the Vermont Public Service Board appointed two entities (Efficiency Vermont and Burlington Electric Department) to provide energy efficiency services, such as technical assistance, rebates and other financial incentives (Vermont Public Service Department, 2014). It was the first energy efficiency utility of its kind in the world and other US states and countries, such as EfficiencyOne in Canada, have now begun to copy the business model (Hamilton et al., 2002; IEA, 2015). These examples are discussed further below.
The premise of the business model for ESCOs is that consumers do not necessarily value the energy itself but the services that it can provide, such as lighting, heating, cooling, washing, cooking and mobility (Boait, 2009; Haas et al., 2008). Energy utilities that set up new business arms to install measures that can achieve these services at reduced cost to the consumer, such as through energy efficiency, 'smart' technologies and micro-generation, could profit from DSM. As Strbac (2008) argues, a concentration on energy services could help traditional utilities to overcome a lack of understanding of the benefits of DSM solutions. The purpose of the ESCO business model is to meet the needs of customers' energy service demands with lower levels of energy supply than traditional utilities (Hannon et al., 2013).
There is a range of different business models for ESCOs. Traditional utilities that offer energy services as an additional line of their business is the simplest model, as it does not require a fundamental change in the way utilities earn revenues—utilities can still earn revenues from selling more electricity and/or gas. A further benefit is that the model can be implemented in any type of market (from vertically integrated state-owned utilities in monopoly markets to fully liberalised, competitive markets).
In some markets, public and regulatory bodies have set up large-scale energy efficiency organisations as a business model to deliver demand-side activities. As discussed above, in North America, two notable sub-national state-level examples include Efficiency Vermont (State of Vermont, USA) and EfficiencyOne (Province of Nova Scotia, Canada). The former was created in 2000 and the latter was established in 2010 (Efficiency Vermont, 2016a; EfficiencyOne, 2015a).
Efficiency Vermont claims that in 2015, energy savings of 104,998 MWh and total resource benefits of USD $111,859,662 were achieved (Efficiency Vermont, 2016b). Data from Efficiency Vermont's annual report suggests that since it was created, it has achieved a cumulative 1,026 GWh of energy savings through installing energy efficiency measures, which represents 14.5% of the state's electricity requirements in 2015 (Efficiency Vermont, 2016b). Measures include both electric efficiency (e.g., Light Emitting Diode (LED) lighting) and thermal efficiency (e.g., insulation), and cover the local community, business and residential sectors (Efficiency Vermont, 2016a).
EfficiencyOne claims that in 2015, electricity savings of 137.9 GWh (70 GWh from the domestic sector and 68 GWh from the non-domestic sector) and 144,316 GJ of non-electricity energy savings were achieved (EfficiencyOne, 2015b). Electricity efficiency programmes included appliance retirement, home energy assessments and business energy rebates, and non-electricity efficiency programmes included residential solar and low-income direct installations. The 2015 annual report highlights that CAD $110,000,000 of energy savings were achieved through > 30,000 energy efficiency projects across the domestic and non-domestic sectors (EfficiencyOne, 2015b).
In India, the concept of large-scale energy efficiency organisations covering whole jurisdictions has been extended to the national level with the creation of Energy Efficiency Services Limited (EESL) in 2009 through the Companies Act 1956 (EESL, 2015). EESL was set up by the Indian Ministry of Power to help to develop the ESCO and energy efficiency industry in India, as well as to lead the market-related aspects of the National Mission for Enhanced Energy Efficiency (NMEEE). NMEEE aims to strengthen the market for energy efficiency by developing favourable regulatory and policy models in the country, and stimulating the development of innovative business models (Bureau of Energy Efficiency (BEE), 2015).
Another example at the national level is the Federal Energy Management Program (FEMP) in the USA. FEMP focuses on reducing the energy intensity of the 350,000 federal buildings and structures, and the 600,000 road vehicles (Department of Energy (DoE), 2017). The programme provides the relevant organisations and agencies with the information, tools and assistance required in order to meet energy-related requirements and targets (DoE, 2017). Since 1975, FEMP has reduced the energy intensity of its buildings by > 40% through business models such as energy savings performance contracts, utility energy service contracts, on-site renewable power purchase agreements, and various federal and state energy incentives programmes (FEMP, 2016). Of particular prominence are performance-based contracts (FEMP, 2016).
Energy performance contracting is the most common form of ESCO financing, which is based on the ESCO financing the installation of measures, such as loft insulation, cavity wall insulation, micro-generation and improved window glazing, and the consumer paying for the installations through the future energy cost savings resulting from reduced energy consumption (Marino et al., 2011; Marino et al., 2010). The concept aims to overcome one of the more significant barriers to consumer engagement with DSM—high upfront costs (see figure two in sub-section 2.2). There are three main types of energy performance contracting: shared-savings, guaranteed savings and 'chauffage'. A key part of all three of the business models is the importance of the ESCO monitoring and verifying the performance of energy efficiency projects (Boait, 2009).
With all three of the business models, the financing is usually provided by a third-party financial institution rather than the ESCO (ICF, 2007). Options include: financing marketplaces (i.e., large institutional lenders) or financing vehicles (such as tax-exempt lease purchase agreements, local government leasing pools, local government bonds, revolving loan pools or power purchase agreements—see ICF, 2007 for more details).
In the shared-savings model, the ESCO finances the upfront costs and is responsible for repaying any financial lender, and the consumer pays the ESCO a percentage of its achieved savings, which must be large enough to cover repayment costs, monitoring and verification costs and other costs (International Finance Corporation (IFC), 2011). A benefit for the customer is that the ESCO assumes the performance and credit risk, and can serve customers that do not have access to financing (European Commission, 2015). However, the model favours larger ESCOs, as smaller ESCOs become too leveraged to do a greater number of projects (European Commission, 2015).
In the guaranteed savings model, the customer applies for a loan to finance the measures and provides periodic repayments to the financial lender. The ESCO guarantees energy savings from the measures, which usually equals the customer's repayments (IFC, 2011). Thus, the customer is protected from any performance risk (Dreessen, 2003). The main difference between the shared-savings model and the guaranteed savings model is that in the former, the ESCO guarantees the cost of energy saved, whereas in the latter, the ESCO guarantees the level of energy saved (European Commission, 2015). A benefit of the guaranteed savings model is that financial lenders, such as banks, are better able to manage a customer's credit risk than ESCOs. However, the model requires a financial sector that has familiarity with project financing and sufficient expertise for energy efficiency projects (European Commission, 2015).
The 'chauffage' model, common in Europe, is based on ESCOs offering customers conditioned space at a specified price per energy unit or other unit. The ESCO manages all supply and demand efficiencies (IFC, 2011).
Mourik et al. (2017) argues that forward-looking utilities find emerging energy efficiency services attractive, such as "integrated or one-stop shop or bundled offerings around retrofitting, smart (grid) services, lighting-as-a-service, heating-as-a-service [and] smart energy management as a service". Furthermore, Bigliani et al. (2015-cited in Mourik et al., 2017) identifies that such utilities are seeking to decouple energy services from conventional energy supply contracts. As Bigliani et al. (2015) primarily examine North American and European utilities, this suggests that some form of decoupling is possible in the European context. However, further research is required to validate this finding.
Mourik et al. (2017) also highlight the challenges for many European ESCOs that are start-up SMEs (see Kangas et al., 2018 (Finland) and Bertrand et al., 2019 (Luxembourg) for specific country examples) and this contrasts with the better-resourced large-scale energy efficiency organisations discussed previously. The research is based on Task 25 of the International Energy Agency's DSM Technology Collaboration Programme (IEA DSM TCP), which began in 2014 and is investigating business models for energy services. The authors, amongst others, argue that energy service business models that focus on the perspectives of customers and their motivations for purchasing energy efficiency are important steps in developing the energy efficiency market (Mourik et al., 2017; Nilsson et al., 2012; Hiernerth et al., 2011).
The main purpose of this sub-section is to highlight the variety of business models for energy services, as the concept, like other aspects of DSM, is not new. There are no homogenous approaches to policy models that stimulate the development of business models for energy services. Examples include direct mandated approaches, indirect developments from mandatory approaches (such as new business arms being set up as a result of utility obligations), direct (financial or other) incentives, or voluntary approaches (e.g., utilities proactively developing new business arms to offer energy services). However, it is clear that the relatively slow development of the ESCOs market is partly due to the barriers highlighted in sub-section 2.2. For example, in Finland, Kangas et al. (2018) highlight that a lack of technical skills, disinterest in energy efficiency improvements and non-functional regulation are hindering the business models of ESCOs. However, in contrast, in China, Chen et al. (2017) found that government subsidies had a large impact on rapidly developing the ESCOs market and stimulating competition (from 782 ESCOs in 2010 to 4182 ESCOs in 2013). This also led to increased innovation by ESCOs, which was deterred in the absence of subsidies.
4.
Conclusions
Demand-side management (DSM) is a crucial part of meeting the goals of the Paris Agreement and improving the efficiency of resource use. Utilities are key actors in the energy system and consequently have an important role to play in accelerating the implementation of DSM activities. Business and policy models to financially incentivise utility engagement with DSM have been extensively studied in the grey literature and in certain countries, such as the USA and Australia, from an applied perspective. However, the academic literature remains relatively limited from a theoretical perspective with much of the previous work focussed on demand response rather than other categories of DSM. This theoretical review paper aimed to contribute to filling this gap by first reviewing the benefits and challenges for utilities to engage with DSM, and then discussing theoretical frameworks for four key categories of business models and how they relate to policy models that enable their implementation: Decoupling, capacity market participation, utility obligations and Energy Service Companies (ESCOs).
The review identified that the key benefits for utilities engaging in demand-side activities include those related to value creation, regulatory influence and consumer engagement. Despite this, there remain key challenges for utilities, particularly market-based issues and operational-based issues. Although the benefits and challenges of DSM have been extensively researched in the literature, this paper has built on existing reviews by focusing on the private finance perspective and taking a more holistic perspective of DSM rather than focusing on specific types of DSM, such as demand response or energy efficiency.
There are various theoretical frameworks for business and policy models to enable the decoupling of revenues from the amount of electricity or gas that a utility sells. The models vary in the degree of cost recovery that is authorised by regulators, from decoupling without cost recovery to the recovery of potential lost revenue, DSM programme costs and additional profit above supply-side options. In North America, a large number of utilities operate locally or regionally and are usually publicly- or investor-owned but with a strong degree of regulation from state public commissions. In Europe, utilities are often large, private and operate in fully liberalised, competitive markets across different countries. Thus, the applicability of decoupling policies in fully liberalised markets warrants further research. The review proposed a theoretical framework for identifying the investment implications of different types of policy models for decoupling, which forms one of the central contributions of the paper to the academic literature.
Capacity markets have proved to be commercially viable markets for utilities to extract value from demand-side resources. Much of the previous research has focussed on the role of on-site back-up generation (such as diesel generators in industry) and 'turn-down' demand response, rather than other types of DSM, such as the role of energy efficiency and behind-the-meter storage in capacity markets. The role of demand-side resources in capacity markets appears to transcend contexts, having been implemented or piloted in countries with different contexts, such as the USA and the UK. The ability for utilities to extract value from demand-side resources in markets beyond capacity (and energy) markets requires further research, in particular, the ability of utilities to create viable business models in the reserve markets.
Following the successful experiences in the UK and the USA, an increasing number of countries are implementing utility obligations. The policy has the potential to stimulate innovation and new business arms in traditional utilities without changing their underlying business model to increase revenues through increased electricity and gas sales. Utilities may use the mandatory obligations as a way to diversify their business model and offer new demand-side-based services to their customers. Further research should investigate the commercial viability of utilities expanding their demand-side business arms to develop services in the more expensive or more complex options as the opportunities for installing the least expensive measures decrease over time (such as insulation and efficient lighting). The applicability of utility obligations appears to transcend different contexts, as an increasing number of countries are implementing the policy.
ESCOs are another category of business models that appear to transcend different contexts, partly due to the variety of specific business models that have been tested around the world. ESCO business models often revolve around energy performance contracting, though there are various specific forms that this can take, such as shared-savings, guaranteed savings and 'chauffage' models. ESCOs vary in size from independent start-ups through being part of traditional utilities as new business arms, to large-scale ESCOs set up through regulatory or government influence to cover whole jurisdictions, such as countries or sub-national states. The applicability of the business models for large-scale ESCOs from the countries that have set them up (such as the USA, Canada and India) to other countries is an important area for further research.
Overall, the theoretical review concludes that business and policy models for decoupling, demand-side participation in capacity markets, utility obligations and ESCOs have the potential to financially incentivise the engagement of utilities with DSM. Although further research is required on the applicability of decoupling policies in fully liberalised, competitive markets, demand-side participation in capacity markets, utility obligations and ESCOs appear to be applicable across contexts. It is clear from the review that there remains an important role for governments to facilitate the conditions necessary to incentivise private finance for DSM through these four promising approaches.
Acknowledgements
This research was made possible by UK EPSRC support, grant number EP/H009612/1. The author would like to thank the anonymous peer reviewers for their helpful comments.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: