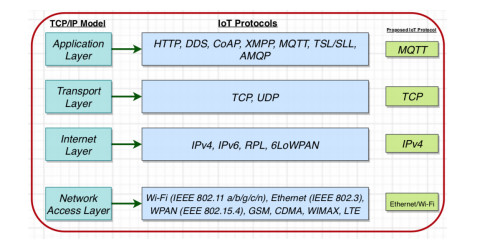
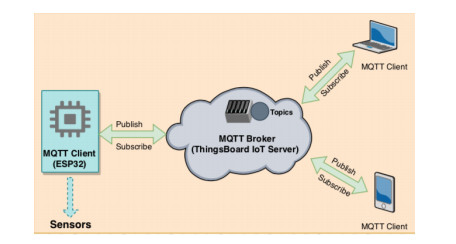
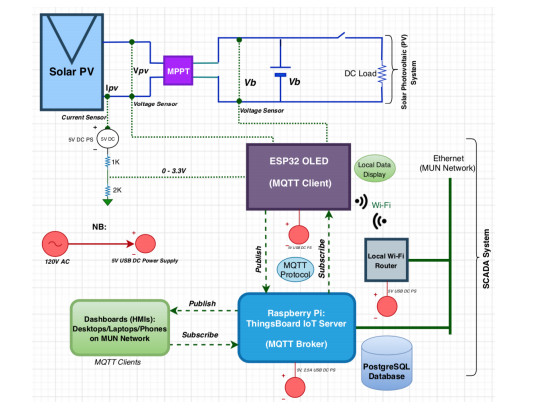
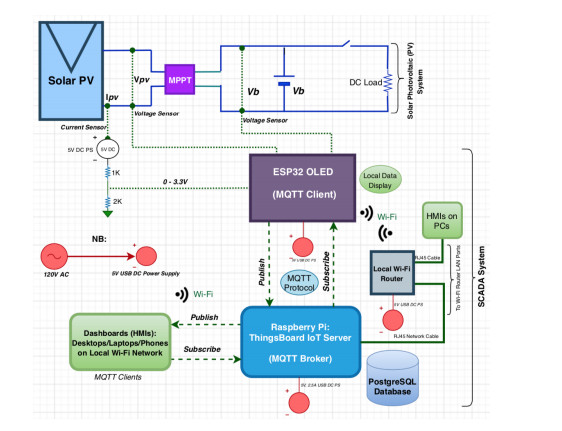
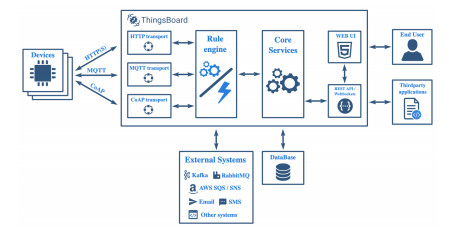
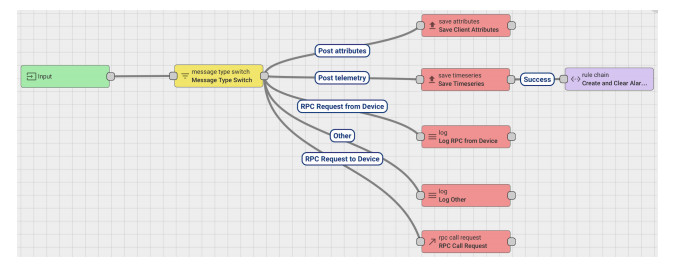
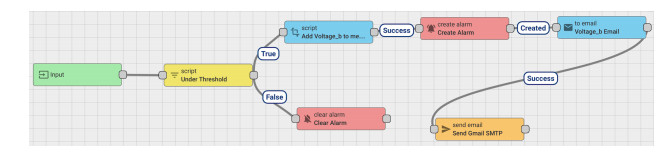
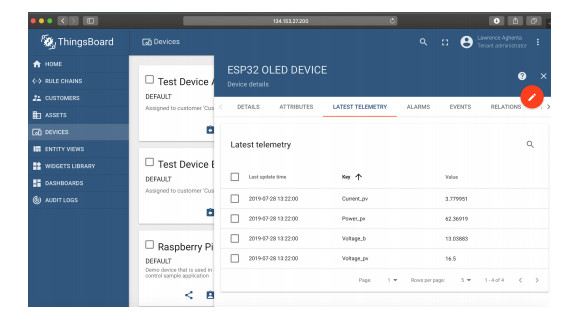
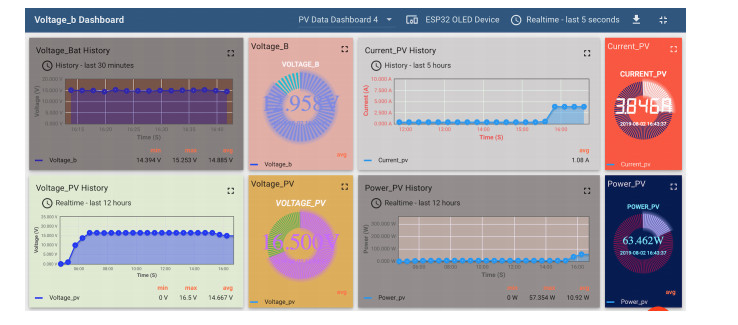
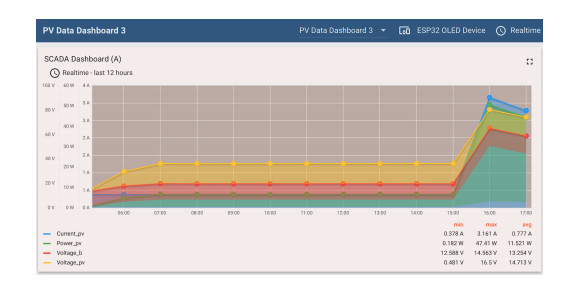
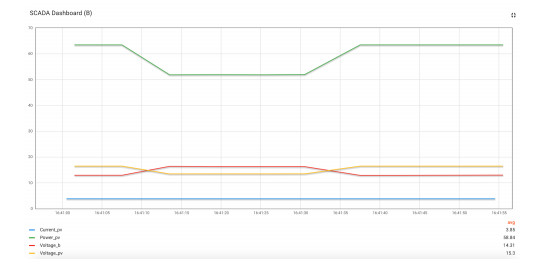
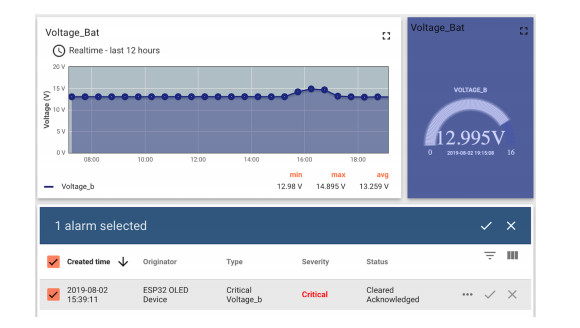
Distributed assets, such as hybrid power system components, require reliable, timely, and secure coordinated data monitoring and control systems. Supervisory Control and Data Acquisition (SCADA) is a technology for the coordinated monitoring and control of such assets. However, SCADA system designs and implementations have largely been proprietary, mostly pricey and therefore economically unjustifiable for smaller applications. With proprietary SCADA systems, there is also the problem of interoperability with the existing components such as power electronic converters, energy storage systems, and communication systems since these components are usually from multiple vendors. Therefore, an open source SCADA system represents the most flexible and most cost-effective SCADA option for such assets. In this paper, we present the design and implementation of a low-cost, open source SCADA system based on the most recent SCADA architecture, the Internet of Things (IoT). The proposed SCADA system consists of current and voltage sensors for data collection, an ESP32 micro-controller with organic light-emitting diode (OLED) display, for receiving and processing the sensor data, and ThingsBoard IoT server for historic data storage and human machine interactions. For the sensor data transfer from the ESP32 to the ThingsBoard IoT server, Message Queuing Telemetry Transport (MQTT) protocol is implemented for data transfer over a local Wi-Fi connection with the MQTT Client configured on the ESP32, and the ThingsBoard server node serving as the MQTT Broker. The ThingsBoard IoT server is locally installed with PostgreSQL database on a Raspberry Pi single-board computer and hosted locally on MUN Network for data integrity and security. To test the performance of the developed open source SCADA system solution, it was setup to acquire and process the current, voltage and power of a standalone solar photovoltaic system for remote monitoring and supervisory control. The overall system design procedures and testing, as well as the created dashboards and alarms on the ThingsBoard IoT server platform are presented in the paper.
1.
Introduction
The memristor is the fourth basic circuit element, and it was firstly proposed by Chua in 1971 [1]. The first memristor device was realized in 2008 [2], and since then it has received much attention from research area, such as neural networks, signal processing and artificial intelligence. As a particular type of neural networks, memristive neural networks (MNNs) have become an interesting topic for researchers [3,4,5,6]. MNNs can be regarded as a switch system since the memristive connection weights switch according to the system states. Compared with the traditional network model, MNNs have more equilibrium points and can better modify the dynamics of neurons in human brains. Lately, the dynamical analysis of MNNs has attracted great attention [7,8,9].
As we know, reaction-diffusion influences are important and common in chemistry, biology and neuroscience. Since the electrons in circuits move in a nonuniform electric field, the state of the electrons dose not only depend on time but also on the spatial information. Due to this reason, MNNs with reaction-diffusion terms can better modify the real-world systems than the traditional MNNs. Recently, the research on dynamics of reaction-diffusion MNNs has made great progress, such as stability [10], passivity [11,12], and asymptotical synchronization [13,14]. However, most of these results only focus on the cooperative interactions between neurons, while the competitive relationships have not been considered yet.
In the real world, competition and cooperation relationships coexist in many dynamic systems. For instance, in biological systems, interactions between cells may be cooperative or competitive; in social networks, relationships between people may be hostile or friendly. Hence, it is meaningful and necessary to consider the model of coopetition networks, in which the competition and cooperation relationships coexist [15,16,17,18,19,20,21]. Due to the existence of competition relationships, the traditional synchronization cannot be realized, and instead we will consider bipartite synchronization. In Reference [15], the idea of bipartite consensus in coopetition networks was first proposed, it requires that all nodes' states will reach the consensus in modulus but may not in sign. Recently, bipartite synchronization of coopetition networks has attracted the attention of many scholars [18,19,20,21]. In Reference [19], by designing an adaptive control strategy, the bipartite synchronization of coupled coopetition MNNs is investigated. In Reference [20], the model of inertial MNNs with antagonistic interactions is considered, and the criteria for bipartite synchronization are derived in both the leaderless and leader-following case. However, the above works only focus on the asymptotic or exponential synchronization, and how to improve the convergence speed in bipartite synchronization still remains an open topic.
Synchronization is an important phenomenon in engineering and biological systems. As we know, the convergence speed is an important issue in synchronization. To overcome the constraints of long convergence time, the issue of finite-time synchronization (FTS) is proposed [24]. Different from asymptotic synchronization [22,23], FTS guarantees the system will reach synchronization in a finite time. However, the convergence time of FTS is related to the initial conditions [24,25,26,27], which may be unmeasurable in practice. To solve this problem, the idea of fixed-time synchronization (FxT) is introduced [28]. Although the FxTS control removes the limitation of initial dependence, its settling time is related to the control parameters [28,29,30,31]. Hence, the settling time of traditional FTS and FxTS control still depend on the initial conditions and system parameters, which is a great limitation for some practical applications. To solve this problem, prespecified-time synchronization (PTS) control is proposed [32,33,34,35], in which the settling time is independent of both initial value and control parameters. As we know, the investigation of prespecified-time control is still very limited, especially for the coupled networks with competitive interactions.
This paper is intended to explore the prespecified-time bipartite synchronization (PTBS) of CRDMNNs with both cooperative and competitive relationships. The main contributions of this work are as follows:
1) Different from most previous results that only focus on cooperative interactions, this paper considers the model of CRDMNNs with both cooperative and competitive relationships between neurons.
2) By designing a novel control protocol, criteria for leader-following PTBS and leaderless PTBS of CRDMNNs are derived. It is shown that under the proposed protocol, all nodes' states will reach synchronization in modulus (but might not in sign) within a prescribed time.
3) Different from the traditional FTS and FxTS methods, the prespecified-time control method in this work can lead to a predetermined settling time, which is independent of both initial values and system parameters.
Notations. In this paper, sgn(⋅) denotes the signum function. The symbol T denotes vector transposition. C1 denotes the set of continuous functions. λmax(A) is the maximal eigenvalue of matrix A. ⊗ denotes the Kronecker product. Ω={x=(x1,⋯,xϑ)T|hmk≤|xk|≤hMk,k=1,⋯,ϑ} is a bounded compact set with smooth boundary ∂Ω.
2.
Preliminaries and model formulation
A signed graph is represented by G={P,J,G}, where P={p1,p2,⋯,pN} is the node set, J⊂P×P={(pi,pj)|pi,pj∈P} denotes the edge set, G=[Gij]∈RN×N is the adjacent matrix satisfying that Gij≠0 if (pi,pj)∈J, and Gij=0 otherwise. It is assumed that Gii=0. If the relationship between nodes pi and pj is competitive (cooperative), then Gij<0 (Gij>0). Due to the existence of negative edges, the elements in the Laplacian matrix L of a signed graph are given as
Definition 1. For a signed graph, it is called structurally balanced if the node set P can be divided into two subgroups P1 and P2, where P1∪P2=P and P1∩P2=∅, such that Gij≥0 for ∀pi,pj∈Pl(l∈{1,2}) and Gij≤0 for ∀pi∈Pl,pj∈Pk(k≠l,k,l∈{1,2}) [15].
Lemma 1. Suppose L is the Laplacian matrix of a signed graph G. If G is structurally balanced, then there is a gauge transformation matrix S=diag(s1,⋯,sN) with si∈{−1,1}, such that SLS has allnonnegative entries [15].
The model of CRDMNNs with competitive interactions is:
where zp(t,x)=(zp1(t,x),⋯,zpn(t,x))T∈Rn denotes the state of the pth neural network at time t and space x∈Ω⊆Rz. f(zp(t,x))=(f1(zp1(t,x)),⋯,fn(zpn(t,x)))T∈Rn denotes the activation function. Δ=∑ϑk=1(∂2∂x2k) is the Laplace diffusion operator. D=diag(d1,⋯,dn)>0. C=diag(c1,c2,⋯,cn)>0. A(zp(t,x))=[akj(zpj(t,x))]n×n stands for the memristive connection weight matrix. σ is a positive number denoting the coupling strength, and Np is the neighbor set of node p. Γ=diag(γ1,γ2,⋯,γn)∈Rn×n is the inner coupling matrix. up(t,x) is the control input to be designed. G=(Gpq)N×N is the symmetric weighted adjacency matrix of the signed graph, representing the competitive-cooperation relationship between neurons. The memristive connection weights akj(zpj(t,x)) can be described as
where Tj>0 is the switching jump, and ˊakj,ˊakj are real numbers. Define
The initial condition and Dirichlet boundary condition of zp(t,x) are
Remark 1. In this article, the reaction-diffusion term is contained in the MNNs model, and it is closer to the real networks because spatial location is considered. So, our results are more general than previous results in [19,20].
Next, we make the following assumptions.
Assumption 1. The cooperative-competitive network G is structurally balanced and connected.
Assumption 2. The activation function fp(⋅) is bounded, and there existconstants σp and Υ such that
In addition, define F=diag(σ1,⋯,σn)∈Rn×n.
Lemma 2. If η(x)=η(x1,⋯,xϑ):Ω→R satisfies that η(x)∈C1(Ω) and η(x)|∂Ω=0, then [12]
Based on the feature of Laplacian matrix L of the signed graph, we have:
Hence, CRDMNN (2.1) can be written as
Definition 2. The CRDMNNs System (2.5) is said to reach leaderless PTBS, if there exists a time T, which is a prespecified constant for any initial values, such that
Remark 2. In this work, we use zq(t,x)−zp(t,x) to represent the cooperation relationship between nodes p and q, and we use zq(t,x)+zp(t,x) to depict the competitive relationship between nodes p and q.
The System (2.5) can be rewritten as the following matrix form:
where
To achieve the main results, two classes of matrices are given. Define
Definition 3. For the CRDMNN System (2.6), define:
where M=M⊗In. Then, the networks' states can reach leaderless PTBS, if there exists a time T, which is a prescribed constant for any initial values, such that
Lemma 3. For the Laplacian matrix L∈RN×N, there is a matrix H∈R(N−1)×(N−1) given by H=MLJ, so that the following condition is satisfied:
For convenience, define
3.
Main results
To achieve leaderless PTBS, the following controller for System (2.5) is introduced:
where K=diag(k1,k2,⋯,kn)>0, ξp>0 and ψ>0 are control gains to be designed. r is a positive constant, and T>0 is a prespecified time chosen by users. Let tb=t0+T, and μ(t) is a function defined as:
The derivative of μ(t) can be calculated:
With the control protocol (3.1), the theorem can be achieved.
Theorem 1. Under Assumptions 1 and 2, if the control gains constants kj,ξp satisfy the following conditions
where ˜ξ=minp{ξp}, and ϕ>0 is a positive constant, then the leaderless bipartite prespecified-time synchronization for CRDMNN (2.6) can be achieved with controller (3.1).
Proof. Before proceeding, let y(t,x)=Mz(t,x), and then we get yi(t,x)=sizi(t,x)−si+1zi+1(t,x),i=1,⋯,N−1. Consider the Lyapunov functional
Computing the derivative along (2.6), it follows that
From Lemma 2, we get
Note that
Based on Assumption 2, we have
Similarly, we get
By Lemma 3, we get
and
From the condition in Theorem 1, we derive that
According to the definition of μ(t), defining Ω(t)=μr(t) yields
Multiplying Ω2ψ(t) on both sides of (3.12) yields
Solving the above inequality yields
Then, we have
Note that
which yields
Hence, limt→t−b‖y(t,x)‖=0, and the systems can reach synchronization in prespecified time T.
Next, we prove that the synchronization can be maintained on [tb,+∞).
where ˆθ=ϕ+2ψrT>0.
Then, we can get
So, we obtain that V(t)≡0 over [tb,+∞). Hence, ‖y(t,x)‖≡0 on [tb,+∞). Based on Definition 3, leaderless PTBS for Systems (2.6) can be realized with controller (3.1). The proof is complete.
Remark 3. Different from [33,34,35], the competitive relationship between network nodes is considered in this paper, which is described by negative edges in the signed graph. It can be seen that the prescribed-time synchronization in the above papers is a special case of the bipartite prescribed-time synchronization in this work. On the other hand, compared with the asymptotic bipartite synchronization criteria in [19,20], our approach ensures that the CRDMNNs can reach bipartite synchronization within prespecified time tb, which is independent of initial values and control parameters.
Remark 4. Since there are switching parameters in the memristor system, the first term of controller (3.1) is designed to remove the influence of the memristor parameters. Then, the terms −ξpzp(t,x) and −ψrTμ(t)zp(t,x) are devoted to realizing the convergence in a prespecified time. The function μ(t) plays an important role to ensure the prespecified-time synchronization. It can be seen from (3.17) that μ(t0)2rψ=1,limt→t−bμ(t)−2rψ=0. In practical applications, there may exist a leader in the community. In this case, leader-following synchronization is a meaningful issue to be considered.
Next, we aim to investigate leader-following PTBS of CRDMNNs. Considering the following system with coupling delays:
The reference target system is:
where z0(t,x)=(z01(t,x),z02(t,x),⋯,z0n(t,x))T∈Rn is the leader node.
Definition 4. For the CRDMNN System (3.21), it is said that the network can reach leader-following PTBS, if there exists a prespecified constant T, which is independent of any initial values or control parameters, such that
where sp=1 if p∈P1, and sp=−1 if p∈P2.
Define synchronization error δp(t,x)=zp(t,x)−spz0(t,x), and since ∑Nq=1lpqsq=0, we have
Then, the error system can be obtained:
Define the norm
The prespecified-time controller up(t,x) is designed as
where K=diag(k1,k2,⋯,kn) with ki>0, ξp,ϕ,ψ>0 are the control gains. sgn(δp(t,x))=(sgn(δp1(t,x)),⋯,sgn(δpn(t,x)))T∈Rn. T, r and μ(t) are defined the same as in controller (3.1).
Theorem 2. Under Assumptions 1 and 2, suppose the following conditions hold:
where ϕ>0 is given in controller (3.25), ˜ξ=minp{ξp}, cmin=min{c1,c2,⋯,cn}, and dmin=min{d1,d2,⋯,dn}. Then, leader-following PTBS for Systems (3.21) and (3.22) can be achieved under controller (3.25).
Proof. Design the Lyapunov functional
Computing the derivative along (3.24), we get
Based on Lemma 2, we get
According to Assumption 2, we have
For the coupling terms, it can be yielded that
For the control term (3.25), we get
By combining the above inequalities, one has
Following the discussion in Theorem 1, we derive limt→t−b‖zp(t,x)−spz0(t,x)‖2=0 and ‖zp(t,x)−spz0(t,x)‖2≡0 on [tb,+∞). Thus, leader-following PTBS for Systems (3.21) and (3.22) can be realized with controller (3.25).
Remark 5. Different from [12,13,14], the competitive relationship and coupling delay are considered in this paper, which can better modify the real network model. Due to the existence of antagonistic interactions and coupling delays, the traditional synchronization methods in [12,13,14] cannot be directly used to realize PTBS. Moreover, the convergence speed is required to be prescribed instead of asymptotic in this work, and thus the Theorem in our work greatly generalizes the previous results on bipartite synchronization.
Remark 6. In Reference [27], by applying nonsmooth analysis and some novel inequality techniques in the complex field, several nonseparation method-based fixed-time synchronization criteria are derived. In Reference [30], the FXTS of dynamic systems are reconsidered in this article based on special functions from the view of improving the estimate accuracy for settling time and reducing the chattering caused by the sign function. In this paper, the convergence time is prescribed in advance according to actual requirements, and thus our criteria are less conservative and more flexible.
4.
Numerical examples
To verify our theorem, two simulation examples are proposed in this section. We consider a network with 3 nodes, and since the structural balance condition is satisfied, the node set V can be separated into V1={1,2} and V2={3}. Then, one has s1=s2=1 and s3=−1. We first consider Theorem 1.
Example 1. Choose the CRDMNNs with 2 neurons as below:
where zp(t,x)=(zp1(t,x),zp2(t,x))T, D=diag(1,1),C=diag(2,2), and Ω={x|−1≤x≤1}. The memristive matrix A(zp(t,x)) switches between ˇA and ˆA, where
The activation functions are chosen as
It can be checked that F=0.5I2 and Υ=0.5. Hence, the conditions in Assumption 2 are satisfied. Choose Γ=I2 and σ=1. The Laplacian matrix is
The controller is
Choose feedback matrix K=0.6I2, ξp=0.5,ψ=1.5,r=2, ϕ=1. Let t0=0, and set the prespecified time tb=2. It can be checked that
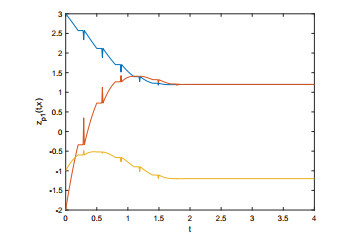
Thus, the conditions in Theorem 1 are satisfied. Choosing initial values in [−3,3], Figures 1 and 2 depict the evolutions of states zp1(t,x) and zp2(t,x). It can be seen that system (4.1) can reach leaderless PTBS in prespecified time tb under control law (4.4).
Next, we consider the leader-following PTBS in Theorem 2.
Example 2. Consider the following 2-node CRDMNN with coupling delays:
where τ=0.5. Other parameters are the same as in Example 1. The desired reference target is
Let εp(t,x)=zp(t,x)−spz0(t,x), and the error system is
The prespecified-time controller up(t,x) is chosen as (3.25). Choose ki=2,ξp=2. Other parameters are the same as in Example 1. It can be checked that
Thus, the condition in Theorem 2 holds, and the leader-following PTBS is achieved. Take initial random conditions in the interval [−3,3], and Figure 3 describes the synchronization error εp(t,x) between system (4.5) and (4.6) with controller (3.25). From the simulations, leader-following synchronization can be achieved in prescribed time tb=2.
5.
Conclusions
This paper investigates the prespecified-time bipartite synchronization (PTBS) of CRDMNNs with both cooperative and competitive interactions. Two types of PTBS are considered in our work: leaderless PTBS and leader-following PTBS. In addition, the coupling delays are considered in the leader-following case. By designing suitable Lyapunov functionals and novel control protocols, two criteria are derived for leaderless PTBS and leader-following PTBS based on a structural balance condition. Compared with FTS and FxTS, the settling time in our theorem can be predetermined according to the task, which is independent of the initial values and control parameters.
Our future study will focus on 1) PTBS control of neural networks under time-scale and 2) PTBS control of quaternion-valued neural networks.
Acknowledgments
This work is supported by the Natural Science Foundation of Jiangsu Province (Grant No. BK20210635).
Conflict of interest
The authors have no conflict of interest.









 DownLoad:
DownLoad: