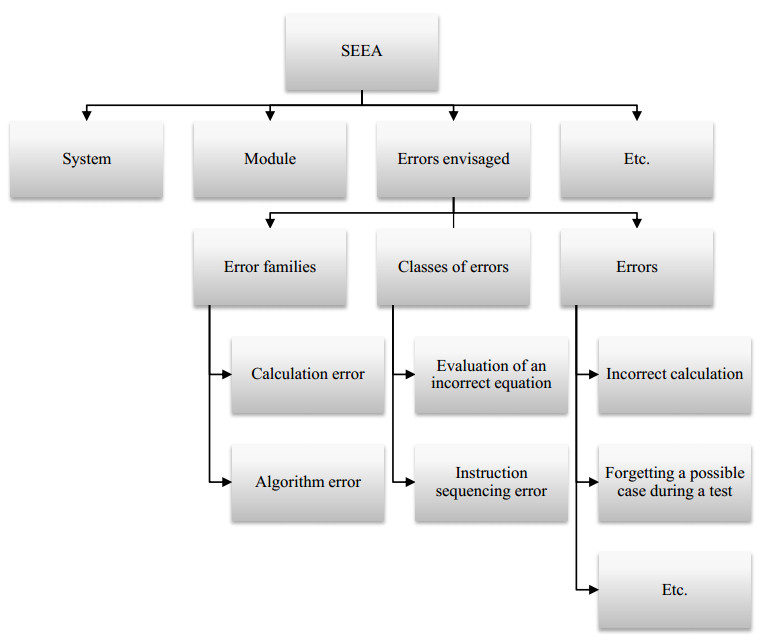
The harmful consequences of rail accidents, which sometimes lead to loss of life and the destruction of the system and its environment, are at the basis of the implementation of a "experience feedback" (REX) system considered as the essential means to promote the improvement of safety. REX seeks to identify adverse events with a view to highlighting all the causes that contributed to the occurrence of a particular accident and therefore to avoid at least the reproduction of new accidents and similar incidents. Accident and incident investigation reports provide a wealth of informative information for accident prevention. It would be appropriate to exploit these reports in order to extract the relevant information and suggest ways to avoid the reproduction of adverse events. In this context, knowledge of the causes of accidents results mainly from the contribution of lessons learned and experiences gained, whether positive or negative. However, the exploitation of information and the search for lessons from past events is a crucial step in the REX process. This process of analyzing and using data from experience can be facilitated if there are methods and tools available to technical investigators. It seems advisable to consider the use of artificial intelligence (AI) techniques and in particular automatic learning methods in order to understand the origins and circumstances of accidents and therefore propose solutions to avoid the reproduction of similar insecurity events. The fact that the lessons one can learn from a REX depends on the experiences of the situations experienced in the past, constitutes in itself a key argument in favor of machine learning. Thus, the identification of knowledge about rail accidents and incidents and share them among REX actors constitute a process of learning sequences of undesirable events. The approach proposed in this manuscript for the prevention of railway accidents is a hybrid method built around several algorithms and uses several methods of automatic learning: Learning by classification of concepts, Rule-based machine learning (RBML) and Case-based reasoning (CBR).
1.
Introduction
Under addressing global competition, manufacturing companies strive to produce better and cheaper products more quickly. For a complex system such as an aircraft, the design problem is intrinsically a daunting optimization task often involving multiple disciplines, nonlinear mathematical model, and computation-intensive processes during manufacturing process. Here is a reason to develop a high performance algorithm based on soft computing technique for finding an optimal solution to the engineering design and/or optimization problems [1,2]. An engineering optimization problem can be defined as a problem to find an optimal solution while satisfying complex constraints that consist of various types of design variables, including integers, 0–1 variables, and discrete and continuous variables. Since the types of design variables are varied and they are used together in constraints, various approaches to efficiently manage them have been developed in prior research [3,4,5,6,7].
Amir and Hasegawa [3] suggested an approach to solve the reinforced concrete beam design problem with three design variables that consisted of an integer variable, a continuous variable, and a predefined discrete variable. To handle three design variables, they converted the continuous and integer variables into discrete ones using the modified Rosenbrocks orthogonalization procedure. However, this led to the loss of some decimal values of the continuous variable in the process of converting the variable types. Therefore, the best solution obtained using this process may not be the optimal solution. Sandgran [4] suggested a branch and bound (B & B) method to solve the gear train and pressure vessel design problems, wherein discrete, continuous and integer variables are used together in constraints. To apply the B & B method to the gear train and pressure vessel design problem, he converted the discrete and integer variables into continuous variables. However, during this conversion process, the search ranges of discrete and integer variables were also changed, which may have led to the B & B method finding a feasible solution, but not an optimal one.
Similar to Sandgran [4], Fu et al. [5] also considered the gear train and pressure vessel design problems. They suggested the integer-discrete-continuous nonlinear programming (IDCNLP) method that changes the type of variables by introducing a penalty function to the discrete and integer variables. However, in the process of introducing a penalty function, the original search space of the design variables may be changed, which may cause the IDCNLP method to not locate the optimal solution or attain premature convergence by getting stuck at a local optimum.
The conventional studies mentioned above usually either converted the type of design variables or introduced a penalty function to the original design variables. However, during conversion or penalty function introduction, either the quality of the obtained solution deteriorates or a premature convergence occurs. To mitigate this situation, various metaheuristic approaches have been developed. A major advantage of applying metaheuristic approaches to engineering optimization problems is that the original design variable types can be maintained without any conversion process [8,9,10,11,12]. Some conventional studies that have implemented such approaches are noted below.
Wu and Chow [9] suggested a genetic algorithm (GA) approach to solve a coil compression spring design problem with a mixture of discrete, continuous and integer design variables. They proved the efficiency of the GA approach by comparing it with the conventional approaches suggested by Amir and Hasegawa [3], Sandgran [4], and Fu et al. [5]. The efficiency of applying the GA approach to various engineering optimization problems was also demonstrated by Lin and Hajela [8] and Yokota et al. [10]. Gandomi et al. [11] solved a corrugated bulkhead design problem and three-bar truss design problem using a cuckoo search (CS) approach. In a recent study, Maputi and Arora [12] suggested a teaching and learning-based optimization (TLBO) approach. As a repeating and searching approach, the TLBO can guide the search direction to an optimal solution through discussing and learning processes between a teacher and their students. The TLBO approach was applied to a weight gear design problem and a gear transmission system design problem. They proved that applying a TLBO approach outperformed the GA, simulated annealing (SA), and particle swarm optimization (PSO) approaches.
Since most of the conventional studies using various metaheuristic approaches mentioned above can handle the type of original design variables without any conversion process, they have the merit in solving various engineering optimizations when compared with Amir and Hasegawa [3], Sandgran [4], Fu et al. [5], Kuo et al. [6], and Yarushkina [7].
However, in recent years, several studies have shown that a hybrid metaheuristic approach that combines the merits of multiple metaheuristic approaches is more efficient than applying a single metaheuristic approach such as GA, SA, PSO, TLBO, etc. [13,14,15,16,17,18,19,20]. For instance, while GA approach has high performance in global searchability, it has low performance in local searchability. However, SA and hill climbing (HC) approaches have strong local searchability. Therefore, a hybrid approach using GA and SA (or HC) approaches is more efficient than the individual GA, SA, or HC approaches.
In this paper, a hybrid metaheuristic approach is proposed and demonstrated to efficiently solve various engineering optimization problems. The proposed hybrid metaheuristic approach, called the GA-PSO-TLBO approach, combines the GA approach's global searchability, PSO approach's local searchability, and TLBO approach's learning ability. The performance of the GA-PSO-TLBO approach is compared with those of conventional single and hybrid metaheuristic approaches using various engineering optimization problems through a case study. The main contributions of this paper when compared with conventional studies are as follows:
● It presents an efficient hybrid metaheuristic approach by combining the GA approach's global searchability, PSO approach's local searchability, and TLBO approach's learning ability.
● It proves the efficiency of the GA-PSO-TLBO approach by comparing it with conventional single and hybrid metaheuristic approaches.
● It shows the robustness of the GA-PSO-TLBO approach through additional analyses using changes in the number of populations at the initial stage and that of the offspring at the TLBO search process.
This paper is organized as follows: Section 2 describes the definition and characteristics of engineering optimization problems. The detailed implementation procedure of the GA-PSO-TLBO approach is described in Section 3. Section 4 shows the computational results and analyses using various engineering optimization problems to prove the efficiency of the GA-PSO-TLBO approach compared to some conventional single and hybrid metaheuristic approaches, and also includes an additional analysis for providing the robustness of the GA-PSO-TLBO approach. Finally, Section 5 concludes for this paper and suggests a potential future research direction.
2.
Mathematical model for engineering optimization problem
Considering minimization problem, the general structure of an engineering optimization problem is as follows [21]:
where f : a scalar objective; x = {x1,…,xJ}T = {xD,xI,xA,xC}T; xLj: set of lower bounds on design variables xj; xUj: set of upper bounds on design variables xj; xD∈RD: feasible subset of discrete variables; xI∈RI: feasible subset of integer variables; xA∈RA: feasible subset of 0–1 variables; and xC∈RC: feasible subset of continuous variables.
Equation (1) represents the minimization of the design or manufacturing cost under consideration in the engineering optimization problem, which is generally represented as a linear or nonlinear function type. If Eq (1) is represented as a nonlinear function type with a mixture of discrete, continuous, integer, and 0–1 design variables, the conventional approach dictates that all design variables be converted into a single variable type to locate the optimal solution [3,4,5,6,7]. However, as mentioned previously, this may cause either the quality of the obtained solution to deteriorate or premature convergence to occur. Eqs (2)–(4) represent the constraints and each design variables type for solving the minimization problem of Eq (1).
3.
Proposed GA-PSO-TLBO approach
As mentioned in Section 1, previous research has shown that applying a hybrid metaheuristic approach that combines the merits of multiple metaheuristic approaches is more efficient than applying those metaheuristic approaches individually [13,14,15,16,17,18,19,22]. This paper proposes the GA-PSO-TLBO approach as a hybrid metaheuristic approach that aims to efficiently solve engineering optimization problems with various types of design variables. Since the GA-PSO-TLBO approach has the merits of each metaheuristic approach (GA, PSO and TLBO) in its search processes, effectively combining their merits is an important problem.
First, the characteristics of the GA, PSO and TLBO approaches for hybridization are analyzed as follows. The GA approach starts its search process using a randomly generated population. The population consists of some individuals with varying fitness values and can provide global searchability, allowing the GA to have more chances to find an optimal solution than local search approaches such as SA and HC. However, since the GA is a population-based search approach and conducts its operators (i.e., selection, crossover and mutation operators) using all individuals in the population, it may have a slow convergence tendency [23]. To mitigate this disadvantage of the GA while maintaining a population-based search, an efficient alternative may be to use only a few individuals in the population, not its entirety [24].
In this paper, the sub-population (50%) with superior fitness values in the initial population is used for the GA loop, because using the sub-population (50%) with superior fitness values improves the chances of finding an optimal solution rather than using the sub-population with inferior fitness values. While the sub-population with superior fitness values may be highly similar and thus, using it may increase the risk of premature convergence, this similarity and risk can be mitigated using the GA search process because its global searchability can enhance the diversity of individuals in the population.
However, unlike the sub-population with superior fitness values, using the sub-population with inferior fitness values can reduce the chance of finding an optimal solution [23]. This means that if GA starts its search process using the sub-population with inferior fitness values, then the chance of finding an optimal solution is lower than applying its search process using the sub-population with superior fitness values, since GA searches a wide range of values as a way of increasing the diversity of individuals in the population. Therefore, one must actively reduce the diversity of the sub-population with inferior fitness values and therefore, achieve a rapid search process to an optimal solution. Applying PSO to the sub-population with inferior fitness values can be a good alternative because it rapidly improves the fitness values of current individuals using their velocities and positions [23,24].
In this paper, the sub-population (50%) with inferior fitness values in the initial population is used for the PSO loop, because by applying the PSO search process, the fitness values of the individuals in the sub-population may be improved, which makes PSO feasible for rapidly obtaining the optimal solution. In addition, several recent studies [23,24] have shown that further improvement is possible by applying the TLBO search process using elite individuals obtained after applying the GA search process. Since GA lacks an adequate learning ability for the elite individuals during its search process, applying the TLBO search process to some individuals with superior fitness values can provide higher chances to find an optimal solution. In this paper, the sub-offspring (50%) with superior fitness values obtained after GA and PSO loops are used for the TLBO search process.
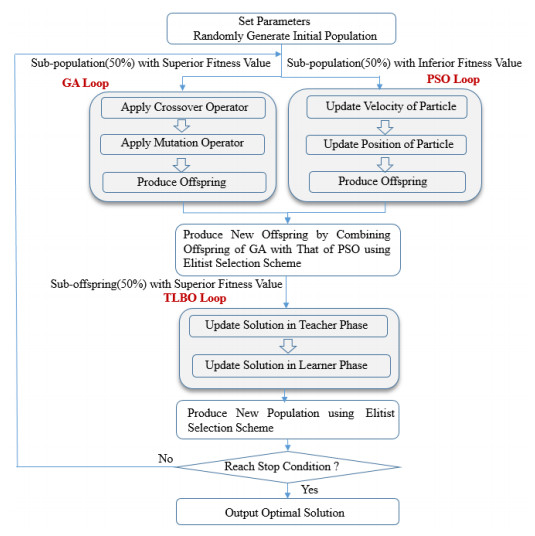
Secondly, a conceptual flow of the GA-PSO-TLBO approach is shown in Figure 1.
As shown in Figure 1, using a randomly generated initial population, the sub-population (50%) with superior fitness values and the sub-population (50%) with inferior fitness values are applied to the GA and PSO loops, respectively. The objective of applying GA is to increase the diversity of the population, while that of applying PSO is to enhance the search speed to an optimal solution. By applying GA and PSO together, the exploration and exploitation can be enhanced simultaneously. Using the combined offspring of GA and PSO, the sub-offspring (50%) with superior fitness values are applied to the TLBO loop. The objective of applying TLBO is to increase the chance of finding the optimal solution.
Lastly, for minimization problem, the detailed implementation procedure of the GA-PSO-TLBO approach is described in Figure 2.
4.
Case studies
In this section, several well-known engineering optimization problems with various types of design variables are described in detail.
4.1. Type 1 (T-1): Reinforced concrete beam design problem
Introduced by Amir and Hasegawa [3], Shih and Yang [26], Yun [27], and Gandomi et al. [11], T-1 is the problem of designing a reinforced concrete beam. Three types of design variables (continuous, discrete and integer) are used in this problem. It may be assumed that while x1 can only take 40 numbers of certain predetermined discrete values, x2 and x3 can take any continuous values and integer values, respectively. The objective for this problem is to minimize the total cost of concrete and reinforcing steel of the beam. The mathematical formulation is expressed as follows.
where x1 is discrete, x2 continuous, and x3 integer.
4.2. Type 2 (T-2): Gear train design problem
T-2 was introduced by Sandgren [4], and Gandomi et al. [11] and its main objective is to produce a gear ratio as close as possible to 1/6.931. For each gear, the number of teeth must be between 14 and 40, which means that the design variables (x1,x2,x3,x4) are the numbers of teeth that must be integers. The mathematical formulation is expressed as follows.
where xi are all integers.
4.3. Type 3 (T-3): Coil compression spring design problem
T-3 was codified by Wu and Chow [9], and Yun [27]. This problem aims to determine the number of coils (x1), winding diameter (x2) and wire diameter (x3) that result in a minimum mass spring to carry the given loads while satisfying the design constraints. The design variables are an integer, continuous and discrete, respectively. Especially, discrete design variables (x3) use predefined discrete dimensions [9]. The mathematical formulation is expressed as follows.
where x1 is integer, x2 continuous and x3 discrete.
The parameters used above are as follows:
δp=Fp/K, K=Gx43/8x1x32, Fmax=1,000lb, lf=Fmax/K+1.05(x1+2)x3, S=289,000psi, lmax=14.0inch, dmin=1.2inch, Dmax=3.0inch, Fp=300.0lb, δpm=6.0inch, δw=1.25inch, G=11.5×106psi, Cf=(4(x2/x3)−1)/(4(x2/x3)−4)−0.165x3/x2.
4.4. Type 4 (T-4): Corrugated bulkhead design problem
Initially studied by Kvalie [28], T-4 aims to minimize the weight of corrugated bulkheads for a tanker. The design variables used in T-4 are width (x1), depth (x2), length (x3), and plate thickness (x4). The minimum-weight requires the solution of the following optimization problem [11]. The mathematical formulation is expressed as follows.
where x1≥0,x2,x3≤100,0≤x4≤5, and xi are all continuous
4.5. Type 5 (T-5): Pressure vessel design problem
T-5 was studied by Sandgran [4], Fu et al. [5], Wu and Chow [9], and Gandomi et al. [11]. The design variables are the dimensions required for the specifications of vessel. The design variables x1 and x2 are discrete values and have integral multipliers of 0.0625 inch, respectively. The design variables x3 and x4 are continuous values, and the side constraints are 40 ≤ x3 ≤ 80 inches and 20 ≤ x4 ≤ 60 inches, respectively. The mathematical formulation is expressed as follows.
where x1 and x1 are discrete, and x3 and x4 continuous.
4.6. Type 6 (T-6): Speed reducer design problem
T-6 is a benchmark engineering optimization problem proposed by Ray and Saini [29], and Gandomi and Yang [30]. Seven design variables are used in total: face width (x1), module of teeth (x2), number of teeth on pinion (x3), length of shaft 1 between bearings (x4), length of shaft 2 between bearings (x5), diameter of shaft 1 (x6), and diameter of shaft 2 (x7). The objective is to minimize the total weight of the speed reducer. The constraints involve limitations on the bending stress of the gear teeth, surface stress, transverse deflections of shafts 1 and 2 due to transmitted force, and stresses in shafts 1 and 2. The mathematical formulation is expressed as follows.
where 2.6≤x1≤3.6,0.7≤x2≤0.8,17≤x3≤28,7.3≤x4,x5≤8.3,2.9≤x6≤3.9,5.0≤x7≤5.5 and xi are all continuous.
Using the six aforementioned engineering optimization problems, the performance of the GA-PSO-TLBO approach is compared with that of several single and hybrid metaheuristic approaches in Table 1.
All approaches shown in Table 1, including the GA-PSO-TLBO approach, were programmed using MATLAB version 2014b and were simulated on an IBM-compatible PC having a 1.3 GHz processor with 4 GB of RAM. The parameter setting values and operators to implement each approach are summarized in Table 2.
All setting values were obtained after fine-tuning process of each approach. Total number of iterations is 1000. All results are obtained after 10 independent runs to eliminate the randomness in the run of each approach. Three measures of performance are used to compare the performances of all approaches, as shown in Table 3.
Tables 4 and 5 show the comparison results among conventional single metaheuristic approaches (GA, PSO, and TLBO), conventional hybrid metaheuristic approaches (GA-PSO and GA-TLBO) and the GA-PSO-TLBO approach. It can be observed that the performances of GA, PSO, TLBO, GA-PSO and GA-TLBO approaches are worse than that of the GA-PSO-TLBO approach if plus (+) values appeared in Gaps 1 and 2, but the former are better than the latter if minus (−) values appeared in Gaps 1 and 2.
In T-1 of Table 4, the differences between the GA-PSO-TLBO approach and the GA, PSO and TLBO approaches are 0.453, 1.810 and 0.002 %, respectively, in terms of the BS. This means that the GA-PSO-TLBO approach has slightly better performance than the TLBO approach, but has significantly better performance than the GA and PSO approaches. Similar situations are also seen in terms of the AS—the differences among the GA, PSO and TLBO approaches are 2.035, 3.448 and 0.022%, respectively, when compared with the GA-PSO-TLBO approach, indicating that the performance of the GA-PSO-TLBO approach is slightly better than that of the TLBO approach, but significantly better than those of the GA and PSO approaches. However, in terms of CPU, the GA-PSO-TLBO approach is the slowest, and the TLBO approach is the quickest.
In T-2, T-3, T-5 and T-6 of Table 4, the performance metrics of the GA-PSO-TLBO approach are considerably superior to those of the other approaches in terms of the BS and AS, but its search speed is the slowest in terms of the CPU. In T-4 of Table 4, the GA-PSO-TLBO approach shows better performances in terms of the BS and AS than the GA and PSO approaches, but the former does not show any merit in terms of the BS when compared with the TLBO approach.
In T-1 of Table 5, the differences between the GA-PSO-TLBO approach and the GA-PSO and GA-TLBO approaches are 0.205 and 0.003 %, respectively, in terms of the BS, which means that the GA-PSO-TLBO approach has slightly better performance than the GA-TLBO approach, but significantly better performance than the GA-PSO approach. Similar situations are also seen in terms of the AS—the differences of the GA-PSO and GA-TLBO approaches when compared with the GA-PSO-TLBO approach are 3.748, and 0.356%, respectively, which indicates that the performance of the GA-PSO-TLBO approach is considerably better than those of the GA-PSO and GA-TLBO approaches. However, in terms of the CPU, the GA-PSO-TLBO approach has the slowest performance, and the GA-TLBO approach has the quickest performance.
In T-2, T-3, T-5 and T-6, but not in T-4, of Table 5, the GA-PSO-TLBO approach outperforms those of the other approaches in terms of the BS and AS, but the search speed of the former is the slowest in terms of CPU.
For a more detailed comparison, Figures 3 and 4 show the convergence behaviors of all the approaches when the number of iterations is increased to 100.
It is evident from Figure 3 that the GA-PSO-TLBO approach rapidly enhances the optimization in the early stage, while all other approaches (GA, TLBO, GA-PSO and GA-TLBO), except the PSO approach, show various convergence behaviors in their early stages, but inferior overall performance to that of the GA-PSO-TLBO approach in the later stages. Similar convergence behaviors are also shown in Figure 4, where all the competing approaches, except the PSO approach, show various convergence behaviors in their early stages, while the GA-PSO-TLBO approach shows rapid convergence behavior compared to the others, though the former does not show any different convergence behavior than the others in its early stage.
To compare the stability of each approach, the distributions of the best solutions obtained after 10 independent runs for T-5 and T-6 are shown in Figures 5 and 6.
These figures show that the GA-PSO-TLBO approach can provide a more compact distribution with a lower average value than the GA, PSO, TLBO, GA-PSO and GA-TLBO approaches, which indicates its reliability and satisfactory optimization ability.
Through the computation results of Tables 4 and 5 and Figures 3–6, the following conclusions can be reached.
● Among all single metaheuristic approaches using T-1, T-2, T-4, T-5, and T-6, except T-3 in Table 4, the TLBO approach has shown better performance in terms of BS and AS than the GA and PSO approaches, indicating that the search scheme used in the TLBO approach is more efficient than those used in the GA and PSO approaches.
● In the comparison among all hybrid metaheuristic approaches in Table 5, it has been observed that the performance metrics of the GA-TLBO approach are superior to those of the GA-PSO approach in terms of BS in T-4, T-5, and T-6, but not in terms of BS and AS in T-3. This implies that the search scheme used in the GA-TLBO approach is usually more efficient in finding better solutions than that used in the GA-PSO approach.
● In the comparison between single metaheuristic approaches (GA, PSO, and TLBO) and the hybrid ones (GA-PSO and GA-TLBO) of Tables 4 and 5, the latter do not show any merits compared with the former, since some computation results (in terms of the BS and AS for T-1, and AS for T-4, T-5, and T-6) of the TLBO approach have shown better performances than the GA-PSO and GA-TLBO approaches. This means that the hybridization schemes used in the GA-PSO and GA-TLBO approaches do not show sufficient advantages in searching the best solutions in T-1 to T-6 when compared with the GA, PSO, and TLBO approaches, though the former have more search schemes than the latter.
● In the comparison among all approaches, the GA-PSO-TLBO approach outperforms both single metaheuristic approaches (GA, PSO, and TLBO) and hybrid ones (GA-PSO and GA-TLBO) in terms of the BS and AS, except in the case of T-4. This analysis result shows that the success of a hybrid metaheuristic approach, like the GA-PSO-TLBO approach, depends highly on how single metaheuristic approaches are combined.
4.7. Additional analysis of the GA-PSO-TLBO approach
In the GA-PSO-TLBO approach, the sub-population (50%) with superior fitness values is used for the GA loop, while the other sub-population with inferior fitness values is used for the PSO loop. However, some conventional studies [13,18,37,38,39] have used the whole population when they combined several metaheuristic approaches. Yun et al. [18] proposed a GA-CS approach, where the whole population generated at the initial stage was first used for GA loop and then the CS loop was applied using all offspring obtained after the GA loop. Similar studies using the whole population in each metaheuristic approach have also been performed by Castelli and Vanneschi [13] and Zhai et al. [38] who combined the GA approach with the VNS approach and Marinakis and Marinaki [37] who combined the GA approach with the PSO approach. Recently, Gen, et al. [39] proposed hybridized metaheuristics by TLBO with GA and PSO and applied to supply chain network model as one of case studies.
Therefore, it would be worthwhile to compare the performance between the studies using the whole population and the studies using a part of the population in hybrid metaheuristic approaches. For achieving this purpose, the GA-PSO-TLBO approach is divided into two parts, as follows:
● GA-PSO-TLBO1: the whole population (100%) randomly generated in the initial stage is used for the GA and PSO loops. Also, the whole offspring (100%) obtained after the GA and PSO loops is used for the TLBO loop.
● GA-PSO-TLBO2: the sub-population (50%) with superior fitness values is used for the GA loop, while the other sub-population (50%) with inferior fitness values is used for the PSO loop. However, the whole offspring (100%) obtained after the GA and PSO loops is used for the TLBO loop.
The main difference between the GA-PSO-TLBO and GA-PSO-TLBO1 is that the former uses a part of the population in the GA, PSO and TLBO loops, while the latter uses the whole population for those loops. Also, the main difference between the GA-PSO-TLBO and GA-PSO-TLBO2 is that the former uses a part of the whole population in the TLBO loop, while the latter uses the whole population as it is for the same loop. Tables 6 and 7 show the computation results using T-4 and T-6 for the GA-PSO-TLBO, GA-PSO-TLBO1, and GA-PSO-TLBO2 approaches.
In Table 6, it is observed that the performance of the GA-PSO-TLBO approach is equal to that of the GA-PSO-TLBO1 approach in terms of the BS and AS, but in terms of the CPU, the former shows significantly quicker search speed than the latter, indicated by the gaps between them being 130.43 (%) for T-4 and 161.11 (%) for T-6. This implies that using sub-population (50%) and sub-offspring (50%) for the GA, PSO and TLBO loops is more efficient in terms of the CPU than using the whole population and offspring, though they have the same results in terms of the BS and AS.
In Table 7, both the GA-PSO-TLBO and GA-PSO-TLBO2 approaches have the same results in terms of the BS and AS, but the former shows considerably better performance in terms of the CPU than the latter, with the differences between them being 52.17 (%) for T-4 and 33.33 (%) for T-6. This means that applying the sub-offspring (50%) obtained after GA and PSO loops to TLBO loop is more efficient than applying the whole offspring obtained after GA and PSO loops to the TLBO loop.
Through the computation results of Tables 6 and 7, it can be concluded that when combining GA, PSO and TLBO for the GA-PSO-TLBO approach, using sub-population (50%) of the whole population obtained in the initial stage for GA and PSO loops as well as using sub-offspring (50%) of the whole offspring obtained after GA and PSO loops for the TLBO loop are more efficient in reducing search speed than using the whole population and offspring for all three loops.
5.
Conclusions
Over the last three decades, many researchers have developed various approaches to efficiently solve engineering optimization problems. Most conventional studies typically either convert the type of design variables or introduce a penalty function to the original design variables. However, this either results in deterioration of the quality of the obtained solution, or occurrence of premature convergence through the conversion or introduction process. To overcome this disadvantage, various metaheuristic approaches have been developed. The primary advantage of applying metaheuristic approaches to engineering optimization problems is that the original design variable types can be used as without any conversion or introduction process.
In this study, we developed a new hybrid metaheuristic approach called the GA-PSO-TLBO approach. This approach combines the merits of three single metaheuristic approaches, that is, GA approach with global searchability, PSO approach with local searchability, and TLBO approach with learning ability. To improve the time-efficiency of the GA-PSO-TLBO approach, the sub-population (50%) with superior fitness values, sub-population (50%) with inferior fitness values of the whole population obtained in the initial stage, and sub-offspring (50%) with superior fitness values in the whole offspring obtained after the GA and PSO loops, are used for the GA, PSO, and TLBO loops, respectively.
The performance of the GA-PSO-TLBO approach was compared with those of three single metaheuristic approaches (GA, PSO, and TLBO), respectively and two hybrid metaheuristic approaches (GA-PSO, and GA-TLBO) using six well-known engineering optimization problems. The experimental results have proved and demonstrated that the GA-PSO-TLBO approach outperforms the GA, PSO, TLBO, GA-PSO and GA-TLBO approaches in terms of the BS and AS, which implies that the success of a hybrid metaheuristic approach like the GA-PSO-TLBO approach depends highly on how the merits of each constituent metaheuristic approach are combined.
For additional analysis of the GA-PSO-TLBO approach, two competing approaches (GA-PSO-TLBO1 and GA-PSO-TLBO2) have been suggested, and the experimental results have proved that the performance of the GA-PSO-TLBO approach is superior to those of the GA-PSO-TLBO1 and GA-PSO-TLBO2 approaches in terms of the CPU, which implies that when combining GA, PSO, and TLBO for the GA-PSO-TLBO approach, using a sub-population (50%) of the whole population obtained in the initial stage for the GA and PSO loops as well as using a sub-offspring (50%) of the whole offspring obtained after the GA and PSO loops for the TLBO loop, increase the efficiency and reduce the search time than using the whole population and offspring for the GA, PSO and TLBO loops.
However, although the GA-PSO-TLBO approach combines the merits of the GA, PSO, and TLBO approaches, its search speed is slower than those of three single metaheuristic approaches (GA, PSO, and TLBO) and two hybrid metaheuristic approaches (GA-PSO, and GA-TLBO). Therefore, a method to increase the search speed of the GA-PSO-TLBO approach must be found and more comparisons between the GA-PSO-TLBO approach and other hybrid metaheuristic approaches such as GA-SA-TLBO or GA-TS (Tabu search)-TLBO approaches must be conducted; these are potential avenues of future research in this domain.
Acknowledgments
This work was supported by research fund from Chosun University (2022).
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: