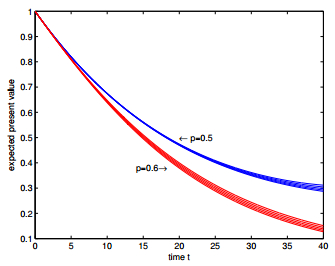
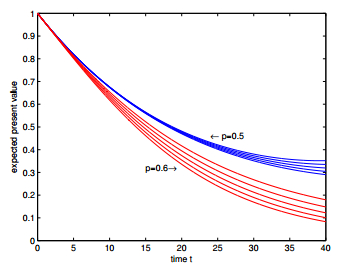
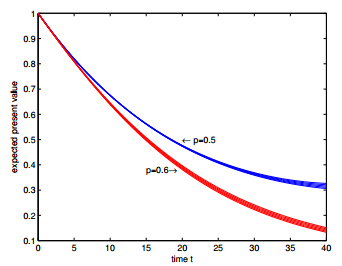
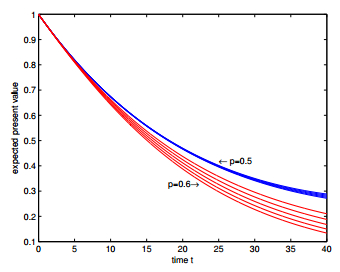
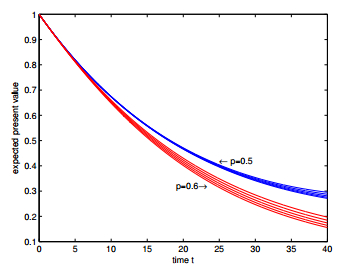
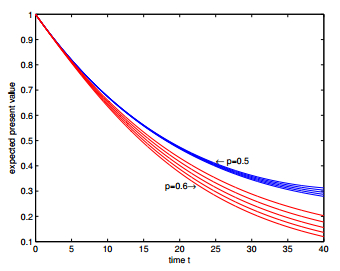
In this paper, we introduce a class of stochastic interest model driven by a compound Poisson process and a Brownian motion, in which the jumping times of force of interest obeys compound Poisson process and the continuous tiny fluctuations are described by Brownian motion, and the adjustment in each jump of interest force is assumed to be random. Based on the proposed interest model, we discuss the expected discounted function, the validity of the model and actuarial present values of life annuities and life insurances under different parameters and distribution settings. Our numerical results show actuarial values could be sensitive to the parameters and distribution settings, which shows the importance of introducing this kind interest model.
1.
Introduction
We consider the Cauchy problem for the nonlinear damped wave equation with linear damping
where N≥1, p,q>1, w∈L1loc(RN), w≥0 and w≢0. Namely, we are concerned with the existence and nonexistence of global weak solutions to (1.1). We mention below some motivations for studying problems of type (1.1).
Consider the semilinear damped wave equation
under the initial conditions
In [12], a Fujita-type result was obtained for the problem (1.2) and (1.3). Namely, it was shown that,
(ⅰ) if 1<p<1+2N and ∫RNuj(x)dx>0, j=0,1, then the problem (1.2) and (1.3) admits no global solution;
(ⅱ) if 1+2N<p<N for N≥3, and 1+2N<p<∞ for N∈{1,2}, then the problem (1.2) and (1.3) admits a unique global solution for suitable initial values.
The proof of part (ⅰ) makes use of the fundamental solution of the operator (∂tt−Δ+∂t)k. In [15], it was shown that the exponent 1+2N belongs to the blow-up case (ⅰ). Notice that 1+2N is also the Fujita critical exponent for the semilinear heat equation ut−Δu=|u|p (see [3]). In [6], the authors considered the problem
under the initial conditions (1.3), where m is a positive natural number, α≥0, and f(t,x)≥0 is a given function satisfying a certain condition. Using the test function method (see e.g. [11]), sufficient conditions for the nonexistence of a global weak solution to the problem (1.4) and (1.3) are obtained. Notice that in [6], the influence of the inhomogeneous term w(t,x) on the critical behavior of the problem (1.4) and (1.3) was not investigated. Recently, in [5], the authors investigated the inhomogeneous problem
where w∈L1loc(RN) and w≢0. It was shown that in the case N≥3, the critical exponent for the problem (1.5) jumps from 1+2N (the critical exponent for the problem (1.2)) to the bigger exponent 1+2N−2. Notice that a similar phenomenon was observed for the inhomogeneous semilnear heat equation ut−Δu=|u|p+w(x) (see [14]). For other results related to the blow-up of solutions to damped wave equations, see, for example [1,2,4,7,8,9,13] and the references therein.
In this paper, motivated by the above mentioned works, our aim is to study the effect of the gradient term |∇u|q on the critical behavior of problem (1.5). We first obtain the Fujita critical exponent for the problem (1.1). Next, we determine its second critical exponent in the sense of Lee and Ni [10].
Before stating the main results, let us provide the notion of solutions to problem (1.1). Let Q=(0,∞)×RN. We denote by C2c(Q) the space of C2 real valued functions compactly supported in Q.
Definition 1.1. We say that u=u(t,x) is a global weak solution to (1.1), if
and
for all φ∈C2c(Q).
The first main result is the following Fujita-type theorem.
Theorem 1.1. Let N≥1, p,q>1, w∈L1loc(RN), w≥0 and w≢0.
(i) If N∈{1,2}, for all p,q>1, problem (1.1) admits no global weak solution.
(ii) Let N≥3. If
then problem (1.1) admits no global weak solution.
(iii) Let N≥3. If
then problem (1.1) admits global solutions for some w>0.
We mention below some remarks related to Theorem 1.1. For N≥3, let
From Theorem 1.1, if 1<p<pc(N,q), then problem (1.1) admits no global weak solution, while if p>pc(N,q), global weak solutions exist for some w>0. This shows that pc(N,q) is the Fujita critical exponent for the problem (1.1). Notice that in the case N≥3 and q>1+1N−1, pc(N,q) is also the critical exponent for utt−Δu=|u|p+w(x) (see [5]). This shows that in the range q>1+1N−1, the gradient term |∇u|q has no influence on the critical behavior of utt−Δu=|u|p+w(x).
It is interesting to note that the gradient term |∇u|q induces an interesting phenomenon of discontinuity of the Fujita critical exponent pc(N,q) jumping from 1+2N−2 to ∞ as q reaches the value 1+1N−1 from above.
Next, for N≥3 and σ<N, we introduce the sets
and
The next result provides the second critical exponent for the problem (1.1) in the sense of Lee and Ni [10].
Theorem 1.2. Let N≥3, p>1+2N−2 and q>1+1N−1.
(i) If
and w∈I+σ, then problem (1.1) admits no global weak solution.
(ii) If
then problem (1.1) admits global solutions for some w∈I−σ.
From Theorem 1.2, if N≥3, p>1+2N−2 and q>1+1N−1, then problem (1.1) admits a second critical exponent, namely
The rest of the paper is organized as follows. In Section 2, some preliminary estimates are provided. Section 3 is devoted to the study of the Fujita critical exponent for the problem (1.1). Namely, Theorem 1.1 is proved. In Section 4, we study the second critical exponent for the problem (1.1) in the sense of Lee and Ni. Namely, we prove Theorem 1.2.
2.
Preliminaries
Consider two cut-off functions f,g∈C∞([0,∞)) satisfying
and
For T>0, we introduce the function
where ℓ≥2 and ρ>0 are constants to be chosen. It can be easily seen that
Throughout this paper, the letter C denotes various positive constants depending only on known quantities.
Lemma 2.1. Let κ>1 and ℓ>2κκ−1. Then
Proof. By (2.1), one has
Using the properties of the cut-off function f, one obtains
which shows that
Next, using the properties of the cut-off function g, one obtains
On the other hand, for Tρ<|x|<√2Tρ, an elementary calculation yields
where
Notice that since T^\rho < r < \sqrt 2T^\rho , one deduces that
Hence, it holds that
and
Therefore, by (2.5) and using the change of variable x = T^\rho y , one obtains
which yields (notice that \ell > \frac{2\kappa}{\kappa-1} )
Finally, using (2.3), (2.4) and (2.6), (2.2) follows.
Lemma 2.2. Let \kappa > 1 and \ell > \frac{\kappa}{\kappa-1} . Then
Proof. By (2.1) and the properties of the cut-off function g , one has
On the other hand, for T^\rho < |x| < \sqrt 2 T^\rho , an elementary calculation shows that
which yields
Therefore, using the change of variable x = T^\rho y and the fact that \ell > \frac{\kappa}{\kappa-1} , one obtains
i.e.
Using (2.4), (2.8) and (2.9), (2.7) follows.
Lemma 2.3. Let \kappa > 1 and \ell > \frac{2\kappa}{\kappa-1} . Then
Proof. By (2.1) and the properties of the cut-off functions f and g , one has
An elementary calculation shows that
which yields (since \ell > \frac{2\kappa}{\kappa-1} )
On the other hand, using the change of variable x = T^\rho y , one obtains
which yields
Therefore, using (2.11), (2.12) and (2.13), (2.10) follows.
Lemma 2.4. Let \kappa > 1 and \ell > \frac{\kappa}{\kappa-1} . Then
Proof. By (2.1) and the properties of the cut-off functions f and g , one has
An elementary calculation shows that
which yields (since \ell > \frac{\kappa}{\kappa-1} )
Therefore, using (2.13), (2.15) and (2.16), (2.14) follows.
3.
Fujita critical exponent
3.1. A general estimate
Proposition 3.1. Suppose that problem (1.1) admits a global weak solution u with (u, \nabla u)\in L^p_{loc}(Q)\times L^q_{loc}(Q) . Then there exists a constant C > 0 such that
for all \varphi\in C_c^2(Q) , \varphi\geq 0 , where
and
Proof. Let u be a global weak solution to problem (1.1) with
Let \varphi\in C_c^2(Q) , \varphi\geq 0 . Using (1.6), one obtains
On the other hand, by \varepsilon -Young inequality, 0 < \varepsilon < \frac{1}{3} , one has
Here and below, C denotes a positive generic constant, whose value may change from line to line. Similarly, one has
and
Therefore, using (3.2), (3.3), (3.4) and (3.5), it holds that
Since 1-3\varepsilon > 0 , one deduces that
Again, by (1.6), one has
where \cdot denotes the inner product in \mathbb{R}^N . Hence, it holds that
By \varepsilon -Young inequality ( \varepsilon = \frac{1}{2} ), one obtains
Next, using (3.7), (3.8), (3.9) and (3.10), one deduces that
which yields
Finally, combining (3.6) with (3.11), (3.1) follows.
Proposition 3.2. Suppose that problem (1.1) admits a global weak solution u with (u, \nabla u)\in L^p_{loc}(Q)\times L^q_{loc}(Q) . Then
for all T > 0 , where \xi_T is defined by (2.1).
Proof. Since for all T > 0 , \xi_T\in C_c^2(Q) , \xi_T\geq 0 , taking \varphi = \xi_T in (3.1), (3.12) follows.
3.2. An estimate related to the inhomogeneous term
Proposition 3.3. Let w\in L^1_{loc}(\mathbb{R}^N) , w\geq 0 and w\not\equiv 0 . Then, for sufficiently large T ,
where \xi_T is defined by (2.1).
Proof. By (2.1) and the properties of the cut-off functions f and g , one has
On the other hand,
Moreover, for sufficiently large T (since w, g\geq 0 ),
Notice that since w\in L^1_{loc}(\mathbb{R}^N) , w\geq 0 , w\not\equiv 0 , and using the properties of the cut-off function g , by the domianted convergence theorem, one has
Hence, for sufficiently large T ,
Using (3.14), (3.15), (3.16) and (3.17), (3.13) follows.
3.3. Proof of Theorem 1.1
Now, we are ready to prove the Fujita-type result given by Theorem 1.1. The proof is by contradiction and makes use of the nonlinear capacity method, which was developed by Mitidieri and Pohozaev (see e.g. [11]).
Proof of Theorem 1.1. (ⅰ) Suppose that problem (1.1) admits a global weak solution u with (u, \nabla u)\in L^p_{loc}(Q)\times L^q_{loc}(Q) . By Propositions 3.2 and 3.3, for sufficiently large T , one has
where \xi_T is defined by (2.1),
and
Taking \ell > \max\left\{\frac{2p}{p-1}, \frac{q}{q-1}\right\} , using Lemmas 2.1, 2.3, 2.4 with \kappa = p , and Lemma 2.2 with \kappa = q , one obtains the following estimates
Hence, by (3.19), (3.21), (3.22) and (3.23), one deduces that
Observe that
So, for sufficiently large T , one deduces that
Notice that the above estimate holds for all \rho > 0 . In particular, when \rho = \frac{1}{2} , it holds that
Next, by (3.20), (3.21), (3.22), (3.24) and (3.25), one deduces that
Similarly, the above inequality holds for all \rho > 0 . In particular, when \rho = \frac{p(q-1)}{q(p-1)} , it holds that
Therefore, it follows from (3.18), (3.26) and (3.27) that
which yields
and
Notice that for N\in\{1, 2\} , one has
which shows that
Hence, for N\in\{1, 2\} , passing to the limit as T\to \infty in (3.28), a contradiction follows ( 0 < C\leq 0 ). This proves part (ⅰ) of Theorem 1.1.
(ⅱ) Let N\geq 3 . In this case, one has
Hence, if p < 1+\frac{2}{N-2} , passing to the limit as T\to \infty in (3.28), a contradiction follows. Furthermore, one has
Hence, if q < 1+\frac{1}{N-1} , passing to the limit as T\to \infty in (3.29), a contradiction follows. Therefore, we proved part (ⅱ) of Theorem 1.1.
(ⅲ) Let
Let
where
and
Note that due to (3.30), the set of \delta satisfying (3.32) is nonempty. Let
Elementary calculations yield
Hence, one obtains
Next, using (3.32) and (3.33), one deduces that
Therefore, for any \delta and \varepsilon satisfying respectively (3.32) and (3.33), the function u defined by (3.31) is a stationary solution (then global solution) to (1.1) for some w > 0 . This proves part (ⅲ) of Theorem 1.1.
4.
Second critical exponent
4.1. An estimate related to the inhomogeneous term
Proposition 4.1. Let N\geq 3 , \sigma < N and w\in I_\sigma^+ . Then, for sufficiently large T ,
where \xi_T is defined by (2.1).
Proof. By (3.14) and (3.15), one has
On the other hand, by definition of I_\sigma^+ , and using that g(s) = 1 , 0\leq s\leq 1 , for sufficiently large T , one obtains (since w, g\geq 0 )
Hence, using (4.2), (4.1) follows.
4.2. Proof of Theorem 1.2
Now, we are ready to prove the new critical behavior for the problem (1.1) stated by Theorem 1.2.
Proof of Theorem 1.2. (ⅰ) Suppose that problem (1.1) admits a global weak solution u with (u, \nabla u)\in L^p_{loc}(Q)\times L^q_{loc}(Q) . By Propositions 3.2 and 4.1, for sufficiently large T , one obtains
where \xi_T , A(\xi_T) and B(\xi_T) are defined respectively by (2.1), (3.19) and (3.20). Next, using (3.26) and (4.3) with \rho = \frac{1}{2} , one deduces that
Observe that
Hence, if \sigma < \frac{2p}{p-1} , passing to the limit as T\to \infty in (4.4), a contradiction follows. Furthermore, using (3.27) and (4.3) with \rho = \frac{p(q-1)}{q(p-1)} , one deduces that
Observe that
Hence, if \sigma < \frac{q}{q-1} , passing to the limit as T\to \infty in (4.5), a contradiction follows. Therefore, part (ⅰ) of Theorem 1.2 is proved.
(ⅱ) Let
Let u be the function defined by (3.31), where
and \varepsilon satisfies (3.33). Notice that since \sigma < N , the set of \delta satisfying (4.7) is nonempty. Moreover, due to (4.6) and (4.7), \delta satisfies also (3.32). Hence, from the proof of part (iii) of Theorem 1.2, one deduces that
On the other hand, using (3.34) and (4.7), for |x| large enough, one obtains
which proves that w\in I_\sigma^- . This proves part (ⅱ) of Theorem 1.2.
5.
Conclusions
We investigated the large-time behavior of solutions to the nonlinear damped wave equation (1.1). In the case when N\in\{1, 2\} , we proved that for all p > 1 , problem (1.1) admits no global weak solution (in the sense of Definition 1). Notice that from [5], the same result holds for the problem without gradient term, namely problem (1.5). This shows that in the case N\in\{1, 2\} , the nonlinearity |\nabla u|^q has no influence on the critical behavior of problem (1.5). In the case when N\geq 3 , we proved that, if 1 < p < 1+\frac{2}{N-2} or 1 < q < 1+\frac{1}{N-1} , then problem (1.1) admits no global weak solution, while if p > 1+\frac{2}{N-2} and q > 1+\frac{1}{N-1} , global solutions exist for some w > 0 . This shows that in this case, the Fujita critical exponent for the problem (1.1) is given by
From this result, one observes two facts. First, in the range q > 1+\frac{1}{N-1} , from [5], the critical exponent p_c(N, q) is also equal to the critical exponent for the problem without gradient term, which means that in this range of q , the nonlinearity |\nabla u|^q has no influence on the critical behavior of problem (1.5). Secondly, one observes that the gradient term induces an interesting phenomenon of discontinuity of the Fujita critical exponent p_c(N, q) jumping from 1+\frac{2}{N-2} to \infty as q reaches the value 1+\frac {1}{N-1} from above. In the same case N\geq 3 , we determined also the second critical exponent for the problem (1.1) in the sense of Lee and Ni [10], when p > 1+\frac{2}{N-2} and q > 1+\frac{1}{N-1} . Namely, we proved that in this case, if \sigma < \max\left\{\frac{2p}{p-1}, \frac{q}{q-1}\right\} and w\in I_\sigma^+ , then there is no global weak solution, while if \max\left\{\frac{2p}{p-1}, \frac{q}{q-1}\right\}\leq \sigma < N , global solutions exist for some w\in I_\sigma^- . This shows that the second critical exponent for the problem (1.1) in the sense of Lee and Ni is given by
We end this section with the following open questions:
(Q1). Find the first and second critical exponents for the system of damped wave equations with mixed nonlinearities
where p_i, q_i > 1 , w_i\in L^1_{loc}(\mathbb{R}^N) , w_i\geq 0 and w_i\not\equiv 0 , i = 1, 2 .
(Q2). Find the Fujita critical exponent for the problem (1.1) with w\equiv 0 .
(Q3) Find the Fujita critical exponent for the problem
where N\geq 1 , p, q > 1 , 0 < \alpha < 1 and w\in L^1_{loc}(\mathbb{R}^N) , w\geq 0 . Notice that in the limit case \alpha \to 1^- , the above equation reduces to (1.1).
(Q4) Same question as above for the problems
and
where 0 < \alpha, \beta < 1 .
Acknowledgments
The author is supported by Researchers Supporting Project RSP-2020/4, King Saud University, Saudi Arabia, Riyadh.
Conflict of interest
The author declares no conflict of interest.













 DownLoad:
DownLoad: