1. Introduction
Comprehension of verbal information has been approached from different perspectives across time. Contemporary study of brain organization with respect to verbal comprehension began in 1874 with Karl Wernicke’s description of a patient who, as a consequence of a left temporal lesion, had fluent speech and normal hearing but poor comprehension of verbal commands. This seminal report initiated further descriptions of clinical-anatomical correlations based on the language deficit exhibited by subjects with local brain lesions [1,2,3,4]. During the middle of the 20th century, a major contribution following this model was advanced by Alexander R. Luria, the eminent Russian neuropsychologist, who had the opportunity to assess thousands of brain injured subjects during the Second World War [5,6,7,8]. Luria’s methodical observation, description, and analysis of iconic clinical cases with cognitive deficits (corresponding to the so-called “clinical model”) significantly progressed the knowledge and understanding of the functional organization of the brain for language. The findings of the “clinical model” were either supported or augmented by the cortico-electrical studies of the North American neurosurgeon Wilder Penfield in subjects undergoing epilepsy surgery [9,10]. Penfield mapped motor, sensory, and cognitive brain functions by stimulating or by eliciting a transient focal functional disruption in the cortex and observing the neurological consequences. Different authors continued this approach during the following years [11]. Until recently, both methods (clinical and cortical stimulation) represented the mainstreams of research aimed to elucidate the brain localization of cognitive functions, including verbal comprehension. Of note is that these methods provided information of brain organization in patients with brain pathology and not in normal subjects.
Since the advent of the functional Magnetic Resonance Imaging (fMRI) during the late half of the past century, brain functions in general, and language in particular, have been intensively investigated in normal subjects [12]. Other contributing techniques like Positron Emission Tomography (PET), Magneto-Encephalography (MEG), Event Related Potentials (ERP), Diffusion Tensor Imaging/Tractography DTI-Tractography, and Transcranial Magnetic Stimulation among others, have also been utilized [13]. However, the versatility, easiness, availability, and lack of invasiveness of the fMRI have made it the most popular method in the scientific community to explore brain functions.
2. Language Canonical and Ancillary Areas
Currently, the following are generally considered as canonical language areas [8,14,15,16,17,18,19,20]: (1) the expressive language area (Broca’s area) represented by Brodmann areas 44 (BA44) and BA45, located in the pars opercularis and pars triangularis respectively, in the left inferior frontal gyrus; and (2) the receptive language area (Wernicke’s area) usually represented by BA21 and BA22, located in the posterior third of the superior/middle temporal gyri. Some authors include BA40, whereas others consider BA39 part of the receptive language areas.
Recent brain connectivity and pooling-data of co-activation studies have demonstrated the relevance of some other ancillary areas in language processing. Among these are BA6 (the mesial segment corresponding to the supplementary motor area) [21] and BA13 (anterior insula) for expressive language [22]. It has also been suggested that BA41, BA42, BA37, BA38, and BA20 may participate in receptive language [23,24].
All but two of these areas are considered multimodal. The remarkable exceptions are BA41 and BA42. The finding is striking as BA41/42 correspond to the primary auditory area [25]. Primary areas are thought to be unimodal, responding only to a type of input and executing very basic level functions. However, there is something unusual in the left BA41/42 that makes this region completely segregated from the opposite homological area and other unimodal areas. It seems to have an important role in receptive language functions, specifically in phoneme perception [26]. Phoneme is understood as a language sound unit capable of conveying meaning [27].
The aim of this article is to present a systematic review about the anatomy, function, connectivity, and functional activation of the primary auditory areas when involved in language paradigms. We will strive to synthesize the different findings and present arguments which support the proposal of including BA41/42 as a perceptual language area. For the sake of this article we will only consider language to be left lateralized as it occurs in the vast majority of normal subjects.
3. The Primary Auditory Cortex (PAC): BA41/42
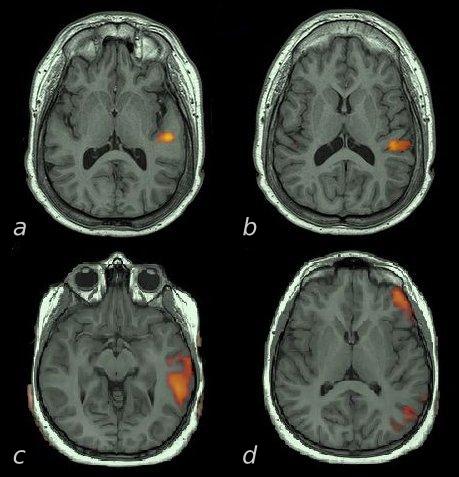
The PAC is located in the posterior third of the superior temporal gyrus, within the transverse temporal gyrus, also known as Heschl’s gyrus (Figure 1).
In transversal MRI views, Heschl’s gyrus has a triangular shape with its truncated sharpest vertice pointing posterior and medial, and its base lateral toward the temporal convexity of the superior temporal gyrus. Heschl’s gyrus abuts the posterior insula boundary medially and the planum temporale posteriorly. Its inferior boundary is part of the superior temporal gyrus and its anterior is the rest of the temporal plane of the sylvian fissure. Heschl’s gyrus is the superior end point of the auditory pathways which have had the olive, the inferior colliculus, and the medial geniculate body as intermediate relay centers. Each PAC has input from both ears, although the predominant input is from the contralateral one. The output pathways of PAC, however, are not well understood yet. Some studies found that PAC connects to 5-6 multimodal areas around it and to the frontal/prefrontal cortex [28,29]. Other important target areas are the left inferior frontal gyrus, its contralateral homologous area [30], and the posterior cingulate cortex (BA30) [31]. Interestingly, there are some results pointing to a cross-unimodality connectivity with the anterior bank of the primary visual area where the visual periphery field is represented [32].
The findings reported by Eckert et al. [32] of a cross-modal link between primary visual and primary auditory area are perplexing as it will necessarily make the area of input a multi-modal area (unless the input is not functional). Since this connection does not fade away while the subjects were performing visual tasks, it suggests the input is toward the auditory cortex. Another interesting aspect of the reported finding is that the connectivity is more precisely between the anterior aspect of the primary visual areas and the Heschls’ gyrus. The anterior primary visual areas are related to the peripheral visual fields. This connectivity is of unknown directionality, and its function is not clear. The fact, also reported in the same work, that visual tasks do not diminish the visual-to-auditory functional connectivity suggests an input to PAC. However, other works seem to point to the opposite direction. An interesting visual illusion has been described: the “sound-induced flash illusion”. If a single flash presented to the peripheral view fields is accompanied by multiple auditory beeps, it is perceived as multiple flashes [33]. In this case, the input would be toward the visual processing areas. Of interest is that stimuli that need to be integrated across different senses require the integrity of the gamma band ( > 30 Hz) brain oscillations mediated by the neurotransmitter gamma-aminobutyric acid (GABA), although the oscillations per se are sustained by activation of metabotropic glutamate receptors [34].GABA concentration in PAC correlates, with the sound-induced flash illusion perception rate while no significant effects were obtained for glutamate concentration, suggesting that the GABA level shapes individual differences in audiovisual perception through its modulating influence on the gamma band multisensory processing.
Although there are some conflicting results in the details, there is agreement that the PAC is organized in a tonotopic manner [35,36,37]. High to low tones are organized from medial to lateral and rostral to posterior manners in both PACs. The left PAC seems to be more sensitive to tones centered at 500 and 4000 Hz than the right one; the right one is in general more sensitive to higher frequencies [35]. Noteworthy, language phonemes mostly in the frequency range 500 to 4000 Hz. Anatomical and functional asymmetries have been also described. Interesting to note, the left planum temporale, including Heschl’s gyrus, is bigger in humans and monkeys [38], suggesting its involvement in human language recognition. Left and right PACs are relatively specialized: temporal resolution —required for phoneme recognition—is better processed on the left, whereas spectral resolution (tones, pitch) is better on the right [39,40]. This is an important asymmetry due to the high dependence of speech for rapidly processing changing broadband sounds, which are defined in temporal domain [41].
The controversy whether phonemes are represented in sensorimotor regions as well as auditory regions remains. Phonemes are often interpreted as multimodal units whose neuronal representations are located across perisylvian cortical regions, including auditory and sensorimotor cortical regions. A different point of view considers phonemes primarily as acoustic entities with posterior temporal localization; according to this position, phonemes are functionally independent from frontal articulatory programs. The question about a causal role of sensorimotor cortex on speech perception and understanding is addressed by reviewing recent TMS studies. Schomers and Pulvermüller [42] argue that frontoparietal cortices, including ventral motor and somatosensory areas, are correlated with phonological information during speech perception and have a direct influence on language understanding (For a further review see [43,44]).
3.1. Functional involvement of PAC
PAC activates with a plethora of diverse basic stimuli such as tones, chords, natural sounds, consonants, and speech. Since the list is significantly long, Table 1 provides examples of publications related to stimuli utilized.
Table 1. Stimuli activating PAC.
| Authors | Year | Stimulus | PAC activation plus: |
| Menéndez-Colino et al. [45] | 2007 | Narrative text (1 subject) Pure tones (750 Hz) | Superior temporal gyrus,rostral to A1 |
| Lasota,et al. [46] | 2003 | Pure tones (1000 Hz) | Planum temporale |
| Yetkin F,et al. [47] | 2004 | Pure tones to left ear 1000,2000 and 4000 Hz | |
| Stefanatos et al. [48] | 2008 | Consonant-vowel speech tokens vs. band- limited noise | |
| Alain et al. [49] | 2005 | Phonetically different vowels presented simultaneously | Left thalamus; planum temporale |
| Liebenthal et al. [50] | 2003 | Sequences of 16 1000-Hz-tones with one deviant tone | Superior temporal plane |
| Hall et al. [51] | 2002 | A single frequency tone and a harmonic tone,either static or frequency modulated | Lateral non-PAC region; superior temporal plane |
| Hart et al. [52] | 2003 | Increasing sound level of high and low tones | |
| Lasota et al. [46] | 2003 | 1000 Hz tone to the right ear at different dB | |
| Patterson et al. [53] | 2002 | Pitch variation to form melodies | Superior temporal plane,Planum temporale |
| Obleser et al. [54] | 2006 | Natural German vowels vs non-speech band-passed noise | Superior temporal plane |
| Izumi et al. [55] | 2011 | Musical sounds | |
| Da Costa et al. [56] | 2013 | Pure tones | |
PAC is also activated in more complex auditory processing such as auditory short-term memory, visualization of speech gestures [57], selective attention to frequency [56], conscious perception [58], and conflicting audio/visual information at syllabic level [59].
3.2. Speech perception
PAC shows specific sensitivity to speech. The processing of auditory language correlates with significant activation in bilateral primary auditory and adjacent areas [60]. At the bottom of the language function is the stage in which, from an auditory-sensorial representation of a vocal sound (sublexical level), a mental representation of speech emerges (phonemes, words). It has been suggested that the initial stage of speech perception takes place in the posterior part of the planum temporale. This activation occurs as a response to basic sublexical processing as some paradigms of passive listening to syllable sequences demonstrate [61]. The processing is automatic and not necessarily related to prior memories or understanding as reversed speech also activates PAC [62].
The involvement of PAC in selective attention mentioned before is of importance in speech perception. In general, speech sounds elicit greater responses on both sides of the brain than non-speech vocalizations in most parts of auditory cortex, including the PAC [63]. However, in spite of this bilateral capability of the auditory cortex, the PAC is strongly left temporal lateralized for the categorical perception of phonemes, as in much auditorily as visually; the latter with lateralized activation of the left visual-word-form area (BA37) [64].
Speech perception is based on a variety of spectral and temporal acoustic features [65,66]. Voice-onset time (VOT) is at the core of the phonemic perception for some phonemes, such as stop phonemes. VOT requires fine temporal feature discrimination between the onset of larynx sound (voicing) and the instant the air column in the trachea is released against the mechanical flow resistance of any point of phonemic articulation in the mouth or pharynx. This discrimination is generally on the order of tens of milliseconds [67]. The advantage of the left auditory areas in processing these acoustic temporal features has been demonstrated by electrophysiological studies (auditory evoked potentials) [68]. However, this “advantage” is not only explained by more proficiency of the left PAC. The right hemisphere, for example, maintains phonological discrimination functions when isolated after the left hemisphere is anesthetized with a short action barbiturate injected in the ipsilateral internal carotid artery—Wada test [69]. However, the right hemisphere function seems to depend somehow on the left hemisphere input as suggested by another Wada test study. In this case, bilateral Wada was administered consecutively with direct disruptive electric stimulation of the left auditory area. Phonological discrimination was kept with either side of the Wada injection (meaning, each hemisphere is “phonological capable” when the contralateral hemisphere is knocked-down). Surprisingly, when only the left auditory area is disrupted electrically, the right hemisphere phonological abilities are lost. These findings strongly suggest an inhibitory input on the right PAC from some area in the left hemisphere that ceases when the entire hemisphere is off. The source of this inhibitory input seems be located on the left planum temporale, according to a recent fMRI study with ultra-high-magnetic field fMRI [70]. Therefore, a combination of truly higher proficiency of the left over the right PAC and an inhibitory tone with left to right direction explains the dominance of the left PAC for phonological processing skills. Noteworthy, phonological discrimination defects in cases of aphasia tend to have a good and rapid recovery [71] suggesting that the right PAC can have a phoneme discrimination role when it is required.
This lateralization probably explains the correlation of clinical findings in some types of fluent aphasia with left posterior temporal lesions. The key concept here is the lack of a minimal phonological/lexical discrimination that gives origin to diminished language comprehension, corresponding to the so-called acoustic-agnosic aphasia according to Luria [8]—one particular subtype of Wernicke’s aphasia [72,73]. Unfortunately, minimal phonological discrimination has received scanty attention from neuroimagenology. Gandour et al. [74] analyzed the differences in hemispheric functions underlying speech perception in Chinese; it was found that pitch contours associated with tones are processed in the left hemisphere by Chinese listeners, whereas pitch contours associated with intonation are processed predominantly in the right hemisphere.
More recently, a study has appeared on phonological discrimination utilizing stop consonants with different points of articulation. This discrimination also requires VOT processing. The study was performed on a 7.0 Tesla MRI providing high resolution. The authors found an overall bilateral activation in auditory areas during the processing of the consonant-vowel syllables. Left lateralization was surprisingly found modulated more by point of articulation than VOT [70].
From the aforementioned findings, it seems speech perception of minimal phonological categories may be processed in either or both primary auditory areas with a functional interplay between them, whereby the left takes precedence in the processing, inhibiting the right counterpart.
3.3. Word-deafness syndrome
Damage in the PAC is associated with so-called “pure word-deafness” (sometimes referred also as “auditory verbal agnosia; ” [75]) [76,77,78]. This syndrome is characterized by an inability to understand spoken language with preserved speech production, discrimination of natural sounds, and reading ability [79]. It is usually regarded as a fragment of Wernicke’s aphasia [80]. Patients with this syndrome have difficulties discriminating phonemic contrasts. For example, they are not able to discriminate voiceless to voiced stop consonants. As a consequence, they exhibit a profound speech perception deficit with subsequent auditory language comprehension impairment. In many features this problem compares with the altered speech perception of late bilinguals unable to discriminate non-native phonemes [81]. Cortical deafness on the other hand is a hearing loss caused by bilateral damage to both auditory radiations and primary auditory cortices [82].
The majority of word-deafness cases due to lesions of the left primary auditory area suggests a purely perceptual deficit, and hence, an auditory (verbal) agnosia. An auditory perceptual problem would limit the discrimination deficit to the auditory presented material, leaving unaffected any phonological processing required from visually presented material. In the detailed case study presented by Caramazza and co-workers in 1983 [83], they demonstrated normal visual-lexical access in a patient with random performance for the same task for auditorily presented information. When this subject was asked to pairing from auditory to visual altered strings sounding like the real name with the name of the object, he performed randomly, demonstrating a problem at a higher perceptual level.
3.4. Developmental trajectories of PAC
A number of studies published between 1978 and 1998 utilizing auditory event-related potentials (ERP) have shown the advantage of the left auditory area for processing phonological differences in infants. Point of articulation (POA) perception has been found as early as in newborns, while VOT detection appears at age 2-3 months [84]. In this study they found a correlation between VOT and POA variables and language skills at age 3 and 8 years. The ability to process sublexical components as early as 2-3 months was also demonstrated by Eimas [85]. It could be speculated that early POA in comparison to VOT is the result of differences in the acoustic information that they contain: POA is based in frequency discrimination whereas VOT depends on the detection of rapid temporal changes in the acoustic signal; this is an ability significantly lateralized to the left hemisphere, and required to distinguish voiced and unvoiced phonemes [26]. Different auditory pathways are involved in these two abilities.
3.5. Neuroimaging contribution
fMRI studies in phoneme perception are not abundant. Areas adjacent to the left middle and superior temporal sulcus have been found responsive to familiar consonant-vowel syllables during an auditory discrimination task [50]. When phonemic discrimination tasks are contrasted with tone discrimination task a pure left superior and middle temporal gyrus activations is obtained [87]. Listening to story is a simple passive task useful in clinical settings as it is suitable for limited-cooperative adults, children and infants. It activates PAC asymmetrically, along with receptive language areas.
Several authors, however, have described similar asymmetries in patients under normal sleep [88,89] and even under light sedation [90,91], mostly on PAC areas. How could this be explained? Listening to story paradigms entails comprehension, that in its turn requires the decoding of words and hence of phonemic discrimination. For a sedate subject a listening-to-a-story paradigm is no more than a paradigm in which the stimulus is actually a succession of phonemes grouped into words. Phonemes are passively decoded though, even during sleep as priming studies with words have clearly found in patients under light anesthesia [92] demonstrating non-conscious-automatic phonological processing.
We have designed an auditory paradigm based on a movie for kids. Excerpts of 30 seconds have been cut and concatenated to a 5 minute video alternating 30-second-scenes with verbal and natural sounds. Natural sounds consist of cracking, squeaking, rumbling, roaring, prattling, clicking, panting, moaning, etc. The verbal epochs consist of scenes where the characters talk; the subject is asked to listen carefully (unpublished). With this approach, the visual activation is canceled, and the pediatric subject’s attention to the task is increased. The paradigm is well accepted by patients with minimal or limited executive function skills (working memory, motor control, attention). In these paradigms, again, the left PAC is dominant in the vast majority of right-handed patients.
3.6. Functional connectivity
New MRI techniques have made it possible to study the discrete functional and structural connectivity of specific areas. Auditory functional connectivity studies are few and limited to the study of patients with tinnitus, auditory hallucinations, etc. [93].
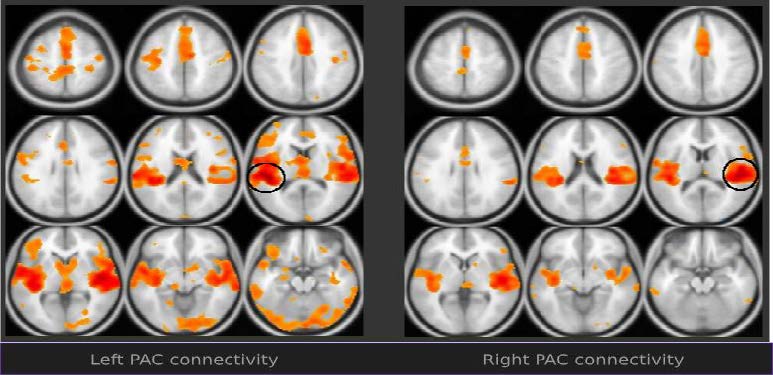
There is a paucity of studies ascertaining the connectivity of PAC in normal subjects. We have observed in a normal subject a particular asymmetry of the connections of BA41 [94]. Indeed, the left BA41 connects asymmetrically with visual and frontal opercular areas as it can be seen in Figure 3. The connectivity with BA19, a secondary visual area, has support from early psychophysics experiments suggesting a hearing modulation for visual functions [95]. More recently, the cross-modal response of V5 (a visual area related to motion detection) to specific auditory stimulus has been demonstrated in normal subjects utilizing fMRI [96]; the same response is observed in early blind subjects, suggesting a structural connectivity between the auditory and visual areas [97]; the response of more extensive visual areas to auditory stimulus is more pronounced in blind subjects [98,99]. Hearing impaired patients also exhibit cross-modal primary and secondary auditory area activation to visual stimuli [100,101]. This interplay seems to substantiate a visual involvement function in speech perception reducing ambiguity and increasing comprehension. Conflicting inputs may show up to the extent that each modality result contributes to the phonological analysis [102]. An elegant and classic experiment in which an auditorily presented /pa/ is overlaid onto a visually presented /ka/ shows that the resultant perception is a sort of fusion into the syllable /ta/ [103].
Asymmetric connectivity of the left BA41 to BA47 (and in general with the frontal operculum) points also to an involvement in language network. Several functional connectivity findings seem to support the contribution of motor/premotor areas in phonological discrimination [104,105,106].
3.7. Structural connectivity
To our knowledge there is only one study assessing the structural connectivity of the primary auditory areas [106]. This study investigated the relevant intra-hemispheric cortico-cortical connections in 20 right-handed male subjects. The connectivity of primary areas consists of a cascade of connections to six adjacent secondary and tertiary areas and from there to the anterior two thirds of the superior temporal gyrus. Graph theory-driven analysis demonstrated strong segregation and hierarchy in stages connecting to PAC. Higher-order areas on the temporal and parietal lobes had more widely spread local connectivity and long-range connections with the prefrontal cortex. Of particular interest is the finding of asymmetric patterns of temporo-parieto-frontal connectivity, a fact that could prompt for structural bases for language development. Upadhyay et al. [107] used stroboscopic event-related functional magnetic resonance imaging (fMRI) to reveal mirror symmetric tonotopic organization consisting of a high-low-high frequency gradient in PAC. The fMRI and DTI results demonstrated that functional and structural properties within early stages of the auditory processing stream are preserved across multiple mammalian species at distinct evolutionary levels.
In humans two different pathways for language have been proposed: ventral and dorsal [108] referred as well as grammatical (frontal) and lexical (temporal) language systems [109,110]. Although the arcuate fasciculus’ posterior terminus is not located in the primary auditory area, it is noteworthy to point that this bundle interconnects secondary auditory areas in the neighborhood of Heschl’s gyrus with areas of the frontal operculum. Temporal functional disruption of this structure with intraoperatory electrical stimulation in awake patients has produced phonological paraphasias [111]. The left arcuate is currently accepted as the dorsal language pathway interconnecting receptive and expressive language areas [112].
Some mention to the mechanisms of coding should be introduced. Sensory regions of cortex are formed of multiple, functionally specialized cortical field maps. In auditory cortex, auditory field maps include the combination of tonotopic gradients—that is, the spectral aspects of sound—and the temporal aspects of the sound [113]. Speech sound involves a mapping from continuous acoustic waveforms onto the discrete phonological units computed to store words in the vocabulary. Localization of auditory fields maps include two levels of sound coding, a tonotopy dimension for spectral properties and a tonochrony dimension for temporal properties of sounds [114].
3.8. Other studies on connectivity
Areas of co-activation within task-related fMRI may be accepted as modules of a network in those paradigms in which the main target area is known a priori. A study of this type investigated the brain areas that are functionally connected during an auditory task. Utilizing a block design paradigm contrasting rest versus hearing human footsteps, areas of activation involved in the task were analyzed using both principal component analysis and structural equation modeling. In addition to Heschl’s gyrus, two connectivity networks were found: (1) involving the planum temporale, posterior superior temporal sulcus (in the so-called “social cognition” area), and parietal lobe. This network is responsible most likely for the perceptual integration of the auditory signal; and (2) a network involving frontal regions related to attentional control: dorsolateral and medial-prefrontal cortex. The authors found a positive influence of the dorsolateral prefrontal cortex (DLPFC) on the auditory areas during the task. The DLPFC activates the auditory pathway when this system conveys the relevant sensory modality [115]. Noteworthy, these results are in agreement with the functional connectivity shown in Figure 3.
4. Conclusion
The aforementioned findings may be summarized in the following points:
1 BA41, and to a lesser extent BA42, are involved in early stages of phonological processing [116,117,118].
2 Phonological processing may take place either on the right or left side, however the left customarily exerts an inhibitory tone over the right, gaining dominance in function [119].
3 Subsequently, a cascade of processes mediated by the left hemisphere predominant connectivity gives the subject a lexico-semantic mental representation [120].
From a clinical perspective, left BA41/42 damage affects phoneme perception, and hence phonological discrimination, which results in auditory verbal agnosia, or word deafness (a subtype of Wernicke’s aphasia). Therefore, it seems evident BA41/42 should legitimately be included as perceptual language areas (Wernicke’s area).
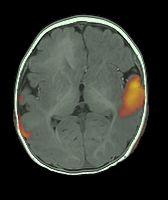
This realization is of utmost importance in the clinical field. Pre-surgical lateralization and localization of language is extremely difficult in young children and adults with poor cooperation. In this group, auditory fMRI under light sedation can demonstrate asymmetries to speech perception that are usually limited to the primary auditory areas [90] (Figure 4). The lateralization of the activation thus demonstrated should be accepted as language lateralization. It would not make sense at all that the side with more “tuned” skills for early stages of language processing resides in the contralateral hemisphere. Of course this could occur in very rare cases, particularly in patients with posterior temporal lesions. In conditions such as this, an interhemispheric dissociation of processing should be considered [121].
In summary, BA41/42 as primary auditory cortices (PAC) harbor complex functions with asymmetrical expression making it possible to include them as core language processing areas (Wernicke’s area).
Acknowledgement
Our sincere gratitude to Deven Christopher for her editorial support and valuable suggestions.
Disclosure
Byron Bernal is owner and President of fMRI Consulting.
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: