1. Introduction
Thiel and his group measured the rise of Ca2+ in Chara cytoplasm (and resulting Cl– channel activation) in response to threshold depolarization of the membrane potential difference (PD) [1,2,3]. They modified animal cell model describing formation of second messenger Inositol 1, 4, 5-triphosphate (IP3) [4,5], which activates Ca2+ channels on internal stores [6]. In our first paper [7] we set up PD rate of change equation, where the transient Ca2+ concentration increase activated Cl– channels and the action potential (AP) form was calculated by numerical integration. To improve the fit of the model to AP data, we introduced prompt Ca2+ transient across plasma membrane. Sharp, positive-going PD spikes at the beginning of the AP data supported this modification. The feature was particularly visible in cells under saline stress, where the APs were spontaneous [7]. The modeling was initially inspired by observation of these prolonged APs in saline stressed cells. We were able to increase the model AP duration by decreasing the values of coefficients in the Hill equation, describing the Ca2+pumps on internal stores (see Figure 6a in [7]). The present paper provides detailed modeling of saline APs, finding that the form is quite variable: "many-or-none" rather than "all-or-none". To fit such diversity in form, some of the Ca2+ channel rate constants also needed modification at the time of saline stress. Different initial IP3 concentrations were explored. As in the first paper [7] the model suggests range of experiments, as well as prompting a discussion how to distinguish AP from other transients. The effect of spontaneous prolonged APs on the cell under salinity stress is discussed.
2. Materials and Methods
2.1. Materials
As described in paper 1 [7] salt-sensitive Chara australis cells survive longer in salinity experiments, if pre-conditioned to osmotic stress in sorbitol artificial pond water (APW: NaCl 1 mM, KCl 0.1 mM, CaCl2 0.1 mM, neutral pH; with added 90 mM sorbitol) for at least 1hr before exposure to Saline APW (KCl 0.1 mM, CaCl2 0.1 mM, neutral pH, 50 mM NaCl). The spontaneous APs with prolonged durations were only observed in the Saline APW. The APs were selected from the whole PD record (data-logged at 0.1 s and stored as text files) and input into Mathematica 10 programs. The evolution of the saline AP form was documented in three cells, numbered in order of the modeling process: Cell 1 (4 APs, AP1 shown in Figure 5 of paper 1 [7]), Cell 2 (5 APs, four APs are shown in Figure 6b of paper 1 [7]) and Cell 3 (5 APs, AP5 from Cell 3 is shown in Figure 6a of paper 1 [7]). The fit parameters for all the APs are shown in Tables 1–3.
Table 1a. Cell 1 fit parameters.
|
Parameter
|
APav, hyper
|
AP1 (20 s) |
AP2 (34 min)
|
AP3 (90 min) |
AP4 (140 min) |
| νr |
0.185 |
|
|
|
|
| γ0 |
0.1 s–1 |
|
|
|
|
| γ1 |
20.5 s–1 |
|
|
|
|
| p1' |
8.5 μM s–1 |
8.89 μM s–1 9.3 red 11.1 blue 13.9 green |
8.63 μM s–1 |
8.89 μM s–1 |
7.8 μM s–1 |
| p2' |
0.035 μM |
0.027 μM 0.027 red 0.025 blue 0.024 green |
0.017 μM |
0.007 μM |
0.007 μM |
| C0 |
1.56 μM |
|
|
|
|
| k1 |
12.0 (μM s)–1 |
|
|
|
|
| k–1 |
8.0 s–1 |
|
|
|
|
| k2' |
15.0 (μM s)–1 |
|
|
|
|
| k–2 |
1.65 s–1 |
|
|
|
|
| k3' |
1.8 (μM s)–1 |
1.38(μM s)–1 1.41 red 0.8 blue 0.8 green |
1.38(μM s)–1 |
1.98 (μM s)–1 |
1.98(μM s)–1 |
| k–3 |
0.04 s–1 |
0.64 s–1 0.635 red 0.47 blue 0.7 green |
0.655 s–1 |
0.935 s–1 |
0.95 s–1 |
| IP3 |
2.5 μM |
0.389 μM 0.49 red 1.0 blue 2.5 green |
0.389 μM |
0.389 μM |
0.389 μM |
| ka |
2 s–1 |
|
|
|
|
| ki |
2 s–1 |
|
|
|
|
| DCa2+ (period of application) |
0.0355 (0.04–0.16 s) |
0.023 (0.04–0.16 s) |
0.04 (0.02–0.16 s) |
0.035 (0.04–0.19 s) |
0.035 (0.04–0.19 s) |
Table 1b. Parameters for the membrane transporters.
|
Parameter
|
APav, hyper
|
AP1 (20 s) |
AP2 (34 min) |
AP3 (90 min) |
AP4 (140 min) |
| κoi |
140 s–1 |
140 s–1 |
102 s–1 |
65 s–1 |
40 s–1 |
| kio0 |
7000 s–1 |
7000 s–1 |
6000 s–1 |
6000 s–1 |
6000 s–1 |
| koi0
|
0.1 s–1 |
|
|
|
|
| κio |
0.1 s–1 |
|
|
|
|
| Gbkg |
0.5 S m–2 |
0.5 S m–2 |
1.5 S m–2 |
1.5 S m–2 |
1.5 S m–2 |
| V50+ |
100 mV |
|
|
|
|
| zg |
1.0 |
|
|
|
|
| NKPK |
6.5 × 10–7 m3 s–1 |
|
|
|
|
| [K+]cyt |
100 mM |
|
|
|
|
| [K+]o |
0.1 mM |
|
|
|
|
| [Cl–]cyt |
10 mM |
50 mM |
|
|
|
| [Cl–]o |
1.3 mM |
50 mM |
|
|
|
| [Ca2+]cyt |
0.02 μM |
|
|
|
|
| [Ca2+]o |
0.1 mM |
|
|
|
|
| GCl, max |
10 S m–2 |
40 S m–2
40 red
43 blue
43 green |
32 S m–2 |
25.5 S m–2 |
19.5 S m–2 |
Table 2a. Cell 2 fit parameters.
|
Parameter
|
APav,
|
AP1 (142 min) |
AP2 (160 min) |
AP3 (168 min) |
AP4 (245 min) |
AP5 (268 min) |
| νr |
0.185 |
|
|
|
|
|
| γ0 |
0.1 s–1 |
|
|
|
|
|
| γ1 |
20.5 s–1 |
|
|
|
|
|
| p1' |
8.5 μM s–1 |
8.4 μM s–1 |
6.8 μM s–1 |
6.8 μM s–1 |
6.8 μM s–1 |
4.8 μM s–1 |
| p2' |
0.035 μM |
0.018 μM |
0.02 μM |
0.015 μM |
0.018 μM |
0.02 μM |
| C0 |
1.56 μM |
|
|
|
|
|
| k1 |
12.0 (μM s)–1 |
|
|
|
|
|
| k–1 |
8.0 s–1 |
|
|
|
|
|
| k2' |
15.0 (μM s)–1 |
|
|
|
|
|
| k–2 |
1.65 s–1 |
|
|
|
|
|
| k3' |
1.8 (μM s)–1 |
1.5 (μM s)–1 |
0.9 (μM s)–1 |
0.55 (μM s)–1 |
0.3 (μM s)–1 |
0.9 (μM s)–1 |
| k–3 |
0.04 s–1 |
0.55 s–1 |
0.21 s–1 |
0.21 s–1 |
0.24 s–1 |
0.1 s–1 |
| IP3 |
2.5 μM |
0.5 μM |
0.35 μM |
0.35 μM |
0.35 μM |
0.3 μM |
| ka |
2 s–1 |
|
|
|
|
|
| ki |
2 s–1 |
|
|
|
|
|
| DCa2+ (period of application) |
0.0355 (0.04–0.16 s) |
0.015 (0.04–0.16 s) |
0.025 (0.04–0.18 s) |
0.025 (0.04–0.18 s) |
0.025 (0.04–0.18 s) |
0.015 (0.04–0.14 s) |
Table 2b. Parameters for the membrane transporters.
|
Parameter
|
APav
|
AP1 (142 min) |
AP2 (160 min) |
AP3 (168 min) |
AP4 (245 min) |
AP5 (268 min) |
| κoi |
140 s–1 |
IOH NOHPOH: 9 × 10–4 m3 s–1 |
IOH NOHPOH: 1 × 10–4 m3 s–1 |
IOH NOHPOH: 1 × 10–4 m3 s–1 |
IOH NOHPOH: 2 × 10–4 m3 s–1 |
IOH NOHPOH: 2 × 10–4 m3 s–1 |
| kio0
|
7000 s–1 |
zg+: 1 zg–: 0.6 |
zg+: 1 zg–: 0.6 |
zg+: 1 zg–: 0.6 |
zg+: 1 zg–: 0.6 |
zg+: 1 zg–: 0.6 |
| koi0
|
0.1 s–1 |
V50+: 350 V50–:– 170 mV |
V50+: 350 V50–: –170 mV |
V50+: 350 V50–: –170 mV |
V50+: 350 V50–: –170 mV |
V50+: 350 V50–: –170 mV |
| κio |
0.1 s–1 |
|
|
|
|
|
| Gbkg |
0.5 S m–2 |
1.8 S m–2 |
1.8 S m–2 |
1.8 S m–2 |
1.8 S m–2 |
1.8 S m–2 |
| V50+ |
100 mV |
|
|
|
|
|
| zg |
1.0 |
|
|
|
|
|
| NKPK |
6.5 × 10–7 m3 s–1 |
|
|
|
|
|
| [K+]cyt |
100 mM |
|
|
|
|
|
| [K+]o |
0.1 mM |
|
|
|
|
|
| [Cl–]cyt |
10 mM |
50 mM |
|
|
|
|
| [Cl–]o |
1.3 mM |
50 mM |
|
|
|
|
| [Ca2+]cyt |
0.02 μM |
|
|
|
|
|
| [Ca2+]o |
0.1 mM |
|
|
|
|
|
| GCl, max |
10 S m–2 |
20 S m–2 |
21 S m–2 |
20 S m–2 |
16 S m–2 |
16 S m–2 |
Table 3a. Cell 3 parameters.
|
Parameter
|
APav
|
AP1 (1 min) |
AP2 (18 min) |
AP3 (82 min) |
AP4 (84 min) |
AP5 (115 min) |
| νr |
0.185 |
|
|
|
|
|
| γ0 |
0.1 s–1 |
|
|
|
|
|
| γ1 |
20.5 s–1 |
|
|
|
|
|
| p1' |
8.5 μM s–1 |
1.65 μM s–1 |
10.5 μM s–1 |
2.1 μM s–1 |
2.8 μM s–1 |
0.651 μM s–1 |
| p2' |
0.035 μM |
0.029 μM |
0.045 μM |
0.045 μM |
0.045 μM |
0.027 μM |
| C0 |
1.56 μM |
|
|
|
|
|
| k1 |
12.0 (μM s)–1 |
|
|
|
|
|
| k–1 |
8.0 s–1 |
|
|
|
|
|
| k2' |
15.0 (μM s)–1 |
|
|
|
|
|
| k–2 |
1.65 s–1 |
|
|
|
|
|
| k3' |
1.8 (μM s)–1 |
1.72 (μM s)–1 |
0.1 (μM s)–1 |
1.7 (μM s)–1 |
1.7 (μM s)–1 |
1.72 (μM s)–1 |
| k–3 |
0.04 s–1 |
0.054 s–1 |
1.4 s–1 |
0.6 s–1 |
0.6 s–1 |
0.695 s–1 |
| IP3 |
2.5 μM |
2.5 μM |
0.23 μM |
2.5 μM |
2.5 μM |
2.5 μM |
| ka |
2 s–1 |
|
|
|
|
|
| ki |
2 s–1 |
|
|
|
|
|
| DCa2+ (period of application) |
0.0355 (0.04–0.16 s) |
0.02 (0.04–0.16 s) |
0.021 (0.04–0.18 s) |
0.02 (0.04–0.18 s) |
0.02 (0.04–0.18 s) |
0.02 (0.04–0.18 s) |
AP1 Extra bump: Ip0 = 0.15 μM, turned on at 18.5 s.
AP5 Extra bump: Ip0 = 0.0065 μM, turned on at 53.05 s. |
Table 3b. Parameters for the membrane transporters.
|
Parameter
|
APav hyper
|
AP1 (1 min) |
AP2 (18 min) |
AP3 (82 min) |
AP4 (84 min) |
AP5 (115 min) |
| κoi |
140 s–1 |
120 s–1 |
70 s–1 |
IOH: NOHPOH: 10 × 10–4 m3 s–1 |
IOH: NOHPOH: 10 × 10–4 m3 s–1 |
50 s–1 |
| kio0
|
7000 s–1 |
6000 s–1 |
|
zg+: 1 zg–: 0.6 |
zg+: 1 zg–: 0.6 |
6000 s–1 |
| koi0
|
0.1 s–1 |
|
|
V50+: 350 V50–: –170 mV |
V50+: 350 V50–: –170 mV |
|
| κio |
0.1 s–1 |
|
|
|
|
|
| Gbkg |
0.5 S m–2 |
1.2 S m–2 |
1.5 S m–2 |
1.8 S m–2 |
1.8 S m–2 |
1.6 S m–2 |
| V50+ |
100 mV |
|
|
|
|
|
| zg |
1.0 |
|
|
|
|
|
| NKPK |
6.5 × 10–7 m3 s–1 |
|
|
|
|
|
| [K+]cyt |
100 mM |
|
|
|
|
|
| [K+]o |
0.1 mM |
|
|
|
|
|
| [Cl–]cyt |
10 mM |
50 mM |
|
|
|
|
| [Cl–]o |
1.3 mM |
50 mM |
|
|
|
|
| [Ca2+]cyt |
0.02 μM |
|
|
|
|
|
| [Ca2+]o |
0.1 mM |
|
|
|
|
|
| GCl, max |
10 S m–2 |
27 S m–2 |
13 S m–2 |
70 S m–2 |
70 S m–2 |
13.5 S m–2 |
2.2. Modeling the saline AP form
The derivation of the Thiel-Beilby model is described in detail in paper 1 [7]. This model was used to simulate all the saline APs. The parameters are listed in Tables 1–3. The programs containing the fitted APs can be found on MJ Beilby website link "Action Potential models": http://newt.phys.unsw.edu.au/~mjb/APproj.html. The standard "APav" modeled to AP data obtained from cells in APW [7] was used to contrast the changes to AP form under salinity stress (see Figure 3, Figure 4 and Tables 1–3).
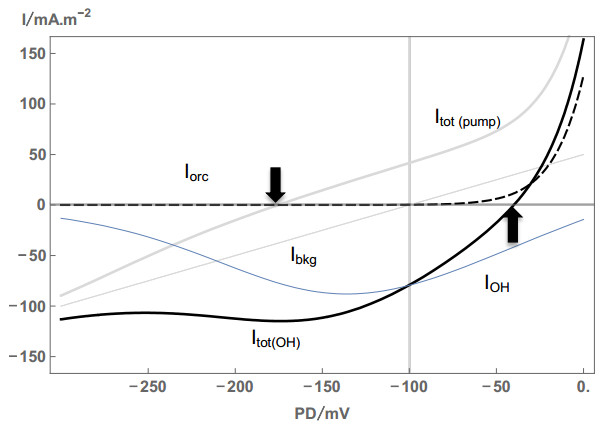
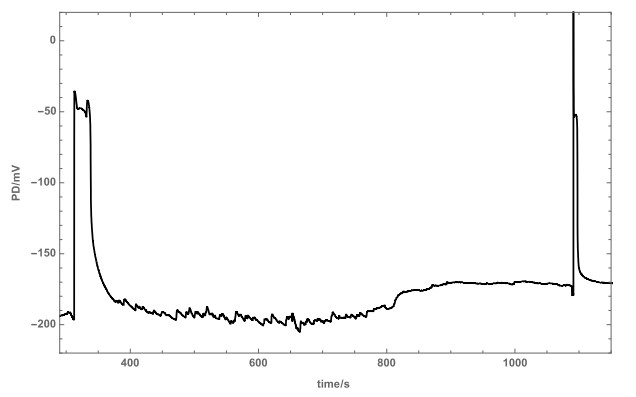
The initial resting PD, RPD, for each cell was adjusted in the model to fit the experimental data. If the RPD was more negative than –100 mV, the appropriate level was obtained by manipulating the proton pump parameters and consequently the Ip/V characteristics (see Figure 1 in paper 1 [7]). At –100 mV the background current, Ibkg, dominated the resting membrane characteristics until the outward rectifier current, Iorc, became important above ~ –30 mV. Cells exposed to Saline APW for longer times depolarized to PDs above –100 mV and exhibited I/V characteristics that could be modeled by growing contribution from OH– channels [8,9]. In this case, the amplitude of OH– current, IOH, was adjusted to match the cell RPD (Figure 1). The IOH was simulated by the Goldmann-Hodgkin-Katz (GHK) equation, multiplied by the Boltzmann distribution of open probabilities, Po– and Po+, to make the PD-dependence stronger [10,11]. For mathematical details see equations 13, 14a, b in paper 1 [7]. The background and reasoning for modelling of IOH can be found in Beilby and Casanova [12].
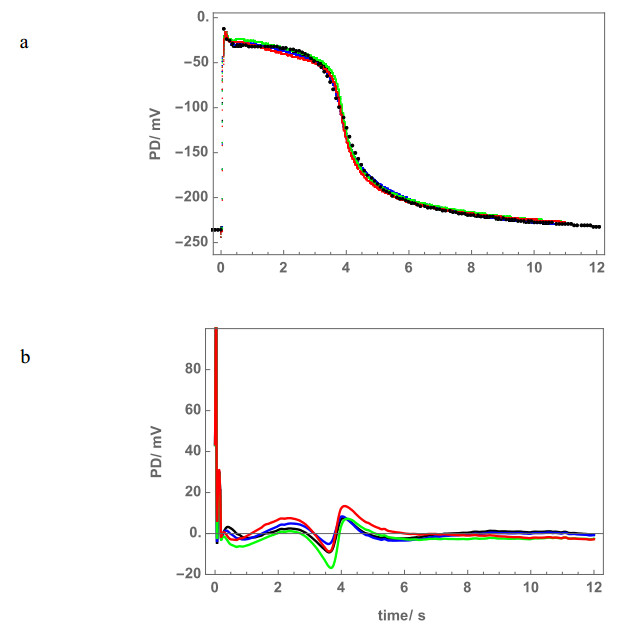
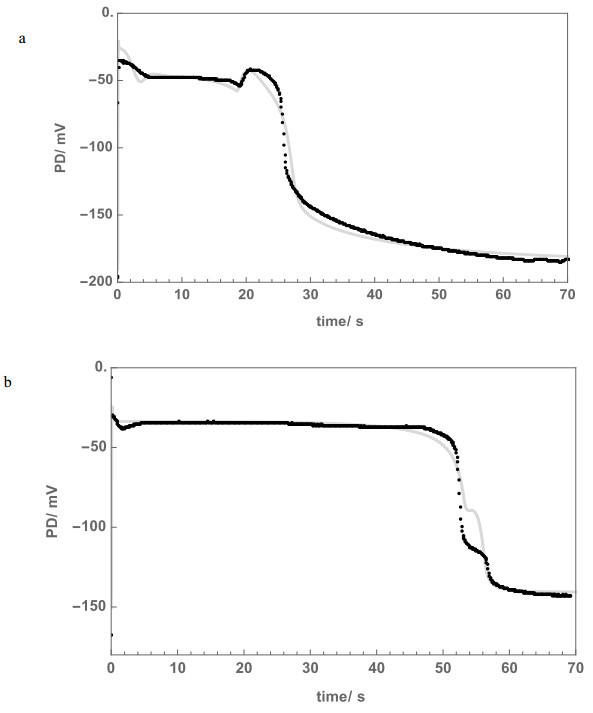
The cytoplasmic Cl– concentration was increased to 50 mM in Saline APW to preserve the AP peak level (see Figure 3). The initial IP3 concentration, I0(see equation 2 in paper 1 [7]), did interact with the other parameters, affecting the AP form in a subtle manner (Figure 2a). The goodness of the model fit was judged by eye, aided by computation of the area difference: area under the data AP—the area under the simulated AP (Figure 2b).
The prompt Ca2+ inflow across plasma membrane, ITRP, Ca, was simulated as in paper 1 [7]. The data-logging speed in the experiments was too slow to reveal detailed shape of the PD spike (see Figure 3 and Figure 4), so square current pulse was used and the fraction of Ca2+ reaching the channels on the stores was adjusted to fit the depolarizing phase of the AP.
3. Results
3.1. AP evolution with time in Saline APW
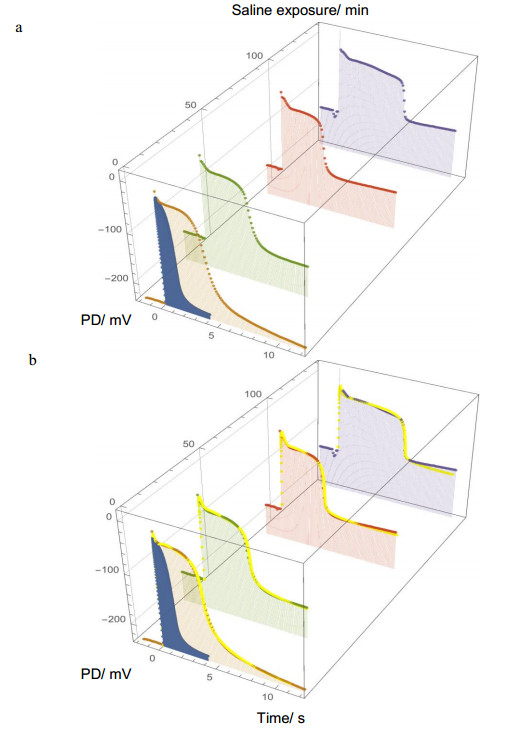
Cell 1 AP1 demonstrated how fast the AP form responded to exposure to Saline APW. After only 20 s, with the RPD still very negative at –235 mV, the AP duration had more than doubled (Figure 3a, see also Figure 5a in paper 1 [7]). However, the repolarizing stage followed similar trend to APav (included in Figure 3a in blue). This gradual repolarization presented first modeling challenge, as changing the Hill coefficients, p1' and p2', in the Ca2+ pump model alone did not provide the right shape. The rate constants k3' and k–3, controlling the backward and forward transition between the activated Ca2+ channel state and final inactivated Ca2+ channel state (see equation 1 in paper 1 [7]), had to be modified to achieve reasonable fit (Table 1a, Figure 3b). AP2 (34 min of saline exposure) looked very similar to AP1, but the duration was slightly longer and the repolarization stage slightly shorter (see Table 4 for summary of AP data and Figure 3a). AP3 (90 min saline exposure) form had changed further: there was a distinct overshoot bulge at the beginning of the AP, reminiscent of the peak of APav, and the repolarization stage was more abrupt, giving the AP square appearance. AP4 (140 min saline exposure) was similar in initial stages, but had much longer duration of almost 6 s and repolarized even more abruptly (Figure 3a, Table 4). The membrane RPD has depolarized for the last two APs to –175 and –155 mV, respectively (Table 4). Figure 3b shows that modeled APs, superimposed on the data as yellow lines, provide satisfactory fit, describing the main features of each AP.
Table 4. Summary of AP parameters.
|
Saline Exposures/min
|
cell 1: 0.3, 34, 90, 140 |
| cell 2: 142, 160, 168, 245, 268 |
| cell 3: 1, 18, 82, 84, 115 |
|
RPD/mV
|
cell 1: –235, –178, –175, –155 |
| cell 2: –74, –88, –97, –81, – 87 |
| cell 3: –196, –177, –90, –75, –167 |
|
Repolarization time/s
|
cell 1: 8, 3.8, 2.2, 1 |
| cell 2: 2.9, 2.8, 1.9, 1.4, 1.2 |
| cell 3: 45, 3.2, 12, 10, 10, 2.9 |
|
Spike peak/mV (multiple peaks in brackets) |
cell 1: –11, –12, –13, +46 |
| cell 2: +51, (+34, +48), (+8, +16), +57, +6 |
| cell 3: –28, +10, +16, –6, +51 |
|
AP peak/mV Average: –38.9 ± 3.8 –29.0 ± 3.8 |
cell 1: –31 to –34, –38 to –48, –40 to –48, –35 to –52 |
| cell 2: –27 to –36, –26 to –35, –23 to –38, –24 to –38, –29 to –35 |
| cell 3: –46 to –52, –52 to –58, –2 to –11, –1 to –11, –32 to –48 |
|
Duration/s Average: 12.8 ± 4.1 |
cell 1: 2.5, 3.2, 3.1, 5.7 |
| cell 2: 3.7, 2.9, 4.4, 7.3, 3.2 |
| cell 3: 19 + 6 (secondary peak), 5.8, 33, 30, 50 |
The initial IP3 concentration, I0 (see equation 2 in paper 1 [7]) subtly influenced the AP form (Figure 2a). The best fit of the model for Cell 1 was found with I0 = 0.389 μM. The small changes in AP form for other concentrations are shown with different colors, the quality of the fit is expressed as area difference (see Methods, Figure 2b). Changing I0 required adjustment in p1', p2', k3', k–3 and GCl, maxparameters for the best fit (Table 1). Such parameter interaction increased complexity of the fitting process.
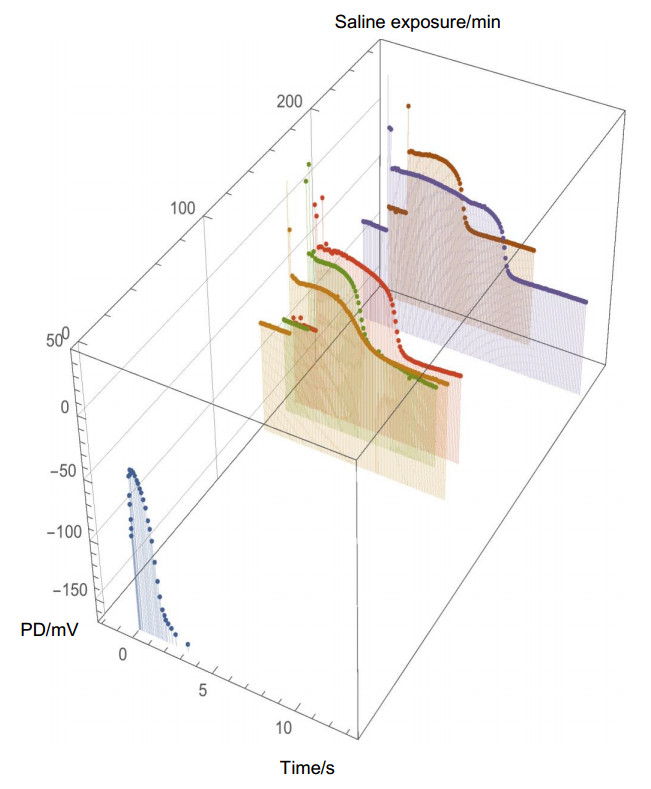
The Cell 1 data suggest that the duration of AP may increase with saline exposure. Following the evolution of Cell 2 dispels that hypothesis: the durations of the five APs seem to vary at random, with the last AP5 being the second shortest (Figure 4, Table 4). Similarly in Cell 3 AP1 is much longer than AP2 (Figure 5). However, the repolarization once again became faster with longer saline exposures in both Cell 2 and Cell 3 APs (Figure 4, Table 4).
3.2. Refractory period
Cell 3 provided another insight. Apart from AP2, all other APs displayed long durations (Table 4, Figure 6). AP1 and AP5 both featured secondary peaks towards the end of the transient (Figure 6a, Figure 6b). The refractory period of Chara AP under normal conditions was found to be between 6 and 60 s [14]. Shepherd et al. 2008 [15] observed spontaneous repetitive APs in 100 mM NaCl/0.1 mM CaCl2 medium of 30 s duration and between 26 and 37 s apart. Consequently the secondary peaks in present data were treated as re-excitation and smaller amount of IP3 was introduced into the model. While the simulation produced secondary peaks, detailed fit was difficult (Table 3, Figure 6).
3.3. Statistical summary
The data were collected from 14 spontaneous APs coming from 3 cells. The exposures to saline stress varied between 0.3 and 268 min, with RPDs ranging from –235 to –74 mV. The repolarization times mostly decreased for all cells as function of the saline exposure time. The initial spikes, thought to be due to prompt Ca2+ transient across plasma membrane, exhibited varying shapes and amplitudes. Some of the variation arises from insufficient data-logging speed (see methods). The maximal PDs of the measured spikes varied from –28 to +58 mV (Figure 3, Figure 4, Table 4). Some cells exhibited multiple spikes (Cell 2: APs 2, 3 and 4). The flat prolonged peaks of the APs were often not horizontal, so we defined maxima and minima for each AP (Table 4). The average level section of the AP varied between –29 and –39 mV (Table 4). The duration varied between 2.5 and 50 s, with average of 12.8 ± 4.1 s (Table 4). However, even the shortest saline APs had longer durations than APav.
4. Discussion
4.1. Can AP be distinguished from other transients?
Under salinity stress, the APs in salt-sensitive Chara australis become "many-or-none", rather than "all-or-none" transient. The diversity involves bulges (e. g. Cell 1: APs 2–4) or dips (e.g. Cell 2: APs 1, 2 and 5, Cell 3: AP5) after the initial prompt spike. The flat part of the AP can slope in hyperpolarizing (Cell 1 APs) or depolarizing (Cell 2: AP 1 and 5) direction. Not only there is a diversity of form, but also the APs at similar saline exposures sometime display large differences (e. g. the two APs in Figure 5). This behavior could only be simulated with the model parameters p1', p2', k3' and k–3varying in almost random fashion (Tables 1–3). These parameters control the Ca2+ inflow into cytoplasm from the stores and pumping Ca2+ back into the stores. Plots of the parameters as function of saline exposure time display a lot of scatter (see supplementary Figure 1 on http://newt.phys.unsw.edu.au/~mjb/APproj.html). However, p1'and p2' mostly decreased with saline exposure time (with exception of Cell 3 p2' at 18, 82 and 84 min saline exposure), while k3' seemed initially unaffected (with exception of Cell 3 at 18 min saline exposure) and decreased at longer exposures, and k–3 increased and then decreased at similar exposures. Clearly more data are needed for conclusive analysis, especially with Cell 3 exhibiting very long APs, which required different combination of parameter values.
Considering the diversity in form, can we be sure that these saline transients are in fact APs? Firstly, we can see the transition from APav after short exposures to Saline APW (Figure 3a, also Figure 5a in paper 1 [7]). Most saline APs start with the positive going spike of putative Ca2+ inflow across plasma membrane. Further, due to cytoplasmic Ca2+ rise, the characean AP is coupled to sudden stoppage of cytoplasmic streaming, which takes ~5 min to recover [16]. This effect was always noted at the time of the experiments. The AP peak, or the plateau in long APs, was found between –30 and –40 mV similar to APav. Finally, the Thiel-Beilby model can accommodate the main features of the diverse saline AP form. Thus we feel fairly confident, that the saline APs are produced by the same mechanisms as APav, but with some of it's many processes affected by salinity. Could we simulate the diverse saline AP form by another model? The alternative scenario is the inflow of Ca2+ from the outside through plasma membrane voltage-dependent channels. The prolonged Ca2+ inflow from the outside under saline stress would probably lead to greater depolarization of the AP peak than observed experimentally, but voltage clamp experiments might be necessary to investigate this possibility.
Interestingly, the shape of the saline AP with the initial spike, the long plateau and the rapid recovery are reminiscent of cardio myocyte AP [17]. While the underlying channels in the myocyte AP are different (fast Na+ channel for the initial spike and two types of K+ channel for repolarization), there is also Ca2+ inflow, followed by more Ca2+ input from internal stores. In both systems the high internal Ca2+ transforms the electrical impulse into mechanical contraction of the heart muscle or the "green muscle" of the cytoplasmic streaming stoppage.
While the re-excitation at the end of AP1 and AP5 of Cell 3 is plausible, as the refractory periods of those durations have been observed [14,15], there is also possibility of superposition of the saline noise [13]. This is more likely in AP1 (Figure 5), where the noise is visible at the end of excitation. However, the secondary bulge is similar to that at the beginning of the AP (Figure 6a) and unlike the spiky saline noise [13]. Alternatively, the long depolarization might produce small amounts of IP3, which would be normally insufficient to start an AP, but as there is still lot of Ca2+ in the cytoplasm, more Ca2+ channels are activated.
4.2. The effect of prolonged APs on the salinity stressed cell
Shepherd et al. [15] compared the effects of 100 mM NaCl with either 1.0 mM or 0.1 mM CaCl2, noting that low external Ca2+ caused depolarization to PDs above the AP threshold and spontaneous repetitive prolonged APs, which usually lead to cell death. In our experiments with Saline APW of 50 mM NaCl/0.1 mM CaCl2, spontaneous APs at shorter intervals also seemed to speed up the cell collapse with RPD close to zero and permanent cytoplasmic streaming cessation (e.g. Cell 2).
Under normal circumstances, the APs signal mechanical deformation or injury to the cell and cessation of cytoplasmic streaming allows the wound healing process to start [18]. So, why is AP so damaging to the cell under salinity stress? The plateau in the saline AP between –30 and –40 mV activates the outward rectifier current (Figure 1) and cell loses K+ (and Cl– through Ca2+-activated Cl– channels) in each AP. With the pump getting gradually inactivated and the RPD depolarizing close to and eventually above –100 mV, the loss of K+ becomes irreversible. In a healthy cell, K+ is one of the most abundant inorganic cations, which activate enzymes, stabilize protein synthesis and contribute to cell turgor [19]. Under salinity stress Na+ enters the cytoplasm through the voltage-independent non-selective channels, that conduct the background current [15], and competes for K+ binding sites, being similar in physicochemical structure. However, the similarity is not close enough for Na+ to perform the same functions and K+-dependent metabolic processes are inhibited [20]. The mechanisms for salinity effects on the Ca2+ channels and pumps on the internal stores are not clear at present. Perhaps K+ stabilizes the channel and pump proteins and the gradual replacement by Na+ leads to somewhat random changes in their function. In general, plants need to maintain high cytoplasmic K+/Na+ ratio to be salt tolerant [19,20]. Cl– is regarded as essential micronutrient, important in oxygenic photosynthesis and needed for turgor generation [21]. With the collapse of the proton electrochemical gradient due to salinity activation of H+/OH– channels [8], the cell is no longer able to import Cl– [22] and export Na+ [23]. Shepherd et al. [15] designated the spontaneous repetitive APs as "point of no return" at the time of saline stress. As Characeae are sister plants to ancestors of land plants [24,25], the lesson of AP contribution to salt stress may be also relevant to agriculturally important plants.
5. Conclusion
The detailed modeling of the Chara AP undergoing salinity stress revealed complex and variable form. The main features of the saline APs could be fitted by the Thiel-Beilby model, varying the parameters of the Ca2+ pump (Ca2+ removal from the cytoplasm), and the activation/inactivation of the Ca2+ channels on the inside stores (Ca2+ inflow into cytoplasm). The initial activating concentration of IP3 also influenced the AP form. Experiments to explore saline Chara AP:
(1) The excitability of Chara cells can be irreversibly abolished by exposure to La3+ [26] and the cells can then be tested for longer survival in Saline APW, compared to untreated cells.
(2) The external Ca2+ is important in cell survival in saline stress [15]. The saline AP can be explored with different Ca2+ content of saline medium. Voltage clamp experiments will resolve whether Ca2+ comes from the outside or internal stores.
(3) Is Na+ the only ion that modifies the AP form? A range of ions similar to Na+ should be tested.
Acknowledgments
MJB thanks Dr. Vadim Volkov for stimulating discussions at the time of modeling of the saline APs and to referees for constructive comments.
Conflicts of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: