Citation: Lars H. Wegner. Cotransport of water and solutes in plant membranes: The molecular basis, and physiological functions[J]. AIMS Biophysics, 2017, 4(2): 192-209. doi: 10.3934/biophy.2017.2.192
| [1] | Wenyuan Xie, Jason Wei Jun Low, Arunmozhiarasi Armugam, Kandiah Jeyaseelan, Yen Wah Tong . Regulation of Aquaporin Z osmotic permeability in ABA tri-block copolymer. AIMS Biophysics, 2015, 2(3): 381-397. doi: 10.3934/biophy.2015.3.381 |
| [2] | Thuy Hien Nguyen, Catherine C. Moore, Preston B. Moore, Zhiwei Liu . Molecular dynamics study of homo-oligomeric ion channels: Structures of the surrounding lipids and dynamics of water movement. AIMS Biophysics, 2018, 5(1): 50-76. doi: 10.3934/biophy.2018.1.50 |
| [3] | Ateeq Al-Zahrani, Natasha Cant, Vassilis Kargas, Tracy Rimington, Luba Aleksandrov, John R. Riordan, Robert C. Ford . Structure of the cystic fibrosis transmembrane conductance regulator in the inward-facing conformation revealed by single particle electron microscopy. AIMS Biophysics, 2015, 2(2): 131-152. doi: 10.3934/biophy.2015.2.131 |
| [4] | Ken Takahashi, Yusuke Matsuda, Keiji Naruse . Mechanosensitive ion channels. AIMS Biophysics, 2016, 3(1): 63-74. doi: 10.3934/biophy.2016.1.63 |
| [5] | Mary Jane Beilby, Sabah Al Khazaaly . Re-modeling Chara action potential: II. The action potential form under salinity stress. AIMS Biophysics, 2017, 4(2): 298-315. doi: 10.3934/biophy.2017.2.298 |
| [6] | Ashwani Kumar Vashishtha, William H. Konigsberg . Effect of different divalent cations on the kinetics and fidelity of DNA polymerases. AIMS Biophysics, 2018, 5(4): 272-289. doi: 10.3934/biophy.2018.4.272 |
| [7] | Mathieu F. M. Cellier . Evolutionary analysis of Slc11 mechanism of proton-coupled metal-ion transmembrane import. AIMS Biophysics, 2016, 3(2): 286-318. doi: 10.3934/biophy.2016.2.286 |
| [8] | Ulrich Lüttge . Physics and the molecular revolution in plant biology: union needed for managing the future. AIMS Biophysics, 2016, 3(4): 501-521. doi: 10.3934/biophy.2016.4.501 |
| [9] | José Luis Alonso, Wolfgang H. Goldmann . Cellular mechanotransduction. AIMS Biophysics, 2016, 3(1): 50-62. doi: 10.3934/biophy.2016.1.50 |
| [10] | Alexander G. Volkov, Yuri B. Shtessel . Electrotonic signal transduction between Aloe vera plants using underground pathways in soil: Experimental and analytical study. AIMS Biophysics, 2017, 4(4): 576-595. doi: 10.3934/biophy.2017.4.576 |
Current concepts of membrane transport in plants are based, among other things, on the (usually implicit, rather than outspoken) assumption that water and solutes are translocated across membranes via separate pathways and interact little during this passage. Hence, water is believed to move passively between compartments, exclusively driven by a difference in water potential (ψ). By contrast, it is widely accepted that solute transport does not necessarily follow the (electro) chemical gradient of a particular solute. In addition to ion pumps such as H+ ATPases, the PPase and the Ca2+ ATPase (s), that directly convert chemical energy into a proton motive force (PMF) and a steep trans-membrane Ca2+ gradient, respectively, cotransporters and antiporters couple transport of one solute to the chemical gradient of another one [1,2]. In summa, the transport process is energetically downhill, but an (electro) chemical gradient of one solute can be employed to transport a second solute against its driving force to establish (or maintain) a gradient of that solute. In plants a PMF is built up across a membrane by proton pumps that energize transport of ions, sugars or amino acids [3]. As a classical example from animal physiology, the Na+-glucose cotransporters belonging to the SGLT family (Sodium dependent glucose transporters) can be considered [4]; a steep Na+ gradient across the plasma membrane is exploited to assure that glucose uptake is maintained irrespective of the actual glucose concentrations on both sides of the membrane. A more detailed account of the many well-studied cases of solute-solute cotransport (and antiport) is beyond the scope of this review. Until recently, water was not considered to be a substrate for the coupling of transport, at least not in plants.
However, this view is starting to change. The possibility that water could also be transported against its driving force by coupling with solute transport has recently been considered in the context of volume regulation of freshwater algae and buoyancy of marine algae [5]. In higher plants, solute-water cotransport was discussed with respect to the generation of root pressure, refilling of embolized xylem vessels, and cell elongation (growth) [6,7,8,9]. In this short review the current molecular basis of these models will be summarized. Since research in this area is still at its infancy, it will rather be a summary of our lack of knowledge, though. This report is intended to identify directions of further research in this area and will hopefully motivate researchers to fill the gaps. First, however, it will be pointed out that coupling of water and solute transport is by no means a new concept in plant physiology. In fact, in the early times of membrane biophysics in the fifties and sixties of the last century, the concept of the thermodynamics of irreversible processes was introduced into this field to adequately treat, among other things, phenomena that result from coupling of water and solute fluxes. Finally, physiological processes are identified for which solute-water cotransport could (potentially) play a pivotal role.
When biological membranes first came into the focus of research in the midst of the last century, it became soon clear that they act as converters of chemical (and electrical) energy. The concept of the thermodynamics of irreversible processes was introduced into membrane biophysics, because this theory provided a framework for taking the mutual coupling of fluxes and driving forces into account. In principle, any driving force contributes to any of the fluxes. The simplest representation is water transport (for practical reasons represented by the volume flow, JV, in units of volume per membrane surface and time) being driven by two forces, a hydrostatic and an osmotic pressure difference across the membrane (ΔP and Δπ, respectively).
| JV=LPΔP+LPDΔπ=LP(ΔP−σΔπ) | eq.1 |
Membrane properties are represented by the linear coupling coefficients, the hydraulic conductance, LP, and the osmotic coefficient, LPD. The reflection coefficient σ is defined as:
| σ=−LPDLP | eq.2 |
For more details, see Figure 1. It was Jack Dainty in his comprehensive review on water relations of plant cells [10] who familiarized plant physiologists with this new concept. The reader is referred to this study, and a later one by Zimmermann and Steudle [11] for a detailed outline of the thermodynamics of irreversible processes and its application to plant membrane transport-it is beyond the scope of this short review. For the topic discussed here, it is most important to point out that Dainty explicitly referred to a possible interaction of water and solutes while passing through the membrane. Prophetically, he suggested the existence of two separate types of membrane pores, those that exclusively transport water, and others that allow passage of both water and solutes. In the latter type, water and solute fluxes are likely to interact in a way that water transport can drive solute transport and vice versa, which can be expressed by frictional coefficients (that are, however, hard to interpret in molecular terms). Solute flow is likely to carry water across the membrane if the hydration shell of the solute is partly or fully retained, or in nanopores when one solutes pushes several water molecules moving in "single file" to the other side of the membrane; special effects have to be considered when ions move through charged pores [12]. Most importantly, water co-transported with a solute counter-acts the osmotic flow which is induced by a concentration difference of that solute across the membrane. Hence, an osmotic pressure gradient induces a smaller volume flow than a hydrostatic gradient of the same magnitude (see Figure 1 for more details). This is expressed by a reflection coefficient significantly smaller than unity. Later work that was undertaken to determine the reflection coefficient experimentally rendered values close to one, suggesting that solute-water cotransport just played a minor role in those cases. However, it has to be taken into account that cotransport of water and solutes may be of minor importance in many cases and only dominates membrane transport in special cell types, and under certain physiological conditions (see below).
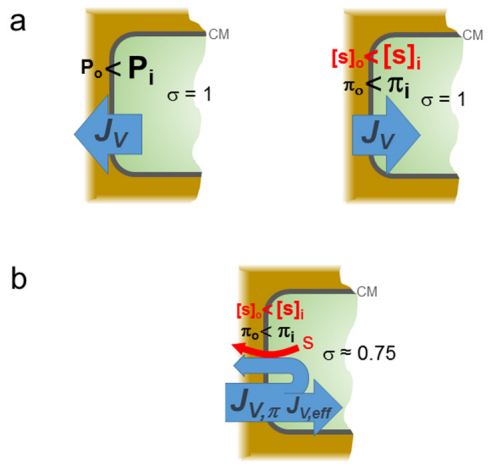 Figure 1. Schematic representation of water fluxes (blue arrows, expressed as volume flow, JV) in a simple arrangement consisting of a cell (subscript "i") separated by a single membrane (CM = cellular membrane) from the extracellular compartment (apoplast; subscript "o"). An osmotic pressure gradient across the membrane is established by a single, uncharged solute "s" that is up-concentrated inside the cell. Besides the osmotic pressure gradient, hydrostatic pressure (P) inside the cell is supposed to exceed the (usually atmospheric) pressure in the apoplast, the difference being the turgor (pressure). In a, the situation for an ideally semipermeable membrane is shown. Note that an osmotic pressure difference between the cell and the extracellular space induces the same JV as a hydrostatic pressure gradient of this magnitude, albeit in opposite direction. This is expressed by a reflection coefficient, σ, of 1. In the steady state, hydrostatic and osmotic JV would cancel each other out, and the net volume flow will be zero. In b, a situation with coupling of water and solute flux across the membrane is shown. As a consequence, part of the water being taken up by the osmotic pressure difference (JV, π) flows back into the apoplast by co-transport with the solute. Therefore, the net volume flow into the cell, JV, eff (and, in turn, the impact of the osmotic pressure difference as reflected by the coefficient LPD) is reduced. Accordingly, the reflection coefficient is below 1 (here, about 0.75). Note that for a small cell this will only be a transient scenario, since the solute gradient and, in turn, osmotic and hydrostatic pressure differences tend to dissipate rapidly. A case of sustained water secretion is shown in Figure 3.
Figure 1. Schematic representation of water fluxes (blue arrows, expressed as volume flow, JV) in a simple arrangement consisting of a cell (subscript "i") separated by a single membrane (CM = cellular membrane) from the extracellular compartment (apoplast; subscript "o"). An osmotic pressure gradient across the membrane is established by a single, uncharged solute "s" that is up-concentrated inside the cell. Besides the osmotic pressure gradient, hydrostatic pressure (P) inside the cell is supposed to exceed the (usually atmospheric) pressure in the apoplast, the difference being the turgor (pressure). In a, the situation for an ideally semipermeable membrane is shown. Note that an osmotic pressure difference between the cell and the extracellular space induces the same JV as a hydrostatic pressure gradient of this magnitude, albeit in opposite direction. This is expressed by a reflection coefficient, σ, of 1. In the steady state, hydrostatic and osmotic JV would cancel each other out, and the net volume flow will be zero. In b, a situation with coupling of water and solute flux across the membrane is shown. As a consequence, part of the water being taken up by the osmotic pressure difference (JV, π) flows back into the apoplast by co-transport with the solute. Therefore, the net volume flow into the cell, JV, eff (and, in turn, the impact of the osmotic pressure difference as reflected by the coefficient LPD) is reduced. Accordingly, the reflection coefficient is below 1 (here, about 0.75). Note that for a small cell this will only be a transient scenario, since the solute gradient and, in turn, osmotic and hydrostatic pressure differences tend to dissipate rapidly. A case of sustained water secretion is shown in Figure 3.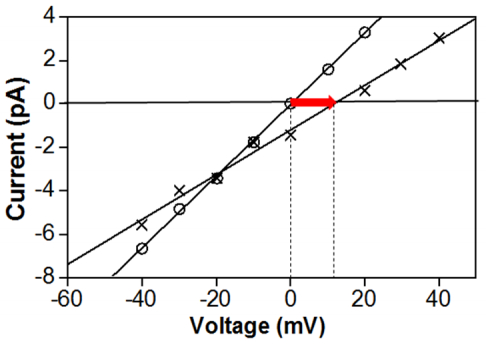 Figure 2. Current-voltage relations of the maxi 130-pS-K+ channel in cytoplasmic droplets from Chara corallina recorded in the inside-out configuration of the patch clamp technique at symmetrical 150 mM KCl concentrations. Recordings were performed before (○) and after (+) addition of 0.65 osmol kg−1 sorbitol to the bath. Note the shift of the reversal potential by~10 mV (red arrow). After [16], with permission. For more details, see text.
Figure 2. Current-voltage relations of the maxi 130-pS-K+ channel in cytoplasmic droplets from Chara corallina recorded in the inside-out configuration of the patch clamp technique at symmetrical 150 mM KCl concentrations. Recordings were performed before (○) and after (+) addition of 0.65 osmol kg−1 sorbitol to the bath. Note the shift of the reversal potential by~10 mV (red arrow). After [16], with permission. For more details, see text.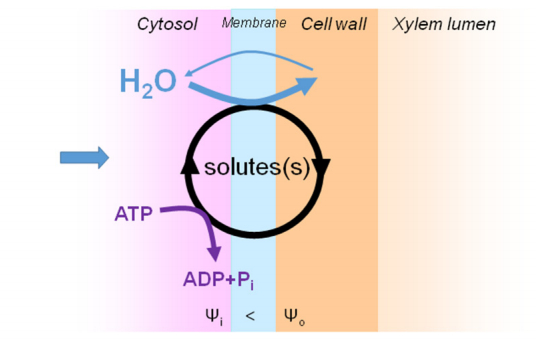 Figure 3. Basic representation of the mechanism of water secretion into the xylem against a water potential gradient as proposed by Wegner [6]. Water is co-transported with solute (s) that are released following their (electro) chemical potential gradient. The gradient is sustained by subsequent re-uptake at the expense of metabolic energy; hence, the solute (s) permanently cycle across the membrane. There will also be some back-flow of water due to the passive hydraulic conductance (LP) of the membrane, but this backflow is supposed to be smaller than water efflux by secretion. Note that secretion is only sustainable if there is an external source of water, to replenish the water loss (blue arrow at the left). In the root, this is, eventually, the soil solution. For a more detailed representation of the model, the reader is referred to Figure 1 in [6].
Figure 3. Basic representation of the mechanism of water secretion into the xylem against a water potential gradient as proposed by Wegner [6]. Water is co-transported with solute (s) that are released following their (electro) chemical potential gradient. The gradient is sustained by subsequent re-uptake at the expense of metabolic energy; hence, the solute (s) permanently cycle across the membrane. There will also be some back-flow of water due to the passive hydraulic conductance (LP) of the membrane, but this backflow is supposed to be smaller than water efflux by secretion. Note that secretion is only sustainable if there is an external source of water, to replenish the water loss (blue arrow at the left). In the root, this is, eventually, the soil solution. For a more detailed representation of the model, the reader is referred to Figure 1 in [6].This brief historical excursion has demonstrated that during the early days of membrane biophysics, water transport was considered part of a tightly coupled network of fluxes and forces, and that is was widely accepted that water and solutes could share the same pathways for trans-membrane passage. Very little was known then about the molecular nature and properties of theses pathways. Some more information is available 60 years later, but our knowledge on plant membranes is still scarce when compared to the animal world, e.g. mammalian epithelia, as described in the following sections.
When membranes of plant origin became accessible to electrical recordings with the patch clamp technique in the mid-eighties of the last century, recordings soon revealed the existence of ion channels in those membranes. By this time, it had already become clear that ion channels are not only involved in the propagation of action potentials, but can have multiple functions whenever electrolyte transport is involved, including nutrient uptake by plant cells [13]. It is important to point out here that ion channels mediate the passage of ions AND water. The latter aspect has frequently been neglected, even though it had quite early been recognized and described quantitatively [14,15,16]. Experimental strategies to determine the number of water molecules per transported ion were introduced, using porines such as gramicidine inserted into artificial lipid bilayers as "model channels". One approach is based on the measurement of "streaming potentials": At identical ion concentrations on both sides of the membrane, an osmotic gradient was imposed that drove mass flow through the pores. Ions dragged with the water flow induced an imbalance of charges that could be measured as a trans-membrane streaming potential. This approach is based on Onsager's reciprocity theorem on mutual interaction of fluxes [11]. Alternatively, electro-osmotic volume flow could be measured that was driven by imposing a voltage difference across the membrane; ion movement following the electrical gradient would drive mass flow. For gramicidin, a stoichiometry of 4 to 12 water molecules per transported ion was obtained.
Few studies on the coupling of ion and water transport in ion channels have been undertaken since then (e.g. [15]), but luckily one is available for a channel from the plant world. The 130 pS "maxi K+ channel" from the giant-celled freshwater alga Chara corallina has frequently been used for biophysical research because it can be studied with comparatively little experimental effort. It is manifest in the membrane covering "cytoplasmic droplets" that spontaneously form once these cells are cut with a razor blade. Membrane material surrounding these droplets was shown to mostly originate from the tonoplast. Homblé and Very [16] investigated interaction of water and K+ fluxes in excised patches using symmetrical 150 mM (300 mosmolal) KCl solutions and imposing an osmotic gradient by adding sorbitol at a concentration of 0.65 osmol kg−1 to the bath. As a result, the reversal potential shifted from 0 mV (as expected under symmetrical conditions) to about +10 mV (Figure 2), a shift that was interpreted as a streaming potential due to water flow dragging K+ through the pore, even against an electrochemical K+ gradient, until K+ backflow would compensate for this "solvent drag". At this voltage, the current-voltage relation would now intersect the line indicating zero net current (Figure 2). Using an equation of Levitt [17], it was calculated that at least 29 water molecules would be translocated per K+ ion. This agreed well with a previous investigation on intact Chara cells [18]. Elegantly, Homblé and Very could show that the streaming potential was largely due to flux coupling in the K+ channel pore, and not due to a local concentration gradient at the membrane surfaces induced by mass flow ("unstirred layer effect"). When Valinomycin, a K+ selective ionophore that inserts into the membrane and just translocates few water molecules together with K+ [15], was added together with sorbitol, the apparent streaming potential was negligible (about 1 mV or less).
The water-ion stoichiometry determined for the maxi K+ channel deviated from values found for gramicidin that translocates ions and water in a "single file mode". It can be concluded that the pore of this maxi K+ channel has a larger diameter and, hence, can translocate a larger volume per turnover. Water transport through the maxi K+ channel could be of physiological relevance (discussed in more detail below), although competing with aquaporins that appear to provide much more efficient pathways. Until recently, plant aquaporins were thought to be highly selective water channels (just allowing the passage of few small neutral molecules such as NH3 and CO2). However, this view is currently changing.
Aquaporins are a superfamily of membrane proteins with several subfamilies that occur with a high abundance in both plasma membrane and tonoplast (denoted accordingly as plasma membrane intrinsic proteins (PIPs) and tonoplast intrinsic proteins (TIPs), respectively. Much work has been devoted to the study of these types of membrane transporters, their molecular structure, cellular expression, regulation, and their role in plant water relations during the last 25 years, and several excellent timely reviews are available (e.g. [20,21]). Aquaporins are small proteins of 21-34 kD consisting of 6 membrane-spanning alpha-helices connected by 5 loops. Besides water, some PIPs have been shown to translocate H2O2, glycerol, and CO2. Permeability of NtPIP1 to CO2 received much interest with respect to the regulation of carbon assimilation in the leaf [21]. Likewise, TIPs not only transport water but also other small polar, neutral molecules such as NH3, glycerol and urea. In another subfamily of aquaporins, the NIPs, that are expressed in nodules of Fabaceae, transport of NH3 and other small molecules even seems to dominate the "original" role of water transport. So, it was well established for quite a while that at least some aquaporins do not exclusively serve as water channels.
Still, it was an utter surprise when Byrt et al. [22] very recently demonstrated for an aquaporin from Arabidopsis thaliana, AtPIP2.1, that this aquaporin when expressed in oocytes is permeable to water and, at the same time, exhibits typical features of non-selective cation channels, predominantly conducting Na+. In fact, AtPIP2.1 exhibited properties very reminiscent of the Nonselective Cation Channels (NSCCs) described for root epidermis cells that are active at low external Ca2+ concentrations and regulated by external pH [23,24]. These NSCCs had been detected and characterized with the patch clamp technique, but their molecular basis was hitherto unresolved. AtPIP2.2, an aquaporin with high homology, did not exhibit an ionic conductance, but showed properties of a "typical" aquaporin with a high selectivity for water. Remarkably, the ionic conductance mediated by AtPIP2.1 vanished when another aquaporin, AtPIP1.2, was co-expressed. By contrast, the hydraulic conductance was apparently retained, since AtPIP1.2 by itself did not mediate any water fluxes. Possibly, heteromeric complexes with a high selectivity for water are preferentially formed upon co-expression of both isoforms. Even though the data available on AtPIP2.1 from the publication of Byrt et al. [22] do not provide direct evidence for a coupling of solute and water fluxes yet, an interaction of fluxes seems highly likely if water and ions simultaneously pass through the same pore. Further experimental work will be required, e.g. to establish that osmotically-induced volume flow generates a streaming potential as shown for the maxi K+ channel from Chara cytoplasmic droplets (see above, [16]). Ion-conducting aquaporins that function as NSCCs have previously been described for mammalian cells (for a review, see [25]). For these "dual function channels", it has been suggested that tetramers assemble forming a central pore that primarily conducts ions, whereas water transport is mediated by each of the monomers, implying, at the first place, independent passage. However, this does not preclude interaction of fluxes via mutual effects on the gating of the monomers. This model was favoured for the human aquaporin-1 (AQP-1). Alternatively, it has been postulated that ions pass through the monomers; this could be a valid interpretation when no osmotic-driven water flow through the aquaporin is observed, such as in the Drysophila Big Brain Aquaporin. It is unclear, whether results obtained on these mammalian channels can be transferred to AtPIP2.1.
In the following, other transport proteins are introduced that could mediate solute-water cotransport, or that could potentially be sites of flux coupling in plant membranes.
Various transport proteins from animal cells mediate both solute and water flow [26,27,28,29]. One class of proteins that received much interest in this context are the cation-chloride cotransporters (CCC proteins) that are inter alia found in epithelia. When the transporter NKCC1 that translocates Na+, K+ and Cl-at a fixed stoichiometry of 1:1:2 was heterologously expressed in oocytes, cell swelling was induced by complementation of a medium that lacked one of the substrates while keeping the osmotic pressure constant, indicating that ion uptake mediated a concomitant uptake of water. Cell swelling became manifest within a second after complementation of the medium with NaCl, excluding the involvement of any unstirred layer effects that need some time to be established. Measurements of ion and water uptake suggested an uptake of 460 water molecules per turnover of the transporter. By contrast, in the same type of experiment the highly homologue isoform NKCC2 started water uptake with a delay (ca. 30 s after complementation of the external medium), indicating that water uptake was favoured indirectly by the generation of a local osmotic gradient, rather than by direct coupling of salt and water fluxes. Compelling evidence for the coupling of water and ion fluxes was also provided for the KCC that translocates KCl and H2O at a stoichiometry of 1:500 [26]. Interestingly, KCl fluxes can drive water transport even against an osmotic gradient (which corresponds, in the absence of a hydrostatic pressure difference, to transport from a lower to a higher water potential). Transporters of the CCC family have also been found in plants. The transporter AtCCC1 from Arabidopsis thaliana required both Na+ and K+ as a substrate (besides Cl-) when being heterologously expressed in oocytes [30], suggesting that it functionally resembles the NKCC type. It was highly expressed e.g. in the growth zone of roots, in root stelar tissue, in leaf hydathodes, and in stamens. CCC proteins were also characterized for rice plants [31]. Unfortunately, no information is currently available if plant CCC proteins transport water at a fixed stoichiometry with salts. Experiments similar to those performed by Zeuthen and McAuley [28] are urgently needed to answer this question.
Transporters of organic molecules have been also shown to permeate water. Prominent examples are the Na+-glucose cotransporters of the SGLT family in animal cells [32]. Per glucose molecule moving from one side of the membrane to the other, 260 water molecules are translocated. Recently, evidence was presented that glucose, Na+ and water share the same pathway when penetrating through the protein [33]. The SGLT family is not found in plants, but co-transport of H+ and sugars by transporters of the SUT type (sucrose transporters, also abbreviated as SUC) play a central role in sucrose loading into the leaf phloem [34,35]. Long-distance phloem transport from source to sink involves a mass flow in the sieve tubes, but no information on a coupling of water with sucrose/H+ transport in these membrane proteins is available from the literature. In sink tissues, phloem sucrose unloading into the apopolast is mediated by transporters of the SWEET type [36], and again no information on their water permeability is available. Amino acid transporters have also been tested with respect to their capacity to mediate water transport. Interestingly, Loo et al. [32] reported co-transport of amino acids, protons and water by the amino acid permease from Arabidopsis thaliana (AAP5) with equal numbers of H+ and amino acids being transported. Preliminary data suggested a coupling ratio of 50 water molecules per transported charge. In the future, transporters of organic molecules from plant origin should routinely be tested with respect to their water permeability, and to cotransport water and solutes at a fixed stoichiometry; it may be highly relevant for various physiological processes, as exemplified in the following section. An overview on the classes of transporters from animal cells that were "positively tested" can be obtained from Zeuthen [26]. It also encompasses the GABA transporters and dicarboxylate transporters.
So far, this review has dealt with the molecular nature of trans-membrane pathways that are potential sites of interaction for water and solute fluxes. The remaining part will be dedicated to a discussion of the physiological function of solute-water cotransport in plants. The focus will be on processes for which this type of cotransport is an essential key element. In other cases, it may just provide an advantage with respect to transport via separate pathways, e.g. to minimize the generation of unstirred layers in the vicinity of the membrane.
For decades, treatment of plant water relations followed the general consensus that water moves across membranes exclusively "passively", i.e. following the difference in the chemical potential of water (expressed, in units of pressure, by the water potential, Ѱ). However, it has repeatedly been observed e.g. for excised roots that root pressure exudation (i.e. the continuous water secretion at the cut surface when the rest of the root is immersed in a nutrient solution) continues even when the exudate is more dilute than the external medium [37,38]. These findings provide evidence for the existence of a non-osmotic "active" component of water transport [37,39]. Elaborating on this earlier work, Wegner [6,7,8] suggested a new mechanism for the generation of root and stem pressure, and refilling of embolized xylem vessels, that included "secondary active" water secretion by the cells bordering on the conducting dead xylem elements. By a cotransport of water with salts, e.g. KCl, with sugars, or with amino acids, the free energy released by an efflux of these solutes from xylem parenchyma cells (XPCs) could be exploited to drive water transport against a water potential gradient across the cellular membrane (Figure 3). According to the model, solutes released by xylem parenchyma cells are subsequently retrieved from the xylem sap at the expense of metabolic energy to maintain the concentration gradient that drives water transport. This model was inspired by previous work on water secretion by mammalian epithelia, e.g. the choroid plexus epithelium [26,28]. Importantly, the model explains how a water potential difference can be maintained between a cell and its environment. Note that such a system operates far from thermodynamic equilibrium, for which ATPase activity in the plasma membrane is constantly required (Figure 3). Wegner [6] favoured CCC proteins as key element for energizing water transport from xylem parenchyma cells into xylem vessels, since CCC proteins are preferentially expressed in root xylem parenchyma cells, and K+ and Cl- gradients between symplast and apoplast in the stele would provide sufficient free energy to fuel water secretion [7,40]. However, two points have recently been raised against this model:
(ⅰ) For playing a key role in water secretion as proposed by Wegner [6], a localization of CCC proteins in the plasma membrane (PM) would be mandatory. However, Henderson et al. [41] investigated the subcellular localization of AtCCC and VviCCC, a transporter identified in grapevine, and came to the conclusion that these transporters are predominantly located in the trans-golgi network rather than in the PM (even though close inspection of their Figure 2 suggests that a minor fraction of the protein may also be located there as judged from the detection of optical markers). The subcellular distribution found by Henderson et al. may not reflect a permanent absence of the transporter from the PM, but rather a temporal internalization. In fact, the trans-golgi network should be considered a "standby-site" that allows rapid trafficking of a membrane protein to the PM if required. Water secretion would not be permanently active but only operate under special physiological conditions (still to be elucidated), implying that otherwise cells would function in the "normal mode" with water fluxes following water potential gradients. In this mode, transporters particularly involved in water secretion may be internalized, and aquaporins exclusively transporting water may be directed to the plasma membrane. Interestingly, cycling of aquaporins between endomembranes and the plasma membrane has been demonstrated in plants [42]. In animal cells, intracellular circulation of cotransporters of the SGLT type involved in water secretion is a common feature [43]. Consistently, Henderson et al. also mention a study [44] that indicated PM localization of CCC transporters (see also [31]). Circumstantial evidence for (at least temporal) PM-localization is also provided by the finding that long-distance ion transport in Arabidopsis and Vitis vinifera was affected in CCC knockdown mutants [28,40]. Henderson et al. argue that CCC proteins may be involved in vesicular shuttling of solutes that originate from the vacuole and are released into the stelar apoplast by exocytosis. Indeed, such a mechanism has been suggested for plants before [45]. However, solute release by exocytosis would be quite inefficient if vesicles contained ions in concentrations found e.g. in the vacuolar sap. An up-concentration in the vesicular lumen with respect to the surrounding cytosol could be achieved by export of salt and water via CCC proteins and subsequent re-uptake of the salts (without the water) by different pathways, energized by the V-ATPase located in the vesicular membrane [46]. At a steady state water influx driven by the osmotic gradient would match water efflux by cotransport. Further experimental work will reveal if such a mechanism of salt exocytosis is feasible, or, alternatively, if conditions can be found that direct a significant fraction of CCC proteins to the PM. Apart from that, it should be noted that the hypothesis of Wegner [6] is by no means exclusively bound to a central role of CCC proteins in solute-water cotransport; potentially, other types of transporters could take over the same function in plants. As stated above, ion channels could serve as pathways for coupled ion and water transport by an electro-osmotic mechanism, with flow being driven by an electrochemical potential difference. Ion release and subsequent retrieval need to occur sequentially coordinated by oscillations of the membrane potential (see Figure 2 in [6])-of course the stoichiometries of ion-water coupling need to differ significantly between ion uptake and release to induce net water transport. Further interesting candidates are aquaporins with dual functions introduced by Byrt et al. [22]. Their data point to a fascinating option how membranes could switch between a "secretory" and a "passive" mode: While AtPIP2.1 provides a pathway for both water and cation transport, co-expression with the "silent" isoform AtPIP1.2 leads to a loss of cation transport function, and to an increase in water permeability of the oocyte. Consistent with Wegner's [6] hypothesis, solute-water cotransport and pores only supporting water transport are regulated antagonistically. For water secretion, down-regulation of the hydraulic conductance is a prerequisite to minimize futile water cycling which is associated with high energetic costs (see the following paragraph).
(ⅱ) In two recent publications, Fricke has scrutinized the energetics of putative water secretion for the generation of root pressure. Initially he stated [40] that water transport into xylem vessels according to the model of Wegner [6] would be feasible from a thermodynamic point of view, and, more so, energetically favourable, since for barley seedlings only 0.12% of the total free energy provided by photosynthesis would be required even if all the transpirational water was delivered by a secretory mechanism. However, in a more recent publication [47] he considered the hypothesis to be "highly unlikely" since aquaporin activity in the PM of xylem parenchyma cells would tend to short-circuit water secretion by a cotransport mechanism, and the proton pump in xylem parenchyma cells could not provide sufficient energy to keep up with the passive backflow once the water potential difference between xylem parenchyma cells and the xylem would exceed about 1 kPa. His calculations are in sharp contrast with those of Wegner [7] who stated that water secretion into the xylem would critically affect the energy budget of the root, but would be energetically feasible. A comparison of the calculations by both authors reveals that they differ with respect to the following assumptions: Firstly, Fricke's calculations are based on a constantly high hydraulic conductance of the plasma membrane of 10-6 m s−1 MPa−1, whereas Wegner assumes that water secretion is associated with a down-regulation of aquaporin activity in xylem parenchyma cells so that the hydraulic conductivity drops to values between 10-7 and 10-8 m s−1 MPa−1. Secondly, both authors use different approaches to quantify the free energy provided by the proton pump. Fricke calculated the free energy difference across the membrane per mol H+, ΔG, which is maintained by the H+ ATPase, from the PMF according to
| ΔG=−n∗F∗PMF | eq.3 |
with
| PMF=MP−2.303∗R∗TFΔpH | (in mV) |
F is the Faraday constant (96.49 kJ mol−1 V−1), n is the number of charges carried by the ion (here n = 1), MP is the membrane potential, and R and T are the gas constant and absolute temperature, respectively. The energy consumption with time, dG/dt, is then calculated by multiplying ΔG by the trans-membrane proton flux generated by the pump. Based on literature data, a value of ‑200 mV was chosen for the PMF by Fricke [47]. However, in a biological membrane the steady state PMF is a result of proton pump activity AND of concomitant energy dissipation by transport processes fuelled by the H+ ATPase, e.g. ion transport driven by the H+ gradient and/or by the membrane potential (that would also be involved in secondary active water transport). Keeping this in mind, eq. 3 seems inappropriate to quantify the total free energy provided by the proton pump. Instead, Wegner [7] calculated the free energy released by ATP hydrolysis, which is available for membrane transport processes, according to
| ΔGATP=RT[ln([Pi]KATP)+ln([ADP]ATP)] | eq.4 |
KATP is the equilibrium constant of ATP hydrolysis; [ATP], [ADP] and [Pi] are the cytosolic concentrations of ATP, ADP and ortho-phosphate, respectively. ATP consumption with time, dnATPdt, is obtained from the pump-driven proton flux, taking the coupling factor λ that relates H+ transport to ATP hydrolysis ("H+/ATP stoichiometry") into account (about 0.8; [48]):
| dnATPdt=−JH+λ | eq.5 |
The energy release with time, dG/dt, is then calculated by multiplying dnATPdt by ΔGATP. With a [Pi] of 1.5 mM, a KATP, of 2.24 × 10-5 mol l−1, and an ADP/ATP ratio of 0.13, ΔGATP amounts to ‑50.8 kJ mol−1 (see [7] for more details), whereas Fricke, using eq. 3, obtained a value for ΔG of just-19.3 kJ mol−1 for the energy invested into membrane transport. Admittedly, eqs 4 and 5 provide us with an upper limit with respect to the energization of the plasma membrane, since a fraction of the energy provided by ATP hydrolysis will be dissipated as heat, being unavailable for transport. However, given the energetic efficiency of biochemical reactions, this will only be a small share.
Water secretion may also be relevant for the refilling of embolized xylem vessels [49,50]. For embolism repair, water is shifted from adjacent cells into (partly) gas-filled vessels; by generating a hydrostatic over-pressure, the gas is dissolved or expelled. The osmotic pressure of the residual xylem sap in these vessels appears to be insufficient in many cases to initiate the refilling process, highlighting the necessity for an alternative mechanism. Moreover, radial water transport can be very fast [51] and may therefore be incompatible with a shift of osmotica preceding passive water transport. The same problem is encountered with fast turgor-driven movements in plants.
Turgor-driven nastic movements in plants have fascinated botanists since the times of Darwin, but research has largely remained on a phenomenological and anatomical level. Only few efforts have been undertaken to study the molecular basis of rapid turgor changes (within a few seconds at most) in pulvini that underlie movements of leafs and leaflets e.g. in Mimosaceae (other movements like the closing of the Venus flytrap may be even more rapid and spectacular, but also involve mechanisms other than changes in turgor and are therefore not considered here). Pulvini function as a kind of hinge, consisting of a flexor (upper part) and an extensor (lower part), that contract and expand antagonistically. This is due to a rapid change in volume and shape of "motor cells". It is frequently believed that pulvini act as "osmotic machines", and that water is re-distributed between flexor and extensor following shifts of osmotica (in particular, potassium salts). However, Morillon et al [52] pointed out that solute fluxes would be rate-limiting in such a process, and, moreover, would be much too slow to explain its rapid kinetics (movements can occur within about a second). They proposed an alternative hypothesis with cotransport of salt and water (mediated by CCC proteins) playing a key role. According to this hypothesis, turgor (and associated cell swelling) is generated by water uptake that is energized by solute transport, e.g. KCl and/or NaCl. Subsequent solute back-transport to maintain the solute gradient is not explicitely mentioned, but it is clear from their presentation of the model that an osmotically unbalanced turgor surplus is established in the motor cell, i.e. a water potential difference between the cell and its environment is maintained. A sudden turgor loss underlying fast leaf (let) movements is achieved by a prompt activation of aquaporins that mediate a fast efflux of water, and subsequent shrinking of the motor cell. Most importantly, with this mechanism the time course of the movement depends on the kinetics of water flux across the motor cell membranes, with no acute osmotic shift being involved. Water transport would indeed be fast enough to provide an explanation of the fast movements. The hypothesis of Morillon et al [52] still awaits rigorous testing, but some observations seem to be in accordance with its predictions: Consistently, Tomos and Pritchard [53] had found for pulvini of Phaseolus that during rapid changes in turgor, osmotic pressures of the cell sap remained unaffected (however, they postulate local osmotic changes in the apoplast (i.e. at the external membrane surface) to control the direction of trans-membrane water fluxes, rather than considering the possibility of a water potential difference across the plasma membrane). Moreover, aquaporins have indeed been found in motor cells [54]. Unfortunately, no direct evidence for solute-water cotransport has yet been obtained for these cells.
Recently, it has been suggested that solute-water cotransport could play a key role in the regulation of plant cell growth [9]. In addition to a passive mechanism of water transport across the plasma membrane of growing cells mediated by aquaporins ("leak") a secondary active water transport ("pump") is postulated in analogy to the mechanism previously demonstrated for mammalian epithelia and suggested for the generation of root pressure (see above). Water is hypothesized to be secreted (transferred into the apoplast) against a trans-membrane water potential difference by cotransport with solutes (salts, sugars, and/or amino acids), taking advantage of the free energy released by this transport step. The solute concentration gradient is supposed to be maintained by a subsequent retrieval of the solutes from the apoplast and back-transport at the expense of metabolic energy (Figure 4), leading to a circulation of the solute across the membrane much as hypothesized above for the generation of root pressure. Extending Lockhart's classical model [55], the relative growth rate (RGR) is then described quantitatively by the following equation:
| RGR=ϕ(JV,CTLP+Δπ−Y)) | eq.6 |
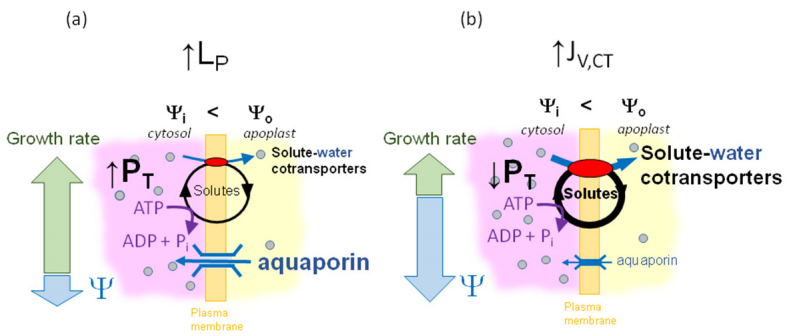 Figure 4. The pump/leak model of cell elongation in the growth zone e.g. of grass roots and leaves according to [9]. Note that cell turgor (PT) and, in turn, growth rate are varied at a constant osmotic gradient across the membrane. Growing cells are frequently characterized by a relatively large water potential deficit; Ѱ is~0.15 to 0.4 MPa lower compared to adjacent non-growing cells. An increase of membrane LP by de-novo synthesis or activation of aquaporins (a) leads to a decrease in the cellular water potential deficit (i.e., a less negative water potentials) and an increase in PT and in growth, whereas an increase in solute-water cotransport (JV, CT) (b) entails a down-regulation of PT and growth, associated with an increase in the water potential deficit. Note that only hydraulic effects are considered, and modulation of cell wall properties is not taken into account. From [9], with permission.
Figure 4. The pump/leak model of cell elongation in the growth zone e.g. of grass roots and leaves according to [9]. Note that cell turgor (PT) and, in turn, growth rate are varied at a constant osmotic gradient across the membrane. Growing cells are frequently characterized by a relatively large water potential deficit; Ѱ is~0.15 to 0.4 MPa lower compared to adjacent non-growing cells. An increase of membrane LP by de-novo synthesis or activation of aquaporins (a) leads to a decrease in the cellular water potential deficit (i.e., a less negative water potentials) and an increase in PT and in growth, whereas an increase in solute-water cotransport (JV, CT) (b) entails a down-regulation of PT and growth, associated with an increase in the water potential deficit. Note that only hydraulic effects are considered, and modulation of cell wall properties is not taken into account. From [9], with permission.With ϕ being the "extensibility" (characterizing rheological properties of the cell wall), JV, CT being the volume flow driven by cotransport with solutes, and Y being a threshold hydrostatic pressure required to initiate cell elongation. The "pump/leak" model of growth can account for two experimental observations that the classical model which is solely based on an osmotic mechanism for the uptake of growth water fails to explain. Theoretical considerations suggest that the cell elongation rate in root cells should be under control of the rheological properties of the cell wall, whereas LP should not be rate-limiting for growth, at least not in roots grown under hydroponic conditions [56]. Consistent with the notion that water should be readily accessible, no radial nor axial turgor pressure gradients have been observed in the root elongation zone. Nevertheless, a dependence of the growth rate on LPand aquaporin expression has frequently been observed [57,58]. Moreover, considerable water potential deficits have been reported for growing tissues (summarized in [9]). A minor water potential difference with respect to non-growing tissue is required to provide growing cells with the necessary growth water, but water potentials deficits reported in the literature are incompatible with the measured growth rates and with the hydraulic conductance of the cellular membrane when the data are interpreted according to Lockhart's model [55]. Considerable negative water potentials on growing cells would, however, be predicted by the pump/leak model.
Water secretion tends to reduce the turgor pressure and to retard growth. The benefit of growth regulation according to the pump/leak model is that turgor and, in turn, the growth rate could be up-regulated very rapidly. Remarkably, this could occur, without any adjustment in the osmolyte deposition rate, just by increasing aquaporin activity and, hence, LP and/or by reducing secondary active water transport, e.g. when the root is exposed to mild osmotic stress (Figure 4), as confirmed by experimental studies.
Plant cells can be exposed to considerable osmotic perturbations that have a direct impact on the turgor pressure; this is not only relevant for cell elongation, but also for the mechanical stability of the plant, and mechanisms for stabilizing the turgor are required. Effects of varying osmotic conditions can be even more severe in the absence of a stable cell wall; in this case, volume regulation is required to prevent rupture or extreme shrinkage of the cell. For unicellular freshwater alga lacking a stable cell wall, or flagellate algae such as Chlamydomonas, Raven and Doblin [5] argued that the cellular sap is always more concentrated than the ambient freshwater and, hence, a water potential gradient across the cellular membrane has to be maintained permanently to prevent rupture. This would require continuous uphill water pumping to out-balance osmotic water uptake, involving a cotransport of water and solutes as proposed by Wegner [6]. In case of Chlamydomonas, such a mechanism should be associated with the contractile vacuole that serves this function (see also Zeuthen [59]), but the molecular mechanism of operation of this vacuole is still unknown.
Of course solute-water cotransport is not necessarily involved in secondary active water transport, but could also operate in accordance with the classical concept of plant water relations. For hypo-osmotic turgor regulation in higher plant cells, e.g., solute efflux for turgor regulation may be most efficient when water is co-transported, instead of water and solutes taking different pathways across the membrane [22].
Zonation of phytoplankton is an important issue in marine biology. The depth of algal habitats varies with the season, and with nutritional constraints. This requires an adjustment of the density of the intracellular (vacuolar) sap. Raven and Doblin [5] suggested that density and, hence, vertical motion of marine algae may be adjusted by secondary active water transport. In particular, accumulation of dense material such as macromolecules would induce sinking of the algae. This could be prevented by water extrusion with a secondary active water transport, involving salt-water cotransport [5]. Consistently, it was found that marine algae may not be at a water potential equilibrium with their environment. It should be noted that both the plasma membrane and the tonoplast could be the site at which a gradient in water potential is maintained.
Many loose ends have been presented here, and further areas of research have been identified, instead of providing the reader with validated information. Clearly, more research on the molecular basis of solute-water cotransport across (plant) membranes, and on its physiological function is required in the near future. So this review ends with a general plea: As a rule, each solute transporter should routinely be tested with respect to its water transport capacity!
The author declares no conflicts of interest in this paper.
| [1] |
Poole RJ (1978) Energy coupling for membrane transport. Annu Rev Plant Physiol 29: 437–460. doi: 10.1146/annurev.pp.29.060178.002253

|
| [2] |
Williams LE, Lemoine R, Sauer N (2000) Sugar transporters in higher plants-a diversity of roles and complex regulation. Trends Plant Sci 5: 283–290. doi: 10.1016/S1360-1385(00)01681-2

|
| [3] |
Bush DR (1993) Proton-coupled sugar and amino acid transporters in plants. Annu Rev Plant Biol 44: 513–542. doi: 10.1146/annurev.pp.44.060193.002501

|
| [4] |
Wright EM, Turk E (2004) The sodium/glucose cotransport family SLC5. Pflüg Arch 447: 510–518. doi: 10.1007/s00424-003-1063-6

|
| [5] |
Raven JA, Doblin MA (2014) Active water transport in unicellular algae: where, why, and how. J Exp Bot 65: 6279–6292. doi: 10.1093/jxb/eru360

|
| [6] |
Wegner LH (2014) Root pressure and beyond: energetically uphill water transport into xylem vessels? J Exp Bot 65: 381–393. doi: 10.1093/jxb/ert391

|
| [7] |
Wegner LH (2015) A thermodynamic analysis of the feasibility of water secretion into xylem vessels against a water potential gradient. Funct Plant Biol 42: 828–835. doi: 10.1071/FP15077

|
| [8] | Wegner LH, (2015) Interplay of water and nutrient transport: A whole-plant perspective, In: Lüttge U, Beyschlag W, Progress in Botany, Springer, 109–141. |
| [9] |
Wegner LH (2017) A pump/leak model of growth: the biophysics of cell elongation in higher plants revisited. Funct Plant Biol 44: 185–197. doi: 10.1071/FP16184

|
| [10] |
Dainty J (1963) Water relations of plant cells. Adv Bot Res 1: 279–326. doi: 10.1016/S0065-2296(08)60183-4

|
| [11] | Zimmermann U, Steudle E (1978) Physical aspects of water relations of plant cells. Adv Bot Res 6: 45–117. |
| [12] |
Dainty J, Croghan PC, Fensom DS (1963) Electro-osmosis, with some applications to plant physiology. Can J Bot 41: 953–966. doi: 10.1139/b63-079

|
| [13] |
Tyerman SD, Schachtman DP (1992) The role of ion channels in plant nutrition and prospects for their genetic manipulation. Plant Soil 146: 137–144. doi: 10.1007/BF00012006

|
| [14] |
Rosenberg PA, Finkelstein A (1978) Interaction of ions and water in gramicidin A channels: streaming potentials across lipid bilayer membranes. J Gen Physiol 72: 327–340. doi: 10.1085/jgp.72.3.327

|
| [15] | Alcayaga C, Cecchi X, Alvarez O, et al. (1989) Streaming potential measurements in Ca2+-activated K+ channels from skeletal and smooth muscle. Coupling of ion and water fluxes. Biophys J 55: 367–371. |
| [16] |
Homblé F, Véry AA (1992) Coupling of water and potassium ions in K channels of the tonoplast of Chara. Biophys J 63: 996–999. doi: 10.1016/S0006-3495(92)81666-1

|
| [17] |
Levitt DG (1990) Streaming potential: Continuum expression applicable to very small nonuniform ion channels. J Chem Phys 92: 6953–6957. doi: 10.1063/1.458282

|
| [18] |
Barry PH, Hope AB (1969) Electro-osmosis in Chara and Nitella cells. Biochim Biophys Acta BBA-Biomembr 193: 124–128. doi: 10.1016/0005-2736(69)90065-0

|
| [19] |
Maurel C, Boursiac Y, Luu DT, et al. (2015) Aquaporins in plants. Physiol Rev 95: 1321–1358. doi: 10.1152/physrev.00008.2015

|
| [20] |
Chaumont F, Tyerman SD (2014) Aquaporins: highly regulated channels controlling plant water relations. Plant Physiol 164: 1600–1618. doi: 10.1104/pp.113.233791

|
| [21] |
Uehlein N, Lovisolo C, Siefritz F, et al. (2003) The tobacco aquaporin NtAQP1 is a membrane CO2 pore with physiological functions. Nature 425: 734–737. doi: 10.1038/nature02027

|
| [22] | Byrt CS, Zhao M, Kourghi M, et al. (2016) Non-selective cation channel activity of aquaporin AtPIP2; 1 regulated by Ca2+ and pH. Plant Cell Environ. Available from: http://onlinelibrary.wiley.com/doi/10.1111/pce.12832/full. |
| [23] |
Roberts SK, Tester M (1997) A patch clamp study of Na+ transport in maize roots. J Exp Bot 48: 431–440. doi: 10.1093/jxb/48.Special_Issue.431

|
| [24] |
Demidchik V, Tester M (2002) Sodium fluxes through nonselective cation channels in the plasma membrane of protoplasts from Arabidopsis roots. Plant Physiol 128: 379–387. doi: 10.1104/pp.010524

|
| [25] |
Yool AJ, Campbell EM (2012) Structure, function and translational relevance of aquaporin dual water and ion channels. Mol Aspects Med 33: 553–561. doi: 10.1016/j.mam.2012.02.001

|
| [26] |
Zeuthen T (2010) Water-transporting proteins. J Membr Biol 234: 57–73. doi: 10.1007/s00232-009-9216-y

|
| [27] |
Meinild AK, Klaerke DA, Loo DDF, et al. (1998) The human Na+-glucose cotransporter is a molecular water pump. J Physiol 508: 15–21. doi: 10.1111/j.1469-7793.1998.015br.x

|
| [28] |
Zeuthen T, MacAulay N (2012) Cotransport of water by Na+-K+-2Cl– cotransporters expressed in Xenopus oocytes: NKCC1 versus NKCC2. J Physiol 590: 1139–1154. doi: 10.1113/jphysiol.2011.226316

|
| [29] |
Loo DD, Hirayama BA, Meinild AK et al. (1999) Passive water and ion transport by cotransporters. J Physiol 518: 195–202. doi: 10.1111/j.1469-7793.1999.0195r.x

|
| [30] |
Colmenero-Flores JM, Martínez G, Gamba G, et al. (2007) Identification and functional characterization of cation-chloride cotransporters in plants. Plant J Cell Mol Biol 50: 278–292. doi: 10.1111/j.1365-313X.2007.03048.x

|
| [31] |
Kong XQ, Gao XH, Sun W, et al. (2011) Cloning and functional characterization of a cation-chloride cotransporter gene OsCCC1. Plant Mol Biol 75: 567–578. doi: 10.1007/s11103-011-9744-6

|
| [32] |
Loo DD, Zeuthen T, Chandy G, Wright EM (1996) Cotransport of water by the Na+/glucose cotransporter. Proc Natl Acad Sci 93: 13367–13370. doi: 10.1073/pnas.93.23.13367

|
| [33] | Zeuthen T, Gorraitz E, Her K, et al. (2016) Structural and functional significance of water permeation through cotransporters. Proc Natl Acad Sci 113: E6887–E6894. |
| [34] | Sauer N (2007) Molecular physiology of higher plant sucrose transporters. Febs Lett 581(12): 2309–2317. |
| [35] |
Geiger D (2011) Plant sucrose transporters from a biophysical point of view. Mol Plant 4: 395–406. doi: 10.1093/mp/ssr029

|
| [36] |
Chen LQ, Qu XQ, Hou BH, et al. (2012) Sucrose efflux mediated by SWEET proteins as a key step for phloem transport. Science 335: 207–211. doi: 10.1126/science.1213351

|
| [37] |
Oertli JJ (1966) Active water transport in plants. Physiol Plant 19: 809–817. doi: 10.1111/j.1399-3054.1966.tb07067.x

|
| [38] | Pickard WF (2003) The riddle of root pressure. II. Root exudation at extreme osmolalities. Funct Plant Biol 30: 135–141. |
| [39] | Zholkevich VN, (1991) Root pressure, In: Waisel Y, Eshel A, Kafkafi U, Plant roots, the hidden half Marcel-Dekker, New York, 589–603. |
| [40] |
Fricke W (2015) The significance of water co-transport for sustaining transpirational water flow in plants: a quantitative approach. J Exp Bot 66: 731–739. doi: 10.1093/jxb/eru466

|
| [41] | Henderson SW, Wege S, Qiu J, et al. (2015) Grapevine and Arabidopsis cation-chloride cotransporters localize to the golgi and trans-golgi network and indirectly influence long-distance ion transport and plant salt tolerance. Plant Physiol 169: 2215–2229. |
| [42] |
Boursiac Y, Boudet J, Postaire O, et al. (2008) Stimulus-induced downregulation of root water transport involves reactive oxygen species-activated cell signalling and plasma membrane intrinsic protein internalization. Plant J 56: 207–218. doi: 10.1111/j.1365-313X.2008.03594.x

|
| [43] |
Hirsch JR, Loo DD, Wright EM (1996) Regulation of Na+/glucose cotransporter expression by protein kinases in Xenopus laevis oocytes. J Biol Chem 271: 14740–14746. doi: 10.1074/jbc.271.25.14740

|
| [44] |
Benschop JJ, Mohammed S, O'Flaherty M, et al. (2007) Quantitative phosphoproteomics of early elicitor signaling in Arabidopsis. Mol Cell Proteomics 6: 1198–1214. doi: 10.1074/mcp.M600429-MCP200

|
| [45] |
MacRobbie EAC (1999) Vesicle trafficking: a role in trans-tonoplast ion movements? J Exp Bot 50: 925–934. doi: 10.1093/jxb/50.Special_Issue.925

|
| [46] |
Brüx A, Liu TY, Krebs M, Stierhof YD, et al. (2008) Reduced V-ATPase activity in the trans-Golgi network causes oxylipin-dependent hypocotyl growth inhibition in Arabidopsis. Plant Cell 20: 1088–1100. doi: 10.1105/tpc.108.058362

|
| [47] | Fricke W (2016) Water transport and energy. Plant Cell Environ. Available from: http://onlinelibrary.wiley.com/doi/10.1111/pce.12848/full. |
| [48] | Briskin DP, Reynolds-Niesman I (1991) Determination of H+/ATP stoichiometry for the plasma membrane H+-ATPase from red beet (Beta vulgaris L.) storage tissue. Plant Physiol 95: 242–250. |
| [49] |
Kaufmann I, Schulze-Till T, Schneider HU, et al. (2009) Functional repair of embolized vessels in maize roots after temporal drought stress, as demonstrated by magnetic resonance imaging. New Phytol 184: 245–256. doi: 10.1111/j.1469-8137.2009.02919.x

|
| [50] | Bentrup FW (2016) Water ascent in trees and lianas: the cohesion-tension theory revisited in the wake of Otto Renner. Protoplasma 254: 627–633. |
| [51] | Ryu J, Hwang BG, Lee SJ (2016) In vivo dynamic analysis of water refilling in embolized xylem vessels of intact Zea mays leaves. Ann Bot 118: 1033–1042. |
| [52] |
Morillon R, Liénard D, Chrispeels MJ, et al. (2001) Rapid movements of plants organs require solute-water cotransporters or contractile proteins. Plant Physiol 127: 720–723. doi: 10.1104/pp.010732

|
| [53] |
Tomos D, Pritchard J (1994) Biophysical and biochemical control of cell expansion in roots and leaves. J Exp Bot 45: 1721–1731. doi: 10.1093/jxb/45.Special_Issue.1721

|
| [54] |
Moshelion M, Becker D, Biela A, et al. (2002) Plasma Membrane aquaporins in the motor cells of samanea saman diurnal and circadian regulation. Plant Cell 14: 727–739. doi: 10.1105/tpc.010351

|
| [55] |
Lockhart JA (1965) An analysis of irreversible plant cell elongation. J Theor Biol 8: 264–275. doi: 10.1016/0022-5193(65)90077-9

|
| [56] |
Pritchard J (1994) The control of cell expansion in roots. New Phytol 127: 3–26. doi: 10.1111/j.1469-8137.1994.tb04255.x

|
| [57] |
Hukin D, Doering-Saad C, Thomas C, et al. (2002) Sensitivity of cell hydraulic conductivity to mercury is coincident with symplasmic isolation and expression of plasmalemma aquaporin genes in growing maize roots. Planta 215: 1047–1056. doi: 10.1007/s00425-002-0841-2

|
| [58] |
Ding L, Gao C, Li Y, et al. (2015) The enhanced drought tolerance of rice plants under ammonium is related to aquaporin (AQP). Plant Sci 234: 14–21. doi: 10.1016/j.plantsci.2015.01.016

|
| [59] | Zeuthen T (1996) Molecular mechanisms of water transport (RG Landes Compagny) Austin, Tx, USA. |
| 1. | Stephen D. Tyerman, Rana Munns, Wieland Fricke, Borjana Arsova, Bronwyn J. Barkla, Jayakumar Bose, Helen Bramley, Caitlin Byrt, Zhonghua Chen, Timothy D. Colmer, Tracey Cuin, David A. Day, Kylie J. Foster, Matthew Gilliham, Sam W. Henderson, Tomoaki Horie, Colin L. D. Jenkins, Brent N. Kaiser, Maki Katsuhara, Darren Plett, Stanley J. Miklavcic, Stuart J. Roy, Francisco Rubio, Sergey Shabala, Megan Shelden, Kathleen Soole, Nicolas L. Taylor, Mark Tester, Michelle Watt, Stefanie Wege, Lars H. Wegner, Zhengyu Wen, Energy costs of salinity tolerance in crop plants, 2019, 221, 0028646X, 25, 10.1111/nph.15555 | |
| 2. | Victoria Vitali, Moira Sutka, Lucas Ojeda, Ricardo Aroca, Gabriela Amodeo, Root hydraulics adjustment is governed by a dominant cell-to-cell pathway in Beta vulgaris seedlings exposed to salt stress, 2021, 306, 01689452, 110873, 10.1016/j.plantsci.2021.110873 | |
| 3. | Tetsuya Ishikawa, Tracey Ann Cuin, Nadia Bazihizina, Sergey Shabala, 2018, 87, 9780128093900, 267, 10.1016/bs.abr.2018.09.006 | |
| 4. | Lars H. Wegner, Sergey Shabala, Biochemical pH clamp: the forgotten resource in membrane bioenergetics, 2020, 225, 0028-646X, 37, 10.1111/nph.16094 | |
| 5. | Park S. Nobel, 2020, 9780128191460, 117, 10.1016/B978-0-12-819146-0.00003-1 | |
| 6. | Borjana Arsova, Kylie J. Foster, Megan C. Shelden, Helen Bramley, Michelle Watt, Dynamics in plant roots and shoots minimize stress, save energy and maintain water and nutrient uptake, 2020, 225, 0028-646X, 1111, 10.1111/nph.15955 | |
| 7. | Thorsten Knipfer, Mathieu Danjou, Charles Vionne, Wieland Fricke, Salt stress reduces root water uptake in barley ( Hordeum vulgare L.) through modification of the transcellular transport path , 2021, 44, 0140-7791, 458, 10.1111/pce.13936 | |
| 8. | Kylie J. Foster, Stanley J. Miklavcic, A Comprehensive Biophysical Model of Ion and Water Transport in Plant Roots. III. Quantifying the Energy Costs of Ion Transport in Salt-Stressed Roots of Arabidopsis, 2020, 11, 1664-462X, 10.3389/fpls.2020.00865 | |
| 9. | Rana Munns, David A. Day, Wieland Fricke, Michelle Watt, Borjana Arsova, Bronwyn J. Barkla, Jayakumar Bose, Caitlin S. Byrt, Zhong‐Hua Chen, Kylie J. Foster, Matthew Gilliham, Sam W. Henderson, Colin L. D. Jenkins, Herbert J. Kronzucker, Stanley J. Miklavcic, Darren Plett, Stuart J. Roy, Sergey Shabala, Megan C. Shelden, Kathleen L. Soole, Nicolas L. Taylor, Mark Tester, Stefanie Wege, Lars H. Wegner, Stephen D. Tyerman, Energy costs of salt tolerance in crop plants, 2020, 225, 0028-646X, 1072, 10.1111/nph.15864 | |
| 10. | Sam Henderson, Stefanie Wege, Matthew Gilliham, Plant Cation-Chloride Cotransporters (CCC): Evolutionary Origins and Functional Insights, 2018, 19, 1422-0067, 492, 10.3390/ijms19020492 | |
| 11. | Kylie J. Foster, Stanley J. Miklavcic, A Comprehensive Biophysical Model of Ion and Water Transport in Plant Roots. II. Clarifying the Roles of SOS1 in the Salt-Stress Response in Arabidopsis, 2019, 10, 1664-462X, 10.3389/fpls.2019.01121 | |
| 12. | Lars H. Wegner, 2019, Chapter 4, 978-3-030-06127-2, 75, 10.1007/978-3-030-06128-9_4 | |
| 13. | Vadim Volkov, Heiner Schwenke, A Quest for Mechanisms of Plant Root Exudation Brings New Results and Models, 300 Years after Hales, 2020, 10, 2223-7747, 38, 10.3390/plants10010038 | |
| 14. | Franck Michaël Zahui, Jean-Marie Pétémanagnan Ouattara, Mahamadou Kamagaté, Lacina Coulibaly, Alexandros I. Stefanakis, Effect of Plant Species on the Performance and Bacteria Density Profile in Vertical Flow Constructed Wetlands for Domestic Wastewater Treatment in a Tropical Climate, 2021, 13, 2073-4441, 3485, 10.3390/w13243485 | |
| 15. | Francisco Jose Valenzuela, Daniela Reineke, Dante Leventini, Christopher Cody Lee Chen, Edward G Barrett-Lennard, Timothy D Colmer, Ian C Dodd, Sergey Shabala, Patrick Brown, Nadia Bazihizina, Plant responses to heterogeneous salinity: agronomic relevance and research priorities, 2022, 129, 0305-7364, 499, 10.1093/aob/mcac022 | |
| 16. | Stephen D. Tyerman, Samantha A. McGaughey, Jiaen Qiu, Andrea J. Yool, Caitlin S. Byrt, Adaptable and Multifunctional Ion-Conducting Aquaporins, 2021, 72, 1543-5008, 703, 10.1146/annurev-arplant-081720-013608 | |
| 17. | Mayank Chugh, Akankshi Munjal, Sean G. Megason, Hydrostatic pressure as a driver of cell and tissue morphogenesis, 2022, 131, 10849521, 134, 10.1016/j.semcdb.2022.04.021 | |
| 18. | Sam W. Henderson, Saeed Nourmohammadi, Maria Hrmova, Protein Structural Modeling and Transport Thermodynamics Reveal That Plant Cation–Chloride Cotransporters Mediate Potassium–Chloride Symport, 2024, 25, 1422-0067, 12955, 10.3390/ijms252312955 | |
| 19. | Riccardo Sacco, Greta Chiaravalli, Giovanna Guidoboni, Anita Layton, Gal Antman, Keren Wood Shalem, Alice Verticchio, Brent Siesky, Alon Harris, Reduced-Order Model for Cell Volume Homeostasis: Application to Aqueous Humor Production, 2025, 30, 2297-8747, 13, 10.3390/mca30010013 | |
| 20. | June I. Medford, Towards sustainable freshwater systems through Plant Synthetic Biology Engineering Plants for sustainability, 2025, 26931257, 100009, 10.1016/j.bidere.2025.100009 |