Abbreviations

C	capacitance;	CCCP	carbonylcyanide-3-chlorophenylhydrazone;
DAQ	data acquisition;	λ	the length of electrotonic potential
V	voltage;	R	resistance;
PXI	PCI extensions for instrumentation;
FCCP	carbonylcyanide-4-trifluoromethoxyphenyl hydrazine;

---

1. Introduction

---

1.1. Plant electrostimulation and nonlinear responses

DC and AC electrostimulation of plants can induce gene expression ^[1,2,3], enzymatic systems activation ^[4], electrical signaling ^[5,6,7], plant movements ^{[8,9,10,11,12,13,14,15,16]}, and influence plant growth ^{[17,18,19,20]}. The electrostimulation by bipolar sinusoidal or triangular periodic waves induces electrical responses in plants and seeds with fingerprints of memristors ^{[21,22,23,24,25,26,27]}.

Electrical signals, as a result of stimulation, can propagate to adjacent cells due to cell-to-cell electrical coupling ^{[28,29,30,31]}. This propagation can be either active, representing an action potential, or passive, described as an electrotonic potential. The action potential can propagate over the entire length of the cell membrane and along the vascular bundles of plant tissue with constant amplitude, polarity, duration, and speed. Amplitude of electrotonic potentials depends on size, shape and polarity of a stimulus. It decreases exponentially with distance from electrostimulating electrodes ^[32,33]. The shape of electrotonic and action potentials in plants is very similar.

In small neurons, electrical potentials decreasing exponentially are referred to as electrotonic potentials ^[34]. The standard term in literature on bioelectrochemistry and neurobiology is“electrotonic potential”, whichdenotes the direct spread of electrical potential or current in tissues by electrical conduction, without the generation of action potentials.

Abiotic stress such as drought, extreme cold or heat, strong winds and biotic stress induced by other living organisms such as bacteria, viruses, fungi, parasites and insects can induce a propagation of electrical signals between phytosensors and phytoactuators in plants.

Electrical signals can propagate along the plasma membrane on long and short distances in vascular bundles, plasmodesmata and protoxylem. Electrostimulation by a square pulse of electrical circuits as was shown on examples of the Venus flytrap, Aloe vera, Arabidopsis thaliana and Mimosa pudica induces electrotonic potentials with amplitude exponentially decreasing along a leaf or a stem ^[32,33].

Electrical stimulation can be used to study mechanisms of plant movements and morphing structures in the Venus flytrap and Mimosa pudica. Electrostimulation of the Venus flytrap induces closing the upper leaf of the Venus flytrap without mechanical stimulation of trigger hairs ^{[11,12,13,14,15]}. The closing time of the Venus flytrap by electrical stimulation is 0.3 s, the same as mechanically induced closing ^[11,12]. The Venus flytrap can accumulate small subthreshold charges. When the threshold value is reached, the trap closes.

Mechanical movements in Mimosa pudica can be induced by electrostimulation of a pulvinus ^[8,9,16]. Volkov et al. ^[16] investigated the mechanical movements of the pinnae and petioles in the Mimosa pudica which were induced by the electrical stimulation of a pulvinus, petiole, secondary pulvinus, or the pinna by a low electrical voltage and charge stimulation. The threshold value was about 1.5 V of applied voltage and 10 µC charge for the closing of the pinnules. Both voltage and electrical charge are responsible for the electrostimulated closing of a leaf (Volkov et al. 2010).

Herde et al. ^[1] found that electrical current application activated pin2 gene expression in tomato plants and also increases endogenous level of abscisic acid. Stanković and Davies ^[3] demonstrated that electrical stimulation of tomato plants induces electrical signals with amplitude of 40 mV and elicits systemic pin2 gene expression.

Favre and Agosti ^[5] described voltage-dependent“action”potentials in Arabidopsis thaliana induced by 3-18 V pulses. Amplitude and velocity of electrical responses were a function of applied voltage. Most probably, voltage-dependent electrical responses in their publication were electrotonic potentials.

Adamatzky ^[35] studied a possibility of making electrical wires from plants and found that a lettuce seedlings acted as a potential divider. Stavrinidou et al. ^[36] manufactured analog and digital organic electronic circuits in vascular bundles of R. floribunda.

There are many publications in literature about electrical signals in plants, such as variation or systemic potentials, with amplitude decreasing with distances. In the same time, there are not any information in literature about their dependencies on distance of propagation and mechanism of their generation.

There exists a significant advantage in an analytical study of the propagation of electrical signals in plants. Information gained from the mathematical modeling, analytical and simulation study can be used not only to elucidate the effects of electrostimulation on higher plants, but also to observe and predict the intercellular and intracellular communication in the form of electrical signals within electrical networks of plants.

The purpose of this work is experimental, analytical and simulation study of electrotonic signal transduction in plants. One of the goals of the experimental study is to discover differentiation property and electrical coupling in leaves of Aloe vera. We present new experimental proofs of existing the electrical differentiators, electrical coupling and cable properties of electrical circuits in Aloe vera. The experimentally study of the differentiation property of cell-to-cell electrical coupling never has been reported out in the literature on plant physiology. Another goal of this work is to present the mathematical model of electrotonic potentials in plants, which is supported by the experimental data, including the differentiation property reported in this work. The information gained from this study/analysis can be used not only to elucidate the effects of electrostimulation on higher plants, but for the evaluation of mechanisms of phytoactuators’responses in plants without stimulation of abiotic biotic stress phytosensors.

---

2. Materials and Methods

---

2.1. Plants

Seventy five Aloe vera L. plants were grown in clay pots. Plants were exposed to a 12:12 hr light/ dark photoperiod (Environmental Corporation) at 21 °C. Aloe vera plants had 20-35 cm leaves. Volume of soil was 1.0 L. The humidity averaged 40-45%. Irradiance was 700-800 µmol photons m⁻²s⁻¹ PAR at plant level. All experiments were performed on healthy adult specimens.

---

2.2. Chemicals

Carbonylcyanide-3-chlorophenylhydrazone (CCCP) and carbonylcyanide-4-trifluoromethoxyphenylhydrazone (FCCP)were obtained from Fluka (New York). CCCP and FCCP were injected in the Aloe vera leaf between Pt and Ag/AgCl electrodes in concentration of 0.1 mM.

---

2.3. Electrodes

All measurements were conducted in the laboratory at 21°C inside a Faraday cage mounted on a vibration-stabilized table. Ag/AgCl electrodes were prepared in the dark from Teflon coated silver wires (A-M Systems, Inc., Sequim, WA, USA) with a diameter of 0.2 mm by electrolysis of 5 mm long silver wire tip without Teflon coating in a 0.1 M KCl aqueous solution. The anode was a high-purity silver wire and the cathode was a platinum plate.

Platinum electrodes were prepared from Teflon coated platinum wires (A-M Systems, Inc.) with diameter of 0.076 mm. In all experiments we used identical Ag/AgCl electrodes as a measuring and as reference electrodes. Platinum electrodes were used for electrostimulation of plants. We allowed plants to rest one hour after electrode insertion.

---

2.4. Data acquisition

High speed data acquisition was performed using microcomputers with simultaneous multifunction I/O plug-in data acquisition board NI-PXI-6115 (National Instruments) interfaced through a NI SCB-68 shielded connector block to Ag/AgCl electrodes. The system integrates standard low-pass anti-aliasing filters at one half of the sampling frequency.

---

2.5. Plant electrostimulation

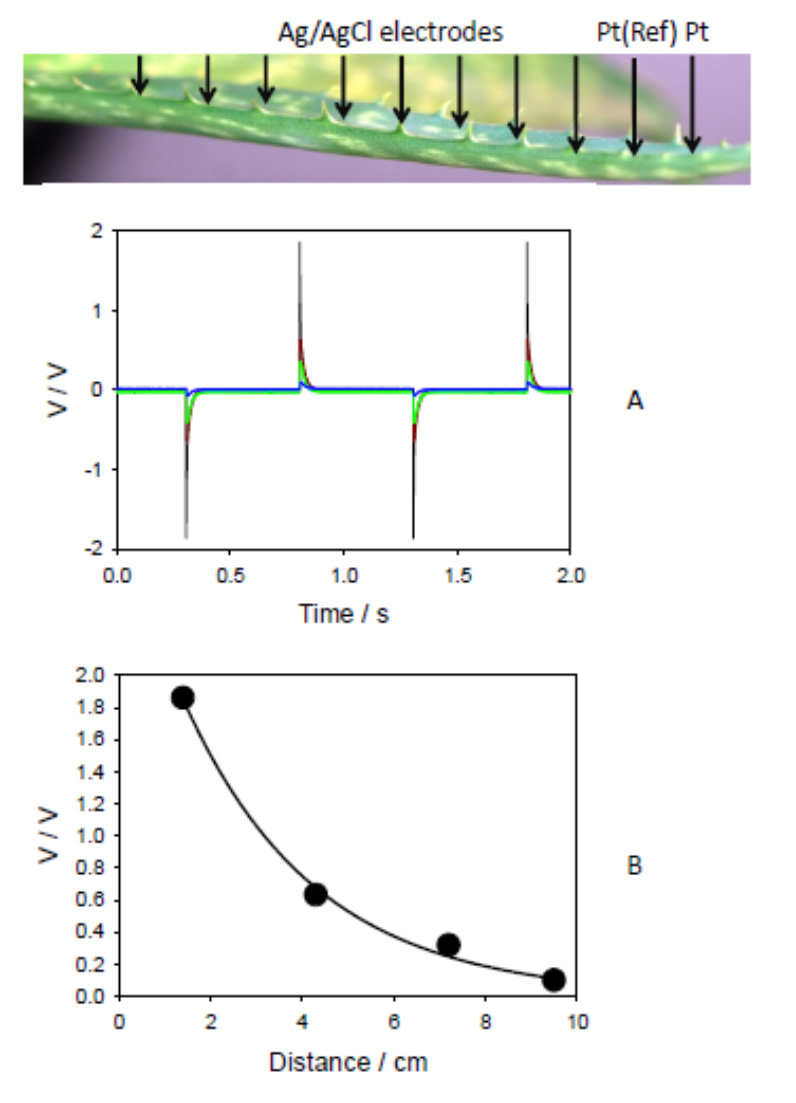
The function generator FG300 (Yokagawa, Japan) was interfaced to NI-PXI-1042Q microcomputer and used for electrostimulation of plants using platinum electrodes inserted to plant tissue. The function generator gives many options for the electrostimulation: shapes, duration, and frequency of stimulation. Ag/AgCl electrodes, inserted to the same leaf were used for detection of plant responses during electrostimulation as shown in Figure 1. Leaf electrostimulation induced reproducible results during a few hours.

---

2.6. Statistics

All experimental results were reproduced at least 25 times. Software SigmaPlot 12 (Systat Software, Inc.) was used for statistical analysis of experimental data.

---

3. Results

---

3.1. Experimental Study

---

3.1.1. Electrotonic potentials in Aloe vera

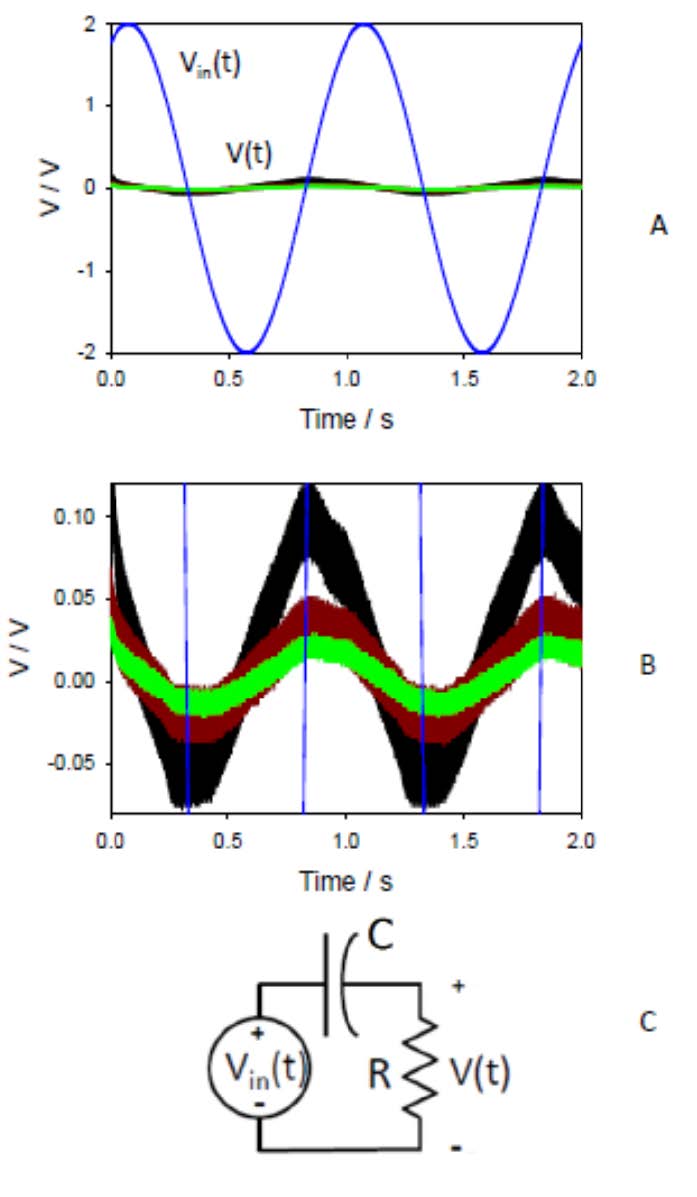
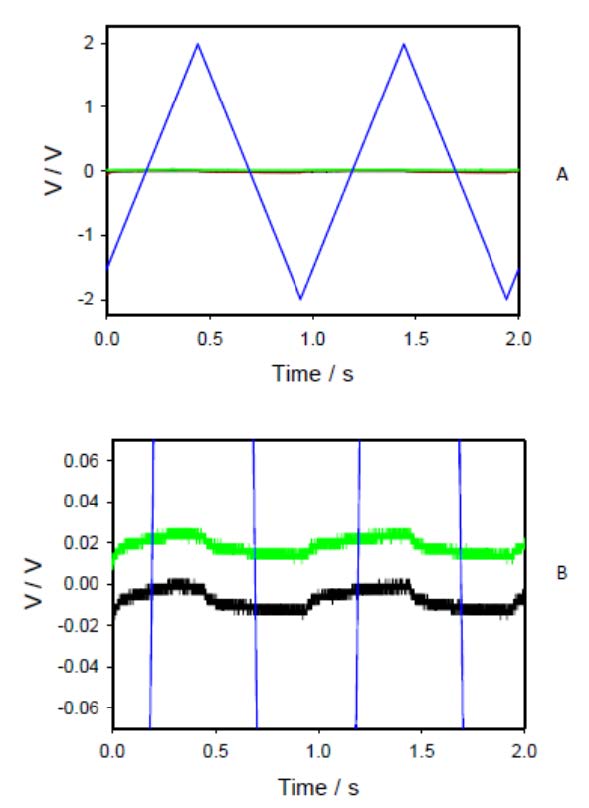
Electrostimulation of a leaf of Aloe vera by a square pulse from a function generator induces percussive electrical signals along the plants. For electrostimulation we used the pulse train (Figure 1), sinusoidal (Figures 2 and 3) and a triangular saw-shape (Figure 4) voltage profiles.

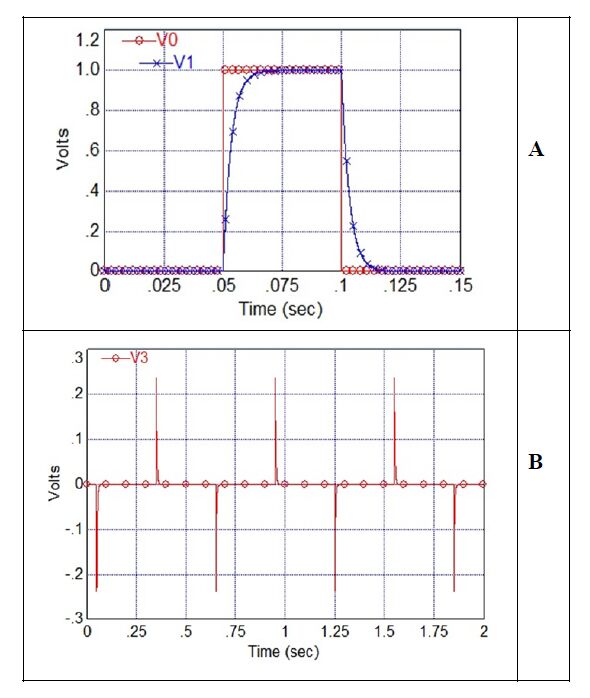
The pulse train voltage is supposed to illustrate the differentiation capabilities of the leaf; the sinusoidal voltage is to demonstrate the phase shift in the voltage propagation. The triangular voltage wave can demonstrate how the time-varying voltage with a constant slope propagates through the leaf. The transformation of such time-varying signal to a constant one is expected due to a possible differential property of a leaf. The amplitude and sign of electrotonic potentials depend on the shape, rise and fall of the applied voltage during electrostimulation, and also the distance from electrostimulating electrodes, amplitude and polarity of the applied voltage (Figure 1A). To understand the nature of these electrical potentials in the lower leaf, we have measured their dependence on the distance from the electrostimulating platinum electrodes. These electrical responses are not action potentials since their amplitude and polarity depend on the applied voltage (Figure 1A). Amplitude of these electrical potentials decreases exponentially with distance (Figure 1B):

$V=a{\text{Exp}}(-{\text{Distance}}/{\lambda })$

(1)

with λ=2.88 cm. Therefore, the constant of length λ, which indicates how far an electrical signal will spread in the leaf of the Aloe vera, is λ=2.88 cm.

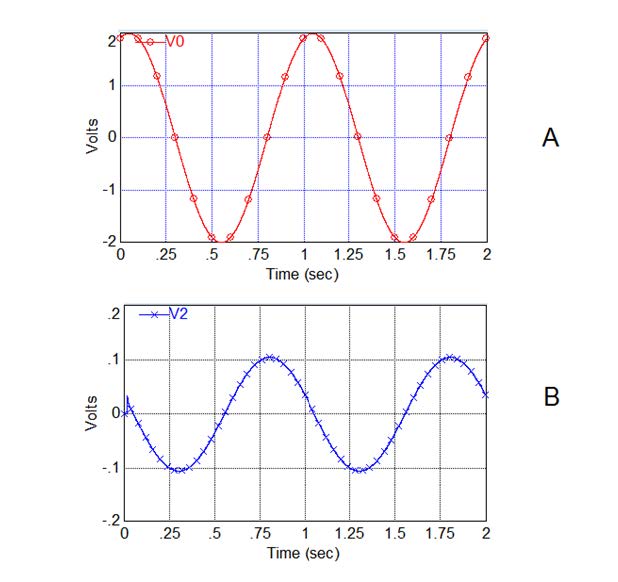
The reaction of the plant strongly depends on the shape of electrical stimulus. Electrostimulation by a sinusoidal wave from a function generator induces electrical response between inserted Ag/AgCl electrodes with a phase shift of 90°(Figure 2 A, B). This phenomenon shows that electrical networks in plant tissue have electrical differentiators (Figure 2C). A differentiator is an electrical circuit that is designed such that the output of the circuit is approximately directly proportional to the rate of change of the input:

$V(t)=RC\frac{d}{{dt}}({V_{in}}(t)-V(t))$

(2)

where V_in is an input voltage, V is an output voltage, R is a resistance and C is a capacitance

If

$\frac{{dV(t)}}{{dt}} \ll \frac{{d{V_{in}}(t)}}{{dt}}$

(3)

then

$V(t)=RC\frac{d}{{dt}}{V_{in}}(t)$

(4)

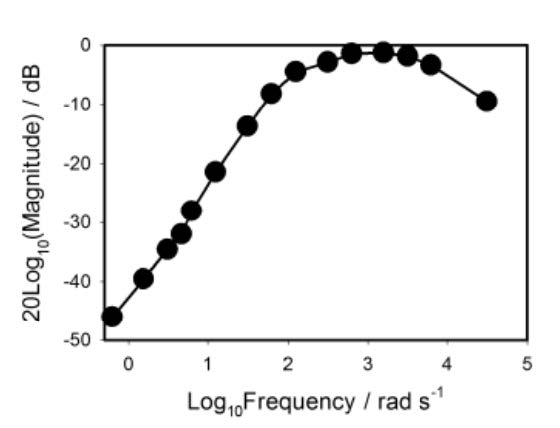
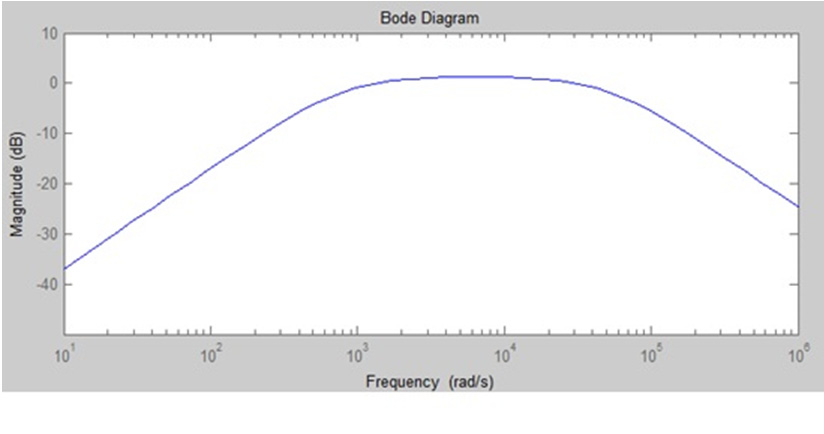
According to eq (4) V_in=A sin(ωt) yields V(t)=ωRCA cos(t), i.e. the 90^o phase shift is expected. Also, if frequency of the applied voltage is below 25 Hz, the amplitude of V(t) is proportional to the frequency of scanning as presented in Figure 3. Next, it is observed from Figure 3 that the amplitude V(t) decreases at high frequencies. Note that the plot at Figure 3 is presented in terms of the amplitude-frequency Bode plot, where the amplitude is computed in decibels, $20{\log _{10}}(Amplitude)$, and plotted versus ${\log _{10}}\omega$.

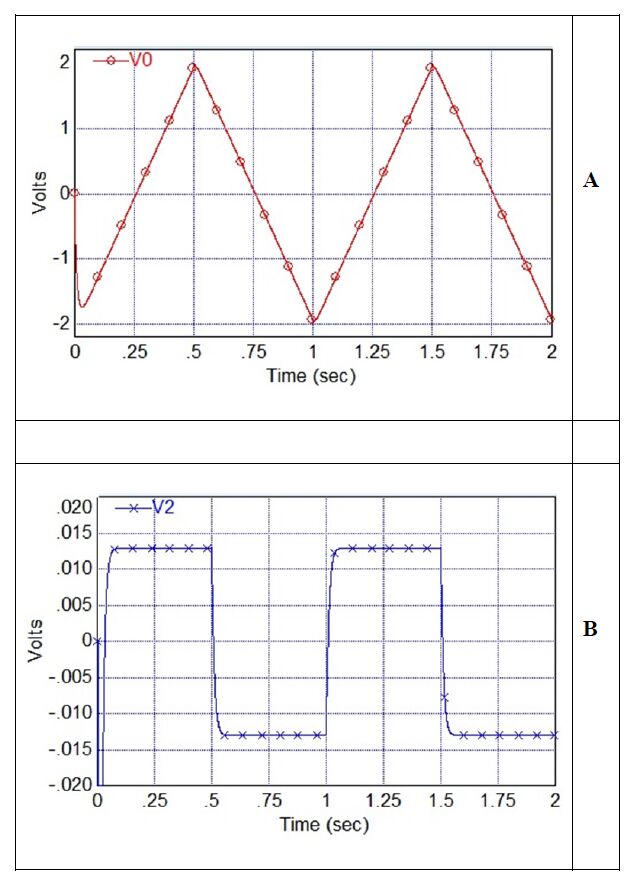
Electrostimulation by a triangular saw-shape voltage profiles demonstrates how the time-varying voltage with a constant slope propagates through the leaf. The transformation of such time-varying signal to a plateau (Figure 4) is expected due to a possible differential property of a leaf (Figure 4).

If the stimulus changes very sharply, the plant’s response is very significant and nonlinear: the square impulses initiate electrical responses with shapes completely different from the stimulating voltage, which look like spikes or“action”potentials. Any stimulation that is not instantaneous, such as a sinusoidal or triangular function, does not induce a nonlinear response, but results in linear responses in the form of electrotonical potentials with small amplitude. Amplitude and the sign of this response depend on the polarity of electrostimulating electrodes and the amplitude of applied voltage. The response does not obey the all-or-none rule and it is not an action potential. Amplitude of these electrical potentials decreases exponentially with distance (Figure 1B).

---

3.1.2. Pharmaceutical analysis

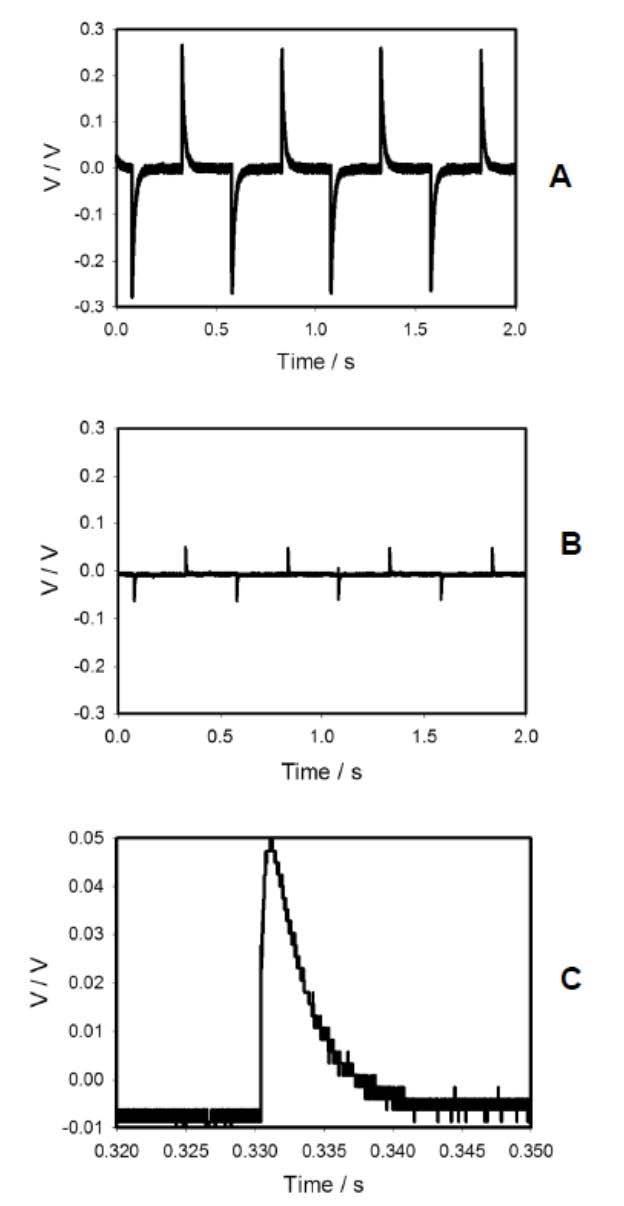
Inhibition of electrical waves in the Aloe vera by uncoupler FCCP is presented in Figure 5. Figure 5A shows the electrical responses before injection of uncouplers into the Aloe vera leaf.

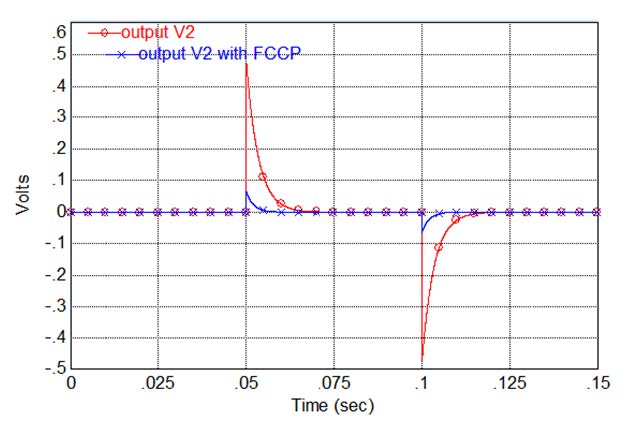
Injection of 50 µL of uncouplers FCCP (Figure 5B and 5C) or CCCP in concentration of 0.1 mM into the Aloe vera leaf only partially suppresses the generation of signals: the amplitude of plant electrical responses decreases about 7 times. Figure 5C shows the same results as Figure 5B in a short time scale. Uncouplers decrease the amplitude and duration of electrotonic potentials in a leaf (Figure 5 C). However, these uncouplers do not completely eliminate the propagation of electrotonic potentials: they continue to propagate along the leaf with smaller amplitude. FCCP and CCCP do not permanently damage electrical machinery of the Aloe vera: their suppression effect is reversible. After a few days the inhibitory effects disappear and propagation ability completely restores to original level as in Figure 5A. It can be caused by decreasing of FCCP concentration between Pt and Ag/AgCl electrodes due to diffusion of FCCP along the massive leave of Aloe vera. This experiment was repeated by another injection of uncouplers to the same Aloe vera leaf and results are similar to findings shown in Figure 5B. The results of the application of uncouplers, FCCP or CCCP, are rather similar.

---

3.2. Analytical study

The mathematical modeling of electrotonic potentials in plants that exponentially decrease with distance is accomplished in this section. Dynamics of the electrotonic potentials, which are induced by electrostimulation of electrical networks in plants and propagate along their leaves and stems, are taken into account.

Electrostimulation of electrical networks in plants can induce electrotonic potentials propagating along their leaves and stems. The instantaneous change in voltage of stimulating potential that generates a nonlinear response in plant tissues is studied via the proposed mathematical model.

The mathematical model is derived based on the classical cable theory that was originally applied to the conduction of potentials in an axon by Hodgkin and Rushton ^[37] and was later applied to the dendritic trees of neurons by Rall ^[38]. The cable theory based mathematical model that is used to describe electric currents and voltages along dendrites ^[38]. In this work it is proposed applying the cable theory-based mathematical mode to describe the dynamics of the electrotonic potentials in plants.

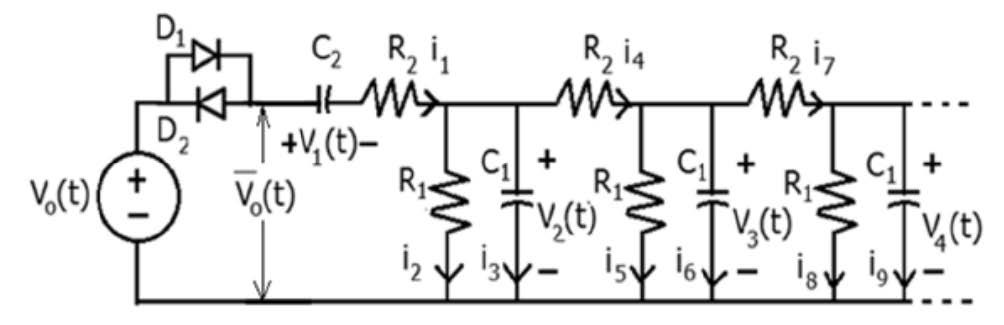
The equivalent electric circuit that approximately describes the propagation of the electrotonic potentials ${V_1}, {V_2}, {V_3}, {V_4}, ...$ in plants along leaves or stems is given in Figure 6, where ${V_0}(t)$ is an electrostimulation potential; ${V_1}, {V_2}, {V_3}, {V_4}, ...$ are electrotonic potentials in intermediate places of plant’s leaf or stem; ${C_1}, {C_2}$ are capacitances due to electrostatic forces; ${R_1}, {R_2}$ are membrane resistance and a resistance along a leaf or stem due to the resistance to a current respectively; ion channels (${D_1}$ and ${D_2}$) are represented by the diodes that constitute a dead band structure, which prevents propagating electrostimulation potential ${V_0}$, while it is below a sensitivity threshold $\left| {{V_0}} \right| \leqslant \varepsilon$, therefore modeling the nonlinear effects as follows

${\bar V_0}=\left\{ {\begin{array}{*{20}{c}} {0, \;if\; \left| {{V_0}} \right| \leqslant \varepsilon \; } \\ {{V_0}, \;otherwise} \end{array}} \right.$

(5)

The capacitances ${C_0}, {C_1}$ and the resistance ${R_1}$ have dimensions per membrane length unit, specifically [$F/m$] and [$\Omega \cdot m$] respectively. On the other hand, the resistance ${R_2}$ is measured per leaf or stem length unit, i.e. in [$\Omega \cdot m$].

The experimental discovery of the differentiation property of cell-to-cell electrical coupling presented in this work (see Figures 1, 2, and 5) is proposed to have studied analytically via including the differentiation capacitor ${C_2}$ in the electrical circuit (Figure 6) that facilitates modeling electrotonic potentials propagating along their leaves and stems. Therefore, the main innovation in the proposed scheme (Figure 6) with respect to the one in ^[38] is in adding the capacitor C₂ that allow mastering of the voltage spikes as shown in the experimental plots in Figure 1. Adding the capacitor C₂ is equivalent to differentiation of the voltage V₀, which explaining the occurrence of the spike in the voltage V₂, V₃, and V₄. However, if the input voltage V₀ has a sinusoidal shape, then, being differentiated on the capacitance C₂, the voltage V₂ repeats this shape with a certain phase shift.

The following assumptions are made concerning the measuring availability of the parameters of the proposed mathematical model:

A1. The specific resistance, $\bar R$ [$\Omega \cdot {m^2}$], and the specific capacitance $\bar C$ [$F/{m^2}$], which correspond to the resistance and the capacitance of one unit area of the membrane respectively, are measured.

A2. The area of a cross-section, and the length of the cross-section contour of the studied leaf or stem are measured and equal to S [m²] and L [m] respectively.

A3. The specific resistance, $\tilde R$ [$\Omega \cdot m$], of the leaf or stem tissue is measured.

Then the parameters of the equivalent circuit in Figure 6 can be calculated as in reference ^[38]:

${R_1}=\frac{{\bar R}}{L}\; \left[{\Omega \cdot m} \right], \quad {R_2}=\frac{{\tilde R}}{S}\; \left[{\Omega /m} \right], \quad {C_1}=\bar CL\; \left[{F/m} \right]$

(6)

The mathematical model of the equivalent electric circuit presented in Figure 6 is derived using Kirchhoff Current Law

$\begin{gathered} {i_1}={i_2} + {i_3} + {i_4}, \quad {i_4}={i_5} + {i_6} + {i_7}, \quad {i_7}={i_8} + {i_9} \hfill \\ {i_1}={C_2}\frac{{d{V_1}}}{{dt}}, \quad {i_3}={C_1}\frac{{d{V_2}}}{{dt}}, \quad {i_6}={C_1}\frac{{d{V_3}}}{{dt}}, \quad {i_9}={C_1}\frac{{d{V_4}}}{{dt}} \hfill \\ \end{gathered}$

(7)

Ohm Law

${i_2}=\frac{{{V_2}}}{{{R_1}}}, \quad {i_5}=\frac{{{V_3}}}{{{R_1}}}, \quad {i_8}=\frac{{{V_4}}}{{{R_1}}}$

(8)

and Kirchhoff Voltage Law

${V_1} + {i_1}{R_1} + {i_2}{R_2}-{V_0}=0, \quad {i_4}{R_2} + {i_5}{R_1}-{V_2}=0, \quad {i_7}{R_2} + {i_8}{R_1}-{V_3}=0$

(9)

The following equations that describe the evolution of the voltages ${V_2}(t), \;{V_3}(t), \;{V_4}(t)$ in three equidistant points along the plant leaf or stem are obtained based on eqs. (7)-(9):

$\left\{ \begin{gathered} \frac{{d{V_1}}}{{dt}}=-\frac{1}{{{R_2}{C_2}}}{V_1}-\frac{1}{{{R_2}{C_2}}}{V_2} + \frac{1}{{{R_2}{C_2}}}{V_0} \hfill \\ \frac{{d{V_2}}}{{dt}}=-\frac{1}{{{R_2}{C_1}}}{V_1}-\left({\frac{1}{{{R_1}{C_1}}} + \frac{2}{{{R_2}{C_1}}}} \right){V_2} + \frac{1}{{{R_2}{C_1}}}{V_3} + \frac{1}{{{R_2}{C_1}}}{V_0} \hfill \\ \frac{{d{V_3}}}{{dt}}=\frac{1}{{{R_2}{C_1}}}{V_2}-\left({\frac{1}{{{R_1}{C_1}}} + \frac{2}{{{R_2}{C_1}}}} \right){V_3} + \frac{1}{{{R_2}{C_1}}}{V_4} \hfill \\ \frac{{d{V_4}}}{{dt}}=\frac{1}{{{R_2}{C_1}}}{V_3}-\left({\frac{1}{{{R_1}{C_1}}} + \frac{1}{{{R_2}{C_1}}}} \right){V_4}\; \hfill \\ \end{gathered} \right.$

(10)

Equations (10) are rewritten in a matrix-vector format

$\left[{\begin{array}{*{20}{c}} {\frac{{d{V_1}}}{{dt}}} \\ {\frac{{d{V_2}}}{{dt}}} \\ {\frac{{d{V_3}}}{{dt}}} \\ {\frac{{d{V_4}}}{{dt}}} \end{array}} \right]=\left[{\begin{array}{*{20}{c}} {-\frac{1}{{{R_2}{C_2}}}} & {-\frac{1}{{{R_2}{C_2}}}} & 0 & 0 \\ {-\frac{1}{{{R_2}{C_1}}}} & {-\left({\frac{1}{{{R_1}{C_1}}} + \frac{2}{{{R_2}{C_1}}}} \right)} & {\frac{1}{{{R_2}{C_1}}}} & 0 \\ 0 & {\frac{1}{{{R_2}{C_1}}}} & {-\left({\frac{1}{{{R_1}{C_1}}} + \frac{2}{{{R_2}{C_1}}}} \right)} & {\frac{1}{{{R_2}{C_1}}}} \\ 0 & 0 & {\frac{1}{{{R_2}{C_1}}}} & {-\left({\frac{1}{{{R_1}{C_1}}} + \frac{1}{{{R_2}{C_1}}}} \right)} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{V_1}} \\ {{V_2}} \\ {{V_3}} \\ {{V_4}} \end{array}} \right] + \left[{\begin{array}{*{20}{c}} {\frac{1}{{{R_2}{C_2}}}} \\ {\frac{1}{{{R_2}{C_1}}}} \\ 0 \\ 0 \end{array}} \right]{V_0}$

(11)

It is worth noting that the derived mathematical model in eqs. (10) and (11) describes linear dynamical processes of electrotonic potentials in the plants. The nonlinear effects presented in Figure 6 by the diodes ${D_1}$ and ${D_2}$ will be added to the mathematical model of the electrotonic potentials in the plants in the following up study.

---

3.3. Simulation study

Electrotonic potentials in Aloe vera, that have been studied experimentally (see Figures 1-5), are studied here using the mathematical model given by eqs. (10) and (11).

Given the parameters ${R_1}=150K\Omega, \;{R_2}=86K\Omega, \;\; {C_1}=0.2 \cdot {10^{-9}}F, \;\; {C_2}=20.0 \cdot {10^{-9}}F$, the coefficients in eqs. (10) and (11) were computed, and the systems (10), (11) becomes

$\left\{ \begin{gathered} \frac{{d{V_1}}}{{dt}}=-581.4{V_1}-581.4{V_2} + 581.4{V_0} \hfill \\ \frac{{d{V_2}}}{{dt}}=-5.814 \cdot {10^4}{V_1}-14.961 \cdot {10^4}{V_2} + 5.814 \cdot {10^4}{V_3} + 5.814 \cdot {10^4}{V_0} \hfill \\ \frac{{d{V_3}}}{{dt}}=5.814 \cdot {10^4}{V_2}-14.961 \cdot {10^4}{V_3} + 5.814 \cdot {10^4}{V_4} \hfill \\ \frac{{d{V_4}}}{{dt}}=5.814 \cdot {10^4}{V_3}-9.147 \cdot {10^4}{V_4}\; \hfill \\ \end{gathered} \right.$

(12)

The system (12) was simulated in Visual Simulation software environment using Runge-Kutta-4 integration algorithm with a step size $\tau={10^{-6}}\; s$, the threshold for the stimulation potential was neglected ($\varepsilon=0$). The results of the simulations are depicted in Figures 7-10, where voltages ${V_0}-{V_4}$ are measured in Volts.

---

3.3.1. Simulation experiment 1

The plot in Figure 7A illustrates shaping of the input voltage pulse by the capacitor ${C_2}$.

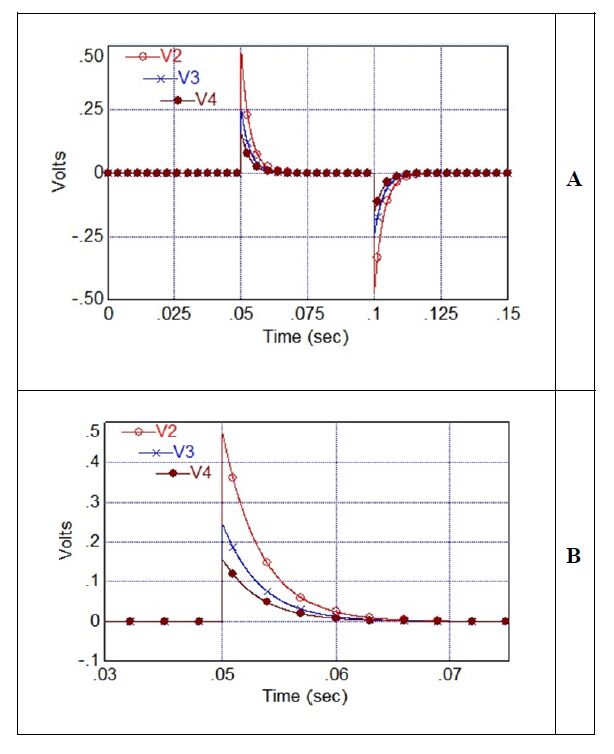
Figure 7B demonstrates a good match with the results of the experiment presented in Figures. 1A, 5A and 5B. Plots of the electrotonic potentials ${V_2}, {V_3}, {V_4}$ in the equidistant intermediate places of Aloe Vera leaf obtained via simulations (see Figures 8A and B) are similar to the experimental results presented in Figures. 1 and 5. The amplitudes of the electrotonic potentials ${V_2}, {V_3}, {V_4}$ are: ${a_1}=0.47, \;{a_2}=0.24, \;{a_3}=0.15$ (V) that confirms the exponential decay (see Figure 1B).

---

3.3.2. Simulation experiment 2

The plots presented in Figures 4A and 4B that demonstrate how the time-varying voltage with a constant slope propagates through the leaf are confirmed via mathematical modeling. The results of the simulations are shown in Figures 9A and 9B.

The experimentally expected transformation of such time-varying signal to a plateau due to a possible differential property of a leaf (Figure 4B) is confirmed on Figure 9B. Figures 10A and 10B that are obtained via simulations illustrate the 90^o phase shift of the sinusoidal input voltage V(t)=ωRCA cos(t) that was experimentally discovered and presented in Figures 2A and 2B. A good match between experimental and analytical results can be observed.

The amplitude frequency characteristic $20\log \left| {G(j\omega)} \right|=20\log \frac{{\left| {{V_2}(j\omega)} \right|}}{{\left| {{V_0}(j\omega)} \right|}}$ experimentally obtained and presented in Figure 3 has been computed using the mathematical model (12), via Matlab application. The mathematical model-based amplitude Bode plots are presented in Figure 11.

In the frequency range $0 \leqslant \omega < 1000\;rad/s$ the amplitude-frequency characteristic corresponds to the differentiator that confirms the experimental results presented in Figure 3. The rest of the frequency characteristic for $\omega \geqslant {10^4}\; rad/\operatorname{s}$ describes a low-pass filter dynamics that is in line with the experimental data plotted in Figure 3.

---

3.3.3. Simulation experiment 3

Effects of uncouplers on amplitude of the electrotonic potentials that is studied experimentally (see Figure 5) are modeled by adding a resistance $\Delta {R_1}=16.67K\Omega \,$ in parallel with the resistance ${R_1}=150K\Omega$. The results of the simulation are shown in Figure 12.

The plot in Figure 12 confirms the experimental results on reduction of the amplitude of the electrotonic potential (Figure 5) caused by shunting the membrane resistance R₁=150 kW by another much smaller resistance△R₁=16.67 kW.

---

4. Discussion

The proposed mathematical model of electrotonic potentials in plants is supported by the experimental data. The exponential decay of the amplitudes of the electrotonic potentials in plants is observed experimentally (Figure 1) and revealed via computer simulation (Figures 8A and B).

For electrostimulation, we used the pulse train, sinusoidal and a triangular saw-shape voltage profiles. The amplitude and sign of electrotonic potentials depend on the amplitude, rise and fall of the applied voltage (Figures 1, 2, 4, 5). Electrostimulation by a sinusoidal wave from a function generator induces electrical response between inserted Ag/AgCl electrodes with a phase shift of 90°(Figure 2). This phenomenon shows that electrical networks in leaves of Aloe vera have electrical differentiators (Figure 2C) in cell-to-cell coupling (Figure 6). The experimental results in Figures 1, 2, 4, 5 are obtain via simulations using the equivalent electrical circuit in Figure 6 and corresponding mathematical models in eqs. (10)-(12). The plots obtained via computer simulations (Figures 7-12) have a good match to the experimental results.

Uncouplers CCCP or FCCP decrease the amplitude and duration of electrotonic potentials in the leaf of Aloe vera (Figure 5). This effect was also predicted and estimated by our mathematical model (Figure 12). CCCP and FCCP, which are soluble in both water and lipids, permeate the lipid phase of a membrane by diffusion and transfer protons across the membrane, thus eliminating a proton concentration gradient and decreasing the transmembrane resistance R₁ in the electrical circuit shown in Figure 6.

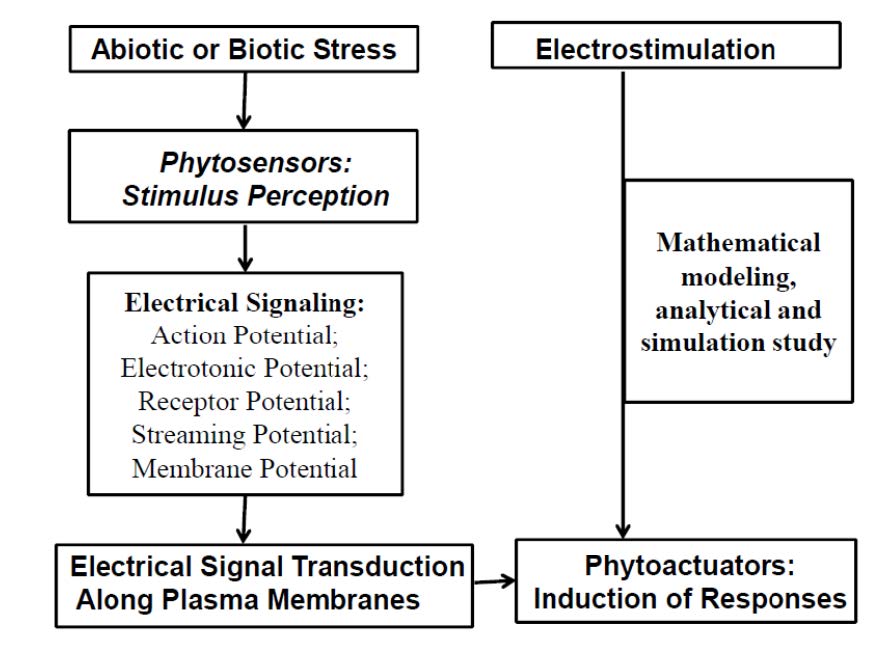
Electrostimulation is an important tool for the direct evaluation of mechanisms of phytoactuators’responses in plants without stimulation of abiotic or biotic stress phytosensors (Figure 13). For example, since the movements in Mimosa pudica are controlled by mechanosensors, it is possible to reproduce leaflets closing and a petiole moving by direct electrostimulation of a phytoactuator in a pulvinus without touching of mechanosensitive hairs and evaluate the mechanism of plant movement ^[16]. Closing of pinnules and a petiole bending can be triggered by electrical discharge (1.5 V) during a few second between electrodes connected to a pulvinus. Another example is the evaluation of the mechanism of the Venus flytrap movement using DC electrostimulation of a plant ^{[11,12,13,14,15]}.

The information gained from this mathematical model and analytical study can be used not only to elucidate the effects of electrostimulation on higher plants but also to observe and predict the intercellular communication in the form of electrical signals within electrical networks of plants.

---

5. Conclusion and Perspectives

Electrostimulation of electrical networks in plants can induce electrotonic potentials propagating along their leaves and stems. The amplitude and sign of electrotonic potentials depend on the amplitude, rise and fall of the applied voltage. Electrostimulation is an important tool for evaluating the mechanisms of phytoactuators’responses in plants without stimulation of abiotic or biotic stress phytosensors. Propagation of electrotonic potentials in plants is studied in this paper experimentally and via mathematical modeling. Electrostimulation by a sinusoidal wave from a function generator induces electrical response between inserted Ag/AgCl electrodes with a phase shift of 90°. This phenomenon shows that electrical networks in leaves of Aloe vera have electrical differentiators and cell-to-cell electrical coupling. The derived mathematical model of electrotonic potentials in plants is supported by the experimental data. The information gained from this mathematical model and the analytical study can be used to observe and predict the intercellular and intracellular communication in the form of electrical signals within electrical networks of the plants.

It is well known that electrostimulation of plants can induce gene expression, enzymatic systems activation, electrical signaling, plant movements, and influence plant growth. In the future work it will be very important to find mechanisms of interaction between electrical signals and phytoactuators in plants.

---

Acknowledgements

This article is based on work supported by the Henry C. McBay (UNCF) Research Fellowship and by National Institute of Health under grant number 1R25GM106994-01.

---

Conflicts of Interest

All authors declare no conflicts of interest in this paper.

---