1.
Introduction
Energy harvesting emerged and gained popularity over the past few years due to the rapid growth of renewable energy. Microscale device production has been increasing for the past decade along with the evolution of technology applications. This raises a new crisis and functionality issue, where a suitable energy source is needed. Besides, the world is now taking more interest in wireless technologies and microelectronics where the power source is either batteries or energy-harvesting devices [1]. However, wireless or portable devices typically have a short lifetime, and the battery size corresponding to the device capability is inadequate, thus making energy harvesting a better option [1,2,3,4,5,6,7].
Energy harvesting is an alternative that captures the surrounding energy (available in the environment) by harnessing motion, vibrations, temperature gradients, etc. [1,8,9]. Energy harvesting allows surveillance or monitoring where sensors are deployed in a remote area, or when the replacement of batteries is inconvenient or costly [2,3,6]. It can be categorized into large scale or small scale. Large-scale energy harvesting includes the extraction of energy from sources such as solar, wind, tidal, geothermal, etc. Meanwhile, small-scale energy harvesting focuses on energy typically represented as noises such as motion, vibrations, or heat [10]. Typical alternatives to extracting the kinetic energy are piezoelectric, electromagnetic, or electrostatic transduction techniques [7,9]. The harvesting mechanism includes a structure where the ambient energy is converted into electrical energy [1].
A pipeline is a long pipe used to convey substances such as water, oil, and gas over a long distance [11,12,13,14,15]. Pipelines induce turbulence vibration while conveying these substances [16,17,18,19,20]. Therefore, this opens an opportunity to exploit the vibration from the pipeline and harvest useful mechanical energy into electrical energy.
The pipeline network's location varies depending on the location of the plant to the destination, including underground and underwater venues [17,21,22,23,24]. Thus, pipelines need to be designed to adapt to their functionality. However, every pipeline has a different lifespan depending on its design and environmental factors [4,15,25,26,27]. As pipeline lengths are typically designed for long distances, the connection is often found in isolated areas where manual inspection by humans is regarded as almost impossible [2].
Over the years, several solutions have been proposed to counter the issues regarding pipeline failures and their potential hazards. To avoid any costly situation resulting from the late detection of pipeline hazards, the pipeline should be monitored by a functional and self-powered sensor that is stable and possesses a fast response [11,28]. Conventional pipeline monitoring sensors usually had to operate using external power sources, long-distance connected wirings, or batteries. Long-distance wiring resulted in power loss [5] and showed potential degradation. Even though batteries can be used as an alternative for self-powered sensors, they can only supply power for a limited amount of time. This method requires regular inspection and maintenance as well as being troublesome and costly [2,3,6]. Due to this, the application of a self-powered pipeline monitoring system based on energy harvesting should be considered, by utilizing the vibration of the pipeline.
Piezoelectric energy harvesting is one of the most common methods used in harnessing energy from vibration. Piezoelectric produces an electric voltage when mechanical energy, such as a strain or stress, is applied to a certain active piezoelectric crystal. At rest, the crystal does not conduct any electric current. When stress is applied, ions that were in balance positive and negative charge shift their position into dipole moment and produce voltage. This is known as the piezoelectric effect.
Mechanical and material piezoelectric properties allow variations in frequency-operating range and power output [29]. Table 1 presents several types of piezoelectric materials. The research on the best materials for piezoelectricity has widely been done, and various types of piezoelectric with different materials can be found in the market. Among them, lead magnesium niobate-lead titanate (PMN-PT) and lead zirconate niobate-lead titanate (PZN-PT) are recognized for their high-efficient piezoelectric properties. However, these materials still present a few downsides, such as being sensitive to temperate change, susceptible to fatigue, and difficult to manufacture. Lead zirconate titanate (PZT) offers various types and grades with different material properties such as PZT-5A, PZT-5H, and PZT-5J. PZT is a preferred material because it is chemically inert and has higher strength, operating temperature, and sensitivity in comparison to other piezoceramic materials. PZT can be easily customized to fit into specific applications and is relatively inexpensive to manufacture, being therefore the most common material used for energy harvesters [30].
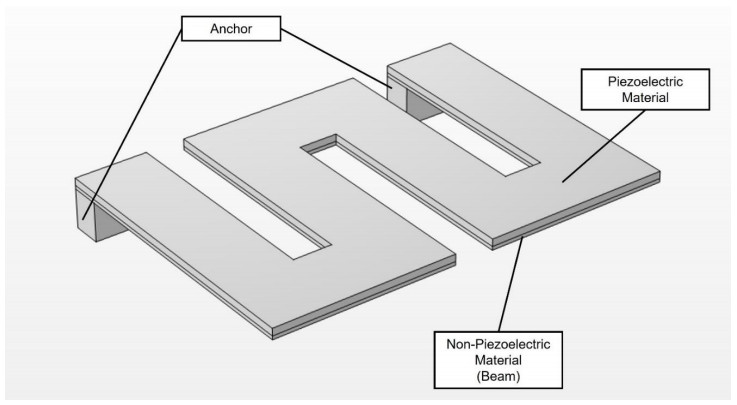
In addition to that, piezoelectric energy harvesters come in different types and shapes depending on their functionality. Some commonly known piezoelectric energy harvester types are piezoelectric stacks, cymbal, and cantilever beams. A cantilever beam is usually made of two layers: a piezoelectric layer and a non-piezoelectric layer near the high-stress fixed end. Some are attached with a proof mass at the tip to lower the resonant frequency and increase stress induced from the vibration [30]. The cantilever beam structure is called unimorph, bimorph, or stacks depending on the number of piezoelectric layers.
In contrast to electrostatic, electromagnetic, and triboelectric energy harvesting, the piezoelectric effect is primarily dependent on the intrinsic polarization of the material and does not require an external voltage source, magnetic field, or interaction with another material, making it a particularly practical approach for harvesting ambient mechanical energy and transforming it into electric power [3,32,33]. Consequently, piezoelectric transduction is by far the most viable ambient energy harvesting technique, having been used in a wide variety of fields including transportation [33,34,35,36,37], traffic [38,39,40], structures [34,36,41,42,43,44,45,46], underwater [47,48,49,50], and biomedical [51].
Various studies on harvesting vibration from pipeline vibration have been conducted over the years. Hafizh et al. [52] presented a design of vortex-induced vibration energy harvesting using a magnetically coupled broadband circular-array piezoelectric patch. Khan et al. [53] presented a novel flow type of electromagnetic-based energy harvester for generating useful electrical power from the flowing fluid in a pipeline. Qureshi et al. [54] suggested a novel scalable design of an in-pipe piezoelectric energy harvester for underwater pipeline monitoring applications. Aramendia et al. [48] developed an energy harvester assembled inside a water pipe with U-shaped geometry as the oscillating body. Lu et al. [55] proposed a uniform composite fluid-conveying pipe, made up of a piezoelectric layer and a substrate layer. In this paper, the proposed design of the fluid-conveying energy harvester involves a piezoelectric layer with a thickness of 12 mm covering 1 m of the pipe portion. A contact-mode triboelectric nanogenerator (TENG) composed of tribo-pair dielectric films connected to a mass-spring base that is fixed on the outer surface of a pipeline was introduced by Li et al. [56]. However, most of the aforementioned studies focused on the development of in-pipe vibration energy harvesters. The quantity of research on pipeline energy harvesters that are fixed to the exterior of the pipe is currently insufficient. Despite that, there are various publications related to vibration energy harvesting that can be utilized to assist this approach. However, the majority of the vibration energy harvesters in these studies were designed to operate at ultra-low frequencies.
The pipeline vibration-based energy harvester developed in this study aimed to improve the existing pipeline monitoring system by giving a novel technique for harnessing pipeline vibration from the pipe's exterior. Aside from that, no major pipeline adjustments are required because the designed energy harvester only has to be mounted on the pipeline's outside surface, and the installation of the energy harvester will have no influence on the pipeline's current operating circumstances. This allows the energy harvester to be installed in a variety of pipeline locations, potentially lowering the cost of maintenance. This piezoelectric energy harvester can offer a continuous power source to the pipeline monitoring sensor, allowing for the creation of a more efficient and sustainable pipeline monitoring sensor. A self-powered device enables sensors to be installed in harsh, remote, or inaccessible areas where wiring is limited and prohibited [5]. This also enables sensors to be self-sustaining modules that do not require external power sources, allowing for a wireless solution.
The research takes into consideration the following hypotheses: (1) The useful energy extracted from the vibration produced by the pipeline is sufficient to initiate the conversion of mechanical energy to electrical energy; (2) The dimension (length, width, thickness) of the piezoelectric cantilever beam will improve the output power of the energy harvester module; (3) The serpentine vibration-based piezoelectric energy harvester module will produce the expected output power for the pipeline monitoring application. This paper presents the investigation of the functionality and performance of the designed serpentine vibration-based piezoelectric energy harvester for the pipeline monitoring application.
2.
Methods
2.1. Proposed design
Pipelines produce various types of vibrations due to their dynamic operations. Some of the common vibrations analyzed for pipeline operations are flow-induced vibration (FIV) [49,57], acoustic-induced vibration (AIV), and vortex-induced vibration (VIV) [16,17,22,58,59,60]. Vibrations may also occur due to external surroundings especially when pipelines are built subsea (vibration due to ocean waves). Moreover, pipelines are built using different diameters depending on their functionality. The various factors of pipeline vibrations cause irregularities in pipeline vibration patterns.
The piezoelectric energy harvester model is designed based on the vibration level and dynamic operations of the pipeline. Vibration is one of the many criteria that need to be considered in pipeline design (usually before the construction of the pipeline). This criterion is highlighted in the API Standard 618, ASME Standard B31.4, and ASME Standard B31.8. API standards cover a wide range of equipment and processes within the oil and gas industry, while the ASME focuses on the mechanical system of the pipe. API Standard 618 outlines the basic design assessments required to prevent possible damage to the compressors or pipe systems due to vibrations. The compressors covered by the API 618 are low-to-moderate speeds (typically between 300 and 750 rpm). The 618 API also covers lubrication systems, controls, instrumentation, heat exchangers, pulsation suppression devices, and other auxiliary equipment [61]. ASME B31.4 prescribes requirements for the design, materials, construction, assembly, inspection, testing, operation, and maintenance of liquid pipeline systems between production fields or facilities, tank farms, above-or belowground storage facilities, natural gas processing plants, refineries, pump stations, ammonia plants, terminals (marine, rail, and truck), and other delivery and receiving points, as well as pipelines transporting liquids within pump stations, tank farms, and terminals associated with liquid pipeline systems [62]. Meanwhile, ASME B31.8 covers gas transmission and distribution piping systems, including gas pipelines, gas compressor stations, gas metering and regulation stations, gas mains, and service lines up to the outlet of the customer's meter set assembly [63]. The maximum allowable vibration level of pipes has not been specified in most publications, including the ASME and API standards.
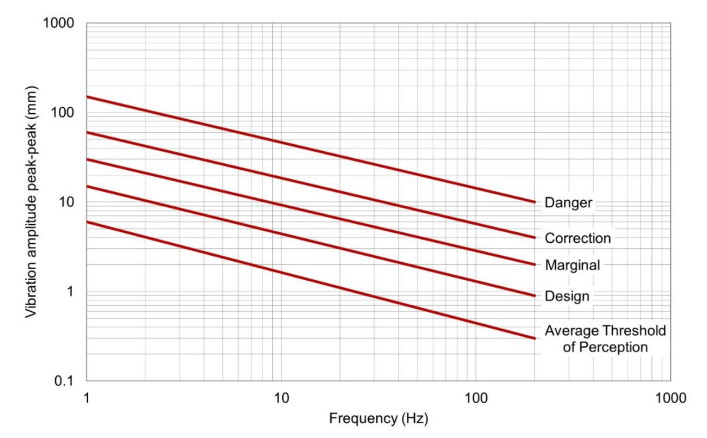
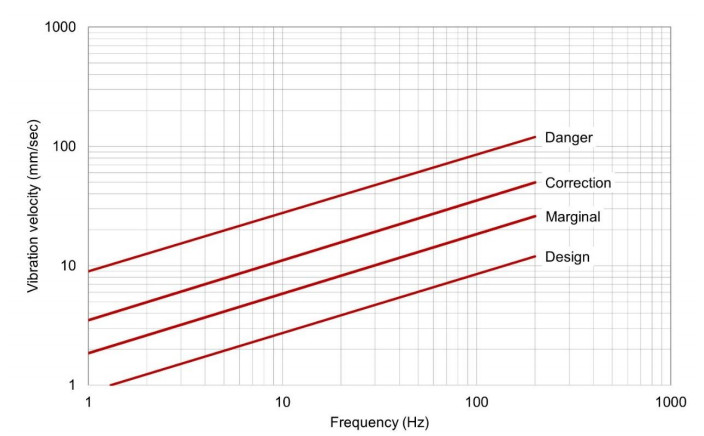
A common evaluation criterion used to identify the safe or allowable range of pipeline displacement or vibration that happens at a certain frequency was introduced by Wachel JC in 1970 [64]. This evaluation criterion has been adopted by many independent companies [65] and mentioned in various publications [65,66,67,68,69,70]. The evaluation criterion is only applicable to frequencies up to 300 Hz, which is satisfactory in evaluating the mechanical vibration of the pipe [66,67]. The evaluation criteria are highlighted in Figure 1, Figure 2, and Table 2.
The assessment of pipelines usually requires modifications or changes to pipe systems to reduce the vibration level into a safe or allowable vibration range. Modification on any pipe systems or pipe supports may negatively alter the mechanical natural frequency of the system.
To develop efficient piezoelectric energy harvesters adapted to pipeline environments, the energy harvester and the pipeline need to operate at similar resonant frequencies. Fitting the energy harvester's natural frequency to a specific design of pipeline is a difficult task and should take into account that the pipeline system operates at different natural frequencies depending on its operation, disregarding any external vibrational factor. The piezoelectric energy harvester proposed is specifically designed to operate according to pipeline design criterion with vibration amplitude of 0.9–14.46 mm and vibration velocity of 1.48–12 mm/sec within the frequencies of 10–300 Hz.
2.1.1. Design specification
The initial model of the piezoelectric energy harvester was evaluated using a PZT-5A piezoelectric layer. PZT-5A is a commonly used material for low-powered applications. This material was chosen due to its material compositions: (1) high permittivity and easily poled, (2) high electromechanical and piezoelectric coupling coefficient, (3) high Curie point, which permits high-temperature operation, and (4) high piezoelectric charge coefficient properties.
Meanwhile, steel will be used on the non-piezoelectric layer, because this material has a lower natural frequency compared to other metals, thus enabling a higher output power to be produced for lower-frequency vibrating sources from infrastructures on pipeline sites.
Table 3 highlights the initial parameters for the serpentine-shaped piezoelectric energy harvester model that will be implemented in the geometry model for analysis in the COMSOL Multiphysics software.
2.2. Finite element modeling
The implementation of finite element analysis (FEA) in this research focuses on the optimization of structure for the serpentine-shaped piezoelectric cantilever beam. This analysis is conducted to evaluate and understand how the piezoelectric energy harvester may behave under various physical conditions. Apart from that, finite element analysis serves as a form of simulation to identify vulnerabilities in design prototypes before the fabrication process. The finite element analysis was conducted using COMSOL Multiphysics Software Version 6.1.
2.2.1. Geometric modeling
The values in Table 3 can be defined in the COMSOL global definitions parameters section and used as reference values to build the 3D component geometry of the piezoelectric energy harvester model as shown in Figure 3. The 3D models are constructed using a structural mechanics module and AC/DC module.
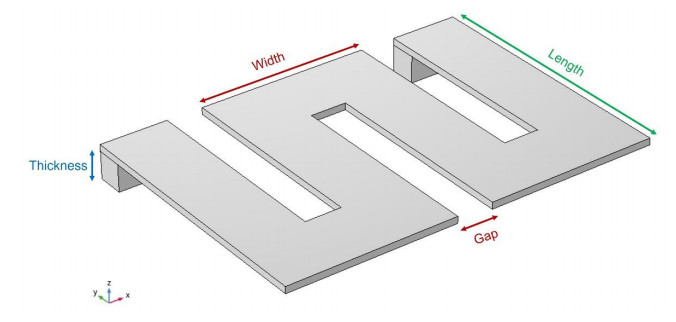
The geometry parts were all built as solid type and positioned at the corner base. The work plane is set to be at the xy plane. The blocks of piezoelectric beam and non-piezoelectric beam are assigned to be in union to create the serpentine-shaped cantilever beam.
Frequency response simulation is done by adding a frequency domain study into the component section. The frequency range of 10–300 Hz was input for the analysis. To create acceleration or load resistance sweep, auxiliary sweep in study extension should be enabled, and parameters from global definition need to be selected.
A separate study called eigenfrequency is added to the component for mode of shape and eigenfrequency analysis.
2.2.2. Definition of material
The piezoelectric layer (PZT-5A) and non-piezoelectric layer (steel) material properties are defined in COMSOL by default. The material needs to be assigned to the respective blocks manually.
The piezoelectric effect constitutive relations are expressed using stress-charge form. The stress-charge form is as follows:
In the above relations, the structural strain is denoted as $ S $, stress is $ T $, the electric field is $ E $, and the electric displacement field is $ D $. The material parameters $ {c}_{E} $, $ e $, and $ {\varepsilon }_{rS} $ correspond to the material stiffness, coupling properties, and relative permittivity at constant strain. $ {\varepsilon }_{0} $ is the permittivity of free space.
The density of the PZT-5A is defined as 7750 kg/m3. For the stress-charge constitutive relation, the elastic matrix of PZT-5A is:
The electromechanical coupling matrix of PZT-5A is:
The relative permittivity matrix of PZT-5A is:
Table 4 highlights the material properties of steel in COMSOL. The values are defined by the COMSOL material library by default.
2.2.3. Component multiphysics
The multiphysics included in the model analysis are electrostatics, electrical circuits, solid mechanics, and piezoelectric effects.
For electrostatics multiphysics, the charge conservation, zero charges, and initial values domain were set by default according to the material defined onto the blocks. The piezoelectric charge conservation domain needs to be manually selected. To ensure the electrical connection is correctly connected, the upper surface of the piezoelectric layer is assigned as the terminal and the lower surface is the ground.
The ground and terminal assigned previously will act as the reference for the electrical circuit multiphysics for electrical connections of the piezoelectric beam (series or parallel). For open-circuit connection, a voltmeter is required to measure the voltage across the probe. For the connection that requires load, the voltmeter is replaced with a resistor, and the value is set manually.
In the field of solid mechanics, isotropic loss factors are user-defined for the damping of linear elastic materials on the beam and mechanical damping of piezoelectric materials. The piezoelectric material property constitutive reactions are analyzed based on the stress-charge form, where the parameters used are from the defined material. Fixed constraint boundary conditions are added to the anchor blocks and the rest are free. An inertia load is applied to the beam structure, with an input acceleration of 1 g. The force per unit volume is defined on the structure body load at the z-axis using the following Eq:
The equation is written as '-solid.rho*g_const*acc' in COMSOL, and the 'acc' parameter is defined in the global definition. The solid density is denoted as $ \rho $, the gravitational force is $ g $, and $ Acc $ is the magnitude of the gravitational force. The gravitational force constant is 9.81 m/s2. The input acceleration variation is determined by the magnitude of gravitational force denoted as 0.5, 1, 1.5, and 2 g throughout this paper. The acceleration of 0.5 g represents half the acceleration of vibration magnitude relative to gravity and 2 g is twice the acceleration.
The physics-controlled mesh element size is assigned to be a finer triangular shape for the whole structure. The mesh element size needs to be smaller than the geometry size. The mesh element size will determine the accuracy of the analysis. A smaller element size represents a more accurate analysis; however, it may take a longer running time for the simulation to be completed.
2.2.4. Characterization of the serpentine-shaped piezoelectric cantilever beam model
The serpentine-shaped design was selected to be tested as the piezoelectric energy harvester from the preliminary studies conducted for this project. This preliminary study employs shape analysis to check whether the modification to the geometry, the additions of the beam, and the anchor can affect the performance of the piezoelectric cantilever beam, in comparison to the traditional one-degree-of-freedom. Figure 4 presents the 13 designs that were analyzed in the previous study [71].
According to data collected from the previous study, Table 5 shows that a design (k) with the shape of serpentine with two anchors obtained the highest output of 40.922 V and 27.0099 mW at the resonant frequency of 119.67 Hz, in comparison to design (a), which is a conventional 1DOF piezoelectric cantilever beam that obtained 17.5763 V and 4.9827 mW at the resonant frequency of 198.86 Hz. The serpentine design from this preliminary study was adopted to be further investigated in this paper.
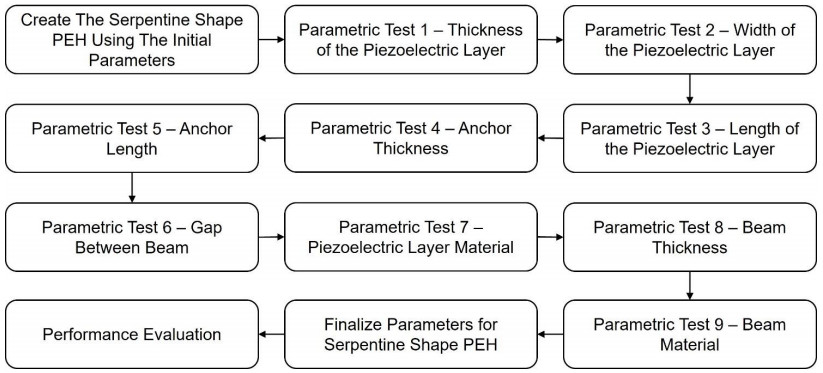
The finite element analysis was carried out on the serpentine-shaped piezoelectric cantilever beam with no proof of mass. The analysis includes characterization of the piezoelectric cantilever beam dimensions such as thicknesses, length, width, and gaps between the beam to obtain an optimal design parameter that can improve its performance. This characterization process is highlighted in Figure 5.
A sinusoidal acceleration is applied to the energy harvester model as the input excitation. In real application, the pipeline's ambient vibrations operate randomly. However, applying sinusoidal input acceleration allows the model to be analyzed through a frequency sweep where a range of frequencies is systematically tested to identify its resonant frequency. The output is evaluated as a function of frequency response for voltage and power, load dependency, acceleration sweep, displacement magnitude, von Mises stress figure, and electric potential figure. The piezoelectric energy harvester cantilever beam vibrates upwards and downwards along the z-axis. The characterization of the dimensions along the x, y, and z axes on the piezoelectric cantilever beam are highlighted in Figure 6 and Table 6.
3.
Results
3.1. Characterization of the model
3.1.1. Parametric test 1—piezoelectric layer thickness
The thickness of the piezoelectric layer ranges from 0.05 to 0.15 cm with intervals of 0.025 cm was tested. The dimension of the piezoelectric layer is set according to Table 3, except for the thickness. This test is conducted to determine the piezoelectric layer thickness that can obtain the highest voltage. The thickness of the piezoelectric layer affects the stiffness of the piezoelectric energy harvester. However, it may increase the electric potential of the piezoelectric layer. Table 7 shows that the piezoelectric layer with a thickness of 0.15 cm has the highest peak output voltage power of 44.9693 V at a resonant frequency of 142.86 Hz.
3.1.2. Parametric test 2—piezoelectric layer width
The width of the piezoelectric layer ranges from 0.5 to 1.5 cm with intervals of 0.25 cm was tested. The dimension of the piezoelectric layer is set according to Table 3, except for the thickness and width. Following the result obtained from Parametric Test 1, the piezoelectric layer thickness is set to be 0.15 cm. This test is conducted to determine the piezoelectric layer width that can obtain the highest voltage. The increment of the piezoelectric layer width may increase the surface area that experiences stress due to the deflection of the piezoelectric layer across the z-axis and thus improve the electric potential. Table 8 shows that the piezoelectric layer with a width of 1.5 cm has the highest peak output voltage of 44.9693 V at a resonant frequency of 142.86 Hz.
3.1.3. Parametric test 3—piezoelectric layer length
The length of the piezoelectric layer ranges from 4 to 6 cm with intervals of 0.5 cm was tested. The dimension of the piezoelectric layer is set according to Table 3, except for the thickness, width, and length. Following the result obtained from Parametric Tests 1 and 2, the piezoelectric layer thickness and width are set to be 0.15 cm and 1.5 cm, respectively. This test is conducted to determine the piezoelectric layer length that can obtain the highest voltage. The increment of the piezoelectric layer length may increase the weight of the beam and thus improve the deflection and stress area. Table 9 shows that the piezoelectric layer with a length of 6 cm has the highest peak output voltage of 44.9693 V at a resonant frequency of 142.86 Hz.
3.1.4. Parametric test 4—anchor thickness
The anchor thickness ranges from 0.2 to 1 cm with intervals of 0.2 cm was tested. The piezoelectric layer will be attached to the anchor, where it will work as the constraint for the piezoelectric cantilever beam. Following the result obtained from Parametric Tests 1, 2, and 3, the piezoelectric layer thickness, width, and length are set to be 0.15 cm, 1.5 cm, and 6 cm, respectively. The dimension of the anchor is set according to Table 3, except for the thickness. This test is conducted to determine whether the thickness of the anchor influences the displacement of the piezoelectric cantilever beam and thus affects its performance.
Table 10 shows that the thickness of the anchor has a low impact on the output values of the piezoelectric cantilever beam. The anchor with a thickness of 0.2 cm has the highest peak output voltage of 44.9731 V at a resonant frequency of 142.86 Hz. However, the thickness of the anchor may limit the deflection of the piezoelectric cantilever; therefore, the anchor thickness is set to 0.6 cm, which can obtain the second highest output voltage of 44.9692 V.
3.1.5. Parametric test 5—anchor length
The anchor thickness ranges from 0.2 to 1 cm with intervals of 0.2 cm was tested. Following the result obtained from Parametric Tests 1, 2, and 3, the piezoelectric layer thickness, width, and length are set to be 0.15 cm, 1.5 cm, and 6 cm, respectively. The dimension of the anchor is set according to Table 3, except for the length. This test is conducted to determine whether the thickness of the anchor influences the stress area of the piezoelectric cantilever beam and thus affects its electric potential. Table 11 shows that the piezoelectric layer with a length of 0.6 cm has the highest peak output voltage of 45.8170 V at a resonant frequency of 152.54 Hz.
3.1.6. Parametric test 6—gap between beam
The gap distance between the beam ranges from 0.2 to 1 cm with an interval of 0.2 cm was tested. Following the results obtained from previous tests, the piezoelectric layer is set to have a thickness, width, and length of 0.15 cm, 1.5 cm, and 6 cm, respectively. The anchor thickness, width, and length are set to be 0.6 cm, 1.5 cm, and 0.6 cm, respectively. The anchor width is not tested and is set to have the same width as the piezoelectric layer. Table 12 shows that a gap distance of 0.8 cm has the highest peak output voltage of 46.8268 V at a resonant frequency of 158.83 Hz.
3.1.7. Piezoelectric material selection
The parametric test of the model was conducted using PZT-5A piezoelectric material. However, different PZT types offer different material properties. Therefore, a material sweep consisting of various PZT types and non-piezoceramic materials was conducted. Table 13 presents the performance of the energy harvester based on the material sweep analysis conducted in COMSOL using the same model. The result shows that PVDF has a lower resonant frequency in comparison to other materials due to its flexibility. Despite that, it produces the lowest output voltage. Meanwhile, PZT-5A was able to produce up to 47.2208 V with a resonant frequency of 159.44 Hz, making it the most suitable material to be used for the model.
3.1.8. Non-piezoelectric beam thickness
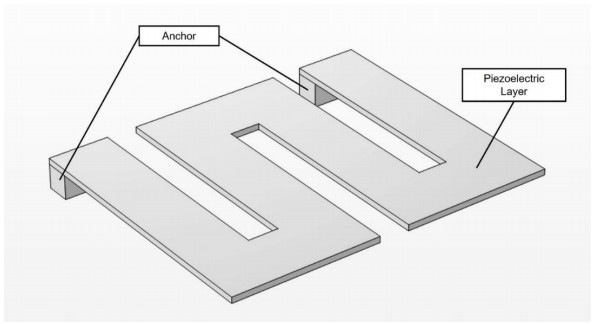
Additional analysis is required where the non-piezoelectric material is added as another layer to support the piezoelectric material, which is called the beam. An illustration of the piezoelectric cantilever beam with piezoelectric and non-piezoelectric layers can be seen in Figure 7. The beam characterization process is carried out by observing the performance of the piezoelectric energy harvester with different beam thicknesses. The characterized thickness values for the beam are set to range from 0.05 to 0.15 cm with intervals of 0.025 cm. Table 14 shows that the beam with a thickness of 0.1 cm produced the highest peak with an output voltage of 11.3433 V at 263 Hz.
3.1.9. Non-piezoelectric beam material selection
The piezoelectric energy harvester undergoes a final test to select the material to be used for the fabrication of the macroscale prototype. Table 15 compiles the results of the material sweep obtained from the analysis for the beam. The results show that the beam layer made of steel contributed to the highest output of 11.3533 V at a resonant frequency of 262.66 Hz.
3.1.10. Parameter after characterization and material selection
Table 16 summarizes the structural parameters and material selection of the serpentine-shaped piezoelectric cantilever beam for the piezoelectric and non-piezoelectric layers based on the parametric test. This parameter specifies the final dimensions for fabricating the serpentine-shaped piezoelectric cantilever beam for the pipeline vibration-based piezoelectric energy harvester. The highlighted parameters can be used to conduct a comprehensive examination of the performance of the energy harvester.
3.2. Performance analysis of the model
Performance for the characterized design of the serpentine-shaped piezoelectric cantilever beam can be analyzed using various methods through a finite element analysis in COMSOL Multiphysics software. A sinusoidal acceleration is applied to the piezoelectric cantilever beam model. The performance analysis of the energy harvester was conducted through the eigenfrequency study and frequency domain study where two datasets for the analysis were generated. The frequency range and parametric sweep can be input into the study setting before running the study. The output is evaluated as a function of the mode of shapes, voltage and power frequency response, load impedance, acceleration magnitude, displacement magnitude, von Mises stress, and electric potential. The same method and studies were used for the characterization process of the serpentine-shaped piezoelectric cantilever beam.
3.2.1. Study 1—eigenfrequency
The eigenfrequency analysis for the model was conducted to identify the first six modes of vibration and their associated frequencies. It is well understood that the piezoelectric energy harvester generates the highest output voltage when the entire system, or specifically the cantilever beam, is excited at its natural frequency. Table 17 compiled the eigenfrequencies of the model.
3.2.2. Study 2—frequency domain—frequency response
The frequency domain study is conducted to construct a frequency sweep plot and identify the resonant frequency of the model. The analysis was conducted by plotting the voltage across 50 Hz to 300 Hz with an interval of 1 Hz.
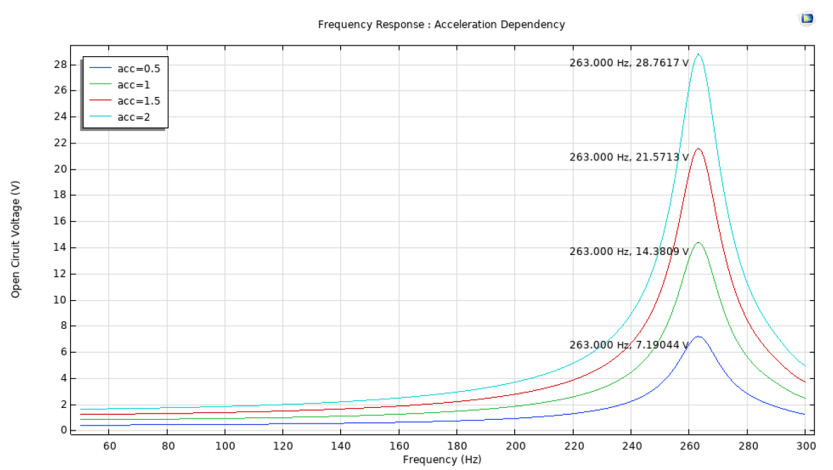
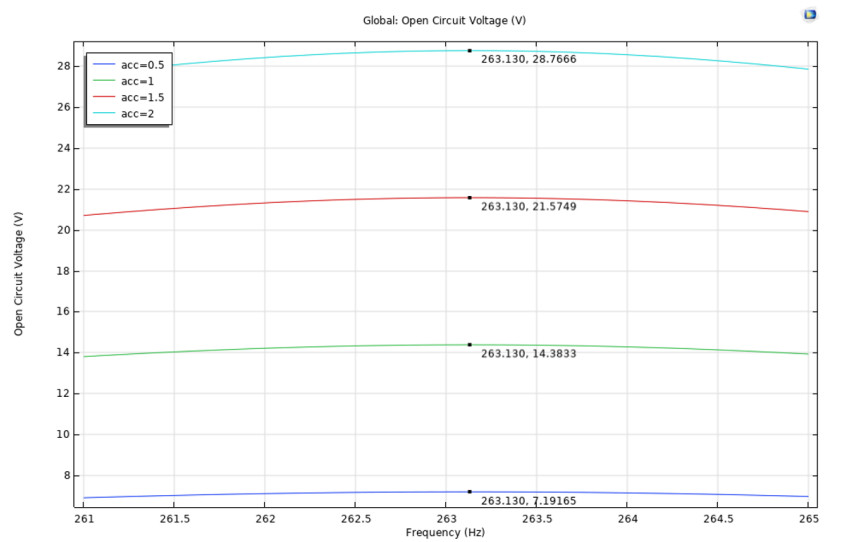
Different input accelerations were applied to check the peak output voltage of the model at its resonant frequency. To obtain a more accurate value of the resonant frequency, the interval can be reduced to a smaller value. However, the running time will increase. To improve the running time speed, the frequency range is reduced. The frequency sweep of the voltage is shown in Figure 8 and 9.
The result from the frequency sweep shows that the model achieved its peak output voltage within the range of 220 to 300 Hz. The peak output voltage increases as the acceleration increases. Figure 9 illustrates the frequency response of the energy harvester using an interval of 0.01 Hz. According to this figure, during the vibration with an input acceleration of 1 g, the model produced an output voltage of 14.3833 V at 263.13 Hz.
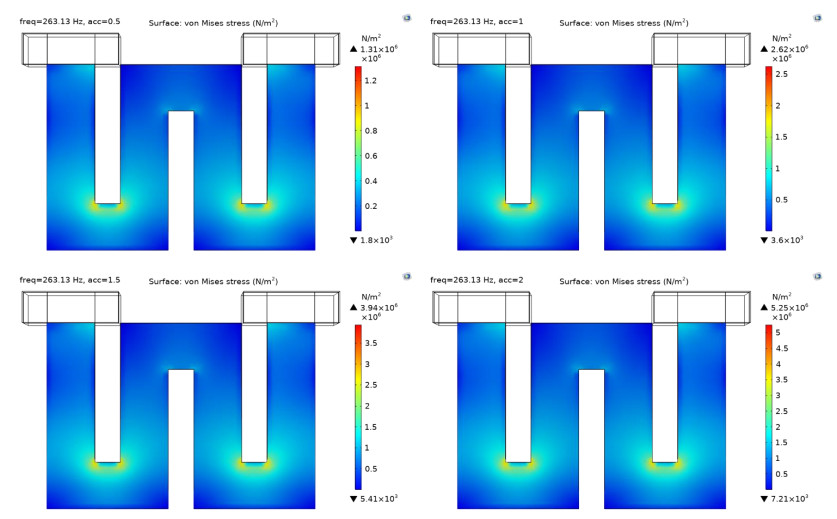
The same frequency sweep dataset was used for additional analysis such as von Mises stress, electric potential, and displacement magnitude on the model. This analysis is conducted to understand the structural performance of the energy harvester that occurs due to the input acceleration of the pipeline vibrations at its respective resonant frequency of 263.13 Hz.
Von Mises stress measures the combined magnitude of all components of stress (tensile, compression, and shear) at any point. The value obtained from the von Mises stress analysis is used to determine if the piezoelectric material will yield or fracture. The stress distribution of the piezoelectric cantilever beam is crucial in determining the electric potential produced by the piezoelectric layer.
The von Mises criterion trend is indicated by the rainbow color-coded maps, which are interpolated from blue to red. The lowest tension is indicated in blue, and the highest tension is indicated in red. The surface areas that experience higher stress can be observed using graphic image mapping generated by the software. Figure 10 illustrates the von Mises stress on the surface area of the model at different accelerations.
The deflection of the inner beam increases the stress area at the connector. It can be seen from Table 18 that the von Mises stress value for the model increases as the acceleration increases. Considering that the von Mises stress is low, it can be assumed that the piezoelectric layer will not break due to the pipeline vibrations.
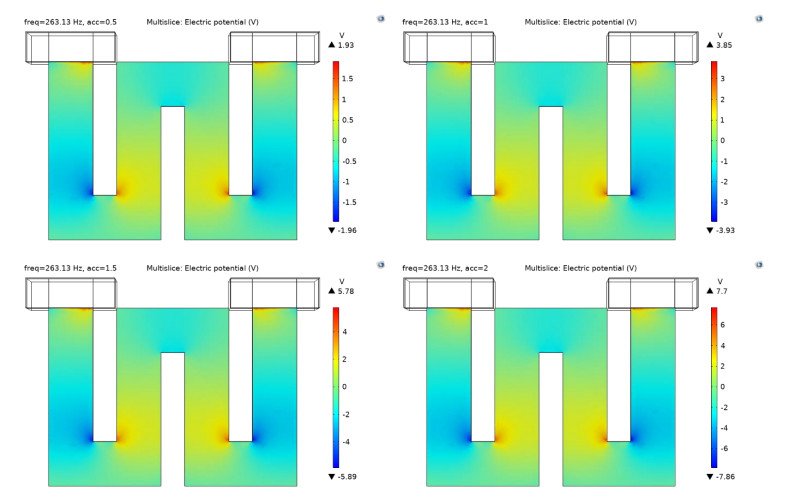
Piezoelectric produce an electric charge proportional to the mechanical stress applied to it. Electric potential is defined as the amount of work done (W) in moving a unit charge (Q) from infinity to a point. It is measured in terms of Joules and is denoted by V. Through this analysis, the electric potential produced by the model with respect to the stress (vibration source) can be obtained. The electric potential criterion trend is indicated by the rainbow color-coded maps, which are interpolated from blue to red. The minimum electric potential is indicated as blue, and the maximum electric potential is indicated as red. Figure 11 illustrates the electric potential distributed on the surface area of the model.
According to Table 19, as the stress exerted on the piezoelectric cantilever beam increases corresponding to the acceleration, it can be seen that the electric potential range of the piezoelectric cantilever beam also gets wider with a bigger total electric potential.
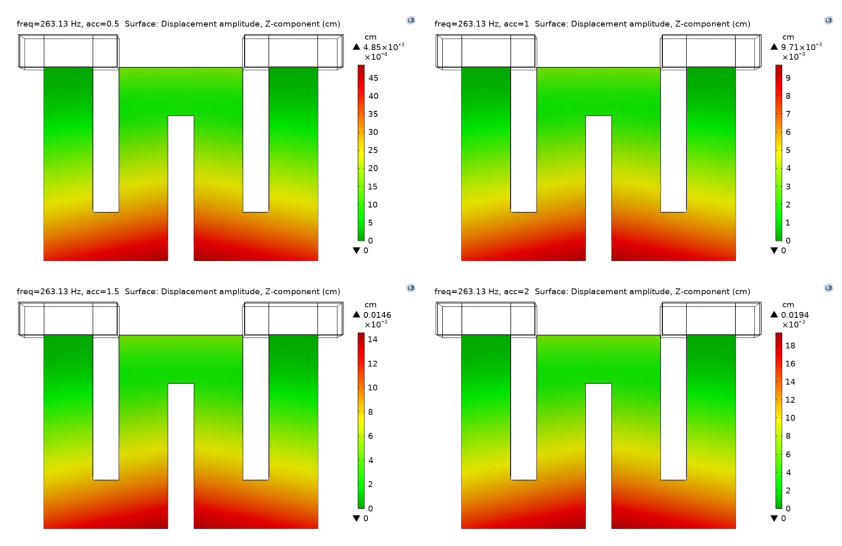
The piezoelectric cantilever beam bends while vibrating (moves up and down) along the z-axis (vertically). The displacement of the cantilever beam is analyzed to check the vibration amplitude of the beam. The bending moment of the cantilever beam at a resonant frequency can be observed through the displacement amplitude value of the model. High displacement results in high stress and thus produces higher electric potential.
The displacement criterion trend is indicated by the traffic light color-coded maps, which are interpolated from green to red. The smaller displacement amplitude is indicated in green, and the larger displacement amplitude is indicated in red. Figure 12 illustrates the displacement amplitude of the model.
The illustration of displacement magnitude for the model shows that the piezoelectric cantilever beam is displaced near the same area. However, the displacement magnitude changed along with the increment of the acceleration. Table 20 shows that the piezoelectric cantilever beam was able to move in the Z-axis direction up to 97.1 μm while operating at 1 g.
3.2.3. Study 3—frequency domain—load dependency
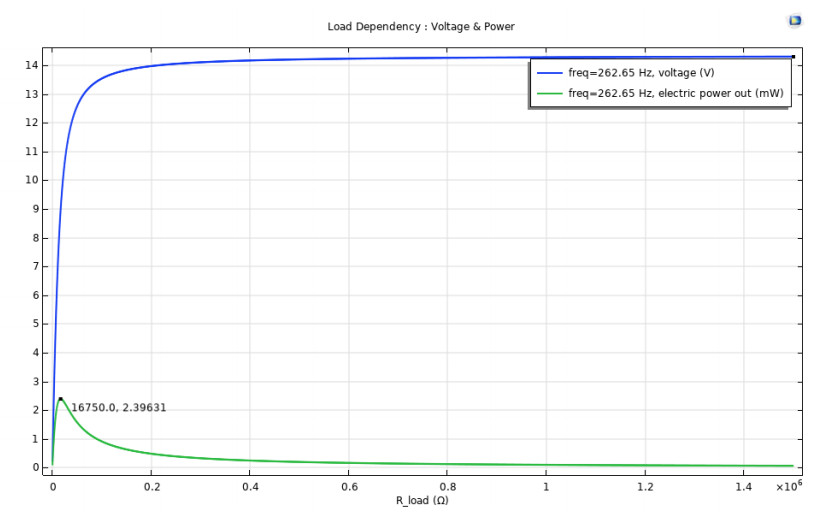
In the open-circuit condition, the model is connected to a voltmeter instead of a resistor. Meanwhile, in short-circuit conditions, the voltmeter is replaced with a resistor where the value of the load resistance is set in the global parameter. A 31 kΩ was used as the test load resistor in the characterization process. To maximize the power output of the piezoelectric cantilever beam, the correct impedance match needs to be identified. The load resistor must be equal to the impedance of the source. A parameter study for the load resistor was conducted to see which value gives maximum power. Due to the nature of the circuit according to Ohm's law, the highest point of the power can only be achieved at its ideal resistance value.
An auxiliary sweep was added into the frequency domain study where load resistance ranged from 250 Ω to 1 MΩ with an interval of 250 Ω. A graph of load resistance versus voltage and power is plotted to identify the ideal range of the load resistance. Voltage increases as the load resistance increases and is concentrated after a certain value. The output power achieved the highest peak at its ideal load resistance range as shown in Figure 13 where the model obtained 2.3963 mW when the load resistance is 16.75 kΩ.
4.
Discussion
4.1. Effect of structural parameters on energy harvester performance
The parametric test was conducted to evaluate the direct influence of the structural parameters on the energy harvester performance. According to the results compiled in Tables 5–10, the modification of structural parameters affects the resonant frequency, the stress area, displacement, and electric potential of the energy harvester.
The flexibility of the energy harvester to deflect in reaction to the pipeline vibrations is dependent on the thickness of the cantilever beam. A cantilever beam with a lower thickness has a higher displacement magnitude in the z-axis direction due to its flexibility. At the same time, this movement causes higher stress exerted on the piezoelectric layer and thus improves its electric potential outcome. A stiffer cantilever beam increased the resonant frequency. Therefore, having a more flexible cantilever beam can reduce the resonant frequency.
Apart from that, based on the stress analysis of the energy harvester, the existence of the inner beam allows the energy harvester to experience displacement on two sides and increase its flexibility.
4.2. Analysis of the energy harvester performance
The performance of the energy harvester can be analyzed based on the open-circuit test and short-circuit test of the model.
The open-circuit study is to analyze the performance of the piezoelectric cantilever beam at its ideal state. The open-circuit situation is defined as an electric displacement that is constant. This occurs because, if the electrodes are open, the charge that was created on them as a result of the material's mechanical deformation stays there, creating a continuous electric displacement in the material. In this case, an electric field is created throughout the material's thickness as a result of the separation of charge between the electrodes.
The short-circuit situation is the state in which the electric field is constant. The electric field across the material stays constant at zero when the electrodes are shorted together because there can be no charge separation between the electrodes. A power source regulates the voltage across the electrodes when a piezoelectric element is utilized as an actuator. To maintain the desired voltage, the power source either adds or subtracts charge from the electrodes. As a result, electrical boundary conditions corresponding to a short circuit or continuous electric field also apply to an actuator connected in this way.
4.2.1. Output voltage of the energy harvester
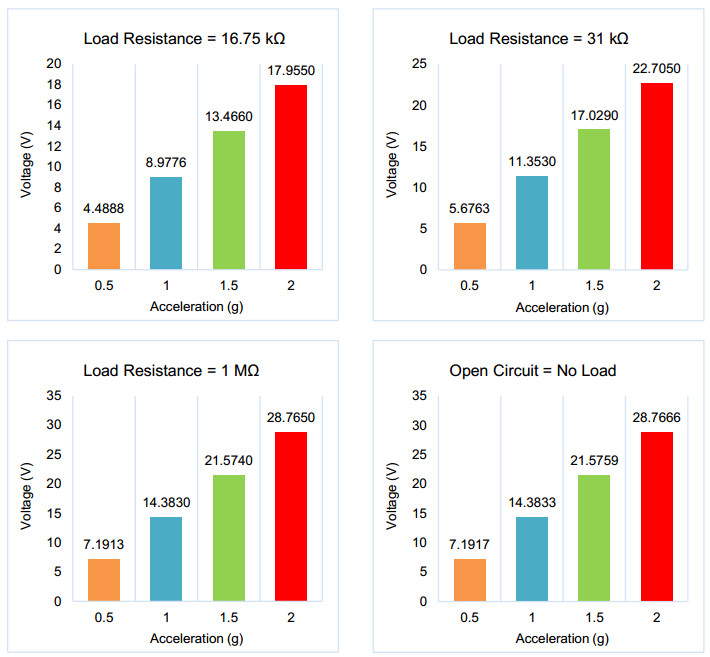
The compiled results show that the open-circuit voltage of the model is higher than its short-circuit voltage. Output voltage produced at different acceleration values is plotted in Figure 14. At an acceleration of 1 g, using the test load resistance of 31 kΩ, the model obtained 11.3530 V at its resonant frequency. Meanwhile, the model obtained 8.9776 V when tested using its ideal load resistance value of 16.75 kΩ. The voltage at 1 MΩ is almost similar to the open-circuit voltage.
4.2.2. Output current of the energy harvester
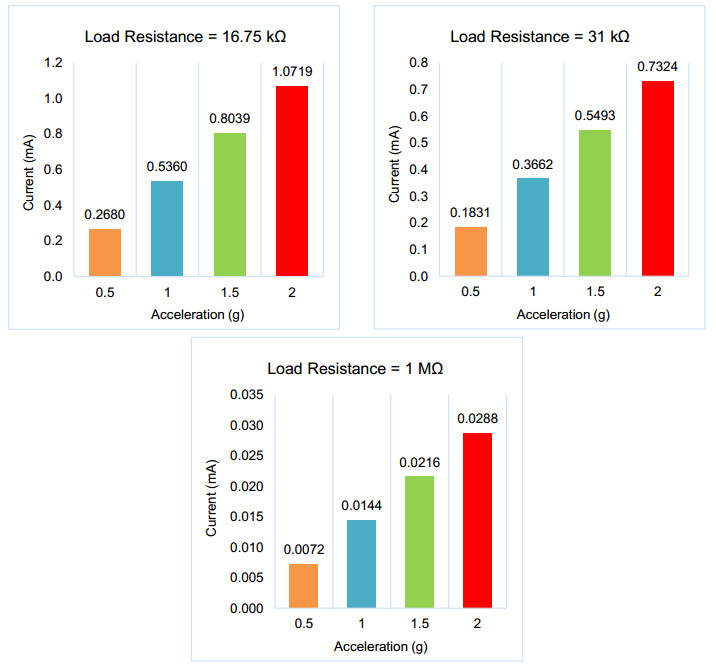
The output current of the model at load resistance of 16.75 kΩ, 31 kΩ, and 1 MΩ are plotted in the figures above. The result from Figure 15 shows that the higher the load resistance, the lower the output current.
At an acceleration of 1 g, the model obtained the highest output current of 0.5360 mW at 16.75 kΩ. The output current of the model with a load resistance of 31 kΩ and 1 MΩ is 0.3662 mW and 0.0144 mW, respectively. In the case of no load, there are no current flows when the circuit is operating in open-circuit conditions.
4.2.3. Maximum output power of the energy harvester
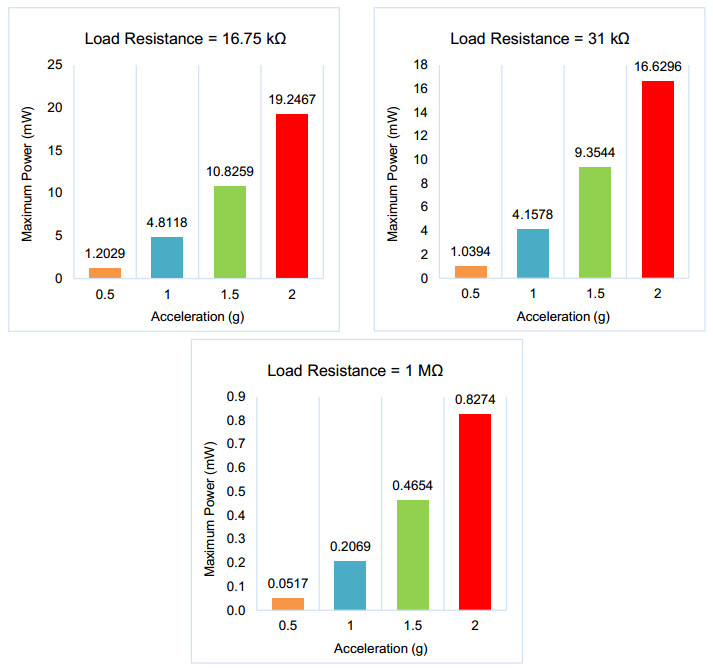
The maximum electrical output power produced by the model can be calculated using Ohm's law. The value of the peak output voltage and current can be obtained when plotting the result from the dataset generated by the frequency domain study.
The maximum power is represented in real values. The calculated values of the maximum electrical output power at different accelerations with 16.75 kΩ, 31 kΩ, and 1 MΩ are plotted in the figures above. The plot of maximum output power indicates that the model achieves a higher range of electrical output power when operating using its ideal load resistance of 16.75 kΩ. In Figure 16, the maximum power obtained by the model at the acceleration of 1 g is 4.8118 mW.
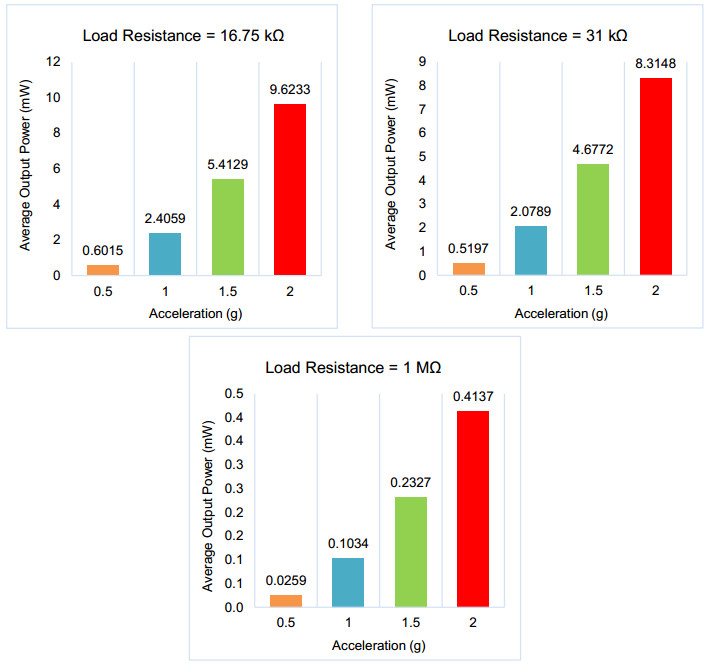
4.2.4. Average output power of the energy harvester
To fully understand the overall performance of the piezoelectric cantilever beam, the average power for the model at each acceleration using 16.75 kΩ, 31 kΩ, and 1 MΩ was tested. According to Figure 17, using the input acceleration of 1 g, the model achieved an average output power of 2.4059 mW, 2.0789 mW, and 0.1034 mW at load resistance of 16.75 kΩ, 31 kΩ, and 1 MΩ, respectively.
4.3. Load dependency of the energy harvester
The piezoelectric cantilever beam only achieved its highest peak output power at its ideal load resistance value and remained lower or concentrated after a certain value. This shows that it is important to determine the ideal and maximum load that can be handled by the piezoelectric energy harvester to achieve the desired output. To ensure the piezoelectric energy harvester is operating efficiently, the maximum load range needs to be identified.
5.
Conclusions
A model of a serpentine-shaped piezoelectric cantilever beam design utilizing pipeline vibrations is simulated and analyzed through FEM using COMSOL Multiphysics software. The model underwent an initial characterization process where the geometric parameters (length, width, thickness) were manipulated to identify the best parameters that can obtain the highest output power within the allowable range of pipeline vibrations level at frequencies of 10–300 Hz.
The frequency bandwidth of the energy harvester was identified to be 220–300 Hz, where the first mode eigenfrequency and resonant frequency of the model is in the range of 262–263 Hz. In open-circuit conditions, the model was able to produce 14.3833 V when an acceleration of 1 g was applied. Through the load dependency test, it is determined that the ideal load resistance required for the model to produce the highest output power is 16.75 kΩ. In the short-circuit condition, the model obtained the highest voltage when the load resistance is 1 MΩ, where the piezoelectric operates similarly to an open-circuit condition. However, the highest maximum output power obtained by the model with acceleration of 1 g is at 16.75 kΩ. The maximum output power produced was 4.8118 mW with an output voltage of 8.9776 V and a current of 0.5360 mA.
The compilation of results based on the analysis conducted for this research agrees with the hypothesis of the study. This study represents meaningful progress in providing a new approach for harnessing vibration energy from pipelines and enhancement of the existing pipeline monitoring system. The table below is a comparison of related studies conducted based on the shape structure of the vibration energy harvester and the research work presented in this paper.
Recommendations for future work include the following: (1) A comprehensive study on improving the efficiency of the energy harvester to operate at a lower frequency by including a proof mass to increase the beam displacement and flexibility, resulting in higher stress and electric potential; (2) the output of the energy harvester can be enhanced using an optimized power management circuit (PMC) where the fluctuating AC output due to irregular vibration can be smoothened and converted to DC output with lower noise; (3) a different structure, such as bimorph, can increase the output voltage of the piezoelectric energy harvester due to an additional piezoelectric layer.
The limitations and functionality of the model require further investigation to identify if the design is suitable for the research application. Other than that, the design can still be improved to produce the best possible outcome. Nevertheless, the simulation results verified that the model has the potential to produce the expected output power for the application.
Use of AI tools declaration
The authors declare they have not used artificial intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors would like to acknowledge the Department of Electrical & Electronics Engineering of Universiti Teknologi PETRONAS for providing the facilities for research development.
Conflict of interest
The authors declare there is no conflict of interest in the writing and publication of this article.
Author contributions
Wan Nabila Mohd Fairuz participated in reviewing the literature related to the study, conducted the methodology through COMSOL Software, compiled the data, provided analysis on the data, wrote the first draft, and revised the manuscript. Illani Mohd Nawi provided supervision on the project and reviewing the manuscript. Mohd Radzi Ahmad is the principal investigator for the project where he initiates the conceptualization, supervise, provide technical advice, and review the final version of the manuscript. Ramani Kannan is the co-supervisor of the project and assists on the research development.
Supplementary Data
Supplementary Data is available online on AIMS Energy website.









 DownLoad:
DownLoad: