A fast second-order block-centered finite difference method for the fractional Cattaneo equation

1.   Introduction

In this paper, we consider the following time fractional Cattaneo equation:

where $\Omega = (x_{L}, x_{R})\; \times\; (y_{L}, y_{R})$, $\partial\Omega$ is the boundary, $T$ is the final time, and $\boldsymbol{n}$ is the unit outward normal to $\partial\Omega$. $p$ is the pressure, $f(x, y, t)$, $\varphi(x, y)$, $\psi(x, y)$ are given known functions, and $a = \text{diag}(a^{x}(x, y, t), a^{y}(x, y, t))$ is a positive definite matrix, i.e., there are two positive constants $a_{\ast}$ and $a^{\ast}$ such that

The Caputo fractional derivative $\sideset{_0^C}{_t^\alpha}{\mathop{D}}p$ is defined by

Equations of this type describe the combined diffusion and wave-like behavior of heat conduction and have been widely used in various fields such as chemistry, biochemistry, thermoelasticity, and fluid mechanics ^[1,2,3]. More discussions of (1.1)–(1.3) are given in ^[4,5].

In recent years, many works have been devoted to numerical methods for the fractional Cattaneo equation. For example, a high-order compact finite difference scheme for the generalized fractional Cattaneo equation was proposed in ^[6], where the Caputo fractional derivative was discretized by the classical $\mathcal {L}1$ formula. Zhao and Sun ^[7] constructed a compact Crank-Nicolson difference scheme for the one-dimensional fractional Cattaneo equation, where both the integer-order and fractional-order time derivatives were discretized by the Crank-Nicolson scheme. Ren and Gao ^[8] developed some compact alternating direction implicit difference schemes for the two-dimensional time fractional Cattaneo equation. Wei ^[9] presented a new finite difference method to approximate the Caputo fractional derivative and then applied it to introduce a fully discrete local discontinuous Galerkin method for the fractional Cattaneo equation. Nikan et al. ^[10] studied a local meshless method for the time fractional Cattaneo model.

The block-centered finite difference (BCFD) method is a powerful tool in computational fluid dynamics ^[11,12,13]. The key idea of this method is to approximate the pressure at the cell center, the $x$-component of velocity at the midpoint of the vertical edges of the cell, and the $y$-component of velocity at the midpoint of the horizontal edges of the cell. The advantage of the BCFD method is that it can guarantee mass conservation and approximate simultaneously the velocity and pressure with second-order accuracy on non-uniform rectangular grids. Recently, the BCFD method has been applied to solve various fractional partial differential equations, such as the time fractional diffusion equation ^[14,15,16], time fractional advection-dispersion equation ^[17], nonlinear fractional cable equation ^[18], and time fractional diffusion-wave equation ^[19]. In particular, the BCFD method combined with the Crank-Nicolson scheme for (1.1)–(1.3) was analyzed in ^[20].

To the best of our knowledge, most of the above methods can only achieve $(3-\alpha)$-order accuracy in time. Moreover, due to the nonlocal dependence of Caputo fractional derivatives, the above methods require the storage of the solutions at all previous time steps, which leads to large computation time and memory. In order to improve computational efficiency, Yan et al. employed the sum-of-exponentials (SOE) approximation to the kernel function and proposed a fast and second-order $\mathcal {F}\mathcal {L}2-1_{\sigma}$ method for the time fractional diffusion equations in ^[21]. Based on the $\mathcal {F}\mathcal {L}2-1_{\sigma}$ formula and a weighted approach, Lyu et al. ^[22] constructed a fast linearized finite difference scheme for the nonlinear time fractional wave equation. Their scheme can achieve second-order accuracy in time and greatly reduces the computational complexity. Subsequently, Bai et al. ^[23] presented a fast second-order finite-difference time-domain method for the time fractional Maxwell system. Although there are some results of fast BCFD methods for the fractional diffusion equations ^[24,25], there are no studies on the fast second-order BCFD method for the fractional Cattaneo equation.

The purpose of this paper is to propose and analyze a fast second-order BCFD method for (1.1)–(1.3). For the spatial discretization, we adopt the BCFD method, and for the time discretization, we apply a proper linear weighted combination of the $\mathcal {F}\mathcal {L}2-1_{\sigma}$ formula for the Caputo fractional derivative ^[22], and establish fitted time approximations for the integer-order terms. Using the special properties of the discrete coefficients and mathematical induction method, we derive the unconditional stability of the proposed method rigorously. Then, by establishing a proper relation between the velocity and the difference of the pressure, we show that the proposed method yields second-order superconvergence in both time and space for the velocity and pressure in discrete $L^{\infty}(L^{2})$-norms on a non-uniform rectangular grid. Compared with the original BCFD method in ^[20], our new method is more accurate and efficient.

The structure of the paper is as follows. In Section 2, we first introduce some notation and basic results, and then develop a fast second-order BCFD method for (1.1)–(1.3), where a special approximation is used for the solution at the first time step. In Section 3, we apply the mathematical induction method to establish the stability of the method. The superconvergent error estimate is derived in Section 4. Finally, in Section 5, three numerical examples are presented to support our theoretical results.

Throughout the paper, we use $C$, with or without subscripts, to denote a generic positive constant, whose value may vary in each occurrence.

2.   The fast second-order BCFD method

To illustrate our fast second-order BCFD method, we introduce the velocity $\boldsymbol{u} = (u^{x}, u^{y}) = -a\nabla p$ and rewrite (1.1) and (1.2) as

For the time discretization, a proper linear weighted combination of the $\mathcal {F}\mathcal {L}2-1_{\sigma}$ formula is applied for the Caputo fractional derivative and fitted time approximations are established for the integer-order terms. Let $N$ be a positive integer, $\tau = \frac{T}{N} < 1$ be the time step, $\sigma = \frac{3-\alpha}{2}$, $t_{\sigma} = \sigma\tau$, and $t_{n} = n\tau, 0\leq n\leq N$. For a smooth function $p$ on $[0, T]$, we define $p^{\sigma} = p(t_{\sigma})$ and $p^{n} = p(t_{n})$. Moreover, we set

The SOE approximation proposed in ^[21,26] reads as:

Lemma 2.1. Let $\beta = \alpha-1$. Then for given tolerance error $\varepsilon\ll1$, and final time $T$, there exist a positive integer $N_{e}$, positive quadrature nodes $s_{j}$, and corresponding positive weights $\omega_{j}$ such that

and the number of quadrature nodes needed is of the order

Denote

For $n = 0$, let

For $n\geq 1$, let

Denote

where

Then, the weighted combination of the $\mathcal {F}\mathcal {L}2-1_{\sigma}$ formula proposed in ^[22] for the Caputo derivative is:

According to ^[27,28,29], we have the following lemmas.

Lemma 2.2. Assume that $p\in C^{4}[0, T]$. Then we have

Lemma 2.3. Assume that $p\in C^{3}[0, T]$. Then we have

Lemma 2.4. The sequence $\{\tilde{b}_{n}\} (n\geq 1)$ satisfies

Lemma 2.5. The sequences $\{ g^{(i+1)}_{0}\} (0\leq i\leq n)$ and $\{g^{(n+1)}_{i}\} (1\leq n\leq N-1, 1\leq i\leq n)$ satisfy

Lemma 2.6. Assume that $u\in C^{2}[0, T]$. Then we have

Lemma 2.7. For any real sequence $\{ F^{n}\} (1\leq n\leq N-1)$, when $\tau$ and $\varepsilon$ are sufficiently small, we have

Lemma 2.8. For integer $n\geq 0$, let $\tau, H$ and $a_{n}, b_{n}, c_{n}, d_{n}, \gamma_{n}$ be non-negative numbers such that

and $\tau\gamma_{n} < 1$. Then

For the spatial discretization, the BCFD method is considered. Let $N_{x}$ and $N_{y}$ be two positive integers. The domain $\Omega$ is partitioned by $\mathscr{G}_{x}\times \mathscr{G}_{y}$, where

For $1\leq i\leq N_{x}$ and $1\leq j\leq N_{y}$, we use the following notations

We assume that $\mathscr{G}_{x}\times \mathscr{G}_{y}$ is regular, that is, there exists a positive constant $C$ such that

Define the grid function spaces:

For a function $\omega(x, y)$, let $\omega_{l, m}$ denote $\omega(x_{l}, y_{m})$, where $l$ may take values $i, i+\frac{1}{2}$ for integer $i$, and $m$ may take values $j, j+\frac{1}{2}$ for integer $j$. Then, we define the differential operators:

For functions $\omega$ and $\psi$, we define the following discrete $L^{2}$ inner products and norms:

For a vector-valued function $\boldsymbol{u} = (u^{x}, u^{y})$, we define the discrete $L^{2}$ norm

For $1\leq i\leq N_{x}$ and $1\leq j\leq N_{y}$, define

Then according to ^[11,20], we have the following lemmas.

Lemma 2.9. If $p$ is sufficiently smooth, then it holds that

Lemma 2.10. If $p$ and $\boldsymbol{u}$ are sufficiently smooth, then for $1\leq n\leq N-1$, it holds that

with the following approximate properties:

Lemma 2.11. For $(v^{x}, v^{y})\in{\boldsymbol{\mathcal {V}}}_{h}$ and $q\in P_{h}$, it holds that

In order to obtain high-order approximations at the first time step, we use the Taylor expansion to get

It follows from Lemmas 2.2 and 2.3 that

which leads to

Define

Then we have

Therefore,

With the above preparations, our fast second-order BCFD method reads as follows: Find $P^{n}\in \mathcal {P}_{h}$ and ${\boldsymbol{U}}^{n} = (U^{x, n}, U^{y, n})\in {\boldsymbol{\mathcal {V}}}_{h}$ such that

with

Here,

3.   Stability of the method

In this section, we study the stability of the method (2.5)–(2.11). The existence and uniqueness of numerical solutions to (2.5)–(2.11) will follow from these stability results.

Taking $(V^{x}, V^{y}, Q_{h}) \in {\boldsymbol{\mathcal {V}}}_{h}\times \mathcal {P}_{h}$, multiplying (2.5) by $h_{i}k_{j}Q_{ij}$, summing over $1\leq i\leq N_{x}, 1\leq j\leq N_{y}$, and using Lemma 2.11, we obtain that for $1\leq n\leq N-1$,

Similarly, for $0\leq n\leq N-1$, it holds that

Theorem 3.1. For sufficiently small $\tau$ and $\varepsilon$, the method (2.5)–(2.11) is unconditionally stable with the following estimate:

where

Proof. To prove the theorem, we only need to show that for $1\leq n\leq N$,

where

Now we prove (3.4) by the mathematical induction method. From (2.6)–(2.11), we easily know that (3.4) holds for $n = 1$. Assume that (3.4) holds for $1\leq n\leq N-1$. Then it is sufficient to show that (3.4) also holds for $n = N$.

A simple computation yields

Thus, choosing $Q = \widetilde{d}_{t}P^{n+1}$ in (3.1) gives

Applying Lemma 2.7 yields

Due to (3.2), we can get

It follows then that

Similarly, using (3.3), we can easily obtain

Using the Cauchy-Schwarz inequality, we have

Substituting (3.7)–(3.10) into (3.6), we conclude that

Summing up (3.11) for $n$ from 1 to $N-1$ and multiplying by $\tau$, we get

Applying Lemma 2.8 to (3.12) gives

By Lemma 2.5, we have

A direct computation shows that

From ^[22], we know that

and

Using Lemma 2.4, (2.8), and (2.9), we obtain

and

Combining estimates (3.13)–(3.19) yields

On the other hand, using the triangle inequality, we have

Substituting (3.21) into (3.20), we get

Now, we discuss the following two cases:

Case (Ⅰ): $\|P^{N}\|_{m}+ \|\widetilde{U}^{x, N-1+\sigma} \|_{x}+ \|\widetilde{U}^{y, N-1+\sigma} \|_{y}\leq \|P^{N-1}\|_{m}+ \|\widetilde{U}^{x, N-2+\sigma} \|_{x}+ \|\widetilde{U}^{y, N-2+\sigma} \|_{y}$.

(ⅰ) If $\|{\boldsymbol{U}}^{N}\|_{TM}\leq \|{\boldsymbol{U}}^{N-1}\|_{TM}$, then $S^{N}\leq S^{N-1}$, and (3.4) follows directly.

(ⅱ) If $\|{\boldsymbol{U}}^{N}\|_{TM}\geq\|{\boldsymbol{U}}^{N-1}\|_{TM}$, then

From (3.5), we get

and thus (3.4) follows directly.

Case (Ⅱ): $\|P^{N}\|_{m}+ \|\widetilde{U}^{x, N-1+\sigma} \|_{x}+ \|\widetilde{U}^{y, N-1+\sigma} \|_{y}\geq \|P^{N-1}\|_{m}+ \|\widetilde{U}^{x, N-2+\sigma} \|_{x}+ \|\widetilde{U}^{y, N-2+\sigma} \|_{y}$.

In this situation, we have

From (3.22), it follows that

(ⅰ) If $\|{\boldsymbol{U}}^{N}\|_{TM}\leq \|{\boldsymbol{U}}^{N-1}\|_{TM}$, then we have

Subcase (1): $S^{N} = \|P^{N}\|_{m}+ \|\widetilde{U}^{x, N-1+\sigma} \|_{x}+ \|\widetilde{U}^{y, N-1+\sigma}\|_{y}$. Then, (3.4) easily follows from (3.23).

Subcase (2): $S^{N} = (2\sigma -1)\|{\boldsymbol{U}}^{N}\|_{TM}\leq (2\sigma -1)\|{\boldsymbol{U}}^{N-1}\|_{TM}\leq S^{N-1}$, which immediately leads to (3.4).

(ⅱ) If $\|{\boldsymbol{U}}^{N}\|_{TM}\geq \|{\boldsymbol{U}}^{N-1}\|_{TM}$, then

From (3.5), we know that

Using (3.23), (3.4) is clarified, and so the proof is finished. □

4.   Superconvergence of the method

In this section, we investigate the superconvergence of the method (2.5)–(2.11).

Let us introduce the error functions:

By (2.4), (2.8)–(2.11), we can easily obtain

Lemma 4.1. Assume that the analytical solution $p$ is sufficiently smooth. Then, it holds that

Proof. Using the Taylor expansion, we have

which, in combination with (2.6) and (2.7), leads to

From (4.1) and (4.2), we then get

and consequently,

Similarly,

We conclude the proof by combining (4.3) and (4.4). □

Using Lemmas 2.2, 2.3, 2.6, 2.9, and (3.1), we easily obtain that for $1\leq n\leq N-1$,

where

and

Using (3.2), (3.3), and Lemmas 2.10 and 4.1, we conclude that for $0\leq n\leq N$,

where

Theorem 4.1. Assume that the analytical solution $p$ is sufficiently smooth. Then for sufficiently small $\tau$ and $\varepsilon$, it holds that

Proof. The proof is similar to that of Theorem 3.1. We only need to apply the mathematical induction method to show

where

By (4.1) and Lemma 4.1, we know that (4.10) holds for $n = 1$. Assume that (4.10) holds for $1\leq n\leq N-1$. Then it suffices to prove that (4.10) also holds for $n = N$.

Taking $Q = \widetilde{d}_{t}\xi^{n+1} = d_{t}\overline{\xi}^{n}$ in (4.5) leads to

Applying Lemma 2.7 yields

By (4.8), we have

and therefore

Similarly, using (4.9), we can obtain

Substituting (4.13)–(4.15) into (4.12) gives

Summing up (4.16) for $n$ from 1 to $N-1$ and multiplying by $\tau$, we conclude that

Using Lemma 2.8, one gets

where

Using (4.2) and Lemma 4.1, we have

Using (4.7) and Lemma 2.5, we obtain

Using (3.16), (3.17), (4.1), and (4.6), we get

By Lemma 2.10, we have

Substituting (4.18)–(4.22) into (4.17), we obtain

Similar to the proof of Theorem 3.1, we can conclude that

Again, we discuss the following two cases:

Case (Ⅰ): $\|\xi^{N}\|_{m}+ \|\widetilde{\eta}^{x, N-1+\sigma} \|_{x}+ \|\widetilde{\eta}^{y, N-1+\sigma} \|_{y}\leq \|\xi^{N-1}\|_{m}+ \|\widetilde{\eta}^{x, N-2+\sigma} \|_{x}+ \|\widetilde{\eta}^{y, N-2+\sigma} \|_{y}$.

In this case, we can obtain $S^{N}\leq S^{N-1}$, and (4.10) follows directly.

Case (Ⅱ): $\|\xi^{N}\|_{m}+ \|\widetilde{\eta}^{x, N-1+\sigma} \|_{x}+ \|\widetilde{\eta}^{y, N-1+\sigma} \|_{y}\geq \|\xi^{N-1}\|_{m}+ \|\widetilde{\eta}^{x, N-2+\sigma} \|_{x}+ \|\widetilde{\eta}^{y, N-2+\sigma} \|_{y}$.

We use (4.23) to obtain

Following similar arguments as in Theorem 3.1, we can get

By combining (4.24) and (4.25), we obtain (4.10), which completes the proof. □

Theorem 4.2. Assume that the analytical solution $p$ is sufficiently smooth. Then for sufficiently small $\tau$ and $\varepsilon$, it holds that

Proof. The proof follows from the triangle inequality, the estimation of $\delta$, and Theorem 4.1. □

Remark 4.1. Theorem 4.2 shows that our method has the second-order temporal accuracy, regardless of the order of the Caputo fractional derivative. It is noteworthy that instead of presenting error estimates for the velocity in discrete $L^{2}(L^{2})$-norm ^[20], we provide rigorous error estimates for the velocity in discrete $L^{\infty}(L^{2})$-norm. Moreover, the application of the SOE approach reduces storage and computational cost. Thus, our method is more accurate and efficient than the original BCFD method in ^[20].

5.   Numerical experiments

In this section, we provide four numerical examples to verify our theoretical results. The first three examples are chosen to demonstrate the accuracy and efficiency of the proposed method for smooth solutions, and the fourth example is chosen to demonstrate the performance of the proposed method for solutions with sharp boundary layers. These examples are taken from ^[20,30] with slight modifications. In all experiments, we choose $\Omega = (0, 1)\times (0, 1), T = 1, a^{x} = a^{y} = 1, \varepsilon = 10^{-9}$, and use the Fast-BCFD method and CN-BCFD method to denote our fast second-order BCFD method (2.5)–(2.11) and the Crank-Nicolson BCFD method proposed in ^[20].

Example 5.1. The initial condition and the right side are chosen according to the exact solution

Example 5.2. The initial condition and the right side are chosen according to the exact solution

Example 5.3. The initial condition and the right side are chosen according to the exact solution

Example 5.4. The initial condition and the right side are chosen according to the exact solution

To compare the accuracy of the Fast-BCFD method and the CN-BCFD method, we take $N_{x} = N_{y} = N$ and compute the solutions on three consecutive meshes with $N = 40, 80,160$. The errors and convergent rates for Examples 5.1–5.3 with different $\alpha$ are shown in Tables 1–3, respectively. These numerical results show that the convergence rates of the velocity and pressure in discrete $L^{\infty}(L^{2})$-norms are all around 2 for the Fast-BCFD method, and are all around $3-\alpha$ for the CN-BCFD method. Clearly, the Fast-BCFD method is more accurate than the CN-BCFD method when $\alpha$ tends to 2.

To compare the computational efficiency of the Fast-BCFD method and CN-BCFD method, we compare the CPU time in seconds of both methods. Since the results for different $\alpha$ are very similar, we only present the results for $\alpha = 1.5$ for brevity. From Table 4, one can check that for small time steps, the Fast-BCFD method is more efficient than the CN-BCFD method.

For Example 5.4, the exact solution exhibits a sharp layer at $x = 0$ and $y = 0$. In order to obtain better accuracy, we adopt the following mesh function:

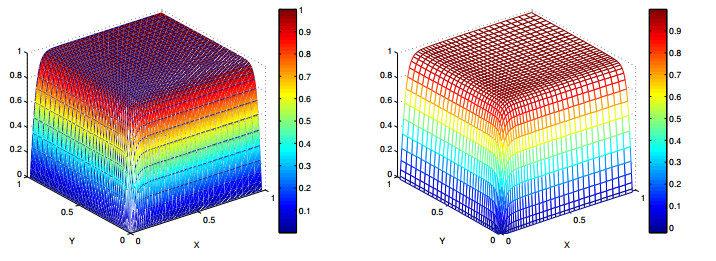
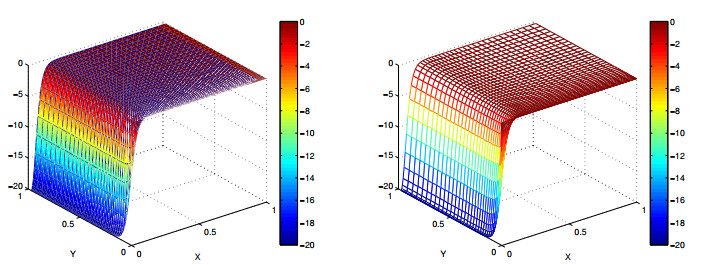
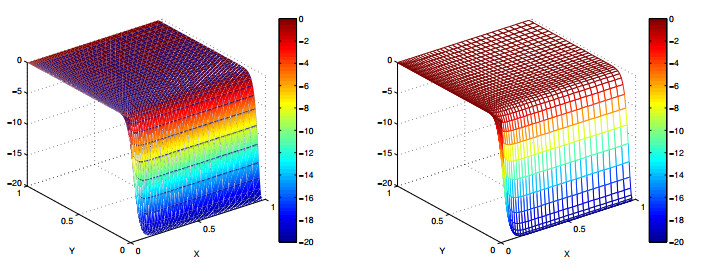
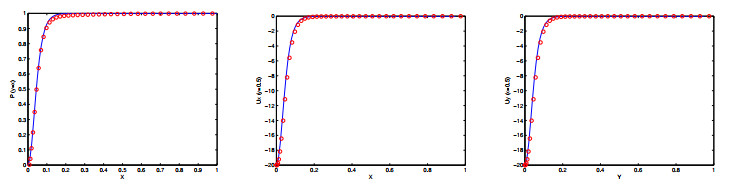
Numerical results for this example with $\alpha = 1.9$ are summarized in Table 5. Obviously, it can be seen that numerical results using a non-uniform grid are also in agreement with our theoretical analysis. Figures 1–3 depict the graphs of the exact solutions and the numerical solutions computed by the Fast-BCFD method at time $T = 1$ on the non-uniform $40\times40$ mesh when $\alpha = 1.9$. For a better comparison, Figure 4 shows the computed pressure profiles along $y = x$, $u^{x}$-velocity profiles along $y = 0.5$, and $u^{y}$-velocity profiles along $x = 0.5$. One can observe that our numerical solutions are in good agreement with the exact solutions.

6.   Conclusions

In this paper, a fast second-order BCFD method based on the $\mathcal {FL}$2-$1_{\sigma}$ formula and a weighted approach was presented for the two-dimensional time fractional Cattaneo equation. The corresponding stability and superconvergence analysis on non-uniform rectangular grids were obtained. The accuracy and efficiency of the proposed method were shown by four numerical examples.

Use of Generative-AI tools declaration

The author declares he has not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the Natural Science Foundation of Ningxia (No. 2023AAC03002).

Conflict of interest

The author declares no conflicts of interest.