1.
Introduction
Of concern is proposing a numerical scheme based on a high-order finite difference/Legendre-Galerkin spectral method for solving the coupled Gross¢Pitaevskii equations in the dimensionless form with time and space fractional derivatives:
with the initial conditions
and the homogeneous boundary conditions
such that Ω=(a,b)⊂R and I=(0,T]⊂R. The parameters δ,β11, β12, β21, β22 and λ are constants to be given and ϕ0(x) and ψ0(x) are given smooth functions.
The temporal fractional derivative is defined in Caputo sense [26], which means
The spatial fractional operator of Riesz type of order α with respect to a≤x≤b [26], namely
where aDαxΨ(x,t) and xDαbΨ(x,t) are the left- and right-Riemann–Liouville derivatives of order α with respect to x∈(a,b), and are defined as
and
Bose and Einstein predicted theoretically Bose-Einstein condensations (BEC) which were detected experimentally by Anderson et al. in 1995 [4]. The link between the spin angular momentum of the electron spin and the orbital angular momentum was performed by the spin-orbit (SO) coupling such as Rasha type and Dresselhaus type. The SO coupling had been extensively discussed experimentally. Bosons and fermions SO coupling was achieved by Jacob et al. in 2008 [20]. A non-dimensionalization and dimension reduction were applied in [12,40]. Then, a two-component BEC with an internal atomic Josephson junction (or an external driving field) can be well modeled by coupled Gross-Pitaevskii equations in dimensionless form.
Lately, Laskin extended the Feynman path integral approach over the more general Lvy-like quantum paths and derived a fractional Schrödinger equation, which modifies the integer equation by invoking the fractional Laplacian. It has been proposed to study BEC of which the particles obey a non-Gaussian distribution law [10,31,32], where fractional Schrödinger was named as fractional Gross¢Pitaevskii Equation (FGPE) and BEC as fractional BEC.
Due to the nonlocality of fractional differential operators, the numerical solutions of the fractional models are more complicated than the classical models. There are several analytical methods to solve fractional differential equations. However, analytical methods do not work well on most of the fractional differential equations, e.g. with nonlinearities or linear equations with time-dependent coefficients. From the numerical implementation point of view, the time-dependent Gross¢Pitaevskii equation describing the dynamics of rotating Bose-Einstein condensates and its discretization with the finite element method were considered in [19]. The approach in [14] exerted some efforts to propose a finite-difference method based on weighted-shifted Grünwald differences for solving the multi-dimensional Gross¢Pitaevskii equation, which considers fractional derivatives of the Riesz type in space, a generalized potential function and angular momentum rotation. An analysis based on a compact finite difference scheme was proposed in [33] for the integer-order coupled Gross¢Pitaevskii equations in one space dimension. That scheme can conserve the total mass and energy at the discrete level. In [21], a sine pseudo-spectral/difference scheme that preserves the discrete mass and energy was produced and analyzed for the integer-order coupled Gross¢Pitaevskii equations with Dirichlet boundary conditions in several spatial dimensions. The approach in [23] was devoted to analyzing the convergence of explicit finite difference schemes for computing the integer-order coupled Gross¢Pitaevskii equations in high space dimensions.
The combination of the efficiency of finite difference quotients based interpolation formulas of L1 or L2-1σ [3] and Galerkin Legendre spectral method is widely used to solve numerically different kinds of fractional order differential problems. For fractional diffusion problems, we refer to [13,36]. For the distributed-order weakly singular integral-partial differential model, we refer to [1]. For nonlinear fractional Schrödinger equations with Riesz space-and Caputo time-fractional derivatives, we refer to [35]. For a coupled system of time and space fractional diffusion equations, we refer to [17]. The propagation of solitons through a new type of quantum couplers called time-space fractional quantum couplers was presented in [18]. Concerning the Gross¢Pitaevskii equation arising in Bose-Einstein Condensation [25] as a generalization of the nonlinear fractional Schrödinger equations, numerous extensions to relevant physical situations are now clarified [6,5,8] (multi-components, nonlocal nonlinear interactions, etc.). For the fractional case, the situation is more complicated and still needs to be analyzed deeply. Serna-Reyes et al. [27] introduced and theoretically analyzed various numerical techniques for approximating the solutions of a fractional extension of a double condensate system that extends the well-known Gross¢Pitaevskii equation to the fractional scenario with two interacting condensates. Antoine et al. [7] proposed numerical schemes for time or space fractional nonlinear Schrödinger equations with some applications in Bose-Einstein condensation. Ainsworth and Mao [2] established the well-posedness of the fractional partial differential equation which arises by considering the gradient flow associated with a fractional Gross¢Pitaevskii free energy functional and some basic properties of the solution. Zhang et al. [39] studied the ground and first excited states of the fractional Bose¢Einstein condensates which are modeled by the fractional Gross¢Pitaevskii equation. They used the weighted shifted Grünwald¢Letnikov difference method to discretize the Gross¢Pitaevskii equation. Liang et al. [22] introduced efficient local extrapolation of the exponential operator splitting scheme to solve the multi-dimensional space-fractional nonlinear Schrödinger equations including the space-fractional Gross-Pitaevskii equation, which is used to model optical solitons in graded-index fibers.
In this paper, our goal is to numerically solve (1.1a)-(1.1b) by implementing a combined high-order numerical approach. This approach is based on the Alikhanov high-order interpolation scheme to be used to approximate the time Caupto fractional derivatives side by side to a Galerkin-type formulation base on Legendre orthogonal polynomials basis to approximate Riesz space fractional derivatives. We used the recently introduced discrete fractional Grönwall inequalities [24] in discrete energy estimates to prove the unconditional convergence of the proposed scheme.
2.
Numerical scheme
We fix the following notations.
● (⋅,⋅)0,Ω denotes the inner product on the space L2(Ω) with the L2-norm ‖⋅‖0,Ω and the maximum norm ‖⋅‖∞.
● C∞0(Ω) denotes the space of non-singular functions with compact support in Ω.
● Hr(Ω) and Hr0(Ω) are Sobolev spaces with the norm ‖⋅‖Hr and semi-norm |⋅|Hr.
● PN(Ω) is the space of polynomials on Ω of degree less than or equal to N.
● The approximation space V0N is defined as
● IN is the interpolation operator of Legendre-Gauss-Lobatto type, IN:C(ˉΩ)→VN,
We also define function spaces [11] which will be used in the construction of the numerical scheme.
Definition 1 (Fractional Sobolev space). The fractional Sobolev space Hη(Ω) for η>0, is defined as
endowed with the semi-norm and norm respectively as
such that Hη0(Ω) is the closure of C∞0(Ω) with respect to ‖⋅‖Hη(Ω). Also, F(˜Ψ) is the Fourier transformation of the function ˜Ψ and the zero extension of Ψ outside Ω denoted by ˜Ψ.
Lemma 1 (Adjoint property). By choosing 1<η<2, then ∀Ψ∈Hη0(Ω) and ν∈Hη/20(Ω), we deduce
Discretization
The temporal domain I is partitioned by tj=jτ, j=0, 1,…,M with τ=T/M. Denote tj+σ=(j+σ)τ=σtj+1+(1−σ)tj, for j=0, 1,…,M−1. We take Ψj+σ=Ψj+σ(⋅)=Ψ(⋅,tj+σ).
Definition 2. Let 0<β<1 and σ=1−β2. Then we define
and
Lemma 2 (see [3]). L2-1σ interpolation formula is given as follows. Assume that Ψ(t)∈C3[0,tj+1], 0≤j≤M−1, is formulated as
where δtΨr=Ψr+1−Ψr.
It can be also given as follows
where d(0,β,σ)1=−d(0,β,σ)0=σ1−β ∀j=0, and ∀j≥1,
Accordingly, L2-1σ Alikhanov formula at the node tj+σ is defined as
Lemma 3. Taylor's theorem can be used directly to obtain that identity
Initiating by L2-1σ formula (2.7) to discretize the time Caputo fractional derivative of (1.1a), leads to
Define the following parameters
Then (2.9) has that equivalent form:
then, the full discrete scheme is to find ψj+1N, ϕj+1N∈V0N, j≥0, ∀ν∈V0N such that
where PN is a projection operator.
3.
Iterative algorithm implementation
Jacobi polynomials Jα,βi(x) by the aid of Via the hypergeometric function can be (for α,β>−1 and x∈(−1,1)) as [29]:
such that the notation (⋅)i represents the symbol of Pochhammer. Then, the equivalent three-term recurrence relation can be yielded
where
The Legendre polynomial Li(x) is a special case of the Jacobi polynomia. This means
The weight function which makes the orthogonality of Jacobi polynomials valid is given as ωα,β(x)=(1−x)α(1+x)β, i.e.,
where δij is the Dirac Delta symbol, and
Lemma 4 (see for example [34]). For α>0, one has
We introduce the following rescale functions:
and we write ∧(x) as ˆx. The basis functions selected for the spatial discretization are given by [37,28]:
The function space V0N can be specified as follows:
The approximate solutions ψj+1N and ϕj+1N may be expressed as
where ˆψj+1i and ˆϕj+1i are the unknown expansion coefficients to be determined. Choosing v=φi, 0≤i≤N−2. Then, the matrix representation of the Alikhanov L2-1σ Legendre-Galerkin spectral scheme has the following representation:
where
Lemma 5 (see [37,29]). The elements of the stiffness matrix S are given by
where
and {x−α2,−α2r,ϖ−α2,−α2r}Nr=0 are Jacobi-Gauss points and their weights with respect to the weight function ω−α2,−α2. The mass matrix ˆM is symmetric and its nonzero elements are given as
Monitoring Hj+1,rq=Hj+1q(ψj+1,rN,ϕj+1,rN), q=1,2, r≥0. Then, the linear system (3.11) can be solved by the following iteration algorithm 1:
4.
Convergence analysis
We fix C to be a generic positive constant which may differ from one inequality to another and is independent of τ, N, and n. Firstly, the following lemma is devoted to introducing the property of the projector operator PN.
Lemma 6 (see [38]). ∀Ψ∈Hα20(Ω)∩Hs(Ω), there exists PN such that:
where ϵ and s are real numbers satisfying s>α2.
The interpolation operator IN achieves the following property:
Lemma 7 (see [29]). Suppose that Ψ∈Hs(Ω) (s≥1). Then,
and the constant C>0 is independent of N.
Lemma 8 (see [30]). For any complex functions Ψ,Φ,ψ and ϕ, we have
Lemma 9 (see [3]). Assume the existence of an absolute continuous function Ψ(t) in [0,T]. Then,
Lemma 10 (Grönwall inequality [26,9]). Let Ψ(t)≥0 be a non-negative function which is locally integrable on [0,+∞] such that |0DβtΨ(t)≤λΨ(t)+b. Then, we have Ψ(t)≤Ψ0Eβ(λtβ)+btβEβ,1+β(λtβ), where the Mittag-Leffler function Eβ(z) and the generalized Mittag-Leffler function Eβ1,β2(z) are defined by
Lemma 11 (see [26,9]). For 0<β1<2, and β2∈R, we assume that there exists μ such that πβ1/2<μ<min(π,πβ2). Then, also there exists a constant C=C(β1,β2,μ) such that |Eβ1,β2(z)|≤C1+|z|, for μ≤|arg(z)|≤π. In addition, if β1∈(0,1), then we have the following properties
By fixing the following notation, and if we denote
then for 1<α≤2, the semi-norm and the norm are defined by
and for any u, v∈Hα/20(Ω). Then, there exist positive constants C1, C2 such that
The orthogonal projection operator PN:Hα20(Ω)→V0N satisfies
Lemma 12 (see [3]). Let Ψ(t) be any function defined on Ω and 0<α<1. If Ψ(σ)=σΨj+1+(1−σ)Ψj then
Lemma 13 (L2-1σ discrete fractional form of Grönwall inequality [24,15]). Suppose that the non-negative sequences {ωj,gj|j=0,1,2,...} satisfy |0Dβτωj+σ≤λ1ωj+1+λ2ωj+gj. Then, there exists of a positive constant τ∗ such that
whenever τ≤(τ∗)β=1/(2Γ(2−β)λ1) and
4.1. Semi-discrete form convergence analysis
Theorem 1. Let {0<β<1,1<α<2,s≥1}. Assume that the solutions {ψ,ϕ} and {ψN,ϕN} of (1.1) and (2.9), respectively, are bounded. Thus, satisfying {ψ,ϕ}∈H1(I;Hα20(Λ)∩Hs(Λ)), such that the external potential function V=V(x) satisfies V∈C(Ω). Then, we get
Proof. The variational formulation is derived by taking the inner product of (1.1a) with v1,
Let e=ψ−ψN, ζe=ψ−PNψ and ηe=PNψ−ψN. Then, we get e=ζe+ηe. Also, let E=ϕ−ϕN, ζE=ϕ−PNϕ and ηE=PNϕ−ϕN. Hence, we get E=ζE+ηE. Now, making use of Lemma 6 and in the case of α≠32, then the following two estimates are obtained:
Subtracting (4.10) from (2.11), then we get
The orthogonality of PN, yields
Taking the inner product of (4.13) with ηe and noting (4.6), and choosing the imaginary part of the resulting equation, we get
Similarly, the imaginary part of the error difference equation concerned with (1.1b) and its semi discrete approximation in (2.11) has the following form
Adding (4.15) and (4.16), and noticing that
yields
Define
then assuming the boundness of the exact solutions {ψ,ϕ} and the approximate solutions {ψN,ϕN} for the system (1.1a)-(1.1d) and invoking Lemma 8 give
Similar analysis leads to
Define G(ε)=|ε|2ε, and making use of Cauchy-Schwarz inequality, we deduce
By Lemma 7, we have
Also,
accordingly and after some rather manipulations and invoking Lemma 9, we finally get
An implementation of Lemmas 10 and 11, yields that (‖ηe‖+‖ηE‖)2≤c7N−2s. The other inequality can be achieved in a similar fashion if α=32 and 0<μ<12. □
4.2. Full-discrete form convergence analysis
Theorem 2 (Convergence of the uniform L2-1σ – Galerkin spectral scheme). Let {ψ,ϕ} and {ψnN,ϕnN} be solutions of (1.1) and (2.9), respectively, with the condition that the external potential function V=V(x) satisfies V∈C(Ω) and suppose that the unique solution {ψ,ϕ}∈L∞([0,T;Hα20(Ω)∩Hs(Ω)) is sufficiently regular in temporal and spatial directions, bounded and ∂βψ∂tβ,∂βϕ∂tβ∈L∞([0,T;Hα20(Ω)∩Hs(Ω)). Then, a positive constant τ∗ is existed such that when 0<τ≤τ∗, the Galerkin spectral scheme (2.9a)–(2.9b) admits a unique solution {ψnN,ϕnN} satisfying
where C is a positive constant that has no dependence on n, τ and N.
Proof. The next variational formula is derived by taking the inner product of (1.1a) with v1,
Let e=ψ−ψN, ζe=ψ−PNψ and ηe=PNψ−ψN, then we get ej+σ=ζj+σe+ηj+σe. Also, let E=ϕ−ϕN, ζE=ϕ−PNϕ and ηE=PNϕ−ϕN, then we get Ej+σ=ζj+σE+ηj+σE. Using Lemma 1, in case of α≠32, we get
Subtracting (4.23) from (2.11), then we obtain
The orthogonality of the operator PN, enables one to write
Taking the inner product of (4.26) with ηj+σe and noting (4.6) and choosing the imaginary part of the resulting equation, we get
Similarly, the imaginary part of the error difference equation related with (1.1b) and its fully discrete approximation in (2.11) has the following form
Adding (4.28) and (4.29), and noticing that
gives
Proceeding as in the proof of Theorem 1, we finally get
Applying the L2-1σ discrete fractional form of Grönwall inequality in Lemma 13, the final result (4.21) is achieved directly. Similarly, we can get the result (4.22) when α=32. This completes the proof of the theorem. □
The stability analysis can be proved similarly following [16].
5.
Numerical experiments
Example 1. Consider the following fractional order Gross–Pitaevskii coupled system:
with homogeneous boundaries
f1(x,t) and f2(x,t) can be deduced by considering the exact solutions
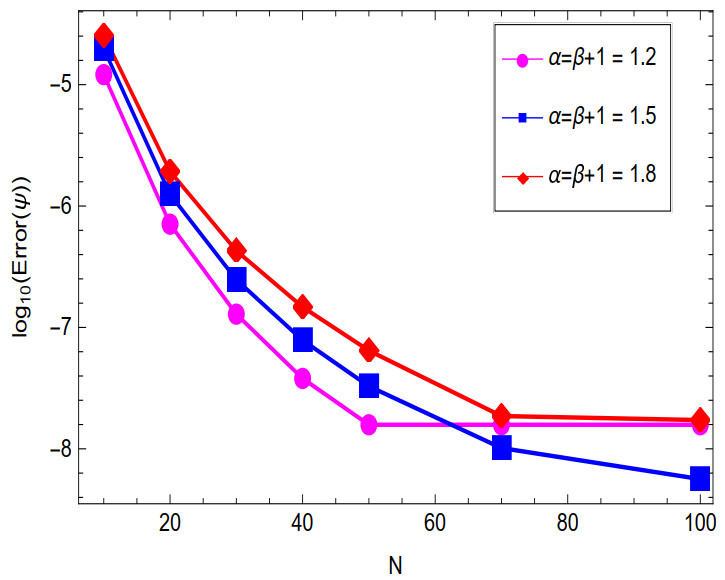
By specifying, α=β+1=1.2, 1.5, 1.8 and N=100 for ϕ and ψ, respectively. It can be shown from Tables 1 and 2, that the resulting L2-errors and the corresponding temporal convergence orders support the theoretical results with convergence order close to 2 in case of the smoothness of the solution. A spectral accuracy of convergence is also shown in Figures 1 and 2 by specifying M=1600 for different α and β.
Example 2. Consider the following Gross¢Pitaevskii system
with the initial conditions
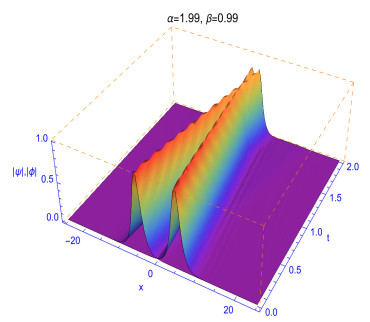
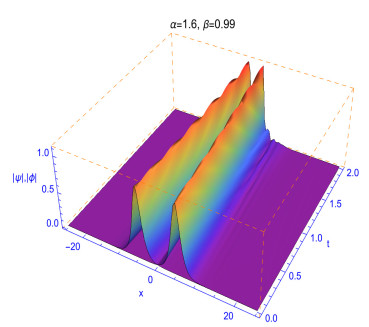
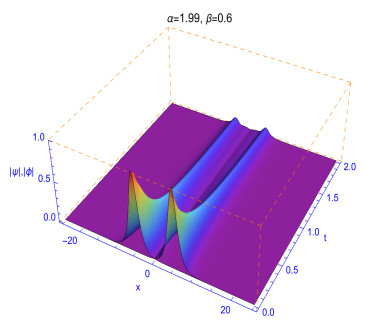
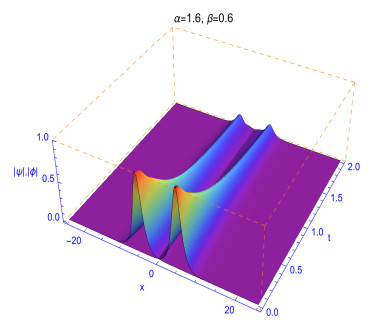
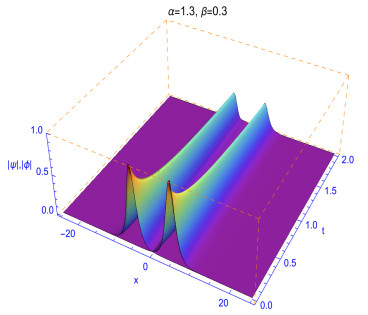
The fractality effects in time with respect to 0<β≤1 and in space with respect to 1<α≤2 affect directly the shapes and stability of the soliton solutions. This can clearly reflected in the numerical solutions given in Figures 3, 4, 5, 6 and 7. The performance of the solutions is represented in the following manner as can be observed from the different experiments. When α≠2 and β≠1, the collision is not elastic and so an influence on the shape of solutions is observed. It can be also observed that the decrease in α values could make the shape of solitons changes faster. As observed in Figures 5, 6, 7 and 8, we conclude that different decay properties in the time direction coming from distinct selections of the fractional-order parameters β. These characteristics can be used in physics to tunable the sharpness of the space-time fractional Gross¢Pitaevskii equations by changing the space fractional order α and the time fractional order β without changing the nonlinearity and dispersion effects.
6.
Conclusions
A high order (second temporal order and a spatial spectral accuracy) convergent numerical approach has been investigated for solving a system of fractional order coupled Gross Pitavskii equations. An algorithmic implementation of the scheme is given to simplify its numerical implementation. A theoretical analysis of the scheme shows unconditional convergence towards the true solution. This is also proven by giving some numerical experiments.
Conflict of interest
The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
M. A. Zaky and A. Aldraiweesh extend their appreciation to the Distinguished Scientist Fellowship Program (DSFP) at King Saud University (Saudi Arabia).
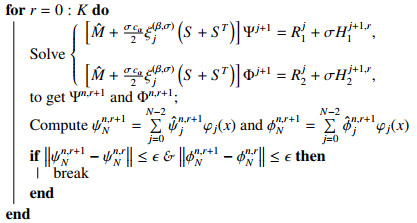









 DownLoad:
DownLoad: