On the well-posedness of the "Bando-follow the leader" car following model and a time-delayed version

1.   Introduction

Neuroblastoma (NB) presents as the most common and aggressive extracranial solid childhood tumor [1],[2]. This malignant tumor arises from neural crest progenitor cells. Primary lesions appear on the migration path of these cells during embryogenesis: abdomen (60–80%), chest (15%), neck (2–5%), pelvis (2–5%) [1],[2]. Pediatric NB accounts for 6–10% of all childhood cancers [1],[2]. The clinical prognosis varies from spontaneous regression to malignant progression [1],[2]. The most important and unfavorable clinical prognostic markers are over 18 months of age at diagnosis and an advanced tumor stage according to the International Neuroblastoma Staging System (INSS) [1]–[4]. NB can be considered a “genetic disease” [1]–[7]. In very rare familial neuroblastoma cases germline mutation in ALK or PHOX2B gene was identified [1]–[7]. A large number of recurrent somatic genetic alterations have been described in this tumor's tissue [8]–[12]. It has been determined that the spectrum of sequence variants associated with clinical outcome and therapeutic application includes the following genes: ALK, ATRX, ARID1, BARD1, LMO1, TERT, TP53 or RAS/MAPK signaling components [8]–[12]. Moreover, rapid tumor progression in NB is associated with MYCN amplification (MNA) and segmental chromosomal aberrations (SCA) [1]–[6]. MYCN amplification occurs in approximately 25% of all NBs and is the most powerful genetic predictor of poor outcome [1]–[6]. The incidence of SCA increases with NB's dissemination up to 59% in the most advanced 4 stage according to INSS [13]–[15]. Recent studies have shown that NB progression, especially to the bone marrow, is associated with accumulation of SCA in primary tumor cells, mostly in older patients. Alternatively, numerical chromosomal alterations (NCA) are observed more frequently in tumors of younger children, with localized disease and good prognosis [7],[13]–[16].

The aim of the study was to identify NCA typical for NB. Over a few decades, well-defined SCA associated with poor prognosis in NB children have been established, e.g., loss of 1p, 3p, 4p, 6q, 9p, 11q, 15q, 18q and gain of 1q, 2p, 12q, 17q [1],[6],[13]–[16]. However, so far no studies have been undertaken to identify NCA that may group NB patients. Identifying effective diagnostic biomarkers for NB is particularly important, in order to optimize treatment. Recent technological advances, such as array CGH (array comparative genomic hybridization), enable the analysis of chromosomal markers in a single step and allow one to define genomic profiles associated with clinical features in NB [13],[17],[18].

2.   Materials and methods

Pangenomic copy number profiling of NB primary tumors was performed with a cytogenetic microarray tool using DNA extracted from fresh samples (N = 94) and formalin-fixed paraffin-embedded (FFPE) specimens (N = 66). Biological samples were analyzed in the Laboratory of Molecular Genetics at the University Children's Hospital in Krakow from June 2016 to August 2021. FFPE tissues were initially de-waxed with xylene and subsequently washed with ethanol. Genomic DNA was extracted from samples with a DNA Tissue Kit (KURABO Industries Ltd, Osaka, JAP) and quantified by OD at 260 nm using a NanoDrop ND-1000 (NanoDrop Technologies, Inc., Wilmington, DE). A total of 200 ng of DNA was used for the manufacturer's array CGH protocol (SurePrint G3 CGH ISCA v2 8x60K, Agilent Technologies, Santa Clara, CA). Copy number alterations in NB tumor genomes were identified using the dedicated software (CytoGenomics 2.9.2.4., Agilent Technologies, Santa Clara, CA) and verified manually. A detection limit of 150 kb was established for appropriate detection of structural chromosomal abnormalities. Categorical variables were coded as a set of binary variables. The χ²-test was used to identify the variables, with a P-value of p ≤ 0.05.

3.   Results

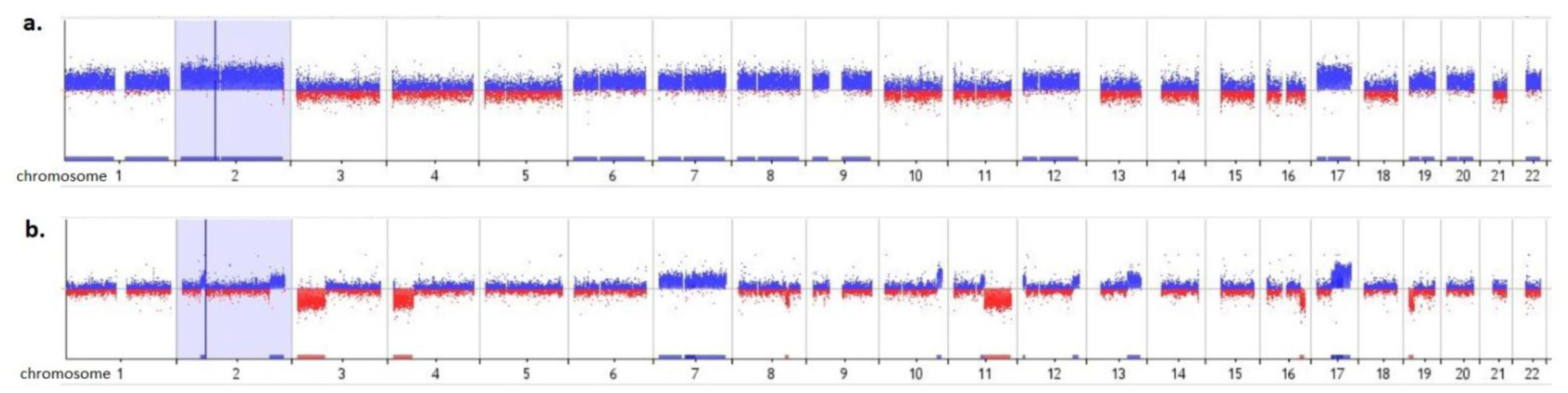
Among 160 NB tumors examined by array CGH, an NCA profile was observed in 72 (45%) cases (Figure 1a and Table 1) and 37 (23%) presented NCA combined with SCA (Figure 1b and Table 1). In analyzed patients 16 (10%) showed MNA in NB tumor tissue and in 35 (22%) patients a normal genomic profile was detected (Table 1). Among samples with NCA, the most frequent abnormalities were an additional copy of whole chromosome 17, 7 and 6 (78%, p = 0.000012; 65%, p = 0.003 and 51%, respectively), whereas copy-loss was observed mainly in chromosome 14, 4 and 19 (57%, p > 0.5; 47%, p = 0.02; 47%, respectively) (Table 1). A majority of NCA cases were under 18 months of age (87.5%, p = 0.000011) (Table 1). Similarly to NCA, patients with a combined NCA and SCA profile were also characterized by whole gain of chromosome 17 and 7 (35%) and loss of chromosome 14 (38%), but with lower frequency (Table 1). Additionally, in the combined NCA and SCA profiles, the loss of whole chromosome 3 (30%, p > 0.5) and 4 (24%) was observed. Moreover, in this NCA+SCA subgroup, typical NB changes such as 1p36 deletion (27%) and 17q gain (41%) were detected, and it was lower frequency than in MNA subgroup (44%) (Table 1). In this group of patients, 19 (51%) were over 18 months of age. In MNA subgroup no specific whole chromosome loss or gain was indicated, but 11q deletion started from the q14.3 subband in comparison to the q13.4 in NCA+SCA subgroup.

Figure 1.  (a) Numerical chromosomal aberrations in NB tumor tissue; (b) Numerical and structural chromosomal aberrations in NB tumor tissue.

DownLoad: Full-Size Img PowerPoint

Table 1.  The frequency of chromosomal alterations in the pangenomic profile of NB primary tumor tissue.

Profile	N = 160	Age > 18	Age < 18	The most frequent chromosomal alterations
*NCA	72 (45%)	9 (12.5%)	63 (87.5%)	+17 (56; 78%) +7 (47; 65%) +6 (37; 51%) +13 (31; 43%) +22 (26; 36%) +2 (25; 35%) +18 (24; 33%) +12 (22; 31%) −14 (41; 57%) −4 (34; 47%) −19 (34; 47%) −21 (31; 43%) −3 (26; 36%)
**NCA + SCA	37 (23%)	19 (51%)	18 (49%)	+7 (13; 35%) +17 (13; 35%) +18 (10; 27%) +22 (10; 27%) +12 (9; 24%) −14 (14; 38%) −3 (11; 30%) −4 (9; 24%) −9 (9; 24%) gain 17q (15; 41%) del 1p36 (10; 27%) del 11q13.4q25 (9; 24%) dup 1q2q44 (7; 17%) del 3p21p26 (6; 16%)
***MNA	16 (10%)	11 (69%)	5 (31%)	gain 17q (7; 44%) del 1p36 (7; 44%) del 11q14.3.4q25 (3; 19%)
Normal	35 (22%)	19 (54%)	16 (46%)

---

Notes: *NCA: numerical chromosomal alterations; **NCA+SCA: numerical and segmental chromosomal alterations; ***MNA: MYCN amplification.

 | Show Table

DownLoad: CSV

4.   Discussion

The study group of NB patients showed both NCA and NCA+SCA genomic profiles. The high occurrence of typical NB NCA such as a gain of whole chromosome 17 and 7 and chromosome 14 loss were previously described [19]. A similar frequency of chromosome 17 polysomy was identified by other authors in 23–100% of NB cases, chromosome 7 in 31–83% and the loss of chromosome 14 in more than 20% cases [16],[19]–[23]. The age in our NB patient subcohorts with NCA and NCA+SCA supports the hypothesis that NCA are more frequent in younger children with good prognosis, whereas SCA are more frequent in older patients with advanced stages of disease and poor outcomes [7],[13]–[16]. Tonini has supported the hypothesis that the initial step of oncogenesis in NB is the generation of whole chromosome gains, followed by segmental alterations [24],[25]. Conversely, the ‘aneuploidy paradox’ where polysomy/monosomy are presented in tumor tissue as indicators of tumor growth, but often lead to reduction in cell proliferation rate [26],[27]. However, there is still a need to evaluate aberration-related genes as molecular markers and their role in NB origin.

The abnormal multiplication of whole chromosome 17 or its long arm (17q) in NB cells and other neoplasms may be related to the location of known oncogenes: HER2 (17q12), TOP2A (17q21.2) and TAU (17q21.31) in this chromosomal region. Gene HER2 amplification is widely utilized as a molecular marker of target treatment in breast cancer. Moreover, in breast cancer the amplification of TOP2A and TAU is also related to the response to anthracycline- and taxane-based chemotherapy [28]. However, nowadays the polysomy of chromosome 17 is not an independent predictive factor in NB, contrary to 17q gain, which occurs in 50–75% of NB and presents co-occurrence with the loss of 1p 3p, 4p, 9p, 11q and 14q as examples of unbalanced translocations [6],[7],[13]–[16]. Genes like NME1, BIRC5 and PPM1D were proposed as potential treatment targets in NB, but their role has not been proven [29],[30]. Moreover, TP53 (17p13) suppressor gene is the most frequently altered gene in human cancers [30].

Stallings et al. have previously discussed the possibility that the gain of whole chromosome 7 or its long arm may contribute to tumorigenesis and progression in NB [22]. Chromosome 7 contains plenty of genes involved in cancer development: BRAF (7q34), CDK6 (7q21q22), EGFR (7p12), ETV1 (7p21.3), IKZF1 (7p12.2), MET (7q31), TRIM24 (7q32q34) [30]. High EGFR gene copy number status related to polysomy of chromosome 7 and EGFR-activating mutations were identified as positive molecular predictors for tyrosine kinase inhibitor responsiveness in non-small cell lung cancer and squamous cell carcinoma [31],[32].

Long arm of chromosome 14 is a region containing IgH and ELK-2 genes, members of the ETS family of oncogenes, and AKT proto-oncogenes [30]. Previous reports suggest that one way of proto-oncogenes activation is a mutation or translocation leading to neoplastic transformation. Losses in 14q are typical in malignant meningiomas and are associated with more aggressive behavior and higher probability of tumor recurrence [33]. Also, for NB 14q deletion is more frequent (20–25%) than the loss of whole chromosome 14. Moreover, 14q loss strongly correlated with 11q loss, unfavorable alteration for NB tumors, and inversely correlated with MNA. Despite this, results do not show more aggressive behavior for patients with 14q deletions, and this alteration is not an independent prognostic marker [13]–[15],[34],[35].

Deletion of 11q is one of the most frequent SCA reported in NB (35–45%). It is an independent prognostic factor associated with poor prognosis and metastatic disease [1],[6],[7],[13]–[16]. Moreover, ositive correlations of 11q loss with 4p loss and 7q gain, and an anti-correlation with MNA have been found [1],[2]. Beside this, it was reported that in 50% of 11q loss cases, deletion was the result of unbalanced translocation - concurrent loss of distal 11q and gain of 17q [36]. An effort was made to identify candidate genes for tumorigenesis in NB: ATM (11q22.3), SDHD (11q23.1), NCAM (11q23.2), CADM1 (11q23.3), H2AFX (11q23.3) and also CCND1 (11q13.3), PHOX2A (11q13.4) [1]. In this study, a difference in spanning 11q deletion between MNA and NCA+SCA subgroup was found (Table 1). Villamón et al. have previously reported the shortest regions of overlap for 11q deletion: from nucleotide 1117.7 Mb to qter (22.8 Mb) [37]. Based on our results, it is possible to outline other genes with loci in 11q13.4 as candidate markers in NB: CTTN (plays a role in the cytoskeleton organization and cell shape, cell migration, focal adhesion, the regulation of neuron morphology and axon growth, the invasiveness of cancer cells and the formation of metastases), NUMA (plays a role in the formation and organization of the mitotic spindle during cell division), FAM168A (protects cells from induced-DNA damage and apoptosis), PPFIA1 (plays a role in the focal adhesions), RPS3 (plays a role in the repair of damaged DNA) [38].

The high incidence of whole chromosome 4 loss may indicate an additional unfavorable genetic factor in the NCA+SCA subgroup of NB patients. Chromosome 4 is the location for genes such as: FGF2 (implicated in nervous system development; 4q26), PHOX2B (a determinate of neurotransmitter phenotype, 4p12), REST (which represses neuronal genes in non-neuronal tissues, tumor suppressor; 4q12) [30]. Monosomy of chromosome 4 is rare in cancer. The loss of chromosome 4, predominantly in regions: 4p15.1–15.3, 4p16.3, 4q25–26 and 4q33–34 was characterized as a potential loci of suppressor genes which play a role in tumor pathogenesis and are associated with poor outcomes in breast, colorectal and lung cancer [39]–[41].

Brinkschmidt et al. using the array CGH technique were one of the first to notice that the pattern of NCA in NB is not random, and irrespective of tumor stage, there is a strong trend towards an additional copy of chromosome: 2, 6, 7, 12, 13, 17, 18 and loss of chromosome: 3, 4, 11, 14 [42]. Brinkschmidt et al. have underlined that this pattern may be connected with up or down regulation of genes engaged in cell cycle and cell growth control [42].

5.   Conclusions

The clinical variability in NB course is strongly linked to diverse genetic changes acquired by tumor cells. To gain new insights into the pathogenesis of NB and to establish molecular targets for diagnosis and therapy, candidate genes in the altered chromosomal regions must be investigated.