Error estimate of BDF2 scheme on a Bakhvalov-type mesh for a singularly perturbed Volterra integro-differential equation

1.   Introduction

Volterra integro-differential equations (VIDEs) with a first-order derivative term arise from population growth models, biology, medicine, physics, and so on ^[1,2,3]. When the first-order derivative of such problems is multiplied by a perturbation parameter $\varepsilon$, these problems are called singularly perturbed Volterra integro-differential equations (SPVIDEs), which are given by

where $0 < \varepsilon\ll1$ is a perturbation parameter and functions $a(x)$, $f(x)$, $K(x, t)$ are sufficiently smooth. In additional, we assume that there exists a positive constant $\beta$ such that $a(x)\geq \beta > 0$. Under these conditions, Eq (1.1) has a unique solution ^[4]. Furthermore, the derivatives of $u(x)$ have following bounds (see [4, Lemma 1.1])

where $C$ is a positive constant, which is independent of $\varepsilon$. Obviously, it can be seen from Eq (1.2) that the exact solution $u(x)$ of Eq (1.1) exists a exponential boundary layer at $x = 0$ as $\varepsilon\to 0$. It is well known that SPVIDEs are widely used to describe a nonlocal reaction-diffusion model in spatially inhomogeneous media that takes into account feedback and nonlocal interactions ^[5].

Due to the presence of perturbation parameter $\varepsilon$, some traditional finite difference and finite element methods on a uniform mesh could not obtain reliable numerical results. Therefore, the layer-adaptive grid (Bakhvalov and Shishkin meshes) and adaptive grid methods are widely used to construct some parameter-uniform numerical methods for solving SPVIDEs, see ^{[6,7,8,9,10,11,12]} and references therein. Among these existing methods, the accuracy of most of these methods is only first-order. For this reason, many researchers studied some second-order accurate numerical methods for Eq (1.1). For example, the authors in ^[13] used the Richardson extrapolation technique to improve the $\varepsilon$-uniform convergence of the adaptive grid method from first-order to second-order. Yapman ^[14] designed a homogeneous (nonhybrid) type difference scheme on Shishkin-type mesh for Eq (1.1), and confirmed that the numerical method was almost second-order convergent.

It is well known that the variable two-step backward differential formula (BDF2) technique has widely used to approximate the time derivative with second-order accurate for linear parabolic equations and differential-algebraic problems ^[15,16,17]. In particular, in ^[17], the authors introduced discrete orthogonal convolution kernels for the first time and utilized them to prove the stability and convergent of the adaptive BDF2 time-stepping scheme in $L^2$ norm. Recently, the authors ^[18] applied the BDF2 technique on a Shishkin mesh to solve the problem in Eq (1.1) and proved that the proposed method was almost second-order uniformly convergent. In addition, the result in ^[19] suggests that the BDF2 all-at-once system utilizing the preconditioned Krylov subspace solvers can be a competitive solution method for Riesz fractional diffusion equations.

Inspired by the BDF2 that we recently used in ^[18], where we designed a novel finite difference scheme to prove $\varepsilon$-uniform convergence for a Shishkin mesh. In this paper, we prove $\varepsilon$-uniform convergence of this finite difference scheme on a Bakhvalov-type (B-type) mesh. The advantage of this paper is that the convergence rate of our numerical method do not contain $\ln N$-factors, where $N$ is the number of mesh steps.

The paper is organized as follows: The construction and characteristics of Bakhvalov-type mesh is introduced in Section 2. This is followed by the stability analysis of the discretization scheme in Section 3. Then the bound of truncation error and the parameter-uniform convergence of the numerical method are proved in Section 4. In Section 5, the statement of the numerical experiment illustrates that our theoretical findings are effective. Finally, some concluding discussions are presented in Section 6.

To simplify the notation we set $g_{i} = g(x_i)$ for any function $g$ and set $K_{i, k} = K(x_i, x_k)$. The maximum norm denoted by $\|K\|: = \max\limits_{(x, t)\in \Omega^2}\left|K(x, t)\right|$ and $\|g\|: = \max\limits_{x\in \Omega}|g(x)|$. In addition, for any sequences $\{\gamma_k\}$ if the index $j > i$, we assume the summation $\sum\limits_{k = j}^i\gamma_k = 0$ and $\prod\limits_{k = j}^i\gamma_k = 1$.

2.   The Bakhvalov-type mesh

Let $\bar{\Omega}^{N}: = \{0 = x_0 < x_1 < \ldots < x_N = 1\}$ be a B-type mesh with the local mesh step size $h_i = x_i-x_{i-1}$, $i = 1, 2, \ldots, N$. Then, for $t_i = i/N$, the B-type mesh points $x_i$ can be obtained by the following generating function ^[20,21]

where $\varphi(t) = -\ln[1-2(1-\varepsilon)t]$, $J = N/2$ and $\mu$ is a positive mesh-parameter that satisfy $\mu\beta\geq2$. For the sake of simplicity, $r_{i} = h_{i}/h_{i-1}$($i = 2, \ldots, N$) represents the $i$-th step-size ratios.

Next, the next two lemmas list some characteristics of the above B-type mesh.

Lemma 2.1. The step sizes of the B-type mesh defined by Eq (2.1) satisfy

Proof. The proof of Eqs (2.2)–(2.4) can be found in [22, Lemma 1]. Here, we just need to prove Eq (2.5). In fact, by using Eqs (2.1) and (2.2), one has

where $\xi_i\in[t_{i-1}, t_{i}]$, $i = 2, \cdots, J-1$, which completes the proof.

Lemma 2.2. Let $\left\{x_i\right\}_{i = 0}^N$ be the B-type mesh generated by Eq (2.1). Then we have

Proof. The proof can be found in ^[23,24].

3.   Discretization scheme and stability analysis

Before constructing a second-order discretization scheme for Eq (1.1), we first give the definition of two-step backward differential formula as follows: For a given function $g$, let $P_{i, k}g$ be the corresponding Lagrange interpolating polynomial over points $x_{i}, x_{i-1}, \ldots, x_{i-k}$. Then the first-order derivative of this polynomial at point $x = x_i$ can be obtained by

where $b_0^1: = 1/h_1$, $b_0^i: = \frac{1+2r_i}{h_{i}(1+r_i)}, \; b_{1}^i: = -\frac{r_i^2}{h_i(1+r_i)}$ and $b_{j}^i: = 0$ for $2\leq j\leq i-1, \; \; i\geq 2$. Therefore, by using Eq (3.1) and the trapezoidal formula to approximate the first-order derivative and the integral term, respectively, we obtain the following discretization scheme

where $u_{i}^{N}$ is the approximation solution of $u(x)$ at point $x = x_{i}$.

To facilitate the analysis of the stability and convergence of the discretization scheme in Eq (3.2), we first define a discrete orthogonal convolution (DOC) kernels $\left\{\theta_{i-j}^i\right\}_{j = 1}^i$, which is given by (see [17, Lemma 2.3])

Then by using the following discrete orthogonal identity

where $\delta_{ik}$ is the Kronecker delta symbol, we obtain

Furthermore, the next lemma list a characteristics of DOC kernels:

Lemma 3.1. [17, Corollary 2.1] The DOC kernels $\theta_{i-j}^i$ has following property

Now, based on the above definition of DOC kernels in Eq (3.3) and the proof of Lemma 2 in ^[18], we list the stability of the above discretization scheme in Eq (3.2).

Lemma 3.2. Under the condition that there exists a constant $\alpha^*$ such that

the solution $u_i^N$ of Eq (3.2) satisfies

Proof. For $i = 1, \cdots, N$, multiplying both sides of Eq (3.2) by the DOC kernels $\theta_{i-j}^{i}$, and summing $j$ from 1 to $i$, we get

Then, combining with Eq (3.5), yields,

Based on Eq (3.7), we have

where we have applied the fact that

Then, from Eqs (3.8), (3.9), it is easy to obtain

Furthermore, we have

where

Obviously, to derive the bound for $\left|u_i^N\right|$, we only need to estimate the bounds of $I_j$, $j = 1, 2, 3$, respectively. For $I_1$, it follows from Lemma 3.1 that

where we have interchanged the order of summation. Similar to Eq (3.12), we get

From Eqs (3.11)–(3.13), we obtain

where the sequences $\{\lambda_k\}$ are defined by

Finally, by using the Grönwall inequality, see [25, Lemma 3.2], one has

which completes the proof.

In order to derive convergence analysis below, we also give the bound of $\left|u_i^N\right|$ for $i = 1, \cdots, J-1$ as follows:

Lemma 3.3. For $i = 1, \cdots, J-1$, we have

Proof. Firstly, for $i = 1$, it follows from Eq (3.2) that

Then, by using Eq (2.3), yields,

In addition, set $\eta_i = \frac{\varepsilon}{h_i}\frac{1+2r_i}{1+r_i}+a_i+\frac{h_iK_{i, i}}{2}$, by using the Eq (2.5), we have $\eta_i\geq C\left(\varepsilon/h_i+\alpha^*\right)$. Furthermore, similarly to Eq (3.11), one has

where the sequences $\{\lambda_k\}$ are defined by

Using the Grönwall inequality, we get

The result of this lemma can be implied by Eqs (3.16), (3.17).

4.   Convergence analysis

Let $e_{i}^{N} : = u_{i}-u_{i}^{N}$, $i = 1, 2, 3, \ldots, N$, denote the error at point $x = x_i$ in the numerical solution. Then we have

where

Lemma 4.1. Under the B-type mesh defined in Eq (2.1), we obtain the following estimations

and

Proof. We first consider the truncation error $\left|R_{1, i}\right|$ when $i = 1$, by using Taylor's expansion formula, Eq (1.2), Lemma 2.1 and Lemma 2.2, we have

For $2\leq i\leq J-1$ and $i\geq J+2$, the step-size ratios $1\leq r_i\leq 3$, then for the reason of Eq (4.7), we can obtain

where we have used fact that

for any positive monotonically decreasing function $\phi$ on $[c, d]$, see ^[26].

Furthermore, for $i = J, \; J+1$, the truncation error $R_{1, i}$ can also be estimated in the following form:

Now, we need to estimate the second term on the right-hand side of Eq (4.9) to obtain a estimate of $\left|R_{1, i}\right|\; \text{for}\; i = J, \; J+1$. Firstly, for $i = J+1$, one has

Secondly, for $i = J$, if $\varepsilon\leq N^{-1}$, by using Eq (2.4) it is easy to get that

On the other hand, if $\varepsilon > N^{-1}$, we can get that

From Eqs (4.8)–(4.12), we get $|R_{1, i}|\leq CN^{-2}$ for $2\leq i\leq N$.

Different from BDF2, the discretization of the integral part in Eq (3.2) does not require two starting points, we can estimate $R_{2, i}$ for $1\leq i\leq N$.

which completes the proof.

Finally, we can get the main result of this paper as follows:

Theorem 4.1. Let $u(x)$ be the solution of Eq (1.1) and $u_i^N$ be the solution of Eq (3.2) on the mesh $\bar{\Omega}^{N}$. Then, under the condition $\beta+\frac{h_iK_{i, i}}{2}\geq\alpha^* > 0$, the error satisfy

Proof. From Eq (3.16), we have $\left|e_1^N\right|\leq CN^{-1}\left|R_{1, 1}+R_{2, 1}\right|\leq CN^{-2}$. In particular, Lemma 3.3 imply that

Next, for $i\geq J$, it follows from Eq (3.3) and Eq (3.15) that

where Lemma 3.1 are used. This completes the proof.

5.   Numerical results and discussion

In this section, to confirm our theoretical results, we present numerical results for two test examples. As the exact solution of this test problem is available, the computed errors and rates of convergence are defined by

respectively, where $u_i^N$ is the solution of the discretization scheme in Eq (3.2). Here, in all numerical experiments below, we choose $\varepsilon = 10^{-k}, \; k = 1, \ldots, 7$ and $N = 2^{m}, \; m = 5, \ldots, 9$. Meanwhile, to obtain the Bakhvalov mesh $\bar{\Omega}^N$, we choose $\mu = 2$ for Example 1 and $\mu = \frac{2}{3}$ for Example 2. All experiments were performed on a Windows 10(64 bit)PC-Intel(R) Core(TM) i7-7500U CPU 2.70GHz 8 GB of RAM using MATLAB R2017a.

Example 1. The first example is taken from ^[14]:

where

The exact solution is $u(x) = 1/\left(1+x\right)+e^{-x/\varepsilon}$. The numerical results of Example 1 are listed in Table 1.

Example 2. We consider the following singularly perturbed Volterra integro-differential equation:

Since the exact solution of this test problem is not available, we use the double-mesh principle ^[14] to calculate the maximum point-wise errors as follows:

where $u^{2N}_i$ is the solution of the Eq (3.2) on the following mesh:

For different values of $\varepsilon$ and $N$, the numerical results of Example 2 are displayed in Table 2.

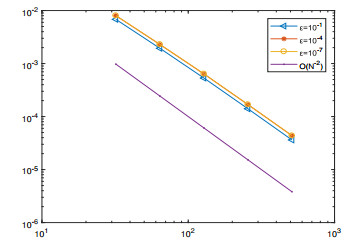
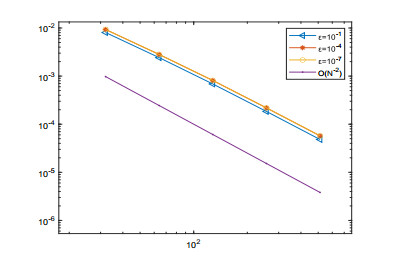
Tables 1–2 illustrate that the errors are robust with respect to $\varepsilon$, and the convergence order is close to 2. Meanwhile, Figures 1–2 display the log-log plot of these errors computed by our presented numerical method. In summary, our numerical results confirm our theoretical results.

6.   Conclusion

We have discussed the $\varepsilon$-uniform convergence of the variable two-step backward differentiation formula of a reduced linear singularly perturbed Volterra integro-differential equation on a Bakhvalov-type mesh. We first proved the stability of our discretization scheme. Then, the proof of $\varepsilon$-uniform convergence can be given by the stability of the numerical method.

Acknowledgments

This work is supported by the key project of the Natural Science Foundation of Guangxi Province (AD20238065), the Natural Science Foundation of Guangxi Province (2020GXNSFAA159010), and the National Science Foundation of China (12261062).

Conflict of interest

The authors declare there is no conflict of interest.