Matrix valued inverse problems on graphs with application to mass-spring-damper systems

1.   Introduction

We study a class of inverse problems where the objective is to find matrix valued quantities defined on the edges or vertices (nodes) of a graph from measurements made at a few boundary nodes. The scalar case corresponds to the problem of finding resistors in a resistor network from electrical measurements made at a few nodes, see e.g. [14]. As in the scalar case, the vector potential at all the nodes can be found from its value at a few nodes by solving a Dirichlet problem, i.e. finding a vector potential satisfying a vector version of conservation of currents (Kirchhoff's node law) and having a prescribed value at certain nodes. We study in detail the Dirichlet problem and give conditions guaranteeing it admits a unique solution (sections 2 and 3). We also include cases where the matrix valued weights are rank deficient and uniqueness of the Dirichlet problem holds only up to a known subspace.

Then we present different inverse problems, where either the matrix valued weights on the edges or the vertices or even their eigenvalues are the unknown parameters that are sought after. All these inverse problems share a common structure that is given in section 4. Any inverse problem that fits this mold has certain desirable properties: mainly the parameter to data map (i.e. the forward map) is analytic and its Jacobian can be computed in terms of products of internal "states" (e.g. solutions to the Dirichlet problem). Analyticity can be used to guarantee local uniqueness for such inverse problems, for almost any parameter within a region of interest provided the Jacobian is injective for one parameter (a generalization of the results in [6]). Moreover, we show that Newton's method applied to such problems is very likely to produce valid steps. Then in sections 5 and 6 we formulate inverse problems with matrix valued weights and determine conditions under which they have the structure of section 4. Some of the inverse problems we consider arise in networks of springs, masses and dampers.

1.1.   Related work

The discrete conductivity inverse problem consists of finding the resistors in a resistor network from voltage and current measurements made at a few nodes, assuming the underlying graph is known. For this problem, the uniqueness results in [13,14,10,12,11] apply to circular planar graphs (i.e. planar graphs that can be embedded in a disk and where the nodes at which measurements are made can be laid on the disk boundary) and real conductivities. A different approach is taken in [9] where a monotonicity property inspired from the continuum [1] is used to show that if the conductivities satisfy a certain inequality then they can be uniquely determined from measurements, without specific assumptions on the underlying graph. The lack of uniqueness is shown for cylindrical graphs in [21]. For complex conductivities, a condition for "uniqueness almost everywhere" regardless of the underlying graph is given in [6]. Uniqueness almost everywhere means that the set of conductivities that have the same boundary data lie in a zero measure set and that the linearized problem is injective for almost all conductivities in some region.

Uniqueness for the discrete Schrödinger problem is considered in the real scalar case on circular planar graphs in [2,3,4]. This problem involves a resistor network with known underlying graph and resistors but where every node is connected to the ground (zero voltage) via a resistor with unknown resistance. These unknown resistors are a discrete version of the Schrödinger potential in the Schrödinger equation, and the goal is to find them from measurements made at a few nodes. A discrete Liouville identity [5] can be used to relate the discrete Schrödinger inverse problem for certain Schrödinger potentials to the discrete conductivity inverse problem, also on circular planar graphs. A condition guaranteeing uniqueness almost everywhere for complex valued potentials without an assumption on the graph is given in [6].

One of the consequences of the present study is a uniqueness almost everywhere result for matrix valued inverse problems on graphs. To the best of our knowledge there are no results for uniqueness of the inverse problem with matrix valued edge or node quantities other than the characterization and synthesis results for networks of springs masses and dampers (discussed in more detail in section 6) that are derived in [7,18,17]. These results solve an inverse problem for networks of springs, masses and dampers that assumes we are free to choose the graph topology. Indeed the constructions in [7,18,17] start from data generated by these networks (displacement to forces map) and give a network that reproduces this data. We emphasize that in the present study, the underlying graph is always assumed to be known.

2.   The matrix valued conductivity and Schrödinger problems

2.1.   Notation

We use the set theory notation $Y^X$ for the set of functions from $X$ to $Y$. For example $u \in ( \mathbb{C}^d)^X$ is a function $u: X \to \mathbb{C}^d$ that to some $x \in X$ associates $u(x) \in \mathbb{C}^d$. For some matrix $a \in \mathbb{C}^{d \times d}$ we write $a \succ 0$ (resp. $a \succeq 0$) to say that $a$ is positive definite (resp. positive semidefinite). When the same notation is used for $a \in ( \mathbb{C}^{d\times d})^X$, the generalized inequality is understood componentwise, e.g. for $a \in ( \mathbb{C}^{d\times d})^X$, $a \succ 0$ means $a(x) \succ 0$ for all $x \in X$. When we write $a\succ b$ (or $a \succeq b$) we mean $a - b\succ 0$ (or $a-b \succeq 0$). We use the notation $a = \text{Re}\, a + \jmath \text{Im}\, a$, for the real $\text{Re}\, a$ and imaginary $\text{Im}\, a$ parts of $a$. The complex conjugate is $\overline{a} = \text{Re}\, a -\jmath \text{Im}\, a$.

By ordering a finite set $X$, it can be identified with $\{1, \ldots, |X|\}$, where $|X|$ is the cardinality of $X$. Thus $( \mathbb{C}^d)^X$ can be identified with vectors in $\mathbb{C}^{d|X|}$. Similarly, upon fixing an ordering for another finite set $Y$, we can identify linear operators $( \mathbb{C}^d)^X \to ( \mathbb{C}^d)^Y$ with matrices in $\mathbb{C}^{d|X| \times d|Y|}$.

For $A \in \mathbb{C}^{m \times n}$, we denote by ${\rm vect}(A) \in \mathbb{C}^{mn}$ the vector representation of the matrix $A$, i.e. the vector obtained by stacking the columns of $A$ in their natural ordering. Similarly for $a \in ( \mathbb{C}^{d \times d})^X$, we denote by ${\rm vect}(a) \in \mathbb{C}^{d^2|X|}$, the vector representation of $a$, i.e. the vector obtained by stacking the vector representations ${\rm vect}(a(x))$ of the matrices $a(x)$, for $x \in X$ in the predetermined ordering of $X$.

In addition to the usual matrix vector product, we also use a block-wise outer product ($\odot$), the Hadamard product ($\circledast$) and the Kronecker ($\otimes$) product. For $u, v \in ( \mathbb{C}^d)^X$, the (block-wise) outer product $u \odot v \in ( \mathbb{C}^{d\times d})^X$ is

The Hadamard or componentwise product of two vectors $a, b \in \mathbb{C}^n$ is denoted by $a \circledast b$ and it is given by $(a \circledast b)(i) = a(i)b(i)$, $i = 1, \ldots n$. The Kronecker product of two matrices $A \in \mathbb{C}^{n\times m}$ and $B \in \mathbb{C}^{p \times q}$ is the $np \times mq$ complex matrix $A \otimes B$ given by (see e.g. [20])

When we write $u^T v$ for $u, v \in ( \mathbb{C}^d)^X$, we mean

and similarly for $u^* v = \overline{u}^T v$, where the bar denotes the complex conjugate (understood componentwise). With this in mind we can define a norm for $u \in ( \mathbb{C}^d)^X$ by $\| u \|^2 = u^* u$.

2.2.   Discrete gradient, Laplacian and Schrödinger operators

We work with graphs $G = (V, E)$, where $V$ is the set of vertices or nodes (assumed finite) and $E$ is the set of edges $E \subset \{ \{i, j\} | i, j \in V, i \neq j\}$. All graphs we consider are undirected and with no self-edges. We partition the nodes $V = B \cup I$ into a (nonempty) set $B$ of "boundary" nodes and a set $I$ of "interior" nodes. The boundary nodes are where we can make measurements and the interior nodes are considered not accessible.

By (discrete) conductivity $\sigma$ we mean a symmetric matrix valued function defined on the edges, i.e. $\sigma \in ( \mathbb{C}^{d \times d})^E$. Here symmetric means $[\sigma(e)]^T = \sigma(e)$, for all $e \in E$. By (discrete) Schrödinger potential $q$ we mean a symmetric matrix valued function defined on the vertices i.e. $q \in ( \mathbb{C}^{d\times d})^V$.

The $d-$dimensional discrete gradient is the linear operator $\nabla :( \mathbb{C}^d)^V \to ( \mathbb{C}^d)^E$ defined for some $u \in ( \mathbb{C}^d)^V$ by

The discrete gradient assumes an edge orientation that is fixed a priori and that is irrelevant in the remainder of this paper.

The weighted graph Laplacian is the linear map $L_\sigma : ( \mathbb{C}^d)^V \to ( \mathbb{C}^d)^V$ defined by

where we used the linear operator ${\rm diag}(\sigma) : ( \mathbb{C}^d)^E \to ( \mathbb{C}^d)^E$, which is defined for some $v \in ( \mathbb{C}^d)^E$ by $({\rm diag}(\sigma) v)(e) = \sigma(e) v(e)$, $e \in E$. Its matrix representation is a block diagonal matrix with the $\sigma(e)$ on its diagonal. The operator $\nabla^T : ( \mathbb{C}^d)^E \to ( \mathbb{C}^d)^V$ is the adjoint of the $d$-dimensional discrete gradient $\nabla$.

The discrete Schrödinger operator associated with a conductivity $\sigma$ and a Schrödinger potential $q$ is a block diagonal perturbation (with blocks of size $d \times d$) of the weighted graph Laplacian, i.e

We now give two concrete examples of problems that can be described using matrix valued conductivities and Schrödinger potentials.

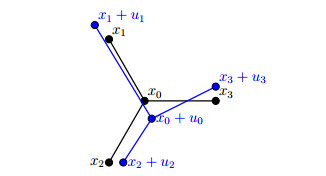
Example 1. We consider a network of springs, masses and dampers based on the graph appearing in black in fig. 1. Since this is a planar network we take $d = 2$. We associate to each edge a spring with spring constant $k_{0i}$ and a damper in parallel with a damping constant being $c_{0i}$, $i = 1, \ldots, 3$. These physical quantities are defined more precisely in section 6. Each node is associated a mass $m_i$ and also a damping constant $\nu_i$, $i = 1, \ldots, 3$, corresponding to the mass moving in a viscous fluid. If we subject the nodes to time harmonic external forces of the form $f_i(t) = \exp[\jmath \omega t] \hat f_i$ (where $t$ is time and $\omega$ the angular frequency) the displacement of the nodes is also time harmonic and satisfies the $8 \times 8$ complex linear system

where $\hat u \equiv [ \hat u_0^T, \hat u_1^T, \hat u_2^T, \hat u_3^T]^T$ and similarly for $\hat f$. The matrices in (6) are given as follows.

● The matrix $M$ is the mass matrix and is given by $M = {\rm diag}(m)$, where $m:V \to \mathbb{R}^{2\times 2}$ associates to each vertex a $2\times 2$ matrix, namely $m(i) = m_i \mathbb{I}$, for $i = 0, \ldots, 3$ and where $\mathbb{I}$ denotes the identity matrix of appropriate dimension.

● The matrix $K$ is the stiffness matrix, and can be written as $K = \nabla^T {\rm diag}(\sigma) \nabla$ where $\nabla$ is the discrete gradient written under the edge ordering of fig. 1

and the "conductivity" $\sigma: E \to \mathbb{R}^{2\times 2}$ given by

where $P_{0i}$ is the orthogonal projector onto direction $x_i-x_0$ of edge $\{0, i\}$, i.e.

● The matrix $C$ is the damping matrix and can be written as $C = C_E + C_V$, where $C_E$ accounts for the edge dampers and $C_V$ for the viscous damping at the nodes. These matrices are given by

where $\mu_E : E \to \mathbb{R}^{2\times 2}$ and $\nu: V \to \mathbb{R}^{2\times 2}$ are given by

The detailed derivation of these relations for general networks of springs, masses and dampers appears later in section 6. Nevertheless we can already see that

is a discrete Laplacian with complex symmetric matrix valued edge weights $\sigma + \jmath \omega \mu_E$. We emphasize that these weights are in general not Hermitian. Moreover

corresponds to complex symmetric matrix valued node weights given by $- \omega^2 m + \jmath \omega \nu$. Again we emphasize that the Schrödinger potential we obtain is in general not Hermitian. Thus we can write the matrix in the system (6) as a discrete Schrödinger operator (5) since

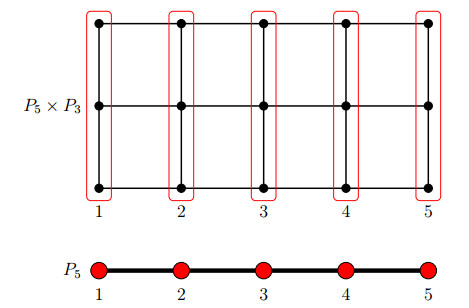
Example 2. We show how to use the matrix valued conductivities and Schrödinger potentials to view the Laplacian of a cylindrical graph $C = P_k \times G$ with scalar weights as a matrix valued Schrödinger operator on the graph $P_k$, a path with $k$ nodes with vertices $V(P_k) = \{1, \ldots, k\}$ and edges $E(P_k) = \{\{1, 2\}, \ldots, \{k-1, k\}\}$. Here $\times$ denotes the Cartesian product between graphs. Such cylindrical graphs arise e.g. in a finite difference discretization of the conductivity equation on a rectangle with a Cartesian grid, as illustrated in fig. 2.

Let $s \in (0, \infty)^{E(C)}$ be a scalar conductivity on the cylindrical graph $C$. We view $s$ as a vector and split it into the sub-vectors $s^{j} \in (0, \infty)^{E(G)}$, $j = 1, \ldots, k$ and $s^{j, j+1} \in (0, \infty)^{V(G)}$, $j = 1, \ldots, k-1$. The sub-vector $s^{j}$ represents the scalar conductivity of the $j-$th copy of the graph $G$. The sub-vector $s^{j, j+1}$ corresponds to the conductivity linking layer $j$ to layer $j+1$. Define the matrix valued conductivity $\sigma \in ( \mathbb{R}^{|V(G)| \times |V(G)|})^{E(P_k)}$ by $\sigma(\{j, j+1\}) = {\rm diag} s^{j, j+1}$, $j = 1, \ldots, k-1$ and matrix valued Schrödinger potential $q \in ( \mathbb{R}^{|V(G)| \times |V(G)|})^{V(P_k)}$ by $q(j) = L_{s^j}$, i.e. the Laplacian of the graph induced by the vertices in the $j-$th copy of $G$, $j = 1, \ldots, k$. Then with an appropriate ordering of the vertices we have

Example 3. To further motivate the symmetry assumptions we make on the matrix valued conductivities and Schrödinger potentials, notice that the Laplacian on the cylindrical graph $C = P_k \times G$ of example 2 can be used to express Kirchhoff's node law in a circuit made of resistors whose conductances are given by $s \in (0, \infty)^{E(C)}$. In other words, the equation $(L_\sigma u)_i = 0$ imposes that the sum of currents at the $i-$th node of $C$ must be equal to zero. If we allow the conductances to be complex, i.e. $s \in \{z \in \mathbb{C} \; |\; \text{Re}\, z > 0\}^{E(C)}$, then $s$ is now the admittance of the circuit elements, at a particular operating frequency. Proceeding as in example 2, the complex matrix valued conductivity $\sigma$, defined on the edges of $P_k$ by $\sigma(\{j, j+1\}) = {\rm diag} s^{j, j+1}$ must be complex symmetric (and not Hermitian). The complex matrix valued Schrödinger potential $q$ defined on the nodes of $P_k$ by $q(j) = L_{s_j}$ must also complex symmetric (and not Hermitian).

2.3.   The Dirichlet problem

For a conductivity $\sigma \in ( \mathbb{C}^{d \times d})^E$ and a Schrödinger potential $q \in ( \mathbb{C}^{d \times d})^V$, the $\sigma, q$ Dirichlet problem consists in finding $u \in ( \mathbb{C}^d)^V$ satisfying

where $g \in ( \mathbb{C}^d)^B$ is the Dirichlet boundary condition and the subscript $I$ (resp. $B$) is used to denote restriction of a quantity in $( \mathbb{C}^d)^V$ to one in $( \mathbb{C}^d)^I$. The Dirichlet to Neumann map, when it exists, is the linear mapping $\Lambda_{\sigma, q} : ( \mathbb{C}^d)^B \to ( \mathbb{C}^d)^B$ defined by

where $u$ solves the Dirichlet problem (15) with boundary condition $u_B = g \in ( \mathbb{C}^d)^B$. We call $\Lambda_{\sigma, q}$ a Dirichlet to Neumann map since this terminology is used when $q = 0$ in the scalar case ($d = 1$), see e.g. [10,13,14]. In the scalar case with $q = 0$, the conditions on the interior nodes (15) correspond to conservation of currents (Kirchhoff's node law) in an resistor network. Similarly (16) represents the net currents flowing out of the boundary nodes $B$, when the voltage is set to $g$ on the boundary. These currents can be interpreted as the Neumann boundary data corresponding to the Dirichlet boundary data $g$, hence the name for $\Lambda_{\sigma, 0}$.

The Dirichlet to Neumann map is well defined e.g. when the solution to the Dirichlet problem is uniquely determined by the boundary condition.¹ Conditions guaranteeing Dirichlet problem uniqueness are given in the next theorem, together with a formula for the Dirichlet to Neumann map.

¹In section 3.3 we consider Dirichlet problems that do not admit a unique solution and yet the Dirichlet to Neumann map is well defined.

Theorem 2.1. The $\sigma, q$ Dirichlet problem on a connected graph with connected interior admits a unique solution when $\sigma \in ( \mathbb{C}^{d\times d})^E$ and $q \in ( \mathbb{C}^{d \times d})^V$ are symmetric and one of the two following conditions is satisfied.

(i) $\mathit{\text{Re}}\, \sigma \succ 0$ and $\mathit{\text{Re}}\, q_I \succ - \lambda_{\min}\left({{(L_{ \mathit{\text{Re}}\, \sigma})_{II}}}\right)$.

(ii) $\mathit{\text{Re}}\, q_I \succ 0$ and $(L_{ \mathit{\text{Re}}\, \sigma})_{II} \succ - \lambda_{\min}({\rm diag}( \mathit{\text{Re}}\, q_I))$.

When any of the two conditions above hold, the Dirichlet to Neumann map can be written as

where we dropped the subscript $\sigma$ in the blocks $(L_\sigma)_{BB}$, $\ldots$ for clarity. This is the Schur complement of block $(L_\sigma + {\rm diag}(q))_{II}$ in the matrix $L_\sigma + {\rm diag}(q)$.

Proof. The proof appears in section 3.2.

In the previous theorem, $\lambda_{\min}(A)$ denotes the smallest eigenvalue of a real symmetric matrix $A$. Recall that we identify operators $A \in ( \mathbb{C}^d)^V \to ( \mathbb{C}^d)^V$ to $\mathbb{C}^{d|V| \times d|V|}$ matrices. We use $A_{XY}$, $X, Y \in \{I, B\}$, to denote the submatrix of $A$ with rows (resp. columns) associated with the vertices in $X$ (resp. $Y$).

Unfortunately theorem 2.1 and the expression (17) of the Dirichlet to Neumann map do not apply to one of the main applications of our results: static spring networks. As we see in more detail in section 6.1, the linearization of Hooke's law we use allows for non-physical floppy modes, i.e. non-zero displacements that can be made with zero forces. A generalization of the static spring network problem is to consider symmetric conductivities with $\text{Re}\, \sigma \succeq 0$. In this situation, floppy modes may also arise if there are edges $e$ for which $\text{Re}\, \sigma(e)$ has a non-trivial nullspace. They can be defined as follows.

Definition 2.2. A non-zero $z \in ( \mathbb{C}^d)^V$, is said to be a floppy mode for a symmetric conductivity $\sigma \in ( \mathbb{C}^{d\times d})^E$ if $z$ solves the equation

If $z$ is a floppy mode, then the solution to the $\sigma, 0$ Dirichlet problem cannot be unique. Indeed if $u$ is a solution to the $\sigma, 0$ Dirichlet problem, then so is $u + \alpha z$ for any scalar $\alpha$. The following theorem shows that even in the degenerate case $\text{Re}\, \sigma \succeq 0$, $q = 0$, there are situations where the Dirichlet problem admits a solution that is unique up to floppy modes.

Theorem 2.3. The $\sigma, 0$ Dirichlet problem on a connected graph with connected interior and $\sigma(e) \neq 0$ for all $e \in E$, admits a unique solution up to floppy modes when $\mathit{\text{Re}}\, \sigma \succeq 0$, and for each $e \in E$ the inclusion $\mathcal{N}( \mathit{\text{Re}}\, \sigma(e)) \subset \mathcal{N}( \mathit{\text{Im}}\, \sigma(e))$ holds. In this case, the Dirichlet to Neumann map can be written as

where for clarity we dropped the subscript $\sigma$ in the blocks $(L_\sigma)_{BB}$ etc. The matrix $Q$ is real with orthonormal columns ($Q^T Q = \mathbb{I}$) and satisfies $\mathcal{R}(Q) = \mathcal{R}(L_{II})$, i.e. its columns form an orthonormal basis of $\mathcal{R}(L_{II})$ and $Q$ is of size $d|I| \times \dim( \mathcal{R}(L_{II}))$. Moreover $Q$ depends only on the ranges of $\mathit{\text{Re}}\, \sigma(e)$ for $e \in E$.

Here we denote the nullspace or kernel of a matrix $A \in \mathbb{C}^{n \times m}$ by $\mathcal{N}(A)$ and the range or column space of $A$ is denoted by $\mathcal{R}(A)$.

Proof. The proof appears in section 3.3.1.

We note that theorem 2.3 applies in particular to the case of real positive semidefinite conductivities.

Remark 1 (Discrete Dirichlet principle). For real $\sigma \succeq 0$ and real $q \succeq 0$, it is easy to show that the Dirichlet problem (15) is equivalent to finding $u \in ( \mathbb{R}^d)^V$ minimizing the energy

subject to $u_B = g$. The function $E(u)$ is the energy needed to maintain a potential $u$ in the network and is the sum of energies associated to each edge and node. The edge terms are akin to the current-voltage product to calculate the power dissipated by a two terminal electrical component. The node terms represent the energy leaked by an electrical component linking the node to the ground (zero potential). The conditions $\sigma\succeq 0$, $q \succeq 0$ guarantee $E(u)$ is a convex quadratic function in $u$. The first equality in the Dirichlet problem (15) is identical to $\nabla_{u_I} E(u) = 0$.

2.4.   Relating boundary and interior quantities

The following lemma is a straightforward generalization to complex matrix valued conductivities and Schrödinger potentials of the interior identities [6,Lemmas 5.1 and 6.1], which are in turn inspired by the continuum interior identities used by Sylvester and Uhlmann [25] to prove uniqueness for the continuum conductivity and Schrödinger problems.

Lemma 2.4 (Boundary/Interior Identity). Let $\sigma_1, \sigma_2 \in ( \mathbb{C}^{d \times d})^E$ be conductivities and $q_1, q_2 \in ( \mathbb{C}^{d \times d})^V$ be Schrödinger potentials. Let $u_1, u_2 \in ( \mathbb{C}^d)^V$ be solutions to the $\sigma_1, q_1$ and $\sigma_2, q_2$ Dirichlet problems:

for some boundary conditions $g_1, g_2 \in ( \mathbb{C}^d)^B$. Then if the Dirichlet to Neumann maps $\Lambda_{\sigma_i, q_i}$, $i = 1, 2$, are well defined we have the identities

where the outer product $\odot$ is as in (1).

Proof. Since $u_1$ solves the $\sigma_1, q_1$ Dirichlet problem we have

Similarly, we have that

Subtracting (22) from (21) gives the first equality. To obtain the second equality, use the definition of the weighted graph Laplacian to see that

By applying for each $e\in E$ the identity $x^T A y = {\rm vect}(xy^T)^T {\rm vect}(A)$, which holds for any $x, y \in \mathbb{C}^d$ and $A \in \mathbb{C}^{d\times d}$, we get

By applying the same identity for all nodes $i \in V$ we get

The third equality follows from identities (23) and (24).

3.   Dirichlet problem uniqueness proofs

We first focus in section 3.1 on proving theorem 2.1 for the particular case where the conductivity is real positive definite and the Schrödinger potential is zero (lemma 3.3). We then complete the proof of theorem 2.1 by considering either $\text{Re}\, \sigma \succ 0$ or $\text{Re}\, q_I \succ 0$ in section 3.2. In both cases the objective is to show that the conditions given in theorem 2.1 are sufficient to guarantee that the matrix $(L_\sigma)_{II} + {\rm diag}(q_I)$ is invertible. The case where $\text{Re}\, \sigma \succeq 0$, $q = 0$ is dealt with in section 3.3 which includes the proof of theorem 2.3, and is more delicate because the matrix $(L_\sigma)_{II}$ may no longer be invertible. However it is still possible to show that the $\sigma, 0$ Dirichlet solution is unique up to floppy modes (definition 2.2).

3.1.   Dirichlet problem uniqueness for positive definite conductivities and zero Schrödinger potentials

The purpose of this section is to establish uniqueness for the $\sigma, 0$ Dirichlet problem for real $\sigma$ with $\sigma \succ 0$ (lemma 3.3). We need two intermediary results on the discrete graph Laplacian $L_\sigma$ with real matrix valued symmetric conductivity $\sigma \succ 0$. The first one is a discrete version of the first Korn inequality (lemma 3.1). The second is to show that a vector potential $u \in \mathcal{N}(L_\sigma)$ must be constant on all connected components of the graph $G$ (lemma 3.2). Using these properties, we can show that when $\sigma$ is a real conductivity with $\sigma \succ 0$, we can deduce that $(L_\sigma)_{II} \succ 0$ which is sufficient to ensure uniqueness for the corresponding $\sigma, 0$ Dirichlet problem.

The following is a discrete version of the first Korn inequality which bounds the elastic energy stored in a body from below by the gradient of the strain, see e.g. [22,§1.12].

Lemma 3.1 (Discrete Korn inequality). Let $\sigma \in ( \mathbb{R}^{d\times d})^E$ be a conductivity with $\sigma \succ 0$. Then there is a constant $C>0$ such that for any $u \in ( \mathbb{R}^d)^V$,

Proof. By using Rayleigh quotients,

Define $\lambda_* = \min_{e\in E} \lambda_{\min}(\sigma(e)) = \lambda_{\min}({\rm diag}(\sigma))$. Clearly $\sigma \succ 0$ implies $\lambda_* > 0$. The inequality we seek follows with $C = \lambda_*^{-1}$ from

The next lemma extends to matrix valued conductivities a well known characterization of the nullspace of (scalar) weighted graph Laplacians (see e.g. [8]).

Lemma 3.2 (Nullspace of graph Laplacian). For real $\sigma \succ 0$, $u \in \mathcal{N}(L_\sigma)$ implies that $\nabla u = 0$. In particular if the graph is connected then $u$ is constant, meaning there is a constant $c \in \mathbb{R}^d$ such that $u(i) = c$ for all $i\in V$.

Proof. If $u \in \mathcal{N}(L_\sigma)$ then $u ^T L_\sigma u = 0$. Using the discrete Korn inequality (lemma 3.1), we get $\nabla u = 0$. This means that for any edge $\{i, j\} \in E$, we must have $u(i) = u(j)$. Therefore $u$ must be constant on connected components of the graph.

We can now prove the first uniqueness result for the Dirichlet problem.

Lemma 3.3 (Uniqueness for real positive definite conductivities). Assume both the graph $G$ and its subgraph induced by the interior nodes are connected. For real conductivities $\sigma$ with $\sigma \succ 0$, the matrix $(L_\sigma)_{II}$ is invertible and the $\sigma, 0$ Dirichlet problem admits a unique solution.

Proof. Our goal here is to show that $(L_\sigma)_{II} \succ 0$ which implies invertibility and therefore uniqueness for the $\sigma, 0$ Dirichlet problem. By definition of the weighted graph Laplacian (4), the matrix $L_\sigma$ must be real and symmetric. Moreover using the discrete Korn inequality (lemma 3.1), there is a constant $C > 0$ such that for all $u \in ( \mathbb{R}^d)^V$:

This implies $L_\sigma \succeq 0$ and hence $(L_\sigma)_{II} \succeq 0$. Now we can write

where $L_{\sigma_I}$ is the weighted graph Laplacian on the subgraph of $G$ induced by the interior nodes $I$ and $f \in ( \mathbb{R}^{d\times d})^I$ is given for $i \in I$ by

Since the sum of positive definite matrices is positive definite, $\sigma \succ 0$ implies $f(i) \succ 0$ for all nodes $i\in I$ that are connected via an edge to some boundary node and $f(i) = 0$ otherwise. This guarantees that ${\rm diag}(f) \succeq 0$.

Now take $v \in ( \mathbb{R}^d)^I$ with $v^T (L_{\sigma})_{II} v = 0$. Since both $L_{\sigma_I}$ and ${\rm diag}(f)$ are positive semidefinite, we must have that

By using (a) and lemma 3.2 on the subgraph induced by the interior nodes (which is connected by assumption), we get that $v$ is constant, i.e. $v(i) = v(j)$ for any $i, j \in V$. By using (b), we get that $v(i)^T \sigma(\{i, j\}) v(i) = 0$ for all $\{i, j\} \in E$ where $i \in I$ and $j \in B$. Hence there must be at least one $i \in I$ such that $v(i) = 0$ (since $G$ is connected). Since the subgraph of $G$ induced by the interior nodes is connected, we conclude that $v = 0$. This gives the desired result $(L_\sigma)_{II}\succ 0$.

3.2.   Proof of theorem 2.1

We start with the following lemma that allows us to extend the uniqueness result from lemma 3.3 to complex conductivities and Schrödinger potentials.

Lemma 3.4. Let $A, B \in \mathbb{R}^{n \times n}$ be symmetric with $A \succ 0$. Then the matrix $M = A + \jmath B$ is invertible.

Proof. The field of values (or numerical range, see e.g. [20]) of $M \in \mathbb{C}^{n \times n}$ is the complex plane region given by

Since $A \succ 0$ we have $v^* A v >0$ for $v \neq 0$. Since $B$ is real symmetric, $v^*B v$ must be real. Therefore $\text{Re}\, (v^* M v) = v^*Av > 0$ for $v\neq 0$ and the field of values $F(M)$ lies on the right hand complex plane, excluding the imaginary axis. Since the spectrum of $M$ is contained in $F(M)$ this means that $0$ is not an eigenvalue of $M$ and that $M$ is invertible.

We are now ready to prove theorem 2.1.

Proof. First assume condition (ⅰ) of theorem 2.1 holds. We want to show that $(L_\sigma)_{II} + {\rm diag}(q_I)$ is invertible when $\text{Re}\, \sigma \succ 0$ and $\text{Re}\, q_I \succ -\zeta$, for some $\zeta>0$ to be determined and depending on $\text{Re}\, \sigma$. By lemma 3.3 and because $\text{Re}\, \sigma \succ 0$, we have that $(L_{ \text{Re}\, \sigma})_{II} \succ 0$. Since we assume $\text{Re}\, q_I \succ -\lambda_{\min}\left({{(L_{ \text{Re}\, \sigma})_{II}}}\right)$, we must have $(L_{ \text{Re}\, \sigma})_{II} + {\rm diag}( \text{Re}\, q_I) \succ 0$. We can now use lemma 3.4 with $A \equiv (L_{ \text{Re}\, \sigma})_{II} + {\rm diag}( \text{Re}\, q_I)$ and $B \equiv (L_{ \text{Im}\, \sigma})_{II} + {\rm diag}( \text{Im}\, q_I)$ to conclude that $(L_\sigma)_{II} + {\rm diag}(q_I)$ is invertible. Uniqueness follows from the definition of the $\sigma, q$ Dirichlet problem.

Then assume condition (ⅱ) of theorem 2.1 holds. By the hypothesis, we have that $(L_{ \text{Re}\, \sigma})_{II} + {\rm diag}( \text{Re}\, q_I) \succ 0$. Hence we can use lemma 3.4 with $A \equiv (L_{ \text{Re}\, \sigma})_{II} + {\rm diag}( \text{Re}\, q_I)$ and $B \equiv (L_{ \text{Im}\, \sigma})_{II} + {\rm diag}( \text{Im}\, q_I)$ to conclude that $(L_\sigma)_{II} + {\rm diag}(q_I)$ is invertible and the desired uniqueness of the $\sigma, q$ Dirichlet problem follows.

It now remains to prove (17). The proof is very similar to the scalar case (see e.g. [13]), but we include it here for completeness. The first equation of (15) can be rewritten as

Since under the hypothesis of theorem 2.1 the matrix $(L_\sigma)_{II} + {\rm diag}(q_I)$ is invertible, we have

The expression (17) of the Dirichlet to Neumann map can be identified from

3.3.   Conductivities with positive semidefinite real part and zero Schrödinger potential

The purpose of this section is to prove theorem 2.3, which deals with the situation $\text{Re}\, \sigma \succeq 0$ and $q = 0$. We start with several intermediary results. The first is a characterization of floppy modes (lemma 3.5) that shows that floppy modes for such $\sigma$ are entirely determined by the subspace $\mathcal{N}({\rm diag}(\sigma))$. Them we establish some relations between the ranges and nullspaces of certain blocks of $L_\sigma$ and of $L_{ \text{Re}\, \sigma}$. One key observation is that floppy modes do not affect the boundary data (lemma 3.7).

First notice that for any $u \in ( \mathbb{C}^d)^V$ and real $\sigma \succeq 0$, we have

where $\sigma^{1/2}(e) = (\sigma(e))^{1/2}$, and the square root of a positive semidefinite matrix is defined by taking the square root of the eigenvalues in its eigendecomposition, see e.g. [20]. We use this identity to give a characterization of the floppy modes for complex conductivities with $\text{Re}\, \sigma \succeq 0$ and $\mathcal{N}( \text{Re}\, \sigma(e)) \subset \mathcal{N}( \text{Im}\, \sigma(e))$, $e \in E$. From this characterization, we can see that floppy modes depend only on the subspaces $\mathcal{R}( \text{Re}\, \sigma(e))$ (or equivalently $\mathcal{N}( \text{Re}\, \sigma(e))$), for $e \in E$.

Lemma 3.5. For conductivities with $\mathit{\text{Re}}\, \sigma\succeq 0$ and $\mathcal{N}( \mathit{\text{Re}}\, \sigma(e)) \subset \mathcal{N}( \mathit{\text{Im}}\, \sigma(e))$, $e \in E$, the following are equivalent.

(i) $z$ is a floppy mode (i.e. it satisfies (18))

(ii) $z$ is a non-zero solution to

(iii) $z$ is such that $z_B = 0$ and $z_I \in \mathcal{N}( (L_{ \mathit{\text{Re}}\, \sigma})_{II} )$.

Proof. $\underline{({\rm ii})\implies {\rm (i)}}$. Assume that $z \neq 0$ satisfies (30). Because of the inclusion $\mathcal{N}( \text{Re}\, \sigma(e)) \subset \mathcal{N}( \text{Im}\, \sigma(e))$, $e \in E$, we also have ${\rm diag}( \text{Im}\, \sigma) \nabla z = 0$ and ${\rm diag}(\sigma) \nabla z = 0$. Hence $L_\sigma z = \nabla^T {\rm diag}(\sigma) \nabla z = 0$,

$\underline{({\rm i}) \implies ({\rm ii}).}$ Now we assume that $z$ is a floppy mode, i.e. (18) holds. Clearly this means that $0 = z^* L_\sigma z = z^* L_{ \text{Re}\, \sigma} z + \jmath z^* L_{ \text{Im}\, \sigma} z$. Since both $L_{ \text{Re}\, \sigma}$ and $L_{ \text{Im}\, \sigma}$ are real symmetric, the scalars $z^* L_{ \text{Re}\, \sigma} z$ and $z^*L_{ \text{Im}\, \sigma}z$ must be real. We can conclude that $z^* L_{ \text{Re}\, \sigma} z = 0$. Now we use (29) to realize that $\| {\rm diag}(( \text{Re}\, \sigma)^{1/2}) z \|^2 = 0$. Since $\text{Re}\, \sigma$ and $( \text{Re}\, \sigma)^{1/2}$ have identical nullspaces, we see that (30) holds as well.

$\underline{({\rm i}) \implies ({\rm iii}).}$ We assume $z \neq 0$ satisfies (18). Since $z_B = 0$ we have $z^* L_\sigma z = z_I^* (L_\sigma)_{II} z_I = 0$. But then

implies that $z_I^* (L_{ \text{Re}\, \sigma})_{II} z_I = 0$. Because of (29) we have $L_{ \text{Re}\, \sigma} \succeq 0$ and also $(L_{ \text{Re}\, \sigma})_{II} \succeq 0$. Therefore $z_I \in \mathcal{N}((L_{ \text{Re}\, \sigma})_{II})$.

$\underline{({\rm iii}) \implies ({\rm ii}).}$ Now let $z$ be such that $z_B = 0$ and $z_I \in \mathcal{N}((L_{ \text{Re}\, \sigma})_{II})$. Again since $z_B = 0$, we have $0 = z_I^* (L_{ \text{Re}\, \sigma})_{II} z_I = z^* L_{ \text{Re}\, \sigma} z$. By (29) we get

which readily implies (30).

Next we continue with a technical result, which is a slight generalization of the elastic network result in [18,Lemma 1].

Lemma 3.6. Let $\sigma$ be a conductivity with $\mathit{\text{Re}}\, \sigma \succeq 0$ and satisfying the inclusion $\mathcal{N}( \mathit{\text{Re}}\, \sigma(e)) \subset \mathcal{N}( \mathit{\text{Im}}\, \sigma(e))$ for $e \in E$. Assume the subgraph induced by the interior nodes is connected. Then we have the following inclusions

(i) $\mathcal{N}((L_\sigma)_{II}) = \mathcal{N}((L_{ \mathit{\text{Re}}\, \sigma})_{II})$

(ii) $\mathcal{N}((L_\sigma)_{II}) \subset \mathcal{N}((L_\sigma)_{BI})$

(iii) $\mathcal{R}((L_\sigma)_{II}) \supset \mathcal{R}((L_\sigma)_{IB})$

Proof. $\underline{{\rm~ Proof ~of ~(i)}.}$ Let $z_I \in \mathcal{N}(L_\sigma)_{II}$. Because $z_I \in \mathcal{N}(L_\sigma)_{II}$ we also have

But the real matrices $L_{ \text{Re}\, \sigma}$ and $L_{ \text{Im}\, \sigma}$ are symmetric so we can conclude that $z_I^* (L_{ \text{Re}\, \sigma})_{II} z_I = 0$. Again by using (29) we see that $L_{ \text{Re}\, \sigma} \succeq 0$ and thus $z_I\in \mathcal{N}((L_{ \text{Re}\, \sigma})_{II})$. Now assume $z_I \in \mathcal{N}(L_{ \text{Re}\, \sigma})_{II}$. By lemma 3.5, the extension $z$ of $z_I$ by zeros on $B$ is a floppy mode, i.e. it satisfies (18). In particular, because $z_B = 0$, we have $0 = (L_\sigma z)_I = (L_\sigma)_{II} z_I = 0$. Thus we get $z_I \in \mathcal{N}( (L_\sigma)_{II})$ and (ⅰ) holds.

$\underline{{\rm Proof~ of~ (ii).}}$ We now proceed as in the proof of lemma 3.3, and write

where $L_{{ \text{Re}\, \sigma_I}}$ is the weighted graph Laplacian on the subgraph $G_I$ induced by the interior nodes and $f \in ( \mathbb{C}^{d\times d})^I$ is given as in (26). Take a $z \in \mathcal{N}(L_\sigma)_{II}$ and multiply (31) on the left by $z^*$ and on the right by $z$ to obtain

By (29) applied to the subgraph $G_I$, we have $L_{ \text{Re}\, \sigma_I} \succeq 0$. By the assumption $\text{Re}\, \sigma \succeq 0$, we also have ${\rm diag}( \text{Re}\, f)\succeq 0$. Thus the two last terms in (32) are non-negative and must be zero by the first equality in (32). We have established that $z^*{\rm diag}( \text{Re}\, f) z = 0$. But $\text{Re}\, f(i)$ is a sum of positive semidefinite matrices (since $\text{Re}\, \sigma \succeq 0$). Thus we must have that

Since conductivities are assumed to have symmetric positive semidefinite real parts, this means that for all $\{i, j\} \in E$, with $i \in I$ and $j \in B$ we have $\text{Re}\, \sigma(\{i, j\}) z(i) = 0$. By the inclusion in the hypothesis of the lemma we get $\text{Im}\, \sigma(\{i, j\}) z(i) = 0$ and also $\sigma(\{i, j\}) z(i) = 0$. Now from the definition of the Laplacian we have

This shows the inclusion (ⅱ).

$\underline{{\rm Proof ~of ~(iii)}.}$ Apply statement (ⅱ) to the conductivity $\overline{\sigma} = \text{Re}\, \sigma -\jmath \text{Im}\, \sigma$ and the fundamental theorem of linear algebra to get $\mathcal{R}((L_{\overline{\sigma}})_{II}^*) \supset \mathcal{R}((L_{\overline{\sigma}})_{IB}^*)$. Since $\text{Re}\, \sigma$ and $\text{Im}\, \sigma$ are symmetric we get the desired result $\mathcal{R}((L_\sigma)_{II})\supset \mathcal{R}((L_{\sigma})_{IB})$.

The following lemma shows that even if there are floppy modes, these do not influence Neumann (or net current) measurements at the boundary. In other words, floppy modes cannot be observed from boundary measurements.

Lemma 3.7. Assume the hypothesis of lemma 3.6 hold. Then floppy modes correspond to zero boundary measurements.

Proof. We need to show that if $z \in ( \mathbb{C}^d)^V$ is a floppy mode, then we have zero Neumann boundary data, i.e. $(L_\sigma z)_B = 0$. Since $z$ is a floppy mode, we see from lemma 3.5 that $z_B = 0$ and $z_I\in \mathcal{N}(L_{ \text{Re}\, \sigma})_{II}$. By inclusions (ⅰ) and (ⅱ) of lemma 3.6 we deduce that $z_I \in \mathcal{N}(L_{\sigma})_{II} \subset \mathcal{N}(L_{\sigma})_{BI}$. We conclude by noticing that $(L_\sigma z)_B = (L_\sigma)_{BB} z_B + (L_\sigma)_{BI} z_I = 0.$

3.3.1.   Proof of theorem 2.3

Proof. If $u$ is a solution to the $\sigma, 0$ Dirichlet problem with boundary condition $g \in ( \mathbb{C}^d)^B$, then $u_B = g$ and

The inclusion (ⅲ) of lemma 3.6 guarantees that equation (33) admits a solution for all $g \in ( \mathbb{C}^d)^B$. The general solution to (33) may be written as

where $z \in \mathcal{N}((L_\sigma)_{II})$ and the symbol $\dagger$ is the Moore-Penrose pseudoinverse. The Neumann boundary data corresponding to such solution is:

However the inclusion (ⅱ) in lemma 3.6 (or lemma 3.7) guarantees that $(L_\sigma)_{BI} z = 0$. Hence the Dirichlet to Neumann map is uniquely defined and can be written as

Now let $Q$ be such that $Q^TQ = \mathbb{I}$ and $\mathcal{R}(Q) = \mathcal{R}((L_\sigma)_{II})$. We can always find a real $Q$ because of lemma 3.6 (ⅰ), and it can be found from $(L_{ \text{Re}\, \sigma})_{II}$ e.g. via a QR factorization or an eigendecomposition. By the fundamental theorem of linear algebra, the space $\mathcal{R}(Q)$ is the orthogonal to the interior components of floppy modes, and thus depends only on the subspaces $\mathcal{R} ( \text{Re}\, \sigma(e))$, $e \in E$ (see lemma 3.5, (ⅱ)). We can use $Q$ to write the pseudoinverse of $(L_\sigma)_{II}$ as follows

and we get the alternate expression (19) for the Dirichlet to Neumann map.

4.   Common structure

The discrete inverse problems we consider share a common structure that we describe in section 4.1 and that is motivated in section 4.2 by the classic uniqueness proof for the continuum Schrödinger inverse problem [25]. Under the assumptions we make here, the linearization of the problem is readily available (section 4.3) and analyticity of the forward map is ensured. This has practical implications that are described in section 4.4.

4.1.   An abstract inverse problem

We denote by $p \in \mathbb{C}^m$ the unknown parameter. As we see later in sections 5 and 6, the parameter $p$ may represent a matrix valued quantity (or its eigenvalues) defined on the edges or nodes of a graph. The forward or parameter to data map associates to the parameter $p$ the matrix $\Lambda_p \in \mathbb{C}^{n \times n}$ (the data), provided the parameter $p$ belongs to an admissible set $R \subset \mathbb{C}^m$ of parameters. The inverse problem is to find $p$ from $\Lambda_p$. Furthermore, we assume that the discrete inverse problems we consider satisfy the following assumptions.

● Assumption 1. The parameter $p$ belongs to an open convex set $R \subset \mathbb{C}^m$ of admissible parameters. The forward map that to a parameter $p \in R$ associates the data $\Lambda_p$ is well defined for $p \in R$.

● Assumption 2. For all $f, g \in \mathbb{C}^n$ and $p_1, p_2 \in R$ the following boundary/interior identity holds:

where $b: \mathbb{C}^\ell \times \mathbb{C}^\ell \to \mathbb{C}^m$ is a bilinear mapping and $S_p \in \mathbb{C}^{\ell \times n}$ is a matrix defined for $p \in R$ that associates to a boundary condition $f \in \mathbb{C}^n$, an internal "state" $S_p f \in \mathbb{C}^\ell$. This identity is motivated in section 4.2 by looking at the continuum Schrödinger problem.

● Assumption 3: Analyticity. The entries of $S_p$ are analytic functions of $p$ for $p\in R$.

Here by "analytic" we mean in the sense of analyticity of several complex variables, see e.g. [19]. For completeness, we recall in appendix A all the results we use from the theory of functions of several complex variables.

4.2.   Motivation of boundary/interior identity

The identity (36) in Assumption 2 is a discrete version of a similar identity that plays a key role in the Sylvester and Uhlmann [25] proof of uniqueness for the continuum Schrödinger inverse problem. To motivate (36) we make a short excursion to the continuum (fully contained within this section) and consider an open connected and bounded domain $\Omega \subset \mathbb{R}^d$ with smooth surface $\partial\Omega$. We say $u$ solves the Schrödinger problem if

where $\Delta = \partial_1^2 + \ldots \partial_d^2$ is the Laplacian and $q$ is a Schrödinger potential and $f$ the Dirichlet boundary data. The Dirichlet to Neumann map is the linear mapping $\Lambda_q$ that maps Dirichlet boundary data $u|_{\partial\Omega}$ to Neumann boundary data $n\cdot \nabla u |_{\partial\Omega}$, where $n$ is the outward pointing unit normal to $\partial\Omega$ and $\nabla u = [\partial_1 u, \ldots, \partial_d u]^T$ is the gradient of $u$. Now if $u_1$ (resp. $u_2$) solves the Schrödinger problem with $u_1|_{\partial\Omega} = f$ (resp. $u_2|_{\partial\Omega} = g$) and Schrödinger potential $q_1$ (resp. $q_2$), then by using Green's identities one gets the following identity that can be found in [25]:

This is called a boundary/interior identity because it relates the boundary data (difference of Dirichlet to Neumann maps for $q_1$ and $q_2$) to a linear functional of $q_1 - q_2$ in the interior of $\Omega$. The linear functional itself is the product of the solutions $u_1$ and $u_2$.

Analogously in the boundary/interior identity (36) we require that the difference in the parameter to data map for two parameters $p_1$ and $p_2$ is given by a linear functional of $p_1 - p_2$, where the linear functional itself is a "product" of the "internal states" corresponding to $p_1$ and $p_2$. What we mean by "product" and "internal state" is left abstract for now, but many concrete examples are given in section 5.

4.3.   The product of solutions matrix and the Jacobian

For a discrete inverse problem satisfying assumptions 1–3, we define the following product of solutions matrix, which is the matrix valued function $W: R \times R \to \mathbb{C}^{m \times n^2}$ with columns given by ²

²We use Matlab style notation where the $j-$th column of a matrix $A$ is $A(:, j)$ and its $i-$th row is $A(i, :)$.

The next lemma shows that the parameter to data map $\Lambda_p$ must be Fréchet differentiable (specialized versions of this lemma appear in [6,lemma 5.4 and 6.3]).

Lemma 4.1 (Linearization of discrete inverse problem). Let $p \in R$. For sufficiently small $\delta p \in \mathbb{C}^m$, we have

Proof. Use the boundary/interior identity (36) with $p_1 = p + \epsilon \delta p$ and $p_2 = p$, for some scalar $\epsilon$. To conclude divide both sides by $\epsilon$ and take the limit as $\epsilon \to 0$. Notice that assumption 3 guarantees that $S_p$ is analytic in $p$, therefore we do have continuity of $S_p$ in $p$ and $S_{p + \epsilon \delta p} \to S_p$ as $\epsilon \to 0$.

A consequence of lemma 4.1 is that $W(p, p)^T$ is a $n^2 \times m$ matrix representation of the Jacobian matrix for the parameter to data map at parameter value $p$. From (39), the matrix representation of the Jacobian is associated to identifying the matrix $\Lambda_p \in \mathbb{C}^{n \times n}$ with the vector ${\rm vect}(\Lambda_p) \in \mathbb{C}^{n^2}$. Clearly the linearized inverse problem about $p$ is injective when $\mathcal{N}(W(p, p)^T) = \{0\}$, i.e. when the product of solutions matrix $W(p, p)$ has full row rank, i.e. $\mathcal{R} (W(p, p)) = \mathbb{C}^m$.

Another consequence of lemma 4.1 is that the Jacobian of $\Lambda_p$ with respect to $p$ must be analytic for $p \in R$ (by assumption 3). Clearly the forward map $\Lambda_p$ must also be analytic for $p \in R$.

4.4.   Analyticity and uniqueness almost everywhere

We look at the impact of analyticity on the uniqueness question:

If $p_1, p_2 \in \mathbb{C}^m$ are parameters with identical data $\Lambda_{p_1} = \Lambda_{p_2}$, can we conclude that $p_1 = p_2$?

For inverse problems satisfying assumptions 1–3, we can only guarantee uniqueness in a weak sense that we call uniqueness almost everywhere (as in [6]). By this we mean that (a) the linearized problem is injective for almost all parameters $p \in R$ and (b) for any $p$, the sets $M_p \equiv \{ q \in R \; |\; \Lambda_q = \Lambda_p \}$ must have zero measure. The set $M_p$ is the equivalence class of all parameters that give the same data as the parameter $p$. If the uniqueness were guaranteed for the inverse problem, we would have $M_p = \{p\}$. In our case we can only guarantee the much weaker statement that $M_p$ has zero measure. Both (a) and (b) follow from analyticity of the forward map and assuming that the Jacobian is injective at a single parameter $\rho \in R$.

First assume analyticity of $\Lambda_p$ and that we can find $\rho_1, \rho_2 \in R^2$ such that $\Lambda_{\rho_1} \neq \Lambda_{\rho_2}$. Define the function $g: R \times R \to \mathbb{C}$ by $g(x, y) = [\Lambda_{x} - \Lambda_y]_{ij}$ for some $i, j\in 1, \ldots, n$. Clearly $g$ is analytic on $R^2$ and we can find $i, j$ such that $g(\rho_1, \rho_2) \neq 0$. By analytic continuation, the set $\{ (p_1, p_2) \in R \times R \; |\; g(p_1, p_2) = 0\}$ must be a zero measure set. In particular if we fix $p \in R$ we have shown that $M_p \times M_p$ has zero measure and so $M_p$ must have zero measure as well. This is a much simpler way of reaching a result similar to that in [6] and was suggested by Druskin [15].

Analyticity can also be used to deduce that if the Jacobian of the forward map is injective at a parameter $\rho \in R$, then it must be injective at almost any other parameter $p \in R$, i.e. (a). Indeed, lemma 4.1 shows that the Jacobian at $p$ can be represented by the $n^2 \times m$ matrix $W(p, p)^T$ defined in (39). If $W(\rho, \rho)^T$ is injective for a $\rho \in R$, then there is a $m \times m$ submatrix $[W(\rho, \rho)]_{:, \alpha}$ of $W(\rho, \rho)$ that is invertible, where $\alpha = (\alpha_1, \ldots, \alpha_m) \in \{1, \ldots, n^2\}^m$ is a multi-index used to represent the particular choice of columns. Thus the function $f: R \to \mathbb{C}$ defined by

is analytic for $p \in R$ and is such that $f(\rho) \neq 0$. By analytic continuation, the zero set of $f$ must be of measure zero. Thus the set of parameters for which the Jacobian is not injective must be a zero measure set.

Finally we note that if we can find a parameter $\rho$ for which the Jacobian $W(\rho, \rho)^T$ is injective, then we can use the constant rank theorem (see e.g. [24]) to show that there is a $p \in R$ in a neighborhood of $\rho$ such that $\Lambda_\rho \neq \Lambda_p$.

4.5.   Applications of uniqueness almost everywhere

Uniqueness a.e. has several practical applications that are illustrated for the scalar discrete conductivity problem in [6]. We give an outline of these applications for completeness. The first application is a simple test to determine whether uniqueness a.e. holds for a particular discrete inverse problem and that may also indicate sensitivity to noise (section 4.5.1). Once we know uniqueness a.e. holds for a particular discrete inverse problem, we can guarantee that the situations in which Newton's method with line search fails can be easily avoided (section 4.5.2). Naturally a statement about zero measure sets can be translated to a probabilistic setting (section 4.5.3).

4.5.1.   A test for uniqueness almost everywhere

Recall from lemma 4.1 that the Jacobian of the discrete inverse problem at a parameter $p$ can be easily computed as a products of solutions matrix (39) with $p \equiv p_1 = p_2$. As discussed in section 4.4, if we can find a parameter $p \in R$ for which the Jacobian is injective, then uniqueness a.e. holds for the problem. A numerical test for uniqueness a.e. can be summarized as follows.

1. Pick a parameter $p \in R$.

2. Calculate the Jacobian $W(p, p)^T$ using (39).

3. Find the largest and smallest singular values $\sigma_{\max}, \sigma_{\min}$ of $W(p, p)$.

4. If $\sigma_{\min} > \epsilon \sigma_{\max}$, where $\epsilon$ is a tolerance set a priori, then uniqueness a.e. holds.

We point out that if $\sigma_{\min} \leq \epsilon \sigma_{\max}$ it is not possible to distinguish between the two following scenarios: (a) uniqueness a.e. holds but $W(p, p)$ is not injective to tolerance $\epsilon$; or (b) uniqueness a.e. does not hold for the problem. Thus the test is inconclusive. However we know that scenario (a) is very unlikely because we would have had to pick $p$ on the zero measure subset of $R$ that contains all parameters for which the Jacobian is not injective. Thus the most likely outcome is (b). Finally we remark that other methods may be used instead of the Singular Value Decomposition (SVD) to find the rank of the Jacobian (e.g. the QR factorization). We prefer the SVD because the ratio $\sigma_{\max}/\sigma_{\min}$ is the conditioning of the linear least squares problem associated with the linearization of the discrete inverse problem, and thus measures the sensitivity to noise of the linearization of the inverse problem about the parameter $p$.

4.5.2.   Newton's method

The discrete inverse problem of finding the parameter $p$ from the data $\Lambda_p$ is a non-linear system of equations that can be solved numerically using Newton's method (see e.g. [23]). Let us denote by $D \Lambda_p = W(p, p)^T$ the Jacobian of the Dirichlet to Neumann map about the parameter $p \in R$. For our particular problem we get the following.

Newton's method

$p^{(0)} =$ given

for $k = 0, 1, 2, \ldots$

Find step $\delta p^{(k)}$ s.t. $D\Lambda_{p^{(k)}} \delta p^{(k)} = {\rm vect}(\Lambda_{p^{(k)}} - \Lambda_{p})$

Choose step length $t_k>0$

Update $p^{(k+1)} = p^{(k)} + t_k \delta p^{(k)}$

The first operation in the Newton iteration is to solve a linear problem for the step $\delta p^{(k)}$. This operation can fail either because ${\rm vect}(\Lambda_{p^{(k)}} - \Lambda_{p}) \notin \mathcal{R}(D\Lambda_{p^{(k)}})$ or because $\mathcal{N}(D\Lambda_{p^{(k)}}) \neq \{ 0 \}$. A remedy to either of these situations is to solve the linear least squares system

and pick $\delta p^{(k)}$ as the minimal norm solution to (42). If uniqueness a.e. holds for the problem at hand then clearly $D\Lambda_{p^{(k)}}$ is injective except on a zero measure set. Therefore we can expect the step in Newton's method to be defined uniquely. Now assume we found a step. If we assume a particular form of analyticity for the entries of $S_p$ (in Assumption 3), then we can guarantee that there are only finitely many choices of the step length $t_k$ for which $D\Lambda_{p^{(k+1)}}$ is not injective. In the unlikely event one encounters one of such points, the step length $t_k$ can be reduced by a small amount to make $D\Lambda_{p^{(k+1)}}$ injective. This is a consequence of the following lemma, which is a generalization of the result for the scalar discrete conductivity inverse problem in [6,Corollary 5.7].

Lemma 4.2. Consider a discrete inverse problem satisfying assumptions 1–3 and further assume that all entries of $S_p$ are rational functions of $p$ (of the form $P(p)/Q(p)$, where $P$ and $Q$ are polynomials). Let $p \in R$ and $\delta p \in \mathbb{C}^m$ and assume the Jacobian of $\Lambda_p$ at $p$ is injective. Then there are at most finitely many $t \in \mathbb{R}$ for which $p + t \delta p \in R$ and either

(i) The Jacobian of $\Lambda_p$ at $p+t\delta p$ is not injective.

(ii) $\Lambda_{p+t\delta p} = \Lambda_p$.

Proof. Since the Jacobian of $\Lambda_p$ is injective at $p \in R$, there is a multi-index $\alpha \in \{1, \ldots, n^2\}^m$ such that the function $f$ defined in (41) satisfies $f(p) \neq 0$. Since the admissible set is open and convex, there is an interval $[a, b]$ containing $0$ such that $t \in [a, b] \implies p + t \delta p \in R$. Since the entries of $S_p$ are rational functions of $p$ and $f$ is defined through a determinant we can see that the function $g(t) = f(p+t \delta p)$ is a rational function of $t$, i.e. it can be written in the form $g(t) = F(t)/G(t)$ where $F(t)$ and $G(t)$ are polynomials. Since $F(t)$ can only have finitely many zeroes, we conclude that there are only finitely many $t$ for which $g(t) = 0$, or in other words, for which the Jacobian at $p + t \delta p$ is not injective. This proves (ⅰ). To prove (ⅱ) we consider the function $h(t) = \det [W(p, p+t\delta p)]_{:, \alpha}$, with $\alpha$ being the same multi-index as in (i). The function $h$ is also a rational function in $t$ with finitely many zeroes. Notice that $h(t) \neq 0$ implies the matrix $W(p, p+t\delta p)$ has full row rank. Using the boundary/interior identity (36) we see that

when $\delta p \neq 0$. Thus there are at most finitely many $t$ for which $\Lambda_{p+t\delta p} = \Lambda_p$, $p, p + \delta p \in R^2$ and $\delta p \neq 0$.

Remark 2. The assumption on the entries of $S_p$ being rational functions of $p$ is satisfied by all the examples of discrete inverse problems on graphs that we consider in sections 5 and 6. This is a simple consequence of the cofactor formula for the inverse of a matrix.

4.5.3.   Probabilistic interpretation of uniqueness almost everywhere

The discussion in section 4.4 has a probabilistic flavor as was remarked for the scalar conductivity problem in [6]. To see this, consider a probability space $(\Omega, \mathcal{F}, \mathbb{P})$ (i.e. a sample space $\Omega$, a set of events $\mathcal{F}$ and a probability measure $\mathbb{P}$) and consider a random variable $P : \Omega \to R\times R$ with distribution $\mu_P$ that we assume is absolutely continuous with respect to the Lebesgue measure on $\mathbb{C}^m \times \mathbb{C}^m$. Note that this assumption precludes the distribution $\mu_P$ from being supported on a set of Lebesgue measure zero in $R \times R$. We write $P \equiv (P_1, P_2)$ when we want to distinguish the components of $P$. If uniqueness a.e. holds for the discrete inverse problem at hand and $M \subset R \times R$ is a measurable set for which $\mathbb{P} \{ P \in M \} > 0$, then we must have

To see this, remark that uniqueness a.e. guarantees that the set

is of measure zero. Since the distribution is absolutely continuous with respect to the Lebesgue measure, this also means $\mu_P(Z) = 0$. Roughly speaking, if we choose two admissible parameters $p_1, p_2$ at random, we have $W(p_1, p_2)$ injective almost surely. Thus we can tell $p_1$ and $p_2$ apart from the data $\Lambda_{p_1}$, $\Lambda_{p_2}$ almost surely.

A similar observation can be made regarding the injectivity of the Jacobian of the problem. Let $Q : \Omega \to R$ be a random variable with distribution $\mu_Q$ that is assumed to be absolutely continuous with respect to the Lebesgue measure. If uniqueness a.e. holds and $N \subset R$ is some measurable set with $\mathbb{P} \{ Q \in N \} > 0$, then we must have

5.   Examples of matrix valued inverse problems on graphs

Here we use the graph theoretical results from section 2 to give examples of matrix inverse problems on graphs that fit the mold of section 4.

5.1.   Matrix valued conductivity inverse problem

Given a graph $G = (V, E)$ with boundary, the problem here is to find the matrix valued conductivity $\sigma \in ( \mathbb{C}^{d\times d})^E$ from the Dirichlet to Neumann map $\Lambda_{\sigma, 0}$. We explain below why this problem satisfies the assumptions of section 4.

● Here we take as admissible set:

This is an open convex set in $( \mathbb{C}^{d \times d} )^E$ which can be identified to an open convex subset of $\mathbb{C}^{d^2|E|}$. The forward map is the map that to $\sigma \in R$ associates the Dirichlet to Neumann map $\Lambda_{\sigma, 0} \in \mathbb{C}^{d|B| \times d|B|}$. This map is well defined for $\sigma \in R$ because of theorem 2.1.

● By lemma 2.4 with $q_i = 0$, $i = 1, 2$, we have the boundary/interior identity

Here we define $S_\sigma \in \mathbb{C}^{d|E|\times d|B|}$ by its action on some $f \in \mathbb{C}^{d|B|}$

where $u$ solves the Dirichlet problem (15), with $q = 0$ and $u_B = f$. The bilinear map $b : \mathbb{C}^{d|E|} \times \mathbb{C}^{d|E|} \to \mathbb{C}^{|E|d^2}$ is defined by $b(u, v) = u \odot v$, where the outer product $\odot$ is defined in section 2.1 and we are implicitly identifying $( \mathbb{C}^d)^E$ with $\mathbb{C}^{d|E|}$ and similarly for $( \mathbb{C}^{d\times d})^E$ and $\mathbb{C}^{|E|d^2}$.

● Analyticity assumption. From theorem 2.1 (see also lemmas 3.3 and 3.4), the solution $u$ to the Dirichlet problem (15) with $u_B = f$, $\sigma \in R$ and $q = 0$ is determined by $u_I = -(L_{II})^{-1} L_{IB} f$, where for clarity we omitted the subscript $\sigma$ from the graph Laplacian $L_\sigma$. Therefore the entries of $S_\sigma$ depend analytically on $\sigma$, for $\sigma \in R$.

5.1.1.   Relation between scalar and matrix valued conductivity problems

Here we show that if the Jacobian for the scalar conductivity problem on a graph is injective at a conductivity $\sigma \in (0, \infty)^E$ then the Jacobian for the matrix conductivity problem on the same graph but with conductivity of edge $e \in E$ given by $\sigma(e) \mathbb{I} \in \mathbb{R}^{d\times d}$ must also also be injective. Because of the discussion in section 4.4, this result shows that if uniqueness a.e. holds for a scalar conductivity problem, then it must also hold for the matrix valued problem. In particular uniqueness a.e. holds on the critical circular planar graphs that are defined in [13,14].

Lemma 5.1. Let $G = (V, E)$ be a graph with boundary and let $s \in (0, \infty)^E$ be a scalar conductivity. Define the conductivity $\sigma \in ( \mathbb{R}^{d \times d})^E$ by $\sigma(e) = s(e) \mathbb{I}$ with $\mathbb{I}$ being the $d \times d$ identity. Then if the Jacobian of the forward problem is injective for the scalar conductivity $s$, it must also be injective for the matrix valued conductivity $\sigma$.

Proof. We need to show that

To this end, we first link the Laplacian $L_\sigma$ for the matrix valued conductivity $\sigma$ (a $d|V| \times d|V|$ matrix) to the Laplacian for a graph $G_d = (V_d, E_d)$ that corresponds to having $d$ copies of the graph $G$ without any edges between the copies, and each copy of $G$ having the same scalar conductivity $s$. To be more precise the vertex set of $G_d$ is $V_d = V \times \{1, \ldots, d\}$, the edge set is

Then with an appropriate ordering of $V_d$, we have $L_\sigma = L_{s_d}$, where the conductivity $s_d \in (0, \infty)^{E_d}$ is defined by

for all $\{v_1, v_2\} \in E$, $\ell_1, \ell_2 \in \{1, \ldots, d\}$, and with $\delta_{\ell_1, \ell_2}$ being the Kronecker delta. Now take a solution $v \in \mathbb{R}^V$ to the Dirichlet problem on $G$ with scalar conductivity $s$ and let $e_i$ be the $i-$th canonical basis vector of $\mathbb{R}^d$. Then up to a reordering of $V_d$, $v \otimes e_i$ solves the Dirichlet problem on $G$ with matrix valued conductivity $\sigma$ and boundary data $v|_B \otimes e_i$, $i = 1, \ldots, d$. Here we used the Kronecker product $\otimes$ which we recall for convenience in (2). Let $v_j$ be the solution to the Dirichlet problem on $G$ with conductivity $s$ such that $v_j|_B = e_j$, $j = 1, \ldots, |B|$. Then we have

where we used the outer product $\odot$ defined in (1). Since $\nabla(v \otimes e_i) = (\nabla v) \otimes e_i$ for any $v \in \mathbb{R}^V$ we should have that

for any $i, i' = 1, \ldots, |B|$ and $j, j' = 1, \ldots, d$. Now let us consider the subspace $M \subset \mathbb{R}^{d^2 |E|}$ spanned by all possible products (43) in vector form, i.e.

Since $\mathcal{R}(W(s, s)) = \mathbb{R}^{|E|}$ we deduce that $M = \mathbb{R}^{d^2|E|}$. Indeed, the $d^2$ subspaces associated with the pairs $(j, j') \in \{1, \ldots, d\}^2$ are mutually orthogonal and each has dimension $|E|$. The desired result follows because we have the inclusion $M \subset \mathcal{R}(W(\sigma, \sigma))$.

5.2.   Matrix valued Schrödinger inverse problem

Given a graph $G = (V, E)$ with boundary, the inverse problem we consider here is to find the symmetric matrix valued Schrödinger potential $q \in ( \mathbb{C}^{d\times d})^V$ from the Dirichlet to Neumann map $\Lambda_{\sigma, q}$, where the conductivity $\sigma \in ( \mathbb{C}^{d \times d})^E$ is symmetric with $\text{Re}\, \sigma \succ 0$ and is assumed to be known. This problem has the structure of the abstract inverse problem of section 4, as we see next.

● The admissible set is

This is an open convex set in $( \mathbb{C}^{d \times d})^V$ which can be identified to an open convex subset of $\mathbb{C}^{d^2|V|}$. The forward map is the map that to $q \in R$ associates the Dirichlet to Neumann map $\Lambda_{\sigma, q} \in \mathbb{C}^{d|B| \times d|B|}$. This map is given by (17) and is well defined for $q \in R$ because of theorem 2.1.

● The boundary/interior identity is given by applying lemma 2.4 with $\sigma_i = \sigma$, $i = 1, 2$:

Here we define $S_q \in \mathbb{C}^{d|V| \times d|B|}$ by its action on some $f \in \mathbb{C}^{d|B|}$

where $u$ solves the Dirichlet problem (15) with $u_B = f$. The bilinear map $b : \mathbb{C}^{d|V| \times d|V|} \to \mathbb{C}^{|V|d^2}$ is defined by $b(u, v) = u \odot v$, where the block-wise outer product $\odot$ is defined in (1) and we implicitly identify $( \mathbb{C}^d)^V$ with $\mathbb{C}^{d|V|}$ and $( \mathbb{C}^{d \times d})^V$ with $\mathbb{C}^{|V|d^2}$.

● Analyticity assumption. From the proof of theorem 2.1, the solution $u$ to the Dirichlet problem (15) with $u_B = f$ and $q \in R$ is determined by $u_I = - (L_{II} + {\rm diag}(q_I))^{-1} L_{IB}f$, where we omitted the subscript $\sigma$ from the graph Laplacian $L_\sigma$. Hence the entries of $S_q$ are analytic for $q \in R$.

5.3.   Rank deficient matrix valued conductivity inverse problem

Here we consider the inverse problem of recovering a conductivity $\sigma \in ( \mathbb{C}^{d\times d})^E$ that is rank deficient from its Dirichlet to Neumann map $\Lambda_{\sigma, 0}$. To simplify the discussion, we assume that the conductivities of all edges have the same rank $r \geq 1$, i.e. ${\rm rank} \sigma(e) = r$ for all $e \in E$. The conductivities we consider here satisfy the inclusion assumption of theorem 2.3, namely that $\mathcal{N} ( \text{Re}\, \sigma(e)) \subset \mathcal{N} ( \text{Im}\, \sigma(e))$, for all $e \in E$. Moreover we assume that $\text{Re}\, \sigma(e)$ and $\text{Im}\, \sigma(e)$ commute so that they can be decomposed on the same basis of real eigenvectors. Therefore the eigenvectors of $\sigma(e)$ are real and we may define $x \in ( \mathbb{R}^{d\times r})^E$ and $\lambda \in ( \mathbb{C}^r)^E$ to write the eigendecomposition of each of the conductivities i.e.

with $x(e)^Tx(e) = \mathbb{I}$ being the $r \times r$ identity. By the hypothesis $\sigma \succeq 0$ we must have $\text{Re}\, \lambda > 0$. We note that the assumptions we make here are more restrictive than those of theorem 2.3, but they suffice for networks of springs, masses and dampers where $r = 1$, as we see later in section 6.1.

● We take as admissible set

Clearly $R$ is an open convex set in $( \mathbb{C}^r)^E$, which can be identified to an open convex subset of $\mathbb{C}^{r|E|}$. The forward map associates to $\lambda \in R$ the Dirichlet to Neumann map $\Lambda_{\sigma(\lambda), 0}$ where $\sigma(\lambda)$ has eigenvectors $x$ and eigenvalues $\lambda$, i.e. $\sigma(\lambda)$ satisfies (44). Theorem 2.3 guarantees that this map is well defined for $\lambda \in R$.

● Let $\lambda_1, \lambda_2 \in R$. By lemma 2.4 with $\sigma_i \equiv \sigma(\lambda_i)$ and $q_i = 0$, $i = 1, 2$, we get the boundary/interior identity

We define the matrix $S_\lambda \in \mathbb{C}^{r|E|\times d|B|}$ by its action on some $f\in \mathbb{C}^{d|B|}$,

where $u$ solves the Dirichlet problem (15) with boundary data $u_B = f$, conductivity $\sigma(\lambda)$ satisfying (44) and $q = 0$. Recall that the Dirichlet problem solution is determined up to floppy modes. However from the floppy mode characterization in lemma 3.5, we see that the definition of $S_\lambda$ is independent of the choice of floppy mode. The bilinear map $b: \mathbb{C}^{r|E|} \times \mathbb{C}^{r|E|} \to \mathbb{C}^{r|E|}$ is simply the Hadamard product, i.e. $b(u, v) = u \circledast v$, and as before we identify $( \mathbb{C}^r)^E$ with $\mathbb{C}^{r|E|}$.

● Analyticity assumption. From the proof of theorem 2.3 (see section 3.3.1), a solution $u$ to the Dirichlet problem (15) with boundary data $u_B = f$, conductivity $\sigma(\lambda)$ satisfying (44) and $q = 0$, is determined by

where $Q$ is a real matrix such that $Q^T Q = \mathbb{I}$ and $\mathcal{R}(Q) = \mathcal{R}((L_\sigma)_{II})$. Since $Q$ depends only on the graph and the (known a priori) eigenvectors $x$, the entries of $u_I$ are analytic for $\lambda \in R$. Hence the entries of $S_\lambda$ must also be analytic for $\lambda \in R$.

6.   Application to networks of springs, masses and dampers

6.1.   Spring networks

Consider a graph $G = (V, E)$ with boundary $B$ and let $p \in ( \mathbb{R}^d)^V$ be a function representing the equilibrium position of each node in dimension $d = 2$ or $3$. Each edge $e \in E$ represents a spring with positive spring constant given by the function $k \in (0, \infty)^E$. Let $u \in ( \mathbb{R}^d)^V$ denote the displacements of the nodes with respect to the equilibrium position. The quantity $\nabla u \in ( \mathbb{R}^d)^E$ is the net spring displacement. By Hooke's law, the force exerted by a spring is proportional to the net spring displacement. Here the proportionality is given by a function $k \in (0, \infty)^E$. For infinitesimally small displacements, the force exerted by spring $\{i, j\} \in E$ is proportional to the projection of the net displacement of spring $\{i, j\}$ on the direction $p(i)-p(j)$. In other words, the forces are ${\rm diag}(\sigma) \nabla u$, where $\sigma \in ( \mathbb{R}^{d\times d})^E$ is the positive semidefinite conductivity

Now assume we displace the boundary nodes by an amount $g \in ( \mathbb{R}^d)^B$. If the interior nodes are left to move freely, the net forces at the interior nodes should be zero, this condition is equivalent to $(L_\sigma u)_I = 0$. Hence finding the displacements in a spring network arising from (static) boundary displacements is the same as solving the Dirichlet problem (15) with the particular matrix valued conductivity (45) and zero Schrödinger potential. Using theorem 2.3, we see that the interior displacements are uniquely determined by the boundary displacements (up to floppy modes) and that the Dirichlet to Neumann map $\Lambda_\sigma$ is given by (19). In this particular case this map is called displacement to forces map.

6.2.   Networks with springs, masses and dampers

We now consider the case where the displacements depend on time, i.e. the function $u: V \times \mathbb{R} \to \mathbb{R}^d$ is defined such that $u(i, t)$ is the displacement about the equilibrium position $p(i)$ of node $i\in V$ at time $t \in \mathbb{R}$. We use the notation $\dot{u} = du/dt$ and $\ddot{u} = d^2u/dt^2$ and we assume that all nodes have a non-zero mass, which is given by the function $m \in (0, \infty)^V$.

6.2.1.   Viscous damping

We consider two kinds of viscous damping. The first is spring damping, which is proportional to the net velocity of a spring and is assumed to be in the same direction as the equilibrium position of the springs, with proportionality constant given by a function $c_E \in [0, \infty)^E$. This corresponds to having a damper in parallel with each spring. The net forces associated with this damping are given by $L_\mu \dot{u}$, where $\mu \in ( \mathbb{R}^{d\times d})^E$ is defined by

The second is node damping, meaning that each node is inside a small cavity containing a viscous fluid and is thus subject to a damping force proportional to the node velocity, with the proportionality constant given by a function $c_V \in [0, \infty)^V$. The forces associated with this kind of damping are ${\rm diag}(q_{\text{damp}}) \dot{u}$ where $q_{\text{damp}} \in ( \mathbb{R}^{d\times d})^V$ is defined by $q_{\text{damp}}(i) = c_V(i) \mathbb{I}$, for $i \in V$ and $\mathbb{I}$ being the $d\times d$ identity matrix.

6.2.2.   Equations of motion in time domain

Putting everything together and applying Newton's second law, we get the equations of motion for a network of springs, masses and dampers:

where $q_{\text{mass}} \in ( \mathbb{R}^{d\times d})^V$ is defined by $q_{\text{mass}}(i) = m(i) \mathbb{I}$ for $i \in V$. The function $f : V \times \mathbb{R} \to \mathbb{R}^d$ is a function representing any external forces, i.e. $f(i, t)$ is the external force exerted on node $i \in V$ at time $t$. This second order system of ordinary differential equations can be written as

where $M = {\rm diag}(q_{\text{mass}})$ is the mass matrix, $C = {\rm diag}(q_{\text{damp}})+ L_\mu$ is the damping matrix and $L_\sigma$ is the stiffness matrix. We recall that $\sigma$ is defined in (45) and $\mu$ in (46).

6.2.3.   Frequency domain formulation and the Dirichlet problem

For a time harmonic displacement $u(i, t) = \exp[\jmath\omega t] \hat u(i, \omega)$, the equations of motion (48) become

Now consider the problem of finding the (frequency domain) displacements $\hat u_I$ at the interior nodes knowing the displacements $\hat u_B$ at the boundary nodes and that there are no external forces at the interior nodes (i.e. $\hat f_I = 0$). We immediately see that we have another instance of the Dirichlet problem (15) with complex conductivity $\sigma + \jmath\omega \mu$ and complex Schrödinger potential $-\omega^2 q_{\text{mass}} + \jmath\omega q_{\text{damp}}$. Unfortunately we cannot apply theorem 2.1 directly because we do not have $\sigma \succ 0$ or $-\omega^2 q_{\text{mass}} \succ 0$. To remedy this, we assume there is always a small amount of damping at the nodes i.e. $c_V \in (0, \infty)^V$, in a way reminiscent of the limiting absorption principle for the Helmholtz equation. We rewrite the equations of motion (49) as follows

Again if $\hat f_I = 0$, this is an instance of the Dirichlet problem (15) with complex conductivity $\mu + (\jmath\omega)^{-1} \sigma$ and complex Schrödinger potential $q_{\text{damp}} + \jmath\omega q_{\text{mass}}$. A positive damping at the nodes guarantees $q_{\text{damp}} \succ 0$. Thus the Dirichlet problem admits a unique solution by theorem 2.1. Indeed the condition $(L_{\mu})_{II} \succ -\lambda_{\min}(q_{\text{damp}})$ always holds in this case because $(L_{\mu})_{II} \succeq 0$. Hence the Dirichlet to Neumann map $\Lambda_{\mu + (\jmath\omega)^{-1} \sigma , q_{\text{damp}} + \jmath\omega q_{\text{mass}}}$ is well defined by (17) and so is the Dirichlet to Neumann map for the original problem: $\Lambda_{\sigma + \jmath\omega\mu, -\omega^2 q_{\text{mass}} + \jmath\omega q_{\text{damp}}}$, as can be seen from a homogeneity argument. Since the latter map associates the frequency domain displacements to frequency domain forces, we also call it displacement to forces map.

6.3.   Spring constant inverse problem: Static case

Let us consider the inverse problem of finding the spring constants $k \in \mathbb{R}^E$ from the static displacement to forces map $\Lambda_{\sigma(k), 0}$ of a network of springs. We assume the equilibrium positions $p \in ( \mathbb{R}^d)^V$ of the nodes are known. Uniqueness a.e. for this inverse problem can be established using the result in section 5.3 for rank deficient matrix valued conductivities, which we adapt here to this particular problem. Since we are not aware of a physically relevant interpretation of complex valued spring constants in the static case, we take spring constants in the admissible set

The forward map associates to $k \in R$, the displacement to forces map $\Lambda_{\sigma(k), 0}$. The conductivity $\sigma(k)$ is defined in (45). For an edge $\{i, j\}$, the spring constant $k(\{i, j\})$ is the only non-zero eigenvalue of the conductivity $\sigma(\{i, j\})$. To write the boundary/interior identity for this problem we introduce the function $x\in ( \mathbb{R}^d)^E$ that to an edge $\{i, j\} \in E$ associates the corresponding normalized eigenvector, i.e.

The boundary/interior identity is then

where $\sigma_i \equiv \sigma(k_i)$, $i = 1, 2$ and $g_1, g_2$ are vectors in $\mathbb{R}^{d|B|}$. The matrix $S_{k_i} \in \mathbb{R}^{|E| \times d|B|}$ is defined such that the vector $S_{k_i} g_i$ contains the components of $\nabla u_i$ along the spring directions, i.e.

where $u_i$ is the displacement arising from displacing the boundary nodes by $g_i$, $i = 1, 2$. Concretely, this problem fits the mold of section 4. Thus from section 4.4, if the linearization of the inverse problem for the spring constants in a spring network is injective for particular spring constants, then it must also be injective for almost all other spring constants.

6.4.   Spring constant inverse problem assuming masses are known

Here we consider the problem where the operating frequency $\omega$, the equilibrium position of the nodes $p \in ( \mathbb{R}^d)^V$, the masses $m \in (0, \infty)^V$ and node dampers $c_V \in (0, \infty)^V$ are all known, but we want to recover the spring constants $k \in (0, \infty)^E$ and spring dampers $c_E \in (0, \infty)^E$ from the displacement to forces map at the frequency $\omega$.

● The admissible set is

where we grouped for convenience the spring constants and spring dampers into a single complex valued edge function $\rho$. To be more precise, if $\rho \in R$ we have $\text{Re}\, \rho = k$ and $\text{Im}\, \rho = \omega c_E$. The forward map associates to $\rho \in R$ the displacement to forces map $\Lambda_{\sigma(\rho), q}$, where $\sigma(\rho)$ is defined as in (45) with $k\equiv \rho$ and $q \equiv -\omega^2q_{\text{mass}} + \jmath\omega q_{\text{damp}}$. The forward map is well defined and given by (16) for all $\rho \in R$ because we assumed damping at the nodes, see section 6.2.3.

● The boundary/interior identity is

where $\sigma_i \equiv \sigma(\rho_i)$, $g_i \in \mathbb{C}^{d|B|}$ and the matrix $S_{k_i}$ is defined as in (51) for $i = 1, 2$.

● Analyticity assumption. We can use theorem 2.1 to guarantee that the solution to the Dirichlet problem with boundary displacements $u_B = f$ is given by $u_I = -(L_{II} + {\rm diag}(q_I))^{-1}L_{IB}f$, where we omitted the subscript $\sigma(\rho)$ from the Laplacian $L_{\sigma(\rho)}$. This implies the entries of $S_{\rho}$ are analytic for $\rho \in R$.

Thus the problem of finding the spring constants when the masses are known fits the mold of section 4. The above argument can be adapted to the case where there are no spring dampers, i.e. $c_E = 0$. In this case the admissible set would be $R = (0, \infty)^E$. However the problem no longer satisfies the assumptions of section 4 if we do not know if spring dampers are present, because with $c_E \in [0, \infty)^E$ the admissible set would not be open.

6.5.   Mass inverse problem assuming spring constants are known

Here we assume that the operating frequency $\omega$, the equilibrium position of the nodes $p \in ( \mathbb{R}^d)^E$, the spring constants $k \in (0, \infty)^E$ and the spring dampers $c_E \in [0, \infty)^E$ are known. The inverse problem is to find the masses $m \in (0, \infty)^V$ and node dampers $c_V \in (0, \infty)^V$ from the displacement to forces map at the frequency $\omega$. As we see next, this problem also satisfies the assumptions of section 4.

● The admissible set is

where we grouped for convenience the masses and node dampers into a single complex valued function $\rho$ defined on the vertices. If $\rho \in R$, then $\text{Re}\, \rho = -\omega^2 m$ and $\text{Im}\, \rho = \omega c_V$. The forward map associates to $\rho \in R$ the displacement to forces map $\Lambda_{\sigma, q(\rho)}$, where $\sigma$ is defined as in (45) with $k \equiv k + \jmath \omega c_E$, and $q(\rho) \in ( \mathbb{C}^{d\times d})^V$ is defined by $q(\rho)(i) = \rho(i) \mathbb{I}$ for all vertices $i \in V$. The displacement to forces map is well defined and given by (16) for all $\rho \in R$ because we assumed damping at the nodes, see section 6.2.3.

● The boundary/interior identity is

where $u_i$ solves the Dirichlet problem (15) with conductivity $\sigma + \jmath \omega \mu$ and Schrödinger potential $q(\rho_i)$, $i = 1, 2$.

● Analyticity follows from the solution $u$ to the Dirichlet problem being well defined from all Schrödinger potentials of the form $q(\rho)$ (see the discussion in section 6.2.3).

7.   Summary and perspectives

We have presented several inverse problems on graphs that share the common structure of section 4. In these inverse problems, the unknowns are matrices (or their eigenvalues) defined on the edges or nodes of a graph (section 2). By giving sufficient conditions under which the Dirichlet problem on a graph with matrix valued weights admits a unique solution we can deduce a set of parameters on which the forward map is analytic. In cases where the weights are rank deficient, the solution is not unique but can be determined up to "floppy modes" that depend only on the nullspaces of the weights (sections 2 and 3). Thus the forward map can still be shown to be analytic in this case. Analyticity of the forward map and its Jacobian have practical consequences that are given in sections 4.4 and 4.5. Particular examples of inverse problems on graphs are given in section 5, with a focus on inverse problems arising on networks of springs, masses and dampers (section 6) at a single frequency. Multi-frequency or time domain problems are left for future studies.

There remains many open questions. For example, it is not clear how to find a graph on which uniqueness a.e. holds for a given problem. This was done in [6] by trying many random graphs drawn from the Erdős-Rényi model [16]. A similar approach could be taken here. It is also not clear whether direct solution methods such as the layer peeling algorithm in [13] exist for these matrix inverse problems on networks. Finally, the theoretical results we present here rely on analytic continuation, which is a notoriously unstable procedure.

Acknowledgments

This work was supported by the National Science Foundation grant DMS-1411577. Most of these results were derived in the Spring 2016 introduction to research class called "Network Inverse Problems", supported by the same grant, at the University of Utah. FGV also thanks support from the National Science Foundation grant DMS-1439786, while FGV was in residence at the Institute for Computational and Experimental Research in Mathematics in Providence, RI, during the Fall 2017 semester. FGV thanks Laboratoire Jean Kuntzmann for hosting him during the 2017-2018 academic year. We thank Vladimir Druskin for his comments on an earlier version of this manuscript. Finally the authors would like to thank the referees for their insightful comments, that among other things simplified the assumptions and proof of theorem 2.3.

Appendix A.   Facts about analytic functions of several complex variables

A function $f : \mathbb{C}^n \to \mathbb{C}$ is analytic on some open set $R \subset \mathbb{C}^n$ if for any $z_0 \in R$, the function $f(z)$ can be expressed as a convergent power series, i.e. we can find complex coefficients $c_\alpha$ for which the series

converges for all $z \in R$. Here we used the notation $z^\alpha = z_1^{\alpha_1} z_2^{\alpha_2} \cdots z_n^{\alpha_n}$, for a multi-index $\alpha \in \mathbb{N}^n$. Rational functions of the form $P(z) / Q(z)$, for $P(z)$ and $Q(z)$ polynomials, are analytic on any connected open set where $Q(z) \neq 0$. Moreover, the product and the sum of two analytic functions is also analytic. The uniqueness lemma below is a consequence of analytic continuation, i.e. if $f(z)$ is analytic for $z\in R$ and we can find $z_0$ such that $f(z_0) \neq 0$, then the zero set of $f$

must be a set of measure zero with respect to the Lebesgue measure on $R$ (see e.g. [19]).