A contiunous-time $SIS$ criss-cross model of co-infection in a heterogeneous population

1.   Introduction

There is a large number of papers with mathematical models of epidemic dynamics. These papers relate to both homogeneous and heterogeneous populations. By heterogeneous population we understand a population with at least two subpopulations that differ in the risk of getting infected. Because of convenience and lack of appropriate data, only two subpopulations are often distinguished. In recent papers ^[1] and ^[2], one can find exemplary models of epidemic spread in such populations with mathematical analysis.

Nowadays, the risk of co-infections is increasing worldwide, including co-infections with COVID-19 ^[3]. This increase is caused by, for example, increased people's mobility ^[4], drug resistance ^[5], impaired immunity after suffering from long COVID-19, and reduction of exposure to microbiota caused by home isolation during the COVID-19 pandemic ^[6]. Also, getting an infection raises the probability of simultaneous development of another illness ^[7]. Co-infection also boosts healthcare costs ^[8] and number of deaths ^[9]. It is therefore essential to put an effort into reducing co-infection cases. This reduction can be achieved by applying mathematical modeling. Thanks to mathematical models of co-infection spreading and their mathematical analysis, one can predict co-infections and implement proper therapeutic approaches. This is desirable since data concerning co-infections are less accessible than for single epidemics.

Generally, models of co-infection dynamics are based on models that describe the spread of a single epidemic. Hence, they have a more complex form and are, consequently, more difficult to analyze. However, one can find literature dealing with mathematical analysis of co-infection spread. A recent paper ^[10] conducted a systemic review of mathematical models. A model of general co-infection for an acute and a chronic disease was presented in ^[11]. The authors in ^[12] proposed and analyzed the model of COVID-19 and tuberculosis $(TB)$ infection. The same type of epidemics, together with measuring impact on isolation, was investigated in ^[13]. Papers ^[14] and ^[15] provide mathematical models for the spread of SARS-CoV-2 with hepatitis B virus and SARS-CoV-2 with human T-cell lymphotropic virus type-I, respectively. The analysis of models concerning individuals suffering from COVID-19 and kidney disease was presented in a recent work ^[16]. An interesting approach is presented in ^[17], where the authors investigated the co-infection of airborne and vector-host diseases, namely COVID-19 and dengue.

Not only COVID-19 is investigated in co-infection modeling. Since $HIV$ infection increases the probability of developing $TB$ ^[18], papers related to the modeling of $TB$ and $HIV$ spread contribute significantly to the literature. Authors in ^[19] distinguish two $TB$ infected classes: fast and slow latent. They also considered acute and chronic $HIV$-infected groups. A recent paper ^[20] focused on an analysis of a $TB$/$HIV$ epidemic spread in Ethiopia, with two infected groups for each disease. Naturally, other co-infections are also analyzed in the literature. Authors in ^[21] investigated the epidemic of $HIV$ and hepatitis C virus, whereas paper ^[22] dealt with co-infection of $TB$ and pneumonia.

In each paper described above, authors assumed that there is only one class of people that are not infected with any disease; this means they are susceptible to both infections. This leads to situations where the probability of co-infection is raised only by encountering a single infection. That supposition implies no population heterogeneity for healthy individuals. Clearly, this case is not valid. Therefore, there is a need to include heterogeneity in a susceptible class. While modeling an epidemic of a single infection for a heterogeneous population, authors assume that values of parameters reflecting a given subpopulation are the same. This assumption actually leads to the case of a homogeneous population. To adequately describe the dynamics of infection, and consequently of co-infection, in a heterogeneous population, one must consider different values of parameters for each subpopulation. Such consideration makes the mathematical analysis of the model more difficult; thus, this approach is uncommon.

Our paper aims to construct and analyze the mathematical models of co-infection in a heterogeneous population consisting of two subpopulations. We assume that parameter values reflecting a given process in each subpopulation differ. This assumption and the heterogeneity in the population make our paper novel among the literature considering the modeling of co-infections. In our model, we also introduce a case of a spread of each disease not only among one subpopulation but also between subpopulations. This introduction enables our system to be classified as a criss-cross model. We propose a system of ordinary differential equations that is a $SIS$-type (susceptible – infected – susceptible) model. In models of such type, there is no immunity after recovery and an individual becomes susceptible again. Including heterogeneity constrains computations. For this reason, we do not incorporate a recovered class to maintain explicit results of the analysis. Our model does not relate to particular diseases. Hence, one can apply the obtained results to different infections. Such applications include co-infections that combine sole airborne illnesses, such as $TB$, COVID-19, or influenza, sexually transmitted diseases, such as gonorrhea, $HIV$, and hepatitis $B$, or incorporate illnesses from both types.

This paper is a continuation of our work from ^[23] and ^[24], in which we investigated the criss-cross model of epidemic spread of a single disease for a heterogeneous population. In ^[23], we conducted the mathematical analysis of the model that was proposed in ^[25]. The aim of that analysis was to confirm, from a mathematical point of view, the medical hypothesis that stated that to control the epidemic spread in the heterogeneous population, one must consider criss-cross illness transmission. Investigating such spread in a single subpopulation does not provide complete insight into the epidemic dynamics. Because of the proposed model's unexpected properties, such as a possible unbounded population growth, we modified the system from ^[23] by assuming a constant inflow into each subpopulation. We analyzed that modified system in ^[24] and again obtained consistency with the medical hypothesis. Considering that the second disease in epidemic dynamics for a heterogeneous population is medically driven by an increasing number of co-infections worldwide and different scenarios regarding individuals' susceptibility can provide mathematical results that can help predict a co-infection course.

In ^[23] and ^[24], we focused on the stability analysis; we indicated stationary states appearing in the given systems and determined the conditions for their local stability. In this paper, we also apply this approach. The model presented herein relies on the system from ^[24].

The paper is organized as follows: In Section 2, we describe and introduce our model. Then we find stationary states of the system and describe conditions for their existence. The basic reproduction number of the model is computed in Section 4. The following section deals with local stability of the found stationary state. We summarize our results in Section 7.

2.   Formulation of a model and its basic properties

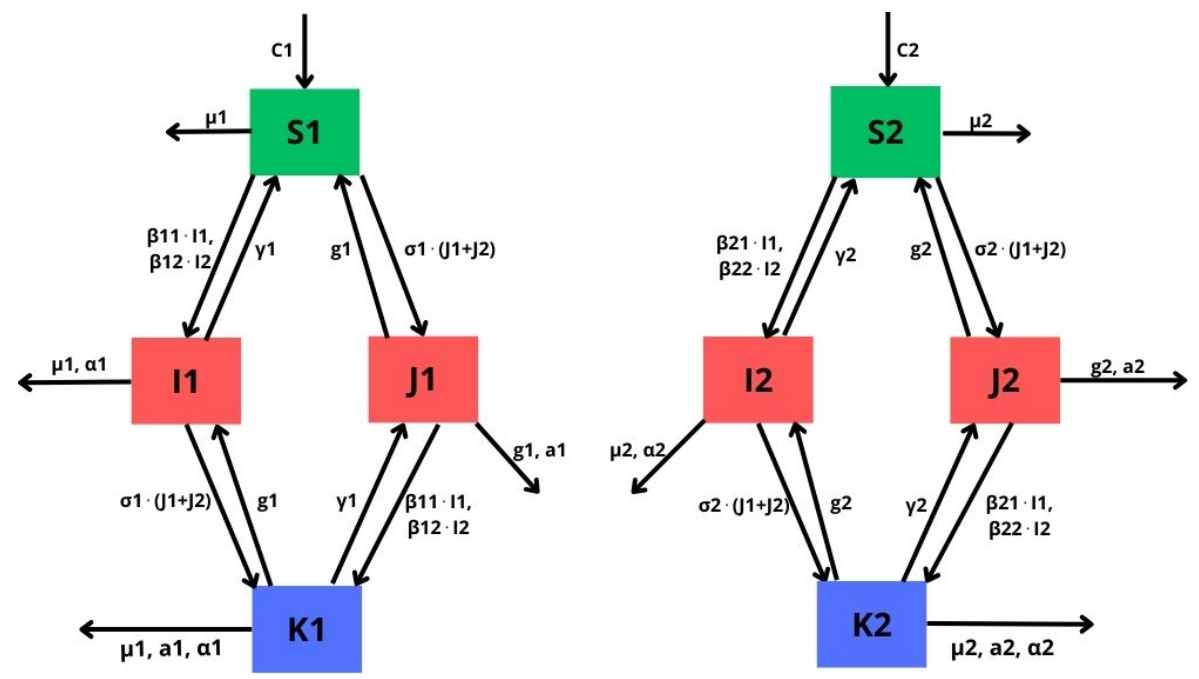
Let us first describe the assumptions concerning the proposed model. In a population, we indicate two subpopulations, a low-risk ($LS$) and a high-risk ($HS$) subpopulation, relating to the risk of getting infected. $LS$ and $HS$ have, respectively, lower and higher susceptibility to each disease. For every variable and parameter, we assign a subscript $i$ equal to 1 and 2 for $LS$ and $HS$ respectively. If $i$ has no assigned value, then $i \in \{1, 2 \}$. By $S_1$ and $S_2$, we denote a density of healthy people in $LS$ and $HS$, respectively. The variables $I_i$ refer to the density of individuals from the given subpopulation that are infected by a pathogen of the disease that we call disease $A$ ($DA$). Similarly, we define $J_i$ as the density of individuals suffering from disease $B$ ($DB$). The density of a group infected by pathogens from both diseases is denoted by $K_i$.

Migrating and newborn individuals join each subpopulation through $S_i$ class with a recruitment rate $C_i$. A natural death rate for each subpopulation is equal to $\mu_i$. For $DA$, we introduce the transmission rates $\beta_{11}$, $\beta_{22}$, $\beta_{12}$ and $\beta_{21}$, reflecting transmission among $LS$, among $HS$, from $HS$ to $LS$, and from $LS$ to $HS$, respectively. These four different rates mean that $DA$ differs in spreading and contracting a pathogen. To get a preliminary insight on co-infection dynamics for the heterogeneous population, for $DB$ we assume that individuals differ only in contracting a pathogen. For this reason, we take only two transmission coefficients for $DB$: $\sigma_1$ for $LS$ and $\sigma_2$ for $HS$. By $\gamma_i$ and $g_i$, we denote the recovery rate for $DA$ and $DB$, respectively. The disease-mortality rate for $DA$ and $DB$ is depicted by $\alpha_i$ and $a_i$.

The proposed model of co-infection is

Each parameter is fixed and positive. In particular, every parameter besides $C_i$ is in the range $(0, 1)$. If we assume that $\sigma_i, g_i, a_i = 0$, the above system would reduce to the system that we introduced and analyzed in ^[24].

Figure 1 is a schematic drawing of the proposed model.

In order to make the form of system (2.1) more transparent, we define:

Now we indicate the basic properties of the model. The form of the right-hand side of system (2.1) implies that its solutions exist and are unique and positive for any positive initial condition. Let us introduce a variable $N_i : = S_i + I_i + J_i + K_i$ that naturally means a density of the whole $HS$ or $LS$. After adding both sides of Eqs (2.1a)–(2.1d) or Eqs (2.1e)–(2.1h), we get

See that we can estimate Eq (2.3) from above by the inequality

which solution is

For $N_i(0) > \tfrac{C_i}{\mu_i}$, we observe a decrease of the population. Clearly, we have

For $N_i(0) < \tfrac{C_i}{\mu_i}$, we have a limited growth of the population, since

where $\tilde{C}$ is any positive constant.

Now we estimate Eq (2.3) by

Combining inequalities (2.4) and (2.5), we get

which produces the invariant set

This set attracts all solutions of system (2.1). We therefore conclude that the variables $S_i(t)$, $I_i(t)$, $J_i(t)$, and $K_i(t)$ are defined for every $t > 0$.

3.   Stationary states

In this section, we indicate stationary states of system (2.1) and determine conditions for their existence.

3.1.   Non-endemic stationary states

Firstly, we find stationary states that are not endemic, meaning that at least one of their coordinates equals zero.

We consider separated cases.

1) Firstly, let us assume that $I_i = J_i = K_i = 0$. We immediately get the form of the disease-free stationary state:

Clearly, this state always exists.

2) Now, consider the case $K_i = 0$. Without loss of generality, we take $K_1 = 0$. From Eq (2.1d) for any stationary, state we have $0 = \sigma_1 I_1 (J_1 + J_2) + \beta_{11} J_1 I_1 + \beta_{12} J_1 I_2,$ which implies

Let us consider the first alternative from (3.2).

a) We first take $I_1 = 0$. From Eq (2.1b), we have $\beta_{12} S_1 I_{2} = 0$, which yields $S_1 = 0$ or $I_2 = 0$. If $S_1 = 0$, then Eq (2.1b) gives the contradiction $0 = C_1 + g_1 J_1$. If $I_2 = 0$, then from Eq (2.1h) we have $K_2 = 0$ and our system reduces to:

The above system's form suggests that there is a stationary state with present $DB$ and absent $DA$. We will investigate the existence of such postulated state later. System (3.3) fulfills the case $I_1 = 0 \land I_1 = 0 \land I_2 = 0$ from (3.2).

Now, assume that $I_1 = 0 \land J_1 = 0 \land J_1 = 0$ holds. Then from Eq (2.1b), we get $\beta_{11} S_1 I_2 + g_1 K_1 = 0$. It provides $S_1 = 0$ or $I_2 = 0$. Case $S_1 = 0$ linked to Eq (2.1a) yields the contrary, $0 = C_1$, hence we must have $I_2 = 0$. Then from Eqs (2.1c) and (2.1h), we get $J_2 = 0$ and $K_2 = 0$, respectively. We obtain state $E_{df}$.

It is easy to check that the case $I_1 = 0 \land J_1 = 0 \land I_2 = 0$ gives $E_{df}$ as well. The case $I_1 = 0 \land I_1 = 0 \land J_1 = 0$ is equivalent to $I_1 = 0 \land J_1 = 0 \land J_1 = 0$.

b) Now assume that $J_1+J_2 = 0$. This assumption obviously provides $J_1 = 0$ and $J_2 = 0$. From Eq (2.1g), we get $\dot J_2 = \gamma_2 K_2$, giving $K_2 = 0$. We obtain the system

where $j = 3-i$. The above system fulfills condition $J_1+J_2 = 0 \land J_1 = 0 \land J_1 = 0$, emerged from (3.2).

If we take $J_1+J_2 = 0$ and simultaneously one of the cases $J_1 = 0 \land I_2 = 0$, $I_1 = 0 \land J_1 = 0$ or $I_1 = 0 \land I_2 = 0$, then we obtain $E_{df}$.

3) Now suppose that $I_1 = 0$. From Eq (2.1b), we get $0 = \beta_{12} S_1I_2 + g_1 K_1$. From $S_1 I_2 = 0$, we get $I_2 = 0$, which gives system (3.3). Choosing $K_1 = 0$ leads to system (3.4).

4) Consider $J_1 = 0$. Then Eq (2.1c) yields $0 = \sigma_1 S_1 J_2 + \gamma_1 K_1$. Both cases $J_2 = 0$ and $K_1 = 0$ provide system (3.4).

5) Assuming $I_1 = 0 \land J_1 = 0$ leads to state $E_{df}$.

6) Supposing $I_1 = 0 \land K_1 = 0$ and $J_1 = 0 \land K_1 = 0$ results in systems (3.3) and (3.4), respectively.

Reasoning from points 1)–6) conducted for the variables with subscript 2 gives the same conclusions.

System (3.4) appears in our previous paper ^[24]. The solution of this system provides the endemic state $E^* = (S_1^*, I_1^*, S_2^*, I_2^*)$. This state is the projection of the state

onto the non-negative subspace $(S_1, I_1, S_2, I_2) \in \mathbb{R}^4$. State $E_A$ reflects the presence of $DA$ and the absence of $DB$. Observe that adding both sides of Eqs (2.1a)–(2.1b) and Eqs (2.1e)–(2.1f) for $E_A$ yields $0 = C_i - \mu_i (I_i + S_i) - \alpha_i I_i$, providing

Relying on results for state $E^*$ from ^[24], we formulate conditions for the existence of state $E_A$.

Proposition 1. In System (2.1), there exists the stationary state $E_A$ defined in (3.5) that reflects the presence of disease $A$ and the absence of disease $B$. This state exists if at least one of three cases holds:

1) $\beta_{11} C_1 \geq\mu_1 k_1$;

2) $\beta_{22} C_2 \geq\mu_2 k_2$;

3) $\beta_{ii} C_i < \mu_i k_i$ and

For $E_A$, we have

Now we focus on system (3.3). Equation (2.3), being the sum of equations from this system, simplifies to $\dot{N}_i = 0 = C_i - \mu_i S_i - (\mu_i + a_i) J_i$, which gives

Computations concerning this system indicate the expected stationary state. Observe that the structure of system (3.3) is analogous to the structure of system (3.4). Based on this analogousness and Proposition 1, we formulate the following proposition concerning the other stationary state.

Proposition 2. In System (2.1), there exists the stationary state

with present disease $B$ and absent disease $A$. This state exists if at least one of three cases holds:

1) $\sigma_1 C_1 \geq\mu_1 q_1$;

2) $\sigma_2 C_2 \geq\mu_2 q_2$;

3) $\sigma_i C_i < \mu_i q_i$ and

For $E_B$, we have

3.2.   The existence of the endemic stationary state

Now we investigate the endemic stationary state, reflecting the presence of both diseases $A$ and $B$. Since it is difficult to obtain its explicit form, we limit our investigation to indicate some properties concerning its existence. Let us define $Z_i : = I_i + J_I + K_i$. Obviously, variable $Z_i$ is the density of individuals from the particular subpopulation infected by disease $A$, $B$, or both. Summing both sides of Eqs (2.1b)–(2.1d) gives

From the above equation for the postulated endemic state, we have

Equation (2.3) and definition of $N_1$ for this state yield

Since $S_1 > 0$, one must fulfill

Combining reorganized Eqs (3.12) and (3.11), we get

where $s_1 : = \alpha_1 + a_1 + \mu_1$ and $w_1 : = g_1 + a_1 + \mu_1$.

From Eqs (2.1a)–(2.1d), we get the formula for coordinates $S_1, I_1, J_1, K_1$:

Positivity of coordinates $I_1$ and $J_1$ yields inequalities:

Combining the above dependences with condition (3.14a), we get

If we substitute Eq (3.14d) into the above inequality, we get

Observe that the reasoning presented in this subsection can be applied to variables with subscript 2. This application provides another condition for the existence of the postulated endemic state.

4.   The basic reproduction number

In this section, we find and investigate the basic reproduction number $\mathcal{R}_0$ of system (2.1). According to the definition from ^[26], $\mathcal{R}_0$ refers to the number of new infections produced by a single infectious individual in a population at a disease-free stationary state. To compute $\mathcal{R}_0$, we will rely on the next generation method described in ^[26]. In this section, we provide a sketch of computations leading to the formula for $\mathcal{R}_0$. We consider the subsystem of system (2.1), including the equations only for infected variables:

where vector $\mathcal{F}$ concerns the terms related to new infections, and vector $\mathcal{V}$ reflects the remaining processes. These vectors read

respectively. We construct matrices $F$ and $V$ that are the Jacobian matrices of $\mathcal{F}$ and $\mathcal{V}$ evaluated at $E_{df}$. These matrices have the form

Then we compute $F V^{-1}$ and obtain

The basic reproduction number is the spectral radius of the matrix $FV^{-1}$. The eigenvalues of this read $\lambda_{1, 2, 3} = 0, \lambda_4 = \tfrac{\sigma_1}{q_1} \widehat{S}_1 + \tfrac{\sigma_2}{q_2} \widehat{S}_2$, and

We finally get

See that $\lambda_4$ consists of terms relying to only infection $B$, whereas $\lambda_6$ refers only to infection $A$.

Now we formulate the theorem relied on the dependence between $\lambda_4$ and $\lambda_6$.

Theorem 4.1. $\mathcal{R}_0 = \lambda_4$ if

where

and

Proof. Observe that $\lambda_4 > \lambda_6$ if

Under fulfillment of

we raise both sides of inequality (4.4) to the square and transform the result to

Using the definition of $\lambda_4$ in the above inequality and transforming the obtained expression, we get

where $u_i$ is defined by Eq (4.2). We rewrite inequality (4.6) as inequality (4.1). Inequality (4.5) with the definition of $\lambda_4$ can be transformed into inequality (4.3). □

Let us strengthen the assumptions from Theorem 4.1 so that we obtain more explicit ones. Suppose that $u_i > 0$, which can be written as

Then condition

suffices fulfillment of inequality (4.1). Moreover, if

then inequality (4.3) is always true. Combining inequalities (4.7) and (4.9) yields

We conclude that

Corollary 1. If inequality (4.10), then $\mathcal{R}_0 = \lambda_4$.

The above corollary confirms the obvious dependence that if the transmission of infection $B$, represented by $\sigma_i$, is sufficiently stronger than the transmission of infection $A$ between different subpopulations, reflected by $\beta_{ii}$, then infection $B$ plays a bigger role in the whole population.

Observe that if in inequality (4.3) we replace sign $>$ by sign $<$, then $\lambda_4 < \lambda_6$. It yields $\mathcal{R}_0 = \lambda_6$, which is the same as $\mathcal{R}_0$ for the system with one infection from ^[24].

From a medical point of view, the desirable situation is when $\mathcal{R}_0 < 1$. Let us check when this case holds. We formulate the theorem

Theorem 4.2. For system (2.1) $\mathcal{R}_0 < 1$ if

and

Proof. Condition (4.11) is obvious from the definition of $\lambda_4$. The part of the proof related to $\lambda_6$ is similar to the proof of Theorem 4.1. The inequality $\lambda_6 < 1$ can be transformed into

Under condition

multiplying both sides of inequality (4.14) yields

which can be written as inequality (4.13). The right-hand side of inequality (4.13) must be positive. It is true when $\widehat{S}_i > \tfrac{k_i}{\beta_{ii}}$ or (4.12). The first case is contrary to inequality (4.15). Hence, inequality (4.12) must hold, which is stronger than inequality (4.15). □

If is easy to check that inequality (4.13) is opposite to inequality (3.7) from Preposition 1 discussing the existence of state $E_A$. Similarly, inequality (4.11) is opposite to inequality (3.10) from Preposition 2 providing conditions for the $E_B$ existence.

5.   Local stability of stationary states

Now we investigate the local stability of states $E_{df}$, $E_A$, and $E_B$. The Jacobian matrix of system (2.1) can be written as $J = \begin{pmatrix} M_1 & M_2 \end{pmatrix}$, where

and

with

We start from the local stability of $E_{df}$.

Theorem 5.1. $E_{df}$ is locally stable if $\mathcal{R}_0 < 1$.

Proof. The Jacobian matrix for state $E_{df}$ reads

Immediately, we get four negative eigenvalues: $- \mu_1$, $-\mu_2$, $-r_1$, $-r_2$. The remaining eigenvalues are the zeros of the characteristic polynomial of the matrix:

This polynomial reads $P(\lambda) = P_1(\lambda) P_2(\lambda)$, where

It is easy to check that their discriminants are positive. The zeros of $P_1$ are negative if inequalities (4.12) and (4.13) hold. Analogously, $P_2$ has negative zeros if

and

Inequality (5.2) can be transformed into inequality (4.11). According to Theorem 4.2, merging inequality (4.11)–(4.13) yields $\mathcal{R}_0 < 1$. Inequality (5.2) yields two exclusive possibilities: $\sigma_i \widehat{S}_i > q_i$ or

The first case is contrary to inequality (5.1), whereas inequality (5.3), under condition (5.2), yields inequality (5.1). Hence, we replace inequality (5.1) by inequality (5.3). We rewrite inequality (5.3) as

Observe that the above inequality is weaker than inequality (4.11); hence, it is omitted in the thesis of Theorem 5.1. □

Theorem 5.1 is in line with the analogical result from ^[24], where we also obtained the local stability of the given disease-free stationary for the basic reproduction number smaller than one.

5.1.   Local stability of $E_A$

Now we provide a theorem guaranteeing the local stability of state $E_A$.

Theorem 5.2. $E_A$ is locally stable if

and

Proof. Let us rearrange matrix $J(E_A)$ so that the characteristic polynomial of the new matrix remains the same. We get $M^* = \begin{pmatrix} M_1^* & \ M_2^* \\ 0 & M_3^* \end{pmatrix},$ where

and

The form of $M_2^* \in M_4(\mathbb{R})$ is not needed for further computations.

We start by investigating matrix $M_1^*$. To simplify computations, we define auxiliary notations:

Thanks to this simplification, matrix $M_1^*$ reads

The characteristic polynomial of $M_1^*$ has the form

where

Observe that if

and

then each coefficient of $P_1$ is positive. Hence, from Descartes' rule of signs, we get that $P_4$ has real negative roots or complex roots with negative real parts. Substituting definition (5.11) into inequalities (5.12) and (5.13) provides inequalities (5.4) and (5.5), respectively.

Let us focus now on matrix $M_3^*$. After using notations:

we rewrite $M_3^*$ as

The characteristic polynomial of the matrix reads $P_3 (\lambda) : = \lambda^4 + c_3 \lambda^3 + c_2 \lambda^2 + c_1 \lambda + c_0$, where

Let us investigate the signs of the coefficients of polynomial $P_3$. Observe that if inequality (5.6) holds, then $t_1, t_2 > 0$, which yields $c_3 > 0$. Conditions $r_1 r_2 > s_1 s_2$ and $r_i t_i > \gamma_i a_i$, which can be written as inequalities (5.7) and (5.8), respectively, yield $c_2 > 0$. See that $c_1 > 0$ if $(t_i + r_i) (t_j r_j - \gamma_j a_j) > s_i (r_j s_j + \gamma_j y_j)$ for $j = 3-i$, which we transform to

Using expressions from (5.14), we rewrite the above inequality as inequality (5.9). Condition $c_0 > 0$ can be written as

With (5.14), the above inequality transforms into inequality (5.10). □

Now let us strengthen conditions from Theorem 5.2 providing the local stability of $E_A$ so that they have a more explicit form. Observe that the condition

yields fulfillment of inequality (5.6). Moreover, from definitions (2.2), clearly we have $r_i > q_i$. Hence, inequality (5.16) implies inequality (5.7).

Again relying on (2.2), we get $r_i > \gamma_i$. Instead of inequality (5.8), it is therefore enough to investigate the inequality

If inequality (5.16) holds, then the left-hand side of the above inequality is always positive. Using Eq (3.6), we transform this inequality into

From the definition of $r_i$, the denominator of the right-hand side of inequality (5.17) is positive if

which is always true. The positivity of the numerator of the right-hand side of inequality (5.17) is maintained if

Now observe that since $r_i > \gamma_i$, inequality (5.9) can be, under fulfillment of inequality (5.16), strengthened to

If inequality (5.16) holds, then one must fulfill

so that inequality (5.19) makes sense. Using Eq (3.6), we transform inequality (5.20) into

which is reasonable if

Observe that inequality (5.22) is stricter than inequality (5.18). Rewriting inequality (5.19), we get

Using again Eq (3.6), we transform the above inequality into

Now we use the dependence $r_i > \gamma_i$ and transform inequality (5.10) into

which can be simplified to

Clearly, inequality (5.24) is stricter than inequalities (5.16) and (5.21).

Using Eq (3.6), we rewrite inequality (5.24) as

We finally conclude that

Corollary 2. If (5.4), (5.5), (5.17), (5.22), (5.23) and (5.25), then $E_A$ is locally stable.

Let us treat the left-hand side of inequality (5.23) as a quadratic trinomial $P(S_j^*)$. If inequality (5.22) holds, then the condition $C_i > \sigma_i S_i^*$ suffices for the constant of $P(S_j^*)$ to be positive. Hence, the form of $P(S_j^*)$ implies that inequality (5.23) is true for $0 < S_j^* < \mathcal{S}$, where $\mathcal{S}$ is the positive zero of $P(S_j^*)$.

5.2.   Local stability of $E_B$

Now we provide the theorem indicating the conditions for the local stability of state $E_B$:

Theorem 5.3. $E_B$ is locally stable if

Proof. Similarly as in the proof of Theorem 5.2, we transform matrix $J(E_B)$ into $M_B = \begin{pmatrix} \bar{M}_1 & \bar{M}_2 \\ 0 & \bar{M}_3 \end{pmatrix},$ where

We start from matrix $\bar{M}_1$. After using notations:

we transform $\bar{M}_1$ to

The characteristic polynomial of matrix $\bar{M}_1$ reads $P_1 (\lambda) = \lambda^4 + c_3 \lambda^3 + c_2 \lambda^2 + c_1 \lambda + c_0$, where

Observe that if

and

then $c_2, c_1, c_0 > 0$. Hence, from Descartes' rule of signs, we get that $P_1$ has real negative roots or complex roots with negative real parts.

Using definitions (5.31), we rewrite inequality (5.32) as inequality (5.6) and inequality (5.33) as

Now we focus on matrix $\bar{M}_3$. With the use of expressions,

we rewrite $\bar{M}_3$ as

which has a similar form as matrix $M_3^*$ from (5.15). This similarity allows us to apply reasoning for $M_3^*$ to $\bar{M}_3$. Analogically to conditions (5.6)–(5.10), we obtain inequalities (5.26)–(5.30). □

Similarly as for Theorem 5.2, let us strengthen conditions from Theorem 5.3 providing the local stability of $E_B$. Since $r_i > g_i$, we replace inequality (5.28) by

which obviously requires fulfillment of inequality (5.26). Using Eq (3.8), we express the above inequality as

under fulfillment of

Again using the dependence $r_i > g_i$, we simplify inequality (5.29) to

Since inequality (5.26) holds, it is enough that inequality (5.36) holds so that inequality (5.39) makes sense.

Inequality (5.30) can be strengthened by

which can be expressed as

The above inequality is always true if

and

Using Eq (3.8), we rewrite inequality (5.42) as

Let us compare inequalities (5.26) and (5.27). Observe that $r_i > k_i$. Moreover, if inequality (5.41) holds, then inequality (5.26) is stronger than inequality (5.27).

Finally, we conclude that

Corollary 3. If inequalities (5.26), (5.37), (5.38), (5.39), (5.40), (5.41), and (5.43) hold, then $E_B$ is locally stable.

6.   Postulated local stability of the endemic state: numerical simulation

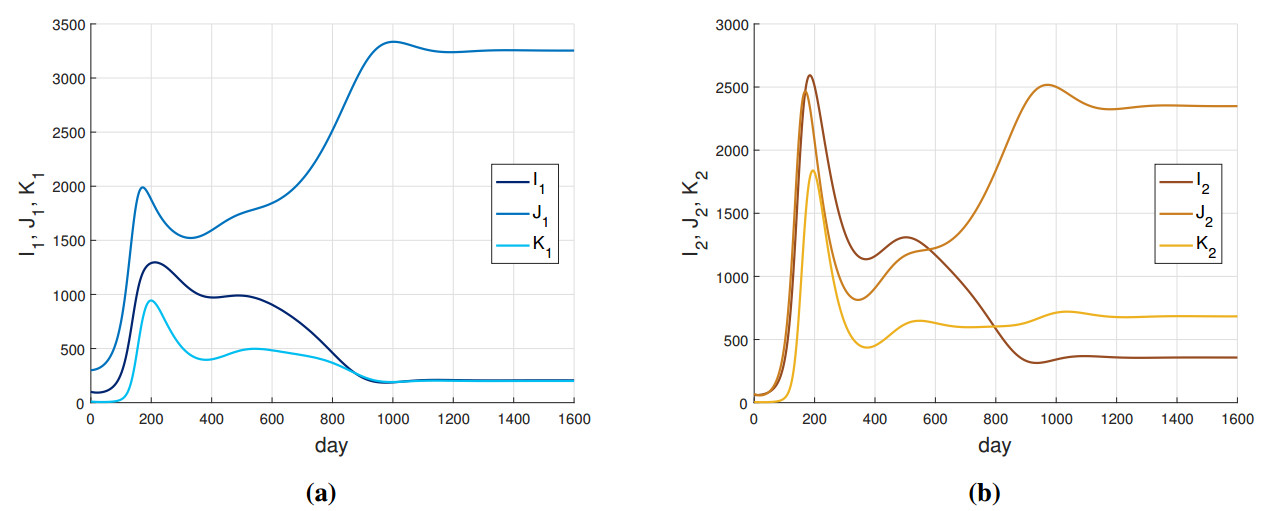
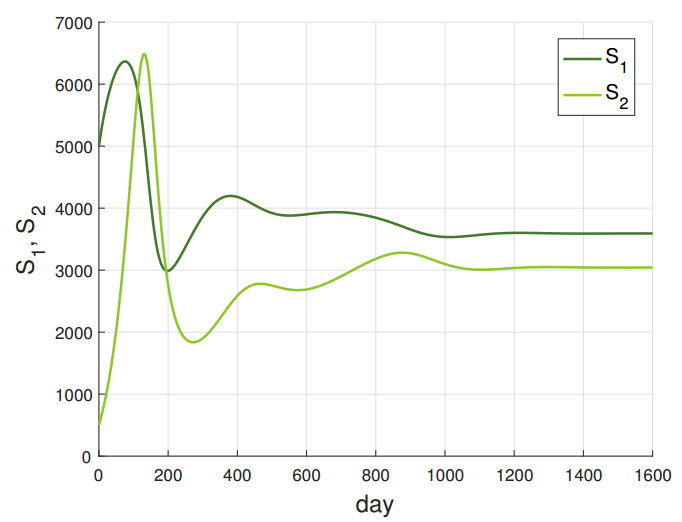
In Subsection 3.2, we provided only a slight analysis of the existence of the endemic stationary state $E_E$, with two diseases present. We are therefore not certain if this state exists. Furthermore, the complexity of the proper Jacobian matrix does not allow us to obtain the explicit conditions for local stability of such a postulated equilibrium. However, the conditions from Theorems 5.2 and 5.3 restrict a set of parameters' values guaranteeing the local stability of existing states $E_A$ and $E_B$. Such restriction suggests that there should be ranges of the values for the $E_E$ local stability under its existence. Indicating these ranges is difficult, even numerically, because of the system's intricacy. For this reason, for each parameter, we only give specific values that yield the desirable local stability. We rely on the values from ^[10] that concern $TB$ and COVID-19. In our system, these diseases correspond to diseases $A$ and $B$, respectively. Since paper ^[10] relates to co-infection dynamics in a homogeneous population, we arbitrarily choose the values of incompatible parameters from our system. These values are chosen so that we reach the $E_E$ local stability. In Table 1, one can find the taken numbers.

We illustrate the local stability of $E_E$ on the plots showing the dependence of the system's solution on time for each particular variable. For the illustration, we use the Matlab software, which provides a built-in $ode45$ function. This function numerically solves a given differential equation system for a specified initial condition ^[27]. For the simulation, we take the parameters' values from Table 1 and the arbitrarily chosen initial condition

Figures 2–3 depict the result of the simulation. For the figures' transparency, we show plots for the infected variables for each subpopulation and the non-infected variables in separate picture graphs. The obtained figures suggest the existence of the stationary state $E_e$ that is locally stable for the parameter values from Table 1.

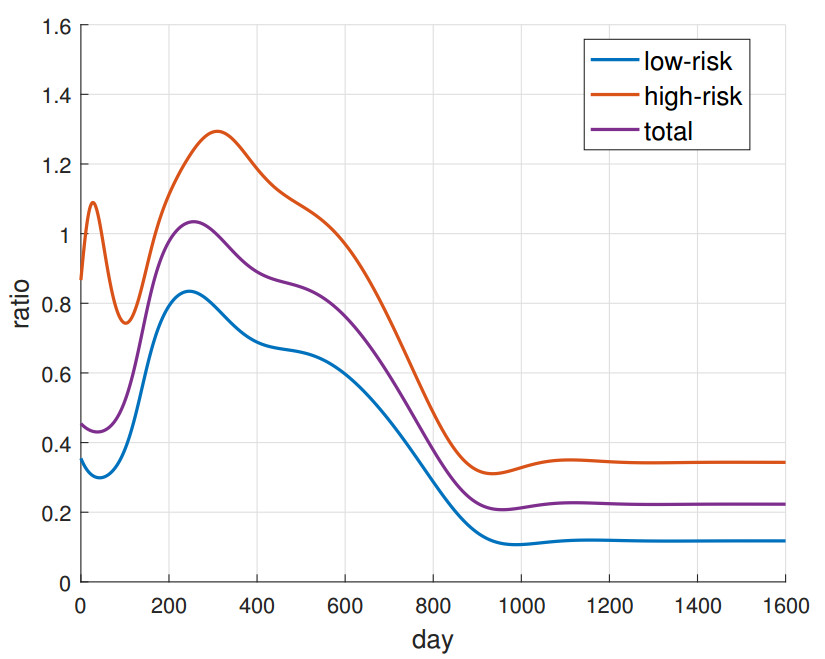
Now for the illustrated example of epidemic, we depict the relative sizes of the infections for time $t$ that we define by ratios:

These ratios correspond to $LS$, $HS$, and the whole population, respectively, and in our case represent the number of $TB$-infected individuals relative to the number of COVID-infected ones. Figure 4 shows the dependence of the relative sizes on time.

For the last point of the simulation timescale, i.e., $\bar{t} = 1600$, we get $R_1(\bar{t}) = 0.1176$ and $R_2(\bar{t}) = 0.3432$. Plots from the figure suggest the convergence of each relative size. We therefore state that for the stabilized co-infection epidemic, for one $TB$-infected person, there are approximately nine and three COVID-infected people in $LS$ and $HS$, respectively.

7.   Conclusions

In this paper, we proposed and analyzed the continuous-time model (2.1) describing co-infection in a heterogeneous population, in which we distinguish two subpopulations. These subpopulations, low-risk $LS$ and high-risk $HS$, differ in the risk of getting infected by any of two diseases, called disease $A$ ($DA$) and disease $B$ ($DA$). The values of the parameters for every subpopulation are different, which guarantees complete population heterogeneity. System (2.1) has three stationary states: disease-free ($E_{df}$), with sole $DA$ or $DB$ ($E_A$ and $E_B$). We also suspect that the endemic state, with two diseases present, exists, but we did not manage to prove it because of complicated computations. State $E_{df}$ exists unconditionally, while provided conditions determine the existence of $E_A$ and $E_B$. For state $E_e$, we only gave insight into its existence because of the complexity of the computations. For system (2.1), we computed the basic reproduction number $\mathcal{R}_0$. This number is the maximum of two terms, whose forms depend on parameters corresponding to the particular sole infection. Later, we investigated the local stability of the stationary state. State $E_{df}$ is locally stable if $\mathcal{R}_0 < 1$, which is expected. Analysis of the local stability for $E_A$ and $E_B$ provided the list of conditions. Importantly, the parameters from both diseases affect the local stability of both states.

The proposed model expands the system from ^[24], where we investigated the epidemic dynamics of one disease in heterogeneous populations. In that system, there are only two stationary states: the disease-free state and the endemic state, which is a counterpart of state $E_A$ of system (2.1). The results for their local stabilities are analogical to those for state $E_{df}$ and $E_A$ in this paper.

The next step of our work will be an analysis of the proposed model with some assumptions simplifying this form. We hope to obtain the endemic state of the simplified model and get explicit results concerning its local stability.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The author declares there is no conflict of interest.