Figure 1.
Molecular structures of Res, PVP and CMCS.
The preparation of amorphous solid dispersions using polymers is a commonly used formulation strategy for enhancing the solubility of poorly water-soluble drugs. However, a single polymer often does not bring significantly enhance the solubility or amorphous stability of a poorly water-soluble drug. We found an application of a unique and novel binary polymeric blend in the preparation of solid dispersions. The main purpose of this study is to optimize and evaluate resveratrol (Res) amorphous solid dispersions with a novel polymeric system of poly (vinyl pyrrolidone) (PVP) and carboxymethyl chitosan (CMCS). The influence of three different release factors, the ratio of CMCS to the polymer mixture (CMCS% = X1), the ratio of Res to the polymer mixture (Res% = X2) and the surfactant (Tween 80 = X3), on the characteristics of released Res at various times (Q5 and Q30) was investigated. The computer optimization and contour plots were used to predict the levels of the independent variables as X1 = 0.17, X2 = 0.10 and X3 = 2.94 for maximized responses of Q5 and Q30. Fourier transform infrared spectroscopy (FTIR) results revealed that each polymer formed hydrogen bonds with Res. The solid performance and physical stability of the optimized ternary dispersions were studied with scanning electron microscopy (SEM), powder X-ray diffraction (XRD), modulated differential scanning calorimetry (MDSC) and dissolution testing. SEM, XRD and MDSC analysis demonstrated that the Res was amorphous, and MDSC showed no evidence of phase separation during storage. Dissolution testing indicated a more than fourfold increase in the apparent solubility of the optimized ternary dispersions, which maintained high solubility after 90 days. In our research, we used CMCS as a new carrier in combination with PVP, which not only improved the in vitro dissolution of Res but also had better stability.
Citation: Gangqi Han, Bing Wang, Mengli Jia, Shuxin Ding, Wenxuan Qiu, Yuxuan Mi, Zhimei Mi, Yuhao Qin, Wenxing Zhu, Xinli Liu, Wei Li. Optimization and evaluation of resveratrol amorphous solid dispersions with a novel polymeric system[J]. Mathematical Biosciences and Engineering, 2022, 19(8): 8019-8034. doi: 10.3934/mbe.2022375
| [1] | Nancy Azer, P. van den Driessche . Competition and Dispersal Delays in Patchy Environments. Mathematical Biosciences and Engineering, 2006, 3(2): 283-296. doi: 10.3934/mbe.2006.3.283 |
| [2] | Philip Gerlee, Alexander R. A. Anderson . Diffusion-limited tumour growth: Simulations and analysis. Mathematical Biosciences and Engineering, 2010, 7(2): 385-400. doi: 10.3934/mbe.2010.7.385 |
| [3] | Jin Zhong, Yue Xia, Lijuan Chen, Fengde Chen . Dynamical analysis of a predator-prey system with fear-induced dispersal between patches. Mathematical Biosciences and Engineering, 2025, 22(5): 1159-1184. doi: 10.3934/mbe.2025042 |
| [4] | Ganjun Xu, Ning Dai, Sukun Tian . Principal stress lines based design method of lightweight and low vibration amplitude gear web. Mathematical Biosciences and Engineering, 2021, 18(6): 7060-7075. doi: 10.3934/mbe.2021351 |
| [5] | Minjuan Gao, Lijuan Chen, Fengde Chen . Dynamical analysis of a discrete two-patch model with the Allee effect and nonlinear dispersal. Mathematical Biosciences and Engineering, 2024, 21(4): 5499-5520. doi: 10.3934/mbe.2024242 |
| [6] | Ali Mai, Guowei Sun, Lin Wang . The impacts of dispersal on the competition outcome of multi-patch competition models. Mathematical Biosciences and Engineering, 2019, 16(4): 2697-2716. doi: 10.3934/mbe.2019134 |
| [7] | Pan Yang, Jianwen Feng, Xinchu Fu . Cluster collective behaviors via feedback pinning control induced by epidemic spread in a patchy population with dispersal. Mathematical Biosciences and Engineering, 2020, 17(5): 4718-4746. doi: 10.3934/mbe.2020259 |
| [8] | Yun Kang, Sourav Kumar Sasmal, Komi Messan . A two-patch prey-predator model with predator dispersal driven by the predation strength. Mathematical Biosciences and Engineering, 2017, 14(4): 843-880. doi: 10.3934/mbe.2017046 |
| [9] | Xiangfen Song, Yinong Wang, Qianjin Feng, Qing Wang . Improved graph cut model with features of superpixels and neighborhood patches for myocardium segmentation from ultrasound image. Mathematical Biosciences and Engineering, 2019, 16(3): 1115-1137. doi: 10.3934/mbe.2019053 |
| [10] | Kwangjoong Kim, Wonhyung Choi . Local dynamics and coexistence of predator–prey model with directional dispersal of predator. Mathematical Biosciences and Engineering, 2020, 17(6): 6737-6755. doi: 10.3934/mbe.2020351 |
The preparation of amorphous solid dispersions using polymers is a commonly used formulation strategy for enhancing the solubility of poorly water-soluble drugs. However, a single polymer often does not bring significantly enhance the solubility or amorphous stability of a poorly water-soluble drug. We found an application of a unique and novel binary polymeric blend in the preparation of solid dispersions. The main purpose of this study is to optimize and evaluate resveratrol (Res) amorphous solid dispersions with a novel polymeric system of poly (vinyl pyrrolidone) (PVP) and carboxymethyl chitosan (CMCS). The influence of three different release factors, the ratio of CMCS to the polymer mixture (CMCS% = X1), the ratio of Res to the polymer mixture (Res% = X2) and the surfactant (Tween 80 = X3), on the characteristics of released Res at various times (Q5 and Q30) was investigated. The computer optimization and contour plots were used to predict the levels of the independent variables as X1 = 0.17, X2 = 0.10 and X3 = 2.94 for maximized responses of Q5 and Q30. Fourier transform infrared spectroscopy (FTIR) results revealed that each polymer formed hydrogen bonds with Res. The solid performance and physical stability of the optimized ternary dispersions were studied with scanning electron microscopy (SEM), powder X-ray diffraction (XRD), modulated differential scanning calorimetry (MDSC) and dissolution testing. SEM, XRD and MDSC analysis demonstrated that the Res was amorphous, and MDSC showed no evidence of phase separation during storage. Dissolution testing indicated a more than fourfold increase in the apparent solubility of the optimized ternary dispersions, which maintained high solubility after 90 days. In our research, we used CMCS as a new carrier in combination with PVP, which not only improved the in vitro dissolution of Res but also had better stability.
The poor water solubility of drugs is one of the main challenges of drug delivery. According to reports, almost 70% of new drugs have water solubility challenges and consequently low oral bioavailability and delivery problems [1]. These drugs are classified as class Ⅱ according to the biopharmaceutics classification system (BCS) [2]. Many methods are used to improve the solubility of poorly soluble drugs and their bioavailability, such as chemical modification, micronization, solid dispersion (SD), pH adjustment, co-solvency, complexation, and micellar solubilization [3,4,5,6,7]. Among the various approaches, SDs are inexpensive, simple and advantageous [8]. It has been shown to be one of the most successful in improving the solubility and bioavailability of poorly soluble active pharmaceutical ingredients [9].
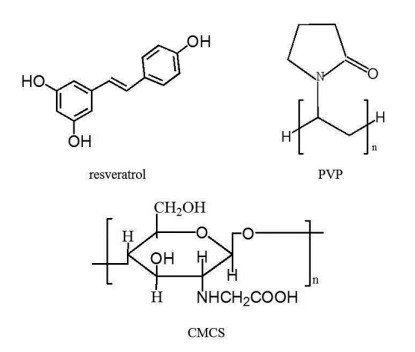
Resveratrol (Res, Figure 1) is a natural active ingredient produced in certain plants [10]. Numerous clinical trials have revealed that Res could help prevent or treat the main threats to health, such as cancer, hypertension and heart disease [11,12]. These tests clearly demonstrated the safety of Res. However, the poor oral bioavailability of Res was also confirmed [13]. The aqueous solubility of Res is low (30 µg/mL) at the pH of the small intestine (6.8). In contrast, Res is highly capable of infiltrating enterocytes. Therefore, it has important implications for exploiting delivery systems to improve the solubility and bioavailability of Res [14,15]. Hydrophilic carriers can increase drug dissolution due to improved wettability, solubility and dispersibility [16]. In the previous literature, various SDs of Res were reported for improving its dissolution using various carriers [17,18,19]. However, SDs of a single carrier presented some drawbacks in terms of formulation, physicochemical properties and physical and chemical stabilities of the vehicle and drug [20,21,22]. An appropriately designed or selected polymer can form a miscible amorphous dispersion with the drug [23]. Therefore, the purpose of this paper is to develop a binary polymeric blend with physicochemical properties and physical and chemical stabilities that meet these requirements. In this study, the use of a polymeric system containing polyvinyl pyrrolidone (PVP) and carboxymethyl chitosan (CMCS) (Figure 1) to improve the dissolution rate of Res has not been reported. CMCS is widely used for biomedical applications because of its good solution, biocompatibility, biodegradability, nontoxicity, and wide availability in Nature. PVP is an amorphous polymer with high water solubility. Both CMCS and PVP contain a carbonyl group (C = O), which forms hydrogen bonds with the hydroxyl group in Res. Hydrogen bonding interactions between polymers and drugs could improve the chemical and physical stability of their SDs [24,25,26]. Our hypothesis is that CMCS and PVP copolymers can protect the Res from recrystallization by hydrogen bonding interactions and maintain the high solubility of the Res. The main purpose of this study is to optimize and evaluate amorphous ternary SDs. We adopted a novel polymeric system that includes PVP, CMCS and Res to improve the dissolution rate and stability of Res SDs.
It is very important for pharmaceutical scientists to design formulations with the smallest number of experiments. A Box–Behnken design was used for the 3-factor and 3-level tests. The optimal process conditions were obtained by regression analysis of response surface methodology (RSM). Box–Behnken design involves the generation of multiple quadratic equations and mapping of the response over the experimental domain to select the optimum formulation [27]. In recent years, many pharmaceutical scientists have used it to design formulations [28,29,30]. In this study, Box–Behnken design was applied to optimize ternary SDs. Independent variables, including CMCS% (X1), Res% (X2), Tween 80 (X3), and their independent and joint effects on Res dissolution were evaluated at 5 minutes (Q5) and 30 minutes (Q30).
Plasdone (poly (vinyl pyrrolidone)) PVPK29/32 was obtained from Ashland Inc. (KY, USA). Carboxymethyl chitosan (CMCS) was purchased from Qingdao Honghai Biotechnology Co., Ltd. (Qingdao, China). Prior to use, PVP and CMCS were dried in a desiccator over powdered phosphorus pentoxide for at least one week. trans-Resveratrol (99%, batch number #111535-202003) from the National Institutes for Food and Drug Control (Beijing, China) was used as a standard. Res was purchased from Hainuo Chemical Company (Shanghai, China). Tween 80 was obtained from Sinopharm Chemical Reagent Co., Ltd. (Shanghai, China). Copper chloride was purchased from Tianda Chemical Company (Tianjing, China). HPLC grade acetonitrile and methanol and analytical grade ethanol and methanol were obtained from Shanghai Macklin Biochemical Co. (Shanghai, China).
Box–Behnken design was performed and statistically analysed using Design Expert software (Version. V8.0.6.1, Stat-Ease Inc., Minneapolis, MN). Single-factor tests were used to ensure that CMCS%, Res% and surfactant were the main factors influencing Res release. To find the optimized amount of carrier used in the SD formulation, independent and dependent variables are listed in Table 1. The polynomial equation was:
| (1) |
| Independent Variables | Level | ||
| low | medium | high | |
| X1: CMCS% | 1:10 | 1:5 | 3:10 |
| X2: Res% | 1:10 | 1:5 | 3:10 |
| X3: Tween 80 | 2 | 3 | 4 |
| Transformed values | -1 | 0 | 1 |
| Dependent variables | Y1 = Percentage of Res released in 5 min (Q5) | ||
| Y2 = Percentage of Res released in 30 min (Q30) | |||
DownLoad:
CSV
where Yi is the dependent variable; b0 is the intercept (arithmetic mean response of 17 runs); b1 to b33 are the regression coefficients; and X1, X2 and X3 are the independent variables that were selected from the preliminary experiments. The main effects of (X1, X2 and X3) represent the average result of changing one factor at a time from its low to high values. The interaction terms (X12, X23 and X13) show how the response changes when two factors are simultaneously changed. All the batches were prepared according to the experimental design in Table 2.
| Batch | X1 | X2 | X3 |
| 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 |
| 3 | 1 | 0 | 1 |
| 4 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 |
| 6 | 0 | -1 | -1 |
| 7 | 1 | -1 | 0 |
| 8 | -1 | 0 | -1 |
| 9 | -1 | 1 | 0 |
| 10 | 1 | 1 | 0 |
| 11 | 1 | 0 | -1 |
| 12 | -1 | 0 | 1 |
| 13 | 0 | 0 | 0 |
| 14 | -1 | -1 | 0 |
| 15 | 0 | 1 | -1 |
| 16 | 0 | -1 | 1 |
| 17 | 0 | 0 | 0 |
DownLoad:
CSV
SDs for all 17 batches were prepared by solvent evaporation. Crystalline Res was dissolved in ethyl alcohol, and then PVP was added to the Res solution. CMCS was added to the solution after the PVP was completely dissolved. After all mixtures formed uniform one-phase solutions, the solvent was removed using a rotary evaporator apparatus (RE-52C, Henan, China) by keeping the solution in a water bath (40 ℃). The SDs were then dried in a vacuum oven (DZF-6050, Shanghai, China) for 24 h. To reduce the particle size, solid dispersions were ground by a mortar with a pestle and sifted by sieve no. 70. The SDs were stored in a desiccator over powdered phosphorus pentoxide before use.
FTIR spectra were obtained using a Bruker Vector 22 (Bruker Optik GmbH, Ettlingen, Germany). KBr pellets of each Res alone and SDs were prepared. All spectra were obtained at a resolution of 4 cm-1, and 64 scans were added.
To examine the morphology of SDs in the dry state, samples were analysed by SEM (JSM-7800F, JEOL, Japan) at a working distance of 6.2 mm. The particles were observed to determine the surface characteristics.
The optimized ternary SDs were placed in weighing bottles without caps and charged for accelerated stability studies for a period of 3 months in ovens set to 40 ± 2.0 ℃ (668, Dalian, China). A saturated copper chloride solution was used to supply the 69 ± 5% RH. The samples were withdrawn after 90 days and evaluated for their solid-state and in vitro Res release.
The MDSC study was performed. The MDSC (Q1000, TA Instruments, New Castle, DE, USA) was equipped with a liquid nitrogen cooling system. The samples were heated to 300 ℃ with modulations of ± 1 ℃/60 s at a 3 ℃/min heating rate under purged dry argon gas (50 mL/min) (n = 3).
XRD patterns were obtained using an X'Pert Pro-1 diffractometer (PANalytical Co., Almelo, the Netherlands) with Cu Kα radiation (λ = 1.5418 Å) at 40 kV and 40 mA. Samples were scanned from 5° to 50° 2θ at a scanning rate of 2°/min with a sampling interval of 0.02°.
Dissolution equipment (RC806, Tianjin, China) was used to determine the release rate of Res dissolution according to the paddle method (USPII method). Each quantity of SDs corresponding to 5 mg Res was placed in the apparatus. The test was performed under the condition of a rotation speed of 100 rpm at 37 ± 0.5 ℃. The dissolution medium consisted of 250 mL of dilute hydrochloric acid (Aladdin Reagent Co., Ltd), pH 1.2. At predefined time intervals, samples (1 mL) were removed from the dissolution medium, and an equal volume of fresh dissolution medium was added after the sample was withdrawn. Samples (1 mL) were filtered through 0.22 μm membranes. The content of Res was analysed by HPLC based on a calibration line of standards of known concentrations. HPLC analysis was performed with a C18 column (200 mm × 4.6 mm, 5.0 μm Kromasil, China) and a UV detector (Waters 2998PAD UV–vis spectrophotometer, USA). The injection volume was 20 μl. The samples were measured at a wavelength of 293 nm to detect Res by UV detection.
The observed values of Q5 (Y1) and Q30 (Y2) for all the batches are shown in Table 3. The Y1 and Y2 values from different batches showed a wide range of changes. The results clearly indicated that the Q5 and Q30 values were strongly affected by the selected variables. The responses (Y1 and Y2) obtained at various levels of the 3 independent variables (X1, X2, and X3) underwent multiple regression to yield second-order polynomial Equations (2) and (3) (full model), respectively. The equation clearly reflects a wide range of values for the coefficients.
| (2) |
| (3) |
| Run | X1 (g/g) | Factors | Responses | ||
| X2 (g/g) | X3 (mL) | Y1 (%) | Y2 (%) | ||
| 1 | 0.1 | 0.2 | 4 | 15.32 | 31.55 |
| 2 | 0.2 | 0.2 | 3 | 17.50 | 33.83 |
| 3 | 0.2 | 0.1 | 4 | 53.42 | 86.38 |
| 4 | 0.2 | 0.2 | 3 | 17.50 | 33.83 |
| 5 | 0.2 | 0.1 | 2 | 54.31 | 83.81 |
| 6 | 0.1 | 0.1 | 3 | 76.42 | 80.09 |
| 7 | 0.1 | 0.3 | 3 | 21.22 | 48.71 |
| 8 | 0.1 | 0.2 | 2 | 14.05 | 25.72 |
| 9 | 0.3 | 0.1 | 3 | 26.79 | 69.67 |
| 10 | 0.2 | 0.2 | 3 | 17.50 | 33.83 |
| 11 | 0.2 | 0.3 | 2 | 25.64 | 51.51 |
| 12 | 0.2 | 0.3 | 4 | 49.59 | 82.91 |
| 13 | 0.3 | 0.2 | 2 | 9.73 | 13.41 |
| 14 | 0.3 | 0.2 | 4 | 7.75 | 13.57 |
| 15 | 0.2 | 0.2 | 3 | 17.50 | 33.83 |
| 16 | 0.3 | 0.3 | 3 | 38.76 | 69.08 |
| 17 | 0.2 | 0.2 | 3 | 17.50 | 33.83 |
DownLoad:
CSV
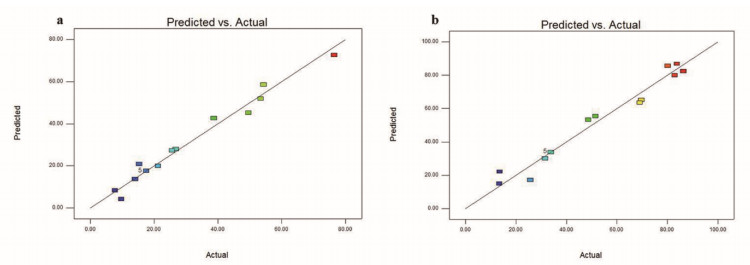
The responses of the experimental values and predicted values are shown in Figure 2. Quadratic regression models of the ANOVA revealed that the response surface models of the three responses were obvious and appropriate (Table 4). In addition, the summary of the model results indicated that the R2 values of all the response models were greater than 0.9, which revealed good and reliable relevance between the actual and predicted responses. In addition, the values of the coefficient of variation were low (CV = 15.6 and 13.52%), indicating a precise and reliable experiment.
| Responses | Models | |||||
| F Value | Prob > F | R2 | Adj. R2 | Adeq. prec. | C. V. (%) | |
| Y1 | 33.33 | 0.0001 | 0.9772 | 0.948 | 20.205 | 15.6 |
| Y2 | 25.18 | 0.0002 | 0.9700 | 0.932 | 14.271 | 13.52 |
DownLoad:
CSV
The interactions between independent variables and the dependent variables, the standardized effects of independent variables with the relative significance of independent variables and the main influence of the independent variables on Q5 and Q30 are summarized in Table 5. Among the 3 independent variables, X2 (Res%) had a prominent effect (b2 = -9.47 and P = 0.0005, b2 = -8.47 and P = 0.0082) on Q5 and Q30. X1 (CMCS%) moderately affected the results (b1 = 2.69 and P = 0.0096) from Q5 and minimally affected the results (b1 = -2.54 and P = 0.31) from Q30, suggesting that CMCS% has an insignificant effect on Q30 (P > 0.05). X3 (Tween 80) also had an insignificant effect on both Q5 and Q30 (P > 0.05). X1 and X2 negatively affected the Q5 and Q30 results.
| Dependent variables | Y1 = Q5 | Y2 = Q30 | ||
| Coefficients | P value | Coefficients | P value | |
| Intercept | 17.50 | < 0.0001 | 33.83 | 0.0002 |
| X1 (CMCS%) | -5.50 | 0.0096 | -2.54 | 0.3100 |
| X2 (Res%) | -9.47 | 0.0005 | -8.47 | 0.0082 |
| X3 (Tween 80) | 2.79 | 0.1163 | 4.99 | 0.0686 |
| X1X2 | 16.79 | 0.0001 | 7.70 | 0.0516 |
| X2X3 | -0.81 | 0.7233 | -1.42 | 0.6791 |
| X1X3 | 6.21 | 0.0259 | 7.21 | 0.0643 |
| X12 | -5.36 | 0.0412 | -11.02 | 0.0108 |
| X22 | 28.66 | < 0.0001 | 44.07 | < 0.0001 |
| X32 | -0.43 | 0.8488 | -1.75 | 0.6010 |
| Note: X1X2, X1X3, and X2X3 represent the interactions between Factors X1, X2, and X3; X12, X22, and X32 are the squared effects of the factors; the underlined represent significant factors (P < 0.05). All values are expressed as the mean ± SD, n = 3. | ||||
DownLoad:
CSV
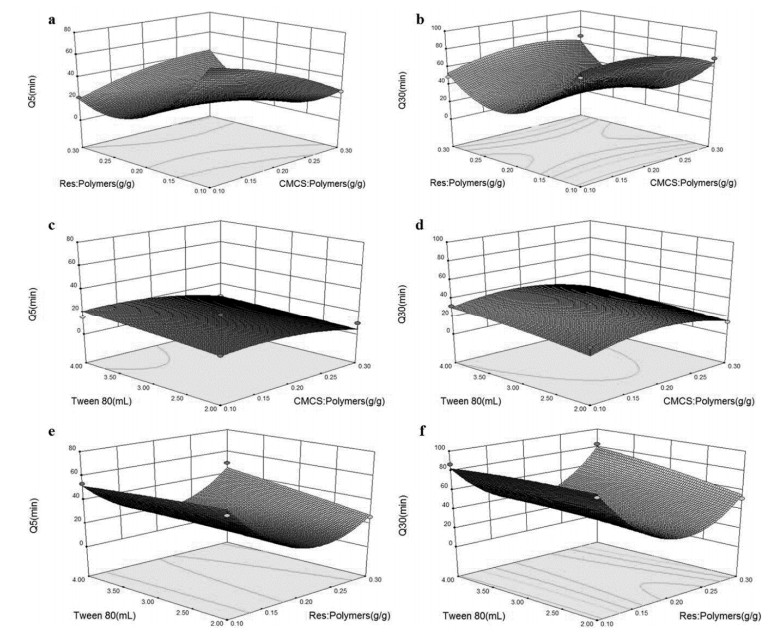
Three-dimensional response plots showed the behaviour of dissolution (% release at 5 min = Q5 and 30 min = Q30), the main effect, the squared effect (nonlinear) and the interactions between the two independent variables (Figure 3). From the three-dimensional response plots, CMCS% and Res%, Res% and Tween 80 had their individual effects on the three responses. CMCS% and Tween 80, and Res% and Tween 80 had a minimal effect on the three responses. It is well known that X1 and X2 negatively affect Q5 and Q30. The three-dimensional response plot clearly shows that at low levels of X1 and X2, Q30 > 80% can be achieved, but at least a medium level or higher is needed to achieve a higher Q5 and Q30 for X3.
The predicted values of the response variables suggested that the prediction error varied between -3.04–12.20% and -0.5–3.99% for Y1 and Y2, respectively (Table 6). Thus, we concluded that Eqs (2) and (3) were valid for predicting Q5 and Q30. A correlation coefficient of linear correlation, R2, was 0.9772 and 0.9700 for the observed and predicted response variables of percentage Res release at 5 and 30 min, respectively, indicating excellent goodness of fit, as shown in Table 4.
| Batch | X1 | X2 | X3 | Y1 (Q5 ± SD) | Predicted Q5 | % Error | P Value |
| Check pt-1 | 0.11 | 0.12 | 3.28 | 59.40 ± 1.11 | 57.98 | 2.45 | 0.157 |
| Check pt-2 | 0.18 | 0.28 | 2.60 | 25.01 ± 0.68 | 22.29 | 12.20 | 0.020 |
| Check pt-3 | 0.13 | 0.13 | 2.07 | 50.13 ± 0.72 | 51.70 | -3.04 | 0.064 |
| Optimized | 0.17 | 0.10 | 2.94 | 61.42 ± 0.47 | 61.64 | -0.36 | 0.509 |
| Batch | X1 | X2 | X3 | Y2 (Q30 ± SD) | Predicted Q30 | % Error | P Value |
| Check pt-1 | 0.11 | 0.12 | 3.28 | 71.75 ± 1.31 | 71.67 | 0.11 | 0.925 |
| Check pt-2 | 0.18 | 0.28 | 2.60 | 49.81 ± 0.56 | 47.90 | 3.99 | 0.027 |
| Check pt-3 | 0.13 | 0.13 | 2.07 | 63.40 ± 1.13 | 62.47 | 1.49 | 0.290 |
| Optimized | 0.17 | 0.10 | 2.94 | 88.38 ± 0.31 | 88.82 | -0.50 | 0.137 |
| Note: All values are expressed as the mean ± SD, n = 3. | |||||||
DownLoad:
CSV
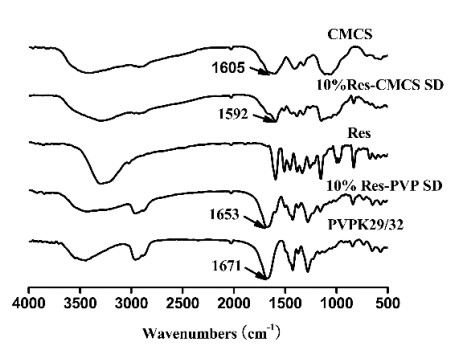
To verify the occurrence of hydrogen bonding between Res and the polymers, FTIR spectra were obtained (Figure 4). The presence of Res caused a significant shift in the C = O stretching of PVP from 1671 cm−1 to a lower wavenumber of 1653 cm−1 and CMCS (C = O stretching) from 1605 cm−1 to 1592 cm−1, indicating the absence of hydrogen bonding between Res and the polymers.
In the SEM report of the optimized ternary SD (Figure 5), the particles were relatively amorphous in comparison to pure Res because the Res was uniformly dispersed throughout the carrier molecules. Based on the SEM and FTIR data, we concluded that the Res was molecularly dispersed as amorphous nanoparticles in the polymers.
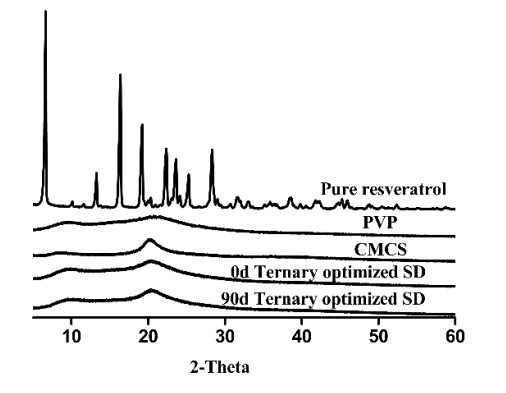
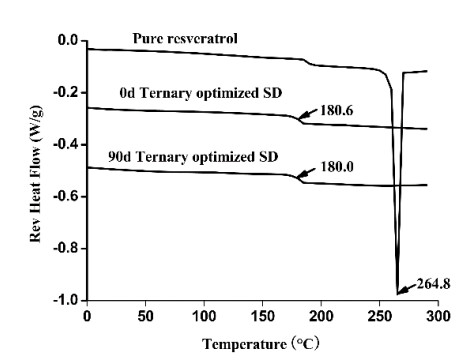
The XRD pattern showed that PVP and CMCS were amorphous chemical compounds (Figure 6). The sharp peaks of pure Res disappeared from the optimized ternary SDs, indicating the amorphous form of Res. The MDSC study indicated that the melting point of Res was 264.8 ℃. However, for amorphous SDs, no melting endotherm was observed, suggesting that no Res crystals were present in the SDs. A single glass transition temperature (Tg = 180.6 ℃) was observed with the 0-day samples (Figure 7).
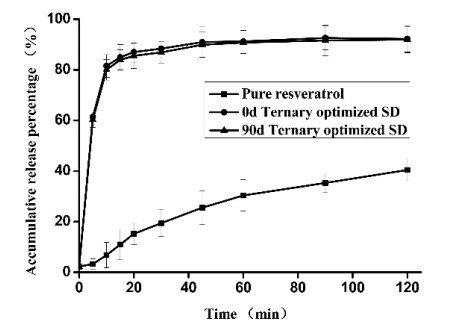
A significant improvement in the dissolution rate profile of the optimized ternary SD batch was observed in comparison to pure Res in hydrochloric acid solution at pH 1.2 (Figure 8). Within 30 minutes, the ternary SD batch showed 88.38% release, while the Res showed only 19.42% release, indicating that the particle size decreased, and the lack of crystallinity increased the wettability of the Res in the solid dispersion.
The XRD pattern demonstrated that the optimized ternary SDs remained amorphous after 3 months (Figure 6). The MDSC results revealed that there was little change in Tg (180.0 ℃) under accelerated conditions (69 ± 5% RH and 40 ± 2 ℃) after 3 months (Figure 7). The cumulative release percentages at 5 and 30 min were > 60 and 86%, respectively, throughout the stability period (Figure 8). From the statistical study (Tukey test), it was clear that there was no significant difference in the accumulative release percentage, as P > 0.05 at the interval of study. Polymers are known to inhibit the recrystallization of drugs and thus maintain supersaturation of the drug in the dissolution fluid. All the results indicate that under accelerated conditions (40 ± 2 ℃ and 69 ± 5% RH), the optimized ternary SD powder was physicochemically stable over 3 months. In this case, the blend of PVP and CMCS was successful in enhancing and maintaining the supersaturation of the amorphous form of Res. Hence, the optimized ternary SD powder is sufficiently stable according to the regulatory requirements.
This study optimized the dissolution profile of Res by Box–Behnken design. The optimized formulation achieved CMCS% = 0.17 (X1 = -0.28), Res% = 0.1 (X2 = -1) and Tween 80 = 2.94 (X3 = -0.6). The experimental values of Q5 and Q30 in all 17 batches and check point batches showed good correspondence with the predicted values, indicating goodness of fit for the models. The dissolution of Res can be predicted by these models under the same dissolution conditions, which provides guidance for optimization of the formulation. In conclusion, CMCS is an enteric polymer that was successfully used in combination with PVP to produce SDs of poorly soluble Res. Ternary optimized SDs were characterized using SEM, FTIR, XRD, and thermal analysis techniques. Ternary SD powder exhibited excellent solubility, dissolution rate and physicochemical stability in comparison with pure Res. If this formulation is scaled up to the manufacturing level, amorphous SDs show more solubility and faster dissolution than their crystalline analogues and provide novel insights into the application of resveratrol. However, many long-term stability, clinical pharmacokinetic studies and preclinical toxicity studies are required before production and commercialization can occur. Over time, amorphous SDs might crystallize, which leads to decreased solubility and a lower dissolution rate of the drug. The use of more than one polymer for formulating SDs might help overcome the storage and stability issues and increase the commercial viability and success of SDs.
This work was supported by the Shandong College Students for innovation and entrepreneurship training program [grant numbers S202110455014] and the Natural Science Foundation of Shandong Province [grant numbers ZR2020MC199] and the Foundation [grant number ZZ20200121] of the State Key Laboratory of Biobased Material and Green Papermaking, Qilu University of Technology, Shandong Academy of Sciences.
The authors declare that they have no competing interests.
| [1] |
S. Rani, R. Rana, G. K. Saraogi, V. Kumar, U. Gupta, Self-emulsifying oral lipid drug delivery systems: Advances and challenges, AAPS PharmSciTech, 20 (2019), 2–12. https://doi.org/10.1208/s12249-019-1335-x doi: 10.1208/s12249-019-1335-x
|
| [2] |
G. Amidon, H. Lennernäs, V. Shah, J. Crison, A theoretical basis for a biopharmaceutic drug classification: The correlation of in vitro drug product dissolution and in vivo bioavailability, Pharm. Res., 12 (1995), 413–420. https://doi.org/10.1023/A:1016212804288 doi: 10.1023/A:1016212804288
|
| [3] |
S. Feng, Y. Yang, Z. Yang, Z. Wang, L. Yan, F. Wang, et al., Hyaluronic acid-endostatin2-alft1 (ha-es2-af) nanoparticle-like conjugate for the target treatment of diseases, J. Controlled Release, 288 (2018), 1–13. https://doi.org/10.1016/j.jconrel.2018.08.038 doi: 10.1016/j.jconrel.2018.08.038
|
| [4] |
S. Watano, M. Matsuo, H. Nakamura, T. Miyazaki, Improvement of dissolution rate of poorly water-soluble drug by wet grinding with bio-compatible phospholipid polymer, Chem. Eng. Sci., 125 (2015), 25–31. https://doi.org/10.1016/j.ces.2014.09.010 doi: 10.1016/j.ces.2014.09.010
|
| [5] |
S. A. Zolotov, N. B. Demina, A. S. Zolotova, N. V. Shevlyagina, G. A. Buzanov, V. M. Retivov, et al., Development of novel darunavir amorphous solid dispersions with mesoporous carriers, Eur. J. Pharm. Sci., 159 (2021), 105700. https://doi.org/10.1016/j.ejps.2021.105700 doi: 10.1016/j.ejps.2021.105700
|
| [6] |
K. Y. Nam, S. M. Cho, Y. W. Choi, C. Park, N. M. Meghani, J. B. Park, et al., Double controlled release of highly insoluble cilostazol using surfactant-driven ph dependent and ph-independent polymeric blends and in vivo bioavailability in beagle dogs, Int. J. Pharm., 558 (2019), 284–290. https://doi.org/10.1016/j.ijpharm.2019.01.004 doi: 10.1016/j.ijpharm.2019.01.004
|
| [7] |
N. Li, N. Wang, T. Wu, C. Qiu, X. Wang, S. Jiang, et al., Preparation of curcumin-hydroxypropyl-β-cyclodextrin inclusion complex by cosolvency-lyophilization procedure to enhance oral bioavailability of the drug, Drug Dev. Ind. Pharm., 44 (2018), 1966–1974. https://doi.org/10.1080/03639045.2018.1505904 doi: 10.1080/03639045.2018.1505904
|
| [8] |
J. Li, I. W. Lee, G. H. Shin, X. Chen, H. J. Park, Curcumin-Eudragit® E PO solid dispersion: A simple and potent method to solve the problems of curcumin, Eur. J. Pharm. Biopharm., 94 (2015), 322–332. https://doi.org/10.1016/j.ejpb.2015.06.002 doi: 10.1016/j.ejpb.2015.06.002
|
| [9] |
M. Shergill, M. Patel, S. Khan, A. Bashir, C. Mcconville, Development and characterisation of sustained release solid dispersion oral tablets containing the poorly water soluble drug disulfiram, Int. J. Pharm., 497 (2015), 3–11. https://doi.org/10.1016/j.ijpharm.2015.11.029 doi: 10.1016/j.ijpharm.2015.11.029
|
| [10] |
J. F. Savouret, M. Quesne, Resveratrol and cancer: A review, Biomed. Pharmacother., 56 (2002), 84–87. https://doi.org/10.1016/S0753-3322(01)00158-5 doi: 10.1016/S0753-3322(01)00158-5
|
| [11] |
J. Sharifi-Rad, C. Quispe, A. Durazzo, M. Lucarini, E. B. Souto, A. Santini, et al., Resveratrol' biotechnological applications: Enlightening its antimicrobial and antioxidant properties, J. Herb. Med., 32 (2022), 100550. https://doi.org/10.1016/j.hermed.2022.100550 doi: 10.1016/j.hermed.2022.100550
|
| [12] |
A. Alesci, N. Nicosia, A. Fumia, F. Giorgianni, A. Santini, N. Cicero, Resveratrol and immune cells: A link to improve human health, Molecules, 27 (2022), 424. https://doi.org/10.3390/molecules27020424 doi: 10.3390/molecules27020424
|
| [13] |
R. B. Rigon, N. Fachinetti, P. Severino, A. Durazzo, M. Lucarini, A. G. Atanasov, et al., Quantification of trans-resveratrol-loaded solid lipid nanoparticles by a validated reverse-phase HPLC photodiode array, Appl. Sci., 9 (2019), 4961. https://doi.org/10.3390/app9224961 doi: 10.3390/app9224961
|
| [14] |
A. C. Santos, F. Veiga, A. J. Ribeiro, New delivery systems to improve the bioavailability of resveratrol, Expert Opin. Drug Delivery, 8 (2011), 973–990. https://doi.org/10.1517/17425247.2011.581655 doi: 10.1517/17425247.2011.581655
|
| [15] |
A. Amri, J. C. Chaumeil, S. Sfar, C. Charrueau, Administration of resveratrol: What formulation solutions to bioavailability limitations, J. Controlled Release, 158 (2012), 182–193. https://doi.org/10.1016/j.jconrel.2011.09.083 doi: 10.1016/j.jconrel.2011.09.083
|
| [16] |
J. S. Sohn, J. S. Kim, J. S. Choi, Development of a naftopidil-chitosan-based fumaric acid solid dispersion to improve the dissolution rate and stability of naftopidil, Int. J. Biol. Macromol., 176 (2021), 520–529. https://doi.org/10.1016/j.ijbiomac.2021.02.096 doi: 10.1016/j.ijbiomac.2021.02.096
|
| [17] |
T. Vasconcelos, F. Prezotti, F. Araújo, C. Lopes, A. Loureiro, S. Marques, et al., Third-generation solid dispersion combining Soluplus and poloxamer 407 enhances the oral bioavailability of resveratrol, Int. J. Pharm., 595 (2021), 120245. https://doi.org/10.1016/j.ijpharm.2021.120245 doi: 10.1016/j.ijpharm.2021.120245
|
| [18] |
B. Li, L. A. Wegiel, L. S. Taylor, K. J. Edgar, Stability and solution concentration enhancement of resveratrol by solid dispersion in cellulose derivative matrices, Cellulose, 20 (2013), 1249–1260. https://doi.org/10.1007/s10570-013-9889-3 doi: 10.1007/s10570-013-9889-3
|
| [19] |
T. Andreani, J. S. Fangueiro, S. José, A. Santini, A. M. Silva, E. B. Souto, Hydrophilic polymers for modified-release nanoparticles: A review of mathematical modelling for pharmacokinetic analysis, Curr. Pharm. Design, 21 (2015), 3090–3096. https://doi.org/10.2174/1381612821666150531163617 doi: 10.2174/1381612821666150531163617
|
| [20] |
L. A. Wegiel, L. J. Mauer, K. J. Edgar, L. S. Taylor, Crystallization of amorphous solid dispersions of resveratrol during preparation and storage-Impact of different polymers, J. Pharm. Sci., 102 (2013), 171–184. https://doi.org/10.1002/jps.23358 doi: 10.1002/jps.23358
|
| [21] |
B. Wang, D. Wang, S. Zhao, X. Huang, J. Zhang, Y. Lv, et al., Evaluate the ability of PVP to inhibit crystallization of amorphous solid dispersions by density functional theory and experimental verify, Eur. J. Pharm. Sci., 96 (2017), 45–52. https://doi.org/10.1016/j.ejps.2016.08.046 doi: 10.1016/j.ejps.2016.08.046
|
| [22] |
B. Démuth, A. Farkas, H. Pataki, A. Balogh, B. Szabó, E. Borbás, et al., Detailed stability investigation of amorphous solid dispersions prepared by single-needle and high speed electrospinning, Int. J. Pharm., 498 (2015), 234–244. https://doi.org/10.1016/j.ijpharm.2015.12.029 doi: 10.1016/j.ijpharm.2015.12.029
|
| [23] |
A. C. Rumondor, L. A. Stanford, L. S. Taylor, Effects of polymer type and storage relative humidity on the kinetics of felodipine crystallization from amorphous solid dispersions, Pharm. Res., 26 (2009), 2599–2606. https://doi.org/10.1007/s11095-009-9974-3 doi: 10.1007/s11095-009-9974-3
|
| [24] |
L. S. Taylor, G. Zografi, Spectroscopic characterization of interactions between PVP and indomethacin in amorphous molecular dispersions, Pharm. Res., 14 (1997), 1691–1698. https://doi.org/10.1023/a:1012167410376 doi: 10.1023/a:1012167410376
|
| [25] |
E. Karavas, G. Ktistis, A. Xenakis, E. Georgarakis, Miscibility behavior and formation mechanism of stabilized felodipine-polyvinylpyrrolidone amorphous solid dispersions, Drug Dev. Ind. Pharm., 31 (2005), 473–489. https://doi.org/10.1080/03639040500215958 doi: 10.1080/03639040500215958
|
| [26] |
G. Z. Papageorgiou, S. Papadimitriou, E. Karavas, E. Georgarakis, A. Docoslis, D. Bikiaris, Improvement in chemical and physical stability of fluvastatin drug through hydrogen bonding interactions with different polymer matrices, Curr. Drug Delivery, 6 (2009), 101–112. https://doi.org/10.2174/156720109787048230 doi: 10.2174/156720109787048230
|
| [27] |
F. A. Maulvi, V. T. Thakkar, T. G. Soni, T. R. Gandhi, Optimization of aceclofenac solid dispersion using Box–Behnken Design: in-vitro and in-vivo evaluation, Curr. Drug Delivery, 11 (2014), 380–391. https://doi.org/10.2174/1567201811666140311103425 doi: 10.2174/1567201811666140311103425
|
| [28] |
Y. Rane, R. Mashru, M. Sankalia, J. Sankalia, Effect of hydrophilic swellable polymers on dissolution enhancement of carbamazepine solid dispersions studied using response surface methodology, AAPS PharmSciTech, 8 (2007), E1–E11. https://doi.org/10.1208/pt0802027 doi: 10.1208/pt0802027
|
| [29] |
R. M. Martins, S. Siqueira, L. A. Tacon, L. A. P. Freitas, Microstructured ternary solid dispersions to improve carbamazepine solubility, Powder Technol., 215 (2012), 156–165. https://doi.org/10.1016/j.powtec.2011.09.041 doi: 10.1016/j.powtec.2011.09.041
|
| [30] |
R. R. Araújo, C. C. C. Teixeira, L. A. P. Freitas, The preparation of ternary solid dispersions of an herbal drug via spray drying of liquid feed, Drying Technol., 28 (2010), 412–421. https://doi.org/10.1080/07373931003648540 doi: 10.1080/07373931003648540
|
| 1. | Quyen Phuoc Le, Vy Nguyen-Thao Le, Tru Van Nguyen, Van Hong Nguyen, 2024, Chapter 27, 978-3-031-44629-0, 333, 10.1007/978-3-031-44630-6_27 | |
| 2. | Merve Tomas, Yuxi Wen, Wei Liao, Lizhu Zhang, Chao Zhao, David Julian McClements, Elifsu Nemli, Mustafa Bener, Resat Apak, Esra Capanoglu, Recent progress in promoting the bioavailability of polyphenols in plant-based foods, 2024, 1040-8398, 1, 10.1080/10408398.2024.2336051 | |
| 3. | Berivan Ajeel Ibrahim, Nozad Rashid Hussein, Huner Kamal Omer, Abdelbary Elhissi, Iftikhar Khan, Enhancing Gliclazide Solubility Using Solid Dispersions with Carboxymethyl Chitosan and Polyvinylpyrrolidone K30 as Polymeric Carriers, 2025, 0363-9045, 1, 10.1080/03639045.2025.2506651 |
Figures(8) / Tables(6)
Gangqi Han, Bing Wang, Mengli Jia, Shuxin Ding, Wenxuan Qiu, Yuxuan Mi, Zhimei Mi, Yuhao Qin, Wenxing Zhu, Xinli Liu, Wei Li. Optimization and evaluation of resveratrol amorphous solid dispersions with a novel polymeric system[J]. Mathematical Biosciences and Engineering, 2022, 19(8): 8019-8034. doi: 10.3934/mbe.2022375
| Independent Variables | Level | ||
| low | medium | high | |
| X1: CMCS% | 1:10 | 1:5 | 3:10 |
| X2: Res% | 1:10 | 1:5 | 3:10 |
| X3: Tween 80 | 2 | 3 | 4 |
| Transformed values | -1 | 0 | 1 |
| Dependent variables | Y1 = Percentage of Res released in 5 min (Q5) | ||
| Y2 = Percentage of Res released in 30 min (Q30) | |||
DownLoad:
CSV
| Batch | X1 | X2 | X3 |
| 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 |
| 3 | 1 | 0 | 1 |
| 4 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 |
| 6 | 0 | -1 | -1 |
| 7 | 1 | -1 | 0 |
| 8 | -1 | 0 | -1 |
| 9 | -1 | 1 | 0 |
| 10 | 1 | 1 | 0 |
| 11 | 1 | 0 | -1 |
| 12 | -1 | 0 | 1 |
| 13 | 0 | 0 | 0 |
| 14 | -1 | -1 | 0 |
| 15 | 0 | 1 | -1 |
| 16 | 0 | -1 | 1 |
| 17 | 0 | 0 | 0 |
DownLoad:
CSV
| Run | X1 (g/g) | Factors | Responses | ||
| X2 (g/g) | X3 (mL) | Y1 (%) | Y2 (%) | ||
| 1 | 0.1 | 0.2 | 4 | 15.32 | 31.55 |
| 2 | 0.2 | 0.2 | 3 | 17.50 | 33.83 |
| 3 | 0.2 | 0.1 | 4 | 53.42 | 86.38 |
| 4 | 0.2 | 0.2 | 3 | 17.50 | 33.83 |
| 5 | 0.2 | 0.1 | 2 | 54.31 | 83.81 |
| 6 | 0.1 | 0.1 | 3 | 76.42 | 80.09 |
| 7 | 0.1 | 0.3 | 3 | 21.22 | 48.71 |
| 8 | 0.1 | 0.2 | 2 | 14.05 | 25.72 |
| 9 | 0.3 | 0.1 | 3 | 26.79 | 69.67 |
| 10 | 0.2 | 0.2 | 3 | 17.50 | 33.83 |
| 11 | 0.2 | 0.3 | 2 | 25.64 | 51.51 |
| 12 | 0.2 | 0.3 | 4 | 49.59 | 82.91 |
| 13 | 0.3 | 0.2 | 2 | 9.73 | 13.41 |
| 14 | 0.3 | 0.2 | 4 | 7.75 | 13.57 |
| 15 | 0.2 | 0.2 | 3 | 17.50 | 33.83 |
| 16 | 0.3 | 0.3 | 3 | 38.76 | 69.08 |
| 17 | 0.2 | 0.2 | 3 | 17.50 | 33.83 |
DownLoad:
CSV
| Responses | Models | |||||
| F Value | Prob > F | R2 | Adj. R2 | Adeq. prec. | C. V. (%) | |
| Y1 | 33.33 | 0.0001 | 0.9772 | 0.948 | 20.205 | 15.6 |
| Y2 | 25.18 | 0.0002 | 0.9700 | 0.932 | 14.271 | 13.52 |
DownLoad:
CSV
| Dependent variables | Y1 = Q5 | Y2 = Q30 | ||
| Coefficients | P value | Coefficients | P value | |
| Intercept | 17.50 | < 0.0001 | 33.83 | 0.0002 |
| X1 (CMCS%) | -5.50 | 0.0096 | -2.54 | 0.3100 |
| X2 (Res%) | -9.47 | 0.0005 | -8.47 | 0.0082 |
| X3 (Tween 80) | 2.79 | 0.1163 | 4.99 | 0.0686 |
| X1X2 | 16.79 | 0.0001 | 7.70 | 0.0516 |
| X2X3 | -0.81 | 0.7233 | -1.42 | 0.6791 |
| X1X3 | 6.21 | 0.0259 | 7.21 | 0.0643 |
| X12 | -5.36 | 0.0412 | -11.02 | 0.0108 |
| X22 | 28.66 | < 0.0001 | 44.07 | < 0.0001 |
| X32 | -0.43 | 0.8488 | -1.75 | 0.6010 |
| Note: X1X2, X1X3, and X2X3 represent the interactions between Factors X1, X2, and X3; X12, X22, and X32 are the squared effects of the factors; the underlined represent significant factors (P < 0.05). All values are expressed as the mean ± SD, n = 3. | ||||
DownLoad:
CSV
| Batch | X1 | X2 | X3 | Y1 (Q5 ± SD) | Predicted Q5 | % Error | P Value |
| Check pt-1 | 0.11 | 0.12 | 3.28 | 59.40 ± 1.11 | 57.98 | 2.45 | 0.157 |
| Check pt-2 | 0.18 | 0.28 | 2.60 | 25.01 ± 0.68 | 22.29 | 12.20 | 0.020 |
| Check pt-3 | 0.13 | 0.13 | 2.07 | 50.13 ± 0.72 | 51.70 | -3.04 | 0.064 |
| Optimized | 0.17 | 0.10 | 2.94 | 61.42 ± 0.47 | 61.64 | -0.36 | 0.509 |
| Batch | X1 | X2 | X3 | Y2 (Q30 ± SD) | Predicted Q30 | % Error | P Value |
| Check pt-1 | 0.11 | 0.12 | 3.28 | 71.75 ± 1.31 | 71.67 | 0.11 | 0.925 |
| Check pt-2 | 0.18 | 0.28 | 2.60 | 49.81 ± 0.56 | 47.90 | 3.99 | 0.027 |
| Check pt-3 | 0.13 | 0.13 | 2.07 | 63.40 ± 1.13 | 62.47 | 1.49 | 0.290 |
| Optimized | 0.17 | 0.10 | 2.94 | 88.38 ± 0.31 | 88.82 | -0.50 | 0.137 |
| Note: All values are expressed as the mean ± SD, n = 3. | |||||||
DownLoad:
CSV
| Independent Variables | Level | ||
| low | medium | high | |
| X1: CMCS% | 1:10 | 1:5 | 3:10 |
| X2: Res% | 1:10 | 1:5 | 3:10 |
| X3: Tween 80 | 2 | 3 | 4 |
| Transformed values | -1 | 0 | 1 |
| Dependent variables | Y1 = Percentage of Res released in 5 min (Q5) | ||
| Y2 = Percentage of Res released in 30 min (Q30) | |||
| Batch | X1 | X2 | X3 |
| 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 |
| 3 | 1 | 0 | 1 |
| 4 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 |
| 6 | 0 | -1 | -1 |
| 7 | 1 | -1 | 0 |
| 8 | -1 | 0 | -1 |
| 9 | -1 | 1 | 0 |
| 10 | 1 | 1 | 0 |
| 11 | 1 | 0 | -1 |
| 12 | -1 | 0 | 1 |
| 13 | 0 | 0 | 0 |
| 14 | -1 | -1 | 0 |
| 15 | 0 | 1 | -1 |
| 16 | 0 | -1 | 1 |
| 17 | 0 | 0 | 0 |
| Run | X1 (g/g) | Factors | Responses | ||
| X2 (g/g) | X3 (mL) | Y1 (%) | Y2 (%) | ||
| 1 | 0.1 | 0.2 | 4 | 15.32 | 31.55 |
| 2 | 0.2 | 0.2 | 3 | 17.50 | 33.83 |
| 3 | 0.2 | 0.1 | 4 | 53.42 | 86.38 |
| 4 | 0.2 | 0.2 | 3 | 17.50 | 33.83 |
| 5 | 0.2 | 0.1 | 2 | 54.31 | 83.81 |
| 6 | 0.1 | 0.1 | 3 | 76.42 | 80.09 |
| 7 | 0.1 | 0.3 | 3 | 21.22 | 48.71 |
| 8 | 0.1 | 0.2 | 2 | 14.05 | 25.72 |
| 9 | 0.3 | 0.1 | 3 | 26.79 | 69.67 |
| 10 | 0.2 | 0.2 | 3 | 17.50 | 33.83 |
| 11 | 0.2 | 0.3 | 2 | 25.64 | 51.51 |
| 12 | 0.2 | 0.3 | 4 | 49.59 | 82.91 |
| 13 | 0.3 | 0.2 | 2 | 9.73 | 13.41 |
| 14 | 0.3 | 0.2 | 4 | 7.75 | 13.57 |
| 15 | 0.2 | 0.2 | 3 | 17.50 | 33.83 |
| 16 | 0.3 | 0.3 | 3 | 38.76 | 69.08 |
| 17 | 0.2 | 0.2 | 3 | 17.50 | 33.83 |
| Responses | Models | |||||
| F Value | Prob > F | R2 | Adj. R2 | Adeq. prec. | C. V. (%) | |
| Y1 | 33.33 | 0.0001 | 0.9772 | 0.948 | 20.205 | 15.6 |
| Y2 | 25.18 | 0.0002 | 0.9700 | 0.932 | 14.271 | 13.52 |
| Dependent variables | Y1 = Q5 | Y2 = Q30 | ||
| Coefficients | P value | Coefficients | P value | |
| Intercept | 17.50 | < 0.0001 | 33.83 | 0.0002 |
| X1 (CMCS%) | -5.50 | 0.0096 | -2.54 | 0.3100 |
| X2 (Res%) | -9.47 | 0.0005 | -8.47 | 0.0082 |
| X3 (Tween 80) | 2.79 | 0.1163 | 4.99 | 0.0686 |
| X1X2 | 16.79 | 0.0001 | 7.70 | 0.0516 |
| X2X3 | -0.81 | 0.7233 | -1.42 | 0.6791 |
| X1X3 | 6.21 | 0.0259 | 7.21 | 0.0643 |
| X12 | -5.36 | 0.0412 | -11.02 | 0.0108 |
| X22 | 28.66 | < 0.0001 | 44.07 | < 0.0001 |
| X32 | -0.43 | 0.8488 | -1.75 | 0.6010 |
| Note: X1X2, X1X3, and X2X3 represent the interactions between Factors X1, X2, and X3; X12, X22, and X32 are the squared effects of the factors; the underlined represent significant factors (P < 0.05). All values are expressed as the mean ± SD, n = 3. | ||||
| Batch | X1 | X2 | X3 | Y1 (Q5 ± SD) | Predicted Q5 | % Error | P Value |
| Check pt-1 | 0.11 | 0.12 | 3.28 | 59.40 ± 1.11 | 57.98 | 2.45 | 0.157 |
| Check pt-2 | 0.18 | 0.28 | 2.60 | 25.01 ± 0.68 | 22.29 | 12.20 | 0.020 |
| Check pt-3 | 0.13 | 0.13 | 2.07 | 50.13 ± 0.72 | 51.70 | -3.04 | 0.064 |
| Optimized | 0.17 | 0.10 | 2.94 | 61.42 ± 0.47 | 61.64 | -0.36 | 0.509 |
| Batch | X1 | X2 | X3 | Y2 (Q30 ± SD) | Predicted Q30 | % Error | P Value |
| Check pt-1 | 0.11 | 0.12 | 3.28 | 71.75 ± 1.31 | 71.67 | 0.11 | 0.925 |
| Check pt-2 | 0.18 | 0.28 | 2.60 | 49.81 ± 0.56 | 47.90 | 3.99 | 0.027 |
| Check pt-3 | 0.13 | 0.13 | 2.07 | 63.40 ± 1.13 | 62.47 | 1.49 | 0.290 |
| Optimized | 0.17 | 0.10 | 2.94 | 88.38 ± 0.31 | 88.82 | -0.50 | 0.137 |
| Note: All values are expressed as the mean ± SD, n = 3. | |||||||
