According to the Warburg effect, there are some significant differences between metabolisms, products and process of respirations of cancer cells and normal cells. For example, normal cells absorb oxygen and glucose and give water molecules, carbon dioxide, ATP molecules and some number of spinors; while cancer cells take glucose and give lactate, less number of ATP molecules and different number of spinors. Using this property, we can design a system from two graphene sheets that are connected by pairing the fourth free electrons of carbons. Then, we can break some pairs and produce some holes. The number of these holes should be equal to the number of radiated spinors by normal cells. Near a normal cell, all holes are filled and the graphene system doesn't emit any electrical current or wave. However, near a cancer cell, some extra holes or spinors remain that their motions produce some electrical currents. These currents force on cancer cell membranes and destroy them and consequently, cause the cell death. Also, these currents emit some electromagnetic waves which detectors could take them out of the human's body and consequently, they could play the main role in imaging.
Citation: Massimo Fioranelli, Hijaz Ahmad, Alireza Sepehri, Maria Grazia Roccia, Faissal Aziz. A mathematical model for imaging and killing cancer cells by using concepts of the Warburg effect in designing a Graphene system[J]. Mathematical Biosciences and Engineering, 2022, 19(3): 2985-2995. doi: 10.3934/mbe.2022137
| [1] | Anshuman Swain, William F Fagan . A mathematical model of the Warburg Effect: Effects of cell size, shape and substrate availability on growth and metabolism in bacteria. Mathematical Biosciences and Engineering, 2019, 16(1): 168-186. doi: 10.3934/mbe.2019009 |
| [2] | G. V. R. K. Vithanage, Hsiu-Chuan Wei, Sophia R-J Jang . Bistability in a model of tumor-immune system interactions with an oncolytic viral therapy. Mathematical Biosciences and Engineering, 2022, 19(2): 1559-1587. doi: 10.3934/mbe.2022072 |
| [3] | Avner Friedman, Kang-Ling Liao . The role of the cytokines IL-27 and IL-35 in cancer. Mathematical Biosciences and Engineering, 2015, 12(6): 1203-1217. doi: 10.3934/mbe.2015.12.1203 |
| [4] | Linglei Meng, XinFang Shang, FengXiao Gao, DeMao Li . Comparative study of imaging staging and postoperative pathological staging of esophageal cancer based on smart medical big data. Mathematical Biosciences and Engineering, 2023, 20(6): 10514-10529. doi: 10.3934/mbe.2023464 |
| [5] | Hassan Ali Khan, Wu Jue, Muhammad Mushtaq, Muhammad Umer Mushtaq . Brain tumor classification in MRI image using convolutional neural network. Mathematical Biosciences and Engineering, 2020, 17(5): 6203-6216. doi: 10.3934/mbe.2020328 |
| [6] | Swati Shinde, Madhura Kalbhor, Pankaj Wajire . DeepCyto: a hybrid framework for cervical cancer classification by using deep feature fusion of cytology images. Mathematical Biosciences and Engineering, 2022, 19(7): 6415-6434. doi: 10.3934/mbe.2022301 |
| [7] | Sushovan Chaudhury, Kartik Sau, Muhammad Attique Khan, Mohammad Shabaz . Deep transfer learning for IDC breast cancer detection using fast AI technique and Sqeezenet architecture. Mathematical Biosciences and Engineering, 2023, 20(6): 10404-10427. doi: 10.3934/mbe.2023457 |
| [8] | Donggu Lee, Aurelio A. de los Reyes V, Yangjin Kim . Optimal strategies of oncolytic virus-bortezomib therapy via the apoptotic, necroptotic, and oncolysis signaling network. Mathematical Biosciences and Engineering, 2024, 21(3): 3876-3909. doi: 10.3934/mbe.2024173 |
| [9] | Nengkai Wu, Dongyao Jia, Chuanwang Zhang, Ziqi Li . Cervical cell extraction network based on optimized yolo. Mathematical Biosciences and Engineering, 2023, 20(2): 2364-2381. doi: 10.3934/mbe.2023111 |
| [10] | Suxiang Yu, Shuai Zhang, Bin Wang, Hua Dun, Long Xu, Xin Huang, Ermin Shi, Xinxing Feng . Generative adversarial network based data augmentation to improve cervical cell classification model. Mathematical Biosciences and Engineering, 2021, 18(2): 1740-1752. doi: 10.3934/mbe.2021090 |
According to the Warburg effect, there are some significant differences between metabolisms, products and process of respirations of cancer cells and normal cells. For example, normal cells absorb oxygen and glucose and give water molecules, carbon dioxide, ATP molecules and some number of spinors; while cancer cells take glucose and give lactate, less number of ATP molecules and different number of spinors. Using this property, we can design a system from two graphene sheets that are connected by pairing the fourth free electrons of carbons. Then, we can break some pairs and produce some holes. The number of these holes should be equal to the number of radiated spinors by normal cells. Near a normal cell, all holes are filled and the graphene system doesn't emit any electrical current or wave. However, near a cancer cell, some extra holes or spinors remain that their motions produce some electrical currents. These currents force on cancer cell membranes and destroy them and consequently, cause the cell death. Also, these currents emit some electromagnetic waves which detectors could take them out of the human's body and consequently, they could play the main role in imaging.
Around 100 years ago, Heinrich Warburg discovered a new mechanism for cancer cell respiration called the Warburg effect. The Warburg effect is a form of modified cellular metabolism found in cancer cells, which tend to favour a specialized fermentation over the aerobic respiration pathway that most other body cells prefer [1,2]. In this mechanism, the final product of glycolysis, pyruvate, is converted into lactate and compared to the normal cellular respiration, fewer numbers of adenosine triphosphate (ATP) are produced [3]. In fact, the metabolism of cancer cells is used to facilitate the uptake and incorporation of nutrients into the biomass (e.g., nucleotides, amino acids and lipids), which are needed for creating a new cancer cell [3,4,5,6,7,8]. Now, the question arises of how the Warburg effect is regulated? Some authors showed that transcription factor SIX1 directly increases the expression of many glycolytic genes, promoting the Warburg effect and tumour growth in vitro and in vivo. In addition, SIX1 regulates glycolysis through HBO1 and AIB1 histone acetyltransferases [5]. Besides this consideration, some other authors indicated that several factors could be involved in occurring Warburg effect; still, the roles of non-coding RNAs (ncRNAs) are highlighted in several types of human cancer. The ncRNAs, including microRNAs, long non-coding RNAs and circular RNAs can all affect metabolic enzymes and transcription factors to promote glycolysis and modulate glucose metabolism to enhance the progression of tumours [6]. These studies and many other parallel investigations could describe some aspects of the Warburg effect. However, the origins of some other aspects are unclear. In another study, it has been shown that the Warburg effect provides the best opportunities to develop therapeutic strategies to preferentially kill cancer cells by targeting the glycolytic pathway [7].
On the other hand, this effect could be the origin of the difference in radiating waves by cancer and normal cells, which could be used in imaging techniques. That's could be achieved by taking radiated waves from cancer cells by some electronic devices and comparing them with radiated waves from normal cells. If observed waves are different from what is expected, it means that some non-desired events occur. For example, a tumour may have emerged.
The differences between cancer and normal cellular respirations cause a significant difference in the production of ions, H+, charges and electrons. These differences lead to radiated waves by charges around cancer and normal cells [8,9]. The waves could be detected by nano-systems like graphene sheets [10,11,12]. Graphene sheets have the potential to produce free radicals [13]. These radicals may have at least one unpaired valence electron. These electrons could carry or emit some waves. Thus, they could capture cellular waves and send them to scopes out of the human's body.
For this reason, they have many applications in imaging and curing diseases [14,15,16,17,18,19,20,21]. These free electrons could act like receivers and absorb radiated waves by cancer cells, strengthen them and send them towards some special detectors out of the human's body. Thus, graphene sheets could help humans to diagnose tumours. On the other hand, one can design a graphene system that acts like a bomb or a weapon against cancer cells and destroy their membranes by shooting electrons. In this research, we propose a model for graphene systems that could be used in imaging and killing cancer cells. These systems are built from two graphene sheets which their electrons are paired. Then, we break some pairs and produce some holes. The number of these holes should be equal to the number of emitted charges by normal cells. Consequently, cancer cells emit different numbers of charges and extra electrons or holes remain. These charges produce some currents and emit some waves. These waves are taken by scopes out of the body and show non-desired events like the emergence of cancers. Also, these currents and extra charges destroy the cancer cell membranes and kill them.
The outline of this paper is as follows: In Section II, we will propose a theoretical model for designing a graphene system by using concepts of the Warburg effect. Then, we will argue about the applications of this system in imaging. Finally, in section III, we will formulate the model and obtain direct electrical currents and magnetic fields around biological cells.
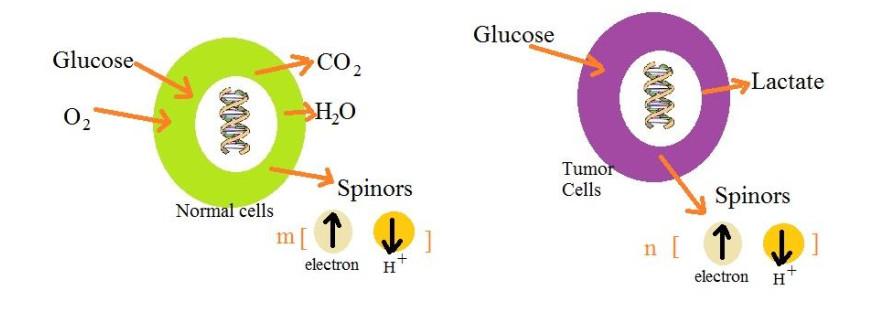
The Warburg effect gives us the best opportunities to diagnose cancers at initial stages and then kill them before metastasis and spreading. This effect states that the respiration process in cancer cells is different concerning respiration and the metabolism process in normal cells [22]. Normal cells absorb glucose and oxygen and give water molecules, carbon dioxide, ATP and some ions and spinors like H+ and electrons (Figure 1):
| Normal Cell:Glucose+O2+…⋯→CO2+H2O+y ATP+w spinors+…… | (1) |
While cancer cells mostly absorb glucose and some other matters and give more lactate and some spinors, including electrons or H+ (Figure 2):
| Cancer cell:Glucose+⋯→Pyruvate+…..→Lactate+x ATP+z spinors…. | (2) |
Number of charges, ions and spinors (H+ and electrons) which are radiated by cancer cells and normal ones are different :
| Difference between number of spinors in cancer and normal cells=nspinors=|[z−w]|spinors | (3) |
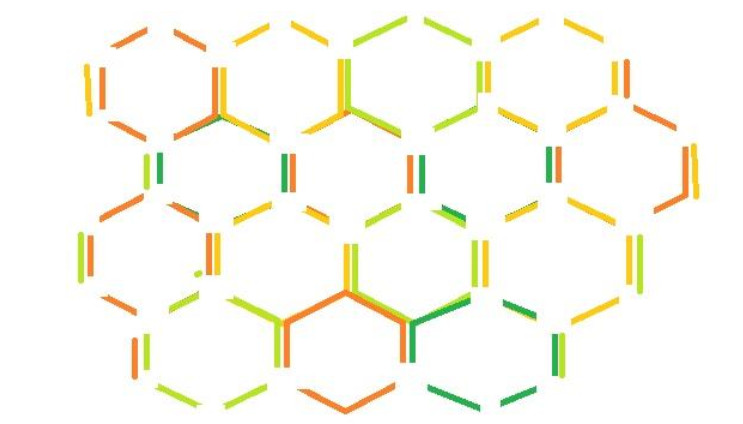
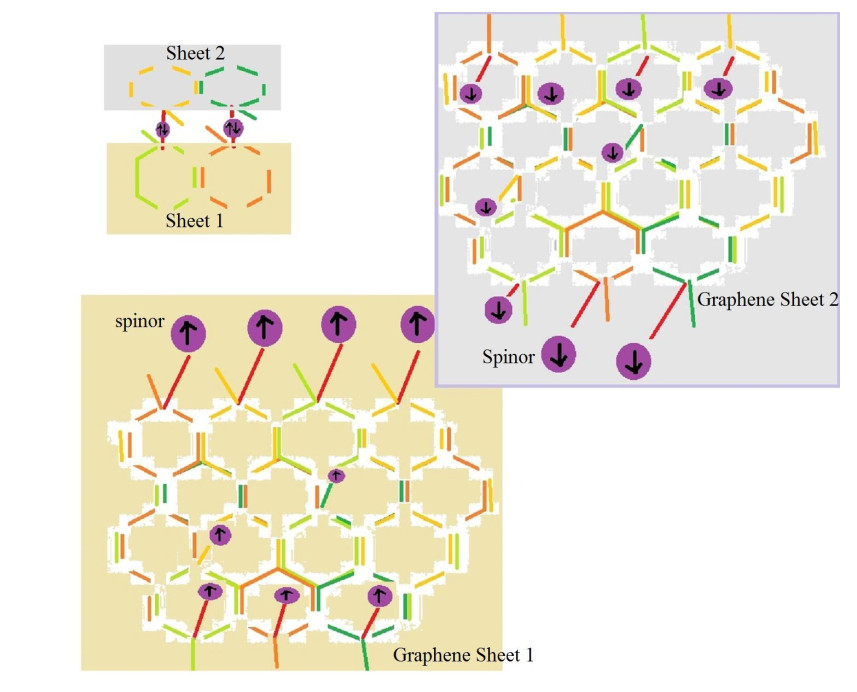
This difference in the number of spinors and charges could help us to propose a new model for imaging cancer cells. Because, spins of spinors produce some magnetic fields, differences in number of spinors cause differences in magnetic fields around cancer and normal cells. To detect these waves, we should use some nanostructures. The best nanostructure could be graphene because it includes hexagonal molecules which each molecule is formed from six carbons. Each carbon has four free electrons which only three of them should be confined with electrons of three other carbons and one electron could be free (Figure 3). Forth free electrons of carbons within a sheet could be paired with the fourth free electrons of carbons in the second sheet (Figure 4). This system could be used as a detector in imaging cancer cells. To this aim:
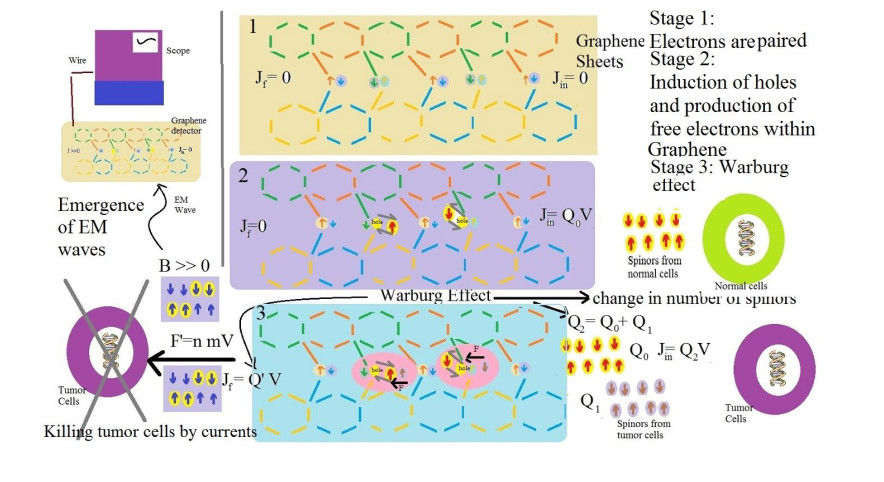
1) At the first stage, we connect the fourth free electron of carbons in one sheet with the fourth free electron of carbons in the second sheet and make a system of two connected graphene sheets.
2) At the second stage, we break some connections between the free electrons of two sheets and produce some holes. The number of these holes should be equal to the number of radiated spinors by normal cells:
| Number of holes between coupled graphene sheets=Number of spinors around normal cells | (4) |
3) We put this graphene system near a cell in the third stage. In normal cells, holes are filled by spinors around normal cells and radiated currents become zero. We have:
| Jin=Q0V | (5) |
Jin is the electrical current produced by spinors around normal cells and before the graphene system, the Q0 charge of spinors and V is their velocity.
Spinors could be electrons or H+. These spinors have different charges. Electrons could fill Holes; however, H+ couldn't be used directly in filling holes. Instead, these spinors could interact with other ions and free some electrons. These new free electrons may fill holes.
On the other hand, a H+ that moves in one direction could act like an electron that moves in a reverse direction. Then, maybe, some (H+)s interact with some free electrons within the graphene sheet, cancel their charges and spins and remove holes. Thus, we can write:
| Jf=0 | (6) |
4) Around a cancer cell, the number of spinors is changed and some extra electrons or H+ (H+)s have emerged. Thus, concerning the normal state, two new states may have emerged (Figure 5):
a) All holes within the graphene system are filled, and some extra charges remain. These charges interact with electrons and break pairs. Consequently, charges move, and some electrical currents are produced.
| Jf=Q′V′ |
| Q′=Q0−Q0+qextra | (7) |
b) Some holes within the graphene system remains. Charges around cells fill these holes. This causes that charges move and some currents have emerged.
| Jf=Q"V" |
| Q"=Q−Q0 | (8) |
5) Currents that are produced by graphene holes have two effects:
a): Currents move, force into cancer cells and kill them.
b): Currents emit some magnetic waves, which detectors may detect out of the human's body (Figure 5).
This section considers the model mathematically and calculates forces and magnetic fields. To begin, we remember a relation between a magnetic field and spin:
| Be∼Se | (9) |
where
| Bpair∼Spair∼Se,up−Se,down∼0 | (10) |
However, by adding a third free electron to this system, the magnetic field finds a relation with a spin of extra particles:
| Btri∼Stri∼Sfree+Se,up−Se,down∼Sfree | (11) |
Thus, the total magnetic of a graphene sheet could be obtained by summing over spins of free electrons. If we suppose that all spins are in one direction, then we can write:
| BGraphene∼nBtri∼nStri∼n[Sfree+Se,up−Se,down]∼nSfree | (12) |
where n is the number of free electrons within a graphene sheet and could depend on the grahene system sizes and quantum parameters (n {graphene sheet sizes and quantum parameters}). When the number of spins increases, their related magnetic fields grow. Using the above magnetic field, we can obtain the energy density of a graphene sheet
| UGraphene→[BGraphene]22μ0→[nSfree]22μ0 | (13) |
Multiplying above energy density by graphene molecular volume, one can obtain the below energy:
| EGraphene=UGrapheneVGraphene | (14) |
where
| VGraphene≈n2RHexagon[RHexagon+x]cos(π6)[LGraphene+x] | (15) |
RHexagon is the radius of the hexagonal molecule, LGraphene (x) is the separation distance between sheets and x is the oscillation parameter. In fact, graphene sheets interact with each other and open or close with the value of x. Substituting results of Eqs (13) and (15) in Eq (14) gives:
| EGraphene≈[nSfree]22μ0n2RHexagon[RHexagon+x]cos(π6)[LGraphene+x] | (16) |
where LGraphene could be a function of x (LGraphene (x) = l0 + g (xn)). The above energy depends on graphene sheet sizes, number and length of spins. Taking derivative respect to x from energy gives the below force approximately:
| FGraphene=dEGrapheneX≈KGraphenex+constant | (17) |
where
| KGraphene≈[nSfree]22μ0n2[RHexagon ]cos(π6) | (18) |
The above force is related to oscillations of graphene sheets and depends on the number of spins and graphene sheet sizes. Using the above equation, we can obtain the below frequency and time period:
| νe≈12π[KGrapheneMe]12=12π[[nSfree]22μ0n2[RHexagon ]cos(π6)Me]12→ |
| Te∼1νe=2π[KGrapheneMe]−12=2π[[nSfree]22μ0n2[RHexagon ]cos(π6)Me]−12 | (19) |
where Me is the electron mass, using the above time, we can obtain the velocity of electrons between
two sheets:
| Ve∼2LGrapheneTe=2LGraphene2π[[nSfree]22μ0n2[RHexagon ]cos(π6)Me]12 | (20) |
This velocity depends on graphene sheet sizes and the number of spinors. Motions of charges produce a current which has the below relation with velocity and charge (Q)
| Je,1∼QVe∼Q2LGraphene2π[[nSfree]22μ0n2[RHexagon ]cos(π6)Me]12 | (21) |
If the number of holes are bigger or less than emitted spinors by cells, this current becomes free and collides with cells. This collision produces a force that depends on a number of spinors (n), their masses (
| Fe,1∼nMeVe∼nMe2LGraphene2π[[nSfree]22μ0n2[RHexagon ]cos(π6)Me]12 | (22) |
The above force depends on graphene sheet sizes and the number of spinors. In addition to this force, electrical currents could produce an extra magnetic field so:
| Be,2∼μ2πRGrapheneJe,1∼μ2πRGrapheneQ2LGraphene2π[[nSfree]22μ0n2[RHexagon ]cos(π6)Me]12 | (23) |
This new magnetic field depends on graphene sheet sizes and the number of spinors or holes. In addition, this field interacts with charges and force on them:
| Fe,2∼QVeBe,2∼μQVe2πRGrapheneJe,1 |
| ∼μQ22πRGraphene[LGraphene2π[[nSfree]22μ0n2[RHexagon ]cos(π6))Me]12]2 | (24) |
The above force depends on electrical charge, graphene sheet sizes and the number of spinors or holes. This force and the previous one put pressure on the structure of cancer cells and destroy their membranes. We can build a neutral graphene system in front of normal cells while fully spinning against cancer cells and acting like a bomb for them. On the other hand, this graphene system produces several currents near cancer cells that emit magnetic waves. It is clear that by increasing graphene sheet sizes, the number of holes or extra spinors increases and stronger currents and fields have emerged. Some detectors could detect these fields out of the human's body.
The Warburg effect shows that cancer cells have different products and metabolisms concerning normal cells. Both types of cells produce H+, electrons and other charges and spinors. However, the number of spinors radiated from cancer cells differs from the number of spinors around normal cells. We have used this property and theoretically designed a system for diagnosing cancer cells and their kill. In this system, we have used two graphene sheets. Each carbon has four free electrons in each sheet, three of which are paired with three electrons of three other carbons and one free electron is paired with a free electron of carbons in the second sheet. Thus, two graphene sheets are coupled by pairing free electrons. Then, we break some pairs and produce some holes. The number of holes should be equal to the number of spinors around normal cells. Consequently, when this graphene system becomes close to a normal cell, all holes are filled and no current emerges. However, some extra holes or spinors remain near a cancer cell, move and produce currents. These currents kill cancer cells and send signals that observers take out of a human's body. We have formulated the model and obtained the electrical currents, forces and emitted magnetic fields in terms of the number of holes and charges.
There is no conflict of interest for this paper.
| [1] |
M. V. Liberti, J. W. Locasale, The Warburg effect: how does it benefit cancer cells?, Trends Biochem. Sci., 41 (2016), 211-218. https://doi.org/10.1016/j.tibs.2015.12.001 doi: 10.1016/j.tibs.2015.12.001
|
| [2] |
K. O. Alfarouk, Tumor metabolism, cancer cell transporters, and microenvironmental resistance, J. Enzyme Inhib. Med. Chem., 31 (2016), 859-66. https://doi.org/10.3109/14756366.2016.1140753 doi: 10.3109/14756366.2016.1140753
|
| [3] |
M. G. V. Heiden, L. C. Cantley, C. B. Thompson, Understanding the Warburg effect: the metabolic requirements of cell proliferation, Science, 324 (2009), 1029-1033. https://doi.org/10.1126/science.1160809 doi: 10.1126/science.1160809
|
| [4] |
C. Yu, J. Xue, W. Zhu, Y. Jiao, S. Zhang, J. Cao, Warburg meets non-coding RNAs: the emerging role of ncRNA in regulating the glucose metabolism of cancer cells, Tumour Biol., 36 (2015), 81-94. https://doi.org/10.1007/s13277-014-2875-z doi: 10.1007/s13277-014-2875-z
|
| [5] |
L. Li, Y. Liang, L. Kang, Y. Liu, S. Gao, S. Chen, et al., Transcriptional regulation of the Warburg effect in cancer by SIX1, Cancer Cell, 33 (2018), 368-385. https://doi.org/10.1016/j.ccell.2018.01.010 doi: 10.1016/j.ccell.2018.01.010
|
| [6] |
H. Mirzaei, M. R. Hamblin, Regulation of glycolysis by non-coding RNAs in cancer: switching on the Warburg effect, Mol. Ther. Oncolytics, 19 (2020), 218-239. https://doi.org/10.1016/j.omto.2020.10.003. doi: 10.1016/j.omto.2020.10.003
|
| [7] |
Z. Chen, W. Lu, C. Garcia-Prieto, P. Huang, The Warburg effect and its cancer therapeutic implications, J. Bioenerg. Biomembr., 39 (2007), 267-274. https://doi.org/10.1007/s10863-007-9086-x doi: 10.1007/s10863-007-9086-x
|
| [8] |
J. Pokorný, J. Pokorný, F. Borodavka, Warburg effect-damping of electromagnetic oscillations, Electromagn. Biol. Med., 36 (2017), 270-278. https://doi.org/10.1080/15368378.2017.1326933 doi: 10.1080/15368378.2017.1326933
|
| [9] |
A. R Liboff, The Warburg hypothesis and weak ELF biointeractions, Electromagn. Biol. Med., 39 (2020), 45-48. https://doi.org/10.1080/15368378.2020.1737810 doi: 10.1080/15368378.2020.1737810
|
| [10] |
T. A. Tabish, R. J. Narayan, Mitochondria-targeted graphene for advanced cancer therapeutics, Acta Biomater., 129 (2021), 43-56. https://doi.org/10.1016/j.actbio.2021.04.054 doi: 10.1016/j.actbio.2021.04.054
|
| [11] |
J. Frontiñan-Rubio, M. V. Gomez, V. J. González, M. Durán-Prado, E. Vázquez, Sublethal exposure of small few-layer graphene promotes metabolic alterations in human skin cells. Sci. Rep., 10 (2020), 18407. https://doi.org/10.1038/s41598-020-75448-0 doi: 10.1038/s41598-020-75448-0
|
| [12] |
C. Martelli, A. King, T. Simon, G. Giamas, Graphene-induced transdifferentiation of cancer stem cells as a therapeutic strategy against glioblastoma, ACS Biomater. Sci. Eng., 6 (2020), 3258-3269. https://doi.org/10.1021/acsbiomaterials.0c00197 doi: 10.1021/acsbiomaterials.0c00197
|
| [13] |
I. S. Donskyi, Y. Chen, P. Nickl, G. Guday, H. Qiao, K. Achazi, et al., Self-degrading graphene sheets for tumor therapy, Nanoscale, 12 (2020), 14222-14229. https://doi.org/10.1039/D0NR02159H doi: 10.1039/D0NR02159H
|
| [14] |
T. A. Tabish, C. J. Scotton, D. C. J. Ferguson, L. Lin, A. V. der Veen, S. Lowry, et al., Biocompatibility and toxicity of graphene quantum dots for potential application in photodynamic therapy, Nanomedicine (Lond), 13 (2018), 1923-1937. https://doi.org/10.2217/nnm-2018-0018 doi: 10.2217/nnm-2018-0018
|
| [15] |
V. Palmieri, M. Papi, Can graphene take part in the fight against COVID-19?, Nano Today, 33 (2020), 100883. https://doi.org/10.1016/j.nantod.2020.100883 doi: 10.1016/j.nantod.2020.100883
|
| [16] |
P. K. Raghav, S. Mohanty, Are graphene and graphene-derived products capable of preventing COVID-19 infection?, Med. Hypotheses, 144 (2020), 110031. https://doi.org/10.1016/j.mehy.2020.110031 doi: 10.1016/j.mehy.2020.110031
|
| [17] |
J. Sengupta, C. M. Hussain, Graphene-based field-effect transistor biosensors for the rapid detection and analysis of viruses: A perspective in view of COVID-19, Carbon Trends, 2 (2021), 100011. https://doi.org/10.1016/j.cartre.2020.100011 doi: 10.1016/j.cartre.2020.100011
|
| [18] | I. Maqbool, F. Rehman, F. Soomro, Z. Bhatti, U. Ali, A. H. Jatoi, et al., Graphene-based materials for fighting coronavirus disease 2019: challenges and opportunities. CBEN, 8 (2021), 67-77. https://doi.org/10.1002/cben.202000039 |
| [19] |
A. Rhazouani, H. Gamrani, M. E. Achaby, K. Aziz, L. Gebrati, M. S. Uddin, et al., Synthesis and toxicity of graphene oxide nanoparticles: A literature review of in vitro and in vivo studies, Biomed. Res. Int., 2021 (2021), 5518999. https://doi.org/10.1155/2021/5518999 doi: 10.1155/2021/5518999
|
| [20] |
D. Samanta, M. P. Karthikeyan, A. Banerjee, H. Inokawa, Tunable graphene nanopatch antenna design for on-chip integrated terahertz detector arrays with potential application in cancer imaging, Nanomedicine, 16 (2021), 1035-1047. https://doi.org/10.2217/nnm-2020-0386 doi: 10.2217/nnm-2020-0386
|
| [21] |
S. F. Adil, M. R. Shaik, F. A. Nasr, A. S. Alqahtani, M. Z. Ahmed, W. Qamar, et al., Enhanced apoptosis by functionalized highly reduced graphene oxide and gold nanocomposites in MCF-7 breast cancer cells, ACS Omega, 6 (2021), 15147-15155. https://doi.org/10.1021/acsomega.1c01377 doi: 10.1021/acsomega.1c01377
|
| [22] |
N. Anjum, J. He, Nonlinear dynamic analysis of vibratory behavior of a graphene nano/microelectromechanical system, Math. Meth. Appl. Sci., 2020 (2020), 1-16. https://doi.org/10.1002/mma.6699 doi: 10.1002/mma.6699
|
| [23] |
T. A. Tabish, M. R. Hamblin, Mitochondria-targeted nanoparticles (mitoNANO): An emerging therapeutic shortcut for cancer, Biomater. Biosyst., 3 (2021), 100023. https://doi.org/10.1016/j.bbiosy.2021.100023 doi: 10.1016/j.bbiosy.2021.100023
|
| [24] |
T. A. Tabish, S. Zhang, P. G. Winyard, Developing the next generation of graphene-based platforms for cancer therapeutics: The potential role of reactive oxygen species, Redox. Biol., 2018 (2018), 34-40. https://doi.org/10.1016/j.redox.2017.11.018 doi: 10.1016/j.redox.2017.11.018
|
| 1. | Aaqid Mohi-Ud Din Bhat, Younis Ahmad Bhat, A Multi-compartment Mathematical Model for HIV–AIDS Transmission and Dynamics, 2023, 2731-8095, 10.1007/s40995-022-01397-0 | |
| 2. | Abeer Hamdan Alblowy, Normah Maan, Abdulkareem Afolabi Ibrahim, Optimal control strategies for SGLT2 inhibitors as a novel anti-tumor agent and their effect on human breast cancer cells with the effect of time delay and hyperglycemia, 2023, 166, 00104825, 107552, 10.1016/j.compbiomed.2023.107552 |
Figures(5)
Massimo Fioranelli, Hijaz Ahmad, Alireza Sepehri, Maria Grazia Roccia, Faissal Aziz. A mathematical model for imaging and killing cancer cells by using concepts of the Warburg effect in designing a Graphene system[J]. Mathematical Biosciences and Engineering, 2022, 19(3): 2985-2995. doi: 10.3934/mbe.2022137
DownLoad:
