1. Introduction
The World Health Organization (WHO) Measles and Rubella Strategic Plan aims to eliminate measles and rubella in at least five WHO regions by the end of 2020 ([18]). However, despite the existence of an inexpensive measles vaccine there are obstacles to achieving this goal. In developing countries the vaccine is not always available. Whether the poorest countries with poor infrastructure for routine health services can achieve sufficiently high coverage is unknown ([18]).
In Europe, the elimination of measles is endangered by non-vaccinated individuals; a growing number of parents refuse to vaccinate their children for various reasons, e.g. too many shots or concern about autism (see e.g. [16]).
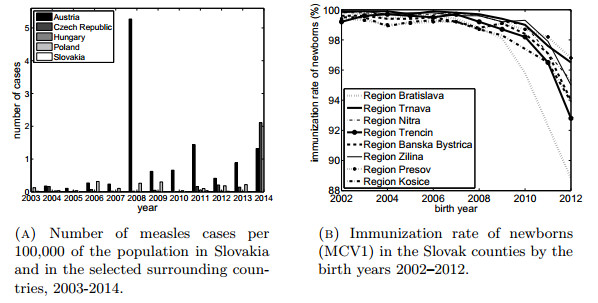
Slovakia is one of the few European countries where vaccination is enacted by law. Vaccination against measles was introduced in 1969. Currently, to prevent measles, children should be vaccinated with the measles, mumps, and rubella (MMR) vaccine. Two doses of this vaccine are needed for complete protection. Children should be given the first dose of MMR vaccine at 15 to 18 months of age. The second dose should be given at the 11th year of life. As Figure 1a indicates, because of the mandatory vaccination, incidence of measles cases in Slovakia is quite low compared to other surrounding countries: in the period 2003-2014 only six measles cases have been registered in Slovakia, all of them imported.
Since becoming independent in 1993, annual immunization rate of newborns for measles-mumps-rubella (MMR) vaccine in Slovakia has been above the critical level needed to achieve herd immunity, which, for measles, is estimated to be approximately 94% (see the theoretical derivation in e.g [12]). However, recent frequent mass media discussions about the adverse effects of vaccination have gradually eroded compliance of parents. As a result, the favorable epidemiological situation started to change, and a decrease in immunization rate of newborns has been observed in recent years. This is especially true for MMR vaccine. Figure 1b depicts the percentage of fully immunized children for MMR vaccine by birth year, starting from 2002 to 2012, in eight Slovak counties. Currently, the drop in vaccination rates has been observed in all regions. For the birth year 2012, the vaccination coverage has decreased bellow the critical level needed to achieve herd immunity in 4 out of 8 Slovak counties. The most significant decline has been observed in the capital, Bratislava region: the annual immunization rate of newborns has dropped from 99% in 2008 to only 88% in 2012.
One can identify several factors responsible for this situation. Firstly, a decline in immunization rates of newborns is most likely related to the increasing activity of the anti-vaccination lobby: their massive campaign has started in the beginning of the year 2010, after the launch of the first web page with anti-vaccination contents in the Slovak language. It is further aided by the present favorable epidemiological situation in Slovakia: the general tendency to underestimate the risk of natural infection and overestimate the risk of the vaccine side effects is stronger during the periods without disease outbreaks. Finally, the penalties for nonvaccinators, as stated by the current law, do not appear to be sufficiently effective: the worst inconvenience for the parents refusing vaccination is a fine of around 330€ per child per vaccination (see: [14]).
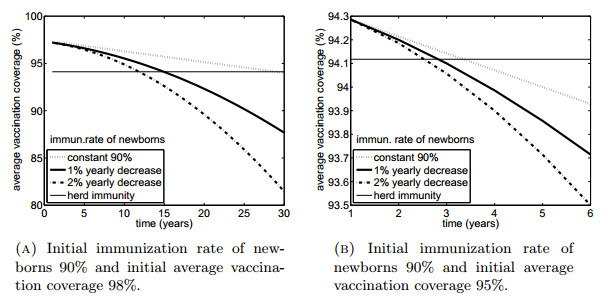
In the light of the above, the question we need to resolve is whether we should worry about the decline in the vaccination rates and coverage. For how long can the past high immunization rates of newborns save us from the future measles outbreaks? Naturally, it all mainly depends on the future dynamics of the immunization rate of newborns. In order to illustrate the problem, we have proposed three potential situations, which are depicted on Figure 2.
The three curves represent temporal dynamics of the average vaccination coverage under three different scenarios, the horizontal grey line depicts the critical vaccination coverage needed to achieve herd immunity. In Figure 2a the initial immunization rate of newborns is assumed to be 90% and the initial average vaccination coverage is 98%. This setup corresponds to the current situation in the Bratislava region. Under the first scenario, the immunization rate of newborns is assumed to stay constant at its initial level 90%. The next two scenarios represent a situation where the immunization rate of newborns declines from its initial level of 90% by 1%, resp. 2% per year. As we can see, it takes from 12 to 28 years to reach the critical boundary. However, if the initial average vaccination coverage were just 95%, the situation would be more critical: as Figure 2b indicates, for the above three scenarios, it would take just 2-4 years to decline below the critical level of vaccination.
The only possible way to get the vaccination coverage back above the critical level appears to be an intervention at the government level. Examples of intervention applied in different countries are summarized e.g. in the study by [15]. The most frequent types are advertisement, education, or law restrictions requiring a proof of vaccination for the school entry.
For the purposes of this study, we have defined intervention in terms of financial or real options terminology as a right but not the obligation to intervene at any time until the end of the planning period. The real options approach can be viewed as an extension of the financial options theory into the investment making process. The standard valuation techniques, such as, for instance, the net present value method (see e.g. [3]), consider a single decision pathway with fixed outcomes only: all decisions are thus prespecified by the expected future revenues path. Moreover, it is assumed that the decision maker follows the original plan irrespectively of changing circumstances. On the other hand, the real options models allow to incorporate flexibility into the model and thus modify business plans taking into account new information. This is particularly important when modeling highly uncertain future outcomes.
In our proposed model setup we assume that the intervention induces costs and results in predetermined increase in immunization rate of newborns in the next period. Our aim is to analyze the cost-effectiveness of intervention and to estimate the moment when it is optimal to intervene. We introduce a real options model, which is a kind of stochastic dynamic problem. It is constructed from the perspective of a policy maker, who faces three types of uncertainties: the stochastic evolution of the future immunization rate of newborns, the random occurrence of an imported measles case and the uncertain outbreak size. Using real options techniques (see e.g. [7], [6]) we determine the level of vaccination coverage at which it is optimal to intervene. A sensitivity analysis shows the importance of early intervention in the population with high initial average vaccination coverage. Furthermore, our numerical results demonstrate that the less certain we are about the future development of the immunization rate of newborns, the more valuable is the option to intervene. To our knowledge, this is the first study analyzing the economic effect of intervention using real options techniques.
During the last two decades many authors attempted to explain human decision-making with respect to vaccination (see e.g.[13]). As the first study within this concept can be probably considered the work [2]. Under the game theory setup authors propose vaccination game and show that it is not possible to eradicate a disease under voluntary vaccination scheme. A number of studies has followed to extend this result. The work [8], resp. [4] seems to be the most relevant to our study. The authors introduce various models of the vaccination behavior dynamics and discuss the impact of information dependence function on the resulting vaccination coverage. In this paper we adopt a different approach: we try to extend the existing studies by establishing a model under the presence of uncertainty in the vaccination behavior. Our assumption reflects the possibility that behavior of a part of parents does not present any rational pattern and therefore cannot be explained by any deterministic model. Furthermore, stochastic setup enables us to study the role of uncertainty in the planning vaccination interventions.
The paper is organized as follows. We first introduce the newly developed real options model, which constitutes a flexible evidence-based dynamic decision making tool. We then present the results of simulations. As a benchmark case, we analyze the model without intervention. In the next step we compare the expected costs with and without the intervention, and thus calculate the value of the option to intervene. We conclude with the most relevant observations following from this modelling exercise.
2. The model
The aim of the policy maker is to minimize the expected costs associated with a measles outbreak during the fixed time period of length T. His/her decision is driven by three types of uncertainties: stochastic evolution of future immunization rate of newborns, random occurrence of imported measles case and uncertain outbreak size. A natural way to describe the stochastic optimization problem is to formulate it via the following Bellman equation:
|
V(t,xt,Xt)=minut{utP+11+rE(˜V(t+1,xt+1,Xt+1|t,xt,Xt))},
|
(1)
|
for t=0,…,T−1. In Equation 1 the strategy costs are represented by the value function V(.) of three state variables: time t, the immunization rate of newborns xt and the average vaccination coverage Xt. For the purpose of this study, the immunization rate of newborns refers to the percentage of vaccinated children born in the same year whereas the average vaccination coverage refers to the average of vaccination rates over all the age cohorts. The symbol E(.|t,.) stands for the conditional expected value operator as seen at the time t, P denotes the amount invested in intervention and r represents the discount rate. The function ˜V(.) is the expectation of the value function V(.) over the random event (see definition in the text below).
The minimization procedure chooses either to intervene (ut=1) or not (ut=0), depending on which action minimizes the sum of the intervention costs plus the discounted expected value of continuation (future) costs. The expected future costs depend on the action chosen, on the uncertain future development of the immunization rate of newborns and on the random occurrence of imported measles cases. More formally, the expected future costs can be expressed as the weighted costs during outbreak plus the expected costs without outbreak occurrence as follows:
|
E(˜V(t+1,xt+1,Xt+1|t,xt,Xt))=pepi(c0E(It|Xt)+E(V(t+1,xmax,Xmax|t,xt,Xt)))+(1−pepi)E(V(t+1,xt+1,Xt+1|t,xt,Xt))
|
(2)
|
In Equation 2 the weight pepi represents the probability of occurrence of an imported measles case. Further, we assume that after the outbreak occurrence, the immunization rate of newborns and the average vaccination coverage reach their maximum values, hereby represented by the variable xmax, resp. Xmax.
The outbreak costs are the product of costs per case c0, and the expected number of cases. We estimate the expected number of cases as a function of the average vaccination coverage using the homogeneous Susceptible-Infected-Recovered (SIR) epidemic model with the constant population size N, transmission rate β and recovery rate γ :
|
dStdt=(1−xt)μN−(βItN+μ)StdItdt=βItNSt−(γ+μ)ItdRtdt=xtμN+γIt−μRt
|
(3)
|
with the initial conditions S0=N−Xt−I0, I0=1, R0=Xt. The resulting function can be described as follows:
|
E(It|Xt)={a0−a1Xt,if Xt<1−1/R00if Xt≥1−1/R0
|
(4)
|
As Equation 4 states, if the average vaccination coverage is below the critical level 1−1/R0 of herd immunity, the dependence of the number of cases on the average vaccination coverage is adequately represented by a linear approximation. For the average vaccination coverage above the critical boundary, the homogeneous SIR model predicts zero incidences. We assume that a1≥0 and that there is continuity at the point Xt=R0.
In order to complete our model specification, we need to describe the dynamics of the state variables. First, we propose that without intervention, the immunization rate of newborns follows Geometric Brownian motion (GBM) process, i.e. the rate xt satisfies the following stochastic differential equation:
where Wt denotes standard Wiener process and α, σ≥0 are assumed to be constant. This assumption has been adopted from the real options theory (see e.g. [7]), but it has an economic interpretation in this case as well. We argue that the decision to vaccinate against measles depends mainly on the country legislation as well as on the primary information parents receive from the health care practitioners rather than on past disease incidence as claimed by e.g. [2], [4]. The latter idea of [2] has been contradicted by, e.g., [5]. Unlike the work presented in [8] which attempts to deterministically model the immunization rate of newborns, we model it as a stochastic proces.
Equation 5 states that the percentage change in the immunization rate of newborns equals the drift term α plus the error term. Although the group of parents making decisions about vaccination changes each year, the global environment (pediatricians, law restrictions) remains the same: the drift term α describes the long-term trend in the incentive to vaccinate as a result of the country vaccination program, while the stochastic term σdWt, represents the random fluctuations which induce uncertainty in vaccination coverage, such as the increasing activity of the anti-vaccination lobby or the measles outbreak in Berlin.
For the modeling purposes, we have used the discretized version of the process 6. We denote the size of the time step by Δt. Uncertainty is now presented by the term εt∼N(0,1), where εt are i.i.d (for more details see derivation in e.g. [11]). Further, we assume that after the intervention has taken place, the immunization rate of newborns in the following time period jumps up from the current level by an amount determined by the function g(.). Our assumptions can be formally stated as follows:
|
xt+1={xt+αxtΔt+σxtεt√Δt if ut=0xt+g(xt) if ut=1
|
(6)
|
Several properties are required for a function g(.) and any xt∈[0,1] in order to represent the jump:
1. xt+g(xt)≤1: the immunization rate of newborns in the next period cannot exceed 100%,
2. g′(xt)≤0: the higher the current immunization rate of newborns, the harder it is to motivate the remaining parents to vaccinate, i.e. the smaller the jump size,
3. g″(xt)≥0: the effect of the increase of vaccinated children induced by the intervention is smaller for the higher immunization rate of newborns.
The above mentioned properties must hold for any 0≤xt≤1 and for all 0≤t≤T. In the numerical analysis we take g(x)=1.5(e−x−e−1). It can be easily verified that this function fulfills all the proposed properties.
The dynamics of the average vaccination coverage is described as follows:
where n denotes the number of the considered age cohorts, and xDt represents the immunization rate of the oldest age cohort1 at time t. Equation 7 has been derived under the assumption that the population can be divided into n equally-sized cohorts. In the numerical analysis, we set n=70. Further, we assume that at the initial time the immunology status of each age cohort is known. These assumptions enable us to reduce the number of state variables.
1We should remark here that the oldest cohorts have not been vaccinated but they are immune thanks to recovery from the natural infection.
3. Model inputs
In terms of the numerical analysis, we perform a case study motivated by the current epidemiological situation in Slovakia as described in Section 1. We chose the Bratislava region as the study area because its decline in the immunization rate of newborns is the most significant in recent years. The region has approximately 400000 inhabitants. In all the simulations the length of the studied time period is set to 20 years. Further parameters represent measles characteristics; the reproduction number, the rate of recovery, and the rate of transmission have all been taken from the literature (see e.g. [17]). In order to simplify the calculations, in our model the birth rate equals the death rate. The parameters of the expected cost curve are fitted by the least squares method in accordance with the homogeneous SIR model (3). The costs per measles case have been determined as an average of direct and indirect costs associated with the disease and potential complications according to the Slovak social and health care system. The value has been taken from the study by [10] and adjusted for inflation. The range of values of intervention costs has been selected subjectively. Parameters of the GBM process have been estimated using historical data on immunization rate of newborns in Europe ([19]). Probability of the occurrence of an imported measles case in Slovakia should be seen as a rough estimate based on historical records from the last 13 years (Source: [19]). Values of all input parameters are summarized in Table 1.
Table 1. Model inputs.
| Time horizon |
T=20 years |
| Population size |
N=400000 |
| Reproduction number |
R0=17 |
| Recovery rate |
γ=0.1 |
| Birth/death rate |
μ=0.01 |
| Expected cases |
a0=0.9789N, a1=1.04 |
| Costs per measles case |
c0=600€ |
| Intervention costs |
P∈⟨0,500000⟩€ |
| Probability of potential outbreak |
pepi=0.1 |
| Drift term of immunization rate of newborns |
α=0.0076 |
| Volatility of immunization rate of newborns |
σ=0.057 |
| Discount rate |
r=1% |
4. Numerical results
Solving the problem formulated in Section 2 requires implementation of a dynamic programming algorithm moving backwards with respect to decision time points. The crucial point is the computation of the conditional expected value. Several techniques can be applied; we have adopted the basic and the most popular one, known as the binomial lattice (see e.g. [11]). The basic idea of this approach is a discrete time approximation of the underlying stochastic process Y. We assume that during each time interval the process Y jumps either up to uY or down to dY. Probability of the moving up is assumed to be pup. The resulting structure is a recombining binomial tree: this fact is important when considering algorithmic aspects. The values of u, d and pup are chosen in such a way that they match the mean and the volatility of Y. More details can be found e.g. in [11].
In order to determine the cost efficiency of intervention, we have performed several numerical experiments. As a basic case, we have analyzed the model without intervention. We have simulated stochastic development of the immunization rate of newborns until the first occurrence of an imported measles case, which happens with exogenously given probability pepi. For each such simulation, we have evaluated the total costs, the number of cases and the vaccination rate at outbreak. Since occurrence of an imported case is random, in order to compare the costs from periods of unequal length, we have expressed the costs in terms of the so called equivalent annual cost (EAC), which can be calculated using the following formula (see e.g. [3]):
Symbol NPV in Formula 8 represents the net present value of the total costs during the period of the length K, i.e. NPV=∑Ki=0Ci(1+r)i. Factor EAC equals to:
|
EAC factor=1−(11+r)Kr,
|
(9)
|
where K stays for the time of outbreak and r denotes the discount rate.
4.1. Case without intervention
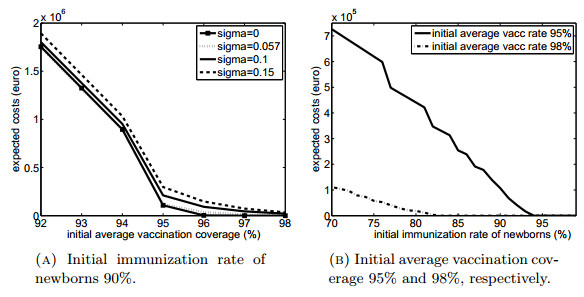
Figure 3a summarizes results for the case without intervention and the initial immunization rate of newborns 90%. The x-axis represents the initial average vaccination coverage; the y-axis depicts expected costs expressed in terms of EAC. The depicted curves differ in the level of uncertainty of the immunization rate of newborns development. The value σ=0.057 corresponds to an estimate from historical data.
Naturally, as the initial average vaccination coverage increases, expected costs decline. However, it is important to realize that this curve declines quite sharply: a decrease of 3% below critical boundary needed to achieve herd immunity in the initial average vaccination coverage increases the cost by almost 1.8mil. per year. Figure 3a further shows how uncertainty of immunization rate of newborns influences the expected costs curve. As we can see, the 15% increase in volatility has no significant impact on the resulting expected costs.
The results of the sensitivity analysis on the initial immunization rate of newborns are presented in Figure 3b. The dashed curve represents the situation when the initial average vaccination coverage is 95% and the solid line represents the case when the initial average vaccination coverage is 98%. As we can see, the high initial average vaccination coverage ensures lower costs. When the initial average vaccination coverage is 98%, the immunization rate of newborns above 82% results in the prediction of zero costs during the next 20 years period, while for the initial average vaccination coverage of 95%, the immunization rate of newborns of at least 94% is needed to ensure zero outbreak costs for the planning period.
4.2. Model with intervention
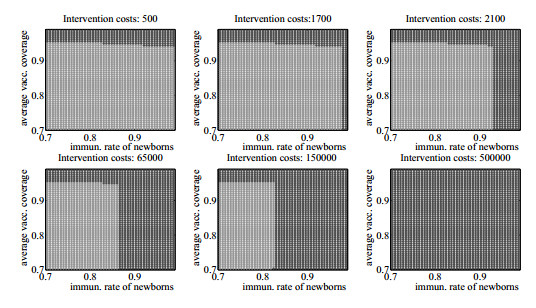
In this section we explore the model incorporating intervention options. In the first step of calculation, the so called decision tool is created. It means that for each combination of state variables we determine whether it is optimal to intervene or not. Figure 4 shows the typical shape of decision diagrams under the stochastic immunization rate of newborns.
On all subfigures, the x-axis corresponds to the immunization rate of newborns, and the average vaccination coverage is shown on the y-axis. The optimality of intervention and non-intervention are reflected by the black and grey areas respectively. The details depend on the exact intervention costs. However, based on the diagrams, several general conclusions can be drawn. If costs are very low, it is optimal to intervene at any level of immunization rate of newborns. On the other hand, if the costs are very high, it is optimal not to intervene at any combination of state variables. Between 500€ and 500000€, the major determinant of the optimal decision is the immunization rate of newborns, although the average vaccination coverage does influence the decision to a certain extent.
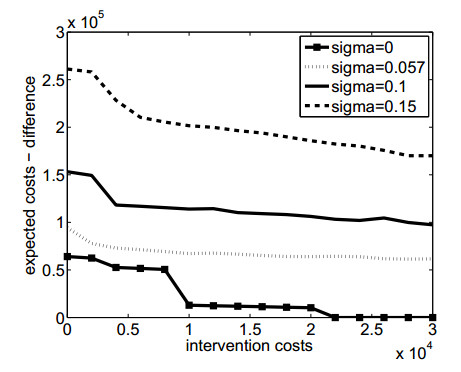
As a further step we have run 100000 simulations and compared the expected costs with and without the intervention, thus producing an estimate for the value of the option to intervene. Figure 5 shows the sensitivity of the option value to the two model parameters: the level of the intervention costs P and the volatility in the immunization rate of newborns σ.
The first observation is rather expected: higher intervention costs decrease costs-effectiveness of an intervention. However, the value of intervention option tends to decrease rather slowly. E.g., the option becomes cost-less for the intervention costs of approx. 2.2×104 under the assumption of constant immunization rate of newborns and for the intervention costs approx. 5×105 for σ=0.057.
Further, the simulations show that under our model setup, an increase in the volatility of the immunization rate of newborns implies an increase in the intervention option value. For the considered range of the intervention costs, the highest considered volatility (σ=0.15) increases the option value approx. two times compared to the case of estimated value (σ=0.057). Moreover, the level of uncertainty has a larger and more significant impact on the option value than the costs invested to intervention.
Table 2a summarizes the estimated percentage of annual savings induced by the intervention. For the initial average vaccination coverage 92% and the initial immunization rate of newborns 90%, the percentage of savings induced by the intervention stays at the same level irrespective of intervention costs. A more significant decline can be observed for low levels of intervention costs only.
Table 2. Savings induced by intervention.
| intervention costs(in thousands of €) |
savings in exp. costs |
|
inital average vacc coverage |
savings in expected costs |
|
| 0 |
8.8% | |
92% |
2.3% |
| 2 |
6.7% | |
93% |
2.9% |
| 4 |
4.0% | |
94% |
4.4% |
| 8 |
3.5% | |
95% |
55.9% |
| 10 |
2.3% | |
96% |
72.5% |
| 20 |
2.0% | |
97% |
78.6% |
| 30 |
1.8% | |
98% |
79.9% |
| (A) Initial immunization rate of newborns 90%, initial average vaccination coverage 92%, σ=0.057. |
|
(B) Initial immunization rate of newborns 90%, initial coverage 10000€, σ=0.057. |
However, these results are highly sensitive to the level of the initial average vaccination coverage. As Table 2b shows, if the initial average vaccination coverage is below the critical level needed to achieve herd immunity, the savings in expected costs induced by intervention reach only around 3%. However, if the initial level of the average vaccination coverage is above or slightly below the critical vaccination coverage needed to achieve herd immunity, the percentage of savings induced by the intervention exceeds 50%.
In Table 3 we present the expected time of the first intervention together with the expected number of interventions during the 20 years planning period. Given intervention costs of P=10000€, the initial average vaccination coverage 95% and σ=0.057, the expected time of the first intervention varies from 6 to 10 years. Not surprisingly, the earliest intervention is observed for the lowest initial immunization rate of newborns. Sensitivity analysis shows that the lower initial immunization rate of newborns is, the earlier it is optimal to intervene. The expected number of interventions is not significantly affected by the level of the initial immunization rate of newborns: during the planning period of 20 years it is optimal to intervene three times on average.
Table 3. Expected time of first intervention and the expected number of interventions. Intervention costs P=10000€, initial average vaccination coverage ˉx=95% and σ=0.057.
| Initial immunization rate of newborns |
Time of first intervention |
Number of interventionss |
| expected |
s.e. |
expected |
s.e. |
|
| 90% |
6.87 |
3.79 |
3.48 |
3.05 |
| 91% |
6.89 |
3.86 |
3.20 |
2.79 |
| 92% |
7.92 |
4.26 |
3.36 |
2.81 |
| 93% |
7.92 |
4.34 |
3.10 |
2.68 |
| 94% |
7.96 |
4.44 |
2.89 |
2.51 |
| 95% |
9.19 |
4.13 |
3.19 |
2.71 |
5. Conclusions
This study provides a detailed valuation analysis of cost effectiveness of an intervention aimed to improve the immunization rates of newborns. The impetus comes from the policy makers in Slovakia who are facing decline of the parents' willingness to vaccinate against measles in all regions. However, since a corresponding decline can be observed worldwide the conclusions are of general interest.
We have introduced a decision model assuming that a policy maker faces uncertainty in the future development of the immunization rate of newborns and a random occurrence of imported measles cases. To our knowledge, the presented study is the first attempt to evaluate the option to intervene using real options techniques. This modern valuation approach enables one not just to estimate the value of intervention option but in addition it provides a way to estimate the optimal time to carry out the intervention.
Numerical results indicate the impact of several factors involved in the decision to intervene. We have demonstrated that the value of the option to intervene decreases for high intervention costs. This result is consistent with our expectations since, under the assumptions of the proposed model, the resulting increase in the immunization rate of newborns is independent of the amount invested in intervention. Furthermore, simulations show the importance of early intervention in the population with a long history of high immunization rate of newborns, e.g. with high initial average vaccination coverage. Intervention directed to improve immunization rate of newborns is more cost effective if the average vaccination coverage remains close to the critical boundary needed to achieve herd immunity. Once the average vaccination coverage falls far below the critical boundary, interventions of this type might not be sufficiently efficient due to a long time period needed for generation-based shift. Another significant role in determination of cost-effectiveness of intervention is played by the level of volatility of the underlying stochastic process. Our results illustrate that the less certain we are about the future development of the immunization rate of newborns the more valuable is the option to intervene. Of course, this is the consequence of the proposed model setup: due to the Markov property of GBM intervention helps not just increase but also stabilize immunization rate of newborns to certain extent.
The presented real options model can be extended in several directions. First of all, the specification of the stochastic model for immunization rate of newborns can be modified: In our study the willingness to vaccinate was modeled via a random variable. According to the real options techniques, we have selected GBM as the first natural candidate. However, one can perform a detailed statistical analysis based on the large data set on historical immunization rates in different countries provided by WHO and thus propose a more sophisticated model. The sensitivity of the option value with respect to the model chosen is another interesting aspect. Another subject to modification is the model of the number of expected cases. In our work, this estimation has been based on the assumption of homogeneous population. However, in reality this is rarely the case: typically, the unvaccinated individuals are members of a single local community (the role of the heterogeneous setup is highlighted e.g in [1]). Examples include religious groups, kindergartens or schools which do not require children to be vaccinated in order to be accepted. In the case of a heterogeneous population, micro-level aspects should also be taken into account. The model, presented in this paper, can be modified for this case. For instance, in the case of a kindergarten, age categories can be modeled as state variables. Another natural extension is to analyze the option value under the assumption of an uncertain effect of intervention. This would cover the case of interventions relying on advertisement and education rather than law or other penalty establishment. Finally, the recent large scale European immigration may increase the likelihood of the occurrence of measles cases in particular countries and change the epidemiological dynamics in general. This fact makes the development of a flexible evidence-based dynamic decision making tools even more urgent.
Acknowledgments
This study was partly supported by Slovak Grant Agency APVV-0096-12.
The author is partly supported by Slovak Grant Agency APVV-0096-12









 DownLoad:
DownLoad: