TODIM method with unknown weights under t-arbicular fuzzy environment for optimal gate security system selection

1.   Introduction

In practice, as systems grow increasingly complex, decision-making experts (DMEs) often face heightened difficulty in identifying the optimal choice from a set of feasible alternatives. While achieving a single objective can be challenging, it remains within reach. Organizations frequently grapple with intricate goals involving employee motivation, achievement, and the development of shared perspectives. Consequently, organizational decisions—whether made by individuals or groups—typically involve multiple concurrent objectives. Each DME strives to derive the most suitable solution, ideally aligning with specific practical needs in real-world scenarios. This ongoing pursuit of more practical and reliable methods for decision-making has fostered an interest in developing approaches grounded in realistic, adaptable methodologies ^[1,2,3,4].

One prominent tool in this field is multi-criteria group decision-making (MCGDM), a structured process that supports DMEs in selecting the most viable option from a limited set by leveraging expert judgment. To address the complexity inherent in such decision-making contexts, Zadeh ^[5] introduced the foundational concept of the fuzzy set (FS), a mathematical framework designed to capture uncertainty. Later, Atanassov ^[6] expanded upon FS, developing intuitionistic fuzzy sets (IFS), which incorporate both membership and non-membership functions to represent uncertainty. IFSs have since been widely applied to resolve complex decision problems, although they occasionally fall short in situations requiring nuanced human responses. For instance, in voting contexts, individuals may express preferences not only as "yes" or "no" but also as "uncertain" or "abstain", responses that traditional FS and IFS frameworks do not fully capture. To address these limitations, Cuong ^[7,8] introduced the picture fuzzy set (PFS), a more flexible model capable of accommodating this expanded range of responses.

In practical scenarios, there are limitations to the application of PFS, especially in cases where the sum of the three degrees—membership (a), neutral (b), and non-membership (c)—exceeds 1, that is $a + b + c > 1$. In such instances, PFS struggles to yield an adequate solution. To address this, researchers in ^[9,10] independently introduced the concept of spherical FS (SFS), relaxing the constraint in PFS by setting $a^2+b^2+c^2\leq 1$. Later, Mahmood et al. ^[11] expanded upon SFS by proposing t-spherical FS (t-SFS), which further relaxed the condition to $a^t+b^t+c^t\leq 1$, where $t$ is any natural number, thereby allowing for greater uncertainty and surpassing traditional fuzzy frameworks in flexibility. Subsequent research has developed some aggregation operators (AOs) for t-SFS to advance MCGDM. Munir et al. ^[12] created Einstein hybrid AOs for t-SFS with applications to MCGDM, while Zeng et al. ^[13] defined Einstein interactive AOs for photovoltaic cell selection. Liu et al. ^[14] proposed novel power Muirhead mean AOs for t-SFS, and Ullah et al. ^[15] introduced the t-spherical (t-SF) Hamacher AOs within an MCDM context. Additionally, Khan et al. ^[16] explored the Schweizer-Sklar power Heronian mean AOs for t-SFS. Mahnaz et al. ^[17] further contributed by developing a set of t-SF-based Frank AOs. Similarly, Ju et al. ^[18] proposed various t-SF interaction AOs, integrating them with the tomada de decisao interativa multicriterio (TODIM) approach to construct an MCGDM model. Acknowledging the significance of input argument prioritization, Mahmood et al. ^[19] explored geometric and averaging AOs founded on t-SF Dombi operational rules. Munir et al. ^[20] introduced immediate probability interactive geometric AOs tailored for TSFS. Additionally, Khan et al. ^[16] proposed a family of power Heronian operators based on t-SF Schweizer-Sklar operational rules, which were subsequently applied to water reuse evaluation. Javed et al. ^[21] described t-SFS that incorporate neutral characteristics and proposed a series of AOs designed to account for these neutral features. Further advancements in t-SF MCGDM methodologies are available in ^{[22,23,24,25]}.

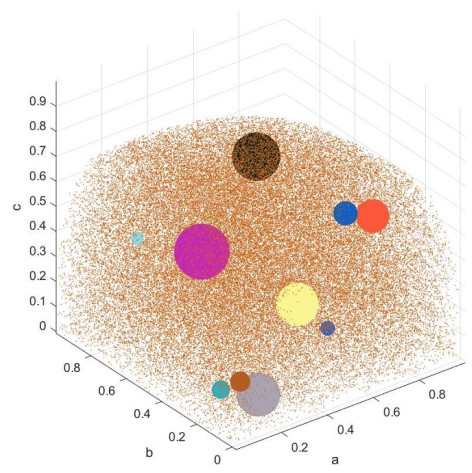
In recent advancements, the t-SF framework has offered DMEs a more versatile tool for assigning degrees of membership, neutrality, and non-membership. The t-SFS thus provides a broader, more adaptive range than traditional IFS, PFS, and SFS ^[20,26]. However, when dealing with high levels of uncertainty, assigning precise triplet values within the closed interval [0, 1] (see Figure 1) can be challenging. These approaches, while rigorous, require DMEs to pinpoint exact numerical values, potentially limiting flexibility in uncertain contexts. To address this limitation, interval-valued t-SFSs ^[27] have been developed, allowing for the assignment of interval values to membership, neutrality, and non-membership degrees. While this provides greater flexibility, managing interval-based representations can still be complex. This paper introduces the t-arbicular FS (t-AFS) as a refined extension of t-SFSs. The proposed t-arbicular fuzzy (t-AF) model, illustrated in Figure 2, employs solid spheres as an intuitive and robust representation mechanism. In this novel framework, an element's degrees of membership, neutrality, and non-membership are represented by solid spheres centered at points $(a, b, c)$ with a radius $r$. The flexible constraint $0 \leq a^t+b^t+c^t\leq 1$ governs the set's boundaries, where the radius $r$ encapsulates the imprecision around the point $(a, b, c)$. This structure effectively expands the t-SF model, which, in the case where $r = 0$, reduces to the standard t-SFS. With this new approach, DMEs can address complex decision-making scenarios by creating solid spheres that reflect a range of possibilities rather than relying on exact numerical values. The introduction of t-AFS enhances both sensitivity and adaptability in decision-making processes, allowing DMEs to handle higher levels of uncertainty with greater ease and accuracy. By enabling the construction of solid spheres with specific attributes, this model supports a more nuanced, flexible approach to managing intricate and uncertain decision-making environments. To further illustrate the necessity of the proposed t-AFS model, consider a real-world scenario involving matrimonial decision-making. In such cases, evaluators often assess not only the potential spouse's individual traits but also the characteristics and history of their family. While the individual's information may be captured using traditional single-point models such as t-SFS, the broader family dynamics—reflecting the cultural, behavioral, and social compatibility—require a more expansive representation. The t-AF framework, by introducing a radius around the central point $(a, b, c)$, effectively models this extended uncertainty domain, enabling decision-makers to incorporate a broader context and capture nuanced preferences that cannot be conveyed using strict point-based methods. A similar situation arises in high-stakes recruitment, such as selecting personnel for aviation security or nuclear facility management. In these cases, evaluators assess not only the candidate's skills and background but also uncertainty surrounding factors like emotional stability, stress response, and potential future adaptability—areas that may not be quantifiable through precise, static assessments. The t-AF framework accommodates such ambiguity by allowing DMEs to assign a solid sphere of values around the candidate's evaluation point. This flexibility supports a more realistic representation of imprecise or indirect knowledge, making the model particularly useful for complex, risk-sensitive decisions.

The TODIM method, initially proposed by Gomes and Lima ^[28], is an outranking technique designed to assist in decision-making by leveraging prospect theory's value function. By modeling the psychological behavior of DMEs, TODIM establishes a relative advantage function that compares each alternative against others, ultimately selecting the most favorable option based on the degree of dominance ^[28]. Over time, TODIM has undergone significant refinement and has become widely adopted across various decision-making domains. Numerous extensions and adaptations of TODIM have been developed to meet the needs of complex decision environments. For instance, Pramanik and Mallick ^[29] applied TODIM to MCGDM problems within a trapezoidal neutrosophic number framework. Other adaptations by Pramanik et al. ^[30,31] involved creating TODIM methods in neutrosophic cubic and bipolar neutrosophic settings. Yin and Liu ^[32] introduced an enhanced Cloud-TODIM approach by integrating the TODIM method with the Cloud model to assess risk levels in a photovoltaic energy storage utilization project in China. Further extensions include the work of Liu et al. ^[33], who proposed a type-2 fuzzy set adaptation to replace traditional quality function deployment, and Liao et al. ^[34], who incorporated cumulative prospect theory into TODIM for probabilistic hesitant fuzzy sets. Zhao et al. ^[35] extended the TODIM model by integrating cumulative prospect theory and entropy weighting within a Pythagorean fuzzy framework, enhancing the rational assessment of criteria weights. Additionally, Su et al. ^[36] leveraged prospect theory within TODIM to rank alternatives while incorporating DMEs' psychological perspectives under specific contexts. This evolving method has shown great versatility, though its further integration with criteria-weighting methods remains essential for optimizing performance across different decision-making scenarios.

Based on the aforementioned research analysis, this paper introduces a novel extension of t-spherical fuzzy sets along with its corresponding technique to address complex MCGDM problems. The primary motivations for this research are as follows:

1). FS theory and its extensions have become foundational tools for managing uncertainty in decision-making. Despite their widespread application, most approaches impose stringent conditions on DMEs, restricting them to specific formats and values to ensure preference validity. For example, in circular Pythagorean and disc spherical FSs, the sum of the square of assessment grades cannot exceed 1, while in q-rung orthopair and t-spherical fuzzy sets, DMEs are constrained to single-point values with limited spaces. Such rigid requirements prevent experts from fully expressing nuanced judgments, confining them to a narrow evaluative framework. Addressing these limitations could allow for a more flexible and expressive approach, empowering experts to convey their insights more comprehensively.

2). While numerous studies have examined the impact of criteria weights in MCGDM problems, some existing approaches assign these weights directly. Predetermined weights can significantly influence decision outcomes and may lack the accuracy needed for complex assessments. Consequently, developing a method that enhances both flexibility and consistency in weight determination is essential for the proposed context. Such an approach would enable more precise assessments and ensure consistency, leading to improved reliability in decision-making outcomes.

3). The ranking method used to select an optimal alternative among multiple options plays a crucial role in practical applications, as different MCGDM methods possess unique characteristics suited to specific fields. Importantly, group decision-making should consider DMEs' risk attitudes and psychological behaviors. The TODIM method has proven effective in capturing such psychological aspects, making it valuable for this purpose. Therefore, generalizing the TODIM method to a larger fuzzy set domain can better accommodate decision-makers' risk attitudes and psychological preferences, enhancing the selection process in uncertain environments.

The core contributions and innovative aspects of this paper are as follows:

1). This paper introduces t-AFS as a novel extension of t-SFS, addressing their limitations in uncertainty representation. Unlike t-SFS, which requires precise triplet values, t-AFS enables DMEs to express uncertainty using solid spheres, allowing for greater flexibility and adaptability in uncertain environments. This extension enhances decision-making models by removing the rigid constraints of t-SFS while preserving interpretability and computational efficiency. Furthermore, we establish comparison laws, operational rules, AOs, and distance measures, extending the applicability of t-AFS in fuzzy MCDM scenarios.

2). The existing CRITIC method relies exclusively on t-spherical fuzzy numbers, and its scoring formula only accounts for membership and non-membership grades, neglecting neutral grades ^[37]. We generalize this method by extending it to the t-AF setting and enhance its effectiveness through the utilization of the proposed score formulation. This extension improves the method, thereby enhancing the rationality and reliability of criteria weight information.

3). This study develops the TODIM method within the t-AF environment. Unlike other methods, this approach not only accommodates t-AF data but also captures the risk-averse tendencies of DMEs, leading to a more rational and credible selection of alternatives.

4). To validate the practical advantages of the proposed framework, we present a case study on gate security system selection. This example demonstrates how the t-AFS-based TODIM method effectively handles uncertainty, showcasing its superiority over t-SFS in modeling expert opinions. The results highlight how t-AFS allows DMEs to express preferences with greater flexibility, leading to more robust and reliable decision-making outcomes. Additionally, comparative and sensitivity analyses confirm the stability and effectiveness of the t-AFS model across different parameter settings, reinforcing its applicability to real-world decision-making problems.

The structure of this paper is organized as follows: Section 2 introduces foundational concepts related to T‐SF sets. Section 3 presents the t-AFS framework, including its basic theory, operational laws, and score function. Section 4 provides various aggregation operators and distance measures, along with an analysis of their beneficial properties. Section 5 outlines the step-by-step CRITIC-TODIM methodology for the t-AF context. Section 6 addresses a real-world application of selecting an optimal gate security system, assessing the stability of the proposed approach through experimental analysis. Section 7 demonstrates the effectiveness of the proposed model by comparing it with existing methods. Finally, Section 8 concludes the study.

2.   Prerequisite knowledge

This section reviews t-spherical fuzzy sets and their relevant concepts to lay the groundwork for our subsequent research.

Definition 1. ^[11] Let $X$ be a universal set, then the t-SFS $T$ is characterized by Eq (2.1)

where $a(x)$, $b(x)$, $c(x)$ $\in [0, 1]$ denote the membership, abstinence, and non-membership degrees, respectively. For these degrees, it is necessary to satisfy the condition $a(x)^t+b(x)^t+c(x)^t \leq 1$; $t$ $\geq$ $1, \forall x\in X$. Furthermore, the degree of indeterminacy is determined as $\pi^t(x) = 1-\left(a^t(x)+ b^t(x)+ c^t(x)\right)$. For simplicity, the triplet $T = \langle a, b, c \rangle$ is called t-spherical fuzzy number (t-SFN).

Definition 2. ^[11] Let $T_1 = \langle a_1, b_1, c_1 \rangle$, $T_2 = \langle a_2, b_2, c_2 \rangle$ be t-SFNs and $\hbar > 0$. Then the basic operations on them are described as follows:

● $T_1 \oplus T_2 = \langle \sqrt[t]{a_1^t+a_2^t-a_1^ta_2^t}, b_1b_2, c_1c_2 \rangle;$

● $T_1 \otimes T_2 = \langle a_1a_2, \sqrt[t]{b_1^t+b_2^t-b_1^tb_2^t}, \sqrt[t]{c_1^t+c_2^t-c_1^tc_2^t} \rangle;$

● $\hbar T_1 = \langle \sqrt[t]{1- (1-a_1^t)^{\hbar}}, b_1^{\hbar}, c_1^{\hbar} \rangle;$

● $T^{\hbar}_1 = \langle a_1^{\hbar}, \sqrt[t]{1- (1-b_1^t)^{\hbar}}, \sqrt[t]{1- (1-c_1^t)^{\hbar}} \rangle.$

Definition 3. ^[18] Let $T_1 = \langle a_1, b_1, c_1 \rangle$ be a t-SFN, then its score function $S(T_1)$ and accuracy function $A(T_1)$ are defined as:

To compare any two t-SFNs $T_1 = \langle a_1, b_1, c_1 \rangle$ and $T_2 = \langle a_2, b_2, c_2 \rangle$, the comparison laws are given as follows:

1. If $S(T_1) > S(T_2)$, then $T_1 > T_2$;

2. if $S(T_1) = S(T_2)$, then

ⅰ. If $A(T_1) > A(T_2)$, then $T_1 > T_2$;

ⅱ. if $S(T_1) = S(T_2)$, then $T_1 = T_2$.

Definition 4. ^[38] Let $T_1 = \langle a_1, b_1, c_1 \rangle$ and $T_2 = \langle a_2, b_2, c_2 \rangle$ be two t-SFNs, then the distance measure between them is given by Eq (2.4)

where $p\geq 1$ denotes the distance parameter.

3.   t-arbicular fuzzy set and its basic concepts

Definition 5. Let $X$ be a universal set, then the t-AFS ${\mathcal{A}}$ is defined as follows:

where the components $a(x), b(x), c(x)$ satisfy the constraints $a, b, c \in [0, 1],$ $a^t(x) + b^t(x) + c^t(x)$ $\leq$ $1, \text{ for } t \geq 1,$ and the radius $r(x)$ lies within the range $r \in \left[0, \sqrt[t]{3} \right].$

Here, $A_r(a(x), b(x), c(x))$ represents the uncertainty region, formally defined as $A_r(a(x), b(x), c(x)) =$ $\left\{ (p_1, p_2, p_3) \mid p_1, p_2, p_3 \in [0, 1] \text{ and } \sqrt[t]{(a(x) - p_1)^t + (b(x) - p_2)^t + (c(x) - p_3)^t} \leq r(x) \right\} \cap R,$ where $R$ is the constraint region given by $R = \left\{ (p_1, p_2, p_3) \in [0, 1] \mid p_1^t + p_2^t + p_3^t \leq 1 \right\}.$

The degree of uncertainty associated with an element $x \in X$ is given by $\pi(x)$ $=$ $\left(1 - \left(a^t(x) + b^t(x) + c^t(x) \right) \right)^{1/t}.$ Moreover, the elements of the t-AFS are referred to as t-arbicular fuzzy numbers (t-AFNs) and are denoted by $\mathcal{A} = \langle a, b, c; r \rangle.$

Notice that here, $(a, b, c)$ represents the center of the solid ball, and the intersection with region $R$ is considered because the radius is $\sqrt[t]{3}$, ensuring that it does not exceed the upper bound of the unit interval, i.e., 1.

Definition 6. Let ${\mathcal{A}}_{1} = \langle a_1, b_1, c_1;r_{1} \rangle$, ${\mathcal{A}}_{2} = \langle a_2, b_2, c_2;r_{2} \rangle$ be t-AFNs, with $\hbar > 0$ and ${\downharpoonleft\upharpoonright} \in \left\{ \min, \max\right\}$. Then the basic operations on them are described as follows:

1. ${\mathcal{A}}_{1}\oplus {\mathcal{A}}_{2} = \langle \sqrt[t]{a^t_{1}+a^t_{2}-a^t_{1}a^t_{2}}, {b}_{1}{b}_{2}, c_{1}c_{2}; {\downharpoonleft\upharpoonright} \left\{r_{1}, r_{2} \right\} \rangle;$

2. ${\mathcal{A}}_{1}\otimes {\mathcal{A}}_{2} = \langle a_{1}a_{2}, \sqrt[t]{{b}^t_{1}+{b}^t_{2}-{b}^t_{1}{b}^t_{2}}, \sqrt[t]{{c}^t_{1}+{c}^t_{2}-{c}^t_{1}{c}^t_{2}}; {\downharpoonleft\upharpoonright} \left\{r_{1}, r_{2} \right\} \rangle;$

3. $\hbar {\mathcal{A}}_{1} = \langle \sqrt[t]{1-\left(1-a^{t}_{1} \right)^{\hbar}}, {b}^{\hbar}_{1}, c^{\hbar}_{1};r_{1} \rangle;$

4. ${\mathcal{A}}^{\hbar}_{1} = \langle a^{\hbar}_{1}, \sqrt[t]{1-\left(1-b^{t}_{1} \right)^{\hbar}}, \sqrt[t]{1-\left(1-c^{t}_{1} \right)^{\hbar}}; r_{1} \rangle;$

5. ${\mathcal{A}}^{c}_{1} = \langle {b}_{1}, c_{1}, a_{1};r_{1} \rangle,$

where ${\mathcal{A}}^{c}_{1}$ marks the complement of ${\mathcal{A}}_{1}$.

Remark 1. In this article, we adopt the maximum operator for the radius component, i.e., ${\downharpoonleft\upharpoonright} = \max$, throughout all definitions and subsequent computations. However, it is worth noting that the minimum operator can also be employed, depending on the DME's preference for conservative or optimistic evaluations.

Theorem 1. Let ${\mathcal{A}}_{1} = \langle a_1, b_1, c_1;r_{1} \rangle$, ${\mathcal{A}}_{2} = \langle a_2, b_2, c_2;r_{2} \rangle$ be t-AFNs, with $\hbar_1, \hbar_2 > 0$, then

1. ${\mathcal{A}}_{1} \oplus {\mathcal{A}}_{2} = {\mathcal{A}}_{2} \oplus {\mathcal{A}}_{1}$;

2. ${\mathcal{A}}_{1} \otimes {\mathcal{A}}_{2} = {\mathcal{A}}_{2} \otimes {\mathcal{A}}_{1}$;

3. $\hbar_1 \left({\mathcal{A}}_{1} \oplus {\mathcal{A}}_{2}\right) = \hbar_1{\mathcal{A}}_{1} \oplus \hbar_1 {\mathcal{A}}_{2}$;

4. $\hbar_1 {\mathcal{A}}_{1} \oplus \hbar_2 {\mathcal{A}}_{1} = \left(\hbar_1+\hbar_2\right){\mathcal{A}}_{1}$;

5. ${\mathcal{A}}_{1}^{\hbar_1} \otimes {\mathcal{A}}_{2}^{\hbar_1} = \left({\mathcal{A}}_{1} \otimes {\mathcal{A}}_{2}\right)^{\hbar_1}$;

6. ${\mathcal{A}}_{1}^{\hbar_1} \otimes {\mathcal{A}}_{1}^{\hbar_2} = {\mathcal{A}}^{\left(\hbar_1+\hbar_2\right)}_{1}$.

Proof. 1. ${\mathcal{A}}_{1} \oplus {\mathcal{A}}_{2} = \langle \sqrt[t]{a^t_{1}+a^t_{2}-a^t_{1}a^t_{2}}, {b}_{1}{b}_{2}, c_{1}c_{2}; {\downharpoonleft\upharpoonright} \left\{r_{1}, r_{2} \right\} \rangle = \langle \sqrt[t]{a^t_{2}+a^t_{1}-a^t_{2}a^t_{1}}, {b}_{2}{b}_{1}, c_{2}c_{1}; {\downharpoonleft\upharpoonright} \left\{r_{2}, r_{1} \right\} \rangle$ $= {\mathcal{A}}_{2} \oplus {\mathcal{A}}_{1}.$

2. Similar to 1.

3. $\hbar_1 \left({\mathcal{A}}_{1} \oplus {\mathcal{A}}_{2}\right) = \hbar_1 \langle \sqrt[t]{a^t_{1}+a^t_{2}-a^t_{1}a^t_{2}}, {b}_{1}{b}_{2}, c_{1}c_{2}; {\downharpoonleft\upharpoonright} \left\{r_{1}, r_{2} \right\} \rangle =$ $\langle \sqrt[t]{1-(1- (a^t_{1}+a^t_{2}-a^t_{1}a^t_{2}))^{\hbar_1}}, {b}^{t}_{1}{b}^{t}_{2}, c^{t}_{1}c^{t}_{2}; {\downharpoonleft\upharpoonright} \left\{r_{1}, r_{2} \right\} \rangle$.

Now $\hbar_1 {\mathcal{A}}_{1}\oplus \hbar_1 {\mathcal{A}}_{2} = \langle \sqrt[t]{1-\left(1-a^{t}_{1} \right)^{\hbar_1}}, {b}^{\hbar_1}_{1}, c^{\hbar_1}_{1};r_{1} \rangle \oplus \langle \sqrt[t]{1-\left(1-a^{t}_{2} \right)^{\hbar_1}}, {b}^{\hbar_1}_{2}, c^{\hbar_1}_{2};r_{2} \rangle =$ $\langle \sqrt[t]{1-(1- (a^t_{1}+a^t_{2}-a^t_{1}a^t_{2}))^{\hbar_1}}, {b}^{t}_{1}{b}^{t}_{2}, c^{t}_{1}c^{t}_{2}; {\downharpoonleft\upharpoonright} \left\{r_{1}, r_{2} \right\} \rangle$. Hence, proved.

4. Similar to 3.

5. ${\mathcal{A}}_{1}^{\hbar_1} \otimes {\mathcal{A}}_{2}^{\hbar_1} = \langle a^{\hbar_1}_{1}, {b}_{1}^{\hbar_1}, \sqrt[t]{1-\left(1-c^{t}_{1} \right)^{\hbar_1}}; r_{1} \rangle \otimes \langle a^{\hbar_1}_{2}, {b}_{2}^{\hbar_1}, \sqrt[t]{1-\left(1-c^{t}_{2} \right)^{\hbar_1}}; r_{2} \rangle =$ $\langle a^{\hbar_1}_{1}a^{\hbar_1}_{2}, \sqrt[t]{1-(1- (b^t_{1}+b^t_{2}-b^t_{1}b^t_{2}))^{\hbar_1}}, \sqrt[t]{1-(1- (c^t_{1}+c^t_{2}-c^t_{1}c^t_{2}))^{\hbar_1}}; {\downharpoonleft\upharpoonright} \left\{r_{1}, r_{2} \right\} \rangle.$

Now $\left({\mathcal{A}}_{1} \otimes {\mathcal{A}}_{2}\right)^{\hbar_1} = \langle a_{1}a_{2}, \sqrt[t]{{b}^t_{1}+{b}^t_{2}-{b}^t_{1}{b}^t_{2}}, \sqrt[t]{{c}^t_{1}+{c}^t_{2}-{c}^t_{1}{c}^t_{2}}; {\downharpoonleft\upharpoonright} \left\{r_{1}, r_{2} \right\} \rangle^{\hbar_1} =$ $\langle a^{\hbar_1}_{1}a^{\hbar_1}_{2}, \sqrt[t]{1-(1- (b^t_{1}+b^t_{2}-b^t_{1}b^t_{2}))^{\hbar_1}}, \sqrt[t]{1-(1- (c^t_{1}+c^t_{2}-c^t_{1}c^t_{2}))^{\hbar_1}}; {\downharpoonleft\upharpoonright} \left\{r_{1}, r_{2} \right\} \rangle.$ Hence, proved.

6. Similar to 5. □

Definition 7. Let ${\mathcal{A}}_{1} = \langle a_1, b_1, c_1;r_{1} \rangle$ be a t-AFN, then the score function is given by

where $S\left({\mathcal{A}}_1\right) \in \left[0, 1 \right]$. The high value of $S\left({\mathcal{A}}_1 \right)$ implies a greater t-AFN ${\mathcal{A}}_1$.

4.   t-arbicular fuzzy operators and distance measure

4.1.   t-Arbicular fuzzy weighted average operator

Definition 8. For a set of t-AFNs $\left\{{\mathcal{A}}_1, {\mathcal{A}}_2, ..., {\mathcal{A}}_n \right\}$, the t-AF weighted average (t-AFWA) is characterized by Eq (4.1)

where $0\leq \vartheta_{j} \leq 1$ and $\sum\limits_{j = 1}^{n}\vartheta_{j} = 1$.

Theorem 2. The expanded form of the t-AFWA operator defined in Definition 8 is given by Eq (4.2)

Proof. To verify Eq (4.2), we apply the principle of mathematical induction. Taking $n = 2$, we have ${\vartheta_1}{\mathcal{A}}_1 = \langle \left(1-(1-a^t_1)^{\vartheta_1}\right)^{1/t}, b^{t}_1, c^{t}_1;r_1 \rangle$, and ${\vartheta_2}{\mathcal{A}}_2 = \langle \left(1-(1-a^t_2)^{\vartheta_2}\right)^{1/t}, b^{t}_2, c^{t}_2;r_2 \rangle$, we have $t-AFWA \left({\mathcal{A}}_1, {\mathcal{A}}_2\right) = {\vartheta_1}{\mathcal{A}}_1 \oplus {\vartheta_2}{\mathcal{A}}_2 = \langle \left(1-(1-a^t_1)^{\vartheta_1}\right)^{1/t}$, $b^{t}_1, c^{t}_1;r_1 \rangle \oplus \langle \left(1-(1-a^t_2)^{\vartheta_2}\right)^{1/t}$, $b^{t}_2, c^{t}_2;r_2 \rangle = \langle \sqrt[t]{1-\prod\limits_{j = 1}^{2}\left(1- a^t_j \right)^{\vartheta_{j}}}$, $\prod\limits_{j = 1}^{2}b^{\vartheta_j}_j, \prod\limits_{j = 1}^{n}c^{\vartheta_j}_j; {\downharpoonleft\upharpoonright} \left\{r_{1}, r_{2}\right\}\rangle$. So, it holds for $n = 2$.

Assume that Eq (4.2) is true for $n = k$, i.e.,

Next, we check it for $n = k+1$:

$t-AFWA \left({\mathcal{A}}_1, {\mathcal{A}}_2, ..., {\mathcal{A}}_{k+1} \right) = t-AFWA \left({\mathcal{A}}_1, {\mathcal{A}}_2, ..., {\mathcal{A}}_{k} \right) \oplus {\vartheta_{k+1}} {\mathcal{A}}_{k+1}$ $= \langle \sqrt[t]{1-\prod\limits_{j = 1}^{k}\left(1- a^t_j \right)^{\vartheta_{j}}}, \prod\limits_{j = 1}^{k}b^{\vartheta_j}_j, \prod\limits_{j = 1}^{k}c^{\vartheta_j}_j; {\downharpoonleft\upharpoonright} \left\{r_{1}, r_{2}, ..., r_{k}\right\}\rangle \oplus \langle \left(1-(1-a^t_{k+1})^{\vartheta_{k+1}}\right)^{1/t}, b^{t}_{k+1}, c^{t}_{k+1};r_{k+1} \rangle$ $= \langle \sqrt[t]{1-\prod\limits_{j = 1}^{k+1}\left(1- a^t_j \right)^{\vartheta_{j}}}, \prod\limits_{j = 1}^{k+1}b^{\vartheta_j}_j, \prod\limits_{j = 1}^{k+1}c^{\vartheta_j}_j; {\downharpoonleft\upharpoonright} \left\{r_{1}, r_{2}, ..., r_{k+1}\right\}\rangle$.

So, Eq (4.2) is true for $n = k+1$. Hence, Theorem 2 is verified. □

Theorem 3. For a set of t-AFNs $\left\{{\mathcal{A}}_1, {\mathcal{A}}_2, ..., {\mathcal{A}}_n \right\}$, if all ${\mathcal{A}}_j(j = 1, 2, ..., n)$ are equal, i.e., ${\mathcal{A}}_j = \langle a, b, c; r_{} \rangle = {\mathcal{A}}$ $\forall j$. Then, we have

Proof. According to Eq (4.2), we have

Since ${\mathcal{A}}_j = {\mathcal{A}} = \langle a, b, c; r_{} \rangle$ $\forall j$. Therefore, we can write

$t-AFWA \left({\mathcal{A}}_1, {\mathcal{A}}_2, ..., {\mathcal{A}}_n \right) = \langle \sqrt[t]{1-\prod\limits_{j = 1}^{n}\left(1- a^t \right)^{\vartheta_{j}}}, \prod\limits_{j = 1}^{n}b^{\vartheta_j}, \prod\limits_{j = 1}^{n}c^{\vartheta_j}; {\downharpoonleft\upharpoonright} \left\{r_{}, r_{}, ..., r_{}\right\}\rangle =$ $\langle \sqrt[t]{1-\left(1- a^t \right)^{\sum\limits_{j = 1}^{n} \vartheta_{j}}}, b^{\sum\limits_{j = 1}^{n}\vartheta_j}, c^{\sum\limits_{j = 1}^{n}\vartheta_j}; r_{}\rangle = \langle a, b, c; r_{} \rangle = {\mathcal{A}}.$ □

Theorem 4. For any two sets of t-AFNs $\left\{{\mathcal{A}}_1, {\mathcal{A}}_2, ..., {\mathcal{A}}_n \right\}$, and $\left\{\widetilde{{\mathcal{A}}}_1, \widetilde{{\mathcal{A}}}_2, ..., \widetilde{{\mathcal{A}}}_n \right\}$ following the conditions: $a_j\geq \widetilde{a}_j$, $b_j\leq \widetilde{b}_j$, $c_j\leq \widetilde{c}_j$ and $r_{j}\geq \widetilde{r}_j$. Then, we have the following inequality:

Proof. Since $a_j\geq \widetilde{a}_j$, $b_j\leq \widetilde{b}_j$, $c_j\leq \widetilde{c}_j$ and $r_{j}\geq \widetilde{r}_j$, we have

$1-a^t_j\leq 1-\widetilde{a}^t_j$ $\Longrightarrow$ $\sqrt[t]{1-\prod\limits_{j = 1}^{n}\left(1- a^t_j \right)^{\vartheta_{j}}}\geq \sqrt[t]{1-\prod\limits_{j = 1}^{n}\left(1- \widetilde{a}^t_j \right)^{\vartheta_{j}}}$, $\prod\limits_{j = 1}^{n}b^{\vartheta_j}_j \leq \prod\limits_{j = 1}^{n}\widetilde{b}^{\vartheta_j}_j$, $\prod\limits_{j = 1}^{n}c^{\vartheta_j}_j \leq \prod\limits_{j = 1}^{n}\widetilde{c}^{\vartheta_j}_j$, and ${\downharpoonleft\upharpoonright} \left\{r_{1}, r_{2}, ..., r_{n}\right\}\geq {\downharpoonleft\upharpoonright} \left\{\widetilde{r}_{1}, \widetilde{r}_{2}, ..., \widetilde{r}_{n}\right\}$. Using Definition 7, we get $t-AFWA\left({\mathcal{A}}_1, {\mathcal{A}}_2, ..., {\mathcal{A}}_n \right)\geq t-AFWA\left(\widetilde{{\mathcal{A}}}_1, \widetilde{{\mathcal{A}}}_2, ..., \widetilde{{\mathcal{A}}}_n \right).$ □

Theorem 5. For a set of t-AFNs $\left\{{\mathcal{A}}_1, {\mathcal{A}}_2, ..., {\mathcal{A}}_n \right\}$, if ${\mathcal{A}}^{+} = \langle \max\limits_{1\leq j\leq n} a_{j}, \min\limits_{1\leq j\leq n} b_{j}, \min\limits_{1\leq j\leq n} c_{j}, \max\limits_{1\leq j\leq n} r_{j} \rangle$, and ${\mathcal{A}}^{-} = \langle \min\limits_{1\leq j\leq n} a_{j}, \max\limits_{1\leq j\leq n} b_{j}, \max\limits_{1\leq j\leq n} c_{j}, \min\limits_{1\leq j\leq n} r_{j} \rangle$. Then, we have

Proof. In light of Theorems 3 and 4, the proof follows directly. □

4.2.   t-arbicular fuzzy weighted geometric operator

Definition 9. For a set of t-AFNs $\left\{{\mathcal{A}}_1, {\mathcal{A}}_2, ..., {\mathcal{A}}_n \right\}$, the t-AF weighted geometric (t-AFWG) is characterized by Eq (4.6)

where $0\leq \vartheta_{j} \leq 1$ and $\sum\limits_{j = 1}^{n}\vartheta_{j} = 1$.

Theorem 6. The expanded form of t-AFWG operator defined in Definition 9 is given by Eq (4.7)

Proof. To verify Eq (4.7), we apply the principle of mathematical induction. Taking $n = 2$, we have

and ${\mathcal{A}}^{\vartheta_2}_2 = \langle a^{t}_2, \left(1-(1-b^t_2)^{\vartheta_2}\right)^{1/t}, \left(1-(1-c^t_2)^{\vartheta_2}\right)^{1/t}; r_2 \rangle$, we have

$t-AFWG \left({\mathcal{A}}_1, {\mathcal{A}}_2\right) = {\mathcal{A}}^{\vartheta_1}_1 \otimes {\mathcal{A}}^{\vartheta_2}_2$ $= \langle a^{t}_1, \left(1-(1-b^t_1)^{\vartheta_1}\right)^{1/t}, \left(1-(1-c^t_1)^{\vartheta_1}\right)^{1/t}; r_1 \rangle \otimes \langle a^{t}_2, \left(1-(1-b^t_2)^{\vartheta_2}\right)^{1/t}, \left(1-(1-c^t_2)^{\vartheta_2}\right)^{1/t}; r_2 \rangle$ $= \langle \prod\limits_{j = 1}^{2}a^{\vartheta_j}_j, \sqrt[t]{1-\prod\limits_{j = 1}^{2}\left(1- b^t_j \right)^{\vartheta_{j}}}, \sqrt[t]{1-\prod\limits_{j = 1}^{2}\left(1- c^t_j \right)^{\vartheta_{j}}}; {\downharpoonleft\upharpoonright} \left\{r_{1}, r_{2}\right\}\rangle$.

So, it holds for $n = 2$.

Assume that Eq (4.7) is true for $n = k$, i.e.,

$t-AFWG \left({\mathcal{A}}_1, {\mathcal{A}}_2, ..., {\mathcal{A}}_k \right) = \langle \prod\limits_{j = 1}^{k}a^{\vartheta_j}_j, \sqrt[t]{1-\prod\limits_{j = 1}^{k}\left(1- b^t_j \right)^{\vartheta_{j}}}, \sqrt[t]{1-\prod\limits_{j = 1}^{k}\left(1- c^t_j \right)^{\vartheta_{j}}}; {\downharpoonleft\upharpoonright} \left\{r_{1}, r_{2}, ..., r_{k}\right\}\rangle.$

Next, we check it for $n = k+1$:

$t-AFWG \left({\mathcal{A}}_1, {\mathcal{A}}_2, ..., {\mathcal{A}}_{k+1} \right) = t-AFWG \left({\mathcal{A}}_1, {\mathcal{A}}_2, ..., {\mathcal{A}}_{k} \right) \otimes {\mathcal{A}}^{{\vartheta_{k+1}}}_{k+1}$ $= \langle \prod\limits_{j = 1}^{k}a^{\vartheta_j}_j, \sqrt[t]{1-\prod\limits_{j = 1}^{k}\left(1- b^t_j \right)^{\vartheta_{j}}}, \sqrt[t]{1-\prod\limits_{j = 1}^{k}\left(1- c^t_j \right)^{\vartheta_{j}}}; {\downharpoonleft\upharpoonright} \left\{r_{1}, r_{2}, ..., r_{k}\right\}\rangle \otimes$ $\langle a^{t}_{k+1}, \left(1-(1-b^t_{k+1})^{\vartheta_{k+1}}\right)^{1/t}, \left(1-(1-c^t_{k+1})^{\vartheta_{k+1}}\right)^{1/t}; r_{k+1} \rangle$ $= \langle \prod\limits_{j = 1}^{k+1}a^{\vartheta_j}_j, \sqrt[t]{1-\prod\limits_{j = 1}^{k+1}\left(1- b^t_j \right)^{\vartheta_{j}}}, \sqrt[t]{1-\prod\limits_{j = 1}^{k+1}\left(1- c^t_j \right)^{\vartheta_{j}}}; {\downharpoonleft\upharpoonright} \left\{r_{1}, r_{2}, ..., r_{k+1}\right\}\rangle$.

So, Eq (4.7) is true for $n = k+1$. Hence, Theorem 6 is verified.

□

Theorem 7. For a set of t-AFNs $\left\{{\mathcal{A}}_1, {\mathcal{A}}_2, ..., {\mathcal{A}}_n \right\}$, if all ${\mathcal{A}}_j(j = 1, 2, ..., n)$ are equal, i.e., ${\mathcal{A}}_j = \langle a, b, c; r_{} \rangle = {\mathcal{A}}$ $\forall j$. Then, we have

Proof. According to Eq (4.7), we have

$t-AFWG \left({\mathcal{A}}_1, {\mathcal{A}}_2, ..., {\mathcal{A}}_n \right) = \langle \prod\limits_{j = 1}^{n}a^{\vartheta_j}_j, \sqrt[t]{1-\prod\limits_{j = 1}^{n}\left(1- b^t_j \right)^{\vartheta_{j}}}, \sqrt[t]{1-\prod\limits_{j = 1}^{n}\left(1- c^t_j \right)^{\vartheta_{j}}}; {\downharpoonleft\upharpoonright} \left\{r_{1}, r_{2}, ..., r_{n}\right\}\rangle$.

Since ${\mathcal{A}}_j = {\mathcal{A}} = \langle a, b, c; r_{} \rangle$ $\forall j$. Therefore, we can write

$t-AFWG \left({\mathcal{A}}_1, {\mathcal{A}}_2, ..., {\mathcal{A}}_n \right) = \langle \prod\limits_{j = 1}^{n}a^{\vartheta_j}, \sqrt[t]{1-\prod\limits_{j = 1}^{n}\left(1- b^t \right)^{\vartheta_{j}}}, \sqrt[t]{1-\prod\limits_{j = 1}^{n}\left(1- c^t \right)^{\vartheta_{j}}}; {\downharpoonleft\upharpoonright} \left\{r_{}, r_{}, ..., r_{}\right\}\rangle =$ $\langle a^{\sum\limits_{j = 1}^{n}\vartheta_j}, \sqrt[t]{1-\left(1- b^t \right)^{\sum\limits_{j = 1}^{n} \vartheta_{j}}}, \sqrt[t]{1-\left(1- c^t \right)^{\sum\limits_{j = 1}^{n} \vartheta_{j}}}; r_{}\rangle = \langle a, b, c; r_{} \rangle = {\mathcal{A}}.$ □

Theorem 8. For any two sets of t-AFNs $\left\{{\mathcal{A}}_1, {\mathcal{A}}_2, ..., {\mathcal{A}}_n \right\}$, and $\left\{\widetilde{{\mathcal{A}}}_1, \widetilde{{\mathcal{A}}}_2, ..., \widetilde{{\mathcal{A}}}_n \right\}$ following the conditions: $a_j\geq \widetilde{a}_j$, $b_j\leq \widetilde{b}_j$, $c_j\leq \widetilde{c}_j$ and $r_{j}\geq \widetilde{r}_j$. Then, we have the following inequality:

Proof. Since $a_j\geq \widetilde{a}_j$, $b_j\leq \widetilde{b}_j$, $c_j\leq \widetilde{c}_j$ and $r_{j}\geq \widetilde{r}_j$, we have

$\prod\limits_{j = 1}^{n}a^{\vartheta_j}_j \geq \prod\limits_{j = 1}^{n}\widetilde{a}^{\vartheta_j}_j$, $1-b^t_j\geq 1-\widetilde{b}^t_j$ $\Longrightarrow$ $\sqrt[t]{1-\prod\limits_{j = 1}^{n}\left(1- b^t_j \right)^{\vartheta_{j}}}\leq \sqrt[t]{1-\prod\limits_{j = 1}^{n}\left(1- \widetilde{b}^t_j \right)^{\vartheta_{j}}}$, $1-c^t_j\geq 1-\widetilde{c}^t_j$ $\Longrightarrow$ $\sqrt[t]{1-\prod\limits_{j = 1}^{n}\left(1- c^t_j \right)^{\vartheta_{j}}}\leq \sqrt[t]{1-\prod\limits_{j = 1}^{n}\left(1- \widetilde{c}^t_j \right)^{\vartheta_{j}}}$, and ${\downharpoonleft\upharpoonright} \left\{r_{1}, r_{2}, ..., r_{n}\right\}\geq {\downharpoonleft\upharpoonright} \left\{\widetilde{r}_{1}, \widetilde{r}_{2}, ..., \widetilde{r}_{n}\right\}$. Using Definition 7, we get $t-AFWG\left({\mathcal{A}}_1, {\mathcal{A}}_2, ..., {\mathcal{A}}_n \right)\geq t-AFWG\left(\widetilde{{\mathcal{A}}}_1, \widetilde{{\mathcal{A}}}_2, ..., \widetilde{{\mathcal{A}}}_n \right).$ □

Theorem 9. For a set of t-AFNs $\left\{{\mathcal{A}}_1, {\mathcal{A}}_2, ..., {\mathcal{A}}_n \right\}$, if ${\mathcal{A}}^{+} = \langle \max\limits_{1\leq j\leq n} a_{j}, \min\limits_{1\leq j\leq n} b_{j}, \min\limits_{1\leq j\leq n} c_{j}, \max\limits_{1\leq j\leq n} r_{j} \rangle$, and ${\mathcal{A}}^{-} = \langle \min\limits_{1\leq j\leq n} a_{j}, \max\limits_{1\leq j\leq n} b_{j}, \max\limits_{1\leq j\leq n} c_{j}, \min\limits_{1\leq j\leq n} r_{j} \rangle$. Then, we have

Proof. In light of Theorems 7 and 8, the proof follows directly. □

4.3.   t-arbicular fuzzy distance measure

In this part, we propose a novel generalized t-AF distance measure that extends the Minkowski distance model.

Definition 10. Let ${\mathcal{A}}_{1} = \langle a_1, b_1, c_1;r_{1} \rangle$, ${\mathcal{A}}_{2} = \langle a_2, b_2, c_2;r_{2} \rangle$ be two t-AFNs with degree of uncertainty $\pi_1 = \left(1-\left(a^{t}_{1}+b^{t}_{1}+c^{t}_{1} \right) \right)^{1/t}$, and $\pi_2 = \left(1-\left(a^{t}_{2}+b^{t}_{2}+c^{t}_{2} \right) \right)^{1/t}$, respectively. Then, the Minkowski‐type distance measure between ${\mathcal{A}}_{1}$ and ${\mathcal{A}}_{2}$ is delineated as shown:

where $p \in \mathbb{Z}^{+}$ symbolizes distance parameter.

Remark 2. In t-AF contexts, the Minkowski-type distance Eq (4.11) serves as a generalized distance metric. To clarify, this distance measure $d_{M}$ is commonly used with the distance parameter $p$ set to either 1 or 2, which correspond to the Hamming-type and Euclidean-type distances, respectively.

When $p = 1$, the Hamming-type distance measure, denoted as $d_{H}$, is defined as follows:

When $p = 2$, the Euclidean-type distance measure, denoted as $d_{E}$, is defined as follows:

Example 1. Let ${\mathcal{A}}_{1} = \langle 0.5851, 0.1749, 0.5322, 0.0800 \rangle$ and ${\mathcal{A}}_{2} = \langle 0.2339, 0.1862, 0.6748, 0.0300\rangle$ be two t-AFNs, then according to Eq (4.13), we have $d_{E}\left({\mathcal{A}}_{1}, {\mathcal{A}}_{2} \right) = 0.2889$.

Theorem 10. Let ${\mathcal{A}}_{1} = \langle a_1, b_1, c_1;r_{1} \rangle$, ${\mathcal{A}}_{2} = \langle a_2, b_2, c_2;r_{2} \rangle$, ${\mathcal{A}}_{3} = \langle a_3, b_3, c_3;r_{3} \rangle$ be three t-AFNs with degree of uncertainty $\pi_1 = \left(1-\left(a^{t}_{1}+b^{t}_{1}+c^{t}_{1} \right) \right)^{1/t}$, $\pi_2 = \left(1-\left(a^{t}_{2}+b^{t}_{2}+c^{t}_{2} \right) \right)^{1/t}$, and $\pi_3 = \left(1-\left(a^{t}_{3}+b^{t}_{3}+c^{t}_{3} \right) \right)^{1/t}$, respectively. Then, the Minkowski‐type distance measure $d_{M}$ fulfills the following properties:

i). $d_{m}\left({\mathcal{A}}_{1}, {\mathcal{A}}_{2}\right)\geq 0;$

ii). $d_{m}\left({\mathcal{A}}_{1}, {\mathcal{A}}_{2}\right)\leq 1;$

iii). $d_{m}\left({\mathcal{A}}_{1}, {\mathcal{A}}_{1}\right) = 0;$

iv). $d_{m}\left({\mathcal{A}}_{1}, {\mathcal{A}}_{2}\right) = d_{m}\left({\mathcal{A}}_{2}, {\mathcal{A}}_{1}\right);$

v). $d\left({\mathcal{A}}_{1}, {\mathcal{A}}_{3} \right)\leq d\left({\mathcal{A}}_{1}, {\mathcal{A}}_{2} \right)+d\left({\mathcal{A}}_{2}, {\mathcal{A}}_{3} \right)$.

Proof. ⅰ). It is clear that $\left|a^{t}_{1}-a^{t}_{2} \right|\geq 0,$ $\left|{b}^{t}_{1}-{b}^{t}_{2} \right|\geq 0,$ $\left|c^{t}_{1}-c^{t}_{2} \right|\geq 0,$ $\left|\pi^{t}_{1}-\pi^{t}_{2} \right|\geq 0$, and $\left|r^{}_{1}-r_{2} \right|\geq 0$. From these inequalities, it can be concluded that $d_{m}\left({\mathcal{A}}_{1}, {\mathcal{A}}_{2}\right)\geq 0$.

ⅱ). It is evident that $\left|{a}^{t}_{1}-{a}^{t}_{2} \right|^{p}\leq \left|{a}^{t}_{1}-{a}^{t}_{2} \right|^{}\leq 1$, $\left|{b}^{t}_{1}-{b}^{t}_{2} \right|^{p}\leq \left|{b}^{t}_{1}-{b}^{t}_{2} \right|^{}\leq 1$, $\left|{c}^{t}_{1}-{c}^{t}_{2} \right|^{p}\leq \left|{c}^{t}_{1}-{c}^{t}_{2} \right|^{}\leq 1$, and $\left|{\pi}^{t}_{1}-{\pi}^{t}_{2} \right|^{p}\leq \left|{\pi}^{t}_{1}-{\pi}^{t}_{2} \right|^{}\leq 1$. As shown by Definition 5, it is understood that ${a}^{t}_{1}+{b}^{t}_{1}+{c}^{t}_{1}+{\pi}^{t}_{1} = 1$, and ${a}^{t}_{2}+{b}^{t}_{2}+{c}^{t}_{2}+{\pi}^{t}_{2} = 1$. As a direct consequence, the maximum possible value of $\left|a^{t}_{1}-a^{t}_{2} \right|+ \left|{b}^{t}_{1}-{b}^{t}_{2} \right| +\left|c^{t}_{1}-c^{t}_{2} \right|+\left|\pi^{t}_{1}-\pi^{t}_{2} \right|$ is equal to 2 while the maximum possible value of $\left|r^{}_{1}-r_{2} \right|^{}$ is equal $\sqrt[t]{3}$ as $r^{}_{1}\leq \sqrt[t]{3}$, and $r^{}_{2}\leq \sqrt[t]{3}$. This implies that $\left(\left|a^{t}_{1}-a^{t}_{2} \right|^{p}+ \left|{b}^{t}_{1}-{b}^{t}_{2} \right|^{p} +\left|c^{t}_{1}-c^{t}_{2} \right|^{p}+\left|\pi^{t}_{1}-\pi^{t}_{2} \right|^{p} \right)\leq 2$ and $\left|r^{}_{1}-r_{2} \right|^{p}\leq \sqrt[t]{3}$. From these, we can easily derive that $d_{m}\left({\mathcal{A}}_{1}, {\mathcal{A}}_{2}\right)\leq 1$.

ⅲ). It is trivially valid.

ⅳ). It is trivially valid.

ⅴ). Since $d_{M}\left({\mathcal{A}}_{1}, {\mathcal{A}}_{3} \right) = \left(\frac{1}{{3}}\left(\frac{\left|r^{}_{1}-r_{3} \right|^{p}}{\sqrt[t]{3}}+ \left(\left|a^{t}_{1}-a^{t}_{3} \right|^{p}+ \left|{b}^{t}_{1}-{b}^{t}_{3} \right|^{p} +\left|c^{t}_{1}-c^{t}_{3} \right|^{p}+\left|\pi^{t}_{1}-\pi^{t}_{3} \right|^{p} \right)\right)\right)^{\frac{1}{p}}$ $= \left(\frac{1}{{3}}\left(\frac{\left|r^{}_{1}-r_{2}+r_{2}-r_{3} \right|^{p}}{\sqrt[t]{3}}+\left(\left|a^{t}_{1}-a^{t}_{2}+a^{t}_{2}-a^{t}_{3} \right|^{p}+ \left|{b}^{t}_{1}-b^{t}_{2}+b^{t}_{2}-{b}^{t}_{3} \right|^{p} +\left|c^{t}_{1}-c^{t}_{2}+c^{t}_{2}-c^{t}_{3} \right|^{p}+\left|\pi^{t}_{1} -\pi^{t}_{2}+\pi^{t}_{2}-\pi^{t}_{3} \right|^{p} \right)\right)\right)^{\frac{1}{p}}$ $\leq \left(\frac{1}{{3}} \left(\frac{\left|r^{}_{1}-r_{2} \right|^{p}}{\sqrt[t]{3}}+ \left(\left|a^{t}_{1}-a^{t}_{2} \right|^{p}+ \left|{b}^{t}_{1}-{b}^{t}_{2} \right|^{p} +\left|c^{t}_{1}-c^{t}_{2} \right|^{p}+\left|\pi^{t}_{1}-\pi^{t}_{2} \right|^{p} \right)\right)\right)^{\frac{1}{p}}$ $+\left(\frac{1}{{3}}\left(\frac{\left|r^{}_{2}-r_{3} \right|^{p}}{\sqrt[t]{3}}+ \left(\left|a^{t}_{2}-a^{t}_{3} \right|^{p}+ \left|{b}^{t}_{2}-{b}^{t}_{3} \right|^{p} +\left|c^{t}_{2}-c^{t}_{3} \right|^{p}+\left|\pi^{t}_{2}-\pi^{t}_{3} \right|^{p} \right)\right)\right)^{\frac{1}{p}}$ (using Minkowski inequality).

Thus, we get $d\left({\mathcal{A}}_{1}, {\mathcal{A}}_{3} \right)\leq d\left({\mathcal{A}}_{1}, {\mathcal{A}}_{2} \right)+d\left({\mathcal{A}}_{2}, {\mathcal{A}}_{3} \right)$. □

5.   Proposed CRITIC-TODIM approach

TODIM method, an MCDM technique rooted in prospect theory (PT), models the bounded rationality of DMEs ^[39]. PT, a behavioral economics theory, posits that DM under uncertainty deviates from normative rationality, influenced by cognitive biases such as probability weighting ^[40]. The TODIM approach incorporates the value function from PT to calculate dominance between alternatives, a nonlinear function reflecting the DME's sensitivity to gains and losses. The method further employs an additive function to aggregate criterion-wise dominance scores, selecting the alternative with the highest overall performance ^[41]. While TODIM has proven effective in various decision contexts, its reliance on crisp values limits its applicability to uncertain and complex problems ^[42]. To address this, researchers have integrated TODIM with various fuzzy set extensions ^[43,44,45] to accommodate ambiguity and uncertainty inherent in real-world decision scenarios.

In this section, we introduce an extended TODIM method tailored for MCDM problems involving t-AF information. Consider a set of $m$ alternatives, $A = \left\{AL_{i}; i = 1, 2, .., m \right\}$ and a set of $n$ criteria, $C = \left\{CR_{j}; j = 1, ,.., n \right\}$. The criteria are weighted by a vector $W = \left(W_{j}; j = 1, ..., n \right)$ such that $0\leq W_{j}\leq n$ and $\sum\limits_{j = 1}^{n}W_{j} = 1$ being completely unknown. A panel of DMEs $E = \left\{E^{(k)}; k = 1, 2, .., e \right\}$ having the weight vector $\varpi = \left(\varpi_{k}; k = 1, 2, .., e\right)$ such that $0\leq \varpi_{k}\leq n$ and $\sum\limits_{k = 1}^{e}\varpi_{k} = 1$ provide the assessment information in the form of t-AFNs ${\mathcal{A}}^{(k)}_{ij} = \langle a^{(k)}_{ij}, b^{(k)}_{ij}, c^{(k)}_{ij}; r^{(k)}_{ij} \rangle$ such that ${a^{(k)}_{ij}}^{t}+{b^{(k)}_{ij}}^{t}+{c^{(k)}_{ij}}^{t}\leq 1$, $r_{ij} \in \left[0, \sqrt[t]{3} \right]$; $t\geq 1$.

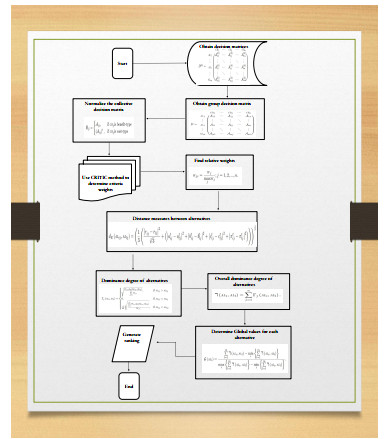
The key steps of the developed method are outlined as follows:

Step 1. Create the decision matrices in the format of t-AFNs derived from DMEs. The resulting decision matrices are presented as follows:

Step 2. Using the t-AFWA or t-AFWG operator, all individual decision matrices $D^{(k)}; k = 1, 2, ..., e$, can be combined into a single group decision matrix $D$ as shown.

In the case where the t-AFWA operator is applied, the aggregation ${\mathcal{A}}_{ij}$ can be expressed as follows:

Alternatively, when the t-AFWG operator is utilized, the aggregation ${\mathcal{A}}_{ij}$ takes the following form:

Step 3. Normalize the decision matrix $D = \left[\mathcal{A}_{ij}\right]_{m \times n}$ according to Eq (5.3).

where $\left(\mathcal{A}_{ij}\right)^c$ presents the complement of $\mathcal{A}_{ij}$.

Step 4. Use the CRITIC technique to determine the weights of the criteria.

Step 4.1. Calculate the score matrix by applying the score formula Eq (3.2) as follows:

Step 4.2. Employ the formula (5.4) to convert the score matrix $S$ into standard form.

where $i = 1, 2, ..., m$ and $j = 1, 2, .., n$.

Step 4.3. Calculate the standard deviations of the criteria by using Eq (5.5) as shown below.

where $\overline{\widetilde{S({\mathcal{B}}_{j})}} = \frac{\sum\limits_{i = 1}^{m}\widetilde{S({\mathcal{B}}_{ij})}}{m}$.

Step 4.4. Calculate the correlation coefficient between the criteria pairs in light of the following equation:

Step 4.5. Analyze the information for each criteria utilizing Eq (5.7).

Step 4.6. In this step, criteria weights are determined through Eq (5.8).

Step 5. Convert the weight components into relative weights according to Eq (5.9).

Step 6. Find the distance measure between alternatives under each criteria with Eq (5.10)

here, $d_{E}\left(AL_{ij}, AL_{lj} \right)$ means distance between $AL_i$ and $AL_l$ under $j$th criteria.

Step 7. Calculate the degree of dominance of alternative $AL_i$ over alternative $AL_l$ with respect to criteria $CR_j$ as follows:

here, ${\Theta} > 0$ represents the attenuation factor for the losses.

Step 8. Calculate the overall degree of dominance of alternative $AL_i$ over alternative $AL_l$ by applying the following formula:

The total domination degrees of alternatives can be presented in the form of a matrix as follows:

Step 9. Determine the global value for $AL_i$ using the following expression.

Then rank the alternatives based on $\mathcal{G}\left(AL_{i}\right)$, where a higher $\mathcal{G}\left(AL_{i}\right)$ value indicates a higher ranking.

The flowchart illustrating these steps is presented in Figure 3.

6.   Case study

To validate the proposed TODIM approach and assess its practical utility, we will present a case study focused on selecting the optimal gate security system. This case study is adapted from a previously published research ^[46].

6.1.   Problem description

In the modern world, security threats pose a significant challenge to organizations across all sectors. Institutions must implement robust security systems at entry points to ensure safety and mitigate vulnerabilities. Whether educational institutions or commercial enterprises like banks, businesses, schools, or universities, the foremost priority remains the creation of a secure environment for staff and students, enabling them to carry out their daily activities without concern. Establishing advanced security mechanisms is not just a precaution but a fundamental responsibility of every institution aiming to provide a safe working and learning environment.

Among the most critical components of an organization's security infrastructure is the gate security system. It serves as a primary line of defense, significantly enhancing protective measures by controlling access and preventing unauthorized entries. By deploying advanced technological solutions, such systems ensure that only verified individuals with the necessary credentials gain entry. These systems provide a comprehensive security solution, creating a physical and technological barrier against potential intrusions. Modern gate security systems are equipped with cutting-edge technology, including ID card scanners, PIN codes, and biometric devices, which streamline access control while reducing the reliance on human security personnel. As technology advances, the challenge for organizations lies in selecting the most suitable and effective security system for their unique needs.

To address this challenge, three domain experts having weight vector $\varpi = \left(0.4, 0.3, 0.3 \right)$ are selected to guide the decision-making process for choosing an optimal security system:

IT expert $(E^{(1)})$: The IT expert evaluates the system's technological compatibility and performance, ensuring that it can be effectively integrated into the organization's existing infrastructure. Finance expert $(E^{(2)})$: The financial expert assesses the system's cost-effectiveness, considering both initial setup and long-term operational expenses. The administrator of the organization ($E^{(3)}$): The administrator evaluates the overall appropriateness of the system, taking into account the organization's personnel needs, local environment, and operational context. Based on expert evaluations, five distinct security systems have been identified:

Card scanner system $(AL_{1})$: This system utilizes keycard readers, which are installed at doors. The reader scans encrypted information stored on cards, such as bank cards, ID cards, or student cards, and unlocks the door upon successful verification.

Fingerprint scanner system $(AL_{2})$: The fingerprint scanner system (FSS) employs optical sensor technology to capture an image of a fingerprint, which is then compared to stored data for authentication. Additional variants include thermal or ultrasonic scanners that operate on similar principles.

Facial recognition system $(AL_{3})$: Facial recognition systems use specialized algorithms, such as convolutional neural networks (CNNs), along with machine learning and artificial intelligence to analyze human facial features. These systems convert facial features into a "face print" (numerical code), requiring significant data storage for accurate recognition.

Iris recognition system $(AL_{4})$: Iris recognition uses mathematical pattern recognition algorithms to identify a person based on the unique and stable patterns in their irises. Infrared light scans the iris, transforming the pattern into an iris code, which is then compared against a database for verification. Iris scanners offer rapid and precise identification.

Voice recognition system $(AL_{5})$: This system records a person's voice and analyzes its unique characteristics—such as tone, pitch, and volume—using algorithms and AI to confirm the individual's identity.

To evaluate and rank these security systems, seven key criteria have been identified:

Cost ($CR_{1}$): This criterion evaluates the approximate cost of installing and maintaining the security system.

Reliability ($CR_{2}$): This refers to the system's ability to function effectively, even in challenging conditions or failure scenarios.

Accuracy ($CR_{3}$): This criterion measures the system's efficiency in accurately capturing and storing data.

Compatibility with existing infrastructure ($CR_{4}$): A system's compatibility with the organization's physical and technological environment is essential for seamless integration and optimal performance.

Durability ($CR_{5}$): This evaluates the longevity and robustness of the system, ensuring that it can function properly over extended periods without significant wear or failure.

IP rating ($CR_{6}$): This assesses the system's resistance to water and dust, ensuring reliable operation in environments where exposure to such elements is possible.

6.2.   Decision process

The selection of the optimal security system using the proposed t-AF framework is detailed as follows:

Step 1. The t-AF decision matrices provided by the DMEs $E^{(1)}$, $E^{(2)}$, and $E^{(3)}$ are tabulated in Tables 1, 2, and 3, respectively.

Step 2. Using Eq (4.2) (setting t = 2 and ${\downharpoonleft\upharpoonright} = \max$), the overall decision matrix is obtained as shown in Table 4.

Step 3. Upon examining the nature of the six selected criteria, it is observed that only criterion $CR_{1}$ is of the cost type, while the remaining criteria are classified as benefit type. By Eq (5.3), the overall decision matrix, as presented in Table 4, has been transformed into its normalized form, as illustrated in Table 5.

Step 4. In the subsequent steps, the proposed CRITIC technique is employed to calculate the unknown weights of the criteria.

Step 4.1. According to Eq (4.1), the score matrix is obtained as shown below.

Step 4.2. In accordance with Eq (5.4), the standardized form of the table is derived as follows:

Step 4.3. Based on Eq (5.5), the standard deviations $£_{j}; j = 1, 2, ..., 6$ are computed as follows: $£_{1} = 0.0596$, $£_{2} = 0.1345$, $£_{3} = 0.1948$, $£_{4} = 0.3934$, $£_{5} = 0.0879$, $£_{6} = 0.3024$.

Step 4.4. Following Eq (5.6), the correlation coefficients among the criteria are computed and are listed in Table 6.

Step 4.5. Equation (5.7) is employed to analyze the details for each criterion as follows: $\amalg_{1}$ $=$ $0.3541$, $\amalg_{2} = 0.5251$, $\amalg_{3} = 0.6730$, $\amalg_{4} = 1.6728$, $\amalg_{5} = 0.5825$, $\amalg_{6} = 1.2631$.

Step 4.6. Under Eq (5.8), the following objective weights are assigned to the considered six criteria. $W = \left(0.0698, 0.1036, 0.1327, 0.3299, 0.1149, 0.2491\right)$

Step 5. The relative weights of the criteria, determined using Eq (5.9), are presented as follows: $W_{1r} = 0.2117$, $W_{2r} = 0.3139$, $W_{3r} = 0.4023$, $W_{4r} = 1.0000$, $W_{5r} = 0.3482$, $W_{6r} = 0.7551$.

Step 6. According to Eq (5.10), the distance measure between each of the two alternatives are constituted in Table 7.

Step 7. Fixing $\Theta = 2$ in Eq (5.11), the degree of dominance of alternatives are obtained in Table 8.

Step 8. The total degree of dominance of alternatives are calculated by Eq (5.12), and the results is tabulated in matrix T.

Step 9. Based on Eq (5.14), the global value $\mathcal{G}\left(AL_{i}\right)$; $i = 1, 2, ..., 5$ is derived as follows:

$\mathcal{G}\left(AL_{1}\right) = 0.0000$, $\mathcal{G}\left(AL_{2}\right) = 1.0000$, $\mathcal{G}\left(AL_{3}\right) = 0.5634$, $\mathcal{G}\left(AL_{4}\right) = 0.3766$, $\mathcal{G}\left(AL_{5}\right) = 0.8746$.

Following the above derived global values, we get the following ranking:

Note that if the operator ${\downharpoonleft\upharpoonright}$ in Eq (4.2) is taken as $\min$ instead of $\max$, an alternative set of results is obtained: $\mathcal{G}\left(AL_{1}\right) = 0.0000$, $\mathcal{G}\left(AL_{2}\right) = 1.0000$, $\mathcal{G}\left(AL_{3}\right) = 0.5633$, $\mathcal{G}\left(AL_{4}\right) = 0.3765$, $\mathcal{G}\left(AL_{5}\right) = 0.8747$.

In this case, the final ranking of alternatives is as follows: $AL_{2} > AL_{5} > AL_{3} > AL_{4} > AL_{1}$. This illustrates the sensitivity of the radius component in aggregation; however, the overall decision pattern remains stable across both scenarios.

6.3.   Influence analysis

This section aims to evaluate the stability of the developed TODIM model under variations in parameters ${\Theta}$ and $t$. In what follows, a comprehensive experimental analysis is conducted to assess the model's sensitivity to these factors.

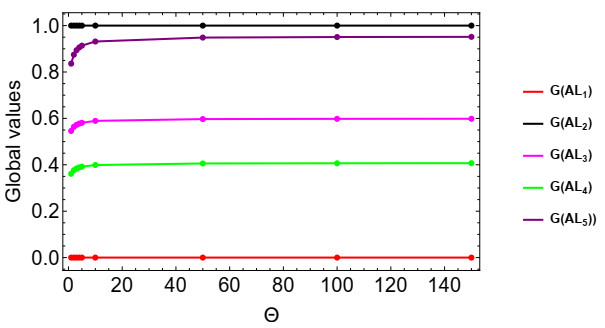
To examine stability concerning ${\Theta}$, we used various values for ${\Theta}$: 1, 2, 3, 4, 5, 10, 50,100, and 150, reapplying the proposed algorithm to the case study with each value. The final ranking results are presented in Table 9 and illustrated in Figure 4. From Table 9, it can be observed that the global values for alternatives $AL_{1}$ and $AL_{2}$ remain constant, while the values for other alternatives increase as ${\Theta}$ grows. Despite these changes, the rankings of alternatives remain consistently unchanged: $AL_{2} > AL_{5} > AL_{3} > AL_{4} > AL_{1}$. This analysis demonstrates that the developed model is robust and insensitive to varying values of ${\Theta}$.

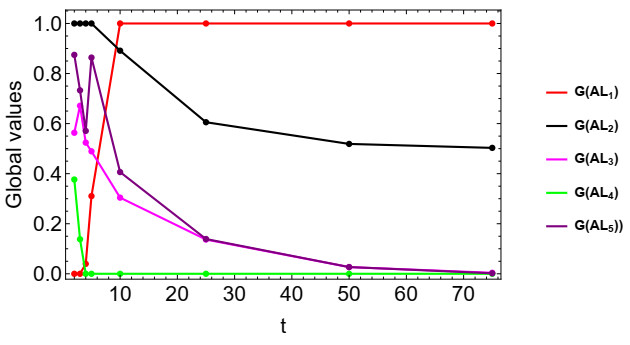
Next, we evaluate the effect of the parameter $t$ on the outcome rankings. For this, we applied different values of $t$ within the proposed approach, with the results shown in Table 10. From Table 10 and Figure 5, we observe that for $t = 2$ and $t = 3$, the ranking is $AL_{2} > AL_{5} > AL_{3} > AL_{4} > AL_{1}$. At $t = 4$ and $t = 5$, alternatives $AL_{4}$ and $AL_{1}$ switch positions. Further analysis reveals that from $t = 10$ to $t = 50$, the ranking changes to $AL_{1} > AL_{2} > AL_{5} > AL_{3} > AL_{4}$, and at $t = 75$, the ranking becomes $AL_{1} > AL_{2} > AL_{3} > AL_{5} > AL_{4}$. This indicates that the proposed TODIM methodology is highly sensitive to changes in $t$; notably, $AL_{1}$, initially the worst alternative at $t = 2$ and $t = 3$, becomes the top choice at higher values of $t$.

The results in Table 10 indicate that the ranking of alternatives varies with different values of $t$, particularly for lower values ($t = 2$ to $t = 5$) and stabilizes for higher values ($t\geq 10$). This variation does not contradict the stability of the proposed methodology but rather highlights the sensitivity of the TODIM-based decision model to parameter selection. The parameter $t$ influences the weight given to hesitation and uncertainty, which affects the dominance degrees of alternatives. To further validate the robustness of our approach, we conducted additional sensitivity analysis, demonstrating that for a sufficiently large $t$, the rankings converge, ensuring stability in decision-making over a reasonable parameter range. This aligns with the expected behavior of fuzzy decision models, where minor fluctuations at lower $t$ values represent initial sensitivity, while higher values provide a more stable preference ordering.

In practical applications, an appropriate value of $t$ can be chosen based on the fundamental constraint $a^{t}+b^{t}+c^{t}\leq 1$, which ensures the valid representation of t-AF elements. The smallest value of $t$ that satisfies this condition is considered the most suitable, as it captures the inherent uncertainty without excessive amplification. For example, in the given case, $t = 2$ is the minimum value satisfying this constraint. However, DMEs may choose higher values of $t$ based on domain-specific sensitivity requirements or robustness preferences.

7.   Results and discussion

For the comparative analysis presented in this section, we utilize the data from Table 5 to evaluate it with established methodologies. Specifically, we incorporated a set of prominent techniques, comparing their ranking outcomes with our initial rankings to validate and highlight the robustness of our proposed theoretical framework. The following methodologies are selected for comparison: Ashraf et al. ^[47] introduced the CRADIS decision model tailored for disc spherical fuzzy (DSF) contexts, while their subsequent work ^[48] elaborated on DSF-based Sugeno-Weber operators. Additionally, Ahmad et al. ^[49] developed Aczel-Alsina (AA) operators for DSF applications, and Ali and Yang ^[50] investigated Dombi AOs in circular q-ROFS frameworks. Anjum et al. ^[37] employed the WASPAS method, and Thilagavathy and Mohanaselvi ^[44] explored the TODIM method within the t-SFS setting. These methods were systematically applied to the dataset in Table 5, using the weight vector $W = \left(0.0698, 0.1036, 0.1327, 0.3299, 0.1149, 0.2491\right)$ generated by the proposed CRITIC method to enhance the accuracy of the comparisons. To enable the application of existing methods—each originally designed for different fuzzy environments (such as DSF, circular q-ROFS, and t-SFS)—to the t-AFNs dataset presented in Table 5, necessary adjustments are made. Specifically, for methods based on circular q-ROFSs ^[50], the neutral membership degrees ($b_{ij}$) are removed to align with the two-component structure of q-ROFSs. For t-SFS-based methods ^[37,44], the radius values were set to zero to match the requirements of the t-spherical structure. Similarly, methods under DSF settings ^[47,48,49] are applied without modification, but they interpret the radius in a less generalized or structurally distinct manner compared to t-AFNs. These transformations, while necessary for compatibility, led to partial loss of evaluation information—particularly the psychological neutrality captured through $b_{ij}$ and the DME's certainty modeled via the radius. Hence, while such modifications allowed for a uniform comparison, they also highlight the advantages of the proposed t-AF TODIM model, which preserves and fully utilizes the three-dimensional structure inherent to t-AFNs, ensuring a more accurate and informative evaluation.

The final computed results are detailed in Table 11.

ⅰ). From Table 11, it is evident that the CRADIS approach ^[47] identifies $AL_{2}$ as the best alternative and $AL_{1}$ as the worst, consistent with the rankings produced by the developed TODIM method. Minor variations are observed in the rankings of other alternatives, which can be attributed to differences in the mathematical formulation structures. Ashraf et al. ^[47] rely on a scoring formula, $S\left({\mathcal{A}}_1\right) = \frac{1}{4} \left(a_1 - b_1 - c_1 + \sqrt{2r_1}(2h - 1) \right),$ where $h \in [0, 1]$, which encounters limitations when $r = 0$, $h = 1$, and where the sums of $b_1$ and $c_1$ are equal to $a_1$. Although this approach works for the current dataset, it may not be applicable in scenarios where the condition $a_1^t + b_1^t + c_1^t \leq 1$ does not hold for $t = 1$ or $t = 2$, limiting its general validity.

ⅱ). Ashraf et al. ^[48] and Ahmad et al. ^[49] have developed methods based on Sugeno-Weber and AA aggregation, respectively, both of which rank $AL_{1}$ as the optimal alternative. This finding stands in stark contrast to our ranking, which identifies $AL_{1}$ as the least favorable option. The primary reason for this significant discrepancy lies in the foundational principles of these existing methods, which rely solely on data aggregation. Their aggregation formulas treat the radius $r$ similarly to membership or non-membership components. In contrast, our developed theory approaches this formulation based on maximum or minimum values, reflecting a fundamentally different perspective. Moreover, the scoring formula is critical in determining the rankings of alternatives, and both existing approaches employ the same scoring formula previously discussed, along with its inherent limitations. This reliance may contribute to the observed differences in results. Despite these drawbacks, the existing methods ^[48,49] possess certain advantages: their operators are more generalized due to the inclusion of Sugeno-Weber and AA parameters, and they are simpler compared to the TODIM technique.

ⅲ). To implement the approach proposed by Ali and Yang ^[50] on the data presented in Table 5, we excluded the neutral grades, denoted as $b_{ij}$, from the t-AFNs. This adjustment transformed the data into circular q-rung orthopair fuzzy context. While this modification allowed Ali and Yang's method ^[50] to be applied, it resulted in the loss of crucial information from the experts, leading to a significant shift in the rankings: as per the framed approach, the best alternative, $AL_{2}$, was moved to the third position, while the worst alternative, $AL_{1}$, ascended to the top rank. Furthermore, this existing aggregation approach is unable to compute criteria weights when faced with scenarios in which this information is unknown.

ⅳ). From Table 11, it is evident that the rankings derived from the methodology of Anjum et al. ^[37] differ significantly from those produced by our proposed t-AF method, similar to previous aggregation-based approaches. In contrast, the rankings from Thilagavathy and Mohanaselvi ^[44] exhibit considerable similarity, except for the switched positions of $AL_{3}$ and $AL_{4}$. Both of these existing methods ^[37,44] are founded on a t-spherical fuzzy context. To enable the application of these approaches, the considered data has been reduced to a t-spherical fuzzy context by setting the radius value of each t-AFN to zero. However, this adjustment may result in the loss of critical information, leading to inaccuracies in the rankings. The similarity between the results of Thilagavathy and Mohanaselvi ^[44] and our proposed approach lies in both utilizing the TODIM methodology and accounting for the DMEs' psychological behavior. The differences arise from the contexts, as Thilagavathy and Mohanaselvi's method is specifically valid for t-SF settings, whereas our proposed method applies to t-AFS, which is a generalization of t-SF. Furthermore, the methodology presented by Anjum et al. ^[37] employs a scoring function defined as $S\left({\mathcal{A}}\right) = a_1^t-c_1^t$, which ranges from -1 to 1. In our case study, several negative values were obtained, rendering the weighted product step of the WASPAS method unworkable. To address this issue and ensure suitability for obtaining the final ranking results, we replaced this scoring function with the formulation proposed by Zedam et al. ^[51].

Based on the analysis presented, we can outline the following advantages of the developed theory and method:

ⅰ). The t-AF context introduced in this article is more general than existing frameworks and is particularly effective in scenarios characterized by greater uncertainty. This fuzzy context can be reduced to a circular spherical fuzzy set by fixing $t = 2$ or to a circular q-rung orthopair fuzzy setting by eliminating neutral grades. Consequently, it offers a broader range for DMEs to articulate their perspectives more clearly.

ⅱ). The proposed novel t-AF TODIM method remains unaffected by variations in the parameter ${\Theta}$, as illustrated in Table 9. This stability enhances the robustness of the approach, allowing for consistent results across different settings.

ⅲ). Utilizing the TODIM method to rank alternatives in MCGDM problems emphasizes the psychological aspects of decision-making. This approach acknowledges the cognitive processes and subjective preferences of DMEs, allowing for a more nuanced evaluation of alternatives. This focus on human psychology contributes to more realistic and applicable results in practical scenarios.

ⅳ). The proposed score computation employs a more accurate formulation that is unaffected by setting the radius values to zero or by equating the sums of neutral and non-membership grades to the membership value, allowing for a clearer and more consistent evaluation of alternatives without the limitations present in previous approaches ^{[47,48,49,50]}.

However, the model does have certain limitations, including:

ⅰ). The criteria weight estimation method determines weights objectively, with limited consideration of subjective input from DMEs.

ⅱ). The presented approach is based on the assumption that the experts weights should be known in advance, which may not align with actual scenarios.

8.   Conclusions

In this paper, we proposed the t-AFS, an extension of several existing fuzzy set frameworks, including FSs, q-ROFSs, circular q-rung orthopair FSs, disc spherical FSs, and t-spherical FSs. This framework effectively represented vagueness and fuzziness in real-world problems by incorporating radius and the parameter $t$, providing DMEs with greater flexibility to express their perspectives. We defined fundamental operations for t-AFNs and established a range of identities, alongside a robust score and accuracy function for comparing t-AFNs. Additionally, we presented a series of aggregation operators with their essential properties and validated distance measures that satisfied the axioms of distance measurement. Building on these developments, we explored the CRITIC method for objective criteria weight determination, leveraging the advantage of capturing correlations among criteria. We also extended the TODIM method to the t-AF context to enable the ranking of alternatives while incorporating the psychological aspects of decision-making. Finally, we presented a case study on selecting an optimal gate security system, followed by a sensitivity analysis and comparative discussion, which demonstrated the stability, validity, and superiority of the developed model.

Future research could focus on enhancing the framework by introducing independent parameters for each grade, as proposed by Ali and Naeem ^[52], to improve flexibility. The model could also be applied to other decision-making problems, such as healthcare, risk analysis, and supply chain management, to validate its effectiveness across domains. Another promising direction is integrating t-AFS with three-way decision-making TWD to refine classification into acceptance, rejection, or a neutral zone, improving decision robustness. Additionally, refining the TODIM method in the t-AFS by incorporating alternative distance measures and adapting it for group decision-making could strengthen its applicability.

Author contributions

Jawad Ali: Conceptualization, methodology, writing-original draft, writing-review and editing; Ioan-Lucian Popa: Conceptualization, methodology, writing-original draft, supervision, language editing, funding acquisition. Both the authors have read and agreed to the published version of the manuscript.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare that they have no conflict of interest regarding this manuscript.