Extended CODAS method for MAGDM with $2$-tuple linguistic $T$-spherical fuzzy sets

1.   Introduction

Market dynamics and technology developments enable businesses to create new items with success. These are the essentials for both startups and enterprises to enhance their present competitive edge and for local firms to expand in a highly competitive climate. Akao ^[1] introduced QFD as a valuable quality technique for converting CRs (customer requirements) into DRs (designing requirements). QFD helps businesses in a variety of ways, including significantly improved customer satisfaction and improved communication. The popular tool QFD was first used in industrial procedures. Product quality, operational effectiveness, and financial performance of the firm may all improve. Through the house of quality (HoQ), QFD manages the relationships between customer requirements and design requirements. An HoQ consists of a number of rooms, each of which is employed in the product design process. Several relationships between these rooms, such as connections between design needs, are not taken into account in the literature. Engineering, control theory mathematics, computer sciences, medical sciences, business and economics, social sciences, human behaviors, and urban planning are just a few of the study fields where fuzzy set (FS) theory has been used to produce effective answers under ambiguity. This paper describes the evaluation and selection of linear delta robots in the 2TL$T$-SF environment using a unique MAGDM approach that combines QFD with CODAS method and the 2TL$T$-SFSs.

The MAGDM complications are crucial aspects of decision theory in which we select the best linear delta robot from a set of finite options based on the overall data. Because of the complexity of real-life situations and the occurrence of vagueness in human judgments, MAGDM problems are complex and challenging. In this context, it is generally believed that knowledge about alternatives would be in the form of real numbers. However, due to the vagueness and inconsistency of the given descriptions, it is difficult for decision makers (DMs) to offer their assessments in crisp values in our immediate environment. Therefore, resolving this ambiguity is a big challenge for DMs. One of the complexities in MAGDM is communicating attribute values in a logical manner. Zadeh's ^[2] FS theory has been widely used to deal with uncertain information due to the ambiguity of evaluative strategies and the uncertainty of MAGDM problems. In FS, Zadeh only demonstrates the membership degree (MD) in the given set. Unfortunately, the non-membership degree (NMD) is not discussed in FS. The absolute uncertainty was not really resolved by FS theory. Consequently, Atanassov ^[3] introduced the intuitionistic fuzzy set (IFS), which involves both MD and NMD. In some circumstances where $\mu + \nu \geq 1$, IFS cannot handle these situations. Yager ^[4] presented the Pythagorean fuzzy set (PyFS), which is categorized with MD and NMD, ensuring that the square sum of MD and NMD is less than or equal to one. Yager ^[5] also suggested the $q$-rung orthopair FS ($q$-ROFS), categorized by MD and NMD, which ensures that the $qth$ sum of MD and NMD is less than or equal to one. As a result, the $q$-ROFS is better than IFS and PyFS for handling ambiguity in actual MAGDM problems. IFS, PyFS, and $q$-ROFS deal with actual inaccuracy and attempt to solve MAGDM problems which would require a human opinion.

The current study goal, according to Ali ^[6], is to investigate a novel $q$-rung orthopair fuzzy scoring function and also to extend the assessment of alternatives and ranking according to compromise solution (MARCOS) approach with unknown weight information to the setting of $q$-ROFNs. The paper given by Ali et al. ^[7] offered a $q$-rung orthopair hesitant fuzzy stochastic approach based on regret theory to represent the psychological behavior of DMs. However, these duplets only address two aspects of human perception: like and dislike. A human opinion, on the other hand, measures the degree of preference. According to Cuong and Kreinovich ^[8] the MD and NMD pairings, that constitute an IFS or its extended form, represent a human perspective, in which the abstinence degree (AD) and refusal degree (RD) are mostly neglected, which entails the loss of knowledge. As a result, they developed a picture fuzzy set (PFS) in the form of triplets MD, AD, and NMD with the condition that the combined sum never exceeds 1. Gündogdu and Kahraman ^[9] advanced PFS structure in the form of a spherical fuzzy set (SFS), that specified some aggregation operators (AOs) with SF information for the multi-attribute decision-making (MADM) problems and enhanced the assigning range of MD, AD, and NMD. Mahmood et al. ^[10] introduced the $T$-spherical fuzzy set (T-SFS). The $T$-SFS is an extension of SFS and PFS. All membership, abstinence, and non-membership grades in the $T$-SFS meet the condition $0 \leq \mu^{q} + \eta^{q} + \nu^{q} \leq 1$ instead of $0 \leq \mu^{2} + \eta^{2} + \nu^{2} \leq 1$ as indicated by the SFS, and $0 \leq \mu + \eta + \nu \leq 1$ as indicated by the PFS. Mahnaz et al. ^[11] developed several generalized operational laws, especially Frank operational laws for $T$-SFNs based on the Frank $t$-norm and $t$-conorm. Ali ^[12] presented a score function, which is a formula for the transformation process of DMs' weight information from the spherical fuzzy form to the classical form. Using the benefits of $T$-SFSs, Garg et al. ^[13] defined various weighted averaging and geometric power aggregation operations. Based on complex $T$-SFSs, Karaaslan and Dawood ^[14] presented the Dombi operations, established several AOs based on Dombi operators, built a MADM technique in the complex $T$-SF environment, and presented an algorithm for the suggested approach. Naeem and Ali ^[15] investigated spherical fuzzy operational rules and their desired properties.

Moreover, maximum choice issues are ambiguous and fuzzy; it is difficult to describe the qualities involved in these decision problems in crisp numbers, as opposed to qualitative data, which can be directly stated using linguistic terms like excellent, great, or good. Zadeh ^[16] suggested the definition of linguistic variables (LVs) since there have been accomplishments in research on linguistic MADM issues. The 2TL representation model was introduced by Herrera and Martí­nez ^[17,18]. Several 2TL-AOs and decision-making approaches have been proposed. Zhang et al. ^[19] developed an approach to two-sided matching decision-making with multi-granular hesitant fuzzy linguistic term sets to resolve two-sided matching problems. As a novel approach to MAGDM problems, Zhao et al. ^[20] developed an enhanced TODIM strategy based on 2TL neutrosophic sets and the cumulative prospect theory. Based on previous research results, the 2TLC$q$-ROF idea was put out by Naz et al. ^[21] by fusing the intricate $q$-rung orthopair fuzzy set using 2-tuple linguistic concepts, such as the fundamental definition, operational guidelines, scoring, and accuracy functions. By assessing the reliability of the information, Chai et al. ^[22] introduced the notion of Z-uncertain probabilistic linguistic variables (Z-UPLVs). Then the operating rules, normalizing, distance and similarity measurements, and Z-UPLV comparative technique were established. Under the dual probabilistic linguistic term sets, Saha et al. ^[23] used the ideas of consistency and similarity amongst DMs to establish the decision-making's subjective and objective weights, respectively. Through certain counter instances, Ali et al. ^[24] demonstrated the limits of the existing distance measurements of dual hesitant fuzzy sets. Akram et al. ^[25,26] developed a new decision-making approach to deal with the MADM problems based on graph theory. Further, Naz et al. ^{[27,28,29,30,31]} as well as other researchers ^{[32,33,34,35,36,37]} introduced several decision-making methods under generalized fuzzy scenarios.

The Hamacher operations, which involve the Hamacher product and Hamacher sum, were first presented by Hamacher ^[38]. In contrast to the algebraic product and algebraic sum, the Hamacher product and the Hamacher sum are both excellent alternatives ^[39]. The Hamacher t-conorm and t-norm are comprehensive and dynamic extensions of the algebraic and Einstein t-conorm and t-norm ^[40]. Akram et al. ^[41] introduced the complex intuitionistic fuzzy (CIF) Hamacher weighted averaging operator, CIF Hamacher ordered weighted averaging operator, CIF Hamacher weighted geometric operator, and CIF Hamacher ordered weighted geometric operator under the CIF environment. Pamucar et al. ^[42] proposed a novel WASPAS approach based on the fuzzy Hamacher weighted averaging function and weighted geometric averaging function for the advantageous prioritization of the sustainable supply chain of the electric ferry. Faizi et al. ^[43] introduced some operational laws for intuitionistic 2TL terms based on Hamacher operations under certain critical properties. They also introduced the intuitionistic 2TL Hamacher weighted average and the intuitionistic 2TL Hamacher weighted geometric operators with the assistance of Hamacher operations and intuitionistic 2TL terms. Garg et al. ^[44] presented the concept of the interval-valued picture uncertain linguistic set to explore the theory, stated some basic operational laws, and investigated their properties. Based on the stated laws, they defined several weighted and ordered weighted generalized Hamacher AOs. Hadi et al. ^[45] proposed the Fermatean fuzzy Hamacher (FFH) arithmetic and geometric AOs by inducing the Hamacher operations and FFS. In the first part, they introduced the concepts of an FFH weighted average operator, an FFH ordered weighted average operator and an FFH hybrid weighted operator. In the second part, they developed the FFH weighted geometric operator, FFH ordered weighted geometric operator and FFH hybrid geometric operator.

Strategy implementation is a crucial part of solving MAGDM problems. For this strategy, DMs used different methods: VIKOR, TOPISIS, EDAS, MABAC, etc. In order to aggregate complex data, Ghorabaee et al. ^[46] developed the CODAS model. To determine the objective weight, Lei et al. ^[47] presented the combined assessment of the objective criteria weights approach. The probabilistic double hierarchy linguistic CODAS approach was developed and used for online shopping platform evaluation. Simic et al. ^[48] used the PFSs to introduce a novel PF-CODAS approach to locate multi-criteria automobile shredding facilities. In MAGDM, Wang ^[49] evaluated the teaching quality of college English. Further, he developed a unique distance-based interval-valued intuitionistic fuzzy CODAS approach based on the traditional CODAS method and interval-valued intuitionistic fuzzy sets. Naz et al. ^[50] enhanced the CODAS approach by creating the 2TL$q$-ROF-CODAS model, that not only accounts for human cognition's uncertainties but also allows DMs a broader area to describe their choices. For the purpose of resolving MAGDM problems, Akram et al. ^[51] devised a 2TL Fermatean fuzzy CODAS technique using the Hamacher aggregation operators.

In the light of the above-mentioned study, there is an area of research that has to be filled in the Hamacher operations and the related AOs for the fusion of 2TL$T$-SFS information. Due to the characteristics that allow it to include the algebraic and Einstein operations, Hamacher operations are more versatile than certain classical operations. The parameterized design of Hamacher operations gives the AOs generality and the power to provide trustworthy results. The development of the expanded CODAS approach for MAGDM based on 2TL$T$-SFSs and suitable Hamacher AOs is strongly encouraged by the attractive theory of the CODAS method and its promise in linguistic decision-making scenarios. This prompts us to think about creating 2TL$T$-SFS Hamacher AOs as part of a comprehensive framework for processing 2TL$T$-SF information.

1.1.   Motivation and objectives

The following points serve as a framework for the motivation of this research article: (1) We utilize 2TL$T$-SFS because it offers a more comprehensive definition of fuzziness and, as a result, a more accurate evaluation of such a decision-making process by allowing DMs to consider a wider range of factors related to the addressed problems' uncertainties, information gaps, and inconsistencies between many expert groups. The 2TL$T$-SFS increases the versatility of $T$-SFS by integrating 2TL and 2TL$T$-SF sets to represent the qualitative data into the 2TL$T$-SFNs. (2) The use of the $T$-FS geometric aggregation operator made it simple to combine the opinions of experts and customers. The spherical fuzzy arithmetic operator has been used, to sum up, both positive and negative correlations. (3) The relationship between the input arguments can be described utilizing the Hamacher operator. Hamacher operations are more flexible than certain standard operations due to the parameters that allow them to cover algebraic and Einstein operations. The parameterized nature of Hamacher operations endows the AOs with generality and efficiency in producing dependable results. Furthermore, the Hamacher operator has one robust parameter to address the various requirements in the information integrating process. There is limited study on using Hamacher operations to build novel operators, according to an analysis of the 2TL$T$-SF-AOs. As a result, a study on AOs utilizing Hamacher operations with 2TL$T$-SF information is required. (4) The CODAS method is the most popular tool for solving the MAGDM problems. Moreover, there is a lack in the application of the CODAS method with 2TL$T$-SFNs. Following is the contribution of this research article according to the above objectives:

(1) By utilizing 2TL$T$-SFS, we propose the new AOs to fuse the given information. In the information integrating process, these new operators minimize the impact of uncertain data and determine the relationship among aggregated arguments, i.e., the 2TL$T$-SFHWA, 2TL$T$-SFHOWA, 2TL$T$-SFHHA, 2TL$T$-SFHWG, 2TL$T$-SFHOWG, and 2TL$T$-SFHHG operators.

(2) In the 2TL$T$-SF environment, we propose a MAGDM approach based on the 2TL$T$-SFHWA and 2TL$T$-SFHWG AOs which is known as the 2TL$T$-SF-CODAS method.

(3) From real-world circumstances, several theorems, properties, and basic definitions of the suggested information aggregation operators are deduced.

(4) A 2TL$T$-SF-CODAS technique is presented to rank the alternatives based on the 2TL$T$-SFHWA as well as 2TL$T$-SFHWG operators. The assessment preferences of DMs are combined using a unique MAGDM model.

(5) A numerical illustration to select the best linear delta robot is conducted to fuse the overall data. The decision-making methods, sensitivity analysis, and comparative analysis are illustrated to prove the accuracy and effectiveness of the proposed technique.

1.2.   Organization

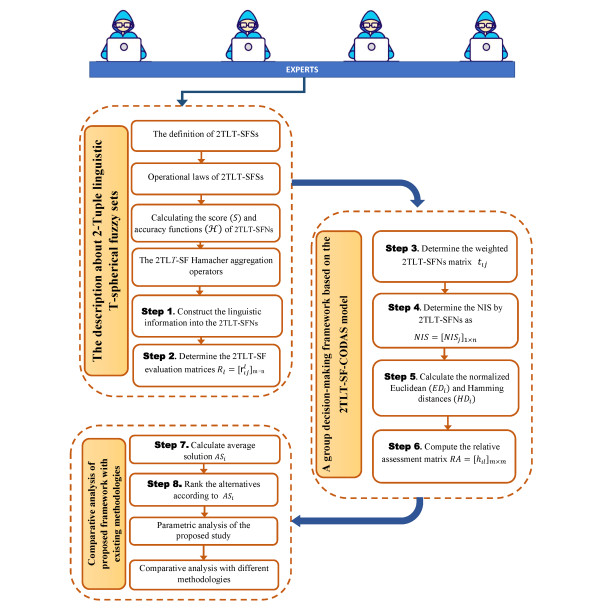
The remaining paper is organized in the following manner to accomplish the goal of this research study. In Section 2, we recap the idea of LTS, 2TL terms, and $T$-SFS. In Section 3, we combine the 2TL$T$-SFS with Hamacher operations and develop the 2TL$T$-SFHWA operator, the 2TL$T$-SFHOWA operator, the 2TL$T$-SFHHA operator, the 2TL$T$-SFHWG operator, the 2TL$T$-SFHOWG operator, and the 2TL$T$-SFHHG operator. In Section 4, we present a novel approach for MAGDM. In Section 5, in order to explain the techniques suggested in this paper, a numerical example to select the best alternative for additive manufacturing of a linear delta robot is described. Section 6 concludes the research article by giving future directions. The flowchart depicts the framework of the proposed study (see Figure 1).

2.   Preliminaries

In this section, some correlative basic concepts of LTS, 2TL terms, and $T$-SFS are recapped to facilitate the next sections.

2.1.   2-Tuple linguistic representation model

In this subsection, the description about 2TL set is recapped.

Definition 1. ^[52] Let there exist a LTS $S = \{s_{\jmath} \, |\; \jmath = 0, 1, \ldots, \tau\}$ with odd cardinality, where $s_{\jmath}$ indicates a possible linguistic term for a linguistic variable. For instance, LTS $S$ having seven terms can be described as follows:

$S = \{ s_{0}$ = none, $s_{1}$ = very low, $s_{2}$ = low, $s_{3}$ = medium, $s_{4}$ = high, $s_{5}$ = very high, $s_{6} = perfect\}$.

If $s_{\jmath}, s_{{k}}\in S$, then the LTS meets the following characteristics:

(i) The set is ordered: $s_{\jmath} > s_{{k}}$, if and only if $\jmath > {k}.$

(ii) Max operator: $\max(s_{\jmath}, s_{{k}}) = s_{\jmath},$ if and only if $\jmath\geq {k}$.

(iii) Min operator: $\min(s_{\jmath}, s_{{k}}) = s_{\jmath},$ if and only if $\jmath\leq {k}$.

(iv) Negative operator: Neg$(s_{\jmath}) = s_{{k}}$ such that $k = \tau-\jmath.$

The 2-tuple fuzzy linguistic representation model based on the idea of symbolic translation, introduced by Herrera and Martínez ^[17,18], is useful for representing the linguistic assessment information by means of a 2-tuple $(s_{\jmath}, \alpha_{\jmath})$, where $s_{\jmath}$ is a linguistic label from predefined LTS $S$ and $\alpha_{\jmath}$ is the value of symbolic translation, and $\alpha_{\jmath}\in[-0.5, 0.5)$.

Definition 2. ^[17,18] Let $\beta$ be the result of an aggregation of the indices of a set of labels assessed in LTS $S$, i.e., the result of a symbolic aggregation operation, $\beta \in [0, \tau]$, where $\tau$ is the cardinality of $S$. Let $\jmath = \rm{round}(\beta)$ and $\alpha = \beta-\jmath$ be two values, such that, $\jmath\in [0, \tau]$ and $\alpha \in [-0.5, 0.5)$ then $\alpha$ is called a symbolic translation.

Definition 3. ^[17,18] Let $S = \{s_{\jmath}\, |\; \jmath = 0, \ldots, \tau\}$ be a LTS and $\beta \in [0, \tau]$ is a number value representing the aggregation result of linguistic symbolic. Then, the function $\Delta$ used to obtain the 2TL information equivalent to $\beta$ is defined as:

Definition 4. ^[17,18] Let $S = \{s_{\jmath}\, |\; \jmath = 0, \ldots, \tau\}$ be a LTS and $(s_{\jmath}, \alpha_{\jmath})$ be a 2-tuple, there exists a function $\Delta^{-1}$ that restores the 2-tuple to its equivalent numerical value $\beta \in [0, \tau]\subset R,$ where

Definition 5. ^[10] A triplet $\Gamma = (m, i, n)$ is referred as a $T$-spherical fuzzy number ($T$-SFN) where $m$, $i$ and $n$ denote respectively the MD, AD and NMD of the $T$-SFN $\Gamma$ provided that for some $q\in Z^{+}$, $0\leq m^{q}+i^{q}+n^{q}\leq1$. The RD in this case is defined as $r = \sqrt[q]{1-(m^{q}+i^{q}+n^{q})}$.

A $T$-SFN is a generalized form of existing fuzzy framework, and it reduces to:

(i) By setting $q = 2$, we obtain spherical fuzzy number (SFN).

(ii) By setting $q = 1$, we obtain picture fuzzy number (PFN).

(iii) By setting $i = 0$, we obtain $q$-rung orthopair fuzzy number ($q$-ROFN).

(iv) By setting $i = 0$ and $q = 2$, we obtain Pythagorean fuzzy number (PyFN).

(v) By setting $i = 0$ and $q = 1$, we obtain intuitionistic fuzzy number (IFN).

(vi) By setting $i = n = 0$ and $q = 1$, we obtain fuzzy number (FN).

2.2.   Hamacher t-norm and Hamacher t-conorm

To extend the existing operations of t-norm and t-conorm, Hamacher ^[38] introduced the Hamacher product t-norm and Hamacher sum t-conorm as generalizations of t-norms and t-conorms, respectively, as follows:

Clearly, when $\varrho = 1,$ the Hamacher t-norm and t-conorm change into the algebraic t-norm and t-conorm as follows:

Again, when $\varrho = 2,$ the Hamacher t-norm and t-conorm reduce to the Einstein t-norm and t-conorm ^[53] as follows:

Inspired by the ideas of 2TL terms and $T$-SFS, Akram et al. ^[54] developed the new concept of 2TL$T$-SFS as an extension of 2TL-PFS and 2TL-SFS. The mathematical representation of 2TL$T$-SFS is described as follows:

Definition 6. ^[54] Let $S = \{s_{\jmath} \, |\; \jmath = 0, 1, \ldots, \tau\}$ be a LTS with odd cardinality. If $(({s_{p}}, \wp), ({s_{r}}, \Re), (s_{l}, £))$ is defined for $s_{p}, s_{r}, s_{l} \in S, \; \wp, \Re, £ \in [-0.5, 0.5)$, where $({s_{p}}, \wp), ({s_{r}}, \Re), and\, (s_{l}, £)$ represent respectively the MD, AD and NMD by 2TLSs. A 2TL $T$-spherical fuzzy set is defined as:

where $0\leq \Delta^{-1}({s_{p}}, \wp)\leq \tau, \; 0\leq \Delta^{-1}({s_{r}}, \Re)\leq \tau, \; 0\leq \Delta^{-1}~~ (s_{l}, £)\leq \tau,$ and $0\leq (\Delta^{-1}({s_{p}}, \wp))^{q} + (\Delta^{-1}({s_{r}}, \Re))^{q} + (\Delta^{-1}~~ (s_{l}, £))^{q} \leq \tau^{q}.$

In order to compare any two 2TL$T$-SFNs, their score value and accuracy value are defined as follows:

Definition 7. ^[54] Let $\mathcal{P} = (({s_{p}}, \wp), ({s_{r}}, \Re), (s_{l}, £))$ be a 2TL$T$-SFN. Then, the score function $\mathcal{S}$ of a 2TL$T$-SFN ${\mathcal{P}}$ can be represented as:

and its accuracy function $\mathcal{H}$ is defined as:

Definition 8. ^[54] Let $\mathcal{P}_{1} = (({s_{{p}_1}}, {\wp_1}), ({s_{{r}_1}}, {\Re_1}), ({s_{{l}_1}}, {£_1}))$ and $\mathcal{P}_{2} = (({s_{{p}_2}}, {\wp_2}), ({s_{{r}_2}}, {\Re_2}), ({s_{{l}_2}}, {£_2}))$ be two 2TL$T$-SFNs; then, these two 2TL$T$-SFNs can be compared according to the following rules:

(1) If $\mathcal{S}(\mathcal{P}_{1}) > \mathcal{S}(\mathcal{P}_{2})$, then $\mathcal{P}_{1}\succ\mathcal{P}_{2}$;

(2) If $\mathcal{S}(\mathcal{P}_{1}) = \mathcal{S}(\mathcal{P}_{2})$, then

● If $\mathcal{H}(\mathcal{P}_{1}) > \mathcal{H}(\mathcal{P}_{2})$, then $\mathcal{P}_{1}\succ \mathcal{P}_{2}$;

● If $\mathcal{H}(\mathcal{P}_{1}) = \mathcal{H}(\mathcal{P}_{2})$, then $\mathcal{P}_{1} \sim \mathcal{P}_{2}$.

3.   The 2TL$T$-SF Hamacher aggregation operators

We present a modified intersection and union on two 2TL$T$-SFNs $\mathcal{P}_{1}$ and $\mathcal{P}_{2}$ in terms of the Hamacher product $\otimes$ and the Hamacher sum $\oplus$. In fact, some Hamacher operations, such as Hamacher product and Hamacher sum of two 2TL$T$-SFNs $\mathcal{P}_{1}$ and $\mathcal{P}_{2}$, with $\varrho > 0$, i.e., Hamacher operational laws for 2TL$T$-SFNs are defined as follows:

Definition 9. Let $\mathcal{P}_{1} = ((s_{p_{1}}, \wp_{1}), (s_{~~ r_{1}}, \Re_{1}), (s_{l_{1}}, £_{1}))$ and $\mathcal{P}_{2} = ((s_{p_{2}}, \wp_{2}), (s_{~~ r_{2}}, \Re_{2}), (s_{l_{2}}, £_{2}))$ be two 2TL$T$-SFNs, with $\varrho > 0$, then the basic Hamacher operations between $\mathcal{P}_{1}$ and $\mathcal{P}_{2}$ are given as follows:

Based on Hamacher operational laws for 2TL$T$-SFNs, we propose some 2TL$T$-SF Hamacher AOs by using weighted average, weighted geometric, and hybrid operators, i.e., 2TL$T$-SFH weighted average (2TL$T$-SFHWA) operator, 2TL$T$-SFH ordered weighted average (2TL$T$-SFHOWA) operator, 2TL$T$-SFH hybrid average (2TL$T$-SFHHA) operator, 2TL$T$-SFH weighted geometric (2TL$T$-SFHWG) operator, 2TL$T$-SFH ordered weighted geometric (2TL$T$-SFHOWG) operator, and 2TL$T$-SFH hybrid geometric (2TL$T$-SFHHG) operator.

3.1.   The 2TL$T$-SFHWA operator

In this subsection, for the purpose of addressing real-world issues, we take into account the significance of the aggregated data and by utilizing the novel Hamacher operational laws in 2TL$T$-SF environment, we propose the 2-tuple linguistic $T$-spherical fuzzy Hamacher weighted average (2TL$T$-SFHWA) operator. Furthermore, we also discuss their properties and some special cases. We define the 2TL$T$-SFHWA operator in terms of Definition 6 and the Hamacher operational laws of Definition 9 as below:

Definition 10. Let $\mathcal{P}_{\jmath} = ((s_{p_{\jmath}}, \wp_{\jmath}), (s_{r_{\jmath}}, \Re_{\jmath}), (s_{l_{\jmath}}, £_{\jmath}))\; \left(\jmath = 1, 2, \ldots, n \right)$ be a collection of 2TL$T$-SFNs, then the 2TL$T$-SFHWA operator is defined as:

where $\varpi = \left(\varpi_{1}, \varpi_{2}, \ldots, \varpi_{n}\right)^{T}$ is the weight vector of $\mathcal{P}_{\jmath}\; \; \left(\jmath = 1, 2, \ldots, n\right),$ and $\varpi_{\jmath} > 0$, $\sum\limits_{\jmath = 1}^{n}\varpi_{\jmath} = 1.$

We derive the following theorem from Definition 10 using the 2TL$T$-SFH operations.

Theorem 1. Let $\mathcal{P}_{\jmath} = ((s_{p_{\jmath}}, \wp_{\jmath}), (s_{r_{\jmath}}, \Re_{\jmath}), (s_{l_{\jmath}}, £_{\jmath}))\; \left(\jmath = 1, 2, \ldots, n \right)$ be a collection of 2TL$T$-SFNs, with $\varrho > 0$. Then, for any $q\geq0$ the aggregated value by utilizing 2TL$T$-SFHWA operator is also a 2TL$T$-SFN, and

where $\varpi = \left(\varpi_{1}, \varpi_{2}, \ldots, \varpi_{n}\right)^{T}$ is the weight vector of $\mathcal{P}_{\jmath}\; \; \left(\jmath = 1, 2, \ldots, n\right),$ and $\varpi_{\jmath} > 0$, $\sum\limits_{\jmath = 1}^{n}\varpi_{\jmath} = 1.$

Proof. We use the mathematical induction principle to prove Eq (3.2).

For $n = 2$, by utilizing the operational laws (1) and (3) of Definition 9, we obtain the following result:

The result in Eq (3.2) holds true for $n = 2$. Suppose the result is true for $n = k$, and

When $n = k+1$, by using the operational laws of Definition 9, we have:

Hence Eq (3.2) is also true for $n = k+1$ and therefore, Eq (3.2) holds for all $n$.

Based on the parameter $\varrho$, we can derive the following special cases of Theorem 1.

Case 1. When $\varrho = 1$, 2TL$T$-SFHWA operator transforms to the 2TL$T$-SF weighted average operator.

Case 2. When $\varrho = 2$, 2TL$T$-SFHWA operator reduces to the 2TL$T$-SF Einstein weighted average operator.

Theorem 2. Let $\mathcal{P}_{\jmath} = ((s_{p_{\jmath}}, \wp_{\jmath}), (s_{r_{\jmath}}, \Re_{\jmath}), (s_{l_{\jmath}}, £_{\jmath}))$ and $\mathcal{P}_{\jmath}^{'} = ((s'_{p_{\jmath}}, \wp'_{\jmath}), (s'_{r_{\jmath}}, \Re_{\jmath}^{'}), (s'_{l_{\jmath}}, £_{\jmath}^{'}))\; \; \left(\jmath = 1, 2, \ldots, n\right)$ be two sets of 2TL$T$-SFNs; then the 2TL$T$-SFHWA operator has following properties:

1) (Idempotency) If all 2TL$T$-SFNs $\mathcal{P}_{\jmath} = ((s_{p_{\jmath}}, \wp_{\jmath}), (s_{r_{\jmath}}, \Re_{\jmath}), (s_{l_{\jmath}}, £_{\jmath}))\; (\jmath = 1, 2, \ldots, n)$ are equal, i.e., $\mathcal{P}_{\jmath} = \mathcal{P} = ((s_{p}, \wp), (s_{r}, \Re), (s_{l}, £))$ for all $\jmath$, then

Proof.

It is simple to follow the properties of boundedness, and monotonicity. As a result, their proofs are omitted.

2) (Boundedness) Let $\mathcal{P}_{\jmath}\; \left(\jmath = 1, 2, \ldots, n\right)$ be a collection of 2TL$T$-SFNs, and let $\mathcal{P}^{-} = \min_{\jmath} \mathcal{P}_{\jmath}$ and $\mathcal{P}^{+} = \max_{\jmath} \mathcal{P}_{\jmath}$, then

3) (Monotonicity) Let $\mathcal{P}_{\jmath}$ and $\mathcal{P}_{\jmath}^{'}\; \left(\jmath = 1, 2, \ldots, n\right)$ be two collections of 2TL$T$-SFNs, if $\mathcal{P}_{\jmath} \leq \mathcal{P}_{\jmath}^{'}$, for all $\jmath$, then

3.2.   The 2TL$T$-SFHOWA operator

The 2TL$T$-SFHWA aggregation operator weights the 2TL$T$-SFNs only. In the MAGDM environment, there are some situations when the ordered positions of the 2TL$T$-SFNs are significantly considered. The definition of ordered weighted averaging operators plays a significant role in these situations, and we define the 2TL$T$-SF Hamacher ordered weighted average (2TL$T$-SFHOWA) operator in terms of Definition 6 and the Hamacher operational laws of Definition 9 as below:

Definition 11. Let $\mathcal{P}_{\jmath} = ((s_{p_{\jmath}}, \wp_{\jmath}), (s_{r_{\jmath}}, \Re_{\jmath}), (s_{l_{\jmath}}, £_{\jmath}))\; \left(\jmath = 1, 2, \ldots, n \right)$ be a collection of 2TL$T$-SFNs, then the 2TL$T$-SFHOWA operator is defined as:

where $\left(\sigma\left(1\right), \sigma\left(2\right), \ldots, \sigma\left(n\right)\right)$ is a permutation of $\left(1, 2, \ldots, n\right),$ such that $\mathcal{P}_{\sigma\left(\jmath-1\right)}\geq \mathcal{P}_{\sigma\left(\jmath\right)}$ for all $\jmath = 2, \ldots, n$, and ${{w}} = \left({{w}}_{1}, {{w}}_{2}, \ldots, {{w}}_{n}\right)^{T}$ is the aggregation-associated weight vector such that ${{w}}_{\jmath}\in [0, 1]$ and $\sum\limits_{\jmath = 1}^{n}{{w}}_{\jmath} = 1$, $\varrho > 0.$

Based on Hamacher operations of the 2TL$T$-SF values described, we can derive the Theorem 3.

Theorem 3. Let $\mathcal{P}_{\jmath} = ((s_{p_{\jmath}}, \wp_{\jmath}), (s_{r_{\jmath}}, \Re_{\jmath}), (s_{l_{\jmath}}, £_{\jmath}))\; \left(\jmath = 1, 2, \ldots, n \right)$ be a collection of 2TL$T$-SFNs, where $\varrho > 0$. Then, for any $q\geq0$, the aggregated value by utilizing 2TL$T$-SFHOWA operator is also a 2TL$T$-SFN, and

Based on the parameter $\varrho$, we can derive the following special cases of Theorem 3.

Case 3. When $\varrho = 1$, 2TL$T$-SFHOWA operator transforms to the 2TL$T$-SF ordered weighted average operator.

Case 4. When $\varrho = 2$, 2TL$T$-SFHOWA operator reduces to the 2TL$T$-SF Einstein ordered weighted average operator.

The 2TL$T$-SFHOWA operator has the same properties as those proposed in Theorem 2.

3.3.   The 2TL$T$-SFHHA operator

The 2TL$T$-SFHWA operator only weights while the 2TL$T$-SFHOWA operator weights the ordered position of the 2TL$T$-SF arguments instead of the arguments themselves. We need to develop such operators that discuss the ordered position as well as the argument itself. To address this problem, we propose the concept of the 2-tuple linguistic $T$-spherical fuzzy Hamacher hybrid average (2TL$T$-SFHHA) operator in terms of Definition 6 and the Hamacher operational laws of Definition 9 that takes into account both the argument and its ordered position.

Definition 12. Let $\mathcal{P}_{\jmath} = ((s_{p_{\jmath}}, \wp_{\jmath}), (s_{r_{\jmath}}, \Re_{\jmath}), (s_{l_{\jmath}}, £_{\jmath}))\; \left(\jmath = 1, 2, \ldots, n\right)$ be a collection of 2TL$T$-SFNs, then the 2TL$T$-SFHHA operator is defined as:

where ${{w}} = \left({{w}}_{1}, {{w}}_{2}, \ldots, {{w}}_{n}\right)^{T}$ is the associated weighting vector such that ${{w}}_{\jmath}\in [0, 1]$ and $\sum\limits_{\jmath = 1}^{n}{{w}}_{\jmath} = 1$, and $\dot{\mathcal{P}}_{\sigma\left(\jmath\right)}$ is the $\jmath^{th}$ largest element of 2TL$T$-SF arguments $\dot{\mathcal{P}}_{\jmath}\left(\dot{\tilde {\varsigma}}_{\jmath} = \left(n\varpi_{\jmath}\right)\mathcal{P}_{\jmath}, \jmath = 1, 2, \ldots, n\right),$ $\varpi = \left(\varpi_{1}, \varpi_{2}, \ldots, \varpi_{n}\right)^{T}$ is the weighted vector of 2TL$T$-SF arguments $\mathcal{P}_{\jmath},$ with $\varpi_{\jmath}\in[0, 1]$ and $\sum\limits_{\jmath = 1}^{n}\varpi_{\jmath} = 1$, and $n$ is the balancing coefficient. Especially, if ${{w}} = \left(1/n, 1/n, \ldots, 1/n\right)^{T}$, then 2TL$T$-SFHHA is reduced to the 2TL$T$-SFHWA operator; if $\varpi = \left(1/n, 1/n, \ldots, 1/n\right)^{T}$, then 2TL$T$-SFHHA is reduced to the 2TL$T$-SFHOWA operator.

Based on Hamacher sum operations of the 2TL$T$-SF values described, we can derive the Theorem 4.

Theorem 4. Let $\mathcal{P}_{\jmath} = ((s_{p_{\jmath}}, \wp_{\jmath}), (s_{r_{\jmath}}, \Re_{\jmath}), (s_{l_{\jmath}}, £_{\jmath}))\; \left(\jmath = 1, 2, \ldots, n\right)$ be a collection of 2TL$T$-SFNs, where $\varrho > 0$. Then, its aggregated value by utilizing 2TL$T$-SFHHA operator is also a 2TL$T$-SFN, and

Based on parameter $\varrho$, we can obtain the following special cases of Theorem 4.

Case 5. When $\varrho = 1$, 2TL$T$-SFHHA operator transforms to the 2TL$T$-SF hybrid average operator.

Case 6. When $\varrho = 2$, 2TL$T$-SFHHA operator reduces to the 2TL$T$-SF Einstein hybrid average operator.

The 2TL$T$-SFHHA operator has the same properties as those proposed in Theorem 2.

3.4.   The 2TL$T$-SFHWG operators

In this subsection, for the purpose of addressing real-world issues, we take into account the significance of the aggregated data. We propose the 2-tuple linguistic $T$-spherical fuzzy Hamacher weighted geometric (2TL$T$-SFHWG) operator in terms of Definition 6 and the Hamacher operational laws of Definition 9.

Definition 13. Let $\mathcal{P}_{\jmath} = ((s_{p_{\jmath}}, \wp_{\jmath}), (s_{r_{\jmath}}, \Re_{\jmath}), (s_{l_{\jmath}}, £_{\jmath}))\; \left(\jmath = 1, 2, \ldots, n \right)$ be a collection of 2TL$T$-SFNs, then the 2TL$T$-SFHWG operator is defined as:

where $\varpi = \left(\varpi_{1}, \varpi_{2}, \ldots, \varpi_{n}\right)^{T}$ is the weight vector of $\mathcal{P}_{\jmath}\; \; \left(\jmath = 1, 2, \ldots, n\right),$ and $\varpi_{\jmath} > 0$, $\sum\limits_{\jmath = 1}^{n}\varpi_{\jmath} = 1.$

Using the 2TL$T$-SFH operations, we deduce the following Theorem from Definition 13.

Theorem 5. Let $\mathcal{P}_{\jmath} = ((s_{p_{\jmath}}, \wp_{\jmath}), (s_{r_{\jmath}}, \Re_{\jmath}), (s_{l_{\jmath}}, £_{\jmath}))\; \left(\jmath = 1, 2, \ldots, n \right)$ be a collection of 2TL$T$-SFNs, where $\varrho > 0$. Then, its aggregated value by utilizing 2TL$T$-SFHWG operator is also a 2TL$T$-SFN, and {

Based on the parameter $\varrho$, we can derive the following special cases of Theorem 5.

Case 7. When $\varrho = 1$, 2TL$T$-SFHWG operator transforms to the 2TL$T$-SF weighted geometric operator.

Case 8. When $\varrho = 2$, 2TL$T$-SFHWG operator reduces to the 2TL$T$-SF Einstein weighted geometric operator.

The 2TL$T$-SFHWG operator has the same properties as those proposed in Theorem 2.

3.5.   The 2TL$T$-SFHOWG operator

The 2TL$T$-SFHWG aggregation operator weights the 2TL$T$-SFNs only. In MAGDM problem, there are some situations when the ordered positions of the 2TL$T$-SFNs are significantly considered. The definition of ordered weighted geometric operator plays a significant role in these situations, and we define the 2-tuple linguistic $T$-spherical fuzzy Hamacher ordered weighted geometric (2TL$T$-SFHOWG) operator in terms of Definition 6 and the Hamacher operational laws of Definition 9.

Definition 14. Let $\mathcal{P}_{\jmath} = ((s_{p_{\jmath}}, \wp_{\jmath}), (s_{r_{\jmath}}, \Re_{\jmath}), (s_{l_{\jmath}}, £_{\jmath}))\; \left(\jmath = 1, 2, \ldots, n\right)$ be a collection of 2TL$T$-SFNs, then the 2TL$T$-SFHOWG operator is defined as:

where $\left(\sigma\left(1\right), \sigma\left(2\right), \ldots, \sigma\left(n\right)\right)$ is a permutation of $\left(1, 2, \ldots, n\right)$, such that $\mathcal{P}_{\sigma\left(\jmath-1\right)}\geq \mathcal{P}_{\sigma\left(\jmath\right)}$ for all $\jmath = 2, \ldots, n,$ and ${{w}} = \left({{w}}_{1}, {{w}}_{2}, \ldots, {{w}}_{n}\right)^{T}$ is the aggregation-associated weight vector such that ${{w}}_{\jmath}\in [0, 1]$ and $\sum\limits_{\jmath = 1}^{n}{{w}}_{\jmath} = 1$.

Theorem 6. Let $\mathcal{P}_{\jmath} = ((s_{p_{\jmath}}, \wp_{\jmath}), (s_{r_{\jmath}}, \Re_{\jmath}), (s_{l_{\jmath}}, £_{\jmath}))\; \left(\jmath = 1, 2, \ldots, n\right)$ be a collection of 2TL$T$-SFNs, where $\varrho > 0$. Then, its aggregated value by utilizing 2TL$T$-SFHOWG operator is also a 2TL$T$-SFN, and

Case 9. When $\varrho = 1$, 2TL$T$-SFHOWG operator transforms to the 2TL$T$-SF ordered weighted geometric operator.

Case 10. When $\varrho = 2$, 2TL$T$-SFHOWG operator reduces to the 2TL$T$-SF Einstein ordered weighted geometric operator.

The 2TL$T$-SFHOWG operator has the same properties as those proposed in Theorem 2.

3.6.   The 2TL$T$-SFHHG operator

The 2TL$T$-SFHOWG operator weights the ordered positions of the 2TL$T$-SF arguments instead of the arguments themselves. As a result, weights in the 2TL$T$-SFHWG and 2TL$T$-SFHOWG operators describe different aspects. However, only one of them is taken into account by both operators. We need to develop such operators that discuss the ordered position as well as the argument itself. To address this problem, in the following subsection, we propose the 2-tuple linguistic $T$-spherical fuzzy Hamacher hybrid geometric (2TL$T$-SFHHG) operator in terms of Definition 6 and the Hamacher operational laws of Definition 9.

Definition 15. Let $\mathcal{P}_{\jmath} = ((s_{p_{\jmath}}, \wp_{\jmath}), (s_{r_{\jmath}}, \Re_{\jmath}), (s_{l_{\jmath}}, £_{\jmath})) \; \left(\jmath = 1, 2, \ldots, n\right)$ be a collection of 2TL$T$-SFNs, then the 2TL$T$-SFHHG operator is defined as:

where ${{w}} = \left({{w}}_{1}, {{w}}_{2}, \ldots, {{w}}_{n}\right)^{T}$ is the associated weighting vector, with ${{w}}_{\jmath}\in [0, 1]$, $\sum\limits_{\jmath = 1}^{n}{{w}}_{\jmath} = 1,$ and $\dot{\mathcal{P}}_{\sigma\left(\jmath\right)}$ is the $\jmath^{th}$ largest element of 2TL$T$-SF arguments $\dot{\mathcal{P}}_{\jmath}$ $\left(\dot{\mathcal{P}}_{\jmath} = \left(\mathcal{P}_{\jmath}\right)^{n\varpi_{\jmath}}, \; \jmath = 1, 2, \ldots, n\right),$ $\varpi = \left(\varpi_{1}, \varpi_{2}, \ldots, \varpi_{n}\right)$ is the weighted vector of 2TL$T$-SF arguments $\mathcal{P}_{\jmath},$ with $\varpi_{\jmath}\in [0, 1]$ and $\sum\limits_{\jmath = 1}^{n}\varpi_{\jmath} = 1$, and $n$ is the balancing coefficient, $\varrho > 0$. Especially, if ${{w}} = \left(1/n, 1/n, \ldots, 1/n\right)^{T}$, then 2TL$T$-SFHHG is reduced to the 2TL$T$-SFHWG operator; if $\varpi = \left(1/n, 1/n, \ldots, 1/n\right)^{T}$, then 2TL$T$-SFHHG is reduced to the 2TL$T$-SFHOWG operator.

Based on Hamacher product operations of the 2TL$T$-SF values described, we can derive the Theorem 7.

Theorem 7. Let $\mathcal{P}_{\jmath} = ((s_{p_{\jmath}}, \wp_{\jmath}), (s_{r_{\jmath}}, \Re_{\jmath}), (s_{l_{\jmath}}, £_{\jmath}))\; \left(\jmath = 1, 2, \ldots, n \right)$ be a collection of 2TL$T$-SFNs, with $\varrho > 0$. Then, its aggregated value by utilizing 2TL$T$-SFHHG operator is also a 2TL$T$-SFN, and

We can derive the following special cases of Theorem 7 based on the parameter $\varrho$.

Case 11. When $\varrho = 1$, 2TL$T$-SFHHG operator transforms to the 2TL$T$-SF hybrid geometric (2TL$T$-SFHG) operator.

Case 12. When $\varrho = 2$, 2TL$T$-SFHHG operator reduces to the 2TL$T$-SF Einstein hybrid geometric (2TL$T$-SFEHG) operator.

The 2TL$T$-SFHHG operator has the same properties as those proposed in Theorem 2.

4.   A novel approach for MAGDM within 2TL$T$-SF environment

In this section, we present a new method to deal with MAGDM problems. The proposed method is known as 2TL$T$-SF-CODAS model based on 2TL$T$-SFHWA and 2TL$T$-SFHWG operators by considering the flexibility of 2TL$T$-SFNs. The desirability of alternatives is calculated using two measures in this method. The largest and most important measurement is the Euclidean distance (ED) between alternatives and the negative-ideal solution (NIS) and the second measure is the Hamming distance (HD). It is clear that the alternative which has greater distance from the NIS is more desirable. The ED and HD measures are used for the relative assessment (RA) of alternatives in order to construct the RA based matrix to fuse the information.

Suppose there are $m$ alternatives ${{A}} = \{{{A}}_{1}, {{A}}_{2}, \ldots, {{A}}_{m}\}$, $n$ attributes $\hbar = \{\hbar_{1}, \hbar_{2}, \ldots, \hbar_{n}\}$, and $g$ experts $E = \{e_{1}, e_{2}, \ldots, e_{g}\}$, and let $\varpi = (\varpi_{1}, \varpi_{2}, \ldots, \varpi_{n})^{T}$ and $\varpi' = (\varpi'_{1}, \varpi'_{2}, \ldots, \varpi'_{g})^{T},$ respectively be the weighting vector of the attributes and weighting vector of the experts satisfying $\varpi_{\jmath}\in[0, 1]$, $\varpi'_{\ell}\in[0, 1]$, $\sum_{\jmath = 1}^{n}\varpi_{\jmath} = 1$, and $\sum\limits_{\ell = 1}^{g} \varpi'_{\ell} = 1$. The technique of implementing the 2TL$T$-SF-CODAS approach is described in the following steps:

$\textbf{Step 1}.$ Switch the linguistic information into 2TL$T$-SFNs $r_{{\imath\jmath}}^{\ell} = (({s_{{p}_{\imath\jmath}^{\ell}}}, {\wp_{\imath\jmath}^{\ell}}), ({s_{{r}_{\imath\jmath}^{\ell}}}, {\Re_{\imath\jmath}^{\ell}}), ({s_{{l}_{\imath\jmath}^{\ell}}}, {£_{\imath\jmath}^{\ell}})) \; (\ell = 1, 2, \ldots, g)$.

$\textbf{Step 2}.$ According to 2TL$T$-SFNs $r^{\ell}_{{\imath\jmath}} = (({s_{{p}_{\imath\jmath}^{\ell}}}, {\wp_{\imath\jmath}^{\ell}}), ({s_{{r}_{\imath\jmath}^{\ell}}}, {\Re_{\imath\jmath}^{\ell}}), ({s_{{l}_{\imath\jmath}^{\ell}}}, {£_{\imath\jmath}^{\ell}})) (\ell = 1, 2, \ldots, g)$ and by utilizing Eqs (3.2) and (3.8), independent panel evaluations can be combined to form the fused 2TL$T$-SFNs matrix $r_{{\imath\jmath}} = (({s_{{p}_{\imath\jmath}}}, {\wp_{\imath\jmath}}), ({s_{{r}_{\imath\jmath}}}, {\Re_{\imath\jmath}}), ({s_{{l}_{\imath\jmath}}}, {£_{\imath\jmath}}))$ as:

$\textbf{Step 3}.$ Calculate the weighted 2TL$T$-SFNs matrix as follows:

where $\varpi_{{\jmath}}$ means the attribute weight of $\hbar_{{\jmath}}$, and $0\leq \varpi_{{\jmath}}\leq 1$, $\sum\limits_{\jmath = 1}^{n}\varpi_{{\jmath}} = 1$.

$\textbf{Step 4}.$ Calculate the NIS by using 2TL$T$-SFNs' score and accuracy functions (if the score functions are similar, the accuracy functions are used to rank the 2TL$T$-SFNs):

$\textbf{Step 5}.$ Calculate the weighted $ED_{\imath}$ and $HD_{\imath}$ as follows:

where HD and ED of two 2TL$T$-SFNs $\mathcal{P}_1 = ((s_{p_{1}}, \wp_{1}), (s_{~~ r_{1}}, \Re_{1}), (s_{l_{1}}, £_{1}))$ and $\mathcal{P}_2 = ((s_{p_{2}}, \wp_{2}), (s_{~~ r_{2}}, \Re_{2}), (s_{l_{2}}, £_{2}))$, defined as:

$\textbf{Step 6}.$ In the following equations, build the relative assessment matrix RA:

where $\ell \in \{1, 2, 3, \cdots, m\}$ and $\mathfrak{g}$ denotes a significant function that could be designed:

where $\Im \in[0.01, 0.05]$ given by DMs. In our study, $\Im = 0.02$.

$\textbf{Step 7}.$ Derive the average solution ($AS_{\imath}$) by using:

$\textbf{Step 8}.$ On the basis of computing outcomes of $AS_{\imath}$, all the alternatives can be ranked. The best option has the highest evaluation score.

5.   Numerical illustration

We choose a case study that focuses on computational architecture and dimensional synthesis of the parallel linear delta robot for additive manufacturing to explain our proposed novel methodology. According to the research, various parallel robots have been introduced, with many of these architectures being genuinely innovative. However, the linear delta robot has by far the most common, has used in pick and place operations, packaging, welding, computer numerical control operations, and additive manufacturing over the years. Two platforms make up a linear delta robot with three degrees of freedom. Each kinematic chain is created by links parallelogram with $T$-spherical joints, and one of the platforms is typically described as mobile. Because of their low inertia, precision, and speed, linear delta robots of this kind perform exceptionally well. Despite both of these benefits, the absence of linear delta robotics result in a decline in working areas. Many experiments have focused on the dimensional optimization of linear delta robots to solve this problem, which assures good results. Regarding that, due to the production group's familiarity with additive manufacturing systems, the customer specifications are established. In their survey, they list $29$ consumers and design criteria that have significant and minor effects on the design of linear delta robots. The most significant customer specifications, according to the article, are the robot capability segment, printing standard, speed burst, massive workspace, long ongoing cycle, and printing with various materials.

In our study, the selected customer requirements (what is) and the design requirements (how is) of the linear delta robots for additive manufacturing are arranged on the decision-making matrix.} Comprehensive above, the set of seven alternatives ${{A}} = \{{{A}}_{1}, {{A}}_{2}, \ldots{{A}}_{7}\}$ is evaluated by four experts $E = \{e_{1}, e_{2}, e_{3}, e_{4}\}$ which are composed of experienced engineers and customers in additive manufacturing at each evaluation stage having weights $\varpi' = (0.2, 0.4, 0.3, 0.1)^{T}$. The four experts use the four attributes such as pace of movement $(\hbar_{1}$), temperature regulation array $(\hbar_{2})$, system total cost $(\hbar_{3})$, and protection criteria $(\hbar_{4})$ with weighting vector $\varpi = (0.17, 0.31, 0.27, 0.25)^{T}$ to select the best alternatives for additive manufacturing of linear delta robot.

The linguistic variables of 2TL$T$-SFNs are recorded in Table 1.

Establish the 2TL$T$-SF evaluation matrix $R_{\ell} = [r^{\ell}_{\imath\jmath}]_{7\times 4}(\ell = 1, 2, 3, 4)$ in Table 2 based on linguistic variables listed in Table 1, which are the assessments of four DMs.

Transformation of the linguistic decision matrix given in Table 2 into 2TL$T$-SF decision matrix shown in Table 3.

5.1.   Results of the case study

5.1.1.   Decision-making procedure based on the 2TL$T$-SFHWA operator

The proposed methodology is used to evaluate seven different additive manufacturing alternatives (linear delta robots) by utilizing 2TL$T$-SFHWA operator.

Individual expert assessments can be integrated into the collective assessing matrix with 2TL$T$-SFNs, according to Tables 2 and 3 and Eq (3.2) (see Table 4).

Determine the weighted assessing matrix with 2TL$T$-SFNs (see Table 5).

Calculate the NIS by Eq (4.4):

Calculate the $ED_{\imath}$ and $HD_{\imath}$:

Determine the RA matrix (see Table 6).

Derive the $AS_{\imath}$ by using Eq (4.12). The results of $AS_{\imath}$ are as follows:

On the basis of computing results of $AS_{\imath}$, all the alternatives can be ranked. The ranking of alternatives is as follows: ${{A}}_1 > {{A}}_6 > {{A}}_7 > {{A}}_4 > {{A}}_2 > {{A}}_3 > {{A}}_5$. So, ${{A}}_1$ is the best alternative.

5.1.2.   Decision-making procedure based on the 2TL$T$-SFHWG operator

Individual expert assessments can be integrated into the collective assessing matrix with 2TL$T$-SFNs, according to Tables 2 and 3 and Eq (3.6) (see Table 7).

Determine the weighted assessing matrix with 2TL$T$-SFNs (see Table 8).

Calculate the NIS by Eq (4.4):

Calculate the $ED_{\imath}$ and $HD_{\imath}$:

Determine the RA matrix (see Table 9).

Derive the $AS_{\imath}$ by using Eq (4.12). The results of $AS_{\imath}$ are as follows:

On the basis of computing results of $AS_{\imath}$, all the alternatives can be ranked. The ranking of alternatives is as follows: ${{A}}_4 > {{A}}_1 > {{A}}_6 > {{A}}_7 > {{A}}_2 > {{A}}_3 > {{A}}_5$. So, ${{A}}_4$ is the best alternative.

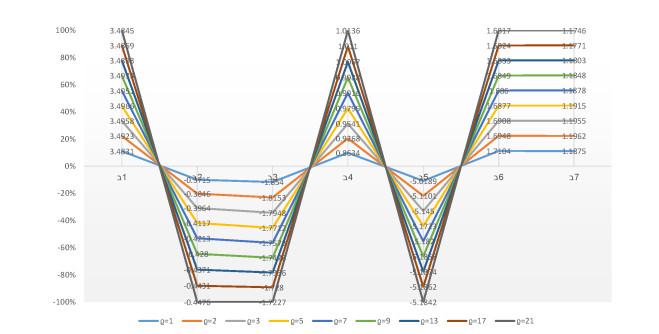
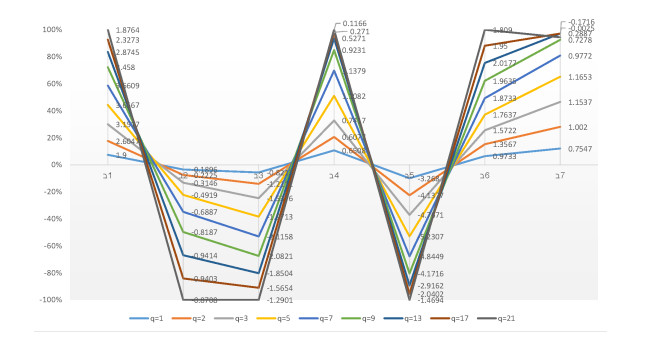
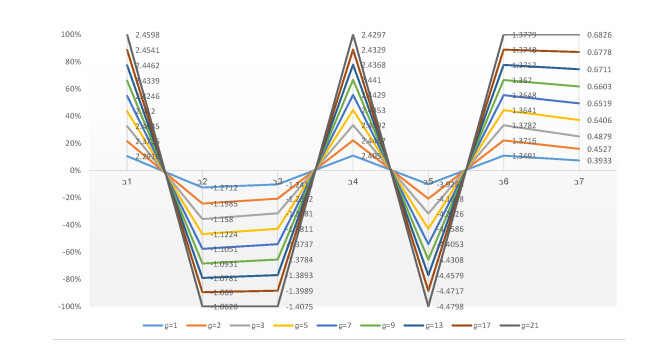
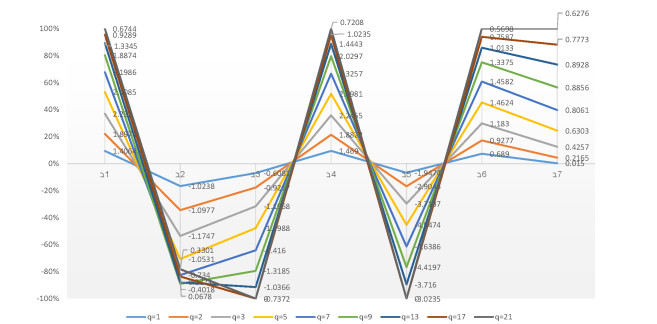
5.2.   Parametric analysis

The parameter $\varrho$ is used in this research study to explain the interdependence of distinct quantifiable attributes and the various numerical values of parameters $\varrho$ illustrate the various decision-making possibilities and circumstances. Under the supposition of preserving $q$ ($q = 4$), the parameter $\varrho$ is given alternate numerical values using the numerical illustration data in Table 3. Numerous rating scoring outcomes for optimal linear delta robot selection are achieved by adjusting the numerical value of the parameter $\varrho$ and the outcomes are shown in Tables 10 and 11 by utilizing the 2TL$T$-SFHWA. The scoring values of each linear delta robot vary depending on the value of parameter $\varrho$ and the derived results are roughly the same. When we allocate distinguishable numerical values to the parameter $\varrho$, the best alternatives are ${{A}}_{1}$ and ${{A}}_{4}$. The order of the results of the analysis tends to vary when $\varrho = 1, 2, 3, 5, 7, 9, 13, 17, 21$ by utilizing the 2TL$T$-SFHWA and 2TL$T$-SFHWG operators. As a result, updating the numerical value of $\varrho$ influences the outcomes for the optimal selection of linear delta robots. The DMs can change the numerical value of parameter $\varrho$ to accommodate the complex scenario and achieve the evaluation results during the actual decision-making procedure. We can also summarize from the appraisal scoring results as shown in Tables 12 and 13 for the 2TL$T$-SFHWG AOs proposed in this research study are the best approaches to summarize aggregated decision information by the 2TL$T$-SFNs because these two operators make the information aggregation procedure more credible with parameters. When $q = 1, 2, 3, 5, 7, 9, 13, 17, 21$, the achieved results vary depending on whether the 2TL$T$-SFHWA or 2TL$T$-SFHWG operator is used. By allocating numerical values to parameter $q$, the range of explaining decision information is expanded and reduces the loss of important aggregated information. Graphical representation of the variation of parameters is given in Figures 2–5.

The score values of each chosen alternative change depending on the value of the parameter, but the resultant outcomes are roughly the same. The ranking order of the alternatives varies due to the basic behavior variation of parameter $\varrho$ and values of $q$. Even so, in most cases, the most appropriate alternatives are the same as shown in Tables 10–13 and Figures 2–5.

5.3.   Comparative analysis

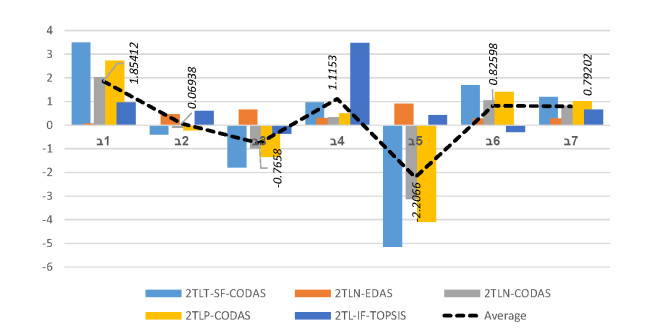
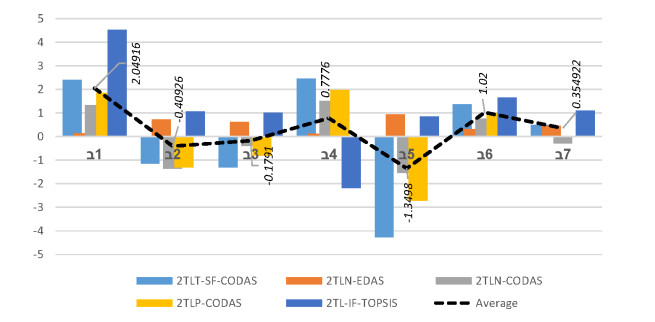
We employ specific validated approaches to deal with the suggested MAGDM problem under this subsection, and we assess the results with developed approach to verify if it is feasible and successful. We compute the evaluation results for the selection of optimal alternative for the manufacturing of linear delta robots by using the different existing and proposed approaches. Tables 14 and 15 summarize the output of the comparison among the developed 2TL$T$-SF-CODAS approach and existing 2-tuple linguistic picture fuzzy (2TLPF-CODAS), 2-tuple linguistic spherical fuzzy (2TLSF-CODAS), 2-tuple linguistic neutrosophic fuzzy-EDAS (2TLNF-EDAS), 2-tuple linguistic neutrosophic fuzzy-CODAS (2TLNF-CODAS), 2-tuple linguistic Pythagorean fuzzy-CODAS (2TLPyF-CODAS), and 2-tuple linguistic IF-TOPSIS methodologies. Further details can be seen in Figures 6 and 7, where the black dotted line represents the average.

There are certain differences in the priority order of alternatives because of the fundamental behavior of several aggregating methodologies. However, as demonstrated in Tables 14 and 15, the most appropriate alternatives are the same in both the present and existing techniques. Hence, from the comparison results with existing 2TLPF-CODAS, 2TLSF-CODAS, 2TLNF-EDAS, 2TLNF-CODAS, 2TLPyF-CODAS, and 2TL-IF-TOPSIS methodologies, we can conclude that the best alternatives for the manufacturing of linear delta robot are same. In a summary, the strategy we propose is broad and applicable to solve MAGDM problems with 2TL$T$-SFNs.

2TLPFS is the special case of 2TL$T$-SFS when $q = 1$. We obtained the same ranking results when comparing the proposed method to the 2TLPF-CODAS method. However, slightly different ranking results are obtained when comparing the proposed method to 2TL$T$-SF-CODAS method, but the preferred alternative is ${{A}}_{1}$ or ${{A}}_{4}$. The range of the 2TLSFS is wider than 2TLPFS but limited in comparison to 2TL$T$-SFS as it is the special case of 2TL$T$-SFS when $q = 2$. Consequently, the proposed approach is more intuitive.

6.   Conclusions

The practical implications of the paper are as follows. Experts can relate the language words listed in Table 2 to the 2TL$T$-SF-QFD model that has been suggested. When people are unsure about two succeeding phrases, they could give intermediate language terms. Their appropriate numerical values were easily extracted from the paper's linguistic scales in Table 3. The use of the 2TL$T$-SF geometric aggregation operator made it simple to combine the opinions of experts and customers. The 2TL$T$-SF arithmetic operator has been used, to sum up, both positive and negative correlations. In contrast to the majority of QFD articles, the suggested model incorporates all of the functions at an HoQ. HoQ implements competitive advantage analysis for both CRs and DRs. The innovative methods 2TL$T$-SF-QFD and 2TL$T$-SF-CODAS are used to assess a company's position among its rivals. The 2TL$T$-Spherical fuzzy sets take ambiguity and imprecision in linear delta robot design into account. Assigning membership, nonmembership, and reluctance separately takes place inside a wider domain. The process of developing a linear delta robot is extensive and is dependent on several clients and design criteria. The suggested model might incorporate all of the many tasks carried out by the HoQ, such as the relationships between customer needs and design specifications and competitive studies from the perspectives of both consumers and specialists. The HoQ can employ linguistic expressions thanks to this concept. It could also consider the degrees of hesitation that customers or experts exhibit while giving assessments on a linguistic scale. The fuzzy set theory-based numerical analysis can include linguistic concepts. The concept has been used to build linear delta robot technology with success. Existing decision-making strategies in the literature were incapable of dealing with 2-tuple linguistic $T$-Spherical fuzzy information. In response, we developed a new MAGDM approach in order to overcome MAGDM problems in the 2TL$T$-SF environment. We introduced novel aggregation operators, given the correlation structure among arguments. The 2TL terms can better reflect human perceptions and $T$-SFSs are more reliable due to the $qth$ power of MD, AD, and NMD. Consequently, we have expanded the arithmetic mean, geometric mean, and hybrid operators into the 2TL$T$-SF environment and utilized Hamacher operational rules to propose six novels AOs which are: the 2TL$T$-SFHWA operator, 2TL$T$-SFHOWA operator, 2TL$T$-SFHHA operator, 2TL$T$-SFHWG operator, 2TL$T$-SFHOWG operator, and 2TL$T$-SFHHG operator. Additionally, we have developed a novel decision-making technique entitled the 2TL$T$-SF-CODAS approach to work out 2TL$T$-SF-MAGDM problems. Finally, we solved the problem of selecting the best alternatives for additive manufacturing of linear delta robot by using our newly developed MAGDM approach. Since this approach efficiently represents the interaction among the many given arguments as well as provides more space for DMs to communicate their fuzzy knowledge, our proposed approach is more generic and versatile than other approaches. The limitation of the study is that the levels of linguistic scale may not be sufficient for experts to assign. Consequently, extra levels might be incorporated into the scale to take into account the range of possible expert opinions. Depending on the technique described in our investigations, the following aspects can be pursued in future research. As fundamental concepts, the 2TL$T$-SFS notion and its corresponding concepts can be further extended, for example, the identification of the similarity and distance assessment between 2TL$T$-SFSs can reveal additional aspects of fuzzy information. Our approach can also be applied to medical diagnoses, purchasing choices, and potential investment evaluation like ^{[59,60,61,62,63]}.

Acknowledgments

The research of Santos-García was funded by the Spanish project ProCode-UCM (PID2019-108528RB-C22) from the Ministerio de Ciencia e Innovación.

Conflict of interest

The authors declare no conflict of interest.