Non-separated inclusion problem via generalized Hilfer and Caputo operators

1.   Introduction

Fractional differential inclusions (FDIs), as an extension of fractional differential equations (FDEs), have gained popularity among mathematical researchers due to their importance and value in optimization and stochastic processes in economics ^[1,2] and finance ^[3]. In addition to their applications in understanding engineering ^[4] and dynamic systems ^[5,6] in biological ^[7,8], medical ^[9], physics ^[10] and chemical sciences ^[11], FDIs are also relevant in various other scientific fields ^[12].

Sousa and Oliveira ^[13] introduced the new fractional derivative $\varsigma$-Hilfer to unify different types of fractional derivatives into a single operator, expanding fractional derivatives to the types of operators with potentially applicable value. After that, Asawasamrit et al. ^[14] investigated the following Hilfer-FDE under nonlocal integral boundary conditions (BCs):

In ^[15], an existence outcome was shown by employing the FPTs (fixed-point theorems) for a sequential FDE of the type,

where $r_{i}\in \left(0, 1\right)$, $i = 1, 2, 3$, $r_{4} = r_{1}+r_{2}\left(1-r_{1}\right)$, $r_{4} +r_{3} > 1$, $\eta _{1}, \eta _{2} \in \mathbb{R}$, $r_{5} > 0$, and $\gimel \in C \big(\mathfrak{B}\times \mathbb{R}^3 \big)$ is a nonlinear function. In 2024, Ahmed et al. ^[16] investigated a class of separated boundary value problems of the form

where $0 < r_1, r_3 < 1$, $r_2 \in [0, 1]$ with $r_4 = r_1+ r_2(1-r_1)$, $r_3+r_4 > 1$ and $\gimel \in C(\mathfrak{B} \times \mathbb{R})$. Lachouri et al., in ^[17], established the existence of solutions to the nonlinear neutral FDI involving $\varsigma$-Caputo fractional derivative with $\varsigma$-Riemann–Liouville (RL) fractional integral boundary conditions:

where $\gimel : \mathfrak{B} \times \mathbb{R} \to \mathcal{P} (\mathbb{R})$ is a set-valued map. Surang et al., in ^[18], studied the $\varsigma$-Hilfer type sequential FDEs and FDIs subject to integral multi-point BCs of the form

where $r_{1}\in \left(1, 2\right)$, $r_{2}\in \left[ 0, 1\right]$, $\gimel \in C\left(\mho \times \mathbb{R}\right)$, $k, \mu _{i}, \theta _{j}\in \mathbb{R}$, and $\eta _{i}, \xi _{j}\in (\tilde{s}, \tilde{b}]$, $i = \overline{1, \, n}$, $j = \overline{1, \, m}$. Etemad et al. ^[19] introduced and studied a novel existence technique based on some special set-valued maps (SVMs) to guarantee the existence of a solution for the following fractional jerk inclusion problem involving the derivative operator in the sense of Caputo–Hadamard

for $\upsilon \in [1, \exp(1)]$, where $r_i \in (0, 1]$, $i = 1, 2, 3$, $\eta \in (1, \exp(1))$, and the operator $\gimel : [1, \exp(1)]\times \mathbb{R}^3 \to \mathcal{P}(\mathbb{R})$ is an SVM, where $\mathcal{P}(\mathbb{R})$ denotes all nonempty subsets of $\mathbb{R}$.

The boundary conditions (BCs) used in (1.1) and (1.2), share a common feature: the requirement of a zero initial condition, which is essential for the solution to be well-defined. Consequently, certain classes of Hilfer FDEs cannot be addressed, including cases with BCs such as,

● $\varkappa (0) = -\varkappa \big(\tilde{b} \big)$, $\varkappa ^{\prime } (0) = - \varkappa ^{\prime } \big(\tilde{b} \big)$ (anti-periodic),

● $\varkappa \left(0\right) +\eta_1 \varkappa ^{\prime }(0) = 0$, $\varkappa \big(\tilde{b} \big) + \eta_2 \varkappa ^{\prime } \big(\tilde{b} \big) = 0$ (separated),

● $\varkappa (0) +\eta_1 \varkappa \big(\tilde{b} \big) = 0$, $\varkappa ^{\prime } \left(0\right) + \eta_2\varkappa ^{\prime } \big(\tilde{b} \big) = 0$ (non-separated), etc.

To address this limitation and study Hilfer FDEs with such BCs, regardless of whether they are anti-periodic, separated, or non-separated, we propose a novel approach in this research. Specifically, we combine the Hilfer and Caputo fractional derivatives, enabling the study of boundary value problems under these conditions. More specifically, we aimed to analyze a class of FDEs for FDI, subject to non-separated BCs of the form,

where $r_{i}\in \left(0, 1\right)$, $i = 1, 2, 3$, $\delta = r_{1}+r_{2}\left(1-r_{1}\right)$, $\delta +r_{3} > 1$, $\eta _{1}, \eta _{2} \in \mathbb{R}$, $\mathbb{y} \in C (\mathfrak{B} \times \mathbb{R})$ and $\gimel : \mathfrak{B} \times \mathbb{R} \to \mathcal{P} (\mathbb{R})$ denotes a SVM, with power set $\mathcal{P} (\mathbb{R})$ of $\mathbb{R}$.

The paper is structured as follows. Section 2 is devoted to discussing the fundamental concepts fractional calculus and set-valued analysis, while Section 3 presents important findings on the qualitative properties of solutions to the $\varsigma$-Hilfer inclusion FDI (1.3) utilizing FPTs. Finally, Section 4, includes three illustrative examples.

2.   Background concepts

2.1.   Fractional calculus

We outline the background material that is pertinent to our study. We consider the Banach spaces $\mathbb{E} = C\left(\mathfrak{B}\right)$ and $L^{1}\left(\mathfrak{B}\right)$ of the Lebesgue integrable functions equipped with the norms $\left\Vert \varkappa \right\Vert = \sup \big\{ \left\vert \varkappa \left(\upsilon \right) \right\vert \, :\, \upsilon \in \mathfrak{B} \big\}$ and

respectively. Let $\varsigma \in C^{n}\left(\mathfrak{B}\right)$ be an increasing function such that $\varsigma ^{\prime } \left(\upsilon \right) \neq 0$, for any $\upsilon \in \mathfrak{B}$.

Definition 2.1 (^[20]). The $\varsigma$-RL fractional integral and derivative of order $r_1$ for a given function $\varkappa$ are expressed by

and

where $n = \left[ r_1 \right] +1$, $n\in \mathbb{N}$, respectively.

Definition 2.2 (^[21,22]). The Caputo sense of $\varsigma$-fractional derivative of the $\varkappa \in C^{n} \left(\mathfrak{B}\right)$ of order $r_1$ is given as,

Lemma 2.3 (^[20,22]). Let $r_1, r_2 > 0$. Then

Lemma 2.4 (^[20]). For $\varkappa\in C^{n}\left(\mathfrak{B}\right)$, we have

and $0 < r_{2} < 1$. Furthermore, if $r_1\in \left(0, 1 \right)$, then ${}^{\mathrm{RL}\!}{ }{\mathfrak{I}}^{r_1, \varsigma } {}^{\mathrm{C}\!}{}{\mathfrak{D}}^{r_1, \varsigma }\ \varkappa \left(\upsilon \right) = \varsigma_0 (\upsilon)$.

Definition 2.5 (^[13]). The $\varsigma$-Hilfer fractional derivative for $\varkappa \in C^n\left(\mathfrak{B} \right)$, of order $n-1 < r_1 < n$ and type $0\leq r_2 \leq 1$, is defined by

Lemma 2.6 (^[13,23]). Let $r_1, r_2, \mu > 0$. Then

Lemma 2.7 (^[13]). For $\mu > 0$, $r_1 \in \left(n-1, n \right)$, and $0\leq r_2\leq 1$,

In particular, if $r_1 \in \left(1, 2 \right)$ and $1 < \mu \leq 2$, then $^{\mathrm{H}\!}{ }{\mathfrak{D}}^{r_1, r_2, \varsigma }\left(\varsigma_0 (\upsilon) \right) ^{\mu-1} = 0$.

Lemma 2.8 (^[13]). If $\varkappa \in C^{n}\left(\mathfrak{B}\right)$, $n-1 < r_1 < n$ and type $0 < r_2 < 1$, then

2.2.   Auxiliary notions of set-valued maps

Consider the Banach space $\left(\mathbb{E}, \left\Vert \cdot \right\Vert \right)$ and SVM $\Theta : \mathbb{E} \to \mathcal{P}\left(\mathbb{E}\right)$. $\Theta$ is a) closed (convex), b) bounded and c) measurable, whenever $\Theta \left(\varkappa \right)$ is closed (convex) for every $\varkappa \in \mathbb{E}$, $\Theta (B) = \cup _{\varkappa \in B} \Theta \left(\varkappa \right)$ is bounded for any bounded set $B \subseteq \mathbb{E}$, that is

and $\forall \rho \in \mathbb{R}$, the function

is measurable, respectively. One can find the definitions of completely continuous and upper semi-continuous in ^[24]. Additionally, the set of selections of $\gimel$ is described as

Next, we take

where $\mathcal{P}_{\mathrm{cl}}$, $\mathcal{P}_{\mathrm{c}}$, $\mathcal{P}_{\mathrm{b}}$, and $\mathcal{P}_{\mathrm{cp}}$ represent the classes of every compact, bounded, closed, and convex subset of $\mathbb{E}$, respectively.

Definition 2.9 (^[25]). An SVM $\gimel : \mathfrak{B} \times \mathbb{R} \to \mathcal{P} \left(\mathbb{R}\right)$ is called Carathéodory if the mapping $\upsilon \to \gimel \left(\upsilon, \varkappa \right)$ is measurable for all $\varkappa \in \mathbb{R}$, and $\varkappa \to \gimel \left(\upsilon, \varkappa \right)$ is upper semicontinuous for almost every $\upsilon \in \mathfrak{B}$. Additionally, we say $\gimel$ is $L^1$-Carathéodory whenever for all $m > 0$, exists $z \in L^1 \left(\mathfrak{B}, \mathbb{R}^+ \right)$ such that for a.e. $\upsilon \in \mathfrak{B}$,

To achieve the intended outcomes in this search, the following lemmas are necessary.

Lemma 2.10 (^[25], Proposition 1.2). Consider SVM $\Theta : \mathbb{E} \to \mathcal{P}_{\mathrm{cl}} (Z)$ with the graph, $\operatorname{Gr} (\Theta) = \big\{ \left(\varkappa, \rho \right) \in \mathbb{E} \times Z \, : \, \rho \in \Theta (\varkappa) \big\}$. $\operatorname{Gr} (\Theta)$ is a closed subset of $\mathbb{E} \times Z$ whenever $\Theta$ is upper semi-continuous. Conversely, $\Theta$ is upper semi-continuous, when it has a closed graph and is completely continuous.

Lemma 2.11 (^[26]). Consider a separable Banach space $\mathbb{E}$ along with a $L^1$-Carathéodory SVM $\gimel: \mathfrak{B} \times \mathbb{R} \to \mathcal{P}_{\mathrm{cp}, \mathrm{c} } \left(\mathbb{E} \right)$ and a linear continuous map $\Upsilon: L^1 \left(\mathfrak{B}, \mathbb{E} \right) \to C \left(\mathfrak{B}, \mathbb{E}\right)$. Then, the composition

is a closed graph map in $C\left(\mathfrak{B}, \mathbb{E} \right) \times C \left(\mathfrak{B}, \mathbb{E} \right)$.

3.   Existence results for fractional differential inclusion (1.3)

In relation to the FDI (1.3), the auxiliary Lemma 3.1 is required.

Lemma 3.1. For $\mathbb{y}, \gimel\in C(\mathfrak{B})$, the solution of linear-type problem

is obtained as follows:

where for $\eta_1, \eta_2\neq -1$,

Proof. Applying the $\varsigma$-fractional integral $^{\mathrm{RL}\!}{}{\mathfrak{I}}^{r_1, \varsigma }$ to the first equation of (1.3), and using Lemma 2.4, we get

where $\delta = r_{1} + r_2 \left(1 - r_1\right)$. Now, by taking $^{\mathrm{RL}\!}{}{\mathfrak{I}}^{r_3, \varsigma }$ in (3.4) from Lemma 2.3, we get

According to Lemma 2.3, we can obtain

Next, by combining the BCs $\varkappa \left(0\right) +\eta _1\varkappa \big(\tilde{b} \big) = 0$ and

with (3.6), we get

From (3.7) and (3.8), we find

By substituting the values of $c_1$ and $c_2$ into (3.5), we arrive at the fractional integral equation (3.2). □

Definition 3.2. An element $\varkappa \in C^1\left(\mathfrak{B}\right)$ can be a solution of (1.3), if there is $\sigma \in L^1 \left(\mathfrak{B} \right)$ with $\sigma \left(\upsilon \right) \in \gimel \left(\upsilon, \varkappa \right)$ for every $\upsilon \in \; \mathfrak{B}$ fulfilling the non-separated BC's, $\varkappa \left(0\right) +\eta _1 \varkappa \big(\tilde{b} \big) = 0$,

and

3.1.   The upper semi-continuous case

The first consequence addresses the convex-valued $\gimel$ using the nonlinear alternative for contractive maps ^[27].

Theorem 3.3. Suppose that

${\rm P1)}$ $\gimel : \mathfrak{B} \times \mathbb{R} \to \mathcal{ P}_{\mathrm{cp}, \mathrm{c}} \left(\mathbb{R}\right)$ is a $L^1$-Carathéodory SVM;

${\rm P2)}$ There is a exist $\widetilde{\varpi }_1 \in C\left(\mathfrak{B}, \mathbb{R}^+ \right)$ and a nondecreasing $\widetilde{\varpi} _2 \in C \left(\mathbb{R}^+, \mathbb{R}^+ \right)$ with,

${\rm P3)}$ There is a constant $l_{\mathbb{y}} < \lambda _2^{-1}$ such that $\left\vert \mathbb{y}\left(\upsilon, \varkappa _{1}\right) -\mathbb{y } \left(\upsilon, \varkappa _2 \right) \right\vert \leq l_{ \mathbb{y} } \left\vert \varkappa _1 - \varkappa _2 \right\vert$;

${\rm P4)}$ There is a exist $\vartheta _{\mathbb{y}}\in C\left(\mathfrak{ B}, \mathbb{R}^+ \right)$ such that $\left\vert \mathbb{y}\left(\upsilon, \varkappa \right) \right\vert \leq \vartheta _{\mathbb{y}} \left(\upsilon \right)$, for each $\left(\upsilon, \varkappa \right) \in \mathfrak{B} \times \mathbb{R}$;

${\rm P5)}$ There is an $\mathcal{N} > 0$ satisfying

where

Then, (1.3) admits a solution of $\mathfrak{B}$.

Proof. At first, to convert the sequential-type FDI (1.3) into a problem of the FP type, we write $\Theta : \mathbb{E}\to \mathcal{P} \left(\mathbb{E}\right)$ as follows:

for $\sigma \in \mathcal{R}_{\gimel, \varkappa }$. Consider two operators $\Psi _1 : \mathbb{E} \to \mathbb{E}$ and $\Psi _2 : \mathbb{E} \to \mathcal{P} \left(\mathbb{E}\right)$ as follows:

and

Obviously, $\Theta = \Psi _1 + \Psi _2$. In the following, we demonstrate that $\Psi _1$ and $\Psi _2$ fulfill the conditions of the nonlinear alternative for contractive maps [27, Corollary 3.8]. Initially, we consider the set,

which is bounded, and show that $\Psi _{\mathring{\jmath}}$ define the SVMs $\Psi_{\mathring{ \jmath}} : \Omega _{\mathtt{γ}^{\ast }} \to \mathcal{P}_{\mathrm{cp}, \mathrm{c}} \left(\mathbb{E}\right)$, $\mathring{\jmath} = 1, 2$. To achieve this, we need to prove that $\Psi_1$ and $\Psi _2$ are compact and convex-valued. The proof will proceed in five steps.

Step 1. $\Psi _2$ is bounded on bounded sets of $\mathbb{E}$. Let $\Omega _{\mathtt{γ}^{\ast }}$ be a bounded set in $\mathbb{E}$. Then for every $z\in \Psi_2 \left(\varkappa \right)$ and $\varkappa \in \Omega_{\mathtt{γ}^{\ast}}$, $\sigma \in \mathcal{R}_{\gimel, \varkappa}$ exists such that,

Let (P1) holds. For any $\upsilon \in \mathfrak{B}$, we obtain,

Indeed, $\left\Vert z\right\Vert \leq \lambda _1 \left\Vert \widetilde{\varpi } _1\right\Vert \widetilde{\varpi }_2 \left(\mathtt{γ}^{ \ast }\right)$.

Step 2. $\Psi _{2}$ maps bounded sets of $\mathbb{E}$ into equicontinuous sets. Let $\varkappa \in \Omega _{\mathtt{γ}^{\ast }}$ and $z\in \Psi_2 \left(\varkappa \right)$. In this case, an element $\sigma\in \mathcal{R}_{\gimel, \varkappa }$ exists such that

Let $\upsilon _1, \upsilon _2 \in \mathfrak{B}$, $\upsilon _1 < \upsilon _2$. Then

As $\upsilon _1 \to \upsilon _2$, we obtain, $\left\vert z(\upsilon _2) - z(\upsilon _1) \right\vert \to 0$. Therefore, $\Psi_2 \left(\Omega _{\mathtt{γ}^{ \ast }}\right)$ is equicontinuous. Combining the results from Steps 1 and 2, and employing the theorem of Arzelà-Ascoli, we can confirm the completely continuity of $\Psi_2$.

Step 3. $\Psi_2 \left(\varkappa \right)$ is convex for all $\varkappa \in \mathbb{E}$. Let $z_1, z_2\in \Psi _2 \left(\varkappa \right)$. Then $\sigma _1, \sigma _2 \in \mathcal{R}_{\gimel, \varkappa }$ exist such that for each $\upsilon \in \mathfrak{B}$

Let $\mu \in \left[ 0, 1\right]$. Then for any $\upsilon \in \mathfrak{B}$,

Since $\gimel$ has convex values, $\mathcal{R}_{\gimel, \varkappa }$ is convex, and for $\mu \in \lbrack 0, 1]$, $\left(\mu \sigma _1 \left(\upsilon \right) +\left(1- \mu \right) \sigma _2 \left(\upsilon \right) \right) \in \mathcal{R}_{\gimel, \varkappa }$. Therefore, $\mu z_1 (\upsilon) + \left(1- \mu \right) z_2 \left(\upsilon \right) \in \Psi _2 \left(\varkappa \right)$, which shows that $\Psi_2$ is convex-valued. Moreover, $\Psi_1$ is compact and convex-valued.

Step 4. We prove that $\operatorname{Gr} \left(\Psi _2 \right)$ is closed. Let $\varkappa _n \to \varkappa_{\ast }$, $z_n \in \Psi _2 \left(\varkappa _n \right)$ and $z_{n} \to z_{ \ast }$. We show that $z_{\ast } \in \Psi_2 \left(\varkappa _{ \ast }\right)$. Since $z_n \in \Psi _2 \left(\varkappa _n \right)$, there is a $\sigma_n \in \mathcal{R}_{ \gimel, \varkappa _n }$ such that,

Therefore, we need to prove the existence of $\sigma _{ \ast }\in \mathcal{R}_{\gimel, \varkappa _{\ast }}$ such that for each $\upsilon \in \mathfrak{B}$,

Let $\Upsilon : L^1 \left(\mathfrak{B}, \mathbb{R} \right) \to C\left(\mathfrak{B}, \mathbb{R}\right)$ be a continuous linear operator defined as follows:

Notice that

when $n \to \infty$. Therefore, by Lemma 2.11, $\Upsilon \circ \mathcal{R}_{\gimel, \varkappa }$ is a closed graph operator. Additionally, $z_n \in \Upsilon \left(\mathcal{R}_{\gimel, \varkappa_n} \right)$. Since $\varkappa_n \to \varkappa _{\ast }$, Lemma 2.11 gives

for some $\sigma _{\ast }\in \mathcal{R}_{\gimel, \varkappa _{\ast }}$. Thus, the graph of $\Psi _2$ is closed. As a result, $\Psi_2$ is compact and upper semi-continuous.

Step 5. We prove that $\Psi _1$ is a contraction in $\mathbb{E}$. Let $\varkappa _1, \varkappa _2 \in \mathbb{E}$. By using the assumption (P3), we get,

Thus, $\left\Vert \Psi _1\varkappa _1- \Psi _1 \varkappa _2\right\Vert \leq l_{\mathbb{y}} \lambda _2 \left\Vert \varphi - \overline{\varphi } \right\Vert$. As $l_{\mathbb{y}} \lambda _2 < 1$, we conclude that $\Psi _1$ is a contraction. Thus, the operators $\Psi _1$ and $\Psi _2$ meet the theorem ^[27] hypotheses. As a result, we conclude that either of the two following conditions holds, (a) $\Theta$ has an FP in $\overline{\mathbb{E}}$, (b) we have $\varkappa \in \partial \mathbb{E}$ and $\xi \in \left(0, 1\right)$ with $\varkappa \in \xi F\left(\varkappa \right)$. We show that conclusion (b) is not possible. If $\varkappa \in \xi \Psi _1 \left(\varkappa \right) + \xi \Psi _2 \left(\varkappa \right)$ for $\xi \in \left(0, 1\right)$. Then, $\sigma \in \mathcal{R}_{\gimel, \varkappa }$ exists such that

which implies that $\left\vert \varkappa \left(\upsilon \right) \right\vert \leq \lambda _1 \left\Vert \widetilde{\varpi }_1 \right\Vert \widetilde{\varpi } _2 \left(\varkappa \right) +\lambda _2 \left\Vert \vartheta _{\mathbb{y} } \right\Vert$, for each $\upsilon \in \mathfrak{B}$. If criterion of [27, Theorem-(b)] is true, then $\xi \in \left(0, 1\right)$ and $\varkappa \in \partial \mathbb{E}$ with $\varkappa = \xi \Theta \left(\varkappa \right)$ exist. Therefore, $\varkappa$ is a solution of (1.3) with $\left\Vert \varkappa \right\Vert = \mathcal{N}$. Now, thanks to $\left\vert \varkappa \left(\upsilon \right) \right\vert \leq \lambda _1 \left\Vert \widetilde{\varpi }_1 \right\Vert \widetilde{\varpi } _2 \left(\varkappa \right) +\lambda _2 \left\Vert \vartheta _{\mathbb{y} } \right\Vert$, we get

which contradicts (3.10). Thus, it follows from the theorem ^[27] that $\Theta$ admits an FP, and it is a solution of (1.3). □

3.2.   The Lipschitz case

We try to establish a more general existence criterion for the FDI (1.3) under new hypotheses. Specifically, we demonstrate the desired existence result for a nonconvex-valued right-hand side using the theorem of Covitz and Nadler ^[28]. For a metric space $\big(\mathbb{E}, \varrho \big)$, we define

where $\varrho \big(\widetilde{R}_1, \widetilde{r}_2 \big) = \inf_{ \widetilde{r}_1 \in \widetilde{R}_1 } \varrho \left(\widetilde{r}_1, \varrho_2 \right)$ and $\varrho \big(\widetilde{r}_1, \widetilde{R}_2 \big) = \inf_{ \widetilde{r}_2 \in \widetilde{R}_2 } \varrho \left(\widetilde{r}_1, \widetilde{r}_2 \right)$. Then $\left(\mathcal{P}_{ \mathrm{b}, \mathrm{cl} } (\mathbb{E}), \mathscr{H}^{\varrho} \right)$ forms a metric space ^[29].

Definition 3.4. An SVM $\Omega : \mathbb{E} \to \mathcal{P}_{\mathrm{cl}} (\mathbb{E})$ is a $\widetilde{\eta }$-Lipschitz if and only if $\widetilde{\eta } > 0$ exists such that

In particular, $\Omega$ is a contraction whenever $\widetilde{\eta } < 1$.

Theorem 3.5. Assume that (P3) and the following conditions hold:

${\rm P6)}$ The map $\gimel : \mathfrak{B} \times \mathbb{R} \to \mathcal{P}_{ \mathrm{cp}} \left(\mathbb{R}\right)$ is such that $\gimel \left(\cdot, \varphi \right) : \mathfrak{B} \to \mathcal{P}_{\mathrm{cp}} (\mathbb{R})$ is measurable for any $\varkappa \in \mathbb{R}$;

${\rm P7)}$ The condition $\mathscr{H}^{\varrho} \left(\gimel \left(\upsilon, \varkappa _1 \right), \gimel \left(\upsilon, \varkappa _2 \right) \right) \leq \mathfrak{n} (\upsilon) \left\vert \varkappa_1 - \varkappa_2 \right\vert$ holds for a.e. $\upsilon \in \mathfrak{B}$ and $\varkappa _1, \varkappa _2 \in \mathbb{R}$ with $\mathfrak{n} \in C \left(\mathfrak{B}, \mathbb{R} ^+ \right)$ and $\varrho \left(0, \gimel \left(\upsilon, 0 \right) \right) \leq \mathfrak{n} (\upsilon)$ for a.e. $\upsilon \in \mathfrak{B}$.

Then FDI (1.3) has at least one solution for $\mathfrak{B}$ whenever $\left\Vert \mathfrak{n} \right\Vert \lambda _1 + l_{ \mathbb{y} } \lambda_2 < 1$, where $\lambda _1, \lambda _2$ are given in (3.11).

Proof. By assumption (P6) and [30, Theorem III.6], $\gimel$ has a measurable selection $\sigma : \mathfrak{B} \to \mathbb{R}$, with $\sigma \in L^1 (\mathfrak{B})$, which implies that $\gimel$ is integrability bounded. Therefore, $\mathcal{R}_{ \gimel, \varkappa } \neq \varnothing$. We demonstrate that the operator $\Omega: \mathbb{E} \to \mathcal{P}(\mathbb{E})$ described in (3.12) meets the conditions required by Nadler and Covitz's FPT. Specifically, we prove that $\Omega (\varkappa)$ is closed for each $\varkappa \in \mathbb{E}$. Assume a sequence such that $\left\{ u_{n} \right\} _{n\geq 0}\in \Omega (\varkappa)$ and $u_n \to u \; (n \to \infty)$ in $\mathbb{E}$. Then $u\in \mathbb{E}$ and $\sigma_n \in \mathcal{R}_{ \mathcal{G}, \varkappa_n }$ exists such that

So there is a subsequence $\sigma _n$ that converges to $\sigma$ in $L^1 \left(\mathfrak{B}\right)$, because $\gimel$ has compact values. As a result, $\sigma \in \mathcal{R}_{ \gimel, \varkappa }$, and we get

Hence $u \in \Omega (\varkappa)$. Next, we show that a $\Delta \in (0, 1)$, $\left(\Delta = \left\Vert \mathfrak{n} \right\Vert \lambda _1 + l_{ \mathbb{y} } \lambda_2 \right)$ exists such that

Let $\varkappa _1, \varkappa _2 \in \mathbb{E}$ and $v_1 \in \Omega \left(\varkappa _1 \right)$. Then $\sigma _1 \left(\upsilon \right) \in \gimel \left(\upsilon, \varkappa _1 \left(\upsilon \right) \right)$ exists such that for all $\upsilon \in \mathfrak{B}$ and

By (P7), we have

Thus, $\chi (\upsilon) \in \gimel \left(\upsilon, \varkappa _2 \right)$ exists such that $\left\vert \sigma _1 \left(\upsilon \right) -\chi \right\vert \leq \mathfrak{n} (\upsilon) \left\vert \varkappa _1 (\upsilon) -\varkappa _2 (\upsilon) \right\vert$, for each $\upsilon \in \mathfrak{B}$. We build an SVM, $\mathcal{O} : \mathfrak{B} \to \mathcal{P} (\mathbb{R})$ as follows:

Notice that $\sigma _1$ and $\omega = \mathfrak{n} \left\vert \varkappa _1 - \varkappa _2 \right\vert$ are measurable, so it follows that $\mathcal{O} (\upsilon) \cap \gimel \left(\upsilon, \varkappa _2 \right)$ is measurable. Next, we select the function $\sigma _2 (\upsilon) \in \gimel \left(\upsilon, \varkappa _2 \right)$ such that,

Define

As a results, we arrive at,

which implies $\left\Vert v_1 - v_2 \right\Vert \leq \left(\left\Vert \mathfrak{n} \right\Vert \lambda _1 + l_{\mathbb{y}} \lambda _2 \right) \left\Vert\varkappa _1 - \varkappa _2 \right\Vert$. Now, by interchanging the roles of $\varkappa _1$ and $\varkappa _2$, we obtain,

Since $\Omega$ is a contraction, it follows that the Covitz and Nadler theorem that $\Omega$ has an FP, which is a solution of the FDI (1.3). □

4.   Examples

In order to validate the theoretical findings, we provide specific cases of FDIs in this section. In fact, we focus on the FDI with the following form:

The examples below are special cases of FDIs given by (4.1).

Example 4.1. Using the FDIs defined by (4.1) and taking $r_1 \in \big\{ \frac{1}{2}, \frac{2}{3}, \frac{5}{6} \big\}$, $r_2 = \frac{1}{3}$, $r_3 = \frac{1}{5}$, $\varsigma (\upsilon) = \upsilon^2$, $\eta _1 = \frac{1}{4}$, $\eta _2 = \frac{1}{6}$, $\delta = 0.666, 0.777, 0.888$, and $\tilde{b} = 1$, the problem (4.1) is reduced to

for $\upsilon \in \mathfrak{B}$. With these data, it follows from (3.3), that we have

We define the function $\mathbb{y}$ and the SVM $\gimel : \mathfrak{B} \times \mathbb{R}\to \mathcal{P} (\mathbb{R})$ as follows:

and

For $\varkappa, \overline{\varkappa }\in \mathbb{R}$, we have

with $l_{\mathbb{y}} = \tfrac{1}{2}$ and also,

Thus, the assumptions (P3) and (P4) hold. It is also clear that the SVM $\gimel$ satisfies the assumption (P1) and

where $\left\Vert \widetilde{\varpi }_1\right\Vert = \frac{1}{4}$ and $\widetilde{\varpi }_2 \left(\left\Vert \varkappa \right\Vert \right) = 1$. Thus, (P2) holds, and by (P5),

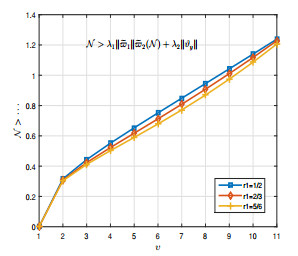
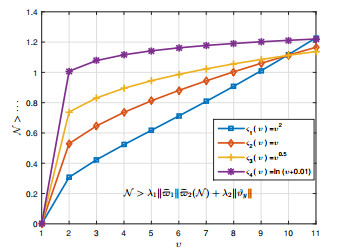
for which the curves are shown in Figure 1, Moreover,

whenever $\mathcal{N} = 1.15$, which it is shown in Figure 2. As seen in Table 1, the effect of the order of the derivative $r_1$ is very insignificant. So all assumptions of Theorem 3.3 are valid. Hence the FDI (4.2) has a solution for $\mathfrak{B}$.

In the next example, we check the changes in the derivative order $r_2$.

Example 4.2. Using the FDI defined by (4.1) and taking $r_1 = \frac{1}{2}$, $r_2 \in \big\{ \frac{1}{15}, \frac{1}{7}, \frac{1}{3} \big\}$, $r_3 = \frac{1}{5}$, $\varsigma \left(\upsilon \right) = \upsilon$, $\eta_1 = \frac{1}{4}$, $\eta _2 = \frac{1}{6}$, $\delta = 0.533, 0.571, 0.666$, and $\tilde{b} = 1$, 4.1 is reduced to

With these data, we find

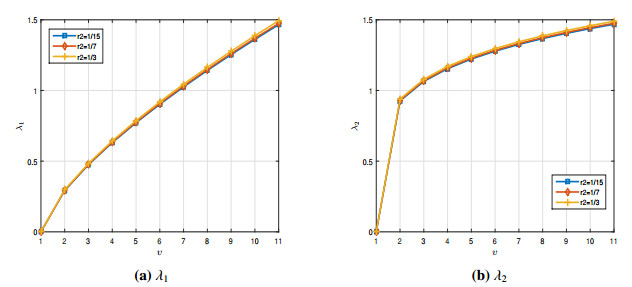
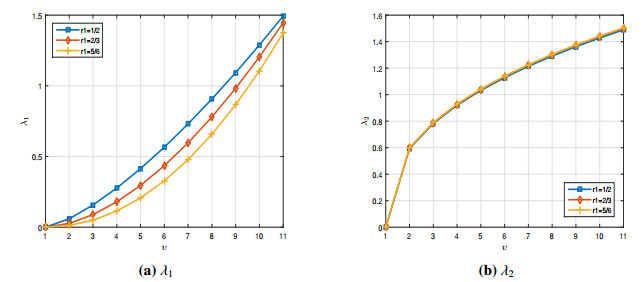
Consider the SVM $\gimel: \mathfrak{B} \times \mathbb{R} \to \mathcal{P} (\mathbb{R})$ is defined by, $\varphi \to \gimel\left(\upsilon, \varkappa \right) = \left[ 0, \, \frac{ \sin \left(\varkappa \right) }{ 5 \sqrt{\upsilon ^2+4}} + \frac{1}{12} \right]$, and the function $\mathbb{y}$ defined in (4.3). From (4.5), we see that the assumption (P3) is satisfied with $l_{\mathbb{y}} = \frac{1}{2}$. Next, we have $\mathscr{H}^{\varrho} \left(\gimel \left(\upsilon, \varkappa \right), \gimel \left(\upsilon, \overline{ \varkappa } \right) \right) \leq \mathfrak{n} (\upsilon) \left\vert \varkappa - \overline{\varkappa }\right\vert$, where $\mathfrak{n}\left(\upsilon \right) = \frac{1}{5 \sqrt{\upsilon ^2+4}}$ and $\varrho \left(0, \gimel \left(\upsilon, 0\right) \right) = \frac{1}{12}\leq \mathfrak{n} (\upsilon)$ for a.e. $\upsilon \in \mathfrak{B}$. Figure 3 shows the curves of $\lambda_i$, $i = 1, 2$, whenever $r_2$ varies in the interval $\mathfrak{B}$. By comparing the curves and data in Table 2, it can be clearly seen that as $r_2$ approaches zero, $\lambda_i$ decreases.

Furthermore, we obtain $\left\Vert \mathfrak{n}\right\Vert = \frac{1}{10}$, resulting in

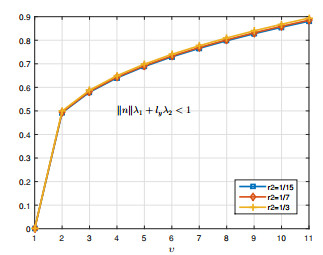
These results are shown in Table 2. Furthermore, the curves of Eq (4.7) for three cases of $r_2$ are shown in Figure 4.

Therefore, all the assumptions of Theorem 3.5 are satisfied, which implies that at least one solution to the problem (4.6) for $\mathfrak{B}$.

In Example 4.3, we examine our proven theorems for changes of function $\varsigma (\upsilon)$.

Example 4.3. Using the FDIs defined by (4.1) and taking $r_1 \in \frac{2}{3}$, $r_2 = \frac{1}{3}$, $r_3 = \frac{1}{5}$,

$\eta _1 = \frac{1}{4}$, $\eta _2 = \frac{1}{6}$, $\delta = 0.777$, $\tilde{b} = 1$, the problem (4.1) is reduced to

for $\upsilon \in \mathfrak{B}$. With these data, it follows from (3.3) that

We define the function $\mathbb{y}$ and the SVM $\gimel : \mathfrak{B} \times \mathbb{R}\to \mathcal{P} (\mathbb{R})$ as follows:

and

For $\varkappa, \overline{ \varkappa } \in \mathbb{R}$, we have

with $l_{\mathbb{y}} = \tfrac{1}{2}$, as well as $\mathbb{y} \left(\upsilon, \varkappa \right) \leq \tfrac{1}{ \exp \left(\upsilon ^2 \right) +1} = \vartheta_{\mathbb{y}} (\upsilon)$, for each $(\upsilon, \varkappa)\in \mathfrak{B} \times \mathbb{R}$. Thus, the assumptions (P3) and (P4) hold. It is also clear that the SVM $\gimel$ satisfies the assumption (P1) and

where $\left\Vert \widetilde{\varpi }_1\right\Vert = \frac{1}{4}$ and $\widetilde{\varpi }_2 \left(\left\Vert \varkappa \right\Vert \right) = 1$. Thus, (P2) holds, and by (P5)

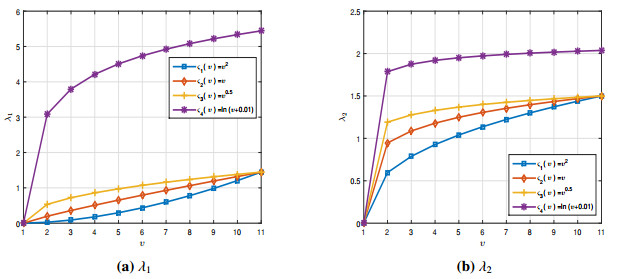
for which the curves are shown in Figure 5. Moreover

whenever $\mathcal{N} = 1.15$, which is shown in Figure 6. As seen in Table 3, the effect of $\varsigma(\upsilon)$ is very remarkable.

So all the assumptions of Theorem 3.3 are valid. Hence the FDI (4.9) has a solution for $\mathfrak{B}$.

5.   Conclusions

In the investigation of FDEs and FDIs that contain Hilfer fractional derivative operators, a zero initial condition is typically required. To address this limitation, we proposed a novel approach that combines Hilfer and Caputo fractional derivatives. In this research, we applied this method to study a class of FDEs for FDIs with non-separated BCs, incorporating both Hilfer and Caputo fractional derivative operators. The existence results are established by examining cases where the set-valued map has either convex or nonconvex values. For convex SVMs, the Leray-Schauder FPT was applied, whereas Nadler's and Covitz's FPTs are used for nonconvex SVMs. The findings are well demonstrated with two relevant illustrative examples. The findings of this study contribute significantly to the emerging field of FDIs. In future work, we aim to apply this method to study other types of FDEs with nonzero initial conditions, as well as coupled systems of FDEs that incorporate both Hilfer and Caputo FDs.

Availability of data and material

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

Author contributions

Adel Lachouri: Actualization, methodology, formal analysis, validation, investigation, initial draft and a major contribution to writing the manuscript. Naas Adjimi: Actualization, methodology, formal analysis, validation, investigation and review. Mohammad Esmael Samei: Actualization, methodology, formal analysis, validation, investigation, software, simulation, review and a major contribution to writing the manuscript. Manuel De la Sen: Validation, review, funding. All authors read and approved the final manuscript.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was funded by the Basque Government, Grant IT1555-22.

Conflict of interest

The authors declare that they have no competing interests.