Nonlinear fractional differential equations and their existence via fixed point theory concerning to Hilfer generalized proportional fractional derivative

1.   Introduction

Fractional calculus has attempted to be accessed as a promising technique in fluid mechanics ^[1], nano-material ^[2], thermal energy ^[3], epidemics ^[4] and other scientific disciplines over recent decades. For example, by provoking interest in both cutting-edge and conventional pure and applied analytical techniques, it has reinforced creative collaboration between different disciplines, existence, and relevant applications in real-world manifestations, see ^[5,6,7]. In 1965, the possibility of fractional calculus depended on the conversation between L'hospital and Leibnitz as letters in ^[8]. After that, many researchers started experimenting in this field, and a large portion of them concentrated on describing novel fractional formulations ^[9,10,11]. Various classifications were raised in this process and were expressed by the advancement of research.

Recently, extensive investigation has been proposed for the qualitative characterization of verification for various fractional differential equations ($FDEs$) with initial and boundary value problems. Several significant approaches regarding the existence, uniqueness, multiplicity and stability have been reported by proposing certain fixed point theorems. Although many of the important problems have been tackled by the classical fractional derivatives ($RL$ and Caputo) ^[12,13,14], it has a few limitations when used to design physical issues as a result of the necessary assumptions are themselves fractional and may be unsuitable for physical problems. The Caputo derivative has the opportunity of being appropriate for physical problems because it only necessitates classical initial conditions ^[15,16].

Khalil et al. ^[17] invented an interesting definition of fractional derivative, which is known to be a conformable derivative. In actuality, this so-called derivative is not a fractional derivative, however, it is it is essentially a first derivative duplicated by an extra straightforward factor. Consequently, this novel concept appears to be a regular extension of the classical derivative. More characterizations and the extended form of this derivative have been expounded in ^[18]. Then authors ^[19] explored an extension of the conformable derivative by considering proportional derivative. This fact leads to the modified conformable (proportional) differential operator of order $\lambda.$ The researchers investigated numerous integral inequalities using classical ^[20], conformable and generalized conformable fractional integrals ^[21,22]. Qurashi et al. ^[23] proposed new fractional derivatives and integrals that have nonsingular kernels. By using the generalized proportional Hadamard fractional integral operator, Zhou et al. ^[24] investigated some general inequalities and their variant forms.

This recently characterized local derivative approaches to the original function as $\lambda\mapsto 0.$ In this manner, they had the option to improve the conformable derivative. Jarad et al. ^[25] presented another kind of fractional operators created from the extended conformable derivatives. The exponential function appeared as a kernel in their examination with outstanding performance ^[26,27,28]. For the interest of readers, we draw in their thoughtfulness regarding some new papers ^[29,30].

In parallel with the concentrated exploration of the fractional derivative, the existence-uniqueness of verification fits to the intense prominent qualitative characterizations of $FDEs,$ see ^{[31,32,33,34]}.

Inspired by the work, we utilize a novel fractional derivative which is known as Hilfer-$GPF$ derivative for finding the existence-uniqueness of solutions for a new class of nonlinear $FDEs$ having non-local boundary conditions. For this we consider the subsequent $BVP$ for a class of Hilfer-$FDEs$:

where $\mathcal{G}:(\varpi_{1}, \varpi_{2}]\times\mathbb{R}\mapsto\mathbb{R}$ be a continuous mapping, $\mathcal{D}_{\varpi_{1}^{+}}^{\lambda, \zeta; \vartheta}(.)$ is the Hilfer-$GPF$ derivative of order $\lambda\in(0, 1)$ and $\mathcal{I}_{\varpi_{1}^{+}}^{1-\delta; \vartheta}(.)$ is the $GPF$ integral of order $1-\delta > 0.$ We find the existence consequences by the fixed point techniques of Schauder, Schaefer and Kransnoselskii. Additionally, the investigation of nonlinear $FDEs$ as far as their information sources (fractional orders, related boundaries, and suitable function) has fascinated the interest of mathematicians because of its importance in Orlicz space (see ^[35]). Rely upon this, the subject of coherence of verification of the Hilfer-$FDEs$ regarding inputs is significant and worth assuming.

The organization of the paper is as follows. In Section 2, we proceed with some basics concepts and detailed consequences as a review literature. In Section 3, we establish an equivalence criterion of integral equation of $BVP$ (1.1) and then proposed the existence consequences for $GPF$-derivative by well-noted fixed point theorem. Also, in Section 4, illustrative examples are presented to check the applicability of the findings developed in Section 3. The conclusion with some open problems is presented in Section 5.

2.   Preliminaries

In what follows, we demonstrate some preliminaries, initial results and spaces which are essential for proving further consequences. Throughout this investigation, let $L^{\mathfrak{p}}(\varpi_{1}, \varpi_{2}), \mathfrak{p}\geq1,$ is the space of Lebesgue integrable mappings on $(\varpi_{1}, \varpi_{2}).$

Assume that $\varpi_{1}, \varpi_{2}\in(-\infty, +\infty)$ be a finite and infinite intervals on $\mathbb{R}.$

Furthermore, we elaborate the subsequent weighted spaces with induced norms defined by (see^[8]). Suppose that $\mathbb{C}[\varpi_{1}, \varpi_{2}]$ is said to be the space of continuous functions defined on $[\varpi_{1}, \varpi_{2}]$ and the norm is defined as follows:

and $\mathcal{AC}^{n}[\varpi_{1}, \varpi_{2}]$ represents the space of $n$-times absolutely continuous differentiable mappings defined as follows:

$\mathbb{C}_{\delta}[\varpi_{1}, \varpi_{2}]$ denotes the weighted space of $\mathcal{G}$ on $(\varpi_{1}, \varpi_{2}]$ is defined as

with the norm

Also, the weighted space of a function $\mathcal{G}$ on $(\varpi_{1}, \varpi_{2}]$ is denoted by $\mathbb{C}_{\delta}^{n}(\varpi_{1}, \varpi_{2}]$ defined as

with the norm

For $n = 0,$ $\mathbb{C}_{\delta}^{n}[\varpi_{1}, \varpi_{2}]$ coincides with $\mathbb{C}_{\delta}[\varpi_{1}, \varpi_{2}].$

Definition 2.1. (^[8]) Assume that $\mathcal{G}\in L_{1}([\varpi_{1}, \varpi_{2}], \mathbb{R}),$ then the $RL$ fractional integral operator of $\mathcal{G}$ of order $\lambda > 0$ is stated as

where $\Gamma(.)$ represents the classical Gamma function.

Definition 2.2. (^[8]) Assume that $\mathcal{G}\in\mathbb{C}([\varpi_{1}, \varpi_{2}]),$ then the $RL$ fractional derivative operator of $\mathcal{G}$ of order $\lambda > 0$ is stated as

where $\Gamma(.)$ represents the Gamma function.

Definition 2.3. (^[8]) Assume that $\mathcal{G}\in\mathbb{C}^{n}([\varpi_{1}, \varpi_{2}]),$ then the Caputo fractional derivative operator of $\mathcal{G}$ of order $\lambda > 0$ is stated as

where $\Gamma(.)$ represents the Gamma function.

Definition 2.4. (^[25]) For $\vartheta\in(0, 1], \, \lambda\in\mathbb{C}, \Re(\lambda) > 0,$ then the left-sided generalized proportional integral of $\mathcal{G}$ of order $\lambda > 0$ is stated as

Definition 2.5. (^[25]) For $\vartheta\in(0, 1], \, \lambda\in\mathbb{C}, \Re(\lambda) > 0,$ then the left-sided generalized proportional derivative of $\mathcal{G}$ of order $\lambda > 0$ is stated as

where $n = [\lambda]+1.$

Definition 2.6. (^[25]) For $\vartheta\in(0, 1], \, \lambda\in\mathbb{C}, \Re(\lambda) > 0,$ then the left-sided generalized proportional integral of $\mathcal{G}$ of order $\lambda > 0$ is stated as

where $n = [\lambda]+1.$

Remark 2.1. Specifically, if $\vartheta = 1$ Definitions 2.4–2.6 reduces to Definitions 2.1–2.3, respectively.

Definition 2.7. (^[25]) For $n\in\mathbb{N}, \lambda\in(n-1, n), \vartheta\in(0, 1], \zeta\in[0, 1],$ then the left/right-sided Hilfer-$GPF$ derivative having order $\lambda,$ type $\zeta$ of $\mathcal{G}$ is stated as follows:

where $\mathcal{D}^{\vartheta}\mathcal{G}(y) = (1-\vartheta)\mathcal{G}(y)+\vartheta \mathcal{G}^{\prime}(y)$ and $\mathcal{I}$ assumed to be $GPF$-integral stated in 2.4.

Specifically, if $n = 1,$ then Definition 2.7 reduces to

In the present investigation, we discuss the case where $n = 1, \lambda\in(0, 1), \zeta\in[0, 1]$ and $\delta = \lambda+\zeta-\lambda\zeta.$

Remark 2.2. It is remarkable to mention that:

$(a)$The Hilfer fractional derivative can be considered as an interpolator between the $GPF$-derivative and Caputo $GPF$-derivative, respectively, as

$(b)$ The following assumptions holds true:

$(c)$ Particularly, if $\lambda\in(0, 1), \, \zeta\in[0, 1]$ and $\delta = \lambda+\zeta-\lambda\zeta,$ then

therefore, we have

where $\Big(\mathcal{D}_{\varpi_{1}^{+}}^{\delta; \vartheta}g_{1}\Big)(\wp) = \frac{d}{d\wp}\Big(\mathcal{I}_{\varpi_{1}^{+}}^{(1-\zeta)(1-\lambda); \vartheta}\mathcal{G}\Big)(\wp).$

Now we define the weighted spaces of continuous mappings on $(\varpi_{1}, \varpi_{2}]:$

and

Since $\mathcal{D}_{\varpi_{1}^{+}}^{\lambda, \zeta; \vartheta} = \mathcal{I}_{\varpi_{1}^{+}}^{\zeta(1-\lambda), \vartheta}\mathcal{D}_{\varpi_{1}^{+}}^{\delta; \vartheta},$ therefore, we have $\mathbb{C}_{1-\delta}^{\delta}[\varpi_{1}, \varpi_{2}]\subset\mathbb{C}_{1-\delta}^{\lambda, \zeta}[\varpi_{1}, \varpi_{2}].$

Theorem 2.1. (^[25]) For $\wp\geq \varpi_{1}, \, \vartheta\in(0, 1], \Re(\lambda), \Re(\zeta) > 0.$ If $\mathcal{G}\in\mathbb{C}([\varpi_{1}, \varpi_{2}], \mathbb{R}),$ then

Theorem 2.2. (^[25]) For $\wp\geq \varpi_{1}, \vartheta\in(0, 1]$ and $\Re(\lambda) > 0$ and let $\mathcal{G}\in L_{1}([\varpi_{1}, \varpi_{2}]),$ then

Lemma 2.1. (^[25]) For $\lambda, \varsigma\in\mathbb{C}$ such that $\Re(\lambda)\geq0$ and $\Re(\varsigma) > 0.$ Then for any $\vartheta\in(0, 1]$ we have

Lemma 2.2. (^[30]) For $\lambda\in(0, 1), \, \vartheta\in(0, 1], \, \zeta\in(0, 1)$ and $\delta = \lambda+\zeta-\lambda\zeta.$ If $\mathcal{G}\in\mathbb{C}_{1-\delta}^{\delta}[\varpi_{1}, \varpi_{2}],$ then

and

Lemma 2.3. (^[30])For $y\in(\varpi_{1}, \varpi_{2}], \, \lambda\in(0, 1), \vartheta\in(0, 1), \zeta\in[0, 1]$ and $\delta\in(0, 1).$ If $\mathcal{G}\in\mathbb{C}_{1-\delta}[\varpi_{1}, \varpi_{2}]$ and $\mathcal{I}_{\varpi_{1}^{+}}^{1-\delta, \vartheta}\mathcal{G},$ then

Lemma 2.4. (^[30]) For $\delta\in[0, 1), \vartheta\in(0, 1]$ and $g_{1}\in\mathbb{C}_{\delta}.$ If $\mathcal{G}\in\mathbb{C}_{\delta}[\varpi_{1}, \varpi_{2}],$ then

Lemma 2.5. (^[30]) For $\lambda\in(0, 1), \zeta\in[0, 1]$ and $\delta = \lambda+\zeta-\lambda\zeta$ and let $\mathcal{G}:(\varpi_{1}, \varpi_{2}]\times\mathbb{R}\mapsto\mathbb{R}$ be a mapping such that $\mathcal{G}\in\mathbb{C}_{1-\delta}[\varpi_{1}, \varpi_{2}]$ for any $y\in\mathbb{C}_{1-\delta}^{\delta}[\varpi_{1}, \varpi_{2}],$ then $y$ satisfies problem (1.1) if and only if $y$ satisfies the Volterra integral equation

3.   Existence of solution

This section consists of the existence of solution to $BVP$ (1.1) in $\mathbb{C}_{1-\delta}^{\lambda, \zeta; \vartheta}[\varpi_{1}, \varpi_{2}].$

Lemma 3.1. For $\lambda\in(0, 1), \, \zeta\in[0, 1],$ where $\delta = \lambda+\zeta-\lambda\zeta$ and suppose there be a function $\mathcal{G}:(\varpi_{1}, \varpi_{2}]\times \mathbb{R}\rightarrow \mathbb{R}$ such that $\mathcal{G}\in\mathbb{C}_{1-\delta}[\varpi_{1}, \varpi_{2}]$ for any $y\in\mathbb{C}_{1-\delta}[\varpi_{1}, \varpi_{2}].$ If $y\in\mathbb{C}_{1-\delta}^{\delta}[\varpi_{1}, \varpi_{2}],$ then $y$ fulfills $BVP$ (1.1) if and only if $y$ holds the following identity

Proof. By means of Lemma 2.5 and utilizing the solution of (1.1) can be expressed as

Employing $\mathcal{J}_{\varpi_{1}^{+}}^{1-\delta; \vartheta}$ on (3.2) and applying the limit $\wp\rightarrow \varpi_{2}^{-1},$ we find

Again, employing $\mathcal{J}_{\varpi_{1}^{+}}^{1-\delta; \vartheta}$ on (3.3), we have

Applying limit $\wp\mapsto \varpi_{1}^{+}$ and utilizing Lemma 2.4 having $1-\delta < 1-\zeta(1-\lambda),$ yields

thus

From boundary condition (1.1), we have

From (3.5) and (3.6), and utilizing (3.4), we have

Setting (3.2) in (3.8), one can find

Conversely, employing $\mathcal{J}_{\varpi_{1}^{+}}^{1-\delta; \vartheta}$ on (3.1), utilizing Lemmas 2.1 and 2.2, and simple computations yields

This shows that $y(\wp)$ satisfies boundary condition (1.1).

Furthermore, employing $\mathcal{D}_{\varpi_{1}^{+}}^{\delta; \vartheta}$ on (3.1) and applying Lemmas 2.1 and 2.2, we have

Since $y\in\mathbb{C}_{1-\delta}^{\delta; \vartheta}[\varpi_{1}, \varpi_{2}]$ and in view of definition of $\mathbb{C}_{1-\delta}^{\delta; \vartheta}[\varpi_{1}, \varpi_{2}],$ we have $\mathcal{D}_{\varpi_{1}^{+}}^{\delta}y\in\mathbb{C}_{n-\delta}^{\vartheta}[\varpi_{1}, \varpi_{2}],$ thus, $\mathcal{D}_{\varpi_{1}^{+}}^{\zeta(1-\lambda); \vartheta}\mathcal{G} = \mathcal{D}\mathcal{I}_{\varpi_{1}^{+}}^{1-\zeta(1-\lambda)}\mathcal{G}\in\mathbb{C}_{1-\delta}[\varpi_{1}, \varpi_{2}].$

For $\mathcal{G}\in\mathbb{C}_{1-\delta}[\varpi_{1}, \varpi_{2}],$ it is noting that $\mathcal{I}_{\varpi_{1}^{+}}^{1-\zeta(1-\lambda)}\mathcal{G}\in \mathbb{C}_{1-\delta}[\varpi_{1}, \varpi_{2}].$ So, $\mathcal{G}$ and $\mathcal{I}_{\varpi_{1}^{+}}^{1-\zeta(1-\lambda); \vartheta}\mathcal{G}$ holds the assumptions of Lemma 2.3. Now, employing $\mathcal{I}_{\varpi_{1}^{+}}^{\zeta(1-\lambda); \vartheta}$ on (3.11), we have

Considering (2.8), (3.11) and Lemma 2.3, we have

By Lemma 2.4, we have $\mathcal{I}_{\varpi_{1}^{+}}^{1-\zeta(n-\lambda)}\mathcal{G}(\varpi_{1}, y(\varpi_{1})) = 0.$ Thus, we have $\mathcal{D}_{\varpi_{1}^{+}}^{\lambda, \zeta; \vartheta}y(\wp) = \mathcal{G}(\wp, y(\wp)).$ Hence, this completes the proof.

Let us evoke some essential assumptions which are required to prove the existence of solutions for the problem mentioned.

$(A_{1})$ Let a function $\mathcal{G}:(\varpi_{1}, \varpi_{2}]\times\mathbb{R}\mapsto\mathbb{R}$ with $\mathcal{G}(., y(.))\in\mathbb{C}_{1-\delta}^{\zeta(1-\lambda); \vartheta}[\varpi_{1}, \varpi_{2}].$ For any $y\in\mathbb{C}_{1-\delta}^{\vartheta}[\varpi_{1}, \varpi_{2}]$ and there exist two constants $\mathcal{M}_{1}, \mathfrak{m}$ such that

$(A_{2})$ The inequality

holds.

Now we are in a position to show the existence results for the $BVP$ (1.1) by employing Schauder's fixed point theorem (see ^[36]).

Theorem 3.1. Suppose that the assumptions $(A_{1})$ and $(A_{2})$ fulfills. Then by Hilfer-$BVP$ (1.1) has at least one solution in $\mathbb{C}_{1-\delta}^{\delta; \vartheta}[\varpi_{1}, \varpi_{2}]\subset\mathbb{C}_{1-\delta}^{\lambda, \zeta; \vartheta}[\varpi_{1}, \varpi_{2}].$

Proof. Defining an operator ${\bf T}:\mathbb{C}_{1-\delta}[\varpi_{1}, \varpi_{2}]\mapsto\mathbb{C}_{1-\delta}[\varpi_{1}, \varpi_{2}]$ by

Assume that $\mathbb{B}_{\varrho} = \Big\{y\in\mathbb{C}_{1-\delta}[\varpi_{1}, \varpi_{2}]:\|y\|_{\mathbb{C}_{1-\delta}}\leq\varrho\Big\}$ having $\varrho\geq\frac{\Omega}{1-\mathcal{G}},$ for $\mathcal{G} < 1,$ we have

The proof will be demonstrated by the accompanying three steps:

Case 1. We will prove that ${\bf T}(\mathbb{B}_{\varrho})\subset\mathbb{B}_{\varrho}.$ Utilizing assumption $(A_{2}),$ we have

Since $\big\vert e^{\frac{\vartheta-1}{\vartheta}\wp}\big\vert < 1.$ Observe that, for any $y\in\mathbb{B}_{\varrho},$ and for every $\wp\in(\varpi_{1}, \varpi_{2}],$ we have

and

Therefore, we get

which leads to

of assumption $(A_{2}),$ we conclude that $\|{\bf T}y\|_{\mathbb{C}_{1-\delta}}\leq\mathcal{G}\varrho+(1-\mathcal{G})\varrho = \varrho,$ Therefore, ${\bf T}(\mathbb{B}_{\varrho})\subset\mathbb{B}_{\varrho}.$

Next we will prove that ${\bf T}$ is completely continuous.

Case 2. We prove that the operator ${\bf T}$ is completely continuous.

Assume that $\{\bar{z}_{n}\}$ is a sequence such that $\bar{z}_{n}\mapsto \bar{z}$ in $\mathbb{B}_{\varrho}$ as $n\mapsto\infty.$ Then for every $\wp\in(\varpi_{1}, \varpi_{2}],$ we have

Since $\Big\vert e^{\frac{\vartheta-1}{\vartheta}\wp}\Big\vert < 1$ and $\mathcal{G}$ is continuous on $(\varpi_{1}, \varpi_{2}]$ and $\bar{z}_{n}\mapsto\bar{z},$ then

which shows that operator ${\bf T}$ is continuous on $\mathbb{B}_{\varrho}.$

Case 3. We show that ${\bf T}(\mathbb{B}_{\varrho})$ is relatively compact. In case 1, we have ${\bf T}(\mathbb{B}_{\varrho})\subset\mathbb{B}_{\varrho}.$ It is observed that ${\bf T}(\mathbb{B}_{\varrho})$ is uniformly bounded. To show operator ${\bf T}$ is equi-continuous on $\mathbb{B}_{\varrho}.$ In fact, for any $\varpi_{1} < \wp_{1} < \wp_{2} < \varpi_{2}$ and $\bar{z}\in\mathbb{B}_{\varrho},$ we have

which approaches to zero as $\wp_{2}\rightarrow \wp_{1},$ independent of $y\in\mathbb{\varrho},$ where $\mathfrak{B}(., .)$ denotes the Euler Beta function.

Therefore, we deduce that ${\bf T}(\mathbb{B}_{\varrho})$ is equicontinuous on $\mathbb{B}_{\varrho},$ that leads to the relatively compactness. As a result, we conclude that by Arzela-Ascoli theorem, the defined operator ${\bf T}:\mathbb{B}_{\varrho}\mapsto\mathbb{B}_{\varrho}$ is completely continuous operator.

By Schauder's fixed point theorem, there exists at least one fixed point $y$ of ${\bf T}$ in $\mathbb{C}_{1-\delta}[\varpi_{1}, \varpi_{2}].$ This fixed point $y$ is the solution of (1.1) in $\mathbb{C}_{1-\delta}^{\delta; \vartheta},$ and this completes the proof.

Now we present another existence result via Schaefer fixed point theorem. For this, we need the following assumption.

$(A_{3})$ Suppose a function $\mathcal{G}:(\varpi_{1}, \varpi_{2}]\times\mathbb{R}\mapsto\mathbb{R}$ such that $\mathcal{G}(., y(.))\in\mathbb{C}_{1-\delta}^{\zeta(1-\lambda); \vartheta}[\varpi_{1}, \varpi_{2}]$ for any $y\in\mathbb{C}_{1-\delta}[\varpi_{1}, \varpi_{2}]$ and there exist a mapping $\eta(\wp)\in\mathbb{C}_{1-\delta}[\varpi_{1}, \varpi_{2}]$ such that

Theorem 3.2. Suppose that assumption $(A_{3})$ satisfies. then Hilfer-$BVP$ (1.1) has at least one solution in $\mathbb{C}_{1-\delta}^{\delta}\subset\mathbb{C}_{1-\delta}^{\lambda, \zeta; \vartheta}[\varpi_{1}, \varpi_{2}].$

Proof. For the proof of Theorem 3.2, one can adopt the same technique as we did in Theorem 3.1 and easily prove that the operator ${\bf T}:\mathbb{C}_{1-\delta}[\varpi_{1}, \varpi_{2}]\mapsto\mathbb{C}_{1-\delta}[\varpi_{1}, \varpi_{2}]$ stated in (3.16) is completely continuous. Now we show that

is bounded set. Assume that $y\in\Delta$ and $\sigma\in(0, 1)$ be such that $y = \sigma {\bf T}y.$ By assumption $(A_{3})$ and (3.16), then for all $\wp\in[\varpi_{1}, \varpi_{2}],$ we have

Since $\big\vert e^{\frac{\vartheta-1}{\vartheta}\wp}\big\vert < 1,$ we have

Since $\sigma\in(0, 1),$ then $y < {\bf T}y.$ The last inequality with (3.29) leads us to the conclusion that

which proves that $\Delta$ is bounded. Utilizing Schaefer fixed point postulate, this completes the proof.

Our last result is the existence result for the problem (1.1) by using the Kransnoselskii's fixed point theorem (see ^[37]), the following assumption is needed:

$(A_{4})$ Suppose that $\mathcal{G}:(\varpi_{1}, \varpi_{2}]\times\mathbb{R}\mapsto\mathbb{R}$ is a function such that $\mathcal{G}(. y(.))\in\mathbb{C}_{n-\delta}^{\zeta(n-\lambda); \vartheta}[\varpi_{1}, \varpi_{2}]$ for any $y\in\mathbb{C}_{n-\delta}[\varpi_{1}, \varpi_{2}]$ and there exists a constant $L > 0$ such that

Also, we note the following assumption as follows: $(A_{5})$ the inequality

is hold.

Theorem 3.3. Suppose that the assumptions $(A_{4})$ and $(A_{5})$ are satisfied. If

Then the Hilfer-$BVP$ (1.1) has at least one solution in $\mathbb{C}_{n-\delta}^{\delta}[\varpi_{1}, \varpi_{2}]\subset\mathbb{C}_{n-\delta}^{\lambda, \zeta; \vartheta}.$

Proof. Considering the operator ${\bf T}$ stated in Theorem 3.1.

First, surmise the operator ${\bf T}$ into sum of two operators ${\bf T}_{1}+{\bf T}_{2}$ as follows

and

Setting $\tilde{\mathcal{G}} = \mathcal{G}(\ell, 0)$ and suppose the ball $\mathbb{B}_{\epsilon} = \{y\in\mathbb{C}_{n-\delta; \psi([\varpi_{1}, \varpi_{2}])}:\|y\|_{\mathbb{C}_{n-\delta}; \psi}\leq\epsilon\}$ having $\epsilon\geq\frac{\sigma}{1-\mathcal{Q}}, \mathcal{Q} < 1,$ where

The proof will be done in three cases.

Case 1. We show that ${\bf T}_{1}y+{\bf T}_{1}\omega\in\mathbb{B}_{\varrho}$ for every $y, \omega\in\mathbb{B}_{\epsilon}.$

Utilizing assumption $(A_{4}),$ then for every $y\in\mathbb{B}_{\epsilon}$ and $\wp\in(\varpi_{1}, \varpi_{2}],$ we have

Since $\big\vert e^{\frac{\vartheta-1}{\vartheta}\wp}\big\vert < 1.$ Therefore, we get

For operator ${\bf T}_{2},$ we have

For every $\omega\in\mathbb{B}_{\epsilon}$ and $\wp\in(\varpi_{1}, \varpi_{2}],$ this shows

From (3.38), (3.40) and utilizing assumption $(A_{5})$ with (3.36), we find

Case 2. We prove that the operator ${\bf T}$ is a contraction mapping on $\mathbb{B}_{\varrho}.$

For any $y, \omega\in\mathbb{B}_{\varrho},$ and for any $\wp\in(\varpi_{1}, \varpi_{2}],$ then by supposition $(A_{4}),$ we have

Since $\big\vert e^{\frac{\vartheta-1}{\vartheta}\wp}\big\vert < 1,$ this yields

Due to assumption (3.33), which shows that the operator ${\bf T}$ is a contraction mapping.

Case 3: Now we show that the operator ${\bf T}_{2}$ is completely continuous on $\mathbb{B}_{\epsilon}.$

From the continuity of $\mathcal{G},$ we deduce that the operator ${\bf T}_{2}:\mathbb{B}_{\epsilon}\mapsto\mathbb{B}_{\epsilon}$ is continuous on $\mathbb{B}_{\epsilon}.$ Furthermore, we prove that for all $\epsilon > 0$ there exists some $\epsilon^{\prime} > 0$ such that $\|{\bf T}_{2}y\|_{\mathbb{C}_{n-\delta}} < \epsilon^{\prime}.$ In view of case 1, for $y\in\mathbb{B}_{\epsilon},$ we have that

which is free of $\wp$ and $y,$ so there exists

such that $\|{\bf T}_{2}(y)\|_{\mathbb{C}_{n-\delta}}\leq\epsilon^{\prime}.$ Therefore, ${\bf T}_{2}$ is uniformly bounded set on $\mathbb{B}_{\epsilon}.$ Finally, to show that ${\bf T}_{2}$ is equicontinuous in $\mathbb{B}_{\epsilon},$ for any $z\in\mathbb{B}_{\epsilon}$ and $\wp_{1}, \wp_{2}\in(\varpi_{1}, \varpi_{2}]$ having $\wp_{1} < \wp_{2},$ we have

Since $\big\vert e^{\frac{\vartheta-1}{\vartheta}\wp}\big\vert < 1.$ It is noting that the right hand side of the aforesaid variant is free of $y.$ So,

This shows that ${\bf T}_{2}$ is equicontinuous on $\mathbb{B}_{\epsilon}.$ According to Arzela-Ascoli Theorem, observed that $({\bf T}_{2}\mathbb{B}_{\epsilon})$ is relatively compact. By Kransnoselskii's fixed point theorem, the problem (1.1) has at least one solution.

4.   Examples

Consider the fractional differential equation with boundary condition which encompasses the Hilfer-$GPF$ derivative of the form

By comparison (1.1) with (2.9), we have $\lambda = \frac{1}{2}, \zeta = \frac{1}{3}, \delta = \frac{2}{3}, m_{1} = \frac{1}{3}, m_{2} = \frac{2}{3}, \vartheta = 1$ and $e_{1} = \frac{2}{5}.$ It is clear that $\wp^{\frac{1}{3}}\mathcal{G}(\wp, y(\wp)) = \wp^{\frac{1}{6}}+\frac{\wp^{7/6}}{16}\sin y(\wp)\in\mathbb{C}([0, 2]),$ So $\mathcal{G}(\wp, y(\wp))\in\mathbb{C}_{\frac{1}{3}}.$ Thus, it follows that, for any $y\in\mathbb{R}^{+}$ and $\wp\in\mathbb{J},$

Hence, the assumption $(A_{1})$ is fulfilled having $\mathcal{M} = 1$ and $\mathfrak{m} = \frac{1}{16}.$ It is easy to verify that the assumption $(A_{2})$ is hold too. In fact, by simple computations, we obtain

Hence, all suppositions of Theorem 3.1 implies that the problem (1.1) has a unique solution in $\mathbb{C}_{\frac{1}{3}}^{\frac{2}{3}}([0, 2]).$

Also, assume that $\mathcal{G}(\wp, y(\wp)) = \wp^{-\frac{1}{6}}+\frac{\wp^{5/6}}{16}\sin y(\wp).$ Thus $\big\vert \mathcal{G}(\wp_{1}, y(\wp))\leq \wp^{-\frac{1}{6}}+\frac{\wp^{5/6}}{16}\big\vert = \eta(\wp)\in\mathbb{C}_{1-\delta}([0, 2]).$ So, $(A_{3})$ is satisfied. Therefore, in view of Theorem 3.2, we conclude that problem (1.1) has a solution in $\mathbb{C}_{1/3}^{2/3}([0, 2]).$

Finally, if $\mathcal{G}(\wp, y(\wp)) = \wp^{-\frac{1}{6}}+\frac{\wp^{5/6}}{16}\sin y(\wp),$ then for $y, \omega\in\mathbb{R}^{+}$ and $\wp\in\mathbb{J},$ we have

Therefore, the assumption $(A_{4})$ is fulfilled having $L = \frac{1}{16}.$ Clearly, assumption $(A_{5})$ and inequality (3.33) are holds. In fact, simple computations yields

and

of Theorem 3.3, shows that problem (1.1) has a solution in $\mathbb{C}_{\frac{1}{3}}^{\frac{2}{3}}([0, 2]).$

5.   Conclusions

In this approach, we have established certain existence consequences for the solution of $BVP$ for Hilfer-$FDEs$ depend on the lessening of $FDEs$ to integral equations. The proposed scheme with the fixed point assertions unifies the existing results in the frame of $RL$ and Caputo $GPF$ sense, respectively. Besides that, the analysis's comprehensive improvements are dependent on various techniques such as Schauder's, Schaefer's and Kransnoselskii's fixed point theorems. Also, the Hilffer $GPF$-derivative comprise two parameters and a proportionality index $\vartheta.$

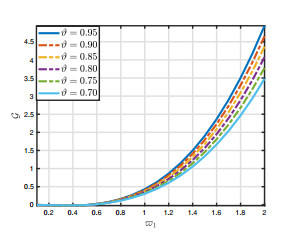
$\bullet$ If $\vartheta\mapsto 1$ and $\lambda = [0, 1],$ then the contemplated problem converted to $RL$ and Caputo fractional derivative ^[8]. If $\vartheta\in(0, 1)$ and $\zeta = 0, 1$ we recaptures the $RL$ and Caputo $GPF$-derivative ^[25], respectively (see Figure 1).

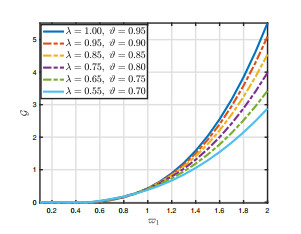
$\bullet$ Clearly, if $\vartheta, \zeta\in(0, 1),$ then the newly employed derivatives amalgamate the existing ones in the adjustment of Hilfer, $RL$ and $GPF$-derivative, (see Figure 2).

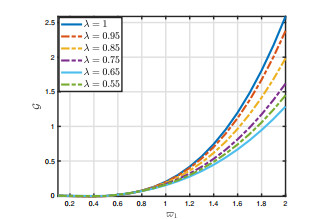
$\bullet$ If $\vartheta\mapsto 1$ and $\zeta, \lambda\in[0, 1],$ then the formulation for this problem enjoys Hilfer factional derivative ^[8], (see Figure 3).

Moreover, a stimulative example is presented to show the efficacy of the established outcomes. We hope that the testified outcomes here will have a considerable impact for more parameters on the stability and other qualitative features of differential equations in the areas of interest of applied sciences.

Conflict of interest

The authors declare that there is no conflict of interests.