The invariant solution with blow-up for the gas dynamics equations from one-parameter three-dimensional subalgebra consisting of space, Galilean and pressure translations

1.   Introduction

The symmetry analysis of differential equations is a powerful method to obtain new exact particular solutions for nonlinear partial differential equations ^[1,2,3]. In this paper, we consider the gas dynamics equations ^[4]. Many solutions for these equations were found from some considerations, for example, using similarity and dimensional methods ^[5]. The outstanding mathematician Lev Ovsyannikov began to obtain new exact solutions to these equations systematically. He succeeded by applying the group analysis of differential equations ^[1] to the gas dynamics equations. As a result of years of research, the "Submodels" program was published ^[6], in which the scientific community proposed to list all submodels in order to simplify the original model that specifies classes of exact solutions and have a lower dimension.

Lev Ovsyannikov has solved the problem of group classification of the gas dynamics equations by an arbitrary element. He obtained 13 special equations of state ^[6]. The transformation group of the gas dynamics equations has additional symmetries for these special state equations. Groups are associated with Lie algebras of infinitesimal generators. However, some Lie algebras are similar. In this paper, we consider a state equation that expands the transformation group to a 12-parameter group. Other authors have not considered this equation of state from the point of view of group analysis of differential equations. In this article, pressure is represented as a sum of density function and entropy function. The transformation group consists of time translation, space translations, Galilean translations, rotations in coordinate planes, space-time uniform dilatation and pressure translation. The 12-dimensional Lie algebra is the direct sum of two ideals. The paper ^[7] presents an optimal system of non-similar subalgebras of the Lie algebra. Simplifications of the original model of lower dimensions can be built for each subalgebra. Invariant submodel is the gas dynamics equations that are written in invariants of subalgebra. The number of independent variables of the submodel is a rank of the submodel. In particular, from a three-dimensional subalgebra one can construct an invariant submodel of rank one. This is a system of gas dynamics equations written in terms of subalgebra invariants with one independent variable. The integration of the system leads to the exact invariant solution of the gas dynamics equations. These solutions can be used at applications. However, the first stage is a representation of the motion of particles on the whole in space. Many authors were engaged in constructing submodels and the study of particle motion. For example, the following recent works can be noted: A solution with collapse on a helicoid was obtained in ^[8]; motion of gas particles based on the Galilean group was studied in ^[9]; examples of invariant solutions describing vortex gas flow with variable entropy, including a point source or sink were considered in ^[10]; in ^[11], three families of exact solutions were obtained and, in a particular case, particle motions were presented; the invariant solutions and submodels in two-phase fluid mechanics generated by three-dimensional subalgebras and describing barochronous flows were presented in ^[12]; a solution with collapse was obtained in ^[13] for a two-phase liquid; for a monatomic gas, an approximate solution on a three-dimensional subalgebra and a description of the motion of particles were presented in ^[14]; for two types of state equations the motions of particles with a linear velocity field were obtained in ^[15].

A submodel of a lower rank can be nested in a submodel of a higher rank ^[16]. This happens when a subalgebra (for a submodel of higher rank) is embedded in a superalgebra (for a submodel of lower rank). This is significant because a solution of a nested submodel is a solution of the submodel of a larger dimension. In order to embed submodels, the invariants should be written in a consistent form. It means that the invariants of the superalgebra should be expressed in terms of the invariants of the subalgebra. All possible embedded subalgebras are given in ^[17] for the gas dynamics equations with an arbitrary state equation. This paper provides an example of embedded submodels for the special state equation.

2.   The main formulas and defenitions

We consider the gas dynamics equations ^[6]

where the total differentiation operator has the form

$t$ is time, $\nabla = \partial_{\vec{x}}$ is a gradient with respect to the spatial independent variables $\vec{x}$, $\vec{u}$ is a velocity vector, $\rho$ is a density and $p$ is a pressure.

In the Cartesian coordinate system, we have ^[18]

where $\vec{i}$, $\vec{j}$, and $\vec{k}$ are an orthonormal basis.

The state equation has the special form ^[6]

where $S$ is an entropy.

The last equation of system (2.1) can be replaced by the equation for entropy:

Equations (2.1) and (2.2) are invariant under the action of 12-parameter transformation group ^[6]:

The 12-dimensional Lie algebra $L_{12}$ corresponds to transformation group (2.3). Lie algebra $L_{12}$ is a direct sum of two ideals $L_{12} = L_{11}\oplus\{Y_1\}$. All nontrivial, non-similar subalgebras of the Lie algebra $L_{12}$ were written in the optimal system of subalgebras in ^[7]. The basis generators of $L_{12}$ in the Cartesian coordinate system have the form ^[6]

The commutators of infinitesimal generators (2.4) are given in Table 1 ^[7], where instead of operators $X_i$, $i = 1...11$, we simply write indices $i$.

3.   Results

3.1.   Invariant submodel and exact solution

The basis generators of the three-dimensional subalgebra 3.35 ^[7] has the form

Invariants of subalgebra (3.1) are

Representation of invariant solution from (3.2) can be written as

In (3.3) the coefficient $\gamma$ has added in order to distinguish the results for three-dimensional subalgebra 3.37 ^[18] of Lie algebra $L_{11}$ from the results for three-dimensional subalgebra 3.35 of Lie algebra $L_{12}$. If we consider $L_{11}$, then $\gamma = 0$. If we mean $L_{12}$, then $\gamma = 1$.

Substituting (3.3) in (2.1) and (2.2), we obtain invariant submodel of rank one

The solution of (2.1) and (2.2) from (3.3) and (3.4) has the form

In solution (3.5) $u_0 = w_0 = Y_0 = 0$, due to Galilean translations with $\vec{b} = (-u_0, 0, -w_0)$ and space translations with $\vec{a} = (0, Y_0, 0)$ (2.3). Using pressure translation with $a_0 = -p_0$, we have in pressure $p_0 = 0$.

Let us consider the solution (3.5) embedded into the solution of invariant submodel of rank three obtained from one-dimensional subalgebra 1.11 from $L_{12}$. This subalgebra is obtained from the sum of subalgebra 1.11 from $L_{11}$ ^[18] and generator $Y_1$. The basis generator of subalgebra 1.11 from $L_{12}$ has the form

Subalgebra (3.6) embeds to subalgebra 3.35 (we assume a = 1) (3.1) if coordinate axes ($x^1$, $x^2$), ($x^4$, $x^5$) are reassigned as ($x^2$, $x^1$), ($x^5$, $x^4$), respectively, then (3.6) is as follows

Invariants of subalgebra (3.7) are

Let us write invariants (3.8) in consistent form with invariants (3.2), then representation of invariant solutions from (3.8) can be written as

The invariant submodel of rank three has the form

If system (3.9) doesn't depend on $x$, $z_1$, then it is the system (3.4) with $a = 1$. This means that the solution for (3.4) with $a = 1$ is also the solution for system (3.9).

3.2.   Particle motion

Particle motion is given by the equation ^[4]:

We investigate the motion of particles for solution (3.5). The world lines in $\mathbb{R}^4(t, \vec{x})$ are given by formulas

where $\vec{x}_0 = (x_0, v_0, z_0)$ are local Lagrangian coordinates. The Jacobian determinant of transformation (3.10) from Lagrangian coordinates to Euler coordinates is

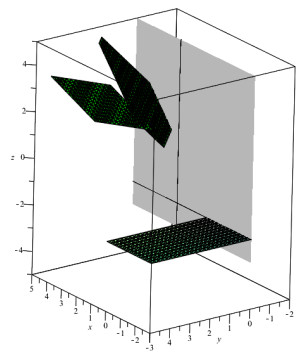
At the moment of time $t = 0$, the Jacobian determinant (3.11) vanishes and the particles collapse. The rank of the Jacobian matrix at this moment of time is equal to two and the blow-up manifold is the plane $y = 0$. Thus, for $t = 0$, the plane $y = 0$ is a flat blow-up or source. Projections of world lines to $\mathbb{R}^3(\vec{x})$ are particle trajectories.

The gas motion is vortex

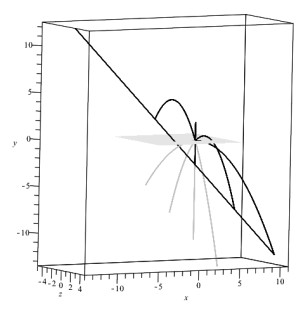
For $z_0\not = av_0$, the particle trajectories are parabolas along the $OY$ axis in the $z = z_0$ planes.

Parabola vertex coordinates are $\left(\dfrac{z_0-av_0}{\gamma}\rho_0v_0+x_0;\dfrac{v_0^2\rho_0}{2\gamma}; z_0\right)$ at $t_{max} = \dfrac{v_0\rho_0}{\gamma}$. The trajectories of such particles, for which $z_0 = av_0$, are rays parallel to the $OY$ axis and scattering from the points $\left(x_0;\dfrac{v_0^2\rho_0}{2\gamma}; av_0\right)$ in the negative direction of the $OY$ axis.

Let us rewrite the gas-dynamic functions in terms of the Lagrangian coordinates

The velocity of the particle changes only in the direction of the $OY$ axis.

From the system (3.10), by separating the Euler and Lagrangian variables, we can obtain the equality

where the left side of which is a combination of the invariants of the subalgebra 1.11 (we assume $a = 1$) (3.8). Thus, from the straight line $x = x_0$ on the blow-up, the particles scatter to the plane (3.12). Also from the straight line $z = z_0$ on the blow-up, the particles scatter to the plane $z = z_0$ (see Figure 1).

At the moment of time $t = 0$, the particles scatter with velocicties $(z_0-av_0;v_0;0)$ from the point $(x_0, z_0)$ of the blow-up plane $y = 0$. In Figure 2 the trajectories are shown for several particles. All particles scattering from one point of the plane are on a straight line, which is the intersection of the planes (3.12) and $z = z_0$, or given by the parametric system (3.10) for fixed $t$ if $v_0$ is a parameter.

The density is uniform in space at any moment of time. At $t \in (-\infty; 0)$ the gas becomes denser, and at $t \in (0;+\infty)$ the gas expands ($\rho \to 0$ as $t \to \infty$). The physical meaning of $\gamma$ is the presence of particle acceleration in the direction $OY$ axis and, accordingly, the presence of the second component of the pressure gradient $p_y$.

From a physical point of view, the blow-up is impossible, and it is necessary to conjugate the solution with another solution (possibly obtained for embedded subalgebras) through weak discontinuities and shock waves.

4.   Conclusions

In this article, we have obtained a new family of exact solutions for the gas dynamics equations with the special state equation when the pressure is prescribed by the sum of density function and entropy function. The solutions have been obtained from invariant submodel of rank one. It has been observed that the solutions of invariant submodel of rank one are embedded into solutions of the submodel with three independent variables. The new solutions of the gas dynamics equations describe the motion of particles in space with a linear velocity field and non-homogeneous deformation. At the one moment of time the solution specifies the blow-up or instantaneous source. The manifold of blow-up or source is a plane. From one point of the source the particles scatter into straight lines. The particle trajectories are parabolas or rays. The gas motion is vortex. The density is uniform in space at any moment of time. The gas becomes denser near the blow-up, and expands as it moves further away from the source.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the state assignment of Mavlyutov Institute of Mechanics UFRC RAS.

Conflict of interest

The author declares no conflict of interest in this paper.