On traveling wave solutions of a class of KdV-Burgers-Kuramoto type equations

1.   Introduction

Many phenomena in physics, engineering and other subjects can be described by nonlinear partial differential equations. In order to well understand various nonlinear phenomena in nature, the exact solutions for the nonlinear partial differential equations has to be studied. Finding effective methods to solve and analyse these equations has been an interesting subject in the field of differential equations. Sometimes, It is difficult to express various wave solutions of nonlinear partial differential equations explicitly in terms of elementary functions. In many cases it is possible to find and prove the existence of traveling wave solutions by the qualitative theory of differential equations and dynamical systems. From the physical point of view, traveling waves usually describe transition processes. Such as solitons and propagation with a finite speed, and thus they give more insight into the physical aspects of the problems. In order to obtain the traveling wave solutions of nonlinear partial differential equations, several powerful approaches to finding the exact solutions have been proposed, such as Backlund transformation method in ^[1], Darboux transformation ^[2,3,4,5,6], Hirota's method ^[7,8,9], the Fokas method ^[10], exp-function method in ^[11,12], tanh-sech method in ^[13], hyperbolic function method in ^[14], first integral method in ^[15,16], homogeneous balance principle in ^[17], Lie symmetry analysis method in ^[18,19] and the references therein ^[20,21,22]. Lie group theory plays an important role in studying the solutions of differential equations, for example, see ^{[23,24,25,26,27,28,29]}. In ^[25], Lie symmetry analysis is performed on the fifth-order KdV types of equations which arise in modelling many physical phenomena, and the exact analytic solutions are obtained.

In this paper, we consider a class of KdV-Burgers-Kuramoto (KdV-BK) type equation with arbitrary power nonlinearity,

where $\alpha, \beta, \gamma\neq0$ and $p\neq0$ are real constants. It contains dispersive terms $u_{xx}, u_{xxx}$ and $u_{xxxx}$ and also the nonlinear term $u^pu_x.$ Here the choice of $p = 1$ leads equation (1.1) to the KdV-Burgers-Kuramoto(KBK) equation

Equation (1.1) is referred to as the generalized KdV-Burgers-Kuramoto(KBK) equation. In ^[30], equation (1.1) was used for explanation of the origin of persistent wave propagation through medium of reaction-diffusion type. In ^[31,32], the motion of a viscous incompressible flowing down an inclined plane is studied by the application of equation (1.1). Mathematical model for consideration dissipative waves in plasma physics by means of equation (1.1) was presented in ^[33]. The equation (1.2) is simultaneously involved in nonlinearity, dissipation, dispersion and instability, and is suggested by Kuramoto ^[34,35]. The KBK equation is a classical nonlinear partial differential equation, which effectively describes the turbulent motion and other unstable motions. It is well known that there are many works to deal with equation (1.2) in recent years, see ^[34,35], ^{[36,37,38,39]} and the references therein. For example, In ^[36,37], The travelling wave periodic solutions of equation (1.2) were considered and obtained.

In this paper, we are mainly interested in equation (1.1). The rest of the paper is organized as follows. In section 2, Lie symmetries for (1.1) are found by differentiating the symmetry condition, and the partial differential equation has traveling wave solutions in this sense is shown. In section 3, the existence of traveling wave solutions of the equation is presented by analysing the corresponding autonomous system. Under the certain parametric conditions, the non-trivial infinitesimal generator of Lie groups admitted by deduced ordinary differential equation is obtained through analysing the determining system in section 4. Based on the Lie symmetry theory, a class of traveling wave solutions of (1.1) is presented by solving the invariant surface condition equation under the certain parametric conditions in section 5. Section 6 is conclusions.

2.   Lie symmetry to the KdV-Burgers-Kuramoto type equation

In this section, we consider Lie symmetry to equation (1.1). Based on Lie symmetry analysis theory ^[19], the generator $X$ of Lie symmetry admitted by (1.1) has the expression

where $\eta(x, t, u) = g(x, t)u+h(x, t),$ and $\xi(x, t), \; \tau(x, t), \; g(x, t), \; h(x, t)$ are function need to be determined. The surface $u = u(x, t)$ is invariant, provided that

when $u = u(x, t).$ (2.1) is called the invariant surface condition. The linearized symmetry condition is as follows:

when $\Delta = 0,$ where

and

Substituting (2.3) into (2.2), one can have

The linearized symmetry condition gives us a systematic approach to finding Lie point symmetries. We can obtain $u_{xxxx}$ from the restriction $\Delta = 0$ and substitute $u_{xxxx}$ into (2.4). According to their dependence on derivative of $u,$ we can get a linear system of determining equation for $\xi, \; \tau\, \; g, \; h:$

We solve the first equation of (2.5) to obtain

where $A(t)$ is an arbitrary function.

Owing to $p\neq0,$ the ninth equation of (2.5) yields

and the tenth equation of (2.5) yields

where $B(t)$ is an arbitrary function. The twelfth equation of (2.5) tells us

where $c_3$ is an arbitrary constant. So,

From the eighth equation of (2.5), we have

The sixth equation of (2.5) gives us the result

Substituting the expression of $\xi_x$ into the third equation of (2.5) yields $c_3 = 0.$ Thus, $g = 0, \xi_x = 0, \; \tau_t = 0.$ The fifth equation of (2.5) is satisfied apparently. One can get $\xi_t = 0$ from the seventh equation of (2.5). So, the generator of Lie symmetry is

where $c_1, \; c_2$ are arbitrary constants.

The derived above generator X implies that (1.1) has a invariant solution in the form

where $c$ is an arbitrary constant.

3.   The analysis of the traveling wave solutions of the KdV-Burgers-Kuramoto type equation

Substituting the traveling wave solution of the form $u = u(v), \; v = x-ct$ into (1.1), we can get the traveling wave solution equation as follows,

For (3.1) with $p\neq-1$, performing the integration once, one has the following traveling wave solutions equation

where $k$ is an integration constant. Let $R = \dfrac{du}{dv}, \; w = \dfrac{dR}{dv}, k = 0,$ (3.2) can be rewritten as

As we know, a solitary wave solution of (1.1) corresponds to a heteroclinic orbit of system (3.3). We will prove that the heteroclinic orbit of system (3.3) does exist when the parametric conditions are satisfied correspondingly.

For convenience, we consider $p$ being a positive integer. When $p$ is an even number and $(p+1)c > 0,$ (3.3) has three equilibrium points

When $p$ is an odd number, (3.3) has two equilibrium points

The coefficient matrix $A_1$ of the linearization system of (3.3) about the equilibrium point $u_1^*$ is

Then, the characteristic equation for $A_1$ is

Similarly, one can get the coefficient matrix $A_2$ of the linearization system of (3.3) about the equilibrium points $u_{2, 3}^*.$ The matrix is

Then, the characteristic equation for $A_2$ is

We have the following result for (3.3).

Theorem 3.1. If $\alpha, \beta, \gamma$ and $c$ are of same sign, $p$ is a positive integer and $pc\gamma-\alpha\beta < 0,$ then the equilibrium point $A_1$ of (3.3) has a one-dimensional unstable manifold and the equilibrium point $A_{2, 3}$ (or $A_{2}$) of (3.3) has a three-dimensional stable manifold.

Proof. The proof is based on Argument Principle. For proving the equilibrium point $A_1$ of (3.3) possessing a one-dimensional unstable manifold, one needs to prove the characteristic equation (3.4) has only one root in the right half complex plane, and for proving the equilibrium point $A_{2, 3}$ (or $A_{2}$) of (3.3) possessing a three-dimensional stable manifold, one needs to prove the characteristic equation (3.5) has three roots in the left half complex plane.

Let us to consider $f_1(\lambda)$ firstly. Since $f_1(\lambda)$ is analytic in complex plane, the number of roots in the right half complex plane is

where $C$ is composed of $\Gamma_R:\; \; z = Re^{i\theta}, \; -\dfrac{\pi}{2}\leq\theta\leq\dfrac{\pi}{2},$ a straight line $\overrightarrow{(Ri, -Ri)}$ is on the imaginary axis and $\Delta_C arg f_1(z)$ denotes the total change quantity in the argument of $f_1(z)$ along $C.$ Apparently, (3.6) equals

The first part of the above formula is

The second part of that formula is

where $f_1(iy) = (-\dfrac{\beta}{\gamma}y^2-\dfrac{c}{\gamma})+(\dfrac{\alpha}{\gamma}y-y^3)i,$ and $f_1(0) = -\dfrac{c}{\gamma}.$ Because $\beta, \gamma$ and $c$ are of same sign, $\dfrac{\beta}{\gamma} > 0, \; \dfrac{c}{\gamma} > 0.$ So $Re(f_1(iy)) < 0$ and $f(0) < 0,$ the image $f_1(iy)$ only lies on the left complex plane. For $|R|\rightarrow\infty,$ $f_1(iy)$ has the asymptotic behavior,

So,

The number of roots of $f_1(\lambda) = 0$ in the right half complex plane is $1.$ Therefore, the equilibrium point $A_1$ of (3.3) has a one-dimensional unstable manifold.

Similarly, we consider the number of roots of $f_2(\lambda) = 0$ in the left half complex plane. Since $f_2(\lambda)$ is analytic in complex plane, the number of roots in the left half complex plane is

where $C$ is composed of $\Gamma_R:\; \; z = Re^{i\theta}, \; \dfrac{\pi}{2}\leq\theta\leq\dfrac{3\pi}{2},$ a straight line $\overrightarrow{(-Ri, Ri)}$ on the imaginary axis and $\Delta_C arg f_2(z)$ denotes the total change quantity in the argument of $f_2(z)$ along $C.$ Apparently, (3.7) equals

The first part of the above formula is

The second part of that formula is

where $f_2(iy) = (-\dfrac{\beta}{\gamma}y^2+\dfrac{pc}{\gamma})+(\dfrac{\alpha}{\gamma}y-y^3)i$ and $f_2(0) = \dfrac{pc}{\gamma}.$

We first compute the quantity $\Delta_{(-\infty, 0)}arg(f_2(iy)).$ Note that

it is obvious that as $y$ increases from $-\infty$ to $0,$ $Re(f_2(iy))$ increases monotonously from $-\infty$ to $\dfrac{pc}{\gamma},$ and $Im(f_2(iy))$ decreases monotonously from $+\infty$ to $-\dfrac{2\alpha}{3\gamma}\sqrt{\dfrac{\alpha}{3\gamma}}$ afterwards increases monotonously to $0.$ Owing to $\sqrt{\dfrac{\alpha}{\gamma}} > \sqrt{\dfrac{pc}{\beta}}$ from the assumption $pc\gamma-\alpha\beta < 0,$ as $y$ increases from $-\infty$ to $0,$ the image $f_2(iy)$ starts in second quadrant of complex plane, intersects the minus Re-axis, passes through the third quadrant, intersects the Im-axis at a certain point, passes through the forth quadrant and finally ends up the point $(\dfrac{pc}{\gamma}, 0)$ of the positive Re-axis. So, $\Delta_{(-\infty, 0)}arg(f_2(iy)) = \dfrac{3\pi}{2}.$ Similarly, we can get $\Delta_{(0, +\infty)}arg(f_2(iy)) = \dfrac{3\pi}{2}.$ Therefore, The number of roots of $f_2(\lambda) = 0$ in the left half complex plane is $3.$ Therefore, the equilibrium point $A_{2, 3}$ (or $A_{2}$) of (3.3) has a three-dimensional stable manifold. This completes the proof.

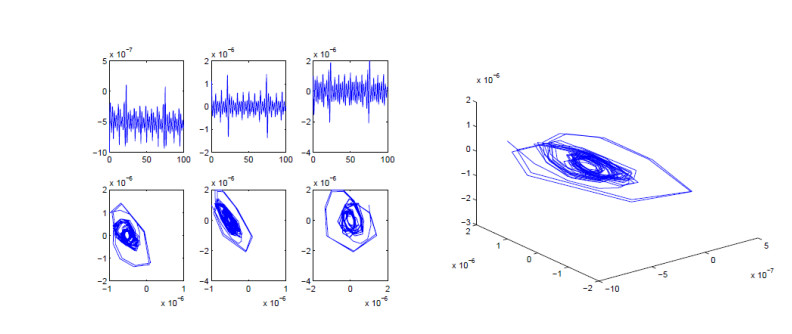
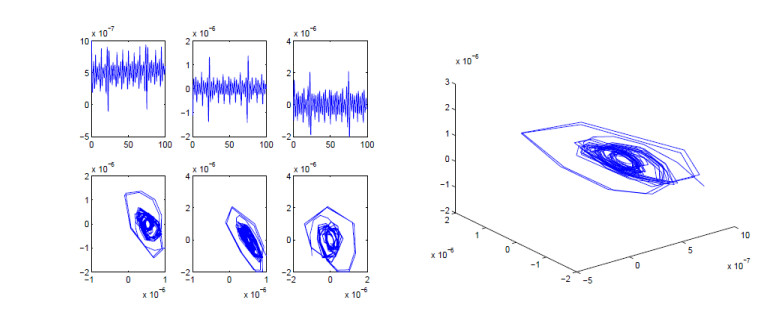
The local trajectory in the neighborhood of these equilibrium points of (3.3) are shown in Figures 1 and 2. In Figure 1, we let $\alpha = 710, \beta = 200, \gamma = 170, p = 4, c = 1,$ and the initial value is $(0.000001, -0.000001, -0.000001).$ In Figure 2, we let $\alpha = 710, \beta = 200, \gamma = 170, p = 4, c = 1,$ and the initial value is $(-0.000001, 0.000001, 0.000001).$ In these Figures, there are the images in coordinate plane $(t, u), (t, R), (t, w), (u, R), (u, w), (R, w)$ and in coordinate space $(u, R, w),$ which show that the equilibrium point $(0, 0, 0)$ is unstable and the equilibrium points $(\pm\sqrt[p]{(p+1)c}, 0, 0)$ is stable.

Theorem 3.2. When $\alpha, \beta, \gamma, c$ are of same sign, $p$ is a positive integer and $pc\gamma-\alpha\beta < 0,$ (3.3) has potentially a heteroclinic orbit.

Proof. Owing to Theorem 3.1, the sum of the dimension of the unstable manifold $W^u(A_1)$ and the stable manifold $W^s(A_{2, 3})$ is four. The dimension of the phase plane of (3.3) is three. Therefore, these two manifolds potentially intersect in $R^3$ along one-dimension curve, which is a heteroclinic orbit of (3.3).

As we know, the heteroclinic orbit of (3.3) corresponds a traveling wave solution of (1.1). Motivated by the above results, we will consider to obtain traveling wave solutions of (1.1) by using Lie symmetry method.

4.   Lie symmetry to the traveling wave solutions equation

In the section, we consider to search for Lie symmetries admitted by (3.2).

4.1.   $p\neq-1$

We suppose that $V = \xi(x, y)\dfrac{\partial}{\partial x}+\eta(x, y)\dfrac{\partial}{\partial y}$ is the infinitesimal generator of Lie symmetry admitted by (3.2). Here, for convenience, symbols $y$ and $x$ are in place of $u$ and $v,$ respectively.

Therefore,

is the 3th-extended infinitesimal generator, where

The linearized symmetry condition

where $f(x, y, y', y'') = -\dfrac{y^{p+1}}{\gamma(p+1)}+\dfrac{c}{\gamma}y+\dfrac{k}{\gamma}-\dfrac{\alpha}{\gamma}y'-\dfrac{\beta}{\gamma}y''.$ Plugging (4.1) to (4.2) and replacing $y'''$ by $f(x, y, y', y''),$ This yields

Both $\xi$ and $\eta$ are independent of $y'$ and $y'',$ After setting the coefficients of the powers $(y')^i(y'')^j (i, j = 0, 1, 2, 3, 4)$ in (4.3) to zero, one can get the determining equations system,

The equation (4.7) gives

After putting (4.13) into equation (4.8) yields

where $a_1(x)$ and $a_2(x)$ are functions of $x.$ Equation (4.4), (4.5), (4.6) and (4.9) are satisfied by (4.13) and (4.14). Substituting (4.13) and (4.14) into (4.10), (4.11) and (4.12), we have the system

The third equation of (4.15) is a polynomial of $y$ with degree $p+1$ which is zero if and only if each variable coefficient is set to zero,

So the above set of differential equations of $a_1(x)$ and $a_2(x)$ can be solved according to the following two cases,

Case 1: $k = 0$

Substituting $\xi'$ derived from (4.16) into the first equation of (4.15), under the condition $p\neq-3,$ one has

and

where $c_1$ is an integration constant. Substituting $\xi'$ and $a_1(x)$ into the second equation of (4.15), one can get a parametric condition

The other parametric condition can be obtained by pulling $a_1(x)$ to (4.18) and it is

Integrating $\xi'$ and using $a_1(x), a_2(x),$ we have

and

where $c_2$ is an arbitrary constant. The infinitesimal generator

If $p = -3,$ we can get $a_1(x)$ and $\xi'(x)$ being all zeros form substituting $\xi'$ into the first equation of (4.15). So, $\xi = c, \eta = 0,$ where $c$ is an arbitrary constant. The infinitesimal generator is $X = c\partial_x.$

Case 2: $k\neq0,$

In this case, from (4.16) and (4.19), we can have $a_1(x) = 0, \xi'(x) = 0.$ Furthermore, (4.15) and (4.18) hold. We can obtain

where $c$ is an arbitrary constant. The infinitesimal generator is $X = c\partial_x.$

4.2.   $p=-1$

For equation (3.1) with $p = -1$, performing the integration once, one has

Similarly, we can obtain the system satisfied by generators of the Lie group admitted by (4.23) by the linearized symmetry condition (4.2).

Thus, we can get

where $c$ is an arbitrary constant. In this case, the infinitesimal generator of Lie symmetry is $X = c\partial_x.$

Therefore, we can have the following result about the Lie symmetries admitted by (3.2).

Theorem 4.1.

Case 1. $p\neq-1, p\neq-3$ and $k = 0.$

when (4.20) and (4.21) are satisfied, (3.2) accepts Lie symmetry with the infinitesimal generator (4.22).

Case 2. $p\neq-1, p\neq-3$ and $k\neq0.$

(3.2) accepts Lie symmetry with the infinitesimal generator $X = c\dfrac{\partial}{\partial x},$ where $c$ is an arbitrary constant.

Case 3. $p = -1$ or $p = -3.$

(3.2) accepts Lie symmetry with the infinitesimal generator is $X = c\dfrac{\partial}{\partial x},$ where $c$ is an arbitrary constant.

5.   The invariant solutions of the KdV-Burgers-Kuramoto type equation

In the section, we consider to obtain the traveling wave solutions of the KdV-Burgers-Kuramoto type equation under the parametric conditions in Section 4 using the invariant curve condition

If the infinitesimal generator of Lie symmetry admitted by (3.2) is

then

that is, a trivial solution $y = constant$ is obtained. The trivial solution has no new useful meaning. So, we consider the following case.

Under the parameter conditions of (4.20) and (4.21), the infinitesimal generator is (4.22). Inserting $\xi(x)$ and $\eta(x, y)$ of (4.22) into (5.1), one has

After solving the above equation, we can have

where $c_3$ is an integration constant. Using the identity $\frac{e^{2x}}{1+e^{2x}} = \frac{1}{2}\tanh x+\frac{1}{2}$ and choosing $\frac{c_1}{c_2} = -\frac{\beta}{\gamma(p+3)},$ we obtain the invariant solutions of (1.1),

where $c_3$ is an arbitrary constant.

When $p = 1,$ (1.1) becomes (1.2), the parametric conditions (4.20) and (4.21) change to

and

Substituting (5.3) into (5.4) yields the condition

Accordingly, under the conditions (5.3) and (5.5), one can get a traveling wave solution of (1.2),

where $c_3$ is an arbitrary constant. After using the identity $sech^2t = 1-\tanh^2t,$ the traveling wave solution can be turn to

The solution is be equivalent to that in the existing literatures, for example ^[35,39].

When $p = 2,$ the parametric conditions (4.20) and (4.21) change to

and

Substituting (5.6) into (5.7) yields the condition

Accordingly, under the conditions (5.6) and (5.8), one can get traveling wave solutions of (1.2)

where $c_3$ is an arbitrary constant. The solution is a new solution of (1.1) compared with the results in ^[40].

6.   Conclusions

In this paper, we consider the solutions of a KdV-Burgers-Kuramoto type equation with an arbitrary power nonlinearity $u^pu_x.$ Firstly, we present the condition of the existence of traveling wave solutions of the equation based on the qualitative theory of differential equations. Then, with $p\; (p\neq-1, \; p\neq-3)$ being an arbitrary constant, when $k = 0,$ and the corresponding parametric conditions (4.20) and (4.21) are satisfied, we derive the invariant solutions of the KdV-Burgers-Kuramoto equation by solving the determining system and the invariant curve condition equation. When $p = 2,$ the KdV-Burgers-Kuramoto equation with the nonlinearity term $u^2u_x$ is the equation in ^[40]. Compared with the results in ^[40], a new solution is obtained.

For the case $\gamma = 0$ in (1.1), the KdV-Burgers-Kuramoto type equation with an arbitrary power nonlinearity can be turn to the KdV-Burgers type equation. One can not directly get the traveling wave solutions from the traveling wave solutions of (1.1) with $\gamma = 0$ because the equation has singular points. Thus, the dynamical properties and the qualitative analysis to the traveling wave solutions equation have to be studied. These will be investigated in our future work.

Acknowledgement

The first author would like to thank Prof. Zhaosheng Feng (University of Texas-Rio Grande Valley) for his discussions and helpful suggestions.

Conflict of interest

All authors declare no conflicts of interest in this paper.