This paper introduces an approximate-analytical method (AAM) for solving nonlinear fractional partial differential equations (NFPDEs) in full general forms. The main advantage of the paper is to apply the proposed AAM to solve the fractional Korteweg-de Vries (KdV) equations. Moreover, the analytical travelling wave solutions for the fractional KdV equation and the modified fractional KdV equation are successfully obtained. The numerical solutions are also obtained in the forms of tables and graphs. The fractional partial derivatives are considered in Caputo sense.
1.
Introduction
Fractional partial differential equations (FPDEs) have emerged from numerous research fields of science, engineering and physics, see [1,3,7,8,15,16,23]. There are many works devoted to the development of efficient methods for solving FPDEs but we should note that finding an analytical or approximate solution is a challenging problem, therefore, accurate methods for finding the solutions of FPDEs are still under investigation (see, e.g., new analytical technique for solving a system of nonlinear fractional partial differential equations [21], analytical solutions for conformable space-time conformable fractional partial differential equations [18], modified least squares homotopy perturbation method for solving FPDEs [19], conformable natural extension of the theory of conformable fractional calculus [22]). Several analytical and numerical methods for solving FPDEs exist in the literature, for example; the Generalized differential transform method[12] and the method was proposed to solve a space- and time-fractional diffusion-wave equation, homotopy perturbation method [6] for fractional Fornberg–Whitham equation, a homotopy perturbation technique [4], and so on. There are, however, a few solution methods for only travelling wave solutions, for example; the multiple exp-function algorithm [10]), fractional complex transformation [25] where the method was employed to solve fractional partial differential equations in the sense of the modified Riemann–Liouville derivative, Lie symmetries, symmetry reductions and conservation laws [2], new modification of Adomian decomposition method for solving a system of nonlinear fractional partial differential equations Research [20] and some references cited therein.
As a modern mathematical discipline nonlinear wave theory frequently explores asymptotic regimes (such as varying over many scales, high frequency or large amplitude) which are not easily accessible via numerical simulations. Moreover, the nonlinear wave theory plays an important role to the understanding of real water waves, the interaction of light with matter, optical fiber transmission, traffic flow, earthquakes, galaxy formation and the steepening of short gravity waves on the crests of long waves. In this paper, two types of the well-known nonlinear wave equations with a fractional order are studied; one is the nonlinear KdV equation and another one is the modified KdV equation (see [2,13,17,24]).
Briefly, a nonlinear wave equation of Korteweg de Vries type has the following form:
where the subscripts denote partial derivatives and parameters a,b can be scaled to any real number.
The goal of this paper is to apply an AAM to solve full general NFPDEs without any assumption and that it gives good results in analytical and numerical experiments. The rest of the paper is organized in as follows: In Section 2, we present basic definitions and preliminaries which are needed in the sequel. In Section 3, we introduce an AAM for solving full general NFPDEs. Approximate analytical and numerical solutions for fractional KdV equations are obtained in Section 4.
2.
Basic definitions and preliminaries
There are various definitions and properties of fractional integrals and derivatives. In this section, we present modifications of some basic definitions and preliminaries of the fractional calculus theory, which are used in this paper and can be found in [5,9,11,14] and some references cited therein.
Definition 1. Let q∈R∖N and q≥0. Then, the Riemann-Liouville fractional partial integral denoted by Iqt of order q for a function u(x,t)∈Cμ, μ>−1 is defined as:
where Γ is the well-known Gamma function.
Theorem 2.1. Let q1,q2∈R∖N,q1,q2≥0 and p>−1. Then, for a function u(x,t)∈Cμ, μ>−1, the operator Iqt satisfies the following properties:
Definition 2. Let q,t∈R,t>0,m−1<q<m∈N and u(x,t)∈Cmμ. Then, the Caputo fractional partial derivative of order q for a function u(x,t) denoted by Dqtu(x,t) is defined as follows:
Theorem 2.2. Let t,q∈R,t>0 and m−1<q<m∈N. Then
3.
AAM for solving NFPDEs
In this section, we present a AAM to solve NFPDEs with initial values of the following form:
where L and N are linear and nonlinear operators, respectively, of u(ˉx,t) and its partial derivatives, which might include other fractional partial derivatives of orders less than q; f(ˉx,t) is known analytic function; and Dqt is the Caputo partial derivative of fractional order q, and ˉx=(x1,x2,…,xn)∈Rn. The proposed AAM has much more computational power in obtaining piecewise analytical solutions.
To introduce the AAM, first we need to present the following results.
Lemma 3.1. For u(ˉx,t)=∑∞k=0pkuk(ˉx,t), the linear operator L(u) satisfies the following property:
Theorem 3.2. Let u(x,t)=∑∞k=0uk(ˉx,t), for the parameter λ, we define uλ(ˉx,t)=∑∞k=0λkuk(ˉx,t), then the nonlinear operator N(uλ) satisfies the following property:
Proof By the help of the Maclaurin expansion of N(∑∞k=0λkuk) with respect to λ, we have
Definition 3. The polynomials En(u0,u1,…,un) can be defined as:
Remark 3.1. Let En=En(u0,u1,…,un) be as in Definition 3. Then by using Theorem 3.2, the nonlinear operator N(uλ) can be expressed in terms of En as:
3.1. Existence theorem
The following theorem introduces the approximate analytical solution obtained by the AAM for the nonlinear fractional partial differential equation with initial value given by (3.1).
Theorem 3.3. Assume that f(ˉx,t),fi(ˉx) are defined as in (3.1) and for m−1<q<m∈N. Then, equation (3.1) admits at least a solution given by
where L(−q)t(u(k−1)) and E(−q)(k−1)t denote the fractional partial integral of order q for L(uk−1) and E(k−1) respectively with respect to t.
Proof. Let the solution function u(ˉx,t) of equation (3.1) be as in the following analytical expansion:
To solve the initial value problem (3.1), we consider
with initial conditions given by
Next, we assume that, the initial value problem (3.8) has a solution given by
By applying Riemann-Liouville fractional partial integral of order q with respect to t to both sides of the initial value problem (3.8) and using Theorem 2.2, we obtain
By using the initial condition given by (3.1), equation (3.11) can be rewritten as:
By substituting (3.10) into (3.12), we obtain
By using Lemma 3.1 and Theorem 3.2, equation (3.13) becomes
Next, we use Definition 3 in equation (3.14), we obtain
By equating the terms in equation (3.13) with identical powers of λ, we obtain the following components:
Substituting the components from (3.16) into equation (3.10) gives the solution of equation (3.8). Now, from equations (3.7) and (3.10), we obtain
By using the first equations of (3.17), we see that ∂iu(ˉx,0)∂ti=limλ→1∂iuλ(ˉx,0)∂ti, which implies that gi(ˉx)=fi(ˉx). Inserting (3.16) into (3.17) completes the proof.
3.2. Convergence and error analysis
In the following results, we establish the convergence theorem and maximum absolute error theorem of the analytical solution given by (3.6) for the nonlinear partial differential equation given by (3.1).
Theorem 3.4. Let B be a Banach space. Then the series solution of equation (3.16) converges to S∈B for , if there exists γ,0≤γ<1 such that, ‖un‖≤γ‖u(n−1)‖ for ∀n∈N.
Proof. Define the sequence Sn of partial sums of the series given by equation (3.16) as:
and we need to show that {Sn} is a Cauchy sequence in Banach space B. For this aim, we introduce
For every n,n′∈N,n≥n′, by using equation (3.19) and triangle inequality successively, we have
Since 0<γ<1, so 1−γn−n′≤1. Then
Since u0(ˉx,t) is bounded, then
Therefore, {Sn} is a Cauchy sequence in the Banach space B, so the series solution defined in equation (3.7) is convergent and the proof is complete.
Theorem 3.5. The maximum absolute truncation error of the series solution (3.7) of the nonlinear fractional partial differential equation (3.1) is estimated to be
where the region Ω⊂Rn+1.
Proof. From Theorem 3.4, we have
But we assume that Sn=∑nk=0u(ˉx,t) and since n→∞, we obtain Sn→u(ˉx,t), so equation (3.24) can be rewritten as:
Therefore, the maximum absolute error is
and this completes the proof.
4.
Applications to fractional KdV equations
In this section, we present examples of some well-known nonlinear fractional partial differential equations, namely, fractional KdV equations. The following examples are chosen due to their closed form solutions which are available in the literature or they have been solved previously by some other well-known methods.
Example 4.1. Consider the following Korteweg-de Vries (KdV) equation of fractional order with initial value:
For q=1, the exact solitary wave solution of the mKdV equation (4.1) is given by
To solve equation (4.1) along with the initial condition, we compare (4.1) with equation (3.1), we obtain
where we assume N(u)=−u(x,t)ux(x,t).
Next, we assume equation (4.1) has a solution given by
To obtain the approximate solution of equation (4.3), we consider the following equation:
subject to the initial conditions given by
and we assume that equation (4.5) has a solution of the following form:
By applying Riemann-Liouville fractional partial integral of order q with respect to t to both sides of equation (4.5) and by using Theorem 2.2 and equation (4.6), we obtain
We use Remark 3.1 and equation (4.7) into equation (4.8), we obtain
We equate the terms in equation (4.9) with identical powers of λ, we obtain the following components:
for k=2,3,… where E(k−1) can be obtained by using Definition 3.
By using equations (4.4) and (4.7), we can write
By using equation (4.11), we have u(x,0)=limλ→1uλ(x,0), it gives that g(x)=u(x,0).
Consequently, we use the components from (4.10) into (4.11), using Definition 3 and by Mathematica software, we obtain the first few components of the solution for the initial value problem (4.1) as follows:
Therefore, the approximate solution of third-order term for equation (4.1) is given by
Example 4.2. Consider the following modified Korteweg-de Vries (mKdV) equation of fractional order with initial value:
where α is a constant. When q=1, the exact solitary wave solution of the mKdV equation (4.14) is given by
To obtain the solution for equation (4.1) along with the initial condition, we compare (4.14) with equation (3.1), we obtain
where we assume N(u)=α(u(x,t))2ux(x,t).
Further, we suppose that equation (4.1) has a solution given by
To get a solution of equation (4.16), we consider the following equation:
subject to the initial conditions given by
and we assume that equation (4.18) has a solution of the following form:
By applying the Riemann-Liouville fractional partial integral of order q with respect to t for both sides of equation (4.18) and by using Theorem 2.2 and equation (4.19), we obtain
Using Remark 3.1 and equation (4.7), in equation (4.8), we obtain
We equate the terms in equation (4.22) with identical powers of λ, we obtain the following components:
for k=2,3,…, where the nonlinear polynomial E(k−1) can be obtained by using Definition 3.
From equations (4.17) and (4.20), we can write
We use equation (4.11) into (4.24), we have u(x,0)=limλ→1uλ(x,0), it gives that g(x)=u(x,0).
Consequently, we use the components from (4.23) into (4.24) and using Definition 3 with the help of Mathematica software, the first few components of the solution for the initial value problem (4.14) are obtained as follows:
and so on. Therefore, the approximate solution of third-order term for equation (4.14) is given by
5.
Numerical results and discussion
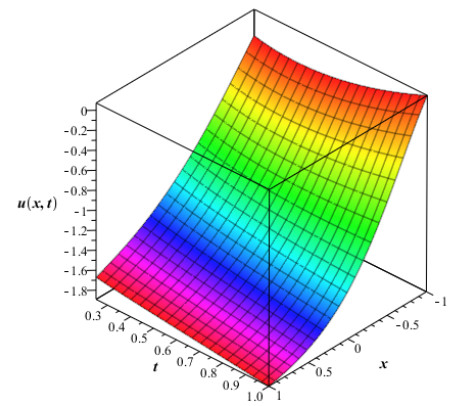
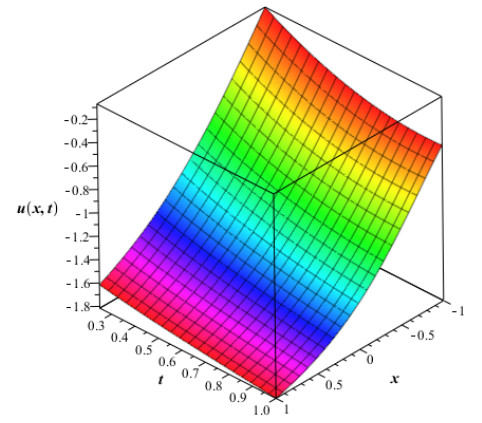
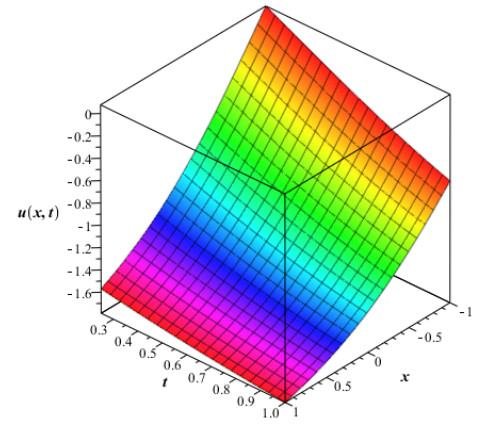
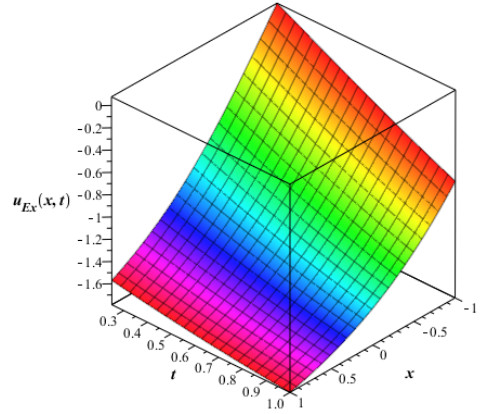
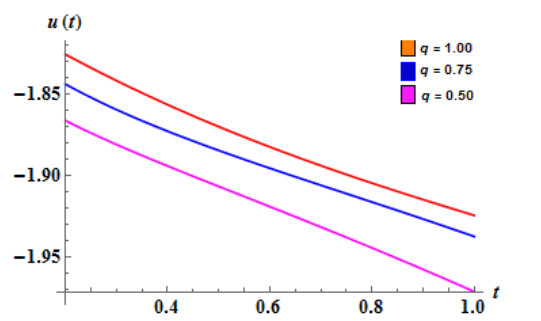
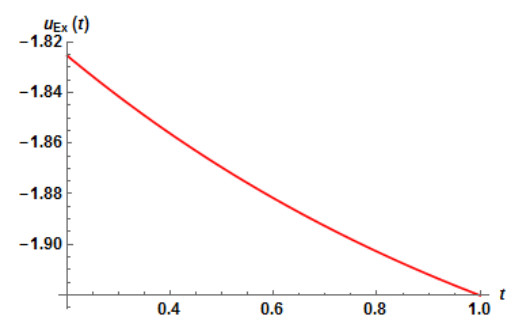
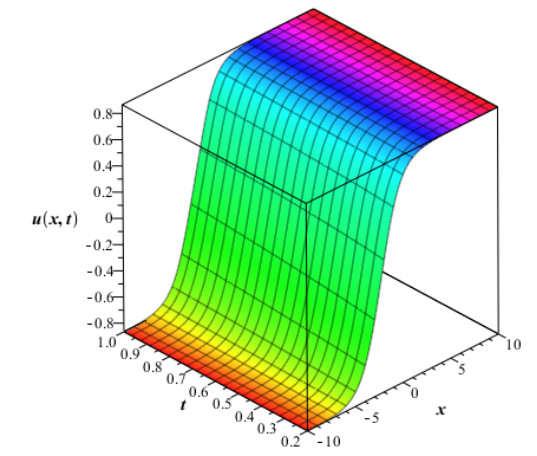
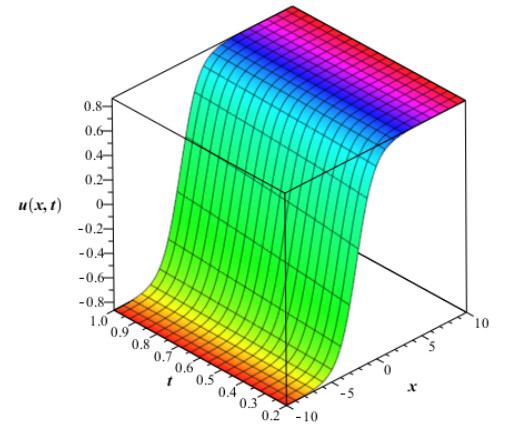
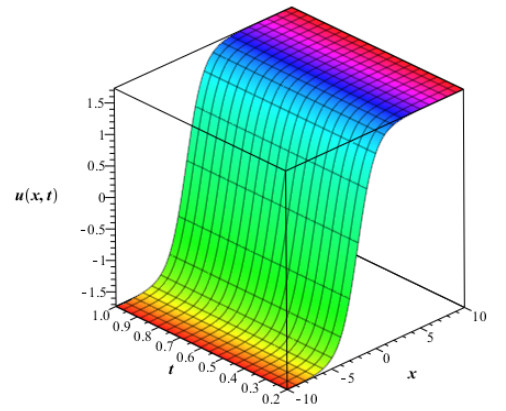
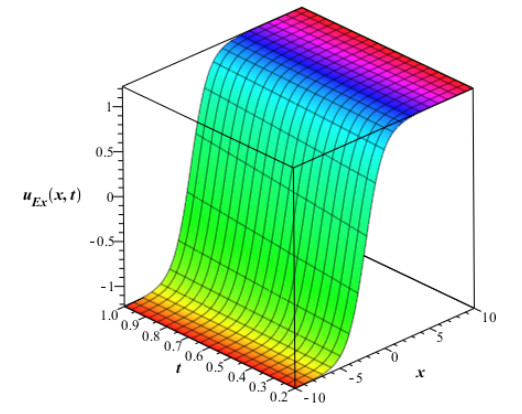
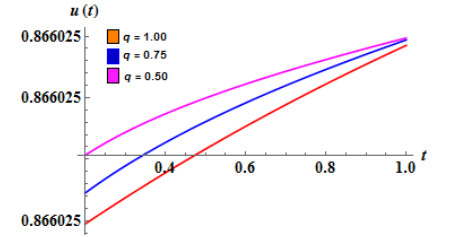
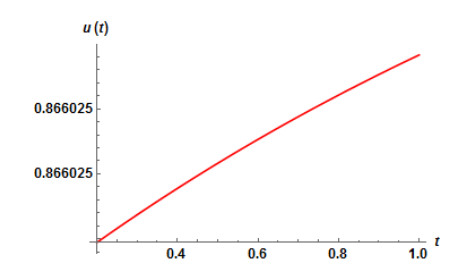
The numerical values in Table 1 are of approximate solution uAAM(x,t) obtained by the proposed AAM and the exact solution uEx(x,t) given by equation (4.2) through different values of x,t when q=0.5,0.75 and 1 for Example 4.1. The Figure 1 and Fig. 2 show the graphs of the approximate solution among different values of x,t when q=0.50 and q=0.75 respectively for Example 4.1. In Fig. 3, we plotted the graph of the approximate solution among different values of x,t when q=1 for Example 4.1. The Fig. 4 shows the graph of the exact solution among different values of x,t for Example 4.1. In Fig. 5 and Fig. 6, we plotted the graphs of the approximate and exact solutions respectively among different values of t,q when x is fixed for Example 4.1. From the Fig. 5, we observe that the approximate solution for Example 4.2 decreases when t and q decrease for fixed values of x. In Fig. 6, the exact solution for Example 4.1 decreases when t decreases for fixed values of x.
In Table 2, we evaluated the numerical values of the approximate solution uAAM(x,t) obtained by the proposed AAM and the exact solution uEx(x,t) given by equation (4.15) through different values of x,t when q=0.5,0.75,1 to make a numerical comparison between uAAM and uEx. The Fig. 7 and Fig. 8 show the graphs of the approximate solution among different values of x,t for α=2 when q=0.50 and q=0.75 respectively for Example 4.2. The Fig. 9 shows the graph of the approximate solution among different values of x,t when q=1 and α=2 for Example 4.1. In Fig. 10, we plotted the graph of the exact solution among different values of x,t when α=2 for Example 4.2. In Fig. 11 and Fig. 12, we plotted the graphs of the approximate and exact solutions respectively among different values of t,q when x is fixed and α=2 for Example 4.2. From the Fig. 11, we observe that the approximate solution for Example 4.2 increases when t increases and q decreases for fixed values of x and α=2. In Fig. 12, the approximate solution for Example 4.2 decreases when t increases for fixed values of x and α=2. From the previous argument and from the numerical values in Table 1 and Table 2, we observe that absolute error is very small which means that the proposed AAM is very effective to obtain the analytical solutions for NFPDEs easily without any assumption.
6.
Conclusion
An approximate-analytical method for solving full general NFPDEs was introduced in this paper and it was efficaciously applied to solve fractional KdV equations with the aid of the Caputo derivative. The obtained travelling wave solutions to the fractional KdV equations can be applied for further study in analytical fields such as stability analysis in the area of applied sciences for instance mathematics and physics. The real benefit of the AAM is that it provides extra general and a great number of original travelling wave solutions by way of some unrestricted parameters. It is valued to state that putting into practice of the proposed method is very dependable, well-organized and it applicable to solve further fractional nonlinear wave equations. We used Maple and Mathematica software to obtain the numerical values and plotting the graphs.
Author contributions: Hayman Thabet and Subhash Kendre contributed substantially to this paper. Hayman Thabet wrote this paper; Subhash Kendre Supervised development of the paper and James Peters helped to evaluate and edit the paper.
Acknowledgments
The research by James Peters has been supported by the Natural Sciences & Engineering Research Council of Canada (NSERC) discovery grant 185986, Instituto Nazionale di Alta Matematica (INdAM) Francesco Severi, Gruppo Nazionale per le Strutture Algebriche, Geometriche e Loro Applicazioni grant 9 920160 000362, n.prot U 2016/000036 and Scientific and Technological Research Council of Turkey (TÜBİTAK) Scientific Human Resources Development (BIDEB) under grant no: 2221-1059B211301223.
The authors thank the referees for their valuable comments and suggestions.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: