A survey of KdV-CDG equations via nonsingular fractional operators

1.   Introduction

In recent centuries, nonlinear evolution equations (NEEs) have considerably gotten scientists and engineers. The most common and well-known NEE is the Korteweg-de Vries (KdV) equation, which has been used to analyze shallow water waves. Physicists have significantly modified the basic KdV equation by combining it with other equations. For instance, Su and Gardner proposed the KdV-Burger equation for the first time ^[1]. In the literature ^[2,3], the KdV and the KdV-Sawada-Kotera equation has been studied. In the literature, several other modifications exist in KdV equations ^[4,5]. We consider the Korteweg-de Vries-Caudrey-Dodd-Gibbon (KdV-CDG) equation ^[6] as follows:

where $c_{1}, c_{2}$ are real constants. Equation (1.1) is reduced to the KdV equation for $c_{2} = 0$ and to the CDG equation for $c_{1} = 0$. There is an increased interest in examining the Kdv-CDG equation since it is used in many different problems in the mathematics and natural sciences.

Nowadays, fractional and integer order PDEs are frequently implemented by scholars in the modeling of physical processes ^{[7,8,9,10,11]}. Fractional operators can provide past information and the history of a physical process since they preserve memory and have heredity characteristics. Over the last few decades, mathematicians and scientists have proposed several operators with different kinds of kernels ^[12]. The Caputo operator is the most well-known fractional operator, dependent on the Power-Law kernel. Caputo operators were applied to many mathematical models in applied sciences. For instance, researchers have used Caputo operators in engineering ^[13,14,15] and physical sciences ^[16,17]. Hosseini et al. studied nonlinear water wave equations under the Caputo operator ^[18]. Later, Caputo and Fabrizio declared the singularity problem in the Caputo operator. Therefore, they modified the old definition by changing the power-law kernel with a nonsingular exponential-decay kernel ^[19]. Using homotopy analysis method (HAM), the authors have studied the Sharma-Tasso-Olver-Burgers equation under the Caputo-Fabrizio operator ^[20]. In the last five years, the Caputo-Fabrizio operator has frequently been used in several fields of applied sciences ^[21,22]. In 2016, Atangana and Baleanu indicated a problem of locality in the kernel of the CF operator. Thus, they defined a new operator by replacing the exponential-decay kernel with a generalized Mittag-Leffler kernel ^[23]. We can call this operator the Atangana-Baleanu-Caputo (ABC) operator. It has gained attention in the scientific community due to its unique advantages over other fractional derivative operators. Unlike some other fractional derivative operators, the ABC is non-singular and continuous. This means that it does not produce infinite or undefined values and can be applied to a wider range of functions. The ABC is non-local, meaning it takes the entire history of the function being differentiated into account. This makes it useful for describing systems with either long-range interactions or memory effects. The ABC operator has plenty of applications in different fields of science. For instance, Xu et al. investigated the chaotic behaviour of a piecewise HIV-1 model in the sense of ABC ^[24]. Saifullah et al. studied the shock wave solutions of the Klein-Gordan equation under the ABC operator ^[25]. Hosseini et al. investigated the Cauchy reaction-diffusion equation under the ABC fractional operator ^[26]. Bayrak et al. analyzed partial differential equations under ABC fractional operator ^[27]. Some other applications of ABC operators can be found in ^[28,29].

Inspired by the above works on the ABC operator, we study Eq (1.1) under the ABC fractional operator. Consider the Eq (1.1) under the ABC fractional operator as:

where $^{\mathscr{ABC}}D_{t}^{ \text{h}}u(x, t)$ denotes the ABC fractional derivative of $u(x, t).$

In this paper, the KdV-CDG equation is investigated under the ABC operator. Fixed point theory is utilized to derive the results of the existence, uniqueness and stability of solution. The Laplace transformation (LT) coupled with the Adomian decomposition method (ADM), is implemented to find an approximate solution to the considered equations. The MATLAB-2020 program is used for simulations. The rest of the paper is organized as follows: Section 2 gives the basic concepts of fractional calculus. The existence and uniqueness results of the considered equation are carried out in Section 3. Section 4 is devoted to the solution of the considered problem. Section 5 deals with the convergence and stability analyses of the proposed method. Section 6 gives graphical analysis of the obtained solutions. The conclusions of the paper are given in Section 7.

2.   Preliminaries

Here, we give the definition of the ABC fractional derivative and integral.

Definition 1. ^[23] Let $0 < \text{h} < 1$ and $u\in H^{1}(c, d),$ then the $\mathscr{ABC}$ fractional order derivative of order $\text{h}$ is expressed as

where $\mathrm{AB}(\text{h})$ is the normalization function such that $\mathrm{AB}(0) = \mathrm{AB}(1) = 1.$ The symbol $E_{ \text{h}}$ is Mittag-Leffler function which is defined as

Definition 2. ^[23] Let $0 < \text{h}\leq1$ and $u\in H^{1}(0, T).$ Then the $\mathscr{ABC}$ fractional integral of order $\text{h}$ is defined as

Definition 3. ^[23] The LT of $\mathscr{ABC}$ FD of $u(t)$ is expressed by

Definition 4. Let $H$ be a Banach space and $X$: $H\rightarrow H$ be a mapping. Then $f$ is said to be Picard X-stable, if for all $\xi, m\in H$, we have

where $\mathrm{p}\geq0$ and $\mathrm{q}\in[0, 1]$. Moreover, the mapping admits a fixed point.

3.   Study of the considered KdV-CDG equation

As was said in the introductory section, a nonlinear process' entire past knowledge is provided by a fractional operator. Due to this, one may formulate the KdV-CDG equation (1.1) with the ABC operator as follows:

Here, we examine some analytical findings regarding the equation under consideration. Using the LT and ADM, we obtain analytical results. We demonstrate the solution's convergence and stability.

The certain findings related to the existence and uniqueness of the solution will be established. Equivalently, we can write

Let

Then, the above equation can be expressed as

Applying the $\mathscr{AB}$ fractional order integral, we get

Now, we want to prove the Lipschitz condition for the kernel $\mathrm{Z}(x, t;u).$ For this, take two bounded functions $u$ and $v,$ so $\left\Vert u\right\Vert \leq\nabla_{1},$ and $\left\Vert v\right\Vert \leq\nabla_{2}$ where $\nabla_{1}, \nabla_{2} > 0$ and consider

Since, $u$ and $v$ are bounded functions. Hence, their partial derivative fulfills the criteria of the Lipschitz condition and there exists non negative constants $K_{1}, L, M, N, O, P, Q,$ such that

This implies that

where

For an additional analysis, we create an iterative method as follows:

where $u_{0}(x, t) = u(x, 0).$ The difference between two successive terms can now be calculated as

Additionally, from the above equation, we have

Theorem 1. Let $u(x, t)$ be a bounded function. Then

Proof. Since,

Utilizing mathematical induction, we will obtain the desired theorem. For $\zeta = 1$, we have

Assume that the result is valid for $\zeta-1$, i.e.,

Now,

Hence, the proof is completed. □

Theorem 2. If the following relation holds at ${t = t_{0}\geq0},$ where

Then at least one solution of the new KdV-CDG equation under the $\mathscr{ABC}$-fractional derivative exists.

Proof. Since,

At ${t = t_{0}\geq0},$ we have

Since,

This means that the sequence $u_{\zeta}(x, t)$ is convergent. Therefore, it is bounded for all $\zeta$. Next, assume that

Since $u_{\zeta}(x, t)$ is bounded, thus

We achieve:

Applying the limit, we get

Thus,

Hence the proof is finished. □

Theorem 3. The inequality

satisfies for ${t = t_{0}\geq0}$. Then, the considered equation possesses a unique solution.

Proof. Let $u$ and $v$ be two solutions of the Eq (1.1). Consider

Since,

This leads us to the fact that $\left\Vert u(x, t)-v(x, t)\right\Vert = 0.$ More specifically, $u(x, t) = v(x, t).$

This shows the uniqueness of the solution. □

4.   Solution of the considered equation

In this portion, we derive a general solution of the considered equation using LT and ADM. We provide two examples to check the accuracy and simplicity of the suggested method. Consider

Applying LT, we have

Further, we reach:

The approximate solution is represented by

Thus,

where $\mathbb{\varLambda}_{i\zeta}$ for $i = 1, 2, 3, 4,$ is represented by the Adomian polynomial, i.e.,

The following can be obtained by comparing the corresponding terms, where one reaches the following:

Applying $\mathscr{L}^{-1}$, we get the series solution as

Here, we present two examples of the considered KdV-CDG equation.

Example 1. Here, we choose the initial condition as:

Applying the above procedure, we get:

Using Mathematica, we get

In a similar manner, Mathematica is used to obtain additional terms. The series solution is given by

Example 2. We take the initial condition as

Applying the above procedure, we get

Using Mathematica, we get

In a similar manner, Mathematica is used to obtain additional terms. The series solution is given by

5.   Convergence of the solution and Picard-stability analysis

In this part, we deliver certain results on the convergence and stability of the suggested equation. Following is a theorem that illustrates convergence.

Theorem 4. Consider a Banach space ${H}$ and $T$: $H\rightarrow H$ be an operator. Suppose that $u$ be the exact solution of the suggested problem. Let $\exists \; \varpi$ so that

$\forall \; \zeta\in\mathbb{W}$ (whole numbers), then the acquired solution $\sum_{\zeta = 0}^{\infty}u_{\zeta}$ converges to $u$.

Proof. To prove the theorem, we will construct a series in the form of:

At first glance, we have to show that the sequence $\left\{ \mathbb{S}_{\zeta}\right\} _{\zeta = 0}^{\infty}$ is a Cauchy sequence in ${{H}}.$ Thus

For each $\zeta, \ m\in\mathbb{N}, \ \zeta > m$, one gets

Given that $0 < \varpi < 1,$ then $1-\varpi^{\zeta-m-1} < 1.$ Hence,

We reach to the fact that

As a result, $\left\{ \mathbb{S}_{\zeta}\right\} _{\zeta = 0}^{\infty}$ is a Cauchy sequence in ${{H}}.$ However, ${{H}}$ is a complete space. Therefore, we can find $u\in{{H}}$ so that $\underset{\zeta\rightarrow \infty}{\lim}\mathbb{S}_{\zeta} = u.$ This complete the proof.□

The next theorem then describes the stability of the suggested scheme.

Theorem 5. Let ${X}$ denote a self mapping such that

Then, the suggested scheme is ${X}$-stable in $L^{1}\left[a, b\right]$ if

holds.

Proof. We first demonstrate that the mapping $X$ has a unique fixed point via the Banach contraction argument. Let us consider the bounded iteration for $(\zeta, m)\in\mathbb{N}\times\mathbb{N}$. Let $\nabla_{1}, \nabla_{2} > 0$ such that

Then,

Under the norm, one may have

As $u_{\zeta}$ and $u_{m}$ are bounded. This gives:

where $\mathrm{Z}_{r}, r = 1, 2, 3, ..., 8,$ denotes expressions achieved from $\mathscr{L}^{-1}\left[\frac{(1- \text{h})s^{ \text{h}}+ \text{h}}{\mathscr{M}(\text{h})s^{ \text{h}}}\mathscr{L}\left[\bullet\right]\right].$ Since

Hence, ${X}$ fulfills the criteria of contraction. Thus, ${X}$ admits a unique fixed point. Additionally, ${X}$ fulfills the criteria of Picard's ${X}$-stability having

Therefore, the required theorem is proved. □

6.   Graphical analysis and simulations

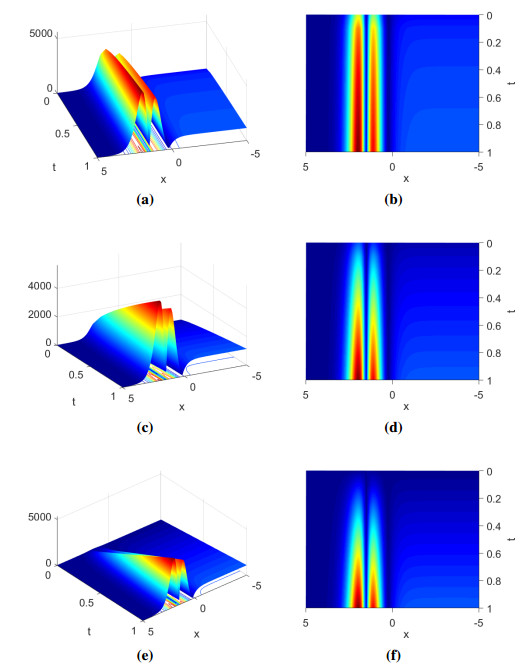
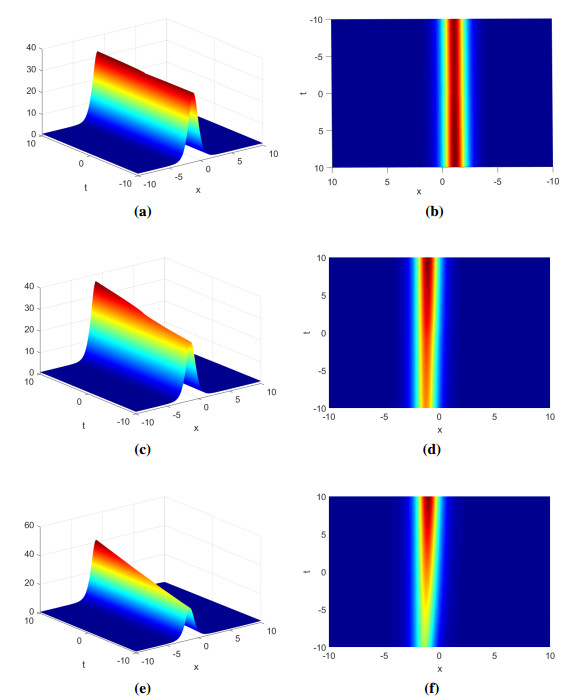
Here, we illustrate the behaviour of the solutions achieved in both problems for several fractional orders (FOs). We portray the evolution of each solution in 3D and density plots. The left panels in Figures 1 and 2 show the 3D behaviour, while the right panels show the density plots. Figure 1 portrays the behaviour of the solution of the Example 1 for $\mathrm{h} = 0.6, 0.8, 1.$ Contour plots and 3D models are used to depict all of the behaviors in Figure 1. In general, the result of the Example 1 gives the bright soliton behaviour. Moreover, the bright soliton behaviour is changed by varying the FO $\mathrm{h}$.

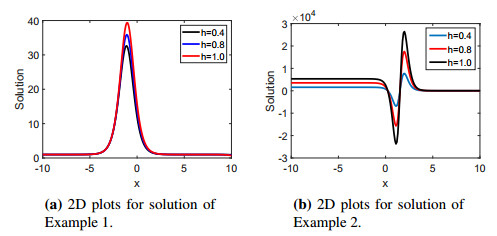
For lower FOs, we notice a bright soliton with a uniform amplitude. For instance, for a fractional order of 0.6, we see a bright soliton wave with a uniform amplitude, as shown in Figure 1(a, b). This behaviour is not observable in integer order, as seen in Figure 1(c). Thus, the solution to Example 2 is shown in Figure 2. The result is simulated for a few FOs: 0.6, 0.8 and 1. The solution of Example 2 shows a hybrid bright soliton behaviour. Nevertheless, the shape of the bright soliton behaviour is significantly influenced by the fractional order. As fractional order declines, the M-shaped wave form drastically changes, as seen in Figure 2(a–d). As seen in Figure 2(e, f), such evolutions are not possible in integer order. To analyze the effect of the FO $\mathrm{h}$ in 2D space, the solutions of the Examples 1 and 2 are displayed in Figure 3. The subfigure 3(a, b) is plotted for a few values of $\mathrm{h}$. The wave dynamics changes with an increase of the fractional order. From 3D figures, we observe that the fractional operator plays a vital role in the study of the waves behaviour of the proposed equation.

7.   Conclusions

In this study, we have investigated the extended KdV-CDG equation using an FO. Specifically, we have utilized a non-singular and non-local kernel in the convolution of the FO. Our goal was to derive several qualitative characteristics regarding the existence, uniqueness, and stability of the solution. To solve the KdV-CDG equation, we employed the Lie symmetry analysis technique combined with the Adomian decomposition method, which we refer to as the LADM method. The LADM is an easy and computationally efficient approach which can produce a series type to nonlinear problems in short time. Additionally, it does not require the assumption of either small or large parameters, making it a more general method. Therefore, the LADM method enabled us to obtain solutions to the equation, which we then analyzed using 3D and contour plots. We observed hidden dynamics behavior in the graphical analysis of the solutions, which were not apparent for integer order. To illustrate the impact of the FO on the shape of solutions, we examined two cases and generated Figures 1 and 2. The results have been shown for various values of FOs in the Figure 3. The graphs tell us that the FO effects the amplitude of the waves. Additionally, it has been noticed that the graph gets closer to the integer order curve when the FO $\mathrm{h}$ tends to unity. Our results showed that the FO had a significant impact on the shape waves solutions for the proposed KdV-CDG equation. In near future, we will apply the more advanced operators to study the advanced features of the considered equation.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The researchers would like to acknowledge Deanship of Scientific Research, Taif University, Saudi Arabia for funding this work.

Conflict of interest

The authors declare that they have no competing interests.