New inequalities via Caputo-Fabrizio integral operator with applications

1.   Introduction

Fractional calculus rapidly developed because of its numerous applications, including mathematics and many other areas such as image processing, physics, machine learning and networking. Fractional calculus is a new field in applied mathematics that developed from the open problems of how to solve some differential equations with fractional order derivatives. The solution to these problems have led many scholars to search for new subjects that many mathematicians have been interested in recent years. The fractional derivative has received rapid attention among experts from different branches of science. Most of the applied problems cannot be modeled by classical derivations. Fractional integral and derivative operators propose solutions that are extremely appropriate for real world problems and establish the connections between mathematics and other fields in terms of application areas. We refer to the readers ^{[1,2,3,4,5,6,7,8,9,10,11,12,13]} and the references therein. Fractional calculus plays a very significant role in the development of inequality theory. To study convex functions, Hermite-Hadamard inequality is particularly important in many areas of mathematics and its applications and its orignal version is defined as follows ^[14]:

Many fractional operators are used to generalized Hermite-Hadamard inequality. Here, we will restrict ourselves to Caputo-Fabrizio fractional derivative. The features that make the operators different from each other comprise singularity and locality, while kernel expression of the operator is presented with functions such as the power law, the exponential function, or a Mittag-Leffler function. The unique feature of the Caputo-Fabrizio operator is that it has a nonsingular kernel. The main feature of the Caputo-Fabrizio operator can be described as a real power turned in to the integer by means of the Laplace transformation, and consequently, the exact solution can be easily found for several problems. In 1993, V. Mihesan et al. ^[15] established the class of $(s, m)$-convex functions. Hudzik et al. ^[16] considered the class of $s$-convex functions in the second sense. N. Eftekhari ^[17] discussed the class of $(s, m)$-convex function in the second sense by involving the concept of $s$-convexity in the second sense with $m$-convexity in 2014. Xiaobin wang et al. ^[18] discussed the Hermite-Hadmard type inequality for modified $h$-convex functions utilizing Caputo-Fabrizio integral operator. Butt et al. ^[19] obtained various inequalities for $s$ and $(s, m)$-convex functions exponentially utilizing Caputo fractional integrals and derivatives. Moreover, Kemali et al. ^[20] obtained Hermite-Hadamard type inequality for $s$-convex functions in the second sense utilizing Caputo-Fabrizio integral operator. Abbasi et al. ^[21] proved new variants of Hermite-Hadamard type inequalities for $s$-convex functions using the Caputo-Fabrizio integral operator. Li et al. ^[22] gave analogous inequalities for strongly convex functions.

Motivated by ongoing studies in past years on generalizations of Hermite-Hadamard type inequalities for different convexities involving certain fractional integral operators, we developed novel fractional version left-hand side of the Hermite-Hadamard type inequalities for functions whose absolute value of the second derivative is convex utilizing Caputo-Fabrizio integral operator. The organization of the paper is as follows: First, in Section 1, we have discussed some well known definitions and results regarding the Caputo-Fabrizio fractional integral, which are used in the consequent sections to present our main results. In Section 2, new Hermite-Hadamard type inequalities are presented regarding the fractional operator. In Section 3, some interesting applications related to matrix and spacial means are discussed. Furthermore, in Section 4 conclusion and some future extensions are presented.

Definition 1.1. ^[16] A function $f:I\subseteq \mathbb{R} \rightarrow \mathbb{R} _{0} = \left[ 0, \infty \right)$ is said to be $s$-convex if

for some $s\in \left(0, 1\right]$, where $\xi _{1}, \xi _{2}\in I, \; \varrho \in \left[ 0, 1\right].$

Definition 1.2. ^[23] A ${f}$unction $f:\left[ \xi _{1}, \xi _{2}\right] \rightarrow \mathbb{R}$ is said to be strongly convex with modulus $\mu \geq 0,$ if

is valid for all $\xi _{1}, \xi _{2}\in I, \; \varrho \in \left[ 0, 1 \right].$

Definition 1.3. ^[24] A function $f:I\subseteq \mathbb{R} \rightarrow \mathbb{R} _{0}$ is said to be strongly $s$-convex with modulus $\mu \geq 0,$ and some $s\in \left(0, 1\right]$, if

is valid for all $\xi _{1}, \xi _{2}\in I, \; \varrho \in \left[ 0, 1 \right].$

Definition 1.4. ^[25,26] Let $H^{1}\left(\xi _{1}, \xi _{2}\right)$ be the Sobolev space of order one defined a;

where

Let $f\in H^{1}\left(\xi _{1}, \xi _{2}\right)$, $\xi _{1} < \xi _{2}, \; \alpha \in \left[ 0, 1\right]$, then the notion of left derivative in the sense of Caputo-Fabrizio is defined as:

and the associated integral operator is

where $B\left(\alpha \right) > 0$ is the normalization function satisfying $B(0) = B(1) = 1$. For $\alpha = 0$ and $\alpha = 1$, the left derivative is defined as follows;

For the right derivative operator, we have

and the associated integral operator is

where $B\left(\alpha \right) > 0$ is a normalization function that satisfies $B\left(0\right) = B\left(1\right) = 1.$

Dragomir ^[27] demonstrated the following version of Hermite-Hadamard inequality.

Theorem 1.1. Let $I$ be a real interval such that $\xi _{1}, \xi _{2}\in I^{o}$, the interior of $I$, with $\xi _{1} < \xi _{2}.$ Let $f:I \; \subseteq \mathbb{R} \rightarrow \mathbb{R}$ be a differentiable mapping on $I^{o}$, $\xi _{1}, \xi _{2}\in I$ with $\xi _{1} < \xi _{2}.$ If $f^{\prime }\in L \; \left[ \xi _{1}, \xi _{2} \right]$, then the following equality holds:

Sarikaya et al. ^[28] proved the following form of fractional Hermite-Hadamard inequality.

Theorem 1.2. Let $f:[\xi _{1}, \xi _{2}]\rightarrow \mathbb{R}$ be a positive mapping with $0\leq \xi _{1}\leq \xi _{2}, \; f^{\prime }\in L\left[ \xi _{1}, \xi _{2}\right]$ and $I_{\xi _{1}^{+}}^{\alpha }f$ and $I_{\xi _{2}^{-}}^{\alpha }f$ be a fractional operator. Then, the following inequality for fractional integral holds if $f$ is a convex function:

Dragomir ^[29] demonstrated the following fractional form of Hermite-Hadamard inequality.

Theorem 1.3. ^[29] Let $f:[\xi _{1}, \xi _{2}]\rightarrow \mathbb{R}$ be a positive function with $\xi _{1} < \xi _{2}$ and $f^{\prime }\in L_{1}[\xi _{1}, \xi _{2}]$. If $f$ is a convex function on $[\xi _{1}, \xi _{2}],$ then the following inequality for fractional integral holds:

Abbasi established the fractional version of the Hermite-Hadamard inequality for differentiable $s$-convex functions as follows.

Theorem 1.4. ^[21] Let $I$ be a real interval such that $\xi _{1}, \xi _{2}\in I^{o},$ the interior of $I$ with $\xi _{1} < \xi _{2}.$ Let $f:I$ $\subseteq \mathbb{R} \rightarrow \mathbb{R}$ be a differentiable function on $I^{o}$, $\xi _{1}, \xi _{2}\in I$ with $\xi _{1} < \xi _{2}.$ If $f^{\prime }\in L \; \left[ \xi _{1}, \xi _{2} \right]$ and $0\leq \xi _{2}\leq 1,$ the following inequality holds:

where $k\in \left[ \xi _{1}, \xi _{2}\right]$ and $B\left(\alpha \right) > 0$ is a normalization function.

Theorem 1.5. ^[21] Let $I$ be a real interval such that $\xi _{1}, \xi _{2}\in I^{o},$ the interior of $I$, with $\xi _{1} < \xi _{2}.$ Let $f:I \; \subseteq \mathbb{R} \rightarrow \mathbb{R}$ be $s$-convex on $\left[ \xi _{1}, \xi _{2}\right]$ for $s\in \left(0, 1\right)$ and $f^{\prime }\in L \; \left[ \xi _{1}, \xi _{2}\right]$. If $0\leq \xi _{2}\leq 1,$ then we have the following double inequality holds:

Sahoo obtained the generalized midpoint-type Hermite-Hadamard inequality associated with the Caputo-Fabrizio fractional operator:

Theorem 1.6. ^[30] Let $f:\left[ \xi _{1}, \xi _{2}\right] \rightarrow \mathbb{R}$ be a differentiable function on $I^{o}$(the interior of $I$) such that $\left(\xi _{1}, \xi _{2}\right) \in I$, with $\xi _{1} < \xi _{2}$ and $f^{\prime }\in L\left[ \xi _{1}, \xi _{2}\right]$. Then for $\alpha \in \left[ 0, 1\right]$ the following fractional equality holds:

Theorem 1.7. ^[30] Let $f:\left[ \xi _{1}, \xi _{2}\right] \rightarrow \mathbb{R}$ be a differentiable function on $I^{o}$(the interior of $I$) such that $\left(\xi _{1}, \xi _{2}\right) \in I$ with $\xi _{1} < \xi _{2}$ and $f\in L\left[ \xi _{1}, \xi _{2}\right]$. If $|f^{\prime }|$ is a convex function then for $\alpha \in \left[ 0, 1\right]$, the following fractional inequality holds:

2.   Main results

The following lemma is the main motivation behind the study, that establishes Hermite-Hadamard type inequalities for Caputo-Fabrizio integral operator.

Lemma 2.1. Suppose a mapping$\ f:I \; \subset \mathbb{R} \rightarrow \mathbb{R}$ is differentiable on $I^{o}$(the interior of $I$) such that $\xi _{1}, \xi _{2}\in I$ with $\xi _{1} < \xi _{2}$. If $f^{\prime \prime }\in L \; \left[ \xi _{1}, \xi _{2}\right]$ and $\alpha \in \left[ 0, 1\right]$, then the following equality holds:

where $k\in \left[ \xi _{1}, \xi _{2}\right]$, and $B\left(\alpha \right) > 0$, is a normalization function.

Proof. Integration by parts

Multiplying both sides of equality $\left(2.1\right)$ with $\frac{ \alpha \left(\xi _{2}-\xi _{1}\right) ^{3}}{16B\left(\alpha \right) }$ and subtracting $\frac{2\left(1-\alpha \right) }{B\left(\alpha \right) } f\left(k\right)$ we get,

Multiplying both sides of equality $\left(2.3\right)$ with$\ \frac{ \alpha \left(\xi _{2}-\xi _{1}\right) ^{3}}{16B\left(\alpha \right) }$ and subtracting $\frac{2\left(1-\alpha \right) }{B\left(\alpha \right) } f\left(k\right)$

We get the result by adding the inequalities $\left(2.2\right)$ and $\left(2.4\right)$ and then multiplying both sides by $\left(\xi _{2}-\xi _{1}\right)$. This completes the proof.

Theorem 2.1. Let $f:\left[ \xi _{1}, \xi _{2}\right] \rightarrow \mathbb{R}$ be a twice differentiable function on $\left(\xi _{1}, \xi _{2}\right)$ such that $f^{^{\prime \prime }}\in L\left[ \xi _{1}, \xi _{2} \right]$, for $\xi _{1} < \xi _{2}.$ If $|f^{\prime \prime }|$ is strongly $\left(s, m\right)$-convex with modulus $\mu \geq 0,$ for $\left(s, m\right) \in \left(0, 1\right] \times \left(0, 1\right]$, then the following inequality for fractional integral operator holds;

Proof. Using the Lemma 1 and the strongly $\left(s, m\right)$-convexity of $|f^{^{\prime \prime }}|,$ we have

Note that,

This completes the proof.

Corollary 2.1. If we choose $\mu = 0$ in Theorem 8$,$ then we have the following inequality

Corollary 2.2. If we choose $\mu = 0$ and $m = 1$ in Theorem 8$,$ then we have the following inequality

Corollary 2.3. If we choose $\mu = 0$ and $s = 1$ in Theorem 8$,$ then we have the following inequality

Corollary 2.4. If we choose $s = 0$ and $m = 1$ in Theorem 8$,$ then we have the following inequality

Corollary 2.5. If we choose $s = 1$ and $m = 1$ in Theorem 8$,$ then we have the following inequality

Remark 2.1. It is observed that, our result Theorem 8 presents the generalization of the inequality (Proposition 1 ^[32]) obtained by Sarikaya et.al in classical sense. This is indeed true since if we choose $\alpha = s = \; m = 1, \; \mu = 0,$ and $B\left(0\right) = B\left(1\right) = 1$, in Theorem 8$,$ we have the following inequality

Theorem 2.2. Let $f:[\xi _{1}, \xi _{2}]\rightarrow \mathbb{R}$ be a twice differentiable function on $(\xi _{1}, \xi _{2})$ such that $f^{\prime \prime }\in L[\xi _{1}, \xi _{2}]$, for $\xi _{1} < \xi _{2}.$ If $|f^{\prime \prime }|^{q}$ is strongly $(s, m)$-convex with modulus $\mu \geq 0,$ for $(s, m)\in (0, 1]\times (0, 1]$ and $q > 1,$ then the following inequality for fractional integral operator:

Proof. Using Lemma 1, the Hölder inequality$i$and the strongly $\left(s, m\right)$-convexity of $\ |f^{^{\prime \prime }}|^{q},$ we have

Now, put $\frac{1+\varrho }{2}\xi _{1}i+i\frac{ 1-\varrho }{2}\xi _{2} = \varrho \xi _{1}+(1-\varrho)\xi _{2}$.

Note that, $\int_{0}^{1}\left(1-\varrho \right) ^{s}d\varrho = \int_{0}^{1}\left(\varrho \right) ^{s}d\varrho = \frac{1}{s+1}.$ This completes the proof.

Corollary 2.6. If we choose $\mu = 0$ in Theorem 9$,$ then we have the following inequality

Corollary 2.7. If we choose $\mu = 0$ and $m = 1$ in Theorem 9$,$ then we have the following inequality

Corollary 2.8. If we choose $\mu = 0$ and $s = 1$ in Theorem 9$,$ then we have the following inequality

Corollary 2.9. If we choose $s = 0$ and $m = 1$ in Theorem 9$,$ then we have the following inequality

Corollary 2.10. If we choose $s = 1$ and $m = 1$ in Theorem 9$,$ then we have the following inequality

Theorem 2.3. Let $f:[\xi _{1}, \xi _{2}]\rightarrow \mathbb{R}$ be a twice differentiable function on $(\xi _{1}, \xi _{2})$ such that $f^{^{\prime \prime }}\in L[\xi _{1}, \xi _{2}],$ for $\xi _{1} < \xi _{2}.$ If $|f^{^{\prime \prime }}|^{q}, \; q\geq 1,$ is strongly $(s, m)$ -convex with modulus $\mu \geq 0,$ for $(s, m)\in (0, 1]\times (0, 1],$ then the following inequality for fractional integral operator holds:

Proof. Using Lemma 1, the power-mean inequality$i$and the strongly $\left(s, m\right)$-convexity of $|f^{^{\prime \prime }}|^{q},$ we have

Now, put $\frac{1+\varrho }{2}\xi _{1}i+i\frac{ 1-\varrho }{2}\xi _{2} = \varrho \xi _{1}+(1-\varrho)\xi _{2}$.

Note that, $\int_{0}^{1}\left(1i-i\varrho \right) ^{2}\varrho ^{s}d\varrho = \frac{2}{6+11s+6s^{2}+s^{3}}$ and $\int_{0}^{1}\left(1i-i\varrho \right) ^{2}\left(1-\varrho \right) ^{s}d\varrho = \frac{1}{s+3}$. This completes the proof.

Corollary 2.11. If we choose $\mu = 0$ in Theorem 10$,$ then we have the following inequality

Corollary 2.12. If we choose $\mu = 0$ and $m = 1$ in Theorem 10$,$ then we have the following inequality

Corollary 2.13. If we choose $\mu = 0$ and $s = 1$ in Theorem 10$,$ then we have the following inequality

Corollary 2.14. If we choose $s = 0$ and $m = 1$ in Theorem 10$,$ then we have the following inequality

Corollary 2.15. If we choose $s = 1$ and $m = 1$ in Theorem 10$,$ then we have the following inequality

Theorem 2.4. Let$\ \ f \; :\left[ \xi _{1}, \xi _{2}\right] \rightarrow \mathbb{R}$ be twice differentiable function on $\left(\xi _{1}, \xi _{2}\right)$ with $\xi _{1} < \xi _{2}$. If $f^{\prime \prime }\in L \; \left[ \xi _{1}, \xi _{2}\right]$ and $\left\vert f^{\prime \prime }\right\vert ^{q}$ is $s$-convex on $\left[ \xi _{1}, \xi _{2}\right]$, for some fixed $s\in \left(0, 1\right]$ and $q > 1,$ then the following inequality for fractional integral operator holds:

where $k\in \left[ \xi _{1}, \xi _{2}\right]$, and $B\left(\alpha \right) > 0$ is a normalization function, $p^{-1} = 1-q^{-1}.$

Proof. Using Lemma 1, we have

By using the Young$^{, }$s inequality as

Theorem 2.5. Let $f \; : \; \left[ \xi _{1}, \xi _{2}\right] \rightarrow \mathbb{R}$ be twice differentiable function on $\left(\xi _{1}, \xi _{2}\right)$ with $\xi _{1} < \xi _{2}$. If $f^{\prime \prime }\in L \; \left[ \xi _{1}, \xi _{2}\right]$ and $\left\vert f^{\prime \prime }\right\vert ^{q}$ is concave on $\left[ \xi _{1}, \xi _{2}\right]$, for some fixed $s\in \left(0, 1\right]$ and $q\geq 1,$ then the following inequality for fractional integral operator holds:

Proof. Let $qi = i1$, then from Lemma 1 and the Jensen integral, we obtain

Which proves the case for $q = 1$. Now, by using the Hölder inequality for $q > 1,$ and then the Jensen integral inequality, we obtain

This completes the proof.

Remark 2.2. It is observed that, our result Theorem 12 presents the generalization of the inequality (Proposition 5 ^[32]) obtained by Sarikaya et al. in classical sense. This is indeed true since if we choose $B\left(0\right) = B\left(1\right) = 1$, $\alpha = 1$ in Theorem 12$,$ we have the following inequality:

3.   Applications

3.1.   Matrix inequalities

Consider that $s\in \left(0, 1\right]$ and $\xi _{1}, \; \xi _{2},$ $c\in \mathbb{R}.$ We define a mapping $f:\left[ 0, \infty \right) \rightarrow \mathbb{R}$ as

If $\xi _{1}\geq 0$ and $0\leq c\leq \xi _{1},$ then $f\in k_{s}^{2}$ in (see ^[16] for proof). Thus, for $\xi _{1} = c = 0,$ and $\xi _{2} = 1,$ we have $f\left(x\right) = x^{s}$ and $f:\left[ \xi _{1}, \xi _{2}\right] \rightarrow \mathbb{R}$, with $f\in k_{s}^{2}.$ Suppose $f:I_{1}\rightarrow \mathbb{R} _{+}$ be a non- decreasing and $s$-convex function on $I_{1}$ and $f:J\rightarrow I_{2}\subseteq I_{1}$ is a non-negative convex function on $J,$ then $f\circ \psi$ is $s$-convex on $I_{1}.$

Corollary 3.1. Suppose $\psi :I\rightarrow I_{1}\subseteq \left[ 0, \infty \right)$ is a non- negative convex function on $I,$ then $\psi ^{s}\left(x\right)$ is $s$-convex on $\left[ 0, \infty \right), \; 0 < s < 1.$

Example 3.1. We denote the set of all $n\times n$ complex matrices by $C^{n}$, and we denote $M_{n}$ to be the algebra of all $n\times n$ complex matrices, and by $M_{n}^{+}$ we mean the strictly positive matrices in $M_{n}.$ That is, $A\in M_{n}^{+}$ if $\langle A_{\xi _{1}}, \xi _{1}\rangle > 0$ for all nonzero $\xi _{1}\in C^{n}.$ In ^[31] Sababheh proved that the function $\psi \left(\theta \right) = \left\Vert A^{\theta }XB^{1-\theta }+A^{1-\theta }XB^{\theta }\right\Vert, \; A, B\in M_{n}^{+} \; , \; X\in M_{n}$ is convex for all $\theta \in \left[ 0, 1\right]$, $s\in \left(0, 1\right).$ Then by using Corollary 2, we have

3.2.   Special means inequalities

We shall consider the following special means.

$\left(\text{a}\right)$ The arithmetic mean:

$\left(\text{b}\right)$ The Geometric Mean:

$\left(\text{c}\right)$ The Harmonic Mean:

$\left(\text{d}\right)$ The Logarithmic Mean:

$\left(\text{e}\right)$ The Generalized Logarithmic Mean:

It is well known that$\ L_{r}^{r}$ is monotonically nondecreasing over $r\in \mathbb{R}$ with $L_{-1} = L.$ In particular, we have the following inequalities

Proposition 3.1. For an $n\in Z\left\{ -1, 0\right\}$, $0\leq \xi _{1} < \xi _{2}$, we have

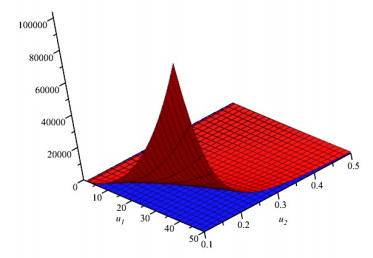
Proof. The assertion directly follows from Theorem $8$ applying for $f\left(x\right) i = ix^{n}$ and $\alpha i = s = m = i1$, and $\mu = 0$, $B\left(0\right) = B\left(1\right) = 1$. For a graphical depiction of this see Figure 1.

Proposition 3.2. For some $0\leq {\xi _{1}} < \xi _{2},$ then we get,

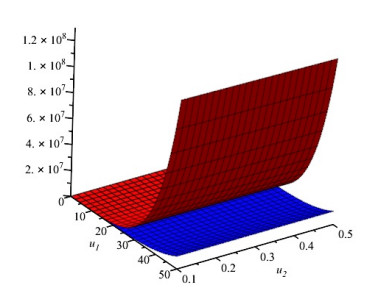
Proof. The assertion directly follows from Theorem $8$ applying for $f\left(x\right) i = ix^{-1}$ and $\alpha i = s = m = i1$, and $\mu = 0$, $B\left(0\right) = B\left(1\right) = 1$. For a graphical depiction of this see Figure 2.

Proposition 3.3. For some $\xi _{1}, \xi _{2}\in \mathbb{R}, \; 0 < \xi _{1} < \xi _{2},$ and$\ q\geq 1,$ then we get

Proof. The assertion follows from Theorem 12 applying for $f\left(x\right) = \frac{1 }{x}, \; x\in \left[ \xi _{1}, \xi _{2}\right] \; \alpha = 1$ and $B\left(0\right) = B\left(1\right) = 1.$

4.   Conclusions

Fractional calculus is an interesting subject with many applications in the modelling of natural phenomena. We are always in need to enhance and improve our ability to generalize the results directly related to the topic of fractional calculus. Many mathematicians have generalized a variety of fractional integral operators using the techniques and operators of fractional calculus. In this paper, we have established several inequalities accomplished for the functions whose second derivatives are strongly $(s, m)$ -convex functions via Caputo fractional derivatives. The main results show a generalization of Hermite-Hadamard-type inequalities for the strongly $(s, m)$-convex function via Caputo-Fabrizio integral operator. Lemmas 1 is established to get novel inequalities regarding Caputo-Fabrizio integral operator, which are applied to obtain some special means inequalities and an inequality involving the matrix function. The Lemma 1 is also appropriate to get new bounds and error estimates for midpoint inequalities. Moreover, the novel study of this article that are discussed in Theorem 5 and Theorem 9 are generalization of the inequalities proved in (Proposition 1 and Proposition 5 ^[32]). Similar types of inequalities can be obtained with the different classes of convex functions. In the future, scholars may explore inequalities of the Ostrowski type, Jensen-Mercer type, and Hermite-Hadamard-Mercer type with modified Caputo-Fabrizio fractional operators and modified A-B fractional operators.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by the Research Project of Optimization of Plant Cell Automation Production Model (H2139) from Ansebo (Chongqing) Biotechnology Co., Ltd.

Conflict of interest

We declare that there are no conflicts of interest between the authors.