Certain inequalities in frame of the left-sided fractional integral operators having exponential kernels

1.   Introduction

The portfolio selection problem has always been a focal point of attention in the field of financial engineering. The core of this issue is to study how to allocate assets rationally in order to diversify risks and achieve returns higher than those obtained from bank deposits and government bonds. Markowitz's ^[1] introduction of the mean–variance (MV) portfolio model marked the beginning of modern portfolio theory. Since then, the balance between returns and risks has been an important theme in portfolio selection, which means maximizing investor returns while minimizing losses as much as possible. In recent years, many scholars have proposed significant models that incorporate new indicators of returns and risks ^[2,3,4,5]. However, due to the uncertainty of asset returns, constructing a portfolio that satisfies investors has become a challenging problem.

In the real securities market, there are many hard-to-quantify uncertainty factors that can prevent investors from obtaining accurate and effective market information. This, in turn, may lead investors to make erroneous judgments. It was not until Zaden ^[6] introduced fuzzy set theory that these problems were addressed. Since then, other scholars began to study the fuzzy portfolio selection problem. Wang et al. ^[7], among others, proposed risk measurement methods such as variance, entropy, and value at risk (VaR) in a fuzzy environment, evaluating investment risk from different perspectives. They also established a multi-objective model based on these measurement methods to assess their collective impact on portfolio selection. Solving the portfolio problem using this theory firstly requires clarifying how to handle the uncertainty of portfolio returns, which is typically approximated using fuzzy numbers with possible distributions or credibility distributions to represent the returns of risky assets. For instance, Enriqueta Vercher ^[8] assumed that the returns of the portfolio are lr-type fuzzy variables and generated efficient portfolios within the fuzzy mean–absolute deviation framework. Additionally, studies on portfolio problems based on fuzzy set theory have been conducted by other scholars ^[9,10,11,12] as well. Meanwhile, methods for measuring risk in portfolio problems have also garnered increasing attention from researchers, leading to the introduction of various risk measurement methods. Among the more common ones are variance (V), absolute deviation (SAD), value at risk (VaR), conditional value at risk (CVaR), and entropy. To date, these risk measurement methods remain widely used internationally.

Jagdish Kumar Pahade ^[13] extended Markowitz's mean–variance portfolio selection model to the mean–variance–skewness portfolio selection model, and presented a polynomial objective programming method to solve it. Kaur et al.^[14] constructed optimal combination of Markowitz's mean–variance model with and without radix constraints. The effectiveness and efficiency of the proposed model as an advanced method for portfolio optimization were verified by experiments. In addition, Mostafa Abdolahi Moghadam ^[15] used the interval semi-absolute deviation criterion to control investment risk and established a portfolio selection model considering many different factors. W. Yue ^[16] took semi-variance risk measures and semi-absolute deviation risk measures as risk measures to provide additional advantages and flexibility, established a portfolio selection model under the framework of low partial risk, and designed a new and efficient multi-objective evolutionary algorithm calculation model. J. K. Pahade ^[17] established a portfolio selection model by using the possibilistic semi-absolute deviation risk measure method. Since value at risk is not a coherent measure of risk, it is not subadditive and convex. Therefore, considering value at risk and conditional value at risk as risk measures with different confidence levels in the model is considered in the financial literature as a new way to manage and control risk. Hossein Babazadeh ^[18,19] used extreme value theory (EVT) to estimate VaR. A new non-dominated sorting genetic algorithm (NSGA-II) has been proposed to solve this problem. C. Jiang ^[20] tested the validity of the model for portfolio selection based on VaR. Other studies related to value at risk are ^[21,22,23]. Second, the conditional value at risk (CVaR), as the conditional expectation of loss exceeding VaR, not only focuses on the threshold of potential losses (VaR), but also considers the average level of losses exceeding this threshold. As a result, CVaR is able to more fully assess the risks posed by extreme events. Moris S. Strub^[24] studied a discrete-time average risk portfolio selection problem whose risk is measured by CVaR, and the results suggest that the risk measured by CVaR may help to understand the long-standing mystery of the equity premium. Taras Bodnar ^[25] presented the correlation quantities required for VaR and CVaR calculations, and expressed the optimal portfolio weights using only observed data. The optimal portfolio allocation of VaR and CVaR as risk measures has been studied from a Bayesian perspective. S. Benati ^[26] combined expected returns, CVaR, and regret measures to propose a robust optimization model under two sources of uncertainty. K. Su ^[27] combined three different hedging models, namely parametric, non-parametric and semi-parametric minimum CVaR hedging models, and constructed a hybrid hedging model to reduce the uncertainty of the model.

Due to the complexity of the financial transaction market and the impact of multiple factors such as transaction costs, management costs, and transaction complexity existing in investment, selecting too many types and numbers of assets in the portfolio will lead to investors not having too much energy to manage these assets, resulting in investment damage. In order to make the portfolio model more in line with the real investment environment, it is necessary to limit the number of assets in the portfolio during investment, that is, a base constraint. Man-Fai Leung ^[28] proposed a neurodynamics-based collaborative optimization method for radix-constrained portfolio selection. In the same year, he also proposed a dual time-scale dual neurodynamics method ^[29] and applied it to solving recombination portfolio optimization problems with cardinality constraints. J. He ^[30] established a fuzzy portfolio model considering the cardinality constraint and transaction cost constraint, and this was solved by a differential evolution algorithm. Loke et al. ^[31] proposed an adaptive step search algorithm to solve the radix-constrained portfolio optimization problem. However, most of the abovementioned studies were processed by a simple intelligent method or a multi-objective method. Multi-objective methods have priority and needs to sacrifice other goals to fulfill another goal. This process will indeed be more flexible, but many investors want to strike a balance between risk and return. Therefore, we have a new way, using the form of fractions, in which the two objectives of risk and return are divided into fractions, and strive to achieve a balance between the two objectives. This method adds another approach to the current multi-objective approach in portfolio optimization research.

Although there have been many excellent works on portfolio optimization, there are not many studies that introduce fractional programming into portfolio optimization modeling. Under the framework of optimization theory, the fractional programming concept is introduced into the portfolio optimization model modeling, which has a theoretical basis and development prospects. Therefore, this paper integrates the concept of fractional programming into the construction of a portfolio model, and establishes four kinds of fractional programming portfolio optimization models with different risk measures by combining radix constraints and transaction costs within the fuzzy framework. These four models are mixed integer programming problems, which are difficult to solve by general methods. Therefore, an internal and external double-loop hybrid heuristic algorithm (IEDCHA) is designed in this paper. The main idea of this algorithm is to use the genetic algorithm to deal with cardinality constraints, and this part is used as an external loop. After that, the differential evolution algorithm is used to process the assets to get a set of solutions that meet the requirements of the model, and this part is regarded as an inner loop. The internal and external double-loop mechanism formed by this algorithm combines the advantages of the qualified differential evolution algorithm of the genetic algorithm, which not only improves population diversity but also ensures the acquisition of a global optimal solution. The rationality and effectiveness of the four models and the proposed algorithm (IEDCHA) are verified by the simulation experiments, which calculate the portfolio strategies of the four models under different parameters. Secondly, we also use other optimization algorithms to solve the four models and compare the numerical results.

1.1.   Distinguishing features of the proposed research

The significant differences between this paper and other relevant studies are as follows.

(1) Compared with the single-objective portfolio optimization model, which only selects a certain objective that investors pay the most attention to for modeling, and the multi-objective optimization model, which uses most constraints as the target for modeling, this paper adopts a new method to process the two objectives in the form of fractions. The purpose is to ensure that the extreme values of the two targets are approximated to find the balance point of the two targets. This can avoid the limitations of single-goal processing and the defects of multi-goal processing that require sacrificing the weight of other goals to fulfill another goal. Therefore, the fractional programming method adopted in this paper is a valuable and novel contribution to the existing research.

(2) Compared with using $\sum_{i = 1}^{n}z_{i} = K$ as cardinality constraint ^{[32,33,34,35]} method, this article will take $\sum_{i = 1}^{n}z_{i}\leq K$ as the cardinality constraint. The method of the article ^{[32,33,34,35]} is to stipulate that the number of assets selected in each investment is equal to its given $K$, which will limit the allocation of proportion of assets in the portfolio selection process to a certain extent. The base constraint method adopted in this paper not only ensures that the investment base will be within a certain range but also makes portfolio selection and asset allocation more flexible. Compared with the method of a fixed maximum base, the method adopted in this paper can obtain a more sophisticated portfolio strategy to a certain extent.

(3) Considering that there are few studies on fuzzy portfolio models based on fractional programming at present, and conditions such as cardinality constraints, threshold constraints, and transaction costs are not taken into account at the same time, there is still a large research space in this aspect. In light of this, four fuzzy portfolio optimization models based on variance, semi-absolute deviation, value at risk, and conditional value at risk (VaR) are established in this paper based on realistic constraints such as cardinality constraints and threshold constraints. These four models comprehensively include the more mainstream risk measurement methods in the world. In the experimental part, this paper makes a detailed analysis and comparison of the portfolio strategy and the numerical results of the simulated investment of these four models.

(4) In this paper, based on the characteristics of two heuristic methods that have been thoroughly studied in the field of optimization, a new internal and external double-loop hybrid heuristic algorithm (IEDCHA) is proposed. In the numerical experiment part, the numerical results of different risk measurement models are compared and analyzed, and the results show the applicability of different risk measurement methods. It makes a valuable and novel contribution to the existing portfolio optimization model solution methods.

1.2.   The rest of the work arrangement

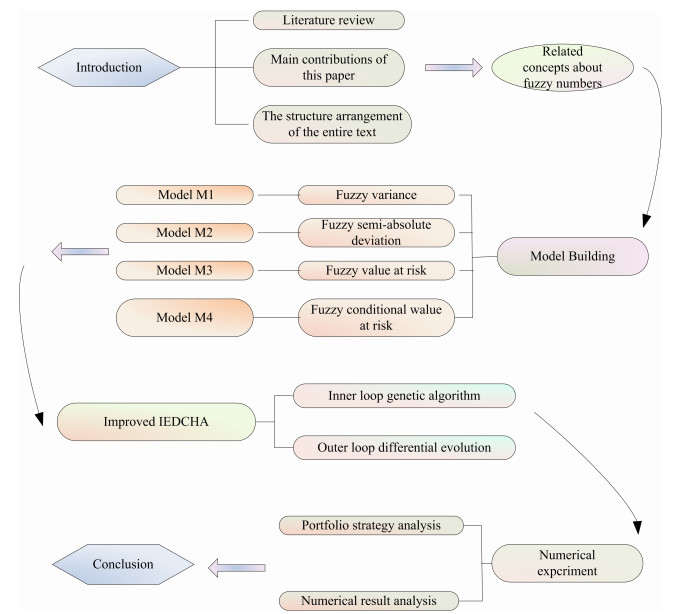
Section 2 explains the related topics of fuzzy set theory in short. Section 3 establishes four alternative risk metrics of fuzzy fractional programming portfolio optimization models based on practical limitations such as cardinality limits. Section 4 proposes an internal and external double-loop cycle hybrid heuristic algorithm (IEDCHA) that combines the properties of the genetic and differential evolution algorithms. This algorithm provides the best balance of exploration and development. In Section 5, we utilize historical data to replicate an investment experiment in order to validate the model's logic and the efficacy of IEDCHA. Section 6 contains the conclusion to the full text. In addition, the graphic abstract of this paper is shown in Figure 1.

2.   Preliminaries

Some scholars use fuzzy figures to represent the uncertainty of potential asset returns. In the sense of selecting the best choice in a judgment issue, they approach the portfolio selection problem mathematically ^[36]. Fuzzy numbers are used to describe financial market returns, and the meaning of fuzzy numbers is the main topic of this part.

Definition 1. ^[6] Let $\widetilde{X}$ be a map from $X$ to the interval $[0, 1]$, $\widetilde{A}: X \longrightarrow[0, 1], X\longrightarrow\widetilde{A}(x)$, where $\widetilde{X}$ is a fuzzy set on $X$, the function $\widetilde{A}(.)$ becomes the subordinate function of the fuzzy set $\widetilde{A}$, and $\widetilde{A}(x)$ is called the subordination of $x$ to the fuzzy set $\widetilde{A}$.

Definition 2. ^[6] A fuzzy set $\widetilde{A}$ has an affiliation function $\widetilde{A}(x): X\longrightarrow[0, 1]$, and to be called a fuzzy number $\widetilde{A}$, it must satisfy the following conditions:

(1) $\widetilde{A}$ is regular, $x_{0}\in R$ exists such that $\widetilde{A}(x_{0}) = 1$;

(2) $\widetilde{A}(x)$ is convex, that is, $x, y\in R$ when $\forall\lambda\in[0, 1]$, with $\widetilde{A}(\lambda x+(1-\lambda)y)\geq min\{\widetilde{A}(x), \widetilde{A}(y)\}$;

(3) $\widetilde{A}(x)$ is upper semi-continuous and bounded, i.e, $\forall\varepsilon\in[0, 1]$, and thus $\widetilde{A}_{\varepsilon} = \{x\in R|\widetilde{A}(x) > \varepsilon\}$ is a fuzzy branch of $\widetilde{A}$;

(4) The branch $sup\widetilde{A}$ of $sup\widetilde{A} = \{x|x\in R, \widetilde{A}(x) > 0\}$ is a tight set.

Definition 3. ^[37] Let $A\in F$ be a fuzzy number, let $\gamma$ be the horizontal intercept set $[\widetilde{A}]^{\gamma} = [\underline{a}(\gamma), \bar{a}(\gamma)], \gamma\in[0, 1]$. Then the likelihood kurtosis of the fuzzy number $A$ is defined as

In short, the fourth-order moments of the fuzzy numbers are used instead of the kurtosis of the possibilities, denoted $K_{A} = E(A-E(A))^{4} = \int_{0}^{1}\gamma[(\underline{a}(\gamma)-E(A))^{4}+ (\bar{a}(\gamma)-E(A))^{4}]d\gamma$. The statistical definition of possibility kurtosis measures the kurtosis of the possibility distribution of a fuzzy variable, where high kurtosis means the increase in the variance of possibility is caused by extreme differences at low frequencies greater or less than the mean of the possibility.

According to the aforesaid analysis, if $\widetilde{A} = (a, b, \alpha, \beta)$ is a trapezoidal fuzzy number, then its subordination function can be expressed as

Let the $\gamma$ of the trapezoidal fuzzy number $\widetilde{A}$ be the horizontal intercept set of $\gamma$: $[\widetilde{A}]^{\gamma} = [\underline{a}(\gamma), \bar{a}(\gamma)]$, where $\underline{a}(\gamma) = a-\alpha(1-\gamma)$, $\bar{a}(\gamma) = b+\beta(1-\gamma)$, $\forall\gamma\in[0, 1]$; $\gamma$ is called the confidence level or confidence level; and $\underline{a}(\gamma)$ and $\bar{a}(\gamma)$ are the left and right endpoints of the $\gamma$-horizontal intercept, respectively.

Definition 4. ^[38] Let the fuzzy number $\widetilde{A}\in F(U)$, $\widetilde{A} = (a, b, \alpha, \beta)$ be the number of trapezoidal fuzzy numbers on the interval $[a, b]$, let $\alpha$ be the left width of the fuzzy number, and let $\beta$ be the right width of the fuzzy number. From this, we can deduce $\widetilde{A}$ in the $\gamma$-horizontal intercept possibility mean of the following:

3.   Portfolio models

3.1.   Realistic constraint

In this paper, we assume that the investment is carried out in a security market composed of $n$ kinds of risky assets, and the returns of each asset are independent of each other. Here, $r_{i}$ denotes the return of the $i$th asset, $x_{i}$ represents the proportion of the investor's investment in the $i$th asset, $X = (x_{1}, x_{2}, \ldots, x_{n})$ is the vector of risky assets to total assets, and the expected return of the portfolio is obtained as

Considering transaction costs, the total transaction costs of the asset portfolio in period $t$ are

Based on this, the trapezoidal fuzzy number is introduced and the net gain in the fuzzy environment is obtained as

Variance is a measure of the difference between the source data and the expected value. The term "variance" was first coined by Ronald Fisher ^[39]. The difference in probability theory is used to measure the degree of deviation between a random variable and its mathematical expectation (i.e., the mean). The variance in statistics (sample variance) is the average of the squared values of the difference between each sample value and the mean of the total sample value. In many practical problems, it is of great significance to study variance, namely the degree of deviation. The probability variance of the returns based on the fuzzy number $r_{i}$ can be expressed as

The probability variance (FV) of the returns of a portfolio $r$ based on fuzzy numbers can be denoted as

Semi-absolute deviation is a statistic used to measure the degree of dispersion between observations in a data set and their mean. The advantage is that it has less effect on outliers because it uses the median rather than the mean to measure dispersion. It is widely used in areas such as financial statistics to measure risk and volatility. The semi-absolute deviation $(FSAD)$ of the portfolio based on the fuzzy number is

Let $A$ be a fuzzy number, where $\mu(A)$ is an affiliation function, $r$ represents a real number, and the plausibility function ^[40] of $A\leq r$ is expressed as follows:

The credibility measure is a self-pairing set function, i.e., $Cr\{A\leq r\} = 1-Cr\{A > r\}$, which describes the credibility of an event with respect to a fuzzy variable. Assuming that $A$ represents the future return of a security, then $Cr\{A\geq 0.4\} = 0.95$ implies that the level of confidence that the future returns are greater than or equal to 0.4 is $90\%$. Moreover, the $Pos\{\cdot\}$ and $Nec\{\cdot\}$ of the equation above are the probability and necessity measures of the credibility measure, respectively.

For a trapezoidal fuzzy number $\widetilde{A} = (a, b, \alpha, \beta)$, the probability of a fuzzy event $\{A\leq r\}$ is

To Make portfolio returns be independent of each other, $\zeta$ represents the fuzzy loss variable of a portfolio ^[41], and the risk confidence interval is $\rho\in(0, 1)$, then

VaR is the maximum possible loss of a financial asset (or portfolio of securities) over a specified period of time in the future at a certain level of confidence. According to the equations above, the fuzzy value-at-risk FVaR of $\zeta$ in the $1-\rho$ confidence interval ^[41] is

From the upper equation, the maximum loss of investment at a confidence level of $1-\rho$ is $\lambda$.

In addition to Eq (3.12), for a trapezoidal fuzzy variable in a fuzzy environment, the corresponding value-at-risk FVaR ^[41] is

Similarly, by virtue of Eq (3.13), the fuzzy conditional value-at-risk FCVaR under $\rho$ ^[42,43] is

where $M\{\zeta\leq x\}$ is axiomatic uncertainty estimator, which represents the probability of the occurrence of uncertain event $\zeta\leq x$. CVaR (conditional value at risk) is an investment risk measurement method developed on the basis of VaR (value at risk). CVaR refers to the average loss of a portfolio under the condition that the portfolio loss is greater than a given VaR value. Compared with VaR, CVaR satisfies sub-additivity, positive homogeneity, monotonicity and transfer invariance, so CVaR is a consistent risk measurement method.

For trapezoidal fuzzy variables, the corresponding FCVaR ^[42,43] is

Considering the cardinality constraint in the portfolio, the asset holdings for portfolio selection can be shown as follows:

This equation suggests that when $z_{i} = 1$, asset $i$ is held, and when $z_{i} = 0$, asset $i$ is not held. Assuming a maximum limit of $K$ on the number of assets in a portfolio, there is a cardinality constraint as follows:

From formula above, the threshold constraint for the portfolio is

In investment processes, it is generally assumed the sum of investment ratios on assets is 1, i.e.,

3.2.   Portfolio models with different risk measures

Building on Eqs (3.1)–(3.19), we construct the following four fractional planning portfolio selection models, M1, M2, M3, and M4, which adopt fuzzy likelihood variance (FV), fuzzy semi-absolute deviation (FSAD), fuzzy value-at-risk (FVaR), and fuzzy conditional value-at-risk (FCVaR) as risk measures, respectively. The advantages of introducing fractional programming are twofold: (1) it simplifies the complexity of the problem by making it a single-objective problem instead of a dual-objective one; (2) it seeks to minimize the risk and maximize the benefit when optimising the risk and benefit compared with methods that introduce pessimistic coefficients, and treats both objectives in the same order, without prioritisation.

(1) A cardinality constrained fractional planning portfolio selection model M1 with FV as the risk measure:

Equation (3.20) represents a cardinality constraint fractional planning portfolio selection model M1 with variance as the numerator and returns as the denominator of the objective function. The returns and variances are calculated according to Eqs (3.3) and (3.5), respectively. The first constraint indicates that the returns cannot be negative; the second constraint means the number of assets in portfolio must be less than or equal to a pre-determined $K$; the third constraint represents a portfolio's holdings of an asset as a 0-1 vector; the fourth constraint is a proportional limit on the assets $i$ that can be invested, i.e., a boundary constraint, requiring the proportion of funds invested in asset $i$ to be between $0\leq l_{i}\leq \mu_{i}\leq1$; the fifth constraint means the sum of investment proportions is 1.

(2) A cardinality constrained fractional planning portfolio selection model M2 with FSAD as the risk measure:

Equation (3.21) represents a fractional programming portfolio selection model M2 with fuzzy semi-absolute deviation as the numerator and returns as the denominator of the objective function. The returns and variances are calculated according to Eqs (3.3) and (3.6), respectively. The constraints in the model and their meanings are same as the M1 model.

(3) A cardinality constrained fractional planning portfolio selection model M3 with FVaR as the risk measure:

Equation (3.22) represents a fractional programming portfolio selection model M3 with fuzzy value-at-risk as numerator and returns as the denominator of the objective function. The returns and variances are calculated according to Eqs (3.3) and (3.13), respectively. Since the fuzzy value-at-risk of this model is calculated differently at different confidence levels $\rho$, it should be discussed separately when simulating investments at different confidence levels. Similarly, the constraints in this model and what they represents are also same as in M1.

(4) A cardinality constrained fractional planning portfolio selection model M4 with FCVaR as the risk measure:

Equation (3.23) represents a fractional programming portfolio selection model M4 with fuzzy conditional value-at-risk as the numerator and returns as the denominator of the objective function. The returns and variances are calculated according to Eqs (3.3) and (3.15), respectively. Since the fuzzy conditional value-at-risk of this model is calculated differently at different confidence levels $\rho$, it should be discussed separately when simulating investments at different confidence levels. Similarly, the constraints in this model and what they represents are same as in M1.

4.   Solution method for the model

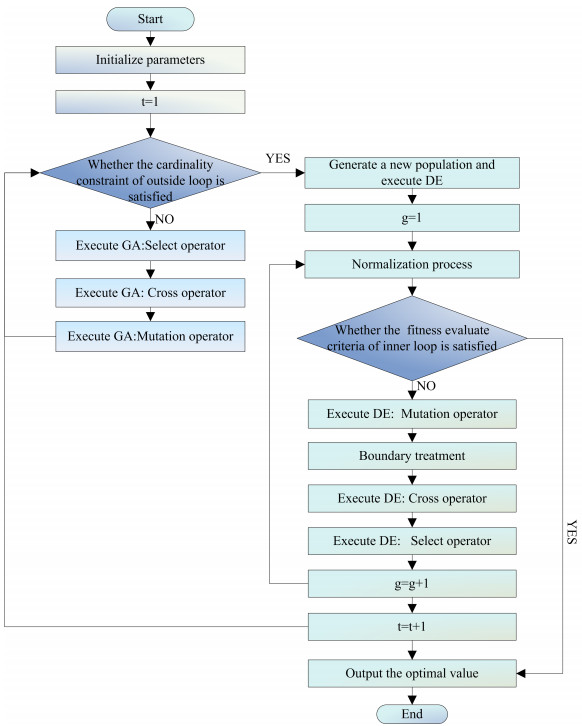
In this part, we go over the Markowitz mean–variance model's solution with a cardinality constraints and fractional programming as additions. The optimization issue is transformed into a 0-1 mixed integer programming problem by the addition of the cardinality constraints. The suggested hybrid heuristic algorithm with internal and external double cycles (IEDCHA) method consists of two sections and uses two optimisation techniques to tackle the issue. The cardinality constraint is used by the genetic algorithm (GA) as an evaluation indication in the first step of the hybrid IEDCHA method to discover viable spots. In light of this, the second stage of the hybrid IEDCHA algorithm uses the differential evolutionary (DE) method to minimize the objective function.

4.1.   Basic ideas of two evolutionary algorithms

Natural selection and population genetic dynamics are the foundation of the genetic algorithm (GA), a computerized stochastic search and optimization tool. It operates according to natural genetics' chromosomal processing and evolutionary principles. At the start of a GA, a set of initial solutions is generated randomly. These initial solutions are then assessed using the fitness function, which produces a fitness value. Using this fitness value, certain individuals are chosen to produce the following generation. The process of selection adheres to the adage "survival of the fittest". The chosen individuals are then united again by a crossover and mutation operation, or j, to create c, a new generation, which improves on the previous generation by inheriting some of its best traits. Therefore, a genetic algorithm may be seen as initial evolutionary process of a population of feasible solutions.

The differential evolutionary (DE) algorithm is a population-based, global optimization method that is based on the principle of "survival of the fittest", which may be approximated by the impacts of heredity, variation, and selection in nature, which drive organisms to evolve from lower to higher levels. This algorithm keeps the population-based global search method, unlike evolutionary algorithms. This method decreases the complexity of the operation by using a real number encoding, a straightforward variation operation based on difference, and a one-to-one competitive survival strategy. Significantly, the differential evolution algorithm's special memory capability enables it to constantly watch the current search environment and adjust its search strategy without using problem-specific knowledge, resulting in significant convergence and resilience.

4.2.   The proposed of IEDCHA

Through relevant research, this paper summarizes the characteristics of genetic algorithms and differential evolution algorithms as follows:

(1) The genetic algorithm is proficient in global searches, allowing it to explore wider regions within the search space; however, it may fall into local optima due to excessive selection pressure. In contrast, the differential evolution algorithm exhibits strong local search capabilities and fast convergence, enabling it to refine solutions more effectively through optimization in the local neighborhood.

(2) The genetic algorithm can lead to a reduction in population diversity during the selection and crossover processes, which may negatively impact its search effectiveness. Conversely, the differential evolution algorithm introduces new solutions through differential operations, effectively enhancing population diversity and mitigating the risk of premature convergence.

(3) The parameters of the genetic algorithm have a significant influence on the optimization results, while the differential evolution algorithm has fewer parameters that are easier to adjust, facilitating a more flexible optimization process.

According to the aforementioned characteristics, the combination of the two algorithms allows for broad exploration while achieving rapid convergence, thereby enhancing overall search efficiency. By integrating the two, the diversity provided by the genetic algorithm, along with the efficient refinement of the differential evolution algorithm, effectively maintains population diversity while improving the solution's quality. In this combined approach, the flexibility of differential evolution's parameters can be leveraged to optimize the performance of the genetic algorithm. This complementary nature of the parameters enables greater adaptability in various problem environments, leading to improved performance.

The integration of genetic algorithms and differential evolution algorithms can create a more robust and flexible optimization framework, where both algorithms complement each other. This synergy allows for the full utilization of their respective strengths when tackling complex problems, resulting in superior solutions and enhanced overall optimization capability. Although this setup may increase time complexity, the improved results justify the additional time investment.

4.2.1.   The basic content of the proposed IEDCHA

The dual-loop processing mechanism designed in this algorithm combines the advantages of genetic algorithms and differential evolution algorithms, creating a more robust and flexible optimization framework where both approaches complement each other. The outer loop first addresses the cardinality constraints within the model to obtain a unit matrix $Z$ that satisfies these constraints. The inner loop then builds upon $Z$ by incorporating the constraint $l_{i}z_{i}\leq x_{i}\leq \mu_{i}z_{i}$ to generate an initial population $X$ that meets both the cardinality and threshold constraints. Subsequently, differential evolution operations are applied to derive the optimal solution that satisfies all constraints. Throughout this process, the outer loop serves as the preliminary constraint processing step, while the inner loop represents the primary computation phase, ultimately producing the optimal solution.

(1) Chromosome coding. An $N$-dimensional vector is randomly generated using binary coding. Each chromosome is adopted as a 0-1 vector to represent the investor's strategy of investing or not investing in risky assets.

(2) Fitness function. The fitness function is a measure of the degree of dominance of an individual in the survival of a population. It is mainly used to determine the fitness of an individual through individual characteristics, and is used to differentiate between "good" and "bad" individuals. The outer loop's fitness function is

The four intra-model circularity fitness functions are

(3) GA selection operator. The probability that an individual $i$ is selected is $p_{i}(x) = \frac{F_{i}(x)}{\sum F_{i}(x)}$, where $F_{i}$ is the fitness value of individual $i$ and $\sum F_{i}(x)$ is the sum of the fitness values of all individuals in the population.

(4) GA crossover operator. Two individuals are chosen at random, to swap combinations, to pass the parent's superior genes to next generation, and produce a new superior individual. The $k$th chromosome $a_{k}$ crosses with the $l$th chromosome $a_{l}$ at position $j$ as follows.

where b is a random number in the interval [0, 1].

(5) GA mutation operator. The number of variant genes is generated with a certain probability, and individuals from the population are selected for mutation to produce better individuals by a random method. The mutation operation for the $j$ th gene $a_{ij}$ of the $i$th individual is

where $a_{max}$ is upper limit of $a_{ij}$, $a_{min}$ is lower limit of $a_{ij}$, $f(g) = r_{2}(1-\frac{g}{G_{max}})^{2}$, $r_{2}$ is a random number, $g$ is the current number of iterations, $G_{max}$ is the maximum number of iterations, and $r$ is a random number of $[0, 1]$.

(6) DE algorithm mutation operator. The DE/rand/1 tactics is used to perform mutation as follows. For the current individual vector $X$, this operator first selects three randomly different individual vectors from the parent as $X_{r1}$, $X_{r2}$, $X_{r3}$, and then performs a difference operation on $X_{r2}$ and $X_{r3}$ to obtain the difference vector; finally, the difference vector is scaled by the scaling factor $F$ and summed with the base vector $X_{r1}$ to obtain a new vector, denoted as the variational individual. Finally, the difference vector is scaled by the scaling factor $F$ and summed with the base vector $X_{r1}$ to obtain a new vector, denoted the variational individual vector $V_{i}$. The equation is as follows:

where the initial scaling factor $F_{0} = 0.5$, and the scaling factor $F$ is calculated by

(7) Non-feasible solution treatment. If $X = (X_{1}, X_{2}, \cdots, X_{n})$ is a non-feasible solution, there are infeasible elements in $X$. If $X_{i}$ is not in the feasible domain $[l_{i}z_{i}, \mu_{i}z_{i}]$, we will correct $X_{i}$ by the following formula:

(8) DE algorithm crossover operator. First, the crossover operator generates a random dimension identifier $j_{rand}$ to ensure that at least one dimension of the final test individual is from the variant, thus avoiding identity with current individual and ensuring population diversity. Otherwise, the dimension of the test individual is from the current individual. The formula is given below.

(9) DE algorithm selection operator. The selection operator serves to guide the evolution of the population, mainly through the evaluation of fitness values. For each current individual vector $x_{i, G}$, a corresponding test individual vector $U$ is obtained by the previous variation and crossover operations. Then the selection operator uses one-to-one selection to compare $x_{i, G}$ with $U$ and select the one with the best fitness value as the next-generation population. The exact formula is illustrated below.

4.2.2.   The steps and flow chart of IEDCHA

Based on a several basic operations as described above, we design an algorithm as follows. The pseudo-code for the inner loop algorithm is shown in Algorithm 1, the pseudo-code for the outer loop algorithm is shown in Algorithm 2, and the overall pseudo-code for the proposed algorithm is shown in Algorithm 3. In addition, please refer to Figure 2 for the flowchart of the proposed algorithm.

5.   Numerical experiments

In this study, we combine genetic algorithms with differential evolutionary algorithms to solve the models M1, M2, M3, and M4. In this paper, all stocks in the SSE-50 index are selected for the study. However, since the 50 stocks in the SSE-50 index are adjusted every six months, the fund will also adjust its position, so it is somewhat bearish for the stocks that are moved out and somewhat positive for the stocks that are moved in. According to the above, since the 50 stocks in the SSE-50 index are dynamically adjusted, we have taken into account the concept of stability of the sample, and in order to ensure that the results are more informative, we have screened the 50 stocks in the SSE-50 index by removing the stocks with obvious problems, few selections, missing data and inconsistent data, and those stocks that were relatively stable (no obvious problems, consistently selected, and with complete and consistent data) in the SSE-50 index's dynamically adjusted list were retained, resulting in a set of 30 alternative stocks with stable performance. The data of all trading days of these stocks from January 2017 to January 2020 were selected as raw data for numerical experiments. The data were obtained from https://tr.investing.com/. The selected sample covers a wide range of sectors with different income characteristics, satisfying decentralization, which can effectively reduce the unsystematic risk in investments and better match the choice of investors' wishes, as well as adding meaning to the empirical study of the portfolio model.

The experiment consists of five main parts. (1) To analyze the portfolio strategies of each of four models in the framework of designed algorithm; (2)to analyze the portfolio strategy under upstream and downstream constraints at different investment ratios, with the aim of examining the impact of various parameters of the upper and lower bounds of investment ratios on the portfolio; (3) to compare the numerical results under different transaction cost rates to illustrate the impact of adjusting the transaction cost parameters on the numerical outcomes; (4) to analyze the investment returns and risks of different models with different cardinality constraints by adjusting the number of investable assets, and to compare the performance of four models in terms of returns and risks, in order to reflect the impact of base constraints on investment; and (5) to compare the numerical results of different algorithms for solving the fours models to verify the effectiveness of the IEDCHA proposed in this paper. All experiments were performed in MATLAB2016a with [Intel(R) Core(TM) i7-10700 CPU @ 2.90 GHz 2.90 GHz] in Windows 10.

The returns of the stocks are trapezoidal fuzzy numbers, and a method of objective fuzzy frequency statistics was adopted to approximate the trapezoidal fuzzy number of returns. The fuzzy return distributions of the 30 sample stocks obtained according to this method are shown in Table 1.

The previous and subsequent limit parameters of investment ratios were adjusted to simulate investments in order to analyze the impact of different upper and lower bounds on the four model portfolios. Subsequently, the numerical results were analyzed. By comparing the simulated investments' numerical results of the four models under varying transaction cost rates, this demonstrates how adjustments in cost rate parameters influence the outcomes.

Tables 2–4 shows the investment results of different models under different parameters. The numerical results of IEDCHA using four different risk measurement models to simulate investment under various transaction cost rates are presented in Table 2. These models consider constraints such as base constraints, threshold constraints, and transaction costs. It is evident from the results that the optimal performance of all four models is observed at a cost rate of 0.005. Table 3 illustrates the comparison of the numerical results obtained by IEDCHA for the four models with different lower limits, while keeping the upper limit fixed at 0.5. It can be observed from the results that the optimal performance of all four models is achieved when the lower limit is set to 0.005. Table 4 presents a comparison of the numerical results obtained by IEDCHA for the four models with different upper limits, while maintaining a lower limit of 0.005. It can be seen from these results that the optimal performance of all four models is observed when the upper limit is set to 0.5. Note that there are negative values in the results, which are due to both the formulas used for the different risk measures and the historical data used, so it is normal here.

In a follow-up experiment, we labeled these 30 stocks as Stock 1, Stock 2, ..., Stock 30 in order. To verify the effect of different cardinality constraints on the portfolio results, this four models were solved by IEDCHA, and the portfolio strategies for different models with different cardinality constraints are shown in Tables 5–9.

The portfolio strategies of these four models with a cardinality restriction of $K = 10$ are shown in Table 5. The number of stocks in the M1 model portfolio is 10, and the proportional weighting of investment is focused on Stocks 2, 3, and 6, which are assigned higher proportional weights, indicating that these three stocks are more likely to generate higher returns than other stocks among the 30 assets. The number of stocks in the M2 model is 10, and the proportional weighting is concentrated on Stocks 1, 2, 3, 4, 9, 10, 17, 28, 29, and 30, with a higher proportional weighting on stocks 1, 3, 10, 28, and 29, indicating that among these 30 assets, the proportional weighting is higher than 1, 3, 10, 28, and 29. The higher weighting of Stocks 1, 3, 10, 28, and 29 indicates that, among the 30 assets, investing in these five stocks is more likely to yield high returns than other stocks. The number of stocks in the M3 portfolio is six, and the proportional weighting is mainly on Stocks 2, 5, 13, 22, 25, 27, 28, and 30. The higher weighting of Stock 30 indicates that, among the 30 assets, investing in this stock is more likely to yield high returns than other stocks. The number of stocks included in the M4 model is nine, and the proportional weighting is concentrated on Stocks 1, 5, 10, 11, 15, 21, 23, 24, and 26, with a higher weighting on Stocks 1, 11, 21, 23, 24, and 26. This indicates that investing in these six stocks is more likely to yield high returns than other stocks across the 30 assets. These four models allocate the highest number of investments to Stocks 2 and 28, followed by Stocks 1, 3, 5, 10, 15, 17, 22, 25, and 30 among the 30 stocks, and less to the rest.

Table 6 depicts the portfolio strategies of these four models under the cardinality constraint $K = 15$. From Table 3, we can know that the number of stocks in the portfolio of M1 is fifteen, and the proportional weighting is mainly on Stocks 2, 3, 4, 6, 9, 10, 12, 13, 14, 18 and 20, 22, 25, 27, and 30, with a higher proportional weighting for Stocks 2, 3 and 4, indicating that these three stocks are more likely to generate higher returns than other stocks across the 30 assets. The number of stocks in the M2 model is 12, and the proportional weights are concentrated in Stocks 1, 3, 6, 8, 11, 14, 16, 19, 23, 26, 27, and 28, with higher weights in Stocks 1, 11, 23, and 27. The higher weighting of Stocks 1, 11, 23, and 27 indicates that among these 30 assets, investing in these four stocks is more likely to yield high returns than other stocks. The number of stocks in the M3 model is seven, and the proportional weighting is concentrated on Stocks 6, 10, 15, 20, 28, and 30, with a higher weighting on Stock 30, indicating that this stock is more likely to generate higher returns than other stocks across the 30 assets. The number of stocks in the M4 model is 12, and the proportional weighting is mainly on Stocks 1, 3, 7, 8, 9, 14, 15, 16, 19, 21, 23, and 24, with higher weights on Stocks 3, 9, and 15, indicating that among the 30 assets, the proportional weighting is higher than the proportional weighting of Stock 30. These three stocks are more likely to generate higher returns than other stocks in these 30 asset classes. The four models allocate the highest number of investments to Stocks 3, 6, and 14, followed by Stocks 1, 8, 9, 10, 15, 16, 19, 20, 21, 23, 27, 28, and 30, and less to the rest of the 30 stocks.

Table 7 displays the portfolio strategies of these four models under the cardinality constraint $K = 20$. From above Table 4, we can find that the number of stocks included in the portfolio of M1 is twenty, and the proportional weighting is concentrated on Stocks 3 to 13 and 15, 17, 20, 21, 24, 26, and 28 to 30. The higher proportional weights for Stocks 4, 5, and 8 indicate that these three stocks are more likely to yield higher returns than other stocks across the 30 assets. The number of stocks in the M2 portfolio is thirteen and the proportional weights are concentrated in Stocks 1, 2, 4, 5, 7, 9, 10, 16, 20, 23, 26, 28, and 29, with higher weights in Stocks 1, 4, and 10. The higher weighting of Stock 1, Stock 4, and Stock 10 indicates that these three stocks have a higher probability of generating high returns compared with other stocks across the 30 assets. The number of stocks in the M3 portfolio is eight, and the proportional weighting is mainly on Stocks 4, 8, 14, 20, 22, 23, 28, and 30, with a higher proportional weighting on Stocks 4 and 30, suggesting that investing in these two stocks is more likely to yield higher returns than other stocks across the 30 assets. The higher weighting of Stock 4 and Stock 30 indicates that, among the 30 assets, investing in these two stocks is more likely to yield higher returns than the other stocks. The number of stocks in the M4 portfolio is eighteen, with the proportional weighting on Stocks 1 to 5, 7 to 12, 14, 20, 22, 24, 25, 27, and 28, with a higher proportional weighting on Stocks 2, 10, 22, and 27. All this indicates that investing in these four stocks is more likely to yield higher returns than the other stocks across the 30 assets. The four models allocate the highest number of investments to Stocks 4, 20, and 28, followed by Stocks 5, 7, 8, 9, and 10, and even fewer to the rest of the 30 stocks.

Table 8 shows the portfolio strategies of the four models with the cardinality constraint $K = 25$, from which we can see that the number of stocks included in portfolio of the M1 is twenty-four, with the proportional weighting concentrated on Stocks 1 to 12, 16 to 18, 20, 22, 24, 25, 26 to 28, and 30, with a higher proportional weighting for Stock 2 and Stock 5, indicating that these two stocks are more likely to generate higher returns than other stocks across the 30 assets. The number of stocks in the M2 is thirteen, and the proportional weighting is mainly on Stocks 1, 2, 4, 5, 7, 9, 10, 16, 20, 23, 26, 28, and 29, with a higher weighting on Stocks 1, 2, 4, and 5. The higher weighting of Stocks 1, 2, 4, and 5 indicates that among the 30 assets, investing in these four stocks is more likely to yield high returns than the other stocks. The number of stocks included in the M3 model is eight, and the proportional weighting is mainly on Stocks 2, 5, 9, 10, 13, 15, 20, and 30. The higher weighting of Stock 9 and Stock 30 indicates that, among the 30 assets, investing in these two stocks is more likely to yield higher returns than the other stocks. The number of stocks in the M4 is eighteen, and the proportional weighting is mainly on Stocks 1, 3 to 6, 8 to 10, 12, 14, and 23 to 30, with a higher weighting on Stocks 9 and 14, indicating a higher probability of high returns compared with the other stocks across this thirty assets, These two stocks are more likely to generate higher returns than the other stocks in the 30 assets. The four models allocate the highest number of investments to Stocks 5, 9, and 10, followed by Stocks 1, 2, 4, 20, 26, 28, and 30, and even less to the rest of the 30 stocks.

It can be seen from Table 9 that with the cardinality constraint $K = 30$, the investment results of the four models are the same as those when the cardinality constraint is $K = 25$. This indicates that the investment strategy does not change after the number of investable stocks exceeds 25. That is, after the number of investments exceeds 25, adding new investments does not have a positive impact on the returns.

From Tables 5–9, the M1 model invests the same amount of risky assets at different cardinality constraints and reaches the maximum limit; the M2 model invests all at $K = 10$ and more at $K = 15$, while the number of investments at $K = 20$, $K = 25$, and $K = 30$ is the same and does not increase much compared with $K = 15$. The number of investments for the M3 model increases incrementally for $K = 10$, $K = 15$, and $K = 20$, and for $K = 25$ and $K = 30$, the number of investments is the same as for $K = 20$, indicating that the optimal investment strategy for the M2 model has 13 assets after the cardinality constraint exceeds 20. The number of investments at $K = 25$ and $K = 30$ is the same as that at $K = 20$, indicating that after cardinality constraint exceeds 20, the change in $K$ has little effect on the behavior of investors using the M3 model for simulated investments, i.e, the optimal number of assets for values of $K$ above 20 is 8; the M4 model has an increasing number of investments in risky assets at $K = 10$, $K = 15$, and $K = 20$, with $K = 15$ and $K = 20$. The number of investments at $K = 25$ and $K = 30$ is the same as the number of investments at $K = 20$, suggesting that the optimal number of assets is 18 after the cardinality constraint exceeds 20, and that increasing the number of investments in risky assets has little positive effect on investors and may lead to capital losses due to poor management.

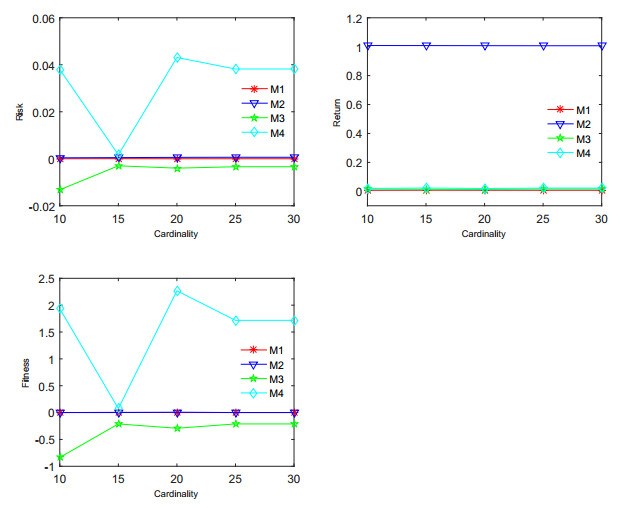
Table 10 and Figure 3 all displays the values of risk, return, and fitness function for four models with varying cardinality constraints. For cardinality $K = 10$ to $K = 30$, the M3 model has the lowest risk, followed by M1, M2, and M4. Otherwise, M2 has the highest return, followed by M4 in second place, M3 in third, and M1 in fourth place. For $K = 10$ and $K = 20$, the M3 model has the lowest adaption index, followed by M1 in second place, M2 in third place, and M4 in fourth place. For $K = 15$, $K = 25$, and $K = 30$, the M3 model has the smallest fitness, M2 has the second largest, M1 has larger fitness, and M4 has the largest fitness. The M1 model is less risky and yields the least returns, the M2 model is less risky and yields the most returns, the M3 model is the least risky but yields less returns, and the M4 model is the most risky but yields more returns. The M3 model is suitable for risk-conservative investors in the portfolio strategy analysis, the M4 model is suitable for risk-seeking investors in the portfolio analysis, and the M1 and M2 models are suitable for risk-neutral investors in the portfolio analysis. Notice that the different line segments in Figure 3 are too close together, which is caused by the small gap between the data, but this does not affect understanding.

Finally, the effectiveness of the IEDCHA method is validated by comparing the numerical results obtained from four different risk measurement models solved using various algorithms. The parameters of the comparison algorithm are set in Table 11. The '$-$' in Table 11 indicates that the parameter is not used by the algorithm.

The numerical results of IEDCHA and the four comparison algorithms solving the four models are compared, as presented in Table 12. When applying the comparison algorithm to solve the model, the constraints within the model are addressed using the classical penalty function method. Additionally, Table 12 displays a selection of four algorithms for comparing their results with those obtained by IEDCHA for each problem. All computations were performed on MATLAB2016a, utilizing an Intel(R) Core(TM) i7-10700 CPU @ 2.90GHz processor running a Windows 10 operating system. From Table 12, it is evident that IEDCHA achieves superior outcomes when compared with several other comparison algorithms. However, due to its double-loop mechanism design, each cycle requires a certain amount of time, which leads to longer computation times for IEDCHA in contrast to other algorithms.

6.   Conclusions

This paper explores the notion of fractional programming in a fuzzy portfolio framework and builds four fractional programming portfolio selection models with distinct risk metrics in an attempt to address the complexity and fundamental structure of current portfolio models. The suggested models analyze risk and return at the same level without prioritization, minimizing the drawbacks of standard techniques that entail compromising one goal to accomplish another. The suggested model is solved using a hybrid IEDCHA strategy that avoids the drawbacks of the penalty function method. The four models' performance is further tested by comparing portfolio strategies under various risk measures and base limitations via simulated investments.The numerical results of the four models are also compared to analyze the various conditions for which they are appropriate. However, since the IEDCHA algorithm designed in this paper is specifically designed for the specific form of the four models we established, and the constraints in the model are gradually processed in the algorithm calculation process, the algorithm designed in this paper has certain limitations, which is also a common problem faced by this type of research. Therefore, on the basis of model innovation, the design of a wider range of optimization algorithms will be the focus of our subsequent research. Second, the incorporation of investing behavior and investment psychology into portfolio modeling provides for a more realistic model, as investors are the major decision-makers. At the same time, the fractional programming described in this study is only applicable to bi-objective issues; more research is required for optimisation problems with more than two goals, or the model might be solved directly using a multi-objective intelligent algorithm. These two notions are also the subject of our subsequent examination.

Author contributions

All authors contributed to the conception and design of the study. C. Y. Hu: Methodology, Writing-original draft, Writing-review and editing; Y. L.Gao: Data curation, Conceptualization, Funding acquisition, Writing-review and editing; E. Y. Gao: Data curation, Writing-original draft.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported in part by the Natural Science Foundation Key Projects of Ningxia 2022AAC02043, in part by the Construction Project of First-class Subjects in Ningxia Higher Education NXYLXK2017B09, in part by the Major Special Fund of North Minzu University ZDZX201901, and in part by the Nanjing Securities Support Basic Discipline Research Project NJZQJCXK202201.

Conflict of interest

The authors declare no conflict of interest.