A new class of Shariah-compliant portfolio optimization model: diversification analysis

1.   Introduction

Numerous studies have confirmed the consistent outperformance of Islamic finance in comparison with the conventional system during financial crises, attracting the attention of investors and policymakers ^[1,2]. Particularly, the Islamic finance industry began to receive a surge of confidence after the global financial crisis in 2008, in which the Islamic indices and Islamic funds had shown a contrasting performance to conventional assets, recording high assets growth of 29% in addition to a good diversification level, and outstanding stability ^[3,4]. Today, the situation is further amplified following the substantial growth of the Muslim population, which stimulated the demand for Shariah-compliant investments due to the devotion of Muslims to integrating religious beliefs into daily conduct ^[5]. With nearly a quarter of the world population and high expectations, given the historically superior performance in risk management, Islamic finance has become one of the fastest-growing segments in the global financial system ^[3].

The outbreak of COVID-19 at the beginning of 2020 had rendered a severe downturn in global equity market value. According to Ashraf, Rizwan and Ahmad ^[6], the global market was hit hard by the crisis, where the population recorded a more intense panic level than in the global financial crisis of 2008. Within a month, the stock market volatility rose sharply from 14x to approximately 85x, causing apprehensiveness among investors about the outlook for the future economy. Consistent with earlier findings, Islamic indices outperformed the conventional benchmarks despite the adverse market condition. Furthermore, the pandemic exacerbated the previously weakened investment climate due to cyclical factors, including the dynamic nature of global demand. The sudden outbreak of the COVID-19 pandemic served as a reminder of the crucial role of financial crisis readiness.

Islamic finance advocates for risk-sharing, social justice and equity, ethical investing, and the practicability of commercial transactions ^[7]. Its distinctive characteristics include the prohibition of riba, gharar, maysir, and the payment of zakat, as outlined in a study conducted by Lim, Goh and Sim ^[8]. Generally, riba refers to interest or usury, in which the practice of imposing interest or a predetermined payment beyond the principal amount is impermissible ^[9]. On the other hand, gharar refers to risk, uncertainty, hazard, and ambiguity. While prohibiting maysir that is defined as speculation or gambling, Islamic finance also forbids haram and unethical activities such as tobacco and liquor, in which Muslims are restricted from engaging in investments associated with ventures whose core operations involve this range of activities. Finally, zakat is the Islamic obligation to make annual donations to the poor and needy upon reaching a minimum threshold of wealth, known as nisab ^[10]. The payment serves to purify the inevitable impermissible income while promoting the redistribution of wealth to improve income inequality.

Previous crises had showcased the inadequacy of the conventional market over the Islamic market due to the instability originating from Islamic-prohibited factors, such as richness in derivatives, leverage, and short selling. Although these instruments or mechanisms are commonly used for risk hedging with high profit-making opportunities, Islamic jurists and scholars claim them as non-compliant with Shariah ^[11,12]. As highlighted by Lim, Goh and Sim ^[8], derivatives and short-selling involve high uncertainties of undelivered assets in addition to the violation of the factor of ownership that leads to gharar. The associated deferred payments also oppose Islamic finance that advocates for an equal exchange between parties, deeming them as riba. Moreover, the expectation of a decrease or increase in future prices leads to speculation. Notwithstanding, leveraging that serves as margin trading involves borrowing funds that promote debt-based interest, which is against Islamic finance.

Hodžić and Sijerčić ^[13] regarded conventional finance as secular and unethical, supporting the assertion that conventional finance is faulty under Shariah. Being justified as lowly sustainable, cyclical changes and financial crises can substantially impact the global economy. Numerous studies also concluded that Islamic portfolios are at least on par with conventional portfolios, if not superior ^[14,15,16]. Notably, Charfeddine, Najah and Teulon ^[17] observed an absence of a long-run relationship between the Islamic and conventional indices.

Furthermore, the Sustainable Development Goals (SDGs) have received renewed interest, with one of the objectives dedicated to promoting sustainable investment. While the SDGs aim to create a resilient investment line corresponding to social, environmental, and climate change issues, relating it to Socially Responsible Investing (SRI) that promotes both ethical and socially conscious investments, covering the environmental context, social justice, corporate ethics, and criticism of discrimination, Islamic finance can align with these efforts to achieve the same goals. As stated by OECD ^[18], Islamic finance is in a good position to maximize social impact and fulfil the SDGs upon its progressive adoption of sustainability principles. Likewise, there was no statistically significant difference between the returns of Islamic and SRI funds across all regions ^[19].

Bauer, Ruof and Smeets ^[20] highlighted three reasons for the massive support for sustainable investment. First, investors have high expectations of sustainable investing due to the corresponding underlying principles. Second, investors put social priorities in support of sustainable investments. Third, the authors found a lack of conscious awareness of investors, in which there were no clear reasons for the preference of sustainable investment over the conventional approach. Overall, the authors testified the second reason such that two-thirds of the respondents prioritized SDGs-considered companies over those with better financial performance. The significant development of the SDGs could be due to the investing behavior of millennials, which favors investments in alignment with personal values. Given that millennials are to inherit more than US$30 trillion, the demand for sustainable investment is anticipated to grow accordingly ^[21]. Thus, this changing demographic for investing must be recognized to support the coming surge of continual demand for sustainable investment by shifting investment strategies.

Collectively, it is apparent that the way of market conduct has to be adjusted corresponding to the integration of enhanced economic knowledge and the renewed interest in sustainability to help relieve global stress and meet future investment demands. Despite the superiority of Islamic finance in portfolio management, the modelling of Islamic portfolio optimization has not been treated in much detail. As summarized in the review paper by Lim, Goh and Sim ^[8], there remains a significant gap in the Islamic portfolio optimization modelling literature as most studies focused on the screening methodology of Islamic securities instead of model construction until the very first Shariah-compliant model introduced by Masri ^[22]. While several more attempts were made to model Islamic portfolios, the securities were typically optimized using conventionally structured models with a reduced asset universe of Shariah-compliant assets.

In addition, the suggestion of an inverse relationship between portfolio diversification and causality between sectors of the securities in the portfolio could encourage the investigation of evaluating causal relationships between securities ^[23]. Hence, understanding spillovers across assets is worthwhile to dampen the impact of financial turmoil. Following the recommendations and findings of the prior studies, this paper aims to construct an Islamic portfolio optimization model as a worthy competitor to the conventional models in supporting the financial system against any unforeseen crisis in the future while incorporating higher moral and ethical values to facilitate the progress of the SDGs, as well as strengthening confidence in Muslims, further encouraging high participation in portfolio investment to boost the economic growth. Additionally, this study evaluates the causal relationships between securities within the resulting portfolios, considering the importance of dynamic relationships for portfolio diversification.

With respect to the consistent ranking as first on the Global Islamic Economy Indicator (GIEI) for eight consecutive years, Malaysia has established itself as a global Islamic finance leader, suggesting a more progressive and competent position in the industry. Thus, this study was constructed within the framework of the Malaysian capital market, which the beneficial habitat of Malaysia could elevate the validity and reliability of the research study. The remainder of this paper is structured as follows: Section 2 highlights the relevant scholarly works; Section 3 presents the sample of data used in the study; Section 4 presents the methodology of constructing the proposed model; Section 5 devotes to the methods of evaluating portfolio performance; Section 6 presents the empirical findings; lastly, the paper ends with the conclusions.

2.   Literature review

The development of Islamic finance has been remarkable over the decade, with Shariah-compliant investment emerging as one of the fastest-growing SRI funds for its recognized resilience and stability, particularly during financial crises. While concerns have been raised regarding the potential opportunity cost of the funds following the exclusion of certain profitable stocks through screening, research has justified a comparable performance to conventional investments in addition to a lower expense due to a lower tendency to speculate ^[22,24].

Several attempts were taken to construct Shariah-compliant portfolio optimization models, including Derigs and Marzban ^[24], who introduced a new paradigm for Shariah-compliant portfolio optimization by emphasizing the application of sector and financial screenings. The study challenged the conventional viewpoint and suggested a greater focus on the Shariah compliance of the optimal portfolio after purification over single assets. The strategy had a notable advantage as it prevented the significant reduction of the asset universe through a carefully constructed pre-process that allows only Shariah-compliant asset classes, such as sukuk.

Masri ^[22] made a notable contribution to the field by presenting the first Shariah-compliant portfolio optimization model, developed by extending the mean-variance (MV) model with the incorporation of a multi-objective stochastic program and the selection of beta coefficient as the risk measure. The model adhered to four main Islamic principles. Firstly, the asset universe was restricted to Shariah-compliant securities to avoid unlawful income. Secondly, risk-free securities were excluded to prohibit riba. Thirdly, the model included 2.5% of the total wealth above nisab to account for zakat. Lastly, the model asserted an upper limit on the beta coefficient, representing the risk for Islamic market return to control Gharar Fahish (intolerable gharar). Masri also concluded that CAPM was suitable for evaluating security returns within the Islamic finance framework. Overall, the model aimed to maximize portfolio returns while minimizing the divergence of portfolio risk from the market risk and portfolio return from the zakat rate. The objective of the model was to create portfolios that closely exhibit the performance of the market benchmark.

On the other hand, Bagheri ^[25] developed the first Shariah-compliant multi-goal program using deterministic goal programming with covariance as the risk measure. The author included additional objectives of minimizing the price/earnings per share ratio and price/book value per share ratio, along with the common objectives of maximizing return and minimizing risk. The model permitted 10–25% impermissible income for constructing the Islamic funds, with different levels of Shariah compliance, namely 90%, 85%, and 75%.

A recent study by Braiek, Bedoui and Belkacem ^[16] proposed a new methodology for Islamic portfolio optimization using CoVaR as the systemic risk and the mean-risk approach as the base model. The model focused on minimizing the potential losses arising from systemic risk in addition to considering sector-level risk rather than institutional-level risk to avoid excessive risk.

Besides, different proxies were used to represent the risk-free rate in evaluating the performance of Islamic portfolios, including the zero-beta portfolio by Black ^[26]; zakat rate by Ashker ^[27]; US Treasury Bill rate by Hakim and Rashidian ^[28], Hassan, Khan and Ngow ^[29]; the 1-year yield of AAA-rated sukuk and the removal of risk-free rate by Hakim, Hamid and Mydin Meera ^[30]; government bond yield by Hussin, Saring, Zahid et al. ^[31], Hoque, Rakhi, Hassan et al. ^[32]; United Arab Emirates Interest Rate by Bagheri ^[25]; Shariah-compliant risk-free references, such as Islamic interbank lending rates by Sandwick and Collazzo ^[15].

Although much of previous research claimed to be an Islamic model, much of the studies concerned only the inclusion of Shariah-compliant assets using conventionally structured models or focused on the screening methodology of Shariah-compliant securities. Among various models examined, only Masri's model emerged to fulfil its objective of constructing a Shariah-compliant model without deviating from its purpose.

Notwithstanding, forming an efficient portfolio was challenging as it involved diversification. Chen and Chiang ^[33] emphasized the importance of evaluating the degree of co-movement among different assets to access their diversification performance, commonly by examining the correlation between them. In accord with the suggested use of the Granger causality test in identifying the dynamic of assets within portfolios to enable effective rebalancing during highly volatile markets, Lim, Goh, Sim et al. ^[34] supported the use of the Granger causality test to test for co-movement.

3.   Empirical sample

The model was tested using the historical closing prices of 154 securities that are averagely priced at RM1 to RM5, filtered from a list of 746 Shariah-compliant securities approved and updated by the Shariah Advisory Council (SAC) of the Securities Commission Malaysia (SC) dated 28 May 2021, the FTSE Bursa Malaysia EMAS Shariah Index (FTSEESI) as the Islamic benchmark index, and the FTSE Bursa Malaysia KLCI (FBMKLCI) as the market benchmark, from 2011 to 2020. The sample data were converted into logarithmic returns:

with P_t and P_t-1 denoting the closing prices at time t and t-1, respectively.

4.   Model construction

The model construction involves four phases, starting from the selection of the base model, the risk measure used, Islamic and practical concerns, and lastly, the resulting model.

4.1.   Base model

This study considers the use of a mean-risk analysis built upon the theoretical framework of the MV model that was well-known to suit risk-averse investors ^[35]. Within the selected framework, this study adopted the principle of maximizing return subject to risk constraint to better address the needs of Muslims in avoiding gharar:

Maximize

Subject to

with ${w_i}$ and ${r_i}$ denoting the weight and return of the i-th security, respectively; $\rho ({r_p})$ refers to the portfolio risk; R^* is the upper limit on the risk of portfolio return.

The mean-risk model consists of long-only constraints to avoid riba and gharar, such that the weight of each security must be non-negative, preventing short-selling, in addition to the budget constraint that limits the sum of weights to 1. Besides, the risk constraint is in line with the Islamic model design for better risk control.

4.2.   Risk measure

This study utilized Conditional Value-at-Risk (CVaR) as the risk measure for modelling Islamic portfolio optimization. CVaR is a percentile risk measure used to account for losses beyond the Value-at-Risk (VaR) threshold, specifically by measuring the average loss in the worst-case scenario ^[36]. Denoted as $CVa{R_\alpha }(X)$, CVaR at a given tail probability α is the conditional expectation of loss, X subject to $X \geqslant Va{R_\alpha }(X)$. As indicated by the definition, a portfolio with an optimal CVaR will have a low VaR. Mathematically, CVaR is represented as:

In modelling time series, CVaR is explicitly estimated without imposing any distributional model using:

which could be solved using a convex program for optimization, where ${r_i}$ denotes the observed returns and ${r_{(k)}}$ is the sorted sample such that ${r_{(1)}} \leqslant {r_{(2)}} \leqslant \ldots \leqslant {r_{(n)}}$; $\left\lceil {n\alpha } \right\rceil$ refers to the smallest integer larger than $n\alpha$; θ is the VaR level ^[37]. Although it is common to reduce the formula into an equivalent Eq (8) solvable using a linear program, the reduction is at the expense of an increasing problem dimension, where an increased number of observations will cause the matrix that was defining the linear constraints to be more non-sparse, reducing the efficiency of the linear problem.

Thus, the advantage of simplifying the problem eventually contra the increasing problem dimension ^[37]. In this context, this study maintained the utilization of Eq (7).

There has been a growing body of literature regarding mean-CVaR in portfolio optimization following the efficiency of a worst-case scenario in evaluating investment losses, in which many of the studies adopted heuristic methods to solve the optimization problem for a shorter computational time. Conversely, a convex program is tractable for optimizing a problem, and this study opts to develop a mathematical model that is highly accessible and easily understandable for laypersons.

In comparison, Masri's model, namely the only Shariah-compliant model that fulfils the Islamic construction purposes found thus far, employed the beta coefficient as the risk measure and constructed the portfolio beta to adhere as closely as possible to the Islamic market beta. The methodology used in Masri's model focused on achieving portfolio risk that approaches the risk of the market benchmark. In contrast, the risk constraint used in this study aims to generate the highest possible profits while providing access and control on the near-maximum investment risk, thus allowing the making of informed decisions.

4.3.   Zakat

The annual zakat rate is 2.5%, calculated on the market value of shares, and is payable once3 in a lunar year ^[38]. With Z denoted as zakat,

Equivalent to

depending on the units used, with ${\omega _i} = {w_i}F$ indicating the amount invested in security i in Ringgit Malaysia.

4.4.   Rebalancing strategy

A rebalancing strategy refers to the periodic adjustment of the composition of a portfolio to ensure a consistently diversified investment that satisfies the changing investors' goals. A portfolio that is held without modification for a prolonged period may be subject to the risk of overweighting certain asset investments since the investment value of a portfolio changes correspondingly to different rates over time in addition to changing investment objectives. Tokat and Wicas ^[39] concluded that a portfolio that has not been rebalanced since its inception would eventually shift to high-risk-return investment. Regular portfolio rebalancing could help to capitalize on market opportunities while managing trading fees. Besides, Dai, Zhu and Zhang ^[40] highlighted the necessity to rebalance portfolios with strong time-varying volatility spillovers and conditional correlations.

While Tokat and Wicas ^[39] claimed that the frequency of portfolio monitoring is crucial to determine portfolio performance, the authors concluded that there is no optimal rebalancing strategy due to the different preferences of financial institutions. The authors argued that most financial managers are indifferent to small deviations, whereby they more frequently select a wide rebalancing threshold with comparatively infrequent portfolio monitoring. Meanwhile, it is imperative to acknowledge that Islamic finance prohibits speculations (maysir) that often relate to relatively short-term investments. Considering these and the nature of zakat that is payable annually, this study proposes an annual rebalancing strategy to reduce the risk associated with speculation while promoting sustainable growth in the global financial system that is in accordance with Islamic principles. The rebalancing process involved applying the optimal allocations generated from each subperiod as the initial composition for the subsequent subperiod.

4.5.   Transaction costs

In addition, it is apparent that portfolio rebalancing directly relates to transaction costs which are crucial in justifying the worthiness of reallocation. This study considers transaction costs specified in Bursa Malaysia, including the brokers' commission, stamp duty, and clearing fees ^[41].

The brokerage fee for investment less than RM100,000 is RM40 or 0.6% of the contract value, whichever is higher, whereas for investment above RM100,000 is the higher amount between RM40 and 0.3% of the contract value. The stamp duty is 0.15% on the transaction value, capped at RM1,000. Lastly, clearing fees account for 0.03% of the transaction value, not exceeding RM1,000 per contract. With C representing the total transaction costs for the portfolio, $C = \sum\nolimits_{i = 1}^3 {{C_i}}$, the respective transaction costs were denoted by C₁, C₂, and C₃, generalized as:

The constraints are written as:

For j = 1

For j = 2, 3

where ${\omega _{it}}$ and ${\omega _{it - 1}}$ equal the amount invested in security i over the period t and t-1, respectively; j is the type of transaction cost; c is the rate of transaction costs; y is the contract values.

4.6.   Holding constraints

Commonly known as the holding constraints, the limit on security weights is crucial for portfolio optimization. It is best to avoid placing too much weight on any asset or industry for better diversification. Moreover, an extremely small active position would have a very limited contribution to the portfolio return besides incurring more transaction costs that would offset the positive returns ^[42]. The box-type constraint was used to exert the maximum and minimum holdings of an individual asset in the portfolio, employing a maximum weightage of 15% each ^[15] and a post-optimization elimination of securities lesser than 7% ^[43], making the holding constraint:

4.7.   The developed model

This study proposes an annually rebalanced mean-CVaR model that attempts to control the possible extreme losses up to an acceptable level to avoid Gharar Fahish. While wealth purification through zakat compensates for the inevitable ribawi transactions in trading, the deduction of zakat as a penalty cost reveals more closely the profits gained by investors. Additionally, transaction costs play a similar role with higher volatility than the zakat payment. Thus, the objective function in Eq (2) was replaced by:

Maximize

where T refers to the total period, and F is the total available fund for investment. Lastly, the proposed model can be simplified as:

Maximize

Subject to

The model was solved using Generalized Reduced Gradient (GRG), a non-linear algorithm commonly used to solve portfolio optimization problems.

5.   Portfolio evaluation

The portfolio performance was evaluated using several measures, including the comparison against the Islamic benchmark index using performance ratios, the comparison against the MV model, the Mean Arctangent Absolute Percentage Error (MAAPE) to examine the forecast accuracy, and correlation coefficient and Granger causality tests to analyze the inter-stock relationships.

5.1.   Performance ratios

This portfolio performance was tested using Sharpe Ratio, Treynor Ratio, and Jensen Alpha ^[44,45,46]. The use of different performance measures helps to reflect a comprehensive image of the portfolio performance.

Sharpe ratio is the simplest and most well-known portfolio performance measure that accesses the portfolio excess return per unit of risk represented by standard deviation. With R_p, R_f, and ${\sigma _p}$ indicating portfolio risk, risk-free rate, and the standard deviation of the portfolio, respectively, the Sharpe ratio is expressed as

The Treynor Ratio is the first portfolio performance measure that takes into account the risk factor, where it provides investors with a universal measure applicable to all risk preferences. By adopting the theory of Capital Asset Pricing Model (CAPM), Treynor proposed the use of the security market, with the beta coefficient, ${\beta _p}$ representing the sensitivity of portfolio returns to the market.

Jensen Alpha is one of the most popular investment performance measures, where it focuses on evaluating the contribution of the forecasting ability of a portfolio manager in increasing the risk-adjusted portfolio returns. Likewise, it uses beta as the systematic risk measure evaluated within the CAPM formulation, expressed as:

with

${R_m}$ is defined as the market return represented by FBMKLCI.

Notwithstanding, the Malaysian Islamic Treasury Bill (MITB) rate was used as the Islamic risk-free reference to substitute the risk-free rate defined in each performance ratio to avoid riba.

5.2.   Mean-variance (MV) model

The MV model that maximizes return while limiting the risk level and asset weights was used to compare the computational efficiency with the proposed model.

Maximize

Subject to

where ${\sigma _{ij}}$ denotes the covariance between ${r_i}$ and ${r_j}$, and R^* is the upper limit on portfolio volatility.

5.3.   Mean absolute percentage error (MAPE) and mean arctangent absolute percentage error (MAAPE)

The forecast accuracy of the proposed model was measured using MAPE. The metric was used to evaluate the average percentage difference between the estimated portfolio returns and the actual observed returns using back testing. The sample data was split into the training set as predicted values and the testing set as actual values:

where ${A_t}$ and ${F_t}$ are the actual and forecasted values, respectively. The forecast accuracy levels are concluded in Table 1 ^[47]. While MAPE was proven to be one of the best methods to account for forecast accuracy, it was also known to yield skewed and biased results easily. Given the limitations of the MAPE in returning extremely high values due to the proximity of the actual values to zero ^[48], the study further examined the MAAPE introduced by Kim and Kim ^[49] to obtain reasonable results:

5.4.   Correlation coefficient test

Correlation analysis was done to measure the strength of linear association between securities within the optimal portfolios, calculated using:

where ${\sigma _{ij}}$ refers to the covariance between series i and j.

The value ranges from −1.00 to 1.00. A higher coefficient indicates a stronger relationship between the movements of the variables. Generally, a correlation of 1.00 denotes a perfect positive correlation, such that the variables move in the same direction. Conversely, a correlation of −1.00 refers to a perfect negative correlation, where the variables move in the opposite direction. Meanwhile, a zero correlation indicates no association between the variables, implying independence. The p-value is computed using a t-distribution with (n–2) degrees of freedom, given by:

where the hypothesis test is written as:

The null hypothesis is rejected if the test statistic is less than the significance level, implying a correlation between the variables.

5.5.   Stationarity test

The return series must be stationary to proceed with the Granger causality test. Stationarity refers to the situation where the statistical measures such as mean, variance, and autocorrelation are consistent and time-invariant, such that the passage of time will not change the distributional shape of the series to ensure good forecasting. This study employed the Augmented-Dickey Fuller (ADF) and Phillips-Perron (PP) tests to examine stationarity, in which a time series with a unit root indicates an unpredictable systematic pattern, implying non-stationarity. The null hypothesis of a unit root is rejected if the statistical test is significant. Conversely, differencing could be done to transform the series into stationary. The series is known to be integrated of order d after d times of differencing to become stationary. The first differencing, $R_t'$, is calculated by subtracting the return at time t-1 from the return at time t, expressed as:

5.6.   Granger causality test

The Granger causality test proposed by Granger ^[50] refers to a statistical hypothesis test used to examine the causality between time series and identify the associated correlation patterns. It helps to evaluate the ability of a time series in causing another time series. The test is commonly performed by fitting the series with the Vector Autoregressive Model (VAR) and is expressed as:

${\alpha _0}$ and ${\beta _0}$ in Eqs (31) and (32) refer to the respective constants, and p denotes the lag length determined using the Akaike Information Criterion (AIC), Schwarz's Bayesian Information Criterion (SBIC), Final Prediction Error (FPE), and Hannan-Quinn Criterion (HQ). The hypothesis is written as:

Generally, the Granger causality test suggests a short-run causal effect of one time series to the other, such that a significant p-value that causes the rejection of the null hypothesis implies a causal relationship between them.

6.   Empirical results

The study assumes a total fund of RM100,000 and a maximum CVaR limit of 10%, at a tail probability α = 5%. Although no explicit guidelines were provided to categorize CVaR based on risk tolerance, a threshold of 10% was selected as a representative range for relatively risk-averse investors. This value strikes a balance between avoiding excessive risk (gharar) and enabling the potential for profit earning, consistent with Shariah that encourages the acquisition and accumulation of wealth. The optimal portfolios generated using the proposed model are presented in Table 2.

The empirical results have testified to the feasibility of the proposed model by optimizing portfolios with an average computing time of 7.6 minutes, which was significantly more efficient than the MV model, which consumed an average of 1.5 hours with similar results. While the CVaR limit was set to 10%, the resulting average portfolio CVaR was remarkably low at 5.61%, corresponding to approximately RM5,610 for a total investment of RM100,000, with an average standard deviation of 1.65%, equating to an estimated RM1,650.

Over the decades, the proposed model generated an average of 7 stocks and was considered appropriate for a well-diversified portfolio without high managing fees. Although improved diversification is commonly associated with an increased portfolio size, the superior performance of the portfolio is merely due to the greater number of assets rather than its skilful selection ^[51]. Evans and Archer ^[52] explored a decline in diversification performance as the number of assets increased after reaching a threshold, knowingly due to the high managing fees that would eventually outweigh the marginal benefits. Several studies provide empirical evidence supporting a portfolio size of 7 stocks for effective diversification. For instance, Alexeev and Dungey ^[51] concluded an 85% reduction of portfolio risk with an average of 7 stocks irrespective of the data frequency or selected time period. Also, a study by Jimbo, Ngongo, Andjiga et al. ^[53], which employed CVaR as a risk measure, observed that portfolios consisting of 7 stocks yielded the highest portfolio return and relatively low risk with the best reliability.

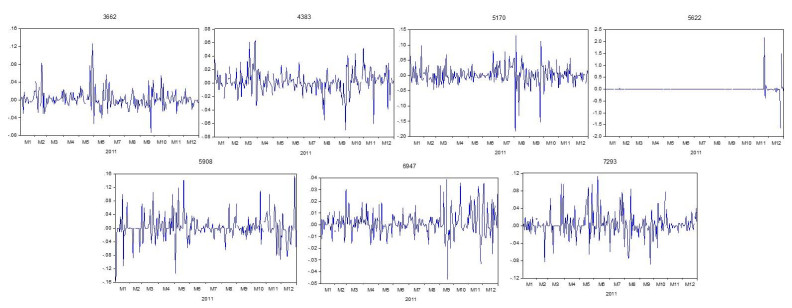
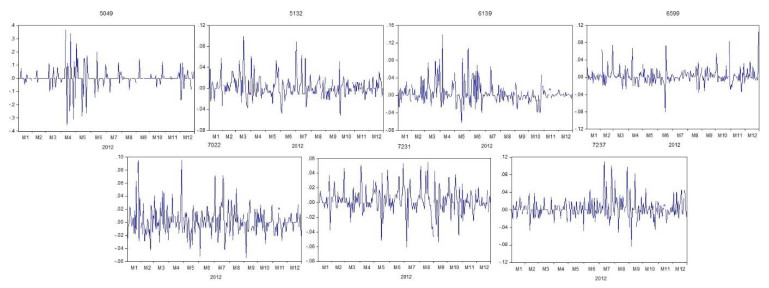
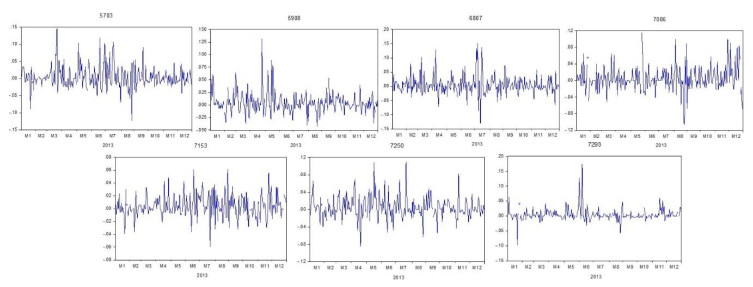
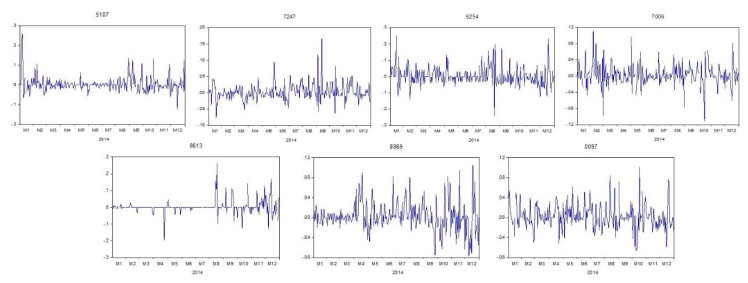
As shown in Figures 1–10, the fluctuating time series plots of the securities within the portfolios indicated time-varying volatility besides the evidence of volatility clustering, emphasizing the need to rebalance a portfolio. Additionally, the return series exhibited mean reversion based on the time series plots, which is a characteristic of a stationary time series. As presented in Table 3, the stationarity of the series was proven by the significant ADF and PP tests that led to the rejection of the null hypothesis of a unit root, implying that the series were stationary at level. Thus, the analyzed series were deemed suitable for modelling purposes, and no differencing was required to proceed with the Granger causality test.

Portfolios generated using the MV model closely resembled those obtained from the proposed model, except for portfolios 2014 and 2020, as shown in Table 4. The similar results to the classic model implied that the proposed model was reliable and feasible for optimizing a portfolio. With a 12x shorter computational time than the MV model, the proposed model was justified as a viable alternative with higher efficiency in addition to considering other trading concerns and Islamic obligations.

According to the performance ratios in Table 5, the optimal portfolios from the proposed model successfully outperformed the Islamic benchmark index (FTSEESI) throughout the study period. Additionally, the beta coefficients of the portfolios and the FTSEESI were examined, where portfolio beta is commonly used to represent the non-diversifiable systematic risk. Apart from 2013 and 2014, which recorded higher volatility than the market (FBMKLCI) with a beta value greater than 1, the remaining optimal portfolios were less volatile than the market. The results showed that the optimal portfolios were less sensitive to market movements, indicating a less risky investment. On the other hand, 6 out of 10 beta coefficients of the FTSEESI in the studied period were greater than 1, implying a higher sensitivity to changes in the overall market. Collectively, the comparison against the Islamic benchmark index showed the outperformance of the proposed model.

Moreover, the better performance of the generated portfolios with an average of 7 stocks over the FTSEESI constituting more than 200 securities, and FBMKLCI with 30 stocks, is consistent with prior studies that claimed that more assets do not necessarily lead to improved diversification. The superiority in terms of uncertainty and systematic risk measures endorsed the proposed model and verified CVaR as a viable measure to reduce market risk.

The MAPE and MAAPE results are shown in Table 6. As anticipated, all portfolios yielded MAPE values greater than 100% due to the metric's limitation in dealing with a significant proportion of actual values clustered around zero. Consistent with projections, the MAAPE had generated reasonable results against the MAPE. While the MAAPE values were less than favourable, the efficiency of a portfolio optimization model was not contingent on the results since it is apparently impractical to expect perfectionism from a real-world investment that is subject to uncertainties. Collectively, given the outperformance of the proposed model to the conventional portfolio optimization model and the Islamic benchmark index, the significance of the MAAPE results was deemed negligible in this study.

As shown in Table 7, the correlation coefficient test highlighted weak to moderate correlations between the resulting series, such that the majority were weakly correlated. The resulting low correlations were desirable to help reduce the overall portfolio risk. However, correlation results may not reflect the complete image of the inter-stock relationships since it does not signify causation ^[34,54,55]. As summarized in Table 8, the securities exhibited less than five causations in 2011, 2014, and 2020. These three portfolios shared the same trait, where the particular years were marked by several significant events that affected the Malaysian capital market.

In 2011, the debt ceiling crisis of the US recorded the highest market volatility since the global financial crisis in 2008. Standard & Poor's radically lowered the credit rating of the US government and federal agencies from AAA to AA+ for the first time in more than 70 years. Following the announcement of degradation, the global stock markets dropped in addition to a decline in all three major US stock indices in the range of 5% to 7% intraday. Moreover, the eurozone debt crisis, which was a consequence of the Greece crisis in 2009 worsened in 2011 with a sharp drop in economic growth ^[56]. While the European crisis seemed distantly related to Malaysia, it greatly affected the US market for being the major trading partner for Europe, with a unidirectional causal effect on Malaysia's stock market ^[57]. According to Kang, Uddin, Troster et al. ^[58], Malaysia was the largest net recipient of volatility spillovers during financial crises.

In 2014, several significant events occurred, including the disappearance of Malaysia Airlines Flight 370, also known as MH370, and the historical oil price crash. While the management in the aftermath of the disappearance of the MH370 caused a sharp decline in Malaysia's reputation and overall economy, investor confidence was further lowered following the crash of Malaysia Airlines Flight MH17, which recorded a more deadly incident than the MH370. On the other hand, oil prices recorded the biggest drop in modern history starting in mid-2014 due to an increased supply market ^[59]. As the second largest oil producer in Southeast Asia, Malaysia faced a significant macroeconomic deterioration. According to Ghorbel, Abdelhedi and Boujelbene ^[60], oil prices and investor sentiment had a strong contagion effect on Islamic indices.

On 30 January 2020, the World Health Organization (WHO) declared the outbreak of the COVID-19 pandemic as a Public Health Emergency of International Concern, and the pandemic became widespread across the globe, including Malaysia, by March 2020. The pandemic further led to nationwide lockdowns and triggered a significant economic disruption, resulting in a global economic recession. The resulting portfolio in 2020 confirmed the impact of the pandemic on the stock market, with Health Care stocks constituting more than half of the portfolio first time over the decade, in addition to one Technology stock and one Industrial Products and Services stock. The result was supported by He, Sun, Zhang et al. ^[61], who explored the contrasting performance of the Health Care and Technology industries during the pandemic.

Within the year, the collapse of the ruling coalition governments led to the Malaysian political crisis, which resulted in a substantial decline in investor confidence and an increased risk-aversion level that gave rise to increased market volatility, followed by the depreciation of the Malaysian currency. The finding was in agreement with several studies that confirmed the relationship between the exchange rate and the Malaysian capital market ^[62,63,64].

Remarkably, the portfolios in 2011, 2014, and 2020 recorded the highest CVaR compared to other portfolios, corresponding to the financial turmoil in the respective years. The results deduced an inverse relationship between the number of causalities and portfolio CVaR using the proposed model. Despite the high portfolio risk in 2020, the portfolio exhibited the highest return in the studied decade. This result could indicate an outperformance of the proposed model in managing risk during financial crises. In addition, the portfolios in 2014 and 2020 recorded the highest forecast accuracy as analyzed using the MAAPE. The above findings evidenced the effectiveness of the proposed model in solving high-performance portfolios, especially during financial crises.

Notwithstanding, the causalities within the optimal portfolios using the MV model were examined through the varied portfolios in 2014 and 2020. The comparison showed an increase in causal relationships between securities in 2014, from 4 unidirectional causal relationships to 1 bidirectional and 11 unidirectional causal relationships, whereas the number of causalities remained the same in 2020. The comparison could imply a more consistent diversification by the proposed model.

7.   Conclusions

The model was structured to avoid riba, gharar, and maysir, in addition to purifying the inevitable unlawful incomes. The proposed model could be generalized as an annually rebalanced mean-CVaR model, with CVaR as the risk constraint while incorporating other market trading concerns and Islamic obligations, such as transaction costs, holding constraints, and zakat payments. As CVaR reflects the expected worst-case scenario, adopting it as the risk constraint could benefit investors in making informed decisions, thus, being well-suited for Islamic risk management since Muslims are prohibited from associating with risky investments.

The rebalancing strategy and additional constraints were concluded as essential for a successful implementation of a competitive Islamic portfolio optimization model given the analyzed characteristics of time series. Theoretically, the proposed model effectively addressed most of the limitations of the classical models, including the computational ease, investor's perspective on risk or risk definition, assumption of return distributions, transaction costs, rebalancing needs, and other practical considerations. On the other hand, the proposed model was well-suited for Islamic finance, such that the properties included in the model as well as the setting and proxies used, were specially tailored for Islamic asset allocation. Generally, the model was comprehensive while offering ease of understanding and reporting.

The performance ratios confirmed the efficiency of the proposed model, where it outperformed the Islamic and market benchmark indices. Also, the short computational time in solving the Islamic portfolios validated the feasibility and superiority of the model as a viable and better alternative to the MV model. Aside from the desirably weak correlations between securities within each portfolio, the causality test suggested a limited number of causal relationships for portfolios within turbulent periods, including the financial crises and bear market in 2011, 2014, and 2020. In addition to the higher forecast accuracy during the bear market, the implication of the reduced spillovers between assets during financial turmoil showed the efficacy of the proposed model in offering better-diversified portfolios that could help anticipate and manage financial crises. Conversely, the MV model was observed to produce a notably higher number of causal relationships than the proposed model in 2014, inferring that the proposed model was more consistent in addressing signals of financial turbulence. The evident result of the study showed that the model could act as a hedging method in optimizing portfolios.

In conclusion, the Shariah-compliant optimal portfolios showed outstanding performance in comparison with the benchmark index, market index, and MV portfolios in terms of performance ratios, computational efficiency, and causality consistency. The study contributes a new Islamic portfolio optimization model to the scarce literature on Islamic portfolio management, in addition to providing new insights into the importance of the number of causal relationships between securities for risk management. Collectively, the results implied good shock absorbance of the proposed model, and the findings suggest a role for the proposed model in managing future crises. The model would be useful for fund managers in providing guidance to clients and benefiting individuals in the decision-making process.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors would like to thank the Ministry of Higher Education Malaysia (MOHE) under Fundamental Research Grant Scheme (FRGS) (Ref. No: FRGS/1/2019/SS01/QUEST/02/2) for supporting this research.

Conflict of interest

We declare no conflicts of interest in this paper.