Further results on stability analysis of time-varying delay systems via novel integral inequalities and improved Lyapunov-Krasovskii functionals

1.   Introduction

As is known to all, time delays exist in the natural dynamic systems, such as transport, communication, or measurement widely. Time delay causes undesirable dynamic behaviors such as oscillation, performance deterioration, limit cycles and even instability in the model^[1,2]. Thus the research about stability analysis of time-delay systems has been of great significance^{[3,4,5,6,7,8,9]}. It has attracted enormous attention of many researchers^{[10,11,12,13,14,15,16,17,18]}.

In general, the problem of stability analysis for time-delay systems can be divided into two categories. That are constant and time-varying delay systems. The stability criteria of time-varying delay systems are less conservatism than that of constant delay systems, owing to the full use of time delay information in stability analysis of time delay systems. The stability analysis of constant delay systems is described in literature^[19].

However, more efforts have been paid to analyze stability of time-varying delay systems. The main approach to measure conservatism is calculating the maximal admissible delay upper bounds(MADUPS). There are two major directions to reduce conservatism, namely the Lyapunov-Krasovskii functional(LKF)^[20,21] structure and Linear matrix inequality(LMI) technique. There are two approaches to construct suitable LKF, namely, augmented Lyapunov-Krasovskii functional approach(ALFA) and multiple integral Lyapunov-Krasovskii functional approach(MILFA). The former introduces more state information into the vector of the positive quadratic terms. The latter adopts multiple integral terms to the LKF. Literature^[22,23] proposed a new formed LKF for time-varying delay systems. Although the conservatism of the stability criteria for time-varying delay systems is reduced in the above literatures. They all introduce the constant matrix in the positive quadratic terms, such as $\int_{t-\tau}^{t}\dot x^T(s)Q\dot x(s)ds$, which makes the conclusion conservative. Secondly, for LMI techniques, there are some useful inequalities were developed, for example, Jensen's inequality(JI)^[24], Wirtinger-based integral inequality(WBII)^[25], free matrix-based integral inequality(FMBLL)^[26] and other LMI techniques^{[27,28,29,30,31,32,33,34,35]}.

$\blacklozenge$ A new type of LKF with time-varying delay dependent matrix is constructed, which is $\int^{t-h_1}_{t-h(t)}\dot x^T(s)(Q_{10}+(h_1-h(t))Q_{11})\dot x(s)ds+\int^{t-h(t)}_{t-h_2}\dot x^T(s)(Q_{20}+(h_2-h(t))Q_{21})\dot x(s)ds$, which makes more use of the time-varying delay information in time-varying delay systems. And the influence of the time-varying rate on the stable operation of system is considered, which plays an important role in reducing the conservatism of the system.

$\blacklozenge$ Two novel time delay partition inequalities are developed in this work for estimating the single integral terms with time-varying delay information. The proposed one can derive bigger MADUPS of time-varying delay systems.

$\blacklozenge$ Two stability criteria of time-varying delay system are established by applying the above LKF and inequalities. Based on three numerical examples, the advantages of the stability criteria are verified through the comparison of MADUPS with different criteria.

Notation: Let ${\mathbb{ R} ^{n}}$ denotes n-dimensional Euclidean space, ${\mathbb{R} ^{n\times n}}$ denotes the set of all $n \times n$ real matrices, $\mathbb{S}_{+}^n$ represents a set of positive definite matrices with $n\times n$ dimensions, $P > 0$ stands for that the matrix $P$ is real symmetric positive definite matrix, $0_{n\times 3n}$ represents the zero element matrix with the $n\times 3n$ dimensions, $X^T$ is the transpose of matrix X, $He\{X\} = X+X^T$. $\star$ in the matrix represents the symmetry of matrix.

2.   Preliminaries

The time-varying delay system model can be obtained from following equation:

where $x(t)\in R^n$ is the state vector. $A$ and $B$ are constant matrices with appropriate dimensions. $\phi(t)$ is a given vector-valued initial function. The time delay, $h(t)$, is a time-varying continuous function that satisfies:

where $0\leq h_1 < h_2$ and $\mu$ is a positive constant. Note that $h_1$ may not be equal to 0. The initial condition, $\phi(t)$, is a continuous vector-valued initial function of $t\in [-h_2, 0]$.

Before deriving the main results, the following lemmas should be introduced. When we set $h_1\neq 0$, and change the single integral terms $-\int^{t}_{t-h(t)}\dot x^T(s)R\dot x(s)ds-\int^{t-h(t)}_{t-h_2}\dot x^T(s)R\dot x(s)ds$ in ^[29] as $-\int^{t-h_1}_{t-h(t)}\dot x^T(s)R\dot x(s)ds-\int^{t-h(t)}_{t-h_2}\dot x^T(s)R\dot x(s)ds$, the following Lemma 1 and 2 can be obtained from Lemma 4 and 6 in ^[29].

Lemma 1. For a block symmetric matrix $\bar R = diag\{R, 3R\}$ with $R\in \mathbb{S}^n_+$ and any matrix $S\in \mathbb{R}^{2n\times2n}$, the single integral terms can be estimated as:

where

Lemma 2. For a block symmetric matrix $\hat{R} = diag\{R, 3R, 5R\}$ with $R\in \mathbb{S}^n_+$ and any matrix $S_1\in R^{3n\times3n}$, the single integral terms can be estimated as:

where

It can be seen that, Lemma 1 and 2 can be applied to estimate the single integral terms with the same Lyapunov matrix.

Different form the Lemma 1 and 2, we consider that the Lyapunov matrix in two single integral terms is different, such as $-\int^{t-h_1}_{t-h(t)}\dot x^T(s)R_1\dot x(s)ds-\int^{t-h(t)}_{t-h_2}\dot x^T(s)R_2\dot x(s)ds$, the following Lemma 3 and 4 can be obtained.

Lemma 3. For the block symmetric matrices $\bar R_{31} = diag\{R_1, 3R_1\}$, $\bar R_{32} = diag\{R_2, 3R_2\}$ with $R_1$ and $R_2\in \mathbb{S}_+^n$, and any matrix $S_2\in R^{2n\times2n}$, the single integral terms can be estimated as:

where

Proof. We can obtain the following equations when setting $\gamma_1(s, a, b) = \frac{2s-b-a}{b-a}$.

The following equations hold based on Schur complement when there exist symmetric matrices $R_1 > 0$, $R_2 > 0$, and any matrices $M_i, i = 1, 2, 3, 4$ with appropriate dimensions.

Then the following inequalities can be obtained.

Where $u_1 = [E_1^T, E_2^T]^T\zeta_1(t)$, $f_1 = \gamma_1(s, t-h(t), t-h_1)$, $f_2 = \gamma_1(s, t-h_2, t-h(t))$.

The matrices $M_i(i = 1, \dots, 4)$ and $S_2$ are defined as following, for any matrices $L_i, i = 1, 2, 3, 4$ with appropriate dimensions.

Based on Eq (2.6), the simple algebraic calculation is as follow:

Then we can obtain the following equation.

The Eq (2.7) can lead to $\Xi_1+\Xi_2\leq 0$. Thus the inequality (2.5) can be derived.

Lemma 4. For the block symmetric matrices $\bar R_{41} = diag\{R_1, 3R_1, 5R_1\}$, $\bar R_{42} = diag\{R_2, 3R_2, 5R_2\}$ with $R_1$ and $R_2\in S_+^n$, and any matrix $S_3\in R^{3n\times3n}$, the single integral terms can be estimated as:

Proof. The following equations can be obtained by setting $\gamma_1(s, a, b) = \frac{2s-b-a}{b-a}$ and $\gamma_2(s, a, b) = \frac{6s^2-6(a+b)s+b^2+4ab+a^2}{(b-a)^2}$.

The following equations also hold based on Schur complement when there exist symmetric matrices $R_1 > 0$, $R_2 > 0$, and any matrices $N_i, i = 1, 2, 3, 4$ with appropriate dimensions.

Then the following inequalities can be derived.

Where $u_2 = [E_3^T, E_4^T]^T\zeta_2(t)$, $S_3 = [L_5, L_6, L_7]^T = [L_8, L_9, L_{10}]$ and matrices $N_i(i = 1, \dots, 6)$ are defined for any matrices $L_i, (i = 5, 6, \dots, 10)$

According to the Eq (2.9) and the similar procedure of the proof for inequality (2.5), the following inequality can be derived.

The Eq (2.10) and (2.11) can lead to $\Xi_3+\Xi_4\leq0$. Thus the Lemma 4 can be proved.

3.   Main results

In this section, the novel LKF with time-varying delay dependent matrix is proposed. By adopting the matrix inequality Lemma 3 and 4 respectively, we can derive two new stability criteria of time-varying delay system (2.1) under the limitation (2.2), which are Theorem 1 and 2. In order to verify the superiority of introducing time-varying delay dependent matrices in reducing the conservatism, we replace the time-varying delay dependent matrices with constant delay matrices as a contrast. As a result, the same Lyapunov matrix is appeared in the single integral terms for the derivation of LKF. So the Lemma 1 and 2 is adopted to deal with the estimation of single integral terms respectively, the Corollary 1 and 2 can be derived.

Theorem 1. Given constant $h_1$, $h_2$, $\mu$, the system (2.1) is asymptotically stable if there exist positive matrices $P\in \mathbb{R}^{6n\times6n}$, $W\in \mathbb{R}^{n\times n}$, $K\in \mathbb{R}^{n\times n}$, and any matrices $Q_{10}\in \mathbb{R}^{n\times n}$, $Q_{11}\in \mathbb{R}^{n\times n}$, $Q_{20}\in \mathbb{R}^{n\times n}$, $Q_{21}\in \mathbb{R}^{n\times n}$, $S_4\in \mathbb{R}^{2n\times 2n}$ satisfying the following LMIs:

Where

$o1$, $o2$, $o3$, $o4$ separately refers to $h(t) = h_1$ and $\dot{h}(t) = \mu$, $h(t) = h_1$ and $\dot{h}(t) = -\mu$, $h(t) = h_2$ and $\dot{h}(t) = \mu$, $h(t) = h_2$ and $\dot{h}(t) = -\mu$. $\psi_{oi}$ for $i = 1, 2, 3, 4$ in inequalities (3.2) is the specific matrix of $\psi$ under $o1, o2, o3, o4$, the four situations respectively. For simplicity, some relevant notations in Theorem 1 are defined in APPENDIX A and the more details about $\psi_{mn}$ are listed in APPENDIX B.

It is worth noting that the inequalities (3.1) must be satisfied under $o_1\cdots o_4$, the four situations. So the inequalities (3.1) are equal to the following linear matrix inequalities:

Proof. Three Lyapunov-Krasovskii functional are adopted as follows

where

The time derivative of $V(t)$ can be calculated as;

According to Lemma 3, the last two single integral terms of $\dot V(t)$ can be calculated as follows:

From the Leibniz-Newton formulas, the following equation is true for any $N\in\mathbb{R}^{n\times n}$.

The Eq (3.6) can be written as:

Adding the Eq (3.7) to the Eq(3.4), the time derivative of $V(t)$ can be rewritten.

Therefore $\Gamma < 0$ leads to $\dot{V}(t)\leq-\sigma\parallel x(t)\parallel^2$ for a sufficient small scalar$\sigma > 0$, the system (2.1) is asymptotically stable with the limitation (2.2).

when $h(t) = h_1$

When $h(t) = h_2$

By applying Schur complement, Formulas $(3.9)$ and $(3.10)$ are also equal to LMIs as Eqs $(3.1)$ and $(3.2)$.

Remark 1. We divide $\int_{t-h_2}^{t-h_1}\dot x^T(s)Q\dot x(s)ds$ into $\int_{t-h(t)}^{t-h_1}\dot x^T(s)Q_1(h(t))\dot x(s)ds$ and $\int_{t-h_2}^{t-h(t)}\dot x^T(s)Q_2(h(t))\dot x(s)ds$. And different from the constant matrices we introduce the time-varying delay dependent matrices $Q_1(h(t)) = Q_{10}+(h_1-h(t))Q_{11}$ and $Q_2(h(t)) = Q_{20}+(h_2-h(t))Q_{21}$ to $V_2(t)$. The integral terms $-\int^{t-h_1}_{t-h(t)}\dot x^T(s)(W+\dot h(t)Q_{11})\dot x(s)ds-\int^{t-h(t)}_{t-h_2}\dot x^T(s)(W+\dot h(t)Q_{21})\dot x(s)ds$ are included in the time derivation of $V(t)$.

However when we divide $\int_{t-h_2}^{t-h_1}\dot x^T(s)Q\dot x(s)ds$ into $\int_{t-h(t)}^{t-h_1}\dot x^T(s)Q_{1}\dot x(s)ds$ and $\int_{t-h_2}^{t-h(t)}\dot x^T(s)Q_{2}\dot x(s)ds$. $Q_{1}, Q_{2}$ are constant matrices, rather than the time-varying dependent matrices. There are only single integral terms $\int_{t-h(t)}^{t-h_1}\dot x^T(s)W\dot x(s)ds$ and $\int_{t-h_2}^{t-h(t)}\dot x^T(s)W\dot x(s)ds$ in $\dot V(t)$, which are obtained from $V_3(t)$.

Obviously, the time-varying dependent matrices $Q_{1}(h(t))$, $Q_{2}(h(t))$ bring more information about time-varying delay than the constant matrices $Q_{1}$, $Q_{2}$.

In order to compare the conservative of stability criterion between time-varying delay dependent matrices and constant matrices, we replace the $Q_{1}(h(t))$, $Q_{2}(h(t))$ with $Q_{1}$, $Q_{2}$ in $V_2(t)$. The stability criteria can be derived as follows:

Corollary 1. Given constant $h_1$, $h_2$, $\mu$, the system (2.1) is asymptotically stable if there exist positive matrices $P_2\in \mathbb{R}^{6n\times6n}$, $W_2\in \mathbb{R}^{n\times n}$, $Q_{1}\in \mathbb{R}^{n\times n}$, $Q_{2}\in \mathbb{R}^{n\times n}$, $K\in \mathbb{R}^{n\times n}$, and any matrix $S_5\in \mathbb{R}^{2n\times 2n}$ satisfying the following LMIs:

Where

Proof. We replace the Lyapunov matrices $Q_{1}(h(t))$ and $Q_{2}(h(t))$ as $Q_1$ and $Q_2$ separately in Lyapunov-Krasovskii functional $V_2(t)$ of the Eq (3.3). Then integral terms $-\int^{t-h_1}_{t-h(t)}\dot x^T(s)W_2x(s)ds-\int^{t-h(t)}_{t-h_2}\dot x^T(s)W_2x(s)ds$ are appeared in the derivation of $V(t)$. Owing to the same Lyapunov matrix $W_2$, the Lemma 1 can be adopted to estimate the single integral terms. The other process is similar to the process of Theorem 1. Therefore the details can be omitted.

It is worth noting that, the subscript of $\Lambda$ in inequalities (3.11) $(oi \quad i = 1, 2, 3, 4))$ separately refers to $h(t) = h_1$ and $\dot{h}(t) = \mu$, $h(t) = h_1$ and $\dot{h}(t) = -\mu$, $h(t) = h_2$ and $\dot{h}(t) = \mu$, $h(t) = h_2$ and $\dot{h}(t) = -\mu$, the four situations. $\Lambda_{oi}$ for $i = 1, 2, 3, 4$ in inequalities (3.11) is the specific matrix of $\Lambda$ under $o1, o2, o3, o4$, the four situations respectively.

Secondly, Theorem 2 for system (2.1) will be derived by Lemma 4. The notations of several parameters are defined in APPENDIX A

Theorem 2. Given constant $h_1$, $h_2$, $\mu$, the system(2.1) is asymptotically stable if there exists matrices $P_3\in \mathbb{R}^{6n\times6n} > 0$, $Q_{10}\in \mathbb{R}^{n\times n}$, $Q_{11}\in \mathbb{R}^{n\times n}$, $Q_{20}\in \mathbb{R}^{n\times n}$, $Q_{21}\in \mathbb{R}^{n\times n}$, $W\in \mathbb{R}^{n\times n} > 0$, $K\in \mathbb{R}^{n\times n} > 0$, $\mathcal{S}\in \mathbb{R}^{3n\times 3n}$ such that the following LMIs hold:

Where

The more details about $\hat\psi_{mn}$ are listed in APPENDIX B. In addition, the process of converting stability condition (3.12) to the linear condition is same as those of the stability condition (3.1) in Theorem 1.

Proof. We adopt the same Lyapunov-Krasovskii functional as (3.3). So the $\dot V(t)$ can be expressed as follows:

According to Lemma 4, the last two single integral terms of $\dot V(t)$ can be calculated as follows:

The Eq (3.6) can also be rewritten as:

Adding the (3.15) to the Eq (3.14), the time derivative of $V(t)$ can be rewritten as follows:

The other process is similar to those of Theorem 1. Then the follow conclusions can be derived.

When $h(t) = h_1$

When $h(t) = h_2$

Similarity, Formulas(3.17) and (3.18) are equal to LMIs as inequalities (3.12) and (3.13) by Schur complement.

$\hat\Psi_{oi}$ for $i = 1, 2, 3, 4$ in inequalities (3.13) is the specific matrix of $\hat\Psi$ under $o1, o2, o3, o4$, the four situations respectively.

Remark 2. Similarity to Remark 1, when we introduce the constant matrices $Q_{1}$, $Q_{2}$ to $V_2(t)$, rather than $Q_{10}+(h_1-h(t))Q_{11}$, $Q_{20}+(h_2-h(t))Q_{21}$. The stability criteria can be derived by Lemma 2 as follow:

Corollary 2. Given constant $h_1$, $h_2$, $\mu$, the system (2.1) is asymptotically stable if there exist positive matrices $P_4\in \mathbb{R}^{6n\times6n}$, $W\in \mathbb{R}^{n\times n}$, $Q_{10}\in \mathbb{R}^{n\times n}$, $Q_{20}\in \mathbb{R}^{n\times n}$, $K\in \mathbb{R}^{n\times n}$, and any matrix $\mathcal{S}_1\in \mathbb{R}^{3n\times 3n}$ satisfying the following LMIs:

Where

$\hat\Lambda_{oi}$ for $i = 1, 2, 3, 4$ in the inequalities (3.19) is the specific matrix of $\hat\Lambda$ under $o1, o2, o3, o4$, the four situations respectively.

4.   Numerical example

In this section, Three numerical examples are used to show the validity of the proposed theorems. The conservation of criteria is checked by calculating maximal admissible delay upper bounds(MADUPS). The symbol of $-$ in Table 1–4 denotes that the result is not listed in the literature. The condition of $\mu$ depends on the results listed in the other literatures.

Example 1. Consider the system (2.1) as follow ^{[20,25,26,29,36,37]}:

For numerical example1, the MADUPS of $h_2$ respecting to $h_1 = 0$ and various $\mu$ calculated by our theorems and existing works are listed in Table 1. We can observe the followings:

Table 1 presents the obtained MADUPS of system 1 for different $\mu$. From Table 1, we can obtain the following conclusions.

$\blacklozenge$ One can confirm that the results of Corollary 1 and 2 are still larger than the other methods listed in Table 1. This means the linear matrix inequality techniques (Lemma 1 and 3) can decrease the conservatism validly.

$\blacklozenge$ The results of Corollary 1 and 2 are smaller than those of Theorem 1 and 2 separately. This means the Lyapunov-Krasovskii functional with time-varying delay dependent matrix plays an important role to reduce the conservatism of stability criterion.

$\blacklozenge$ Theorem 2 is less conservative than Theorem 1 and Corallary 2 is less conservative than Corollary 1, which means the more augmented vectors in Lemma 3 and 4 decrease the conservatism validly.

$\blacklozenge$ It also can be seen that Theorem 1 is less conservative than Corollary 2, which means the time-varying delay dependent matrix proposed in this paper is better than introducing more augmented vectors technique in reducing the conservatism of the stability criterion.

When $h_1\neq0$, the obtained results by applying Theorem 1, Corallary 1, Theorem 2 and Corallary 2 are listed in Table 2 and compared with the results published in previous literatures.

From Table 2, it should be noted that when $h_1\neq0$, the method proposed in this paper is more superior in reducing conservatism than the previous results. And all the results of Theorem 2 listed in Table 2 are better than those of Theorem 1, all the results of Corallary 2 are better than those of Corallary 1. This implies that the Theorem 2 and Corallary 2 effectively reduce the conservatism of stability criteria by introducing more details about time-varying delay in amplification vector than Theorem 1 and Corollary 1 separately. Meanwhile, the results of Corallary 1 and 2 are bigger than the results of ^[38,39], are smaller than those of Theorem 1 and 2 separately. We can infer that the linear matrix inequality technique of Lemma 1– 4 can reduce the conservatism and introducing time-varying delay dependent matrix can reduce conservatism effectively.

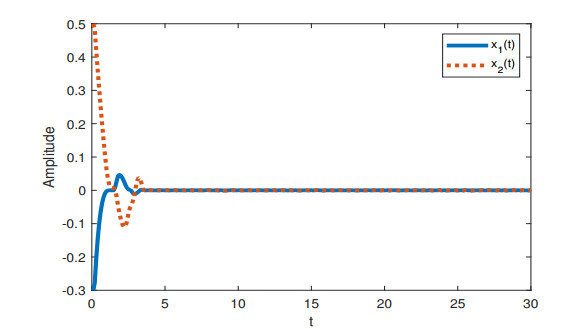
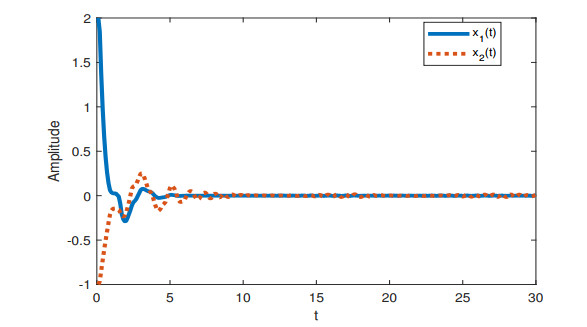
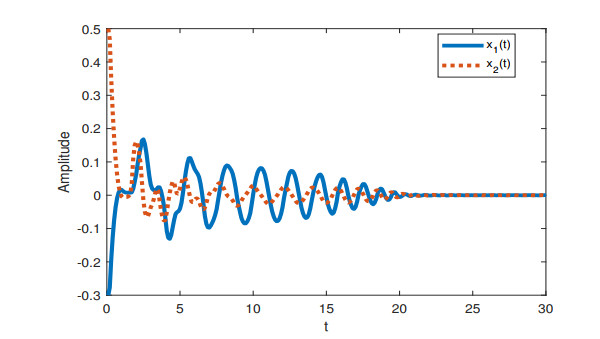
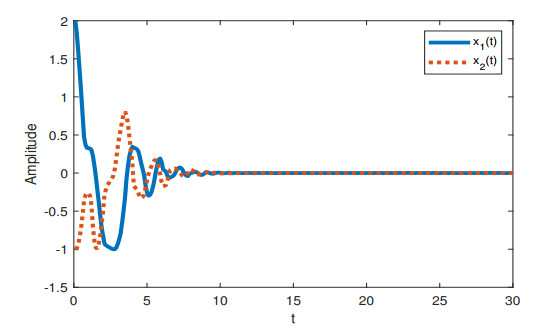
When $h_1 = 0, \mu = 0.1$, Theorem 2 guarantees the stability for [Example 1, $h(t) = 4.952$]. And when $h_1 = 2, \mu = 0.9$, Theorem 2 guarantees the stability for [Example 1, $h(t) = 3.01$]. The state responses under $h_1 = 0, \mu = 0.1$ and $h_1 = 2, \mu = 0.9$ are displayed in Figure 1 and 2. It can be seen that the system is stable under given conditions.

Example 2. Considering the system (2.1) with parameters listed as follow ^{[25,26,29,40,41]}:

Setting $h_1 = 0$, the MADUPS of $h_2$ respecting to various $\mu$ by utilizing the methods of literature ^{[25,26,29,40,41]} and our theorems can be derived, which are listed in Table 3.

From the results in Table 3, one can also see that all the results obtained by Theorem 1 are larger than those obtained by other literatures listed in Table 3, and smaller than Theorem 2, which verify the above inference.

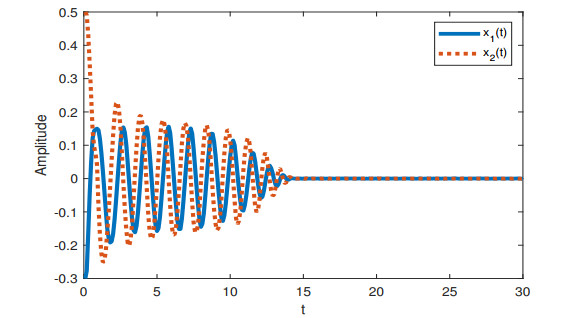
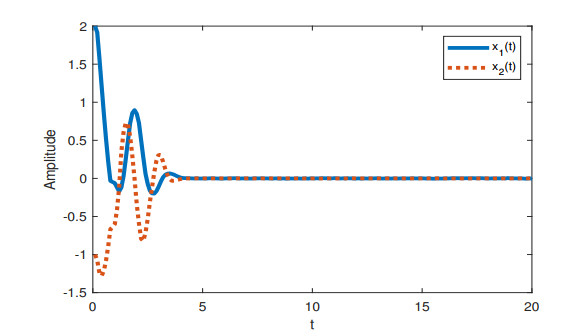
When $h_1 = 0, \mu = 0.1$, Theorem 2 guarantees the stability for [Example 2, $h(t) = 2.71$]. And when $h_1 = 0, \mu = 0.5$, Theorem 2 guarantees the stability for [Example 2, $h(t) = 2.11$]. The state responses under $h_1 = 0, \mu = 0.1$ and $h_1 = 0, \mu = 0.5$ are displayed in Figure 3 and 4. It can be seen that the system is stable under given conditions.

Example 3. Considering the system (2.1) listed as follow ^{[25,26,29,37,42]}:

For numerical Example 3, setting $h_1 = 0$, the comparison of our results obtained by Theorem 1 and 2 with the results in ^{[25,26,29,37,42]} is conducted in Table 4.

The results listed in Table 4 show the Theorem 2 gives slightly larger delay bounds comparing with those of Theorem 1 and other literatures.

When $h_1 = 0, \mu = 0.1$, Theorem 2 guarantees the stability for [Example 3, $h(t) = 7.821$]. And when $h_1 = 0, \mu = 0.8$, Theorem 2 guarantees the stability for [Example 3, $h(t) = 2.657$]. The state responses under $h_1 = 0, \mu = 0.1$ and $h_1 = 0, \mu = 0.8$ are displayed in Figure 5 and 6. It can be seen that the system is stable under given conditions.

5.   Conclusions

This work has investigated the stability analysis issue of linear systems with time-varying delays via some novel approaches. Firstly, two integral inequalities are put forward to deal with the single integral terms with time-varying delay dependent matrices. Secondly, the novel Lyapunov-Krasovskii functionals with the time-varying delay matrix, rather than constant matrix are proposed. Thirdly, improved stability criteria are obtained based on the proposed approaches. Finally the results of three numerical example dealt with our methods and the previous methods, are contrasted to verify the improvement of our proposed methods.

Acknowledgments

This work was supported by the National Natural Science Foundation of China under Grant (No. 61703060, 12061088, 61802036 and 61873305), the Sichuan Science and Technology Program under Grant No. 21YYJC0469, the Project funded by China Postdoctoral Science Foundation under Grant Nos. 2020M683274 and 2021T140092, Supported by the Open Research Project of the State Key Laboratory of Industrial Control Technology, Zhejiang University, China (No. ICT2021B38), Guangdong Basic and Applied Basic Research Foundation (2021A1515011692).

Conflict of interest

The authors declare no conflict of interest.

Appendix

APPENDIX A

The relevant notations in Theorem 1 are defined as follows:

The relevant notations in Theorem 2 are defined as follows:

APPENDIX B

The elements in $\Psi$ are as follows:

The elements in $\hat\Psi$ are as follows: